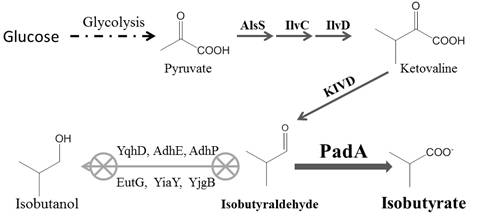
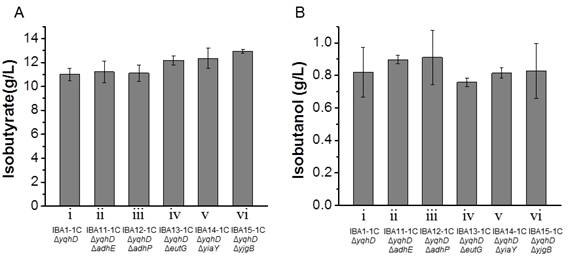
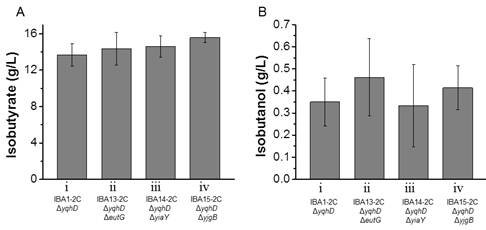
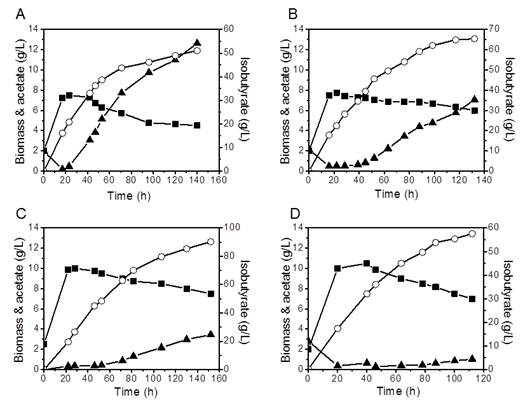
Isobutyrate is an important platform chemical with various industrial applications. Previously, a synthetic metabolic pathway was constructed in E. coli to produce isobutyrate from glucose. However, isobutanol was found to be a major byproduct. Herein, gene knockouts and enzyme overexpressions were performed to optimize further the engineered E. coli strain. Besides yqhD, the knockouts of three genes eutG, yiaY and ygjB increased isobutyrate production in shake flasks. Furthermore, the introduction of an additional padA on a medium copy number plasmid under the constitutive promoter significantly reduced isobutanol formation. The IBA15-2C strain (BW25113, DyqhD, DygjB; carrying two copies of padA) produced 39.2% more isobutyrate (0.39 g/glucose yield, 80% of the theoretical maximum yield) than IBA1-1C strain (BW25113, DyqhD; carrying one copy of padA). A scale-up process was also investigated for IBA15-2C strain to optimize the conditions for the production of isobutyrate in the fermentor. With Ca(OH)2 as the base for pH control and 10% dissolved oxygen level, IBA15-2C strain produced 90 g/L isobutyrate after 144 h. This study has engineered E. coli to achieve biosynthesis of a nonnative compound with the highest titer and opened up the possibility of the industrial production of isobutyrate.
1.
Introduction
We consider characteristic equations, i.e., equations for eigenvalues and eigenfunctions of the class of integral operators on the Hilbert space $ L^2[-l, l] $ of the form
where $ G_{\bf{M}} $ is the Green function [1,2] for the boundary value problem consisting of the fourth-order linear differential equation
and a well-posed two-point boundary condition
Here, $ {\bf{M}} \in \operatorname{gl}(4, 8, \mathbb{C}) $ is called a boundary matrix, where $ \operatorname{gl}(4, 8, \mathbb{C}) $ is the set of $ 4 \times 8 $ matrices with complex entries. For example, the two-point boundary condition $ u(-l) = u^\prime(-l) = u(l) = u^\prime(l) = 0 $ can be expressed by (1.3) with
The differential equation (1.2) is the classical Euler–Bernoulli beam equation [3] which governs the vertical downward deflection $ u(x) $ of a linear-shaped beam with finite length $ 2l $ resting horizontally on an elastic foundation with spring constant density $ k $. The constants $ E $ and $ I $ are the Young's modulus and the mass moment of inertia of the beam respectively, and $ w(x) $ is the downward load density applied vertically on the beam. The beam deflection problem has been one of the central topics in mechanical engineering with diverse and important applications [3,4,5,6,7,8,9,10,11,12].
Throughout this paper, we assume that $ l $, $ E $, $ I $, $ k $ in (1.2) are positive constants and put $ \alpha = \sqrt[4]{k/(E I)} > 0 $. When the boundary value problem consisting of (1.2) and (1.3) is well-posed or, equivalently, when (1.2) and (1.3) has a unique solution, we call the boundary matrix $ {\bf{M}} $ well-posed. The set of well-posed boundary matrices is denoted by $ \operatorname{wp}(4, 8, \mathbb{C}) $. It was shown in [2] that, up to a natural equivalence relation, $ \operatorname{wp}(4, 8, \mathbb{C}) $ is in one-to-one correspondence with the $ 16 $-dimensional algebra $ \operatorname{gl}(4, \mathbb{C}) $ of $ 4 \times 4 $ matrices with complex entries.
For $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, we denote by $ \operatorname{Spec}\mathcal{K}_{\bf{M}} $ the spectrum or, the set of eigenvalues, of the integral operator $ \mathcal{K}_{\bf{M}} $ in (1.1). Since $ \mathcal{K}_{\bf{M}}[w] $ is the unique solution of the boundary value problem (1.2) and (1.3) for every $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, analyzing the behavior of the integral operators $ \mathcal{K}_{\bf{M}} $ is important in understanding the beam deflection problem. In general, spectral analysis for integral operators arising from various differential equations is crucial in many applications such as inverse problem [13] and nonlinear problem [5,6]. In contrast to this importance, there are few explicit spectral analyses for the integral operators $ \mathcal{K}_{\bf{M}} $ which arise from a most fundamental and basic differential equation (1.2) in the history of mechanical engineering.
Choi [14] analyzed $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ of a special integral operator $ \mathcal{K}_{\bf{Q}} $ in detail, where
which is in $ \operatorname{wp}(4, 8, \mathbb{C}) $ [2]. The Green function $ G_{\bf{Q}}(x, \xi) $ corresponding to $ {\bf{Q}} $ is the restriction in $ [-l, l] \times [-l, l] $ of the Green function for the boundary value problem consisting of the infinite version $ E I \cdot u^{(4)}(x) + k \cdot u(x) = w(x) $, $ x \in (-\infty, \infty) $ of (1.2) and the boundary condition $ \lim_{x \to \pm \infty} u(x) = 0 $.
For two positive sequences $ a_n $, $ b_n $, we denote $ a_n \sim b_n $ if there exists $ N > 0 $ such that $ m \leq a_n/b_n \leq M $ for every $ n > N $ for some constants $ 0 < m \leq M < \infty $.
Proposition 1.1 ([14]). For every $ l > 0 $, the spectrum $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ of the operator $ \mathcal{K}_{\bf{Q}} $ is of the form $ \left\{ \mu_n/k \, |\, n = 1, 2, 3, \cdots \right\} \cup \left\{ \nu_n/k \, |\, n = 1, 2, 3, \cdots \right\} \subset (0, 1/k) $, where $ 1 > \mu_1 > \nu_1 > \mu_2 > \nu_2 > \cdots \searrow 0 $. Each of $ \mu_n $ and $ \nu_n $ for $ n = 1, 2, 3, \ldots $ is determined only by the intrinsic length $ L = 2 l \alpha $ of the beam. $ \mu_n \sim \nu_n \sim n^{-4} $, and
Here, $ h : [0, \infty) \to [0, \infty) $ is the strictly increasing real-analytic function defined in Supplementary D, with the properties $ h(0) = 0 $ and $ h^{-1}\left(a_n \right) \sim a_n/L $ for any positive sequence $ a_n $ such that $ a_n \to \infty $. See [14] for numerical computations of $ \mu_n $, $ \nu_n $ with arbitrary precision.
Recently, Choi [2] derived explicit characteristic equations for the integral operator $ \mathcal{K}_{\bf{M}} $ in (1.1) for arbitrary well-posed $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, which are stated in more detail in Section 2. Although these characteristic equations are expressed in terms of the explicit $ 4 \times 4 $ matrices $ \mathcal{G}({\bf{M}}) $, $ {\bf{X}}_\lambda $, $ {\bf{Y}}_\lambda $, they still involve determinants of full $ 4 \times 4 $ matrices, which makes it hard to analyze the structure of $ \operatorname{Spec}\mathcal{K}_{\bf{M}} $ for general well-posed boundary matrix $ {\bf{M}} $.
In this paper, we utilize some of the symmetries in the $ 4 \times 4 $ matrices $ {\bf{X}}_\lambda $, $ {\bf{Y}}_\lambda $ to block-diagonalize them with explicit $ 2 \times 2 $ blocks $ {\bf{X}}_\lambda^\pm $, $ {\bf{Y}}_\lambda^\pm $, which enables us to obtain new and simpler forms of characteristic equations for the integral operator $ \mathcal{K}_{\bf{M}} $ for arbitrary well-posed boundary matrix $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $. In particular, the entries of the $ 2 \times 2 $ blocks $ {\bf{X}}_\lambda^\pm $ and $ {\bf{Y}}_\lambda^\pm $ are represented explicitly with the concrete holomorphic functions $ \delta^\pm(z, \kappa) $ and $ p^\pm(z) $ introduced in Section 3.
Our results significantly reduce the complexity of dealing with determinants of $ 4 \times 4 $ matrices and facilitate to represent $ \operatorname{Spec}\mathcal{K}_{\bf{M}} $ for arbitrary $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $ essentially as the zero set of one explicit holomorphic function composed with the concrete functions $ \delta^\pm(z, \kappa) $. For example, Corollary 1 in Section 3 states that $ 0, 1/k \neq \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ if and only if $ \lambda $ is a zero of the holomorphic function $ \delta^+\left(\alpha l, \chi(\lambda) \right) \cdot \delta^-\left(\alpha l, \chi(\lambda) \right) $, where $ \chi $ is a $ 4 $th root transformation introduced in Section 2. In particular, the holomorphic functions $ \delta^\pm(z, \kappa) $ unify the real-analytic functions which were analyzed in detail in [14,15] to obtain concrete results on $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ such as Proposition 1.1. The fact that $ \delta^\pm(z, \kappa) $ encapsulate condensed information on $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $, and hence on $ \operatorname{Spec}\mathcal{K}_{\bf{M}} $ in general, is demonstrated in Supplementary D by showing that the seemingly complex-looking conditions $ \varphi^\pm(\kappa) = p(\kappa) $, which were derived in [14] with the help of computer algebra systems, can be directly and elegantly recovered from $ \delta^\pm(z, \kappa) $.
Our results open up practical ways to direct and concrete spectral analysis for the whole $ 16 $-dimensional class of the integral operators $ \mathcal{K}_{\bf{M}} $ arising from arbitrary well-posed boundary value problem of finite beam deflection on elastic foundation.
After introducing basic notations, definitions, and previous results relevant to our analysis in Section 2, we state our main results Theorems 1, 2 and 3 in Section 3, which are proved in Sections 4, 5 and 6 respectively. Some remarks and future directions are given in Section 7. In Supplementary D, the conditions $ \varphi^\pm(\kappa) = p(\kappa) $ on $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ in [14] are derived from our holomorphic functions $ \delta^\pm(z, \kappa) $.
2.
Preliminaries
2.1. Basic notations and definitions
We denote $ \mathbb{i} = \sqrt{-1} $. Denote by $ \mathbb{Z} $, $ \mathbb{R} $, and $ \mathbb{C} $, the set of integers, the set of real numbers, and the set of complex numbers respectively. The set of $ m \times n $ matrices with entries in $ \mathbb{C} $ is denoted by $ \operatorname{gl}(m, n, \mathbb{C}) $. When $ m = n $, we also denote $ \operatorname{gl}(m, n, \mathbb{C}) = \operatorname{gl}(n, \mathbb{C}) $. We write $ {\bf{A}} = \left(a_{i, j} \right)_{1 \leq i \leq m, \, 1 \leq j \leq n} $ when the $ (i, j) $th entry of $ {\bf{A}} \in \operatorname{gl}(m, n, \mathbb{C}) $ is $ a_{i, j} $. When $ m = n $, we also write $ {\bf{A}} = \left(a_{i, j} \right)_{1 \leq i, j \leq n} $. For $ {\bf{A}} \in \operatorname{gl}(m, n, \mathbb{C}) $, we denote the $ (i, j) $th entry of $ {\bf{A}} $ by $ {\bf{A}}_{i, j} $. The complex conjugate, the transpose, and the conjugate transpose of $ {\bf{A}} \in \operatorname{gl}(m, n, \mathbb{C}) $ are denoted by $ \overline{{\bf{A}}} $, $ {\bf{A}}^T $, and $ {\bf{A}}^* $ respectively. For $ {\bf{A}} \in \operatorname{gl}(n, \mathbb{C}) $, $ \operatorname{adj}{{\bf{A}}} $ is the classical adjoint of $ {\bf{A}} $, so that, if $ {\bf{A}} $ is invertible then $ {\bf{A}}^{-1} = \operatorname{adj}{{\bf{A}}} /\det{\bf{A}}. $
Regardless of size, the identity matrix and the zero matrix are denoted by $ {\bf{I}} $ and $ {\bf{O}} $ respectively. The zero column vector with any size is denoted by $ {\bf{0}} $. The diagonal matrix with diagonal entries $ c_1, c_2, \cdots, c_n $ is denoted by $ \operatorname{diag}\left(c_1, c_2, \cdots, c_n \right) $.
Definition 2.1. Denote $ \omega = e^{\mathbb{i} \frac{\pi}{4}} = \frac{1}{\sqrt{2}} + \mathbb{i} \frac{1}{\sqrt{2}} $ and $ \omega_n = \mathbb{i}^{n-1} \omega $ for $ n \in \mathbb{Z} $. Denote $ {\bf{\Omega}} = \operatorname{diag}\left(\omega_1, \omega_2, \omega_3, \omega_4 \right) $ and $ {\bf{W}}_0 = \left(\omega_j^{i-1} \right)_{1 \leq i, j \leq 4} $.
$ \omega_1 = \omega $, $ \omega_2 $, $ \omega_3 $, $ \omega_4 $ are the primitive $ 4 $th roots of $ -1 $ and satisfy
Definition 2.2. Denote $ \epsilon_1 = \epsilon_4 = 1 $, $ \epsilon_2 = \epsilon_3 = -1 $, and $ \epsilon_{n+4} = \epsilon_n $ for $ n \in \mathbb{Z} $. Denote $ \mathcal{E} = \operatorname{diag} \left(\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4 \right) = \operatorname{diag}(1, -1, -1, 1) $.
By Definitions 2.1, 2.2 and (2.1), we have
Definition 2.3. Denote
Note that $ {\bf{V}} $ and $ \widehat{{\bf{V}}} $ are orthogonal and
Lemma 2.1. $ {\bf{V}} (ABBA) {\bf{V}}^T = (A+BOOA−B) $ for $ {\bf{A}}, {\bf{B}} \in \operatorname{gl}(2, \mathbb{C}) $.
Proof. By Definition 2.3,
By (2.2) and Lemma 2.1,
By (2.1),
2.2. Previous results
Definition 2.4. For $ \lambda \in \mathbb{C} \setminus \left\{ 0, 1/k \right\} $, define $ \chi(\lambda) $ to be the unique complex number satisfying $ \chi(\lambda)^4 = 1 - 1/(\lambda k) $ and $ 0 \leq \operatorname{Arg}{\chi(\lambda)} < \pi/2 $.
Note that $ \chi $ is a one-to-one correspondence from $ \mathbb{C} \setminus \left\{ 0, 1/k \right\} $ to the set $ \left\{ \kappa \in \mathbb{C} \, |\, 0 \leq \operatorname{Arg}{\kappa} < \pi/2 \right\} \setminus \{ 0, 1 \} $.
Definition 2.5. Let $ 0 \neq \lambda \in \mathbb{C} $ and $ x \in \mathbb{R} $. For $ \lambda \neq 1/k $, let $ \kappa = \chi(\lambda) $. Denote
where $ {\bf{y}}(x) = (eω1αxeω2αxeω3αxeω4αx)^T $ and $ y_{\lambda, j}(x) = \left\{ 1(j−1)!⋅xj−1,if λ=1/k,eωjκαx,if λ≠1/k, \right. \; j = 1, 2, 3, 4 $. Denote $ {\bf{X}}_\lambda(x) = \operatorname{diag}(0, 1, 1, 0) \cdot {\bf{W}}(-x)^{-1} {\bf{W}}_\lambda(-x) + \operatorname{diag}(1, 0, 0, 1) \cdot {\bf{W}}(x)^{-1} {\bf{W}}_\lambda(x) $. When $ \det {\bf{X}}_\lambda(x) \neq 0 $, denote $ {\bf{Y}}_\lambda(x) = {\bf{X}}_\lambda(-x) {\bf{X}}_\lambda(x)^{-1} - {\bf{I}} $.
Definition 2.6. Define $ \mathcal{G} : \operatorname{wp}(4, 8, \mathbb{C}) \to \operatorname{gl}(4, \mathbb{C}) $ by
where $ {\bf{M}}^-, {\bf{M}}^+ \in \operatorname{gl}(4, \mathbb{C}) $ are the $ 4 \times 4 $ minors of $ {\bf{M}} $ such that $ {\bf{M}} = \left(M−M+ \right) $. Define $ \psi : \operatorname{gl}(4, \mathbb{C}) \to \operatorname{gl}(4, 8, \mathbb{C}) $ by
The map $ \mathcal{G} $ in Definition 2.6 is well defined since, for $ {\bf{M}} = \left(M−M+ \right) \in \operatorname{gl}(4, 8, \mathbb{C}) $, $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $ if and only of $ \det \left\{ {\bf{M}}^- {\bf{W}}(-l) + {\bf{M}}^+ {\bf{W}}(l) \right\} \neq 0 $ [2,Lemma 3.1]. $ \mathcal{G}({\bf{M}}) $ is denoted by $ {\bf{G}}_{\bf{M}} $ in [2]. Define the equivalence relation $ \approx $ on $ \operatorname{wp}(4, 8, \mathbb{C}) $ by $ {\bf{M}} \approx {\bf{N}} $ if and only if $ {\bf{M}} = {\bf{A}} {\bf{N}} $ for some invertible $ {\bf{A}} \in \operatorname{gl}(4, \mathbb{C}) $.
Proposition 2.1. (a) ([2,Lemma 6.1]) For $ {\bf{M}}, {\bf{N}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, the following $ \rm(i) $, $ \rm(ii) $, $ \rm(iii) $ are equivalent: $\rm {(i)}\; {\bf{M}} \approx {\bf{N}} $, $ \rm(ii) \; \mathcal{G}({\bf{M}}) = \mathcal{G}({\bf{N}}) $, $ \rm(iii) \; \mathcal{K}_{\bf{M}} = \mathcal{K}_{\bf{N}} $.
(b)([2,Eq 6.4]) For $ {\bf{G}} \in \operatorname{gl}(4, \mathbb{C}) $, $ \psi({\bf{G}}) \in \operatorname{wp}(4, 8, \mathbb{C}) $ and $ \mathcal{G}\left(\psi({\bf{G}}) \right) = {\bf{G}} $.
Denote by $ \operatorname{wp}(\mathbb{C}) $ the quotient set $ \operatorname{wp}(4, 8, \mathbb{C})/\approx $ of $ \operatorname{wp}(4, 8, \mathbb{C}) $ with respect to the relation $ \approx $. For $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, denote by $ [{\bf{M}}] $ the equivalence class in $ \operatorname{wp}(4, 8, \mathbb{C})/\approx $ which contains $ {\bf{M}} $. Then we have the canonical projection $ \pi : \operatorname{wp}(4, 8, \mathbb{C}) \to \operatorname{wp}(\mathbb{C}) $ defined by $ \pi({\bf{M}}) = [{\bf{M}}] $. By Proposition 2.1, the map $ \pi \circ \psi : \operatorname{gl}(4, \mathbb{C}) \to \operatorname{wp}(\mathbb{C}) $ is a one-to-one correspondence, and we denote its inverse by $ \mathrm{\mathrm{\Gamma}} : \operatorname{wp}(\mathbb{C}) \to \operatorname{gl}(4, \mathbb{C}) $. Thus we have the commutative diagram in Figure 1 which holds for any invertible $ {\bf{A}} \in \operatorname{gl}(4, \mathbb{C}) $. Here, the map $ P_{\bf{A}} : \operatorname{wp}(4, 8, \mathbb{C}) \to \operatorname{wp}(4, 8, \mathbb{C}) $ is defined by $ P_{\bf{A}}({\bf{M}}) = {\bf{A}} {\bf{M}} $.
By Proposition 2.1, the set of integral operators $ \mathcal{K}_{\bf{M}} $ in (1.1) is in one-to-one correspondence with the set $ \operatorname{wp}(\mathbb{C}) $ of equivalent well-posed boundary matrices, and hence is also in one-to-one correspondence with $ \operatorname{gl}(4, \mathbb{C}) $. Note that both of the maps $ \mathcal{G} $ and $ \psi $ in Definition 2.6 are explicitly computable, hence $ \mathrm{\Gamma} $ and its inverse $ \mathrm{\Gamma}^{-1} $ are explicitly computable. For the special boundary matrix $ {\bf{Q}} $ in (1.4), we have [2,Eq 6.2]
Proposition 2.2. For $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $ and $ \lambda \in \mathbb{C} $, the following $ \rm(a) $ and $ \rm(b) $ hold.
(a) ([2,Theorem 1 and Corollary 1]) $ \mathcal{K}_{\bf{M}}[u] = \lambda \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ \lambda \neq 0 $ and $ u = {\bf{c}}^T {\bf{y}}_\lambda $ for some $ {\bf{0}} \neq {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that $ \left[ \mathcal{G}({\bf{M}}) \left\{ {\bf{X}}_\lambda(l) - {\bf{X}}_\lambda(-l) \right\} + {\bf{X}}_\lambda(l) \right] {\bf{c}} = {\bf{0}} $. $ \mathcal{K}_{\bf{Q}}[u] = \lambda \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ \lambda \neq 0 $ and $ u = {\bf{c}}^T {\bf{y}}_\lambda $ for some $ {\bf{0}} \neq {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that $ {\bf{X}}_\lambda(l) {\bf{c}} = {\bf{0}} $. In particular, $ 0 \neq \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ if and only if $ \det{\bf{X}}_\lambda(l) = 0 $.
(b) ([2,Corollary 2]) Let $ 0 \neq \lambda \in \mathbb{C} \setminus \operatorname{Spec}\mathcal{K}_{\bf{Q}} $. Then $ \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{M}} $ if and only if $ \det \left\{ \mathcal{G}({\bf{M}}) {\bf{Y}}_\lambda(l) - {\bf{I}} \right\} = 0 $.
3.
Main results
3.1. Block-diagonalization of $ {\bf{X}}_\lambda(x) $ for $ \lambda \neq 1/k $
The following is well defined since the range $ \chi \left(\mathbb{C} \setminus \{ 0, 1/k \} \right) $ of $ \chi $ in Definition 2.4 does not contain $ 1, -1, \mathbb{i}, -\mathbb{i} $.
Definition 3.1. For $ \lambda \in \mathbb{C} \setminus \{ 0, 1/k \} $ and $ x \in \mathbb{R} $, denote
where $ z = \alpha x $ and $ \kappa = \chi(\lambda) $.
The following is well defined, since
Definition 3.2. Denote by $ \beta(\kappa) $ any holomorphic branch in $ \mathbb{C} \setminus \{ -1, 1 \} $ satisfying
and denote by $ \gamma(\kappa) $ any holomorphic branch in $ \mathbb{C} \setminus \{ -\mathbb{i}, \mathbb{i} \} $ satisfying
For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{C} \setminus \{ 1, -1, \mathbb{i}, -\mathbb{i} \} $, define
$ \beta(\kappa) $ and $ \gamma(\kappa) $ are holomorphic branches of $ 2 \operatorname{arctanh}{\kappa} $ and $ 2 \arctan{\kappa} $ respectively, which, in turn, are anti-derivatives of $ 2/\left(1 - \kappa^2 \right) $ and $ 2/\left(1 + \kappa^2 \right) $ respectively.
Definition 3.3. Define $ \mathcal{F} : \operatorname{wp}(4, 8, \mathbb{C}) \to \operatorname{gl}(4, \mathbb{C}) $ by $ \mathcal{F}({\bf{M}}) = {\bf{V}} \mathcal{G}({\bf{M}}) {\bf{V}}^T $ and $ \phi : \operatorname{gl}(4, \mathbb{C}) \to \operatorname{wp}(4, 8, \mathbb{C}) $ by $ \phi({\bf{G}}) = \psi\left({\bf{V}}^T {\bf{G}} {\bf{V}} \right) $. $ \mathcal{F}({\bf{M}}) $ is called the fundamental boundary matrix corresponding to the well-posed boundary matrix $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $.
Denote by $ \operatorname{Sim}_{{\bf{V}}^T}, \operatorname{Sim}_{\bf{V}} : \operatorname{gl}(4, \mathbb{C}) \to \operatorname{gl}(4, \mathbb{C}) $ the similarity transforms defined by $ \operatorname{Sim}_{{\bf{V}}^T} {\bf{G}} = {\bf{V}} {\bf{G}} {\bf{V}}^T $ and $ \operatorname{Sim}_{\bf{V}} {\bf{G}} = {\bf{V}}^T {\bf{G}} {\bf{V}} $ respectively, so that $ \mathcal{F} = \operatorname{Sim}_{{\bf{V}}^T} \circ \mathcal{G} $ and $ \phi = \psi \circ \operatorname{Sim}_{\bf{V}} $ by Definition 3.3. By (2.3), $ \operatorname{Sim}_{{\bf{V}}^T}^{-1} = \operatorname{Sim}_{\bf{V}} $, hence, by Proposition 2.1 (b), $ \mathcal{F}\left(\phi({\bf{G}}) \right) = \operatorname{Sim}_{{\bf{V}}^T} \mathcal{G} \left(\psi \left(\operatorname{Sim}_{\bf{V}} {\bf{G}} \right) \right) = \operatorname{Sim}_{{\bf{V}}^T} \operatorname{Sim}_{\bf{V}} {\bf{G}} = {\bf{G}} $ for $ {\bf{G}} \in \operatorname{gl}(4, \mathbb{C}) $. Thus Definition 3.3 gives a new one-to-one correspondence $ \mathrm{\Phi} : \operatorname{wp}(\mathbb{C}) \to \operatorname{gl}(4, \mathbb{C}) $ defined by $ \mathrm{\Phi} = \operatorname{Sim}_{{\bf{V}}^T} \circ \mathrm{\Gamma} $. See Figure 2 for a commutative diagram which expands the one in Figure 1 to incorporate $ \mathrm{\Phi} $.
By Proposition 2.1 and Definition 3.3, the set of integral operators $ \mathcal{K}_{\bf{M}} $ in (1.1) is in one-to-one correspondence with the $ 16 $-dimensional algebra $ \operatorname{gl}(4, \mathbb{C}) $. Both of $ \mathrm{\Phi} $ and its inverse $ \mathrm{\Phi}^{-1} $ are explicitly computable by using the maps $ \mathcal{F} $ and $ \phi $ in Definition 3.3.
Theorem 1. For $ \lambda \in \mathbb{C} \setminus \{ 0, 1/k \} $, the following $ \rm(a) $ and $ \rm(b) $ hold.
$ \rm(a) $ For $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, $ \mathcal{K}_{\bf{M}}[u] = \lambda \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ u = {\bf{c}}^T {\bf{y}}_\lambda $ for some $ {\bf{0}} \neq {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that
$ \mathcal{K}_{\bf{Q}}[u] = \lambda \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ u = {\bf{c}}^T {\bf{y}}_\lambda $ for some $ {\bf{0}} \neq {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that $ (X+λ(l)OOX−λ(l)) {\bf{V}} {\bf{c}} = {\bf{0}} $.
$ \rm(b) $ Let $ \kappa = \chi(\lambda) $ and $ z = \alpha x $. Then, for $ x \in \mathbb{R} $,
The proof of Theorem 1 will be given at the end of Section 4.
By Proposition 1.1, $ 0, 1/k \not\in \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ for every $ l > 0 $. Note that $ \kappa \neq 0 $ and $ \kappa^4 \neq 1 $ when $ \kappa = \chi(\lambda) $ and $ \lambda \in \mathbb{C} \setminus \{ 0, 1/k \} $. Thus, by Proposition 2.2 (a) and Theorem 1, the zero sets of the holomorphic functions $ \delta^\pm(z, \kappa) $ in Definition 3.2 completely describe $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ in Proposition 1.1.
Corollary 1. For every $ l > 0 $, $ \lambda \in \mathbb{C} $ is in $ \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ if and only if $ \lambda \neq 0 $, $ \lambda \neq 1/k $, and $ \delta^+(\alpha l, \chi(\lambda)) \cdot \delta^-(\alpha l, \chi(\lambda)) = 0 $.
3.2. Block-diagonalization of $ {\bf{X}}_{1/k}(x) $
Definition 3.4. For $ z \in \mathbb{C} $, denote $ p_n(z) = \sum_{r = 0}^n \frac{\omega^{n-r}}{r!} z^r $, $ n = 0, 1, 2, 3 $, where it is understood that $ 0^0 = 1 $, and denote
For $ x \in \mathbb{R} $, denote
where $ z = \alpha x $.
Definition 3.5. For $ z \in \mathbb{C} $, denote
Theorem 2. The following $ \rm(a) $ and $ \rm(b) $ hold.
$ \rm(a) $ For $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $, $ \mathcal{K}_{\bf{M}}[u] = \frac{1}{k} \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ u = {\bf{c}}^T {\bf{y}}_{1/k} $ for some $ {\bf{0}} \neq {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that
$ \rm(b) $ For $ x \in \mathbb{R} $,
where $ z = \alpha x $. $ \det {\bf{X}}_{1/k}^\pm(x) \neq 0 $ and $ \det {\bf{X}}_{1/k}(x) \neq 0 $ for $ x > 0 $.
The proof of Theorem 2 will be given at the end of Section 5.
3.3. Block-diagonalization of $ {\bf{Y}}_\lambda(x) $
Definition 3.6. For $ 0 \neq \lambda \in \mathbb{C} $ and $ x \in \mathbb{R} $ such that $ \det {\bf{X}}_\lambda^\pm(x) \neq 0 $, denote $ {\bf{Y}}_\lambda^\pm(x) = {\bf{X}}_\lambda^\pm(-x) \cdot {\bf{X}}_\lambda^\pm(x)^{-1} - {\bf{I}} $.
Theorem 3. The following $ \rm(a) $ and $ \rm(b) $ hold.
$ \rm(a) $ For $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $ and $ 0 \neq \lambda \in \mathbb{C} \setminus \operatorname{Spec}\mathcal{K}_{\bf{Q}} $, $ \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{M}} $ if and only if
$ \rm(b) $ Let $ 0 \neq \lambda \in \mathbb{C} $, $ x \in \mathbb{R} $, and $ z = \alpha x $. Suppose that $ \det {\bf{X}}_\lambda^\pm(x) \neq 0 $. If $ \lambda \neq 1/k $, then
where $ \kappa = \chi(\lambda) $ and $ \operatorname{s}^\pm(\zeta) = \sinh \left(\sqrt{2} \zeta \right) \pm \sin \left(\sqrt{2} \zeta \right) $ for $ \zeta \in \mathbb{C} $. Also,
The proof of Theorem 3 will be given at the end of Section 6.
4.
Block-diagonalization of $ {\bf{X}}_\lambda(x) $ for $ \lambda \neq 1/k $: proof of Theorem 1
Definition 4.1. For $ z, \kappa \in \mathbb{C} $, denote
Proposition 4.1. ([2,Eq 7.9]) For $ \lambda \in \mathbb{C} \setminus \left\{ 0, 1/k \right\} $ and $ x \in \mathbb{R} $, $ {\bf{X}}_\lambda(x) = {\bf{X}}(z, \kappa) $, where $ z = \alpha x $ and $ \kappa = \chi(\lambda) $.
Definition 4.2. Denote $ \mathbb{D} = \mathbb{C} \setminus \{ 0, 1, -1, \mathbb{i}, -\mathbb{i} \} $. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $, denote
By Definitions 4.1 and 4.2, we have
Lemma 4.1. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $, $ \widehat{{\bf{X}}}(z, \kappa) = \left(\frac { e^{\epsilon_i \omega_j \kappa z} } { 1 - \frac{\omega_j}{\omega_i} \kappa } \right)_{1 \leq i, j \leq 4} $.
Proof. By Definition 2.1 and (2.1), $ {\bf{W}}_0^* = \left(\overline{\omega_i}^{j-1} \right)_{1 \leq i, j \leq 4} = \left(\omega_i^{1-j} \right)_{1 \leq i, j \leq 4} $, hence
for $ 1 \leq i, j \leq 4 $. So by Definition 4.2, we have
Thus the result follows by Definition 2.2.
Definition 4.3. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $, denote
Note from Definitions 3.1 and 4.3 that
where $ z = \alpha x $ and $ \kappa = \chi(\lambda) $.
Lemma 4.2. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $, $ {\bf{V}} \widehat{{\bf{X}}}(z, \kappa) {\bf{V}}^T = (ˆX+(z,κ)OOˆX−(z,κ)) $.
Proof. By (2.1), Definition 2.2 and Lemma 4.1,
for $ 1 \leq i, j \leq 2 $, which implies that $ \widehat{{\bf{X}}}(z, \kappa) = (ABBA) $, where we put $ {\bf{A}} = \left\{ \widehat{{\bf{X}}}(z, \kappa)_{i, j} \right\}_{1 \leq i, j \leq 2}, {\bf{B}} = \left\{ \widehat{{\bf{X}}}(z, \kappa)_{i, j+2} \right\}_{1 \leq i, j \leq 2} \in \operatorname{gl}(2, \mathbb{C}) $. So by Lemma 2.1, we have
By Lemma 4.1, we have
hence, by (2.1) and Definitions 2.2, 4.3,
Thus the lemma follows by (4.3).
Lemma 4.3. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $, $ {\bf{V}} {\bf{X}}(z, \kappa) {\bf{V}}^T = (X+(z,κ)OOX−(z,κ)) $.
Proof. By (2.3), (2.4), (4.1) and Lemma 4.2,
Thus the lemma follows by Definition 4.3.
By Proposition 4.1, (4.2) and Lemma 4.3, we have
Lemma 4.4. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $, $ \det \widehat{{\bf{X}}}^\pm(z, \kappa) = \frac {4 \kappa} {1 - \kappa^4} \cdot \delta^\pm(z, \kappa) $.
See Supplementary A for proof of Lemma 4.4.
Proof of Theorem 1. Let $ \lambda \in \mathbb{C} \setminus \{ 0, 1/k \} $ and $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $. By Proposition 2.2 (a), $ \mathcal{K}_{\bf{M}}[u] = \lambda \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ u = {\bf{c}}^T {\bf{y}}_\lambda $ for some $ {\bf{0}} \neq {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that
since $ {\bf{V}} $ is invertible by (2.3). Thus the first assertion in (a) follows, since (4.5) is equivalent to
by (4.4) and Definition 3.3. The second assertion in (a) follows from the first one, since $ \mathcal{F}({\bf{Q}}) = {\bf{V}} \mathcal{G}({\bf{Q}}) {\bf{V}}^T = {\bf{O}} $ by (2.6) and Definition 3.3.
Let $ \kappa = \chi(\lambda) $, $ x \in \mathbb{R} $, and $ z = \alpha x $. By (2.3) and (4.4), we have
By (4.2) and Definition 4.3,
hence, by (2.5) and Lemma 4.4,
So by (4.6), we have
Thus we showed (b), and the proof is complete.
5.
Block-diagonalization of $ {\bf{X}}_{1/k}(x) $: proof of Theorem 2
Definition 5.1. For $ z \in \mathbb{C} $, denote
Proposition 5.1. $ \rm(a) $ ([2,Eq 7.13]) $ {\bf{X}}_{1/k}(x) = \frac{1}{4} e^{-\mathcal{E} {\bf{\Omega}} z} {\bf{P}}(z) \cdot \operatorname{diag}\left(1, \alpha, \alpha^2, \alpha^3 \right)^{-1} $ for $ x \in \mathbb{R} $, where $ z = \alpha x $.
$ \rm(b) $ ([2,Lemma B1]) For $ z \in \mathbb{C} $, $ {\bf{V}} {\bf{P}}(z) \widehat{{\bf{V}}} = \sqrt{2} (P+(z)OOP−(z)) $.
The result in Proposition 5.1 (b) was for $ z \in \mathbb{R} $ in [2] originally, but it can immediately be extended to $ z \in \mathbb{C} $.
By (2.3), we have
By Proposition 5.1 (a) and (2.3),
hence, by (2.4), (5.1) and Proposition 5.1 (b),
Thus, by (2.3) and Definition 3.4, we have
By Definition 3.4 and (2.1), we have
Lemma 5.1. For $ z \in \mathbb{C} $, $ \det {\bf{P}}^+(z) = 2 \mathbb{i} \cdot p^+(z) $ and $ \det {\bf{P}}^-(z) = - 2 \mathbb{i} \cdot p^-(z) $.
Proof. By Definitions 3.4, 3.5, (2.1) and (5.3),
Proof of Theorem 2. Let $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $. By Proposition 2.2 (a), $ \mathcal{K}_{\bf{M}}[u] = \frac{1}{k} \cdot u $ for some $ 0 \neq u \in L^2[-l, l] $ if and only if $ u = {\bf{c}}^T {\bf{y}}_{1/k} $ for some $ {\bf{c}} \in \operatorname{gl}(4, 1, \mathbb{C}) $ such that
since $ {\bf{V}} $ is invertible by (2.3). Thus (a) follows, since (5.4) is equivalent to
by (5.2) and Definition 3.3.
Let $ x \in \mathbb{R} $ and $ z = \alpha x $. By (2.3) and (5.2),
By (2.5), Definition 3.4 and Lemma 5.1,
By (5.5), (5.6), (5.7),
It follows that $ \det {\bf{X}}_{1/k}^\pm(x) \neq 0 $ and $ \det {\bf{X}}_{1/k}(x) \neq 0 $ for $ x > 0 $, since $ p^\pm(z) > 0 $ for $ z > 0 $ by Definition 3.5. Thus we showed (b), and the proof is complete.
6.
Block-diagonalization of $ {\bf{Y}}_\lambda(x) $: proof of Theorem 3
6.1. The case $ \lambda \neq 1/k $
Denote $ {\bf{R}} = (0110) $. For $ a, b, c, d \in \mathbb{C} $, we have
By Definition 4.3,
for $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $. Note from Definition 4.2 that $ \overline{\kappa} \in \mathbb{D} $ if and only if $ \kappa \in \mathbb{D} $.
Lemma 6.1. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $,
Proof. Let $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $. It can be checked from Definition 4.3 and (6.2) that $ \widehat{{\bf{X}}}^\pm(z, \kappa)_{2, 1} = \overline{ \widehat{{\bf{X}}}^\pm(\overline{z}, \overline{\kappa})_{1, 2} } $, $ \widehat{{\bf{X}}}^\pm(z, \kappa)_{2, 2} = \overline{ \widehat{{\bf{X}}}^\pm(\overline{z}, \overline{\kappa})_{1, 1} } $, and $ \left\{ \operatorname{adj} \widehat{{\bf{X}}}^\pm(z, \kappa) \right\}_{2, 1} = \overline{ \left\{ \operatorname{adj} \widehat{{\bf{X}}}^\pm(\overline{z}, \overline{\kappa}) \right\}_{1, 2} } $, $ \left\{ \operatorname{adj} \widehat{{\bf{X}}}^\pm(z, \kappa) \right\}_{2, 2} = \overline{ \left\{ \operatorname{adj} \widehat{{\bf{X}}}^\pm(\overline{z}, \overline{\kappa}) \right\}_{1, 1} } $, which, by (6.1), are equivalent to $ {\bf{R}} \cdot \widehat{{\bf{X}}}^\pm(z, \kappa) \cdot {\bf{R}} = \overline{ \widehat{{\bf{X}}}^\pm(\overline{z}, \overline{\kappa}) } $, $ {\bf{R}} \cdot \operatorname{adj} \widehat{{\bf{X}}}^\pm(z, \kappa) \cdot {\bf{R}} = \overline{ \operatorname{adj} \widehat{{\bf{X}}}^\pm(\overline{z}, \overline{\kappa}) } $. So we have
since $ {\bf{R}}^2 = {\bf{I}} $. Thus the result follows by (6.1).
Lemma 6.2. For $ z \in \mathbb{R} $ and $ \kappa \in \mathbb{D} $,
where $ \operatorname{s}^\pm(\zeta) = \sinh \left(\sqrt{2} \zeta \right) \pm \sin \left(\sqrt{2} \zeta \right) $ for $ \zeta \in \mathbb{C} $.
See Supplementary B for proof of Lemma 6.2.
Definition 6.1. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $ such that $ \det {\bf{X}}^\pm(z, \kappa) \neq 0 $, denote $ {\bf{Y}}^\pm(z, \kappa) = {\bf{X}}^\pm(-z, \kappa) \cdot {\bf{X}}^\pm(z, \kappa)^{-1} - {\bf{I}} $.
By Definitions 3.6, 6.1 and (4.2),
where $ z = \alpha x $ and $ \kappa = \chi(\lambda) $. Note from (2.1) that, for $ a, b, c, d, \delta \in \mathbb{C} $, $ \delta \neq 0 $,
Lemma 6.3. For $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $ such that $ \det {\bf{X}}^\pm(z, \kappa) \neq 0 $,
where $ \operatorname{s}^\pm(\zeta) = \sinh \left(\sqrt{2} \zeta \right) \pm \sin \left(\sqrt{2} \zeta \right) $ for $ \zeta \in \mathbb{C} $.
Proof. Let $ z \in \mathbb{C} $, $ \kappa \in \mathbb{D} $, and suppose that $ \det {\bf{X}}^\pm(z, \kappa) \neq 0 $. By Definition 4.3,
hence, by Definition 6.1,
By Lemmas 4.4 and 6.2,
hence, by (6.5),
Thus the lemma follows by (6.4).
6.2. The case $ \lambda =1/k $ and proof of Theorem 3
By Definition 3.4, we have
Lemma 6.4. For $ z \in \mathbb{C} $, $ {\bf{P}}^\pm(-z) \cdot \operatorname{adj} {\bf{P}}^\pm(z) = \pm 2 \mathbb{i} (p±(−iz)12∓1ωz2∓112∓1¯ωz2∓1p±(iz)) $.
See Supplementary C for proof of Lemma 6.4.
Lemma 6.5. Let $ x \in \mathbb{R} $, $ z = \alpha x $, and suppose that $ \det{\bf{X}}_{1/k}^\pm(x) \neq 0 $. Then
Proof. By Definition 3.4,
So by Definitions 3.4 and 3.6,
By Lemmas 5.1 and 6.4,
hence, by (6.7),
Thus the lemma follows by (6.4).
Let $ 0 \neq \lambda \in \mathbb{C} $ and $ x \in \mathbb{R} $. Suppose that $ \det {\bf{X}}_\lambda(x) \neq 0 $, which is equivalent to $ \det {\bf{X}}_\lambda^+(x) \neq 0 $ and $ \det {\bf{X}}_\lambda^-(x) \neq 0 $ by (4.4) and (5.2). Let $ {\bf{A}} = \left\{ VT,if λ≠1/k,ˆV,if λ=1/k. \right. $ Then by Definition 2.5 and (2.3),
hence, by (2.3), (4.4) and (5.2),
Thus, by (2.3) and Definition 3.6, we have
Proof of Theorem 3. Let $ {\bf{M}} \in \operatorname{wp}(4, 8, \mathbb{C}) $ and $ 0 \neq \lambda \in \mathbb{C} \setminus \operatorname{Spec}\mathcal{K}_{\bf{Q}} $. By Proposition 2.2 (b), $ \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{M}} $ if and only if
since $ {\bf{V}} $ is invertible by (2.3). Thus (a) follows, since (6.9) is equivalent to
by (6.8) and Definition 3.3.
Let $ 0 \neq \lambda \in \mathbb{C} $, $ x \in \mathbb{R} $, and $ z = \alpha x $. Suppose that $ \det {\bf{X}}_\lambda^\pm(x) \neq 0 $. (b) follows from (6.3) and Lemma 6.3 when $ \lambda \neq 1/k $, and from Lemma 6.5 when $ \lambda = 1/k $. Thus the proof is complete.
7.
Conclusions
The boundary conditions usually considered in practice are only a few in number, including clamped, free, or hinged conditions at each end of the beam. An important aspect of our results is that we have obtained explicit and manageable characteristic equations for the whole $ 16 $-dimensional class of integral operators $ \mathcal{K}_{\bf{M}} $ arising from arbitrary well-posed boundary value problem of the Euler–Bernoulli beam equation.
In our characteristic equations in Theorems 1, 2, and 3, the explicit matrices $ {\bf{X}}_\lambda^\pm $ and $ {\bf{Y}}_\lambda^\pm $ are not affected by specific boundary conditions. The effect of the boundary condition $ {\bf{M}} $ is encoded separately in the fundamental boundary matrix $ \mathcal{F}({\bf{M}}) $. The set of equivalent well-posed boundary matrices $ \operatorname{wp}(\mathbb{C}) $, and hence the set of integral operators $ \mathcal{K}_{\bf{M}} $ in (1.1), is in one-to-one correspondence with the $ 16 $-dimensional algebra $ \operatorname{gl}(4, \mathbb{C}) $ via the map $ \mathrm{\Phi} $. $ \mathrm{\Phi} $ and its inverse $ \mathrm{\Phi}^{-1} $ are explicitly computable using the maps $ \mathcal{F} $ and $ \phi $ in Definition 3.3. See Figure 2 in Section 3 for a commutative diagram showing the details.
The $ 2 \times 2 $ matrices $ {\bf{X}}_\lambda^\pm $ and $ {\bf{Y}}_\lambda^\pm $ themselves are pre-calculated in terms of the explicit functions $ \delta^\pm(z, \kappa) $ and $ p^\pm(z) $. Thus our characteristic equations have simple and manageable expressions with the functions $ \delta^\pm(z, \kappa) $ and $ p^\pm(z) $, which are amenable to concrete analysis similar to that in [14].
By inverting the $ 2 \times 2 $ matrices $ {\bf{Y}}_\lambda^\pm(l) $ in Theorem 3, we would have alternate forms of the characteristic equations in Theorem 1 (a) and Theorem 2 (a) with matrix entries also explicitly expressed by $ \delta^\pm(z, \kappa) $ and $ p^\pm(z) $. However, these forms are suppressed in this paper due to the nontrivial problem of identifying the zeros of $ \det{\bf{Y}}_\lambda^\pm(l) $ or $ \det\left\{ {\bf{X}}_\lambda^\pm(-l) - {\bf{X}}_\lambda^\pm(l) \right\} $, which will be dealt in future works.
Although our results are for boundary matrices with complex entries in general, boundary conditions of practical importance are those represented by boundary matrices with real entries. See [2] for the characterization of these real boundary conditions $ {\bf{M}} $ in terms of $ \mathcal{G}({\bf{M}}) $ by using the $ \mathbb{R} $-algebra $ \overline{\pi}(4) \subset \operatorname{gl}(4, \mathbb{C}) $.
An immediate application of our results would be spectral analysis for a few typical boundary conditions encountered frequently in practice. Specifically, concrete spectral analysis for the following combinations of clamped, free, and hinged boundary conditions at each end of the beam are now possible, which will be performed in future works.
$ \bullet $ clamped-clamped or bi-clamped.
$ \bullet $ free-free or bi-free.
$ \bullet $ hinged-hinged or bi-hinged.
$ \bullet $ clamped-free or cantilevered.
$ \bullet $ hinged-free.
$ \bullet $ clamped-hinged.
In fact, it turns out that the fundamental boundary matrices $ \mathcal{F}({\bf{M}}) $ corresponding to the first three symmetric boundary conditions $ {\bf{M}} $ above also have the following block-diagonal form with $ 2 \times 2 $ blocks.
In these cases, our characteristic equations in Theorems 1, 2, and 3 are completely separable into $ 2 \times 2 $ blocks, resulting in further simplified forms which involve determinants of $ 2 \times 2 $ matrices only.
Acknowledgments
The author thanks the anonymous reviewers for their careful and constructive comments which helped to improve the manuscript.
Conflict of interest
The author declares no conflict of interest in this paper.
Supplementary
A.
Proof of Lemma 4.4
By Definition 4.3 and (2.1),
Thus, by Definition 3.2,
B.
Proof of Lemma 6.2
Let $ z \in \mathbb{C} $ and $ \kappa \in \mathbb{D} $. By Definition 4.3, (2.1) and (6.2),
hence, by Definition 3.2,
By Definition 4.3, (2.1) and (6.2),
By Lemma 6.1, (B.1), (B.2) and Definition 3.2,
Thus the lemma follows from (B.1), (B.2), (B.3), (B.4).
C.
Proof of Lemma 6.4
Let $ z \in \mathbb{C} $. By Definition 3.4 and (6.6), we have
So, by (2.1), (5.3) and Definition 3.5,
Note from (C.1) and (C.2) that
So by (C.3), (C.4), (C.5), (C.6),
Thus, by (C.3), (C.4), (C.5), (C.6), (C.7), (C.8), (C.9), (C.10), we have
and the proof is complete.
D.
The functions $ \delta^\pm(z, \kappa) $
We start with some exotic definitions in [14]. For $ \kappa \geq 0 $, let
Here, $ L = 2 l \alpha $ is the intrinsic length of the beam and
where $ \hat{h} : [0, \infty) \to \mathbb{R} $ is defined by
The branch of $ \arctan $ here is taken such that $ \arctan{0} = 0 $. $ \hat{h} $ is a strictly decreasing real-analytic function with $ \hat{h}(0) = 0 $ and $ \lim_{\kappa \to \infty} \hat{h}(\kappa) = -2 \pi $, hence $ h : [0, \infty) \to \mathbb{R} $ is a strictly increasing real-analytic function with $ h(0) = 0 $ and $ \lim_{\kappa \to \infty} h(\kappa) = \infty $.
Proposition D.1. ([14,Eqs 8 and 25]) $ \lambda \in \mathbb{C} $ is an eigenvalue of $ \mathcal{K}_{\bf{Q}} = \mathcal{K}_{l, \alpha, k} $ if and only if $ \lambda = \frac{1}{k} \cdot \frac {1} {1 + \kappa^4} $ for $ \kappa > 0 $ such that $ \varphi^+(\kappa) = p(\kappa) $ or $ \varphi^-(\kappa) = p(\kappa) $.
Now we demonstrate how the seemingly ad hoc and complex conditions $ \varphi^\pm(\kappa) = p(\kappa) $ in Proposition D.1, which were practically unobtainable without help of computer algebra systems as indicated in [14], can be derived so naturally and elegantly from our holomorphic functions $ \delta^\pm(z, \kappa) $.
By Definition 3.2,
where $ \mathbb{D} = \mathbb{C} \setminus \{ 0, 1, -1, \mathbb{i}, -\mathbb{i} \} $ by Definition 4.2.
Lemma D.1. For $ \kappa \geq 0 $, $ p(\kappa) = e^{ \mathbb{i} \left\{ \gamma \left(\omega \kappa \right) - \gamma \left(\overline{\omega} \kappa \right) \right\} } $ and $ e^{-\mathbb{i} \hat{h}(\kappa)} = e^{ \mathbb{i} \left\{ \gamma \left(\omega \kappa \right) + \gamma \left(\overline{\omega} \kappa \right) \right\} } $.
Proof. By (2.1), (D.1), (D.4),
By (2.1) and (D.4),
So we have
hence
Thus, by (D.3),
It follows that $ e^{-\mathbb{i} \hat{h}(\kappa)} = e^{ \mathbb{i} \left\{ \gamma \left(\omega \kappa \right) + \gamma \left(\overline{\omega} \kappa \right) \right\} } $, and the proof is complete.
By (D.2) and Lemma D.1,
So we have $ \cos h(\kappa) = \cos \left\{ L \kappa + \gamma \left(\omega \kappa \right) + \gamma \left(\overline{\omega} \kappa \right) \right\} $, $ \sin h(\kappa) = \sin \left\{ L \kappa + \gamma \left(\omega \kappa \right) + \gamma \left(\overline{\omega} \kappa \right) \right\} $, hence, by (D.1),
By Definition 3.2,
Comparing (D.4) and (D.6), we have $ e^{\mathbb{i} \gamma(\kappa)} = e^{\beta(\mathbb{i} \kappa)} $ for $ \kappa \in \mathbb{D} $, hence
since $ - \mathbb{i} \omega = \overline{\omega} $ by (2.1).
Now let $ \lambda = \frac{1}{k} \cdot \frac {1} {1 + \kappa^4} $ for $ \kappa > 0 $, and let $ z = l \alpha $ so that
By Definitions 2.1 and 2.4,
hence $ \delta^\pm \left(l \alpha, \chi(\lambda) \right) = \delta^\pm(z, \omega \kappa) $. So by Corollary 1, $ \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ if and only if $ \delta^+ \left(z, \omega \kappa \right) = 0 $ or $ \delta^- \left(z, \omega \kappa \right) = 0 $. By Definition 1, $ \sqrt{2} \omega = 1 + \mathbb{i}, $ hence, by Definition 3.2 and (D.7),
So $ \delta^\pm(z, \omega \kappa) = 0 $ if and only if
which is equivalent to $ p(\kappa) = \varphi^\pm(\kappa) $ by Lemma D.1, (D.5) and (D.8). Thus we conclude that $ \lambda \in \operatorname{Spec}\mathcal{K}_{\bf{Q}} $ if and only if $ p(\kappa) = \varphi^+(\kappa) $ or $ p(\kappa) = \varphi^-(\kappa) $, which is exactly the condition in Proposition D.1.










 DownLoad:
DownLoad: