1. Introduction
The correlation between stock returns and bond returns contains information that is useful to investors and economic policy-makers. Movements in this correlation reveal investor expectations in regard of the future performance of the economy and stocks. This information can thus be used to aid in the use of market timing strategies that switch between the two asset classes. Equally, for policy-makers, movements in this correlation act as a window on expected future economic conditions, allowing for corrective policy action to be taken. This information content stems from the view that the stock and bond return correlation acts as a weathervane for risk within these markets and the wider economy. This paper therefore empirically examines the question of whether the stock and bond return correlation contains information content and predictive power for both stock and bond returns themselves, the ability to develop a market timing strategy and for key macroeconomic variables.
A large amount of empirical research seeks to examine the behaviour of the stock and bond correlation, notably attempting to identify the factors driving its movement. Selected examples of this literature include Connolly et al. (2007) who consider how the correlation varies with stock market risk as proxied by the implied volatility index for a range of international markets using a regime-switching analysis. Baele et al. (2010) consider a range of macroeconomic and market variables in a Markov switching factor model. Aslanidis and Christiansen (2012) also use a regime-switching model (albeit a different one) and consider whether transition between regimes is related to specific financial and macroeconomic variables. Aslanidis and Christiansen (2014) adopt a quantile regression to examine the links between the correlation and macroeconomic variables. Sakemoto (2018) also considers the role of implied volatility in the stock and bond correlation and the impact of the financial crisis. While further work includes that of Asgharian et al. (2016), Dimic et al. (2016), Gupta et al. (2017) and Kollias et al. (2013).
Within this research several ways are proposed for measuring the stock and bond correlation. This arises as the correlation itself is an unobserved variable and so different approaches have arisen to proxy for it. A common approach is to model stock and bond returns jointly and thus estimating the covariance between them. Predominantly, this includes a GARCH type approach; for example, Baur and Lucey (2010) use a multivariate-GARCH model, while Yang et al. (2009) consider alternative GARCH specifications and Colacito et al. (2011) use an extension of the DCC model of Engle (2002). An alternative approach builds upon the realised volatility literature (see, McAleer and Medeiros, 2008 for a review of this area) and seeks to construct a realised correlation series. This includes the work of Aslanidis and Christiansen (2012) as well as the more recent work of Harumi and Tatsuyoshi (2016). Notwithstanding these approaches, a relatively simple way to obtain the time-varying correlation is through a moving window. Fan and Mitchell (2017) use a 1-year and 5-year rolling window to illustrate the nature of time-variation, while Rankin and Shah Idil (2014) consider a variety of window lengths. Each of these alternative approaches produce correlation series that closely mirror each other and only differ in the variability of the correlation time series. For example, Figure 1 of Baele et al. (2010) highlights the greater variability in realised correlation approach compared to the DCC based approach of Colacito et al. (2011).
The general consensus across both the academic literature and practitioner research is that there exists a positive correlation between stock and bond returns, but a substantial amount of variation within that relation is also present. For example, the Pimco quantitative research document (Johnson et al., 2013) documents an average correlation of 10% for US assets over the period 1927 to 2012 but with a variability that ranges from –93% to +86%. As noted in this document, the negative correlations arise from changes in investor risk appetite, most notably referred to as a flight-to-safety. This occurs when investors perceive heightened risk and so shun risky equity in favour of safer debt. This paper argues that this time-varying correlation can therefore be utilised as a measure of risk and will thus have predictive power for future movements in both asset returns themselves and the wider economy. A decline in the stock-bond correlation indicates that the two asset classes are moving apart and this can act as a market timing signal for investors. Using the correlation as a predictor, investors should be able to construct improved stock and bond portfolios. Beyond this, a negative correlation implies that investor outlook for future macroeconomic conditions are poor, indicating a future downturn. Such information therefore, would be of use to policy-makers, providing a leading indicator measure.
Moreover, evidence of predictability for both macroeconomic and financial variables would aid in our understanding of the factors that in turn determine movements in the correlation itself. As noted above, several papers argue that movements in the correlation are affected by specific economic variables. This research uses such variables (e.g., Baele et al., 2010 consider inflation, output, interest rates and measures of cash flow and risk) as explanatory factors for the correlation series. However, as financial markets move quicker than real markets, we would also (or perhaps instead) expect to see the direction of causality running from the former to the latter. As investor expectations of future economic conditions deteriorate, they will alter their relative holdings of stocks and bonds. Thus, we will observe a change in the correlation now, while the changing macroeconomic conditions will materialise over subsequent periods. This will result in a Granger causal effect from financial to real markets.
This paper will therefore, examine the nature of the stock and bond return correlation and its predictive power for future movements in stock and bonds returns as well as for a range of macroeconomic variables.
2. The stock/bond return correlation
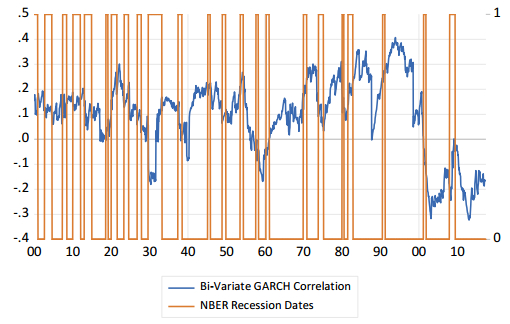
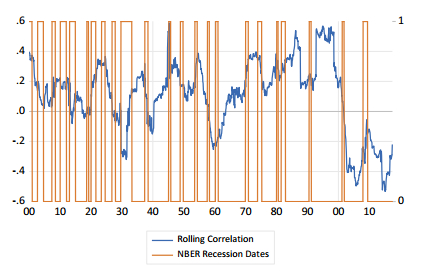
Figure 1 presents the US stock return and bond return correlation based on a rolling window of five years. The data is monthly and over the period from 1900:1 to 2017:6, thus, each window contains 60 observations. The stock return is based on the S & P composite index and the bond return based on a constant maturity 10-year index. Evident within the correlation is the nature of time-variation with the strength of the correlation cycling approximately between –0.6 and +0.6. We can observe notable periods of negative stock and bond return correlation during the great depression period, the recessionary period of the late 1950s and the period following the dotcom crash and extending over the financial crisis. To ensure robustness within the time-varying nature of the stock and bond return correlation, Figure 2 presents the estimated correlation from a bivariate GARCH(1, 1) model. As we can observe the nature of the dynamics within both series are similar. Indeed, the correlation between the two series is approximately 0.90 and the periods of negative correlation overlap.
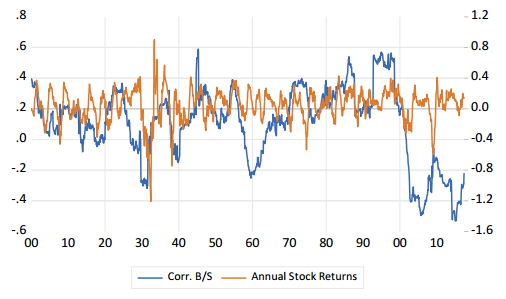
Within both Figures 1 and 2, we include the NBER recession dates, from which we can see a general negative relation between the series. This indicates that a recession is associated with a lower stock and bond return correlation. This supports our view that the negative correlation is an indicator of risk. Figure 3 seeks to further support this view and plots the stock and bond return correlation together with annual stock returns. Here we can see that the negative correlation is associated with negative stock returns. Our view is that within a portfolio setting, under normal conditions, investors will buy stocks and bonds as they diversify across assets. While purchases of equity may outweigh purchases of bonds when they are optimistic, the direction of movement in both assets will be the same.1 However, when risk increases, investors will move from stocks to bonds and thus generating the negative correlation between the two assets and illustrated in Figure 3.
1 Only in periods of extreme optimism (and mania) will investors sell bonds to fund greater purchases of stocks.
While there is perhaps no single unifying theory that determines the nature of the stock and bond return correlation, there is a general view that over a long horizon the correlation will be positive, punctuated by periods of negative values. A positive correlation is suggested by Barksy (1989), Shiller and Beltratti (1992) and Campbell and Ammer (1993). The view here is that under normal economic conditions stock and bond prices respond to changes in economic conditions in a similar manner, resulting in a positive correlation. For example, a rise in interest rates is associated with a fall in the bond price and this occurs in a mechanical fashion given the fixed nature of the bond coupon payment. Equally, a rise in interest rates will typically result in a fall in the stock price through an increase in the rate at which future cash flows are discounted.
Notwithstanding this, while stock and bond asset pricing models have typically developed separately, unifying asset pricing theories are proposed. Mamaysky (2002), Bekaert et al. (2010) and d'Addona and Kind (2006) specify an affine asset pricing model for stocks and bonds. The model specifies a stochastic discount factor that prices all assets in the economy. Generally, the fair price of an asset is calculated by discounting expected future payoffs. For a default-free bond, this is the discounted finite stream of known future cash flows, while for stocks it is the risk adjusted discounted infinite stream of expected future dividends (see d'Addona and Kind, 2006; Cochrane, 2005). In the affine asset pricing model, the expected nominal return on a bond is a function of the real interest rate, expected inflation, the term premium, unexpected real interest rate shocks and unexpected inflation shocks. The nominal return on stocks is a function of the real interest rate, expected inflation, the risk premium, unexpected real interest rate shocks, unexpected inflation shocks and unexpected dividend shocks. The model predicts that real interest rates and expected inflation generally moves stock and bond returns in the same direction. As such, a rise in interest rates and the yield on bonds naturally leads to a fall in bond prices due to an increase in the discount factor. That would also be accompanied by falling stock prices due to a rise in the discount rate. Moreover, an increase in rates may signal an increase in macroeconomic risk and the potential for lower expected future earnings, again causing current stock prices to fall.
In contrast, a negative correlation can arise between stocks and bonds and this is related to an increase in risk, with investors rebalancing their portfolios following flight-to-safety behaviour (see, for example, Gulko, 2002; Connolly et al., 2005; Connolly et al., 2007; Andersson et al., 2008; Baur and Lucey, 2009; Bayraci et al., 2018). In the above asset pricing models, unexpected inflation and dividend shocks are likely to reduce stock-bond comovement via the nominal channel (for a discussion see Li (2002)). In particular, these stocks are likely to be reflected in changes to risk aversion. Ilmanen (2003) suggests that the stock-bond correlation becomes negative during deflationary recessions. Here, investors would prefer the nominally fixed cash flows from arise from bonds as they may increase in real terms while corporate cash flows are more likely to be adversely affected by a loss of corporate pricing power and nominally fixed labour contracts. Shiller and Beltratti (1992) argue that although stocks and bonds represent claims on future cash flows, the nature of those cash flows differ. They argue that while the dividend stream on stocks is fairly stable in real terms, the coupon payment on bonds is stable in nominal terms.
More generally, a negative relation between bond and equity returns would imply that, for example, as interest rates and bond yields fall, so do equity prices, in contradiction of the dividend discount model. Such a negative relation can arise during periods of market stress and poor economic prospects, with investors moving from equities to bonds. As such, higher demand for bonds pushes up their price, while sales of stock leads to price falls. A further fall in interest rates, while leading to higher bond prices given the mechanical nature of the fixed coupon payment will leads to further falls in stock prices, as the lower interest rates confirms investors fear regarding the future economic outlook. Thus, a negative correlation is driven by an increase in risk and investors perception of the future performance of the economy. These changes in the nature of the correlation between stocks and bonds provide useful information not only for investors with regard to the future movements of the respective assets but also to policy makers as it indicates poor future economic prospects.
Turning back to Figure 1, therefore, we can observe that the negative correlation arises during periods of market stress, with all such periods associated with severe recessions. Furthermore, while not all recessions lead to a negative correlation, they are associated with a fall in the correlation. Without listing each recession, we can note the near zero and negative correlations for the sequence of recessions in the 1900s and 1910s, the fall in the correlation associated with the recession of the mid-1920s prior to the great depression, the great depression itself, the negative correlation associated with the recession of the mid-late 1930s, the fall in the correlation from the mid-1950s, the fall in the correlation associated with the oil price shock induced recession of the mid 1970s and the dotcom crash and financial crisis induced recessions of the 2000s.
Table 1 presents summary statistics for stock and bond returns as well as the time-varying correlation and a set of predictor variables used in the analysis below. In terms of the more pertinent points, we can observe, as expected, that stock returns have a higher mean and standard deviation than bond returns, while for both assets the standard deviation is larger than the mean and they exhibit non-normality. The correlation has a positive mean, similar to the value reported by Johnson et al. (2013) and exhibits noticeable negative skewness. Unit root tests are conducted to ensure stationarity of the series and thus reliability in the regression analysis. While all series exhibit stationarity, the result for the correlation series is more marginal and raises the issue of stationary behaviour in a bounded variable. By definition a series that is bounded (in this case between –1 and +1) must be stationary, i.e., its value cannot increase or decrease without end. However, within a sample it could appear to exhibit non-stationary behaviour but care should be exercised in regarding it as a non-stationary series. Notwithstanding this, the possibility of a break within the correlation series exists, which is likely to drive the marginal unit root test result.2 In the analysis below, we allow for both breaks and regimes of behaviour to be present.
Table 1. Summary statistics.
|
Mean |
Std Dev |
Skew |
Kurt |
Unit Root |
| Stock Returns |
0.425 |
5.077 |
–0.517 |
11.245 |
–33.46 |
| Bond Returns |
0.381 |
1.778 |
0.462 |
7.241 |
–8.57 |
| Cor. B/S |
0.106 |
0.239 |
–0.599 |
2.955 |
–1.71 |
| TS |
1.445 |
1.114 |
–0.093 |
2.580 |
–3.89 |
| Δ3-mth TB |
–0.003 |
0.387 |
–1.604 |
23.39 |
–30.39 |
| DP |
1.311 |
0.434 |
–0.575 |
2.843 |
–2.24 |
| FED |
2.086 |
1.432 |
1.650 |
6.262 |
–2.78 |
| Notes: Entries are the mean, standard deviation, skewness and kurtosis statistic for the stock return, bond return and the five-year moving correlation between them over the monthly sample period 1900:1 to 2017:6 (1410 observations). The unit root test is the DF-GLS test with a 5% (10%) significance value of –1.94 (–1.62). |
2 Indeed, a unit root test that allows for a break to occur around the late 1990s period results in a highly significant rejection of a unit root and thus stationary behaviour.
3. Predicting stock and bond returns
3.1. Data and methodology
As noted above, the stock return data is based on the S & P composite index and the bond return on 10-year constant maturity index. In addition to this data, we include alternative financial series, namely, the term structure of interest rates (specifically, the 10-year Treasury bond minus the 3-month Treasury bill) and the log dividend-price (DP) ratio for stocks or the change in the 3-month Treasury bill for bonds. We also consider alternatives to the DP ratio/change in short-term interest rates and include the FED ratio, which is the ratio of the equity yield to 10-year bond ratio and is a measure of relative valuation (see, for example, Asness, 2003; Bekaert and Engstrom, 2010; Maio, 2013). The data is obtained from Datastream and the St Louis FRED database.3
3 We also consider the inclusion of the CAPE instead of the DP produces a similar result to the DP and so is not reported.
We begin the analysis using a linear regression model where the stock and bond correlation series predicts future stock and bond returns:
Where xt refers to the respective asset returns (first-difference of the log price multiplied by 100), ρsb, t is the stock and bond return correlation and εt is a white noise error term.
As can be observed in Figures 1 and 2, the correlation cycles between positive and negative values. To examine the whether the predictive relation changes according to the nature of the correlation, we implement the logistic smooth-transition regression model (LSTR, see the survey paper of van Dijk et al., 2002). This model is an extension of the threshold modelling approach and allows for different regimes of behaviour according to the transition function. The smooth-transition model is given by:
|
xt=α1+β1ρsb,t−1+(α2+β2ρsb,t−1)F(zt−d)+εt
|
(2)
|
Where F(.) is the transition function, with z the transition variables (here, we use the stock and bond return correlation, ρsb) and d is the delay (or lag, for which we use the value of one). As we wish to consider the difference in predictive behaviour across positive and negative values of the lagged correlation, we use the logistic transition function:
|
F(zt−d)=(1+exp(−γ(zt−d−c)))−1;γ>0
|
(3)
|
Where c is the transition point between the positive and negative regimes and while we could impose this to be zero, we prefer to estimate it, and γ is the speed of transition between regimes. As such, in the lower regime, where F(zt–d) = 0 and zt–d < c, the model is given by:
While in the upper regime, where F(zt–d) = 1 and zt–d > c, the model is given by:
|
xt=(α1+α2)+(β1+β2)ρsb,t−1+εt
|
(5)
|
Between these two extreme regimes, the process is given by a combination of the estimated parameters, for example, where F(zt–d) = 0.5 and zt–d = c, the model is given by:
|
xt=(α1+0.5α2)+(β1+0.5β2)ρsb,t−1+εt
|
(6)
|
The STR can thus be seen as exhibiting a continuum of regimes or as having two extreme regimes and a transition phase, the speed of which is governed by the value of γ.
To examine the market timing ability content of the correlation series and whether there are threshold values in which investors switch between stocks and bonds, we estimate the quadratic logistic QLSTR model (Jansen and Teräsvirta, 1996). This model presents an alternative transition function to the LSTR model above. In particular, the QLSTR transition function allows for two threshold points, which can be used to inform the trading strategy. The QLSTR transition function is given as:
|
F(zt−d)=(1+exp(−γ(zt−d−c1)(zt−d−c2))−1;γ>0
|
(7)
|
Thus, we now allow for two threshold points, c1 and c2, which will determine the switch in trading strategy discussed below.
3.2. Empirical results
Panel A of Table 2 reports the estimation results from equation 1 using just the correlation term. The results reveal a positive and significant relation between the stock and bond return correlation and future returns for both stock and bonds. This implies that when the correlation is rising, the next period return on both assets also rises. We can also note that the magnitude of the response of both assets is markedly different, with stocks responding much stronger to a change in correlation.
Table 2. Predicting regression for stock and bond returns.
| Variable |
Stock Returns |
Bond Returns |
| Panel A: 1900:1–2017:6 |
| Cor. B/S |
1.347 (2.24) |
0.457 (2.01) |
| Panel B: 1920:1–2017:6 (TS and DP) |
| Cor B/S |
1.248 (2.02) |
0.555 (2.17) |
| TS |
0.108 (0.69) |
0.170 (2.67) |
| DP/Δ3-mth TB |
0.098 (0.21) |
–0.269 (–1.33) |
| Panel C: 1920:1–2017:6 (TS and FED) |
| Cor B/S |
1.335 (2.25) |
0.507 (2.18) |
| TS |
0.125 (0.81) |
0.159 (2.58) |
| FED |
0.172 (1.81) |
–0.110 (–3.94) |
| Notes: Entries are the coefficient values (Newey-West t-statistics) for the predictive regression of equation 1. Cor. B/S refers to the five-year moving correlation, TS is the term structure of the 10-year Treasury bond minus the 3-month Treasury bill, DP is the dividend-price ratio, Δ3-mth TB is the change in the 3-month Treasury bill and FED is the equity yield to 10-year Treasury bond ratio. |
There exists a large literature that seeks to predict, in particular, stock returns. Therefore, we include two of the more prominent of these variables in our regression to ensure robustness of the results.4 We include the interest rate term structure and either the log dividend-price (DP) ratio for stocks or the change in the 3-month Treasury bill for bonds. We also consider the FED ratio as an alternative to the DP ratio/change in short-term interest rates. These results are reported in Panels B and C of Table 2 and continue to support a significant and positive predictive effect of the stock and bond return correlation for subsequent stock and bond returns. Again, the response of stock returns to changes in the correlation is greater than that of bond returns and the coefficient values are broadly consistent across the different regression specifications. With respect to the other predictor variables, we can see that the term structure has significant predictive power for bond returns, while the FED model has predictive power for both stock and bond returns, although only at the 10% significance level for the former.
4 See, for example, Campbell and Thompson (2008) and Welch and Goyal (2008).
The above results suggest that the stock and bond return correlation has predictive power for subsequent stock and bond returns. Moreover, while stock returns exhibit a larger response to changes in the correlation (greater coefficient magnitude), the above results suggest that the nature of the relation is the same for stocks and bonds, with both exhibiting a positive relation with the correlation. This suggests that a rising correlation leads to both higher stock and bond returns and equally a falling correlation leads to both lower stock and bond returns. This, however, contrasts with the argument above that under certain circumstances the behaviour of the two assets will diverge. Notably, when the correlation is negative, a flight-to-safety effect will drive stock and bond returns apart. Therefore, we re-consider the above regressions and use the logistic smooth-transition (LSTR) model to capture different regimes of behaviour implied by a positive or negative correlation.
Table 3 reports the results of the LSTR model for stock and bond returns respectively. Examining stock returns, we can see that in the lower regime, when the stock and bond return correlation is below the threshold point given by c, we can observe a negative relation between the correlation and subsequent stock returns. Thus, in this regime, a fall in the correlation, as investors perceive worsening economic conditions, leads to higher expected stock returns (falling current stock prices). In the upper regime, we see the positive relation between the correlation and subsequent stock returns observed in Table 2. For bond returns, we can observe the positive relation in both regimes as expected. Of note, we can see that in the upper regime the slope coefficient is not significant. As indicated in equation 5, this suggests that the nature of the relation between the stock and bond return correlation and subsequent bond returns remains broadly constant over the different regimes. This is consistent with the more mechanical nature of bond return behaviour.
Table 3. LSTR predictive regression for stock and bond returns.
|
Stock Returns |
Bond Returns |
| Panel A: LSTR Model |
| α1 |
–0.023 (–2.67) |
0.011 (3.10) |
| β1 |
–0.066 (–2.43) |
0.021 (2.93) |
| α2 |
0.027 (2.98) |
–0.009 (–2.77) |
| β2 |
0.078 (2.69) |
0.006 (0.55) |
| Γ |
2.790 (2.01) |
5.346 (1.01) |
| C |
–0.084 (–2.73) |
–0.090 (–14.02) |
| Panel B: QLSTR Transition Points |
| c1 |
–0.085 (–2.55) |
–0.091 (10.66) |
| c2 |
0.092 (2.17) |
0.102 (1.85) |
| Notes: For Panel A, entries are the coefficient values (Newey-West t-statistics) for the LSTR (logistic smooth transition) regression of equations 2–3. The explanatory variable is the Cor. B/S (the five-year moving correlation). For Panel B, the entries are the estimated transition points for the QLSTR transition function given in equation 7. |
3.3. Market timing
We argue that the nature of the correlation between stock and bond returns indicates the degree of risk that exists in the market. Such knowledge is useful to investors who could then attempt to time the market and move between the two asset classes as the nature of risk changes. Where a higher positive correlation indicates lower risk, investors may wish to increase their holdings of stocks, while a negative correlation would indicate that investors should seek to increase their holdings of bonds. Therefore, using the QLSTR model, we can estimate threshold values at which investors should switch between assets.
Table 3 reports the two threshold values for the stock and bond returns and indicates broad similarity in their respective positions. We do not report the full set of parameter values, as this exercise is intended only to obtain the threshold points. In utilising these values for the trading rule approach, we use the threshold obtained by the stock return model as this is more indicative of trader behaviour.5
5 As noted with the LSTR results, the bond return equation appears to exhibit linearity, which, given the mechanical nature of the relation between bond prices and yields, is not unexpected.
To establish whether using the stock/bond correlation and the identified thresholds allows for improved market timing, we implement a simple trading strategy based on the idea of a balanced 60/40 portfolio (60% in stocks and 40% in bonds). When the correlation is above the upper threshold we believe that risk is low and thus the portfolio switches to an 80/20 proportion in favour of equity. However, when the correlation falls below the lower threshold, we argue that risk is high and so the portfolio becomes 40% equity and 60% bonds. Between the two thresholds, the investor holds the 60/40 portfolio.
Table 4 presents the results of this exercise and compares holding a base 60/40 portfolio, together with a buy-and-hold stock only and bond only portfolio against the switching portfolio outlined above. The reported entries in the table are the average portfolio excess return and standard deviation as well as the Sharpe ratio. The returns are considered as excess over both a 3-month Treasury bill and a 10-year Treasury bond.6 We also report the results across three time horizons. First, for the full sample and then for samples that start in 1955 and 1990. While, these start dates are essentially arbitrary their choice is motivated by first, the period that begins following the end of World War Ⅱ and the immediate recovery therefrom and second, the period that begins after the deregulation of financial markets that took place primarily during the 1980s.
Table 4. Portfolio switching strategy.
|
Mean |
Std Dev |
Sharpe Ratio |
Mean |
Std Dev |
Sharpe Ratio |
|
Risk-Free = 3-Month TB |
Risk-Free = 10-Year TB |
|
Full Sample |
| Stocks Only |
0.191 |
5.342 |
0.036 |
0.039 |
5.080 |
0.008 |
| Bond Only |
0.138 |
1.913 |
0.072 |
–0.006 |
1.773 |
–0.003 |
| 60/40 |
0.172 |
3.360 |
0.051 |
0.021 |
3.188 |
0.007 |
| Switching |
0.234 |
3.685 |
0.064 |
0.075 |
3.509 |
0.021 |
|
Sample 1955:1–2016:12 |
| Stocks Only |
0.019 |
4.211 |
0.005 |
0.033 |
3.736 |
0.009 |
| Bond Only |
0.123 |
2.169 |
0.057 |
–0.003 |
2.162 |
–0.001 |
| 60/40 |
0.161 |
2.740 |
0.059 |
0.035 |
2.729 |
0.013 |
| Switching |
0.168 |
2.801 |
0.060 |
0.042 |
3.048 |
0.014 |
|
Sample 1990:1–2016:12 |
| Stocks Only |
0.353 |
4.163 |
0.085 |
0.195 |
4.165 |
0.047 |
| Bond Only |
0.285 |
2.111 |
0.135 |
0.127 |
2.120 |
0.060 |
| 60/40 |
0.342 |
2.535 |
0.135 |
0.184 |
2.536 |
0.073 |
| Switching |
0.375 |
2.590 |
0.145 |
0.217 |
2.588 |
0.084 |
| Notes: Entries are the values obtained for the portfolio switching strategies based on the QLSTR transition points. The stocks only portfolio represents a buy-and-hold portfolio for the stock index. The bonds only portfolio represents a buy-and-hold portfolio for the bond index. The 60/40 portfolio represents a buy-and-hold portfolio that contains 60% of the stock index and 40% of the bond index. The switching portfolio holds the proportions of stock and bonds at 80%/20%, 60%/40% and 40%/60% is the five-year moving correlation is above the upper transition point, between the two transition points and below the lower transition point respectively. The Sharpe ratio is calculated as the portfolio return minus the risk-free rate, divided by the portfolio standard deviation. For the risk-free rate we consider both the 3-month Treasury bill and the 10-year Treasury bond. |
6 For an interesting discussion on the risk-free rate, see Damodaran (2008).
Focusing on the Sharpe ratio results, we can observe differences according to whether the short or long term Treasury is used as the risk-free rate and over time (especially for the short-rate). Considering the first column of results, which uses the 3-month Treasury bill as the risk-free rate, over the full sample (1920–2017) we can see that the bond only portfolio performs the best. This is particularly achieved through the much lower variance exhibited by this portfolio. The combined stock and bond portfolios perform second and third best, with the switching portfolio preferred over the constant 60/40 portfolio. The equity portfolio performs worse and this is due to the large variance exhibited by this portfolio. When we consider the sub-sample periods, then the switching stock and bond portfolio now performs the best, while the 60/40 and bond only portfolios achieve similar performance. When considering the results where the 10-year Treasury bond yield acts as the risk-free rate, then the results are more consistent. Over the full sample (1900–2017) as well as the two sub-samples, the switching portfolio outperforms the alternative portfolios. The 60/40 portfolio performs second best across the two sub-samples, and third best over the full sample. While the equity portfolio performs second best over the full sample, otherwise it and the bond portfolio perform relatively poorer than the switching portfolio.
Overall, the results of this exercise suggest that a portfolio that switches its weighting of stocks and bonds outperforms a portfolio that holds a constant weight of the two assets or one that holds only one asset type. Moreover, the switching is determined by the correlation between equity and bond returns, which we believe acts as a proxy for risk. Thus, using available information, we are able to improve portfolio performance by switching towards equities when the stock and bond return correlation is higher, which we define as a low risk period, and towards bonds when the correlation is lower (in fact, negative), which we define as a high risk period. By examining the mean and standard deviation of the different portfolios, we can see that this is achieved through obtaining some of the higher equity return but without being exposed to the much larger variance. For example, in each sample and sub-sample, the switching portfolio achieves the highest excess return but only the second highest standard deviation. Moreover, that standard deviation is closer in value to the non-switching 60/40 portfolio than to the equity only portfolio. Hence, using the stock and bond return correlation allow for successful market timing decisions to be made.
3.4. Bull and bear market prediction
To further consider the ability of the stock and bond return correlation for future market movement, we now examine its ability to predict bull and bear market regimes. We define a bull market as one in which the stock price rises over the subsequent 1, 2 or 3 years and thus, a bear market as one in which the price falls over the same time period. This definition is consistent with Chauvet and Potter (2000) who define bull (bear) markets as those that correspond to periods of increasing (decreasing) market prices. This approach eschews measures based around some (arbitrary) threshold for price rises or falls that fail to take account of market trends.7 This general approach is also consistent with Wu and Lee (2015), while the specific use of a three-year average follows Cooper et al. (2004).
7 For example a common definition in the financial press for a bear market is a decline of 20%, although there is no particular rationale for this value.
Having identified bull and bear periods, we then define an indicator variable equal to one in a bull market period and zero in a bear market period. This allows us to run the following regression using a probit approach:
With It indicating whether the subsequent period will see a bull or bear run and ρsb, t the time-varying stock and bond return correlation.
Table 5 presents the estimation results for equation 8, again we run this regression using just the stock and bond return correlation and then including additional predictor variables. The results in Panel A of Table 5 demonstrate that an increase in the stock and bond return correlation is consistent with a bull market phase occurring over the subsequent one, two and three years. The coefficient is positive and statistically significant over each of the three horizons. Moreover, while the coefficient is of a reasonable magnitude for each horizon, it is noticeably larger for the three-year prediction period. The results, thus, equally confirm that a falling stock and bond return correlation has predictive power for a subsequent bear market period.
Table 5. Probit model for bull/bear stock market.
| Variable |
One Year |
Two Years |
Three Years |
| Panel A: 1900:1–2017:6 |
| Cor. B/S |
0.558 (3.79) |
0.451 (2.90) |
0.927 (5.75) |
| Panel B: 1920:1–2017:6 (TS and DP) |
| Cor B/S |
0.546 (3.37) |
0.391 (2.30) |
0.832 (4.68) |
| TS |
0.169 (4.79) |
0.148 (3.96) |
0.166 (4.29) |
| DP |
0.086 (0.94) |
0.438 (4.53) |
0.633 (6.30) |
| Panel B: 1920:1–2017:6 (TS and FED) |
| Cor B/S |
0.599 (3.90) |
0.616 (3.72) |
1.146 (6.57) |
| TS |
0.170 (4.85) |
0.143 (3.88) |
0.161 (4.24) |
| FED |
5.982 (2.26) |
7.017 (2.39) |
16.092 (4.58) |
| Notes: Entries are the coefficient values (t-statistics) for the probit regression of equation 8. The dependent variable takes the value of one if the stock return over the period indicated in the column header is positive, otherwise equals zero. Cor. B/S refers to the five-year moving correlation, TS is the term structure of the 10-year Treasury bond minus the 3-month Treasury bill, DP is the dividend-price ratio and FED is the equity yield to 10-year Treasury bond ratio. |
Panels B and C of Table 5 include additional predictor variables and continues to demonstrate the positive predictive power of the stock and bond correlation for a bull market phase. The results in these two panels also show that a steepening of the term structure is linked to a subsequent bull market run and likewise a flattening of the term structure leads towards a bear market. The dividend-price ratio has no predictive power for one-year ahead, but does so for two and three-year ahead, market movements. A higher dividend-price ratio can occur through either a higher dividend or lower price and so the positive relation indicates either the prospect of improving economic conditions leading to higher dividends or a turning point in the market following a price fall. Likewise, the FED model, as a ratio of the earnings-price ratio (earnings yield) to the 10-year Treasury bond yield may capture the same influence of higher earnings leading to future price rises or a turning point following a price fall. Moreover, for the FED model, in comparison to the dividend-price ratio, we observe significant predictive power across all three horizons. This improved predictive power arising from the FED model over the dividend-price ratio might arise from the inclusion of the bond yield in the former measure. Notably, it is argued that the bond yield is a good predictor of economic growth, which would help sustain a bull run (e.g., Harvey, 1989).
Overall, the results presented in this section support the view that the stock and bond return correlation contains predictive power for future stock returns and for periods that are characterised as bull and bear markets. Additional predictive power is also reported for the term structure and the FED model.
4. Predicting macroeconomic variables
The changing stock and bond return correlation reflects investor outlook regarding future economic prospects and the expected payoffs to the different assets. Thus, in addition to having predictive power for subsequent asset returns, we also believe that movements in the correlation contain information regarding future economic behaviour. As the correlation between stock and bond returns decreases or turns negative, this indicates that investors expect a downturn in future economic prospects and an increase in macroeconomic risk. Thus, investors move out of equities and into bonds, pushing their prices in different directions. Therefore, we repeat the predictive regressions from Section 3 and instead of modelling stock and bond returns we consider several macroeconomic variables.
In examining the relation with the macroeconomy we consider changes in industrial production, changes in personal consumption, inflation and unemployment. Moreover, we consider these at both the monthly and annual horizons. These variables are chosen as they reflect the strength of the economy and thus may exhibit a relation with the stock and bond return correlation if it captures changes in investor perceptions of future economic conditions and risk. Notably, industrial production is a measure of aggregate output, while changes in consumption may be more affected by changes in investor expectations of future risk as opposed to a broader measure of output. Equally, movements in subsequent inflation and unemployment rates will reflect the strength of the economy.
Table 6 presents the results of regressing subsequent macroeconomic variables on the time-varying stock and bond correlation as well as the additional financial predictor variables. Examining the one-month ahead predictive results, we can observe that the coefficient on the stock and bond return correlation is positive and significant for industrial production, consumption and inflation. Thus, a higher correlation is consistent with strengthening macroeconomic conditions. These results remain robust to the inclusion of additional predictor variables. With regard to the other financial variables, there is limited evidence that a steepening term structure leads to a lower unemployment rate in the next month, while a higher dividend-price ratio predicts higher subsequent consumption growth. For the one-year ahead predictive results, the stock and bond return correlation exhibits a marginal (10%) significance for output growth, with a higher level of significance for both consumption growth and inflation. The term structure has significant predictive power for output growth and unemployment, the dividend-price ratio continues to predict consumption, while the FED model exhibits positive predictive power for output growth.8
Table 6. Predicting macroeconomic variables.
|
Ind. Prod. |
Consumption |
Inflation |
Unemployment |
|
Monthly |
| Panel A: |
1919:1–2017:6 |
1959:1–2017:6 |
1900:1–2017:6 |
1948:1–2017:6 |
| Cor B/S |
0.429 (2.02) |
0.360 (5.47) |
0.281 (2.91) |
0.259 (1.52) |
| Panel B: |
1920:1–2017:6 |
1959:1–2017:6 |
1920:1–2017:6 |
1948:1–2017:6 |
| Cor B/S |
0.572 (2.15) |
0.254 (3.55) |
0.428 (4.20) |
0.315 (1.59) |
| TS |
0.089 (1.25) |
–0.025 (–1.52) |
–0.036 (–1.31) |
–0.198 (–1.84) |
| DP |
–0.173 (–0.80) |
0.195 (3.47) |
–0.149 (–1.80) |
0.844 (1.38) |
| Panel C: |
1920:1–2017:6 |
1959:1–2017:6 |
1920:1–2017:6 |
1948:1–2017:6 |
| Cor B/S |
0.488 (2.10) |
0.387 (4.35) |
0.346 (3.89) |
0.198 (1.37) |
| TS |
0.103 (1.44) |
–0.026 (–1.51) |
–0.030 (–1.05) |
–0.233 (–2.03) |
| FED |
0.073 (1.36) |
0.033 (0.78) |
0.723 (0.35) |
0.016 (0.06) |
|
Annual |
| Panel A: |
1919:1–2017:6 |
1959:1–2017:6 |
1900:1–2017:6 |
1948:1–2017:6 |
| Cor B/S |
4.281 (1.82) |
4.496 (6.32) |
3.695 (3.32) |
–0.189 (–0.91) |
| Panel B: |
1920:1–2017:6 |
1959:1–2017:6 |
1920:1–2017:6 |
1948:1–2017:6 |
| Cor B/S |
3.737 (1.87) |
2.945 (4.18) |
5.432 (4.57) |
–0.342 (–0.92) |
| TS |
2.016 (3.23) |
–0.128 (–0.98) |
–0.156 (–0.57) |
0.512 (3.94) |
| DP |
0.022 (1.23) |
2.787 (5.65) |
–1.646 (–1.95) |
0.595 (1.73) |
| Panel C: |
1920:1–2017:6 |
1959:1–2017:6 |
1920:1–2017:6 |
1948:1–2017:6 |
| Cor B/S |
5.152 (1.88) |
4.858 (5.16) |
4.559 (4.45) |
–0.113 (–0.87) |
| TS |
2.079 (3.35) |
–0.142 (–0.98) |
–0.092 (–0.31) |
0.422 (3.14) |
| FED |
1.144 (2.46) |
0.398 (0.87) |
0.115 (0.58) |
–0.259 (–3.00) |
| Notes: Entries are the coefficient values (Newey-West t-statistics) for the predictive regression of equation (1). IP is the monthly rate of change in industrial production, Cons is the monthly rate of change in personal consumption, Infl is the monthly inflation rate, Une is the monthly rate of change in the unemployment rate. Cor. B/S refers to the five-year moving correlation, TS is the term structure of the 10-year Treasury bond minus the 3-month Treasury bill, DP is the dividend-price ratio and FED is the equity yield to 10-year Treasury bond ratio. |
8 This latter result is consistent with the FED model providing predictive power for a subsequent bull market noted earlier.
The above analysis covers a relatively long period and one that has seen numerous events that will impact upon the macroeconomy, including two world wars and other conflicts, as well as technological advances, oil price and other shocks. Thus, we reconsider the results in Table 6 allowing for a break in the nature of the relations using the test of Quandt-Andrews (Andrews, 1993). Inevitably, other breakpoint tests exist but the main purpose of this exercise is to consider how the nature of the predictive relation may change even allowing for only a single break.
Table 7 reports the results of the macro predictive regressions allowing for a break for the one-month ahead relations. The first row in Table 7 presents the breakpoint tests, which indicate a statistically significant break for all macroeconomic series. For the monthly change in industrial production, we can see that the stock and bond return correlation has a similar coefficient value across the breakpoint and is statistically significant in both regimes. However, we can observe that in the post-break period, the term structure variable now exhibits significant predictive power, indicating that a steeper term structure is consistent with improving macroeconomic conditions. For consumption growth, the stock and bond return correlation remains significant across the breakpoint although we note that the coefficient magnitude declines in the latter period. A similar result is found for inflation, with the stock and bond return correlation significant in both regimes but of a reduced value post-break. In contrast to the full sample results, we now observe the correlation having a significant predictive effect for unemployment after the breakpoint. Elsewhere, the term structure continues to predict unemployment, while the remaining results are broadly consistent with those previously reported.
Table 7. Predicting macroeconomic variables—allowing for a break.
|
Ind. Prod |
Consumption |
Inflation |
Unemployment |
| Panel A: Break Test—Quandt-Andrews |
| No Breaks |
16.40 [1938:5] |
76.72 [1985:09] |
95.65 [1942:10] |
21.02 [2001:5] |
| Panel B: Pre-Break Regression Results |
| Cor B/S |
0.504 (3.53) |
0.830 (4.90) |
10.554 (3.92) |
0.796 (1.11) |
| TS |
0.026 (0.09) |
0.028 (1.10) |
0.845 (1.41) |
–0.205 (–2.33) |
| FED |
–0.383 (–0.82) |
0.178 (1.25) |
2.619 (8.43) |
0.315 (0.25) |
| Panel C: Post-Break Regression Results |
| Cor B/S |
0.489 (2.48) |
0.396 (2.78) |
2.977 (4.54) |
3.694 (4.26) |
| TS |
0.085 (2.27) |
–0.027 (–1.41) |
–0.748 (–3.84) |
–0.205 (–2.08) |
| FED |
0.071 (1.35) |
–0.016 (–0.46) |
–0.207 (–1.10) |
–0.574 (–3.77) |
| Notes: Entries are the coefficient values (Newey-West t-statistics) for the predictive regression of equation 1, allowing for a single break following the test of Quandt and Andrews (Andrews, 1993). IP is the monthly rate of change in industrial production (sample 1920:1–2017:6), Cons is the monthly rate of change in personal consumption (sample 1959:1–2017:6), Infl is the monthly inflation rate (sample 1920:1–2017:6), Une is the monthly rate of change in the unemployment rate (sample 1948:1–2017:6). Cor. B/S refers to the five-year moving correlation, TS is the term structure of the 10-year Treasury bond minus the 3-month Treasury bill, DP is the dividend-price ratio and FED is the equity yield to 10-year Treasury bond ratio. |
4.1. Expansion/contraction prediction
In analysing stock return predictability above, we considered the ability of the stock and bond return correlation to predict bull and bear market regimes. Here, we do the equivalent for output growth and seek to predict expansion and contraction regimes. We define an indicator variable that takes the value of one in a contraction and zero in an expansion period. We define a contraction in several ways in order to ensure a robust result. Specifically, a contraction is defined: First, if the month-to-month industrial production growth rate is negative; second, if the monthly annualised growth rate is negative; third, if two consecutive monthly annualised growth rates are negative; fourth, if the growth rate is negative for two consecutive quarters. We also include the NBER recession dates, although as these dates are determined at a time after the event and not in real time, they have less information content.
Table 8 presents the probit regression models with the indicator dependent variable defined as above and the explanatory variables being the stock and bond return correlation, term structure, dividend-price ratio and the FED model. We observe that for all contraction indicators covering the different time horizons there is a negative predictive relation from the stock and bond return correlation. Thus, a rising correlation is consistent with a declining probability of a contraction. Moreover, this relation remains consistent when including additional predictor variables. With regard to the other predictor variables, a steepening of the term structure leads to a lower probability of a recession, while an increase in the dividend-price ratio (a lower stock price relative to fundamentals) is consistent with a higher subsequent probability of a contraction.
Table 8. Predicting contractions.
|
Monthly |
Monthly Annualised |
Two Months |
Two Quarters |
NBER Dates |
| Panel A: 1919:1–2017:6 |
| Cor B/S |
–0.401 (–2.76) |
–0.511 (–3.29) |
–0.528 (–3.34) |
–0.583 (–3.32) |
–0.425 (–2.16) |
| Panel B: 1920:1–2017:6 |
| Cor B/S |
–0.634 (–4.00) |
–1.056 (–5.71) |
–1.021 (–5.42) |
–0.892 (–4.39) |
–1.047 (–4.82) |
| TS |
–0.089 (–2.60) |
–0.431 (–10.54) |
–0.439 (–10.44) |
–0.272 (–6.24) |
–0.092 (–2.24) |
| DP |
0.334 (3.69) |
0.443 (4.35) |
0.400 (3.84) |
0.316 (2.81) |
1.316 (10.63) |
| Panel C: 1920:1–2017:6 |
| Cor B/S |
–0.431 (–2.94) |
–0.758 (–4.59) |
–0.743 (–4.44) |
–0.675 (–3.72) |
–0.569 (–2.01) |
| TS |
–0.099 (–2.91) |
–0.431 (–10.70) |
–0.439 (–10.56) |
–0.272 (–6.31) |
–0.116 (–3.06) |
| FED |
–1.520 (–0.61) |
0.545 (0.20) |
0.322 (0.11) |
0.957 (0.31) |
0.221 (0.08) |
| Notes: Entries are the coefficient values (t-statistics) for the probit regression of equation 8. The dependent variable takes the value of one if the change in industrial production over the period indicated in the column header is negative, otherwise equals zero. Cor. B/S refers to the five-year moving correlation, TS is the term structure of the 10-year Treasury bond minus the 3-month Treasury bill, DP is the dividend-price ratio and FED is the equity yield to 10-year Treasury bond ratio. |
The results in this section thus confirm our view that the stock and bond return correlation has predictive power for key macroeconomic variables, notably, measures of output. Further, that the correlation also has predictive power for expansionary/contractionary regimes. There is also some evidence that the term structure of interest rates also has predictive power for output and regimes of expansion and contraction.
5. Summary and conclusion
This paper argues that the stock and bond return correlation contains information on investor perceptions of future economic conditions and risk. Such information, in turn, will have predictive power not only for subsequent stock and bond returns but also for macroeconomic performance. We argue that a positive correlation indicates that investors expect the economy to grow, with asset prices rising. In contrast, when macroeconomic risk is heightened the paths followed by stock and bond prices diverge as investors seek the safety of bonds. This flight-to-safety behaviour leads to a negative correlation between the two assets and indicates that future economic conditions will worsen. We test this belief by examining the predictive power of the stock and bond return correlation for subsequent returns of the respective assets as well as a selection of macroeconomic variables.
We generate the time-varying stock and bond return correlation using five-year rolling windows but note that the correlation obtained from a bivariate GARCH model is near identical. We use this time-varying correlation as a predictor variable for subsequent stock and bond returns. Further, we include additional, commonly used, predictor variables to ensure that the results for the correlation are not obtained through an omitted variable problem. In addition to predicting returns, we also consider whether the correlation is able to predict bull and bear stock market regimes. Having examined predictability of the asset returns, we subsequently examine whether similar predictability is found for key macroeconomic variables. Again, we consider the ability of the stock and bond return correlation to predict economic conditions and expansion and contractions regimes.
The results suggest the following key points. The stock and bond return correlation exhibits predictive power for both stock and bond returns and this remains robust to the inclusion of additional predictor variables. Further, by using a non-linear regression model, we demonstrate the switching behaviour for stock returns, between negative and positive values of the correlation. Moreover, we can use the information from a threshold model to generate a market timing strategy that switches between stock and bonds and outperforms alternative buy and hold portfolios. Using a probit model, we also demonstrate that the stock and bond return correlation has predictive power for identifying bull and bear market regimes. In conducting the analysis for macroeconomic variables, we reveal predictive power from the correlation for output and consumption growth and inflation, while such power for unemployment exists only in the latter half of the sample period. The stock and bond return correlation also exhibits predictive power for contractionary periods.
Overall, the results provide economically and statistically significant evidence that the stock and bond return correlation has predictive power for asset returns and macroeconomic variables. The nature of the results supports the view that the correlation acts as a proxy for the markets view of future economic conditions and risk. Thus, the correlation contains information content that is of use to investors, policy-makers and those interested in modelling asset price movement. For example, that the measure could be used as a leading indicator for market and macroeconomic movements.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: