Whole body vibration therapy and cognitive functions: a systematic review

1.   Introduction

Hepatitis is an inflammatory liver disease caused by excessive alcohol consumption, pollutants, drugs, and health issues. Hepatitis B, the most dangerous form, is responsible for 600,000 annual deaths from acute or chronic complications, making it a significant global healthcare issue ^[1]. Hepatitis B virus (HBV) is a DNA virus from the Hepadnaviridae family, first identified in an Australian aborigine. It causes severe liver illnesses, targeting hepatocytes. HBV's unique genomic DNA undergoes a molecular template DNA transformation, generating a viral RNA intermediate and reverse-transcribed back into viral DNA. This stable DNA causes perpetual infection and low recovery rates. The complex HBV life cycle has led to the development of antiviral medicines ^[2]. Chronic HBV infection affects 580,000-2.4 million US citizens, increasing the risk of liver cancer and cirrhosis. 69% of the population, particularly non-US citizens, have the virus, particularly during perinatal periods. Despite successful hepatitis B vaccination, 70% of US residents self-reported not receiving it in 2018. Antiviral medication, tracking, and liver cancer diagnosis can help reduce mortality and morbidity ^[3]. Hepatocellular carcinoma (HCC) and liver cirrhosis are diseases caused by the hepatitis B virus. Prevention is crucial, with the first cancer vaccine being the HBV vaccine. The World Health Organization proposes a 90% vaccination goal to eradicate hepatitis B by 2030, making HCC prevention a key part of medical policy ^[4].

For researchers and policy advisers, mathematical modeling is a critical tool for gathering and assessing data from experiments for medical interventions. It combines data from a variety of sources into a coherent structure, enabling an in-depth examination of challenging issues. The consequences of treatments are simulated by mathematical models, which also offer quantitative forecasts for potential population wellness effects. It has a lengthy history and has developed into a crucial instrument for making decisions in the fight against infectious diseases ^[5,6,7,8]. To forecast HBV transmission dynamics and assess a prolonged period efficacy of China's vaccination initiative, Zhao et al. ^[9] created a mathematical model. By creating wave movement using geometrically distinct perturbation and permitting non-monotone propagating characteristics by numerical simulations, the model developed in ^[10] simulates HBV infection with spatial dependency. Two treatment-related hepatitis C virus (HCV) models were observed by Martin et al. ^[11] who discovered various bifurcation patterns. They computed analytical answers for the medication levels required for disease eradication or control and discovered that reachable levels may culminate in control or extinction over diverse prevalence levels. In ^[12], researchers put out an HBV infection model including vaccine and treatment, evaluating dynamic behavior for uniform controls and applying Pontryagin's maximal concept to solve optimal control concerns. The use of mixed control strategies outperformed independent controls, according to numerical findings. The dynamics of HBV are greatly influenced by surroundings like humidity and environmental temperature. In a study ^[13], An effective approach for identifying these implications is stochastic modeling. A stochastic hepatitis B model that takes into account the transmission coefficient's time delay and the Cytotoxic T cells (CTL) immune response class has been constructed. Wodajo et al. ^[14] developed a nonlinear mathematical model for the kinetics of HBV transmission while taking into account the impacts of immunization, medication, migration, and screening.

Mathematical analysis techniques that use fractional calculus to extend differential equations are referred to as fractional differential equations. They are useful in biological contexts because of their intrinsic affinity for memory-based systems, and they are frequently incorporated into epidemiological models ^{[15,16,17,18,19]}, which makes them an important resource for comprehending complicated systems. In science, especially physics and engineering ^{[20,21,22,23,24]}, fractional calculus is frequently employed. Fractional order models are considered more realistic and practical than traditional ordinal order models due to the use of fractional differential equations to differentiate between distinct mathematical models' hereditary and data storage properties. Two models for hepatitis B were presented by Cardoso et al. ^[25], both of which had their foundations on fractional differential equations. Drug therapy factors were absent from the first model whereas they were included in the second. Both models took stability analysis and reproduction number into account, and numerical simulations utilizing unconventional finite difference methods revealed that the solutions tend to an equilibrium point. Khan et al. ^[26] studied the kinetics of HIV using the Caputo-Fabriizo derivative, utilizing the hypothesis of fixed points to get conclusions on uniqueness, and using the Adams-Bashfirth numerical approach to solve the problem. Using the Atangana-Baleanu derivative in Caputo sense, mathematicians created a new epidemic fractional order model to describe HBV in ^[27]. A two-step Lagrange polynomial-based iterative approach was used to determine the solution after the model's nonnegativity, distinction, reproduction number, and equilibria were assessed. Utilizing the Caputo-Fabrizio fractional derivative with immunological delay, Gao et al. ^[28] presented a mathematical model regarding the HBV. Applying the Laplace transform and fixed point theorem, the model's singularity was established. The iterative solutions' stability was examined using the Sumudu transform and Picard iteration. In the study ^[29], Lévy noise-driven HBV infection is analyzed, taking into account the influence of vaccination on the dynamics of the epidemic. It employs a non-integer order, fractal dimension fractional-order scheme. To examine the stochastic model, the theoretical analysis employs the Lyapunov function. In order to conduct additional research and validate the findings, numerical simulations and correlations with deterministic structures were offered. Several numerical techniques for analyzing fractional differential equations have been suggested during the last few decades, with the finite difference and finite element methods serving as the primary instruments. Meshless or mesh-free approaches have recently emerged for studying science and engineering problems, with the problem area represented as a cloud of distributed points ^[30].

In view of their unique properties, enhanced fractional continuous and discrete operators utilizing Mittag-Leffler kernels are especially interesting as discrete equivalents ^[31,32,33]. Employing an improved Atangana-Baleanu fractional difference operator, Farman et al. ^[34] created a fractional-order representation of Bovine Brucellosis. They evaluated the global stability of the Volterra-type Lyapunov function and applied the Lipschitz criterion to guarantee originality. For numerical simulations and emphasizing the consequences of the illness caused by different causes, solutions were generated in the discrete generalized version ^[35]. They conducted assessment using fixed point approaches, looked at the stability of the solution in the Hyers-Ulam meaning, and applied iterative approaches to get an imprecise answer in series. This paper suggests a rarely discussed fractional order model with discrete generalized Mittag-Leffler kernels for the dynamics of HBV. It will also serve as a basis for numerous dynamical problems including their existence, distinctiveness, and numerical simulations.

2.   Preliminaries

Here are some essential definitions that you may find helpful in system analysis.

Definition 2.1. ^[31,36] Consider the reversed jump operator to be $\Im(t) = t-1$.

● The nabla left fractional sum of order $\sigma > 0$ is defined considering a function $\mathrm{X}:\mathbb{N}_j = \{j, j+1, j+2, ...\}\rightarrow \mathbb{R}$ as

The nabla left fractional difference of order $\sigma > 0$ is defined by

● The nabla left fractional sum of order $\sigma > 0$ is defined considering a function $\mathrm{X}:_p\mathbb{N} = \{p, p-1, p-2, ...\}\rightarrow \mathbb{R}$ as

The nabla left fractional difference of order $\sigma > 0$ is defined by

Definition 2.2. ^[31,37] For $\psi\in\mathbb{R} : |\psi| < 1$, and $\sigma, \upsilon, \gamma\in\mathbb{C}$ with $Re(\sigma) > 0$, the nabla discrete Mittag-leffler function of three parameters is defined as:

For $\gamma = 1$, we can calculate the discrete Mittag-Leffler function of two parameters as

For $\gamma = \upsilon = 1$, the discrete Mittag-Leffler function of one parameter is determined by

Remark 2.1. For, $\psi = -\frac{\sigma}{1-\sigma}$ and $\sigma\in(0, \frac{1}{2})$, the initial values of $\mathrm{E}_{\overline{\sigma}}(\psi, t)$ at $t = 0, 1, 2$, and 3 are as follows, taken from ^[38]:

Overall, it is evident that

Conversely, we have that for each $t = 0, 1, 2, ...$, $\mathrm{E}_{\overline{\sigma}}(\psi, t)$ is monotonically decreasing.

Lemma 2.3. ^[31,37] The discrete Laplace transform $(\curlywedge)$ of a function ${\mathrm{X}}$ defined on $\mathbb{N}_j$ (2.1) can be expressed by

Let $\mathrm{Z}$ be a function also defined on $\mathbb{N}_j$, then the discrete Laplace transform of convolution of ${\mathrm{X}}$ and $\mathrm{Z}$ is given by

Lemma 2.4. ^[31,37] For a function ${\mathrm{X}}$ defined on $\mathbb{N}_j$, the outcome is as stated below.

In general,

Lemma 2.5. ^[31,32,39] Specify a real number as $\sigma$. Then, we have

Lemma 2.6. ^[31,32,39] For $\sigma, \upsilon, \psi, \omega\in\mathbb{C}$ with $Re(\upsilon) > 0$, we have

if $|\psi\omega^{-\sigma}| < 1$ with $Re(\omega) > 0$. Also, we can find

Definition 2.7. ^[31,32,39] Assume that ${\mathrm{X}}$ is defined on $\mathbb{N}_j \bigcap {}_p\mathbb{N}$, $j < p$. Then, for $\psi = -\frac{\sigma}{1-\sigma}$ and $0 < \sigma < \frac{1}{2}$, the left discrete generalized Atangana-Baleanu of the Liouville-Caputo sense fractional difference is given by

where $ab(\sigma) > 0$ with $ab(\sigma)\big|_{0, 1} = 1$ is a normalization function. Additionally, the fractional difference of the Liouville-Caputo type right discrete generalized Atangana-Baleanu is described by

The definition of the left discrete Atangana-Baleanu fractional sum is

Definition 2.8. ^[39] Assume that ${\mathrm{X}}$ is defined on $\mathbb{N}_j \bigcap {}_p\mathbb{N}$, $j < p$. Then, for $\psi = -\frac{\sigma}{1-\sigma}$ and $0 < \sigma < \frac{1}{2}$, the we have

Furthermore, the fractional difference of the right discrete Atangana-Baleanu modified Liouville-Caputo type is provided by

The outcomes listed below can be drawn by generalizing using the approach as for $\sigma\in(0, 1)$.

Definition 2.9. ^[39] Assume that $w\in\mathbb{N}_0$, then for $\psi_{w} = -\frac{\sigma-w}{w+1-\sigma}$ and $\sigma\in(w, w+\frac{1}{2})$, the left discrete modified Atangana-Baleanu of the Liouville-Caputo sense fractional difference of a higher order is given by

Also, the right discrete modified Atangana-Baleanu of the Liouville-Caputo type fractional difference of a higher order is given by

3.   Discrete fractional order HBV model

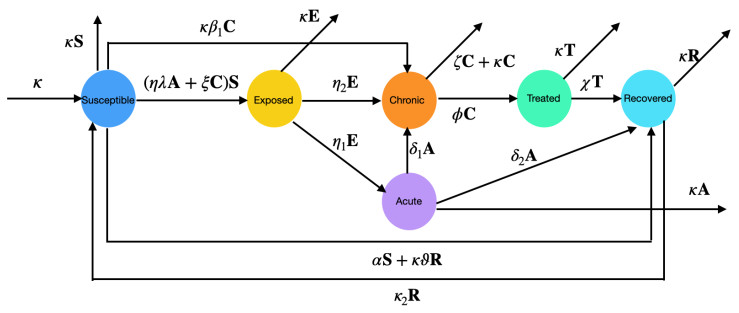
In this section, we look at a SEACTR epidemic model ^[1], which divides the entire population into six time-associated classes according to the form of HBV disease:

● Susceptible class $({\mathbf{S}})$: A susceptible individual is one who lacks immunization or has compromised immunity, permitting the virus to penetrate into the body and get into tissues, replicate, and trigger a reaction, potentially leading to HBV infection if subjected to transmission techniques.

● Exposed class $({\mathbf{E}})$: Individuals who have contracted infection but are yet to become contagious are classified as exposed.

● Acute infective class $({\mathbf{A}})$: Acute infective pertains to people who have been hosts of microorganisms for no longer than six months and who are actively spreading or transmitting HBV or who have the ability of doing so.

● Chronic infective class $({\mathbf{C}})$: Chronic infectious ailments are caused by HBV that continue to exist after a first infection, frequently leading to recurring or chronic illnesses that affect people who seem healthy but are actually harboring infections.

● Treated class $({\mathbf{T}})$: People who receive lamivudine, tenofovir, and various other therapies after developing a chronic infection are believed to be in the treated class.

● Recovered class $({\mathbf{R}})$: People in the recovered class have either had successful medical treatment or have recovered naturally.

Mathematical models with fractional derivatives provide more flexibility when analyzing memory effects and illness dynamics on particular datasets. Hence, the new fractional-order HBV model is developed using the nonlinear fractional differential equations listed below under the left discrete modified Atangana-Baleanu of the Liouville-Caputo type fractional derivative with $0 < \sigma < \frac{1}{2}$.

with nonnegative initial constraints,

Susceptible group increases with the arrival of birth flux rate $\kappa-\kappa\beta_1{\mathbf{C}}-\kappa\vartheta{\mathbf{R}}$. The natural birth/death rate is expressed as $\kappa$. For the purpose of vertical transmission, we suppose that a certain percentage, $\beta_1$, of newborns from infected classes are infected. This percentage is represented by the term $\kappa\beta_1{\mathbf{C}}, \; (\beta < 1)$. Where $\vartheta, \; (\vartheta < 1)$, is used to indicate that a certain percentage of newborns from the recovered class are immunized. Immune response degradation rate of the recovered class is represented by $\kappa_2$. The phrase $\eta\lambda({\mathbf{A}}+\xi{\mathbf{C}}){\mathbf{S}}$ is used to describe the force of HBV infection, where $\eta$ is the per capita interaction rate, $\lambda$ is the likelihood of contracting HBV infection from a single infected person, and $\xi$ is the contamination level of the chronic infected group $({\mathbf{C}})$. The rate of immunization causes proportions of susceptible people to transfer to recovered classes at a rate of $\alpha$. The rate at which susceptible people become chronic HBV carriers is termed $\eta_1$. The rate of transmission from exposed to acutely infected persons is defined as $\eta_2$. $\delta_1$ represents the rate at people gradually become chronic HBV carriers and $\delta_2$ represents the rate at which people who are acutely which infected recover from the disease naturally. The rate of chronically infected people seeking treatment is $\phi$, the rate of HBV disease-related deaths is $\zeta$, and the rate of treatment class recovery is $\chi$. It is also assumed that the number of newborn carriers is less than the total number of carriers who will die and those who will move from carriers to recovery states. We illustrate it in Figure 1.

4.   Qualitative analysis of proposed model

4.1.   Well-posedness

Here we investigate the circumstances that, under the assumption that real-world conditions with pertinent values are present, ensure that the solutions of the proposed model are positive. For this purpose, we find

for all ${t\geq 0}$.

We specify norm for the class ${\mathbf{S}}$:

We can conclude that

The positively invariant set of a dynamical system is defined as one in which the system always stays in the set after emitting from it. We construct a positively invariant region that is closed curve-bounded and encircles the origin.

Theorem 4.1. In straightforward settings, the suggested model (3.1)'s solution is singular and constrained to $\mathbb{R}_{+}^{6}$.

Proof. We shall demonstrate the system (3.1)'s positive solution, and the outcomes are given as follows:

The solution cannot evacuate the hyperplane if $({\mathbf{S}}_0, {\mathbf{E}}_0, {\mathbf{A}}_0, {\mathbf{C}}_0, {\mathbf{T}}_0, {\mathbf{R}}_0) \in \mathbb{R}_{+}^{5}$. The domain $\mathbb{R}_{+}^{6}$ is a positivity invariant set. The following total population is obtained by summing each part of the model (3.1)'s population:

Therefore, a solution of the fractional model (3.1) exists in $\mathfrak{M}$ for all $t > 0$. As such, the suggested HBV model is mathematically and epidemiologically well-posed. Therefore, it is sufficient to examine the fundamental model's dynamics in the feasible region:

□

4.2.   Equilibrium points

The following total population is obtained by summing each part of the model (3.1)'s population:

We can write

Hence, our proposed system reduces to

We employ ${\mathbf{E}} = {\mathbf{A}} = {\mathbf{C}} = 0$ to get the HBV-free equilibrium point $(\mathfrak{E}^{\diamond})$ of system (4.10). We obtain

The system (4.10)'s endemic equilibrium point is indicated by $\mathfrak{E}^{\bullet}$:

where,

4.3.   Reproductive number

It is well recognized that a disease's ability to spread or remain within a community is based on its basic reproductive number. Utilizing the next generation matrix approach on (4.10), we get the reproductive number $(\mathscr{R}_0)$. where

In fact, the HBV will die out, and there will be no epidemic when $\mathscr{R}_0 < 1$. In the meantime, an epidemic will develop if $\mathscr{R}_0 > 1$. Furthermore, the $\mathscr{R}_0$ value shows how contagious the HBV disease is.

4.4.   Sensitivity indices of reproductive $(\mathscr{R})'s$ parameters

It is possible to reduce or regulate the incidence and prevalence of HBV if the key effects of each parameter in the dynamics of the illness are taken into account. It investigates the impact of each parameter on the fundamental reproduction number $\mathscr{R}$. The sensitivity indices for each parameter are listed in the table below (see Table 1).

4.5.   Stability analysis

Systems and control theory heavily relies on the stability analysis of equilibrium points, which are defined by the Lyapunov function. It facilitates the evaluation of equilibrium points' asymptotic stability in both linear and nonlinear systems without the need to explicitly calculate the differential equation's solution. The asymptotic stability of a scalar positive definite function with a negative definite time derivative is known. For identifying infection stages and creating disease management plans, the global stability study of epidemiological algorithms is essential. In terms of disease prevention, the Volterra-Lyapunov matrix theory has become more popular. In order to investigate the global stability of the proposed system, this study compares the stability of risk endemic equilibrium with disease-free equilibrium globally.

Lemma 4.1. ^[40] Let $\mathcal{U}(t)\in\mathbb{R}^{+}$ be a continuous function such that

$\mathcal{U}^{*}\in\mathbb{R}^{+}, \forall \sigma\in(0, \frac{1}{2})$.

Theorem 4.2. The HBV-free equilibrium states $(\mathfrak{E}^{\diamond})$ are globally asymptotically stable provided the reproductive number $(\mathscr{R})$ is less than 1.

Proof. Define a Volterra-type Lyaponuv function $(\mathcal{V})$ by

Using Lemma 4.1, we get

When we substitute the derivative values from (4.10), we discover

Let ${\mathbf{S}} = {\mathbf{S}}-{\mathbf{S}}^{\diamond}$, ${\mathbf{E}} = {\mathbf{E}}-{\mathbf{E}}^{\diamond}$, ${\mathbf{A}} = {\mathbf{A}}-{\mathbf{A}}^{\diamond}$, ${\mathbf{C}} = {\mathbf{C}}-{\mathbf{C}}^{\diamond}$, and ${\mathbf{T}} = {\mathbf{T}}-{\mathbf{T}}^{\diamond}$, then we find

As we can see, for

and ${}_{a}^{MABC}\nabla^{\sigma}\mathcal{V} = 0$ only when

Thus, we draw the conclusion that global asymptotically stable HBV-free equilibrium states $(\mathfrak{E}^{\diamond})$ exist. □

For the endemic Lyapunov function, we assign all independent variables to the suggested model.

Theorem 4.3. The endemic equilibrium points $(\mathfrak{E}^{\bullet})$ are globally asymptotically stable if the calculation of reproduction number $(\mathscr{R}_0)$ is greater than 1.

Proof. Define a Volterra-type Lyaponuv function $(\mathcal{X})$ by

where $\rho_i, \; i = 1, 2, 3, 4, 5, 6$ are future-selectable positive constants. Using Lemma 4.1 and the Eq (4.19) to replace system (4.10), we discover

Substituting the related derivative values from (4.10), we get

Let ${\mathbf{S}} = {\mathbf{S}}-{\mathbf{S}}^{\bullet}$, ${\mathbf{E}} = {\mathbf{E}}-{\mathbf{E}}^{\bullet}$, ${\mathbf{A}} = {\mathbf{A}}-{\mathbf{A}}^{\bullet}$, ${\mathbf{C}} = {\mathbf{C}}-{\mathbf{C}}^{\bullet}$, and ${\mathbf{T}} = {\mathbf{T}}-{\mathbf{T}}^{\bullet}$, then we have

Let ${\rho}_1 = {\rho}_2 = {\rho}_3 = {\rho}_4 = {\rho}_5 = 1$ and after simplifying above, we can express

where

We notice that for $\mathscr{R}_0 > 1$

and when we let ${\mathbf{S}} = {\mathbf{S}}^{\bullet}$, ${\mathbf{E}} = {\mathbf{E}}^{\bullet}$, ${\mathbf{A}} = {\mathbf{A}}^{\bullet}$, ${\mathbf{C}} = {\mathbf{C}}^{\bullet}$, and ${\mathbf{T}} = {\mathbf{T}}^{\bullet}$, then

The system (4.10) is therefore determined to be globally asymptotically stable. □

4.6.   Existence and uniqueness

The presence and uniqueness of the solution are demonstrated in this part by illustrating that the underlying coefficients of the proposed system fulfill the Lipschitz and linear growth requirements.

Consider $\mathfrak{Q} = (\mathfrak{Q}_1, \mathfrak{Q}_2, \mathfrak{Q}_3, \mathfrak{Q}_4, \mathfrak{Q}_5, \mathfrak{Q}_6)$ such that

Let $\mathsf{G} = ({\mathbf{S}}, {\mathbf{E}}, {\mathbf{A}}, {\mathbf{C}}, {\mathbf{T}}, {\mathbf{R}})\in \mathcal{W}$, where $\mathcal{W} = [\mathrm{C}([0, \mathbb{T}], \mathbb{R}_{+})]^6$ is a Banach space built with the norm:

It is evident that $\mathfrak{Q}\in[0, \mathbb{T}]\times \mathcal{W}]^6$ is continuous. Also

To prove the existence and originality of the solution, we must verify the subsequent theorem.

Theorem 4.4. Suppose that there exist positive constants, $\mathfrak{P}_{i}$, $\mho_{i}$, (i = 1, 2, 3, 4, 5, 6) such that

● $|\mathfrak{Q}_{i}(\mathsf{G}, t)|^{2} \leq \mathfrak{P}_{i}(1+|\mathsf{G}|^2) \ \ \ \, \ \ \ \ \ \forall (\mathsf{G}, t)\in \mathbb{R}^{6}\times [0, \mathbb{T}].$

● $|\mathfrak{Q}_{i}(\mathsf{G}_1, t)-\mathfrak{Q}_{i}(\mathsf{G}_2, t)|^2 \leq \mho_{i}|\mathsf{G}_1-\mathsf{G}_2|^2.$

Proof. With linear growth, we start.

Thus, the function satisfies the criteria for growth. We'll now assess the Lipschitz scenario. We have

Here

The solution to our system (3.1) therefore exists and is particularly given the specific conditions.

□

5.   Analysis of proposed model with discrete Atangana-Baleanu, and modified Atangana-Baleanu operators

5.1.   $\chi$-monotonicity investigations

We implement $\sigma$-monotonicity study for the discrete nabla fractional operators in this part. First, as mentioned in ^[39], we review the definitions of $\sigma$-monotones for each $0 \in(0, 1]$ and a function $\wp:\mathbb{N}_j\rightarrow \mathbb{R}$ fulfilling $\wp(j) = 0$.

● $\wp$ is referred to as a $\sigma$-monotone rising function on $\mathbb{N}_j$ in the following case

● $\wp$ is referred to as a $\sigma$-monotone falling function on $\mathbb{N}_j$ in the following case

● On $\mathbb{N}_j$, the function $\wp$ is referred to as a $\sigma$-monotone extremely rising function if

● On $\mathbb{N}_j$, the function $\wp$ is referred to as a $\sigma$-monotone extremely falling function if

Remark 5.1. It is evident that for $\sigma\in(0, 1]$, if $\wp(h)$ is rising or falling on $\mathbb{N}_j$, then we have

or

This indicates that on $\mathbb{N}_j$, $\wp(h)$ is either $\sigma$-monotone rising or falling.

Theorem 5.1. Assume that $\sigma\in(0, \frac{1}{2})$. When functions $\{{\mathbf{S}}, {\mathbf{E}}, {\mathbf{A}}, {\mathbf{C}}, {\mathbf{T}}, {\mathbf{R}}\}:\mathbb{N}_j\rightarrow \mathbb{R}$ fulfill

$\forall t\in\mathbb{N}_{j+1}$, then ${\mathbf{S}}(t), {\mathbf{E}}(t), {\mathbf{A}}(t), {\mathbf{C}}(t), {\mathbf{T}}(t), {\mathbf{R}}(t) > 0$. Moreover, on $\mathbb{N}_j$, ${\mathbf{S}}, {\mathbf{E}}, {\mathbf{A}}, {\mathbf{C}}, {\mathbf{T}}, {\mathbf{R}}$ are $\chi^2$-monotone rising functions.

Proof. From Definition 2.7 and Remark 2.1, we have $\forall t\in\mathbb{N}_j$

Using function ${\mathbf{S}}$, we determine

With the knowledge we have $\frac{ab(\sigma)}{1-\sigma} > 0$ and ${}_j^{ab}\nabla^{\sigma}[{{\mathbf{S}}}(t)]\geq 0$, we can write

Strong induction is used to show that ${\mathbf{S}}(t) > 0$ for each $t\in\mathbb{N}_{j}$. Since ${\mathbf{S}}(j) > 0$ is the underlying assumption, if we further assume that ${\mathbf{S}}(t) > 0$ for each $t\in\mathbb{N}_{j}^{\omega} = \{j, j + 1, ..., \omega\}$, then for some $\omega\in\mathbb{N}_{j}$, we can deduce from Eq (5.11) that

It follows from Remark 2.1 that

Therefore, as required, we draw the conclusion that ${\mathbf{S}}(t) > 0$ for $t\in\mathbb{N}_{j}$.

We rewrite Eq (5.11) as follows in order to demonstrate the $\chi^2$-monotonicity of ${\mathbf{S}}$:

for each $t\in\mathbb{N}_{j+1}$. For every $t\in\mathbb{N}_{j}$, it is demonstrated that ${\mathbf{S}}(t) > 0$. Additionally, from Remark 2.1, we know that $\mathrm{E}_{\overline\sigma}(\psi, t)$ is monotonically decreasing for every $t = 0, 1, ...$ Consequently, Eq (5.14) indicates that

This proves $\chi^2$-monotone increasing of ${\mathbf{S}}$ on $\mathbb{N}_j$. Likewise, we can demonstrate it for ${\mathbf{E}}$, ${\mathbf{A}}$, ${\mathbf{C}}$, ${\mathbf{T}}$, and ${\mathbf{R}}$. □

Remark 5.2. We can infer that ${\mathbf{S}}, {\mathbf{E}}, {\mathbf{A}}, {\mathbf{C}}, {\mathbf{T}}, {\mathbf{R}}$ are $\chi^2$-monotone strictly increasing on $\mathbb{N}_j$ by limiting the conditions in Theorem (5.1) and ${\mathbf{S}}(j), {\mathbf{E}}(j), {\mathbf{A}}(j), {\mathbf{C}}(j), {\mathbf{T}}(j), {\mathbf{R}}(j) > 0$, ${}_j^{abc}\nabla^{\sigma}{\mathbf{S}}(t) > 0$, ${}_j^{abc}\nabla^{\sigma}{\mathbf{E}}(t) > 0$, ${}_j^{abc}\nabla^{\sigma}{\mathbf{A}}(t) > 0$, ${}_j^{abc}\nabla^{\sigma}{\mathbf{C}}(t) > 0$, ${}_j^{abc}\nabla^{\sigma}{\mathbf{T}}(t) > 0$, and ${}_j^{abc}\nabla^{\sigma}{\mathbf{R}}(t) > 0$ for each $t\in\mathbb{N}_{j+1}$.

Theorem 5.2. Let ${\mathbf{S}}, {\mathbf{E}}, {\mathbf{A}}, {\mathbf{C}}, {\mathbf{T}}, {\mathbf{R}}$ be defined on $\mathbb{N}_j$ and increasing on $\mathbb{N}_{j+1}$ with ${\mathbf{S}}(j) = {\mathbf{E}}(j) = {\mathbf{A}}(j) = {\mathbf{C}}(j) = {\mathbf{T}}(j) = {\mathbf{R}}(j) = 0$. For $\sigma\in(0, \frac{1}{2})$, we thus have

Proof. Using Theorem 5.1, we have

By applying Remark 2.1 and raising ${\mathbf{S}}$ on $\mathbb{N}_{j+1}$, it is evident that

This yields

Given that ${\mathbf{S}}$ increases on $\mathbb{N}_{j+1}$ and ${\mathbf{S}}(j) = 0$, we can infer

This implies that

The outcome is therefore proved. We may also prove it for the other compartments in our suggested model. □

Remark 5.3. By equivalent requirements with their accompanying difference operators, the approach outlined above may also be utilized to get all of the aforementioned outcomes for decreasing (or strictly decreasing) functions.

5.2.   Discrete modifications of the discrete Atangana-Baleanu derivative of the Liouville-Caputo-type

Theorem 5.3. ^[38] For $\sigma\in(0, \frac{1}{2})$, the following results hold true:

and

for $t\in\mathrm{N}_{j+1}$.

Proof. Define the following $\forall t\in\mathrm{N}_{j+1}$:

Taking discrete Laplace transform $\curlywedge_j$ on both sides of first equation of (5.24) and utilizing Lemma (2.4), we have

Solving for ${\mathbf{S}}(\omega)$, we have

It follows from ^[38] that

Taking discrete inverse Laplace transform on both sides of (5.27), we have

Also, we can find

The first portion of the theorem is satisfied.

Now let $\forall t\in\mathrm{N}_{j+1}$

Applying discrete Laplace transform $\curlywedge_j$ on ${}_j^{mabc}\nabla^{\sigma}\Upsilon_1$, we get

From (5.26) and (5.27), we have

Also, from (2.19), we find

Equation (5.32) becomes:

Taking inverse Laplace transform on both sides of (5.35), we find

and, also,

In view of Eq (5.30), the second portion of the theorem is satisfied. □

Theorem 5.2. ^[38] The following outcome offers a different series representation of the discrete modified Atangana-Baleanu of the Liouville-Caputo-type fractional difference for $\sigma\in(0, \frac{1}{2})$, which is:

for $t\in\mathrm{N}_{a+1}$.

Proof. From Definitions 2.2 and 2.8, we have

We can demonstrate it for all of the compartments in our suggested system by means of the same approach. □

6.   Solution of proposed system

Our suggested system can be expressed as

From Theorem 5.2, we obtain

7.   Conclusions

Discrete generalized Mittag-Leffler kernels were used in this study to develop a fractional-order model of the HBV epidemic. It addressed the existence and uniqueness of solutions, the positively invariant region, equilibrium states analysis, the fundamental reproduction number, and positivity and boundedness of solutions. A lyapunov function was also used to investigate the global asymptotic stability of the model. The variables that responded the best to the fundamental reproduction number underwent sensitivity analysis. To minimize the number of variables and streamline the issue for optimization, monotonicity analysis is utilized. In specific time scale domains, the study demonstrated that the proposed discrete fractional operators will exhibit $\chi^2$-increasing or decreasing behavior, allowing for effective control of HBV, based on their fundamental features and $\chi$-monotonicity descriptions. The study proposes that the dynamics of hepatitis B in society could be monitored through numerical simulations. The two factors that most inhibit the spread of the disease are vaccination and treatment rates. Raising these rates for both chronically ill patients and newborns is a highly efficient way to halt the spread of HBV. Vaccination, efficient treatment, and stopping the virus's spread all work together to make infection elimination conceivable as well as even possible. Integer-order models lack memory and hereditary properties, while fractional-order models possess these properties. Fractional-order models offer more freedom in derivative order, allowing for more exploration of disease dynamics and memory effects on specific datasets, unlike integer-order models. The proposed model enhances the prediction capacity for the hepatitis B virus in this regard. Policymakers and public health professionals may find the results useful in stopping the spread of hepatitis B. The authors advise more research on the suggested model using a variety of mathematical approaches, such as topological degree theory and upper-lower solution methods, as well as a study of its numerical solution using a variety of numerical techniques.

Author contributions

M. Farman: Conceptualization, Formal analysis, Writing-original draft, Writing review editing; A. Akgül: Conceptualization, Software, Visualization, Writing original draft; J. A. Conejero: Formal analysis, Supervision, Writing-original draft, Writing-review, editing; A. Shehzade: Formal analysis, Writing-original draft, Visualization, Writing-review editing; K. S. Sooppy: Formal analysis, Software, Formatting, Writing review, editing; D. Baleanu: Methodology, Formal analysis, Visualization. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

Prof. J. A. Conejero is the Guest Editor of special issue "Advances in Dynamical Systems and Applications" for AIMS Mathematics. He was not involved in the editorial review and the decision to publish this article. The authors declare no conflict of interest.