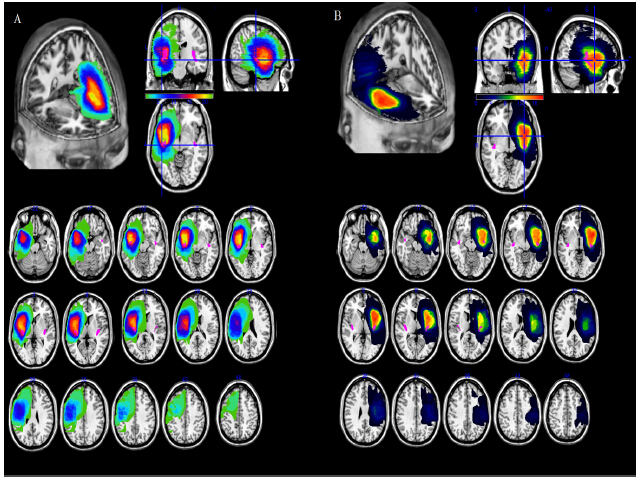
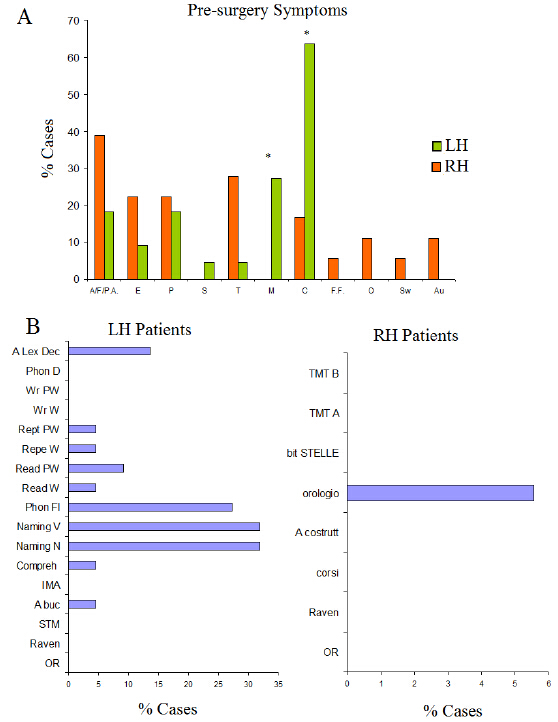
In the present study we investigated the effects of lesions affecting mainly the anterior insula in a series of 22 patients with lesions in the left hemisphere (LH), and 18 patients with lesions involving the right hemisphere (RH). The site of the lesion was established by performing an overlap of the probabilistic cytoarchitectonic maps of the posterior insula. Here we report the patients’ neuropsychological profile and an analysis of their pre-surgical symptoms. We found that pre-operatory symptoms significantly differed in patients depending on whether the lesion affected the right or left insula and a strict parallelism between the patterns emerged in the pre-surgery symptoms analysis, and the patients’ cognitive profile. In particular, we found that LH patients showed cognitive deficits. By contrast, the RH patients, with the exception of one case showing an impaired performance at the visuo-spatial planning test were within the normal range in performing all the tests. In addition, a sub-group of patients underwent to the post-surgery follow-up examination.
1.
Introduction
Many researchers from a variety of fields have focused their efforts on modeling dynamic systems related to growth phenomena. Traditionally, the models used for these purposes have been deterministic, and obtained by means of ordinary differential equations. Among such models, those associated with sigmoidal growth curves stand out: they display slow growth at the beginning, followed by a fast (exponential) growth that slows down gradually until reaching an equilibrium value (usually named carrying capacity or level of saturation). The classic Malthusian, logistic, and Gompertz models gave way to others, amongst which we can mention the Von Bertalanffy, Richards, monomolecular, Blumberg, double sigmoidal, etc., each of which shows some particularity that make them more suitable to study certain growth patterns. Tsoularis and Wallace [1] reviewed these models and proposed a generalization of the logistic curve that assimilates them as particular cases.
The literature on this subject abounds, fruit of the great diversity of fields of application where these models have been used. We may mention, among others, studies concerning phytophenology [2], animal growth [3], and applications in biomedicine: infectious diseases type H1N1 [4], muscle fatigue studies [5], as well as tumor growth [6], and modeling of cancer radiovirotherapy [7]. Another field of interest is the modeling of the exploitation of energy resources [8,9]. All these works include, in turn, numerous references to other application fields.
Today, the need to model growth phenomena has led to two lines of research on the rise: the generalization of classic models and the introduction of new ones. Koya and Goshu [10,11] presented a model that includes the most commonly used classical ways to model biological growth as a particular case; Burger et al. [12] proposed generalizations of the logistic and Gompertz models and applied them to the study of epidemic outbreaks. Tabatabai et al. [13] introduced the hyperbolastic curves, which have proved to be very useful in the study of the evolution of tumor processes and stem cell growth [15]. These models have been the starting point for the development of others, such as the oscillabolastic and T-type models (see [16,17]).
The Weibull curve has been another widely-studied growth curve. Its origins are to be found in the probability distribution of the same name, described in detail by Waloddi Weibull in 1951 [18], although it was previously considered by Fréchet and applied by Rosin and Rammler [19] to describe the distribution of the sizes of certain particles. Its applications are numerous in fields such as Survival Analysis, Engineering and, more currently, in the Theory of Extreme Values.
Like other sigmoidal curves, Weibull's can be obtained from the distribution function of a continuous random variable [20]. This allowed it to be considered as suitable to model growth phenomena in various fields in addition to those previously mentioned. Among others, applications were made to Forestry [21] and population growth [22,23]. In [24] the authors considered the Weibull curve as an extension of the Gompertz model, which also opens up the possibility of using it in fields such as cell proliferation and tumor growth. Along the same line we find the hyperbolastic curve of type Ⅲ, which was introduced in [13] from a generalization of the differential equation that generates the Weibull curve. Also, the need to adjust real data has made essential the development of specific software such as the R-package growth models [25].
Nevertheless, the models mentioned above are deterministic and do not include other information apart from that provided by the variable under study. Including the fluctuations or perturbations that could exist in the system led to the consideration of stochastic differential equations, whose solution are stochastic diffusion processes. Feller was the first author to do so, circumscribing it to the logistic field despite the fact that no expression of the probability transition functions could be obtained in closed-form for the resulting process. Later, other logistic processes were constructed by changing the volatility term of the stochastic differential equation [26].
Among all the diffusion processes obtained from this methodology, those associated with the Gompertz model have been the most widely studied. One of the first formulations of this process can be found in [27]. The fact that this process is especially useful for modeling the evolution of tumors and cell proliferation in general, has made it the object of deep study. This has led to numerous modifications aimed at adapting the model to different tumor cell evolution patterns (see, for instance, [28,29,30,31,32] and references therein).
Other models, such as the one associated with the Bertalanffy curve, have been similarly treated [33]. However, not all the previous diffusion processes verify that their mean function is a growth curve of the same type as the one associated with the starting deterministic model. For this reason, some authors have focused their efforts on obtaining diffusion processes whose mean function is a specific growth curve, which is useful in real applications in which a certain growing pattern is observed. Along this line we may mention the works [34,35,36], focused on the Bertalanffy, logistic and Richards curves respectively, and more recently [37,38] whose goals are the hyperbolastic type-Ⅰ and the multi-sigmoidal Gompertz curves, respectively.
The main goal of the present paper is to develop a new diffusion process whose mean function results in a Weibull-type curve, and its structure is as follows: In Section 2 a wide family of Weibull-type functions is introduced from the generalization of the ordinary differential equation satisfied by the classical Weibull curve. The properties of the curves so defined allow extending the deterministic model to a stochastic one by including a white noise in the ordinary differential equation that originates these curves. This is the objective of Section 3. In Section 4, the hyperbolastic type-Ⅲ diffusion process is introduced as a particular case of the one previously introduced, with its mean function being a hyperbolastic type-Ⅲ function of the type introduced in [13]. Due to the usefulness of such a function for the description of important growth phenomena, a detailed study is carried out on the estimation of the process parameters. The rest of Section 4 deals with this study, with an emphasis on obtaining initial solutions for the resolution of the system of likelihood equations that are obtained. Finally, in Section 5, some simulation examples are considered, whereas Section 6 provides an application to a real case in the context of the qPCR (Quantitative Polymerase Chain Reaction).
2.
A generalization of the Weibull model
Let $ g_{\boldsymbol{\nu}} $ be an integrable real function verifying $ \int^t g_{\boldsymbol{\nu}}(u)du \to +\infty $ as $ t\to +\infty $, where $ \boldsymbol{\nu}\in\mathbb{R}^q $ denotes a $ q $-dimensional real parametric vector. On the basis of this function, we consider the following generalization of the Weibull curve
This curve satisfies the following ordinary linear differential equation of the Malthusian type
where
for $ \varepsilon_{\boldsymbol{\nu}}(t) = e^{-\int^t g_{\boldsymbol{\nu}}(u)du} $.
Taking into account (2.1), equation (2.2) can also be expressed as
which is a generalization of the linear differential equation verified by the Weibull distribution function.
If we consider the initial condition $ f_{\boldsymbol{\nu}}(t_0) = f_0 > 0 $, solving both equations leads to two expressions of the curve (2.1). Concretely, the solution of (2.2) is
where $ \eta = \frac{k}{\alpha} > 0 $, while the solution of (2.4) is
Both expressions can be understood as generalizations of the classic Weibull curve, depending on function $ g_{\boldsymbol{\nu}} $. The main difference between them is the limit value of the system under study, usually called carrying capacity. For curve (2.1) this value depends on the value of the population under study at the initial instant of observation, specifically
whereas for (2.6) this limit is equal to $ k $, and therefore independent on initial value $ f_0 $. This allows us to choose the most appropriate expression depending on the context. For instance, when every path has a particular initial and limit value, despite showing a common Weibull growth pattern, (2.5) would be more adequate. In the present work, we will presume that the carrying capacity depends on the initial values, and therefore this last model will be considered.
Since these models are considered in the context of growth phenomena, we will assume that (2.5) takes positive values. This, together with (2.7), leads to $ \eta > \varepsilon_{\boldsymbol{\nu}}(t) $, $ \forall t\geq t_0 $. As for the inflection points, the candidates will be the solutions of $ \frac{d^2 f_{\boldsymbol{\nu}}(t)}{dt^2} = 0 $, for which we must solve the equation
Note that the classic Weibull curve is a particular case of the one presented here considering $ g_{\boldsymbol{\nu}}(t) = \beta \gamma t^{\gamma-1} $. Other selections of such function lead to different curves, some of which are widely used today. That is the case of the hyperbolastic curve of type Ⅲ, obtained by taking
This curve was introduced in 2005 by Tabatabai et al. [13] to solve the problems found when using classic models, such as logistic, Bertalanffy, or Gompertz, in the study of tumor growth. One of its main features is its increased flexibility, thanks to which data can be adjusted with different evolution patterns to those considered by classic models. It has been successfully applied to several fields. For example, in [13] it was applied to data from the polio epidemic in EEUU (1949) and from multicellular tumor spheroids; in [14] it was used to model the growth of solid Ehrlich carcinoma under a variety of treatments; whereas in [15] it was considered as a mathematical model for studying stem cell proliferation. Note that this curve approaches the Weibull one when $ \theta $ vanishes (in fact, parameter $ \theta $ determines the distance from this model to the Weibull curve).
As we stated before, the inflection time instants are determined by solving equation (2.8). Usually, this type of curve presents a single inflection point, but there are several phenomena in which the maximum level of growth is reached after successive stages, in each of which there is a deceleration followed by an exponential explosion. Consequently, multi-sigmoidal models must be taken into account. Considering the Weibull growth pattern, this can be achieved by taking $ g_{\boldsymbol{\nu}}(t) = \sum_{k = 1}^p \nu_k t^k $ being a polynomial of order $ p $ with real coefficients $ \boldsymbol{\nu} = \left(\nu_1, \dots, \nu_p \right)^T $ and $ \nu_p > 0 $. Then, curve (2.5) becomes a multi-sigmoidal Weibull curve of the form
where $ \omega_k = -\frac{\nu_{k-1}}{k} $, $ k = 1, \ldots, p+1 $. Recent developments in multi-sigmoidal Gompertz functions with random noise can be seen in [38].
3.
The generalized Weibull diffusion process
This section introduces a diffusion process whose mean function is the generalized Weibull curve described in the previous section. We start by observing how curve (2.5) verifies the differential equation of type (2.2). This ensures that the growth phenomenon represented by the curve can be modeled by a non-homogeneous lognormal diffusion process with such a mean function. Several studies have modeled similar growth phenomena (see, for instance [35,36,37]) and obtained diffusion processes whose mean functions are specific growth curves.
Following Román-Román et al. [39], where a general study of the non-homogeneous lognormal diffusion process is carried out, we define the generalized Weibull diffusion process, $ \{X(t); t\in I\} $, as the process solution of the stochastic differential equation
where $ I = [t_0, +\infty) $ is a real interval ($ t_0 \geq 0 $), $ \boldsymbol{\bar{\nu}} = \left(\boldsymbol{\nu}^T, \eta \right)^T $, $ W(t) $ is a Wiener process, independent on the initial condition $ X(t_0) = X_0 $ for $ t\geq t_0 $, and $ h_{\boldsymbol{\bar{\nu}}}(t) $ is obtained from (2.3) by considering $ \eta = \frac{k}{\alpha} $. Here $ \sigma $ represents a diffusion parameter linked to random fluctuations.
An explicit formula for the solution of (3.1) is given, for $ t\geq t_0 $, by
where
being $ \boldsymbol{\xi} = \left(\boldsymbol{\bar{\nu}}^T, \sigma^2 \right)^T $.
In order to find the distribution of the process we must fix the one corresponding to $ X_0 $. In this sense, if $ X_0 $ is distributed according to a lognormal distribution $ \Lambda_1 \left[\mu_0, \sigma_0^2\right] $, or $ X_0 $ is a degenerate variable (i.e. $ P[X_0 = x_0] = 1 $), the finite dimensional distributions of the process are lognormal (note that the second case is a particular case of the former by considering $ \mu_0 = \ln x_0 $ and $ \sigma_0^2 = 0 $). Hence, $ \forall n\in\mathbb{N} $ and $ t_1 < \cdots < t_n $, vector $ (X(t_1), \ldots, X(t_n))^T $ follows an $ n $-dimensional lognormal distribution $ \Lambda_n[{\boldsymbol{\varepsilon}}, {\boldsymbol{\Sigma}}] $, where the components of vector $ {\boldsymbol{\varepsilon}} $ are $ \varepsilon_i = \mu_0+H_{ \boldsymbol{\xi}}(t_0, t_i) $, $ i = 1, \ldots, n $, being $ \sigma_{ij} = \sigma_0^2+\sigma^2(\min(t_i, t_j)-t_0) $, $ i, j = 1, \ldots, n $ those of the matrix $ {\boldsymbol{\Sigma}} $.
The transition probability density functions of the process are also lognormal; concretely,
On the other hand, several characteristics of the process can be deduced from the expression
for different values of $ \lambda = (\lambda_1, \lambda_2, \lambda_3, \lambda_4)^T\in\mathbb{R}^4 $. In particular, the mean function is obtained by taking $ \lambda = (1, 1/2, 1, 1)^T $, $ \tau = t_0 $ and $ y = \mu_0 $, resulting in
whereas the choice of $ \lambda = (1, 1/2, 0, 1)^T $, $ \tau = t_0 $ and $ y = \ln x_0 $ leads to the conditional mean function
Note that both functions belong to the type introduced before, which was what we aimed for when we introduced the present diffusion process.
4.
Hyperbolastic type-Ⅲ difussion process
4.1. Definition of the process
Hyperbolastic curves are a family of curves introduced in [13] with the goal of extending patterns of behavior, such as the logistic (type Ⅰ) and Weibull (type Ⅲ), through the inclusion of hyperbolic functions. This achieves greater flexibility, which in turn allows for the improved representation of certain growth phenomena.
As mentioned above, the hyperbolastic type-Ⅲ curve can be obtained from (2.2) by considering
where $ g_{\boldsymbol{\nu}} $ is given by (2.9). The explicit form adopted by the curve is given by (2.5), being
Following the methodology described in the previous section, we define the hyperbolastic type-Ⅲ process as a diffusion process $ \{X(t); t\in I\} $ that takes values in $ \mathbb{R}^+ $, and with infinitesimal moments
Both the distribution of the process and its main characteristics are derived immediately from the results displayed in the previous section after considering the expression that function $ \varepsilon_{\boldsymbol{\nu}}(t) $ adopts.
4.2. Estimating the parameters of the process
One of the main goals of this process is to develop a tool able to fit growth patterns to real cases, and to this end we will address the estimation of the parameters of the model by means of the maximum likelihood method. The results below are the adaptation, to the present process, of the development described in [39]. There, a general treatment of this question was carried out for the non-homogeneous lognormal process, of which the process dealt with in this paper is a particular case.
For the purposes of estimation our starting point is the observation of $ d $ sample-paths at time instants $ t_{ij} $, $ (i = 1, \ldots, d, \, j = 1, \ldots, n_i) $. Please note that neither the sample sizes nor the times of observation have to be the same, although we will suppose that the first time of observation is common for all sample-paths, that is, $ t_{i1} = t_0 $, $ i = 1, \ldots, d $. Let $ {\bf{X}}_i^T $ be the vector containing the random variables of the $ i $-th sample-path, that is $ {\bf{X}}_i = (X(t_{i1}), \ldots, X(t_{i, n_i}))^T $, $ i = 1, \ldots, d $, and denote $ {\bf{X}} = \left({\bf{X}}_1^T | \cdots | {\bf{X}}_d^T \right)^T $. In addition, we consider a lognormal $ \Lambda_1 [\mu_1, \sigma_1^2] $ distribution as the one followed by $ X_0 $.
From (3.3), and considering the distribution of $ X_0 $, the probability density function of vector $ {\bf{X}} $ is
where $ m_{\boldsymbol{\xi}}^{i, j+1, j} $ and $ \Delta_{i}^{j+1, j} $ are given by
with $ \phi^{i, m, n}_{ \boldsymbol{\bar{\nu}}} = \ln \frac{\eta- \varepsilon_{\boldsymbol{\nu}}(t_{im})}{\eta- \varepsilon_{\boldsymbol{\nu}}(t_{in})} $, $ i = 1, \ldots, d $; $ m, n\in\{1, \ldots, n_{i-1}\}, m > n $.
For a fixed value $ {\bf{x}} $ of $ {\bf{X}} $, expression (4.1) provides the likelihood function, whose logarithm is
where $ n = \sum_{i = 1}^d(n_i-1) $, $ {\boldsymbol{\varsigma}} = (\mu_1, \sigma_1^2)^T $ is the parametric vector of the initial distribution, and
Under the assumption that $ {\boldsymbol{\varsigma}} $ and $ {\boldsymbol{\xi}} $ are functionally independent, the estimate of $ {\boldsymbol{\varsigma}} $ is
while that of $ {\boldsymbol{\xi}} $ is obtained (see [39] for details) from the system of equations
where
Next, we will provide the expression given by the previous system of equations. First, noting
we have
being
From these last expressions, and from those of $ \Omega_{\boldsymbol{\xi}} $ and $ \Psi_{ \boldsymbol{\bar{\nu}}} $, the subsystem of equations (4.2) remains in the form
where we have noted
On the other hand, and since
where
equation (4.3) transforms into
Note that the system of equations (4.4)-(4.5) can not be solved explicitly, and it is therefore necessary to use numerical methods such as Newton-Raphson's, for which an initial solution is required. In the next subsection we present a strategy to provide such a solution according to the information provided by the sample data. This strategy provides an answer to the problems that some authors acknowledge having encountered when finding initial solutions for the adjustment of growth curves (see for example Tabatabai et al. [13]).
4.3. Initial solutions
When selecting initial values of the parameters with the goal of solving the system of equations (4.4)-(4.5), we will distinguish between three cases. The reason is that the calculation of the initial $ \sigma $ value is independent of that made for the rest of the parameters, and $ \eta $ will require initial solutions for $ \beta $, $ \gamma $, and $ \theta $. In any case, the information provided by the sample paths must be used.
The following are the strategies used to obtain these initial solutions.
● It is known that, given a random sample from a lognormal distribution $ \Lambda_1[\eta, \delta] $, the quotient between the arithmetic mean and the geometric one provides an estimation of $ \delta $. By applying this to the distribution of $ X(t) $, we obtain, for each $ t_i $, an estimate of $ \sigma_0^2+\sigma^2\, (t_i-t_0) $; that is, $ \sigma^2_i = 2\ln (m_i/m^g_i) $, $ i = 1, \ldots, n $, where $ m_i $ and $ m^g_i $ are, respectively, the values of the mean and the geometric sample mean of the sample paths at $ t_i $. The initial value of $ \sigma^2 $ is calculated by performing a simple linear regression of the $ \sigma^2_i $ values against $ t_i $. Note that if $ X_0 $ is a degenerate distribution, then $ \sigma_0^2 = 0 $. Otherwise, $ \sigma_0^2 $ is previously estimated from the values of the sample paths at $ t_0 $.
● Regarding $ \beta $, $ \gamma $ and $ \theta $, we do as follows. Firstly, we fix a value of $ \gamma $. Taking into account that hyperbolastic curve of type Ⅲ is an extension of the classic Weibull, and being $ \theta $ the distance between both curves, our approach here is to fit a Weibull model to sample data. The resulting estimated value $ \gamma^0 $ will be considered as the initial value for $ \gamma $. Next, we look for pairs of values $ (\beta, \theta) $ within a two-dimensional bounded region satisfying the inflection condition (2.8) for a predefined error threshold, say $ \epsilon $. That is, it must hold
Note that $ t_{*} $ is the time instant at which the inflection occurs. To obtain it, a spline function is previously adjusted to the mean values of the observed sample paths and, subsequently, the maximum of the derivative of said spline function is calculated.
We propose to use values of $ \epsilon $ between 0.0001 and 0.1, depending on the order of magnitude of the sample data. Finally, initial values $ \beta^0 $ and $ \theta^0 $ will be the mean of the resulting values for each parameter, respectively.
Returning to the value of $ \gamma $, and as shown later in the simulation application, a study has been carried out in order to check the stability of solutions subject to variations of $ \gamma $. As a matter of fact, and taking into account inflection condition (2.8), it follows that increasing values of $ \gamma $ require decreasing values of $ \beta $ to hold the condition. This requires widening the search region for the values of $ \beta^0 $, and more specifically considering lower bounds for $ \beta^0 $. Furthermore, $ \theta $ also increases with $ \gamma $, although to a lesser extent than $ \beta $. However, this also implies an increase in the upper bound for $ \theta^0 $.
● Finally, we must focus our attention on $ \eta $. From (3) it follows that the upper limit for the mean of the process is
from where an initial value for $ \eta $ can be obtained taking into account that
The value of $ k $, in general, will not be known. Therefore, we suggest taking as an approximation the last value of the mean sample path. In addition, if $ t_0 = 0 $, then $ \varepsilon_{\boldsymbol{\nu}}(t_0) = 1 $ and $ \eta^0 $ can be calculated independently of values $ \gamma^0, \beta^0 $, and $ \theta^0 $. Otherwise, the values previously calculated for these parameters must be used.
5.
Simulation-based examples
In this section we present some simulation examples that illustrate the developments made in the context of the hyperbolastic type-Ⅲ diffusion process. One of the main points of interest will be obtaining initial solutions for the subsequent estimation of the parameters of the process.
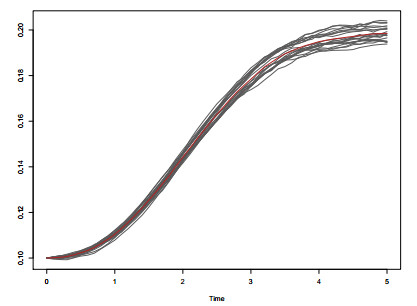
The simulations have been made taking into account the following pattern: by considering expression (3.2), which links the diffusion process being considered and the Wiener process, we have simulated 20 sample paths for time instants ranging from $ t_0 = 0 $ to 50 with step 0.1. This resulted in 501 simulated values for each sample path. $ X_0 $ has been chosen as a degenerate distribution in $ x_0 = 0.2 $.
In order to evaluate the quality of the estimation of the process, we have considered the relative absolute error between the sample mean of the simulated process and the estimated one, that is
where $ m_j $ and $ \hat{m}_j $ are the values of the sample mean function and the estimated ones at $ t_j $, $ j = 1, \dots, n $.
Figure 1 shows the simulated sample paths obtained by taking $ \eta = 2, \:\beta = 0.1, \: \gamma = 2.5, \: \theta = 0.01 $ and $ \sigma = 0.01 $.
By means of the procedure defined in Subsection 4.3, initial values for the resolution of the maximum likelihood system of equations can be obtained. Taking into account that $ t_0 = 0 $, the initial value for parameter $ \eta $ was calculated directly from sample mean values. In this case, $ \eta^0 = 2.015171 $. On the other hand, initial value $ \sigma^0 = 0.007966 $ was obtained by means of simple linear regression, as it has been explained previously. With respect to parameters $ \beta $ and $ \theta $, the first step is to fix an initial value $ \gamma^0 $. In order to do this, a study was carried out concerning the sensibility of the system of equations to variations of parameter $ \gamma $, in terms of how the model fit the data. Indeed, following previous section, a Weibull model was used with original sample mean data. More in detail, study showed that every value in interval $ [2.1, 3.75] $ would be a suitable $ \gamma^0 $. Indeed, and as mentioned in the previous section, increasing values of $ \gamma $ may affect other parameters, mainly $ \beta $. This implies that inflection condition (4.6) may not hold in some situations. In order to address this issue, larger search regions must be considered. In fact, taking into account the lower bounds for $ \beta^0 $ would be a suitable strategy. Then, we apply our methodology with different values of $ \gamma^0 $ in $ [2.1, 3.75] $ to simulated data, establishing $ [0.001, 0.1]\times[0, 0.1] $ as the search region for $ \beta $ and $ \theta $. The results are summarized in Table 1. Final estimations for all cases are $ \hat{\eta} = 2.010156, \:\hat{\beta} = 0.103903, \:\hat{\gamma} = 2.466963, \:\hat{\theta} = 0.008199 $ and $ \hat{\sigma} = 0.017711 $ with $ \mbox{RAE} = 0.000825 $.
It is apparent that high values of $ \gamma^0 $ tend to shrink regions for the search of $ (\beta, \theta) $, and so the number of candidates points become smaller. For example, increasing from $ \gamma^0 = 2.25 $ to $ \gamma^0 = 3.25 $, reduces the number of suitable $ \left(\beta^0, \theta^0 \right) $ values in the same region, from 1195 to just 150. With this in mind, and in order to avoid null search regions in the case of bigger $ \gamma^0 $, lower bounds of $ \beta^0 $ (and even upper bounds of $ \theta^0 $) should be considered.
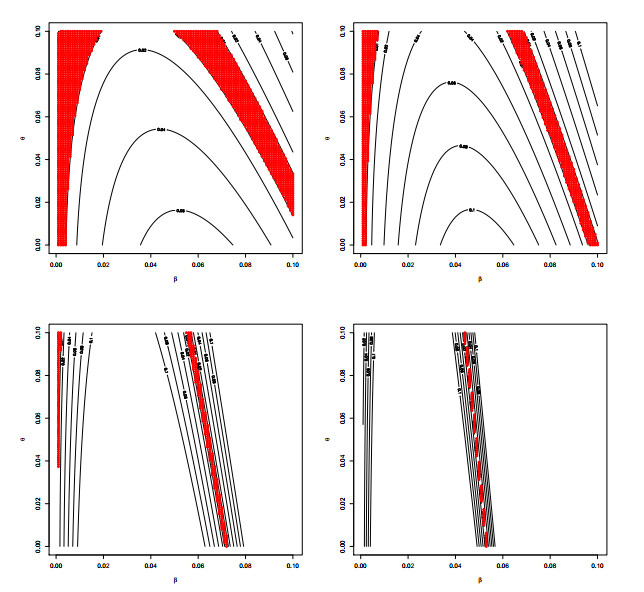
A graphical output of some of this results is shown in Figure 2, where the contour plot of function
is shown with different levels. Selected points in the region, marked in red, are those $ \left(\beta^0, \theta^0\right) $ such that $ I\left(\beta^0, \theta^0\right) < \epsilon = 0.01 $.
Considering a more detailed example, the particular case of $ \gamma^0 = 2.3 $ is shown next. A search was performed over $ 100^2 $ points within the $ [0.001, 0.01]\times[0, 0.1] $ grid. The bounds of this region were established by considering a midpoint between computational costs and a reasonable spectrum of potential solutions. Condition (4.6) was checked taking $ \epsilon = 0.01 $ at inflection time $ t_{*} = 2.1 $. This provided 1079 pairs $ (\beta, \theta) $ meeting the requirements. These pairs of points are marked in red in Figure 3. Any of these pairs would suffice to carry out the numerical method, but mean values were also considered. Indeed, taking the mean value of every dimension resulted in initial values $ \beta^0 = 0.049795 $ and $ \theta^0 = 0.059592 $.
Next, initial value $ \eta^0 $ for parameter $ \eta $ was calculated following (4.7). Regarding this expression, the lower and upper bounds of the sample data must be considered. We propose using the sample mean as a reference to take bounds. Thus, in this case, $ l = 0.1 $ and $ u = 0.1985056 $ were the minimum and the maximum of simulated mean values, respectively. Starting time $ t_0 = 0 $ led to $ \varepsilon_{\boldsymbol{\nu}}(t_0) = 1 $ independently of $ \left(\beta^0, \theta^0\right) $. With this, $ \eta^0 = 2.015171 $. It is worth noting that, in the case $ t_0\neq 0 $, initial values $ \beta^0 $ and $ \theta^0 $ are mandatory in order to get $ \eta^0 $, which indeed always satisfies $ \eta^0 > \varepsilon_{\boldsymbol{\nu}}(t_0) $.
On the other hand, the initial value for diffusion parameter $ \sigma $ was obtained by linear regression over time and values $ \sigma^2_j $ as explained before. Then, initial value $ \sigma^0 = 0.007966 $ was estimated with $ p $-value less than $ 2\times 10^{-16} $.
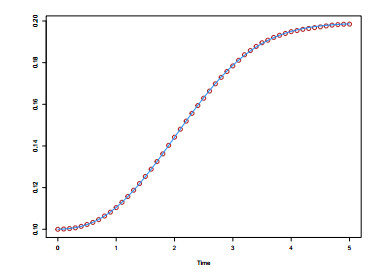
By considering the initial values obtained above, the system of equations (4.4)-(4.5) was solved subject to the constraint $ \eta > \varepsilon_{\boldsymbol{\nu}}(t) $ for every $ t $. Final results are shown in Table 2. In addition, the relative absolute error between the sample mean function and the estimated one (shown in Figure 4) were calculated, resulting in $ \mbox{RAE} = 0.000825 $.
Focusing on diffusion parameter $ \sigma $, simulations with $ \eta = 3, \:\beta = 0.002, \:\gamma = 3 $ and $ \theta = 0.03 $, were carried out for values $ 0.001, 0.005, 0.01, 0.05 $. Note that an increasing value of $ \sigma $ leads to more variability in the sample paths. This can affect the procedures previously used, especially in the calculation of the initial solutions and, therefore, in the adjustment of the model. Results are shown in Table 3.
It can be seen how inflection time decreases as $ \sigma $ increases. This is due to the sample mean function being less smooth, although that does not greatly affect the values of the initial solutions (for example, the values of $ \beta^0 $ remain constant). In addition, it can be observed that, as $ \sigma $ increases, the final estimates of the parameters, which already consider all sample values, lose precision with respect to the theoretical values, which causes a slight increase in the RAE values, as expected.
6.
An application to a real case
In this section, the methodology proposed above is applied to molecular biology. qPCR, standing for quantitative Polymerase Chain Reaction, is a well-known technique, widely used to make copies of an original piece of nucleic acid, both RNA and DNA. This procedure employs the enzyme polymerase to anneal acid (DNA) strands previously isolated with primers, in order to make two copies which are finally elongated. These steps, enclosed in a cycle, are carried out at precise temperatures controlled by a thermocycler.
The main advantage of qPCR over other classical PCR techniques is its ability to quantify the copies in real time. In this case, and thanks to DNA-binding dyes, the level of fluorescence emitted by the copies is constantly monitored by specific mechanisms.
One of the most interesting features of qPCR lies in its potential for mathematical modeling. Models allow the researcher to pinpoint the specific cycle in which a given fluorescence threshold is reached. Traditionally, the logarithm of the fluorescence has been used. Among others, in [41] Rutledge and Côté consider the criteria for a simple mathematical development of the relation between cycles, efficiency, and the log-fluorescence threshold. In addition, other studies such as [40,42,43] or [44] have analyzed the periodicity patterns of the process and the use of fixed fluorescence thresholds.
In this section, the new $ H_3 $ diffusion process (based on the hyperbolastic curve of type Ⅲ) is used to model qPCR data from [41], following the methodology proposed earlier. In order to measure the performance of the new model the RAE is used.
The data originate from 20 sample paths of the fluorescence monitored in 40 cycles of a standard qPCR procedure. The initial distribution, $ X_0 $ at $ t_0 = 0 $, is treated as lognormal with parameters $ \mu_1 $ and $ \sigma^2_1 $ whose estimations, following Section 4.2, are $ -5.407914 $ and $ 0.103251 $, respectively. Thus it follows $ E[X_0] = \exp{\left(\hat{\mu}_1 + \hat{\sigma}_ 1^2/2 \right)} = 0.004718 $.
Initial solutions for numerical procedures, aimed to solve maximum likelihood equations, were obtained following the procedure described in 4.3. Then, $ \gamma^0 = 2.98 $ was estimated by means of a classic Weibull model. Searching in the bounded region $ [0.001, 0.1]\times [0.001, 0.1] $, values $ \beta^0 = 0.001 $ and $ \theta^0 = 0.008 $ were chosen. As in the simulation case, the initial value of $ \eta $ was set from sample mean values. As a matter of fact, $ \eta^0 = 1.011179 $. On the other hand, and by linear regression, $ \sigma^0 = 0.028498 $. With these values, computations of Section 4.2 were performed, following the estimated parameters $ \hat{\eta} = 1.011705, \hat{\gamma} = 3.368802, \hat{\beta} = 0.0009, \hat{\theta} = 0.011912 $ and $ \hat{\sigma} = 0.028876 $. These values are shown in Table 4. The value obtained for RAE is $ 0.011885 $, which shows a good level of performance.
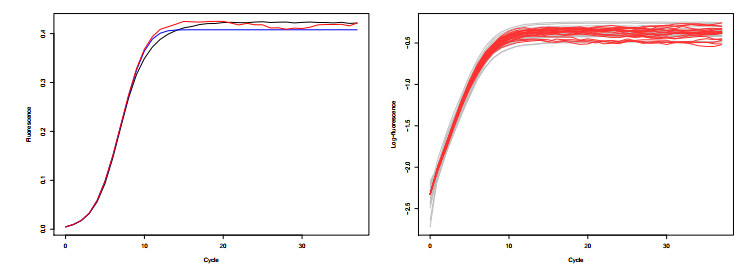
Graphical results can be observed in Figure 5. In the left side, the estimated $ H_3 $ curve and the mean of simulated paths of new diffusion are shown with original mean data. The right side shows the logarithm of paths of a new hyperbolastic diffusion of type Ⅲ (red) over original logarithmic data (grey), as they would show in practical applications.
Similar qPCR data from different replications was used in [37] in the application of the $ H_1 $ model (hyperbolastic of type Ⅰ) by means of the metaheuristic Firefly algorithm. There is no particular reason to use one or the other hyperbolastic model with this kind of data, but the more sophisticated $ H_3 $ model has shown a slightly lower (in the order of $ 10^{-3} $) RAE than $ H_1 $.
7.
Conclusions
Growth curves are commonly used in several fields of research to describe dynamical phenomena. Their main features are their inflection points and their ability to follow sigmoidal patterns. However, the choice of the right curve is no trivial matter, particularly when a single phenomenon exhibits multiple growth patterns.
The present paper considers a generalization of the classic Weibull curve, which is modified by introducing a generic parametric function $ g_{\boldsymbol{\nu}} $. Following the methodology described in [35], among others, we introduce a diffusion process whose mean function covers a wide range of growth curves (depending on the choice of $ g_{\boldsymbol{\nu}} $) derived from the Weibull curve. A convenient choice of $ g_{\boldsymbol{\nu}} $ leads to a diffusion process related to the hyperbolastic curve of type Ⅲ, which has been recently introduced and is currently used in fields of application related to cell growth. Several questions arise when estimating the parameters of the process by means of the maximum likelihood method. Numerical methods are used to obtain a solution, and to this end initial values are required. We propose a general strategy to calculate these initial values using information provided by sample data, and which solves the problems found in this context in the deterministic case. A simulation study is carried out to test the performance of the hyperbolastic model, as well as the strategy to solve the maximum likelihood equations.
Note that when considering a stochastic process for modeling growth phenomena, at each time instant we have a random variable that models the behavior of the variable under study, which allows us to take into account the random fluctuations presented by these phenomena. In addition, by using dynamic models we may study situations that cannot be approached through deterministic or static models. Along this line we may mention some techniques associated with the study of temporal variables such as first-passage times, that is, the time at which the process verifies a certain property for the first time. We may thus determine the time instant in which the process reaches a certain value or in which the growth changes speed (inflection).
Finally, an application based on real data from a study about quantitative polymerase chain reaction has been considered, showing the capability of the process for fitting the fluorescence levels associated with the amplification of amplicons of DNA.
Acknowledgments
This work was supported in part by the Ministerio de Economía, Industria y Competitividad, Spain, under Grant MTM2017-85568-P.
Conflict of interest
The three authors have participated equally in the development of this work, either in the theoretical developments or in the applied aspects. The paper was also written and reviewed cooperatively.









 DownLoad:
DownLoad: