Citation: Gabrielle L. Jenkin, Amber L. Pearson, Graham Bentham, Peter Day, Simon Kingham. Neighbourhood Influences on Children’s Weight-related Behaviours and Body Mass Index[J]. AIMS Public Health, 2015, 2(3): 501-515. doi: 10.3934/publichealth.2015.3.501
| [1] | Fang Wang, Lianying Cao, Xiaoji Song . Mathematical modeling of mutated COVID-19 transmission with quarantine, isolation and vaccination. Mathematical Biosciences and Engineering, 2022, 19(8): 8035-8056. doi: 10.3934/mbe.2022376 |
| [2] | Lei Shi, Hongyong Zhao, Daiyong Wu . Modelling and analysis of HFMD with the effects of vaccination, contaminated environments and quarantine in mainland China. Mathematical Biosciences and Engineering, 2019, 16(1): 474-500. doi: 10.3934/mbe.2019022 |
| [3] | Akhil Kumar Srivastav, Pankaj Kumar Tiwari, Prashant K Srivastava, Mini Ghosh, Yun Kang . A mathematical model for the impacts of face mask, hospitalization and quarantine on the dynamics of COVID-19 in India: deterministic vs. stochastic. Mathematical Biosciences and Engineering, 2021, 18(1): 182-213. doi: 10.3934/mbe.2021010 |
| [4] | Kimihito Ito, Chayada Piantham, Hiroshi Nishiura . Estimating relative generation times and reproduction numbers of Omicron BA.1 and BA.2 with respect to Delta variant in Denmark. Mathematical Biosciences and Engineering, 2022, 19(9): 9005-9017. doi: 10.3934/mbe.2022418 |
| [5] | Xinmiao Rong, Liu Yang, Huidi Chu, Meng Fan . Effect of delay in diagnosis on transmission of COVID-19. Mathematical Biosciences and Engineering, 2020, 17(3): 2725-2740. doi: 10.3934/mbe.2020149 |
| [6] | Fernando Saldaña, Hugo Flores-Arguedas, José Ariel Camacho-Gutiérrez, Ignacio Barradas . Modeling the transmission dynamics and the impact of the control interventions for the COVID-19 epidemic outbreak. Mathematical Biosciences and Engineering, 2020, 17(4): 4165-4183. doi: 10.3934/mbe.2020231 |
| [7] | Chentong Li, Jinhu Xu, Jiawei Liu, Yicang Zhou . The within-host viral kinetics of SARS-CoV-2. Mathematical Biosciences and Engineering, 2020, 17(4): 2853-2861. doi: 10.3934/mbe.2020159 |
| [8] | Hao Wang, Di Zhu, Shiqi Li, Robert A. Cheke, Sanyi Tang, Weike Zhou . Home quarantine or centralized quarantine? A mathematical modelling study on the COVID-19 epidemic in Guangzhou in 2021. Mathematical Biosciences and Engineering, 2022, 19(9): 9060-9078. doi: 10.3934/mbe.2022421 |
| [9] | Kai Wang, Zhenzhen Lu, Xiaomeng Wang, Hui Li, Huling Li, Dandan Lin, Yongli Cai, Xing Feng, Yateng Song, Zhiwei Feng, Weidong Ji, Xiaoyan Wang, Yi Yin, Lei Wang, Zhihang Peng . Current trends and future prediction of novel coronavirus disease (COVID-19) epidemic in China: a dynamical modeling analysis. Mathematical Biosciences and Engineering, 2020, 17(4): 3052-3061. doi: 10.3934/mbe.2020173 |
| [10] | C. K. Mahadhika, Dipo Aldila . A deterministic transmission model for analytics-driven optimization of COVID-19 post-pandemic vaccination and quarantine strategies. Mathematical Biosciences and Engineering, 2024, 21(4): 4956-4988. doi: 10.3934/mbe.2024219 |
A novel coronavirus disease 2019 outbreak, caused by the severe acute respiratory syndrome coronavirus and named SARS-Cov-2, has now spread to more than 200 countries and administrative areas [1]. Most of infected individuals exhibit pneumonia-like symptoms similar to SARS in 2003 and Middle East respiratory syndrome (MERS) in 2013. SARS-Cov-2 virus is primarily transmitted by direct contact with infected people and indirect contact with surfaces in the immediate environment or with objects used by the infected persons. The SARS-Cov-2 emerged in Wuhan, a center city of mainland China in December of 2019. As of March 13th, more than 80 thousands individuals infected by SARS-Cov-2 have been confirmed and nearly 3.5 thousands deaths have been directly caused by SARS-Cov-2 [2,3]. These numbers across the globe are expected to rise with the ongoing disease.
Facing the emerging global health threat, the Chinese government enforced a series of containment strategies, such as city lockdown, traffic restrictions, household quarantine, close contact tracing, face masks etc., to curb SARS-Cov-2 transmission on January 22nd, 2020 [4]. Meanwhile, the mainland China raised the national public health response to the highest state of emergence, Level 1, defined as an "extremely serious evidence" [3,4]. Indeed, those mixed control measures and containments of SARS-Cov-2 had averted a huge number of confirmed cases, decreasing from 744,000 to 29,839 by February 19th [5]. The basic reproduction number had declined from 3.15 to 0.97 before and after those control strategies [5]. The travel restrictions delayed the overall epidemic progression by 3 to 5 days in mainland China [6]. In [8], non-pharmaceutical interventions in China reduced 7–8 fold of daily contacts since most of contacts restricted to the household. They found that the adolescents (0–14 years old) are less susceptible to SARS-Cov-2 infection than adults (15–64 years old). The effectiveness of these containment measures strongly depends on when they are enacted and the proportion of quarantine. However, these enacted containments had substantially changed the transmission pattern of SARS-Cov-2 prevalence in mainland China. Under such enforced control strategies, each family was allowed at most one member going outside for necessities. Therefore, individual contact pattern was approximated to be a contact pattern of inner family, which was closely related to the structures of households of mainland China [9]. How to study the effects of the household heterogeneities on the transmission pattern of SARS-Cov-2 plays a vital role in evaluation of those control measures and the intrinsic dynamics.
Undoubtedly, SARS-Cov-2 has drawn increased attention from mathematicians, biologists, and public health researchers across the globe. Many epidemiological models have been attributed to study the dynamics of SARS-Cov-2 infection and statistic analysis. Most of them have assumed that individual contacts are homogeneous [5,9,10,11,12,13,14]. As the mentioned above, they ignored the structures of households in mainland China. Additionally, under such extreme strategies, the susceptibility of SARS-Cov-2 was suddenly reduced and such a proportion is unclear. How to evaluate and identify such a value is important to understand the evolution of SARS-Cov-2 spread in mainland China. Furthermore, there are few publications considering the case fatality risk (CFR) to examine the severity of SARS-Cov-2 infection in mainland China. Based on a competing risk model, a crude CFR was estimated to be $ 7.24\% $ ($ 95\% $ CI:6.68–8.01$ \% $) for Hubei province and $ 1\% $ ($ 95\% $ CI:0.87–1.18$ \% $) for other provinces of mainland China [15].
In this study, we focus on two aspects: First, we introduce the household structures of mainland China to propose a mean-field model, considering the heterogeneities of individual contacts, to study the dynamics of SARS-Cov-2 infection on complex networks. Second, we identify the susceptibility of SARS-Cov-2 infection and explore the severity of SARS-Cov-2 transmission by inserting a quarantined susceptible compartment and a cumulative confirmed death compartment into the classical SEIR compartmental model. The aim of this paper is to investigate the intrinsic dynamics of SARS-Cov-2 infection and evaluate the public control measures impacted by the structure of households in mainland China.
We picked up the cumulative hospitalized data and death cases of SARS-Cov-2 from the National Health Commission of the People's Republic of China. Since the definition of confirmed cases was changed on February 12th, 2020-the clinically diagnosed cases had been counted in cumulative confirmed cases, we collected the data period from January 31st to March 31st. To obtain the relatively reliable data, we allocated the sudden increment on February 12th to each day in the preceding week in proportion to the original increments of daily documented cases in these days.
All the definitions of suspected cases, death-caused by SARS-Cov-2, hospitalized cases, cured cases were obtained from Chinese Control Disease Center and Prevention [3] (see Figure 1(a)). The households structure was taken from Chinese Population Statistic Yearbook [16] and their distributions were shown in Figure 1(b).
Based on the Chinese Population Statistic Yearbook 2019 [16], the structures of households are classified into ten types by the numbers of each household and its degree distribution $ p(k) = N_k/N $ is shown in Figure 1(b), where $ N_k $ represents the proportion of one family consisting of $ k $ members and $ N = \sum_{k = 0}^{10}N_k(t) $ denotes the total population. In order to address the effects of the household quarantine and self-protection, we divide the total subpopulation $ N_k(t) $ with degree $ k $ into seven different statuses: susceptible class, latent class with no transmission ability, infected class including latent individuals in the transmission phase, asymptomatic individuals and symptomatic individuals, recovery class, unsusceptible class, hospitalized class and cumulative death class, denoted by $ S_k(t) $, $ E_k(t) $, $ I_k(t) $, $ R_k(t) $, $ S_k^Q(t) $, $ H_k(t) $ and $ D_k(t) $, respectively. The subscripts denote the degree of associated nodes. The susceptible individuals are infected by infected individuals and then changed the state as the exposed; the susceptible individuals who are isolated or exercising self-protection become unsusceptible at rate $ \alpha $. The exposed individuals have become infected individuals after $ 1/q $ days periods. The infected individuals are diagnosed as hospitalized individuals at rate $ \lambda. $ The hospitalized individuals are cured and become recovered individuals at rate $ \gamma $, and succumb to the virus and move into the death class at rate $ d $. The above transformation of states are governed in the following equations:
|
$ {dSk(t)dt=−βkSk(t)Θ(t)−αSk(t),dEk(t)dt=βkSk(t)Θ(t)−qEk(t),dIk(t)dt=qEk(t)−λIk(t),dHk(t)dt=λIk(t)−(d+γ)Hk(t),dRk(t)dt=γIk(t),dDk(t)dt=dIk(t),dSQk(t)dt=αSk(t),k=1,2,⋯,10, $
|
(2.1) |
where
|
$ Θ(t)=1⟨k⟩10∑k=0kp(k)Ik(t), $
|
(2.2) |
denotes the probability of any chosen edge connecting to an infected individual at time $ t $, and $ \langle k\rangle = \sum\limits_{k = 1}^{10}kp(k) $ is the average degree. Furthermore, we assume that model (2.1) has the following initial values
| $ S_k(0) = S_{k0} \gt 0,E_k(0) = E_{k0}\ge0,I_k(0) = I_{k0}\ge0,R_k(0) = R_{k0}\ge0, $ |
and
| $ S_k^Q(0) = S_{k0}^Q\ge0, H_k(0) = H_{k0}\ge0, D_k(0) = D_{k0}\ge0. $ |
Summing up all the equations of (2.1) yields $ \frac{dN_k(t)}{dt} = 0, $ which implies that $ N_k(t) = 1. $ The biological means of model parameters and their values of model (2.1) are enclosed in Table 1. Table 2 gives the initial data of model (2.1). Apparently, model (2.1) has a unique disease-free equilibrium
| $ P^0_k = (1,0,0,0,0,0,0,0). $ |
| Parameters | Definition | Values | Standard deviation | Source |
| $ \beta $ | Transmission rate by infected individuals | 0.262 | 0.02575 | MCMC |
| $ 1/q $ | Latent period | 5.2 | - | [5,7] |
| $ 1/\gamma $ | Course of the disease | 7 | - | [3,7] |
| $ \lambda $ | Diagnosed rate | 0.5 | 0.00574 | MCMC |
| $ d $ | Death rate | 0.0055 | 0.00571 | MCMC |
| $ \alpha $ | Quarantine rate | 0.3 | 0.00565 | MCMC |
DownLoad:
CSV
| Parameters | Definitions | Values | Standard deviation | Source |
| $ S_k $ | The proportion of susceptible population | $ p(k) $ | - | [16] |
| $ E_k $ | The proportion of latent population | $ 1.0\times10^{-5}p(k) $ | $ 0.000575 $ | MCMC |
| $ I_k $ | The proportion of infected population | $ 9.8\times10^{-6}p(k) $ | $ 0.000576 $ | MCMC |
| $ H_k $ | The proportion of hospitalized population | $ 9.3\times10^{-6}p(k) $ | - | [16] |
| $ D_k $ | The proportion of death population | $ 1.8\times10^{-5}p(k) $ | - | [16] |
| $ S^Q_k $ | The proportion of unsusceptible population | $ 0.3p(k) $ | - | [16] |
DownLoad:
CSV
With the help of the approach in [17], linearizing model (2.1) at the disease-free equilibrium $ P_0 $, we calculate the basic reproduction number of model (2.1) in form of
|
$ R0=βλ⟨k2⟩⟨k⟩, $
|
(2.3) |
where $ \langle k^2\rangle = \sum_{k = 0}^{10}k^2p(k) $ denotes the two movement of the degree distribution of $ p(k) $.
The monotonicity and continuity of system (2.1) ensure that $ S_k(\infty)\rightarrow S_{k\infty} $, $ E_k(\infty)\rightarrow0 $, $ I_k(\infty)\rightarrow0, $ $ S^Q_k(\infty)\rightarrow S^Q_{k\infty}, $ as $ t\rightarrow+\infty $. Solving $ S_k, E_k, I_k $ and $ S_k^Q $ equations of system (2.1), we obtain that
|
$ 10∑k=1(1−Sk∞−SQk∞)=1R0ln(10∑k=11Sk∞−αT⟨k⟩), $
|
(2.4) |
where $ T $ stands the duration of SARS-Cov-2.
Let $ I_{kT_p} $ denote the peak value of infected individuals at time $ T_p $. Similar to (2.4), the peak value satisfies the following equation:
|
$ 10∑k=1(1−SkTp−(1+qλ)IkTp−SQkTp)=1R0ln(10∑k=11SkTp−αTp⟨k⟩), $
|
(2.5) |
where $ S_{kT_p} $ and $ S_{kT_p}^Q $ represent proportions of susceptible nodes and unsusceptible nodes at peak arrival time $ T_p. $
The details for deriving equations (2.4) and (2.5) are enclosed in the Appendix.
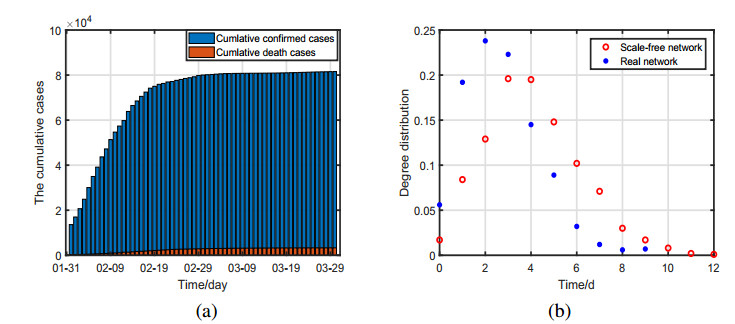
Since the Chinese government has enacted a series of containment strategies, including traffic restriction, household quarantine, and close contact tracing etc., at most one member of each family was allowed to go outside for necessaries during those days. The pattern of contacts was approximated to be a household-to-household network (a real network), which is definitely determined by the structures of the households of the mainland China with the minimum degree $ 1 $, the maximum degree $ 10 $, and the average degree $ \langle k\rangle = 2.75 $; A scale-free network is a configure network with the minimum degree $ 1 $, the maximum degree $ 12 $, and the average degree $ \langle k\rangle = 4.07. $
According to the cumulative number of confirmed cases reported by the National Health Commission of the People's Republic of China from January 31st to March 31st [2], we adopted Markvo Chain Monte Carlo method, together with Metropolis-Hastings (MH) algorithm to fit the model and identified the model parameters. The maximum likelihood function for the data set $ C = \{C_I(t), C_D(t)\}_{t = 0}^{60} $ from January 31st to March 31st is
| $ L(C|P) = \Pi_{t = 1}^{61}\frac{1}{2\pi\sigma_T\sigma_D}\exp\left(-\frac{(C_I(t)-\bar C_I(t))^2}{\sigma_I^2}\right)\exp\left(-\frac{(C_D(t)-\bar C_D(t))^2}{\sigma_D^2}\right), $ |
where
| $ \bar C_I(T) = \sum\limits_{k = 1}^{10}\sum\limits_{t = 0}^{T}\lambda I_k(t),\quad C_I(T) = \bar C_I(T)+\epsilon_I, T = 1,2,\cdots,61, $ |
and
| $ \bar C_D(T) = \sum\limits_{l = 1}^{10}\sum\limits_{t = 0}^{T}d I_l(t),\quad C_D(T) = \bar C_D(T)+\epsilon_D, T = 1,2,\cdots,61. $ |
The small perturbations $ \epsilon_j(j = I, D) $ satisfy normal distributions $ N(0, \sigma_j)(j = I, D) $ with $ \sigma_I = 1000 $ and $ \sigma_D = 100 $ making data fall in a rational region and enabling the iterations converge within a relatively short period. $ P $ denotes the vector of model parameters.
Proceeding the MCMC numerical method running for $ 20,000 $ iterations with a burn-in of $ 11,000 $ iterations, we employed the identification parameters and Eq (2.3) to calculate the basic reproduction number $ \mathcal R_0 = 2.05 $ ($ 95\% $ CI [1.38, 2.87]), which was close to the value reported in [11]. The peak value of documented ill patients of SARS-Cov-2 was approximated to be $ 29766 $ ($ 95\% $ CI [29734, 29868]) on February 7th ($ 95\% $ CI [Feb. 4th, Feb. 10th]). Furthermore, we predicated that the final size was approximated to be 94055 ($ 95\% $ CI [94050, 94059]) at the epidemic duration of 101 days ($ 95\% $ CI [96,104]).
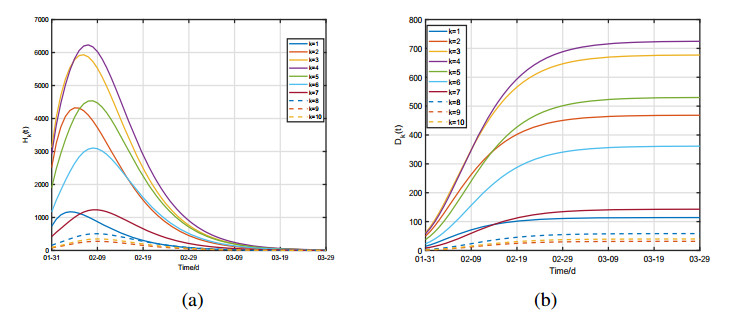
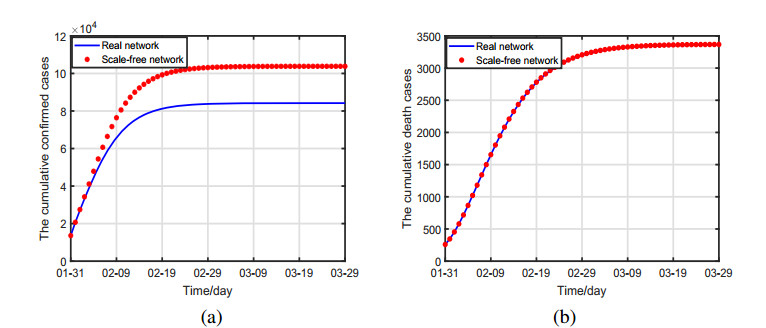
A good-fitting of clinical data and the solution of model are shown in Figure 2. Overall, the epidemic trends of the documented cases and death cases were correlated well with the trends of the model solution and final trends completely fell in a $ 95\% $ confidence interval of the solution of model (2.1). To further calibrate the rationality of model (2.1), we applied reported cumulative cases from April 1st to 15th to validate the fitting effects on the solution of model (2.1). Figure 2 shows that cumulative clinical cases are very consistent with the overall trend of the model, and the fifteen validated points also fell in a $ 95\% $ confidence interval of the solution of model (2.1). All the results of Figure 2 illustrate that model (2.1) successfully addresses the epidemic trend of SARS-Cov-2 in mainland China. On the contrary, Figure 3 displays the epidemic trends of diagnosed cases and deaths caused by COVID-19 in each household of mainland China. We noted that the largest numbers of diagnosed cases and deaths were the family of four; the earliest arrival peak of hospitalized cases was the one-person household. All of these suggested that the greater the household degree distribution and the higher the risk of infection.
In what follows, we studied the household pattern of SARS-Cov-2 prevalence in mainland China on the strict isolation measures mentioned in Section 1. Doing such an issue was in favor of evaluating the effects of the control strategies. First, if the Chinese government didn't enact any extreme strategy, the individual contact networks can be considered as a scale-free network with the average degree $ \langle k\rangle = 4.07 $ and the max degree of $ 12 $, which implies that one person may infect approximately $ 4 $ persons and at most contacts $ 12 $ persons per day. According to Figure 4, we found that the cumulative confirmed cases of SARS-Cov-2 may decrease nearly $ 25\% $, but the cumulative deaths had almost no any change, which mainly depends on the medical resources available. Furthermore, from Table 3, under the current strategies, it follows that the peak value shrank about $ 13\% $ ($ 95\% $ CI [$ 10\% $, $ 18\% $]), the peak arrival time delay $ 5 $ days with $ 95\% $ CI [3, 5] days; the final size has enlarged almost $ 29\% $. However, the epidemic duration may advance nearly 2 days in a scale-free network.
| Biomasses | Real network | $ 95\% $CI | Scale-free network | $ 95\% $CI |
| Peak values | 29766 | [29743, 29868] | 35925 | [35891, 36272] |
| Peak arrival times | Feb.7th | [Feb.6th, Feb.8th] | Feb.11th | [Feb.9th, Feb.13th] |
| Durations | 101 days | [96,104] days | 99 days | [94,102] days |
| Final sizes | 94055 | [94050, 94059] | 121760 | [121700, 121820] |
DownLoad:
CSV
In this paper, we established a mean field SARS-Cov-2 infection model based on a household-to-household network. The contact heterogeneity has been addressed by a certain degree distribution of households chosen from [16]. According to such model, we successfully captured the muti-dimensional data including cumulative diagnosed cases and deaths. Model (2.1) can be used to evaluate the effects of some containment strategies to mitigate SARS-Cov-2 prevalence in China, to some extent.
As we known, there are three primary kinds of modelling approaches, including mean-field model, pairwise model and edge-compartmental approach, to consider the relationship between two nodes on networks. For a pairewise model [9], $ [SSE] $ denotes the numbers of the triple with join structures $ S-S-E $ ($ S $ and $ E $ denote the states of susceptibles and the exposed, respectively), which can be approximated to be in form of
| $ [SSE] = \frac{\langle k\rangle-1}{\langle k\rangle} \frac{[SS][SE]}{[S]}, $ |
where the pairs of $ [SS] $ and $ [SE] $ stand for the numbers of links between susceptibles and susceptibles and the numbers of links between susectibles and the exposed, respectively. $ [S] $ denotes the numbers of susceptibles. For a mean-field model, $ [S_kI] $ represents the numbers of links between susceptibles $ S_k $ with degree $ k $ and infectives $ I $, which can be expressed as follows
| $ [S_kI] = kS_k\Theta(I) = \frac{kS_k}{\langle k\rangle} \sum\limits_llp(l)I_l. $ |
An edge-compartmental model considers all the pairwises as a whole variable by a probability generating function. The different approximated approaches have different concerns. Pairwise models mainly focus on the evolution of each pairwise; Edge-compartmental models primarily focus on the variation of each link; Mean field models are concerned with the evolution of each node with its associated degree. Actually, the contact pattern under household quarantine can be considered as a family-to-family contact, nor a person-to-person contact. Such transmission property can be described by a mean-field modelling approach. Therefore, more details about household transmission patterns were available from our work (see Figure 3).
The basic reproduction number plays a key role in the evaluation of emerging diseases. Generally, the disease will increase exponentially if $ \mathcal R_0 $ is greater than one, whereas it can be eradicated if $ \mathcal R_0 $ is less than one under some certain control measures. Borrowing (2.3), together with the identified parameters, we estimated that the basic reproduction number $ \mathcal R_0 = 2.05 $ is greater than one, which means that each infected individual will produce $ 2.05 $ secondary cases and SARS-Cov-2 will continue to spread in mainland China. We must mention that that our calculated value of $ \mathcal R_0 $ was closely correlated with collected data period. Moreover, compared with no control strategies, the value of $ \mathcal R_0 $ enlarged as a larger value, a great bigger than the current one. The overestimation of $ \mathcal R_0 $ was made up by the following two reasons: one is that the mean field model don't care about the contact correlation and enable its value bigger than one derived by the pairwise model; the other one is that the two movement of a scale-free network is sufficiently larger than its average degree. From (2.3), the value of $ \mathcal R_0 $ become larger than that one conducted by the pairwise modelling approach [9]. This manifests that the household quarantine measure has taken a great beneficial effects on slowing down SARS-Cov-2 spread in mainland China.
In view of Table 3 and Figure 3, we found that the transmission risk primarily depends on the degree distributions of households nor the household members. Under such control strategies, each household was only allowed one member to go outside for necessities and the contact exhibits a household-to-household pattern nor a person-to-person pattern. All of these suggests that the average degree of households determines the transmission risk of SARS-Cov-2 in mainland China. Indeed, the value of the average degree was approximated to be $ 2.75 $ for the current network, but it was to be $ 4.07 $ for a scale-free networks. Figure 3(a) reflects that the family of four has the highest transmission risk than those risks of other households.
Some evidence illustrates that the elderly and those with compromised immune systems are certainly more at risk of getting severe form of SARS-Cov-2. The case fatality rate (CFR), defined as the proportion of cases of a specified condition that are fatal within a specified time, is often used to examine the situation pertaining to SARS-Cov-2, as well as other diseases. By model (2.1), the CFR in mainland China was approximated to be $ 4.0\% $ ($ 95\% $ CI [$ 3.3\% $, $ 4.7\% $]), according with that expected value estimated in [18].
The outbreak of emerging SARS-Cov-2 has caused more than three months and more than 2,000,000 confirmed cases and more than 140,000 death cases as of March 17th, across the globe. How to curtail SARS-Cov-2 outbreaks has been become an urgent issue. The Chinese government had enforced a series of containment strategies, such as household quarantine, traffic restriction, city lockdown etc., to curb the disease spread. Such extreme control measures substantially changed the transmission pattern of SARS-Cov-2 in mainland China. In this study, we employed a mean-field model to investigate the dynamics of SARS-Cov-2 on a household network in mainland China. By fitting the cumulative hospitalized data and death related data, the basic reproduction number was evaluated as $ \mathcal R_0 = 2.05 $ ($ 95\% $ CI [1.38, 2.87]), the peak value of SARS-Cov-2 was nearly $ 29766 $ on February 7th and the epidemic duration will maintain $ 101 $ days. Through the careful analysis, the highest risk household was identified as the family of four. Our results suggested that under the current restrictive control measures, the transmission risk was significantly lower than not implementing a control strategy. Our investigations provided a new insight into the transmission heterogeneities and evaluation the effects of containment strategies in detail for public health decision and policymakers.
This work was supported by the National Natural Science Foundation of China (Nos. 61573016, 61873154), Shanxi Scholarship Council of China (No. 2015-094), and the New Coronavirus (COVID-19) Prevention and Control Project of Shanxi Province (No. 202003D31011 / GZ).
The authors declare no conflict of interest.
In the appendix, we focus on how to derive the final size and peak size by system (2.1). We assume that COVID-19 will die out at the duration $ T $ and arrive at a peak value at time $ T_p. $ The fractions of susceptible nodes, unsusceptible nodes, exposed nodes and infected nodes at the final time $ T $ or at the peak time $ T_p $ are denoted by $ S_{kT}, S_{kT}^Q, E_{kT}, I_{kT} $ or $ S_{kT_p}, S_{kT_p}^Q, E_{kT_p}, I_{kT_p} $, respectively. First, summing up $ S_k, E_k, I_k $ and $ S_k^Q $ equations for system (2.1) yields
|
$ d(Sk(t)+Ek(t)+Ik(t)+SQk(t))dt=−λIk(t). $
|
(5.1) |
Then integrating (5.1) from $ 0 $ to $ T $, we have
|
$ Sk0+Ek0+Ik0+SQk0−(SkT+EkT+IkT+SQkT)=λ∫T0I(t)dt. $
|
(5.2) |
Multiplying $ kp(k)/\langle k\rangle $ on both sides of (5.2) and summing up from $ 1 $ to $ 10 $, one obtains
|
$ ∫T0Θ(t)dt=1λ⟨k⟩10∑k=1kp(k)[Sk0+Ek0+Ik0+SQk0−(SkT+EkT+IkT+SQkT)]. $
|
(5.3) |
Integrating the first equation of (2.1) from $ 0 $ to $ T $, one derives that
|
$ ln(Sk0SkT)=βk∫T0Θ(t)dt+αT. $
|
(5.4) |
Then plugging (5.3) into (5.4) leads to
|
$ ln(Sk0SkT)=βkλ⟨k⟩10∑k=1kp(k)[Sk0+Ek0+Ik0+SQk0−(SkT+EkT+IkT+SQkT)]+αT. $
|
(5.5) |
Multiplying $ kp(k) $ and summing up from $ 1 $ to $ 10 $ again, we get
|
$ 10∑k=1ln(Sk0SkT)=R010∑k=1kp(k)[Sk0+Ek0+Ik0+SQk0−(SkT+EkT+IkT+SQkT)]+α⟨k⟩T. $
|
(5.6) |
Doing the similar process as the above at the peak arrival time $ T_p $, we have that
|
$ 10∑k=1ln(Sk0SkTp)=R010∑k=1kp(k)[Sk0+Ek0+Ik0+SQk0−(SkTp+EkTp+IkTp+SQkTp)]+α⟨k⟩Tp. $
|
(5.7) |
Observing that $ \frac{dI_k(t)}{dt}|_{t = T_p} = 0 $, we have that $ E_{kT_p} = \frac{\lambda}{q}I_{kT_p}. $ Substituting such a quantity into (5.7) results in
|
$ 10∑k=1ln(Sk0SkTp)=R010∑k=1kp(k){Sk0+Ek0+Ik0+SQk0−[SkTp+(1+λq)IkTp+SQkTp]}+α⟨k⟩Tp. $
|
(5.8) |
Remark 1. Since the fractions of exposed nodes and infected nodes are small, we assume that $ S_{k0} = 1, E_{k0} = I_{k0} = S_{k0}^Q = 0. $ Therefore, Eqs (5.6) and (5.8) simplifies as Eqs (2.4) and (2.5).
| [1] | Organisation for Economic Development (2012) OECD Obesity Update 2012. |
| [2] | Ministry of Health (2012) The Health of New Zealand Children 2011/12: Key findings of the New Zealand Health Survey. Wellington: Ministry of Health. |
| [3] | World Health Organization (2012) Obesity and overweight. Factsheet No.311. World Health Organization. |
| [4] |
Ogden C, Yanovski S, Carroll M, et al. (2007) The epidemiology of obesity. Gastroenterology 132: 2087-2102. doi: 10.1053/j.gastro.2007.03.052
|
| [5] | World Health Organization (2003) Diet, nutrition and the prevention of chronic diseases. Geneva: World Health Organization. 916. |
| [6] | World Cancer Research Fund & American Institute for Cancer Research (2007) Food, nutrition, physical activity, and the prevention of cancer: A global perspective. Washington DC: American Institute for Cancer Research. |
| [7] |
Swinburn B, Egger G, Raza F (1999) Dissecting obesogenic environments: The development and application of a framework for identifying and prioritizing environmental interventions of obesity. Prev Med 29: 563-570. doi: 10.1006/pmed.1999.0585
|
| [8] |
Egger G, Swinburn B (1997) An‘ecological’approach to the obesity pandemic. BMJ 315: 477-480. doi: 10.1136/bmj.315.7106.477
|
| [9] |
Giskes K, van Lenthe F, Avendano-Pabon M, et al. (2011) A systematic review of environmental factors and obesogenic dietary intakes among adults: Are we getting closer to understanding obesogenic environments? Obes Rev 12: e95-e106. doi: 10.1111/j.1467-789X.2010.00769.x
|
| [10] |
Morland K, Diez Roux AV, Wing S (2006) Supermarkets, other food stores, and obesity: The Atherosclerosis Risk in Communities Study. Am J Prev Med 30: 333-339. doi: 10.1016/j.amepre.2005.11.003
|
| [11] |
Rundle A, Diez Roux AV, Free LM, et al. (2007) The urban built environment and obesity in New York City: A multilevel analysis. Am J Health Promot 21: 326-334. doi: 10.4278/0890-1171-21.4s.326
|
| [12] | Zick CD, Smith KR, Fan JX, et al. (2009) Running to the store? The relationship between neighborhood environments and the risk of obesity. Soc Sci Med 69: 1493-1500. |
| [13] |
Joens-Matre RR, Welk GJ, Calabro MA, et al. (2008) Rural-urban differences in physical activity, physical fitness, and overweight prevalence of children. J Rural Health 24: 49-54. doi: 10.1111/j.1748-0361.2008.00136.x
|
| [14] | Liu J, Bennett KJ, Harun N, et al. (2008) Urban-rural differences in overweight status and physical inactivity among US children aged 10-17 years. 24: 407-415. |
| [15] | Ji-Hong l, Jones S, Sun H, et al. (2012) Diet, physical activity, and sedentary behaviors as risk factors for childhood obesity: An urban and rural comparison. Childhood Obesity 8: 440-448. . |
| [16] |
Wang Y (2001) Cross-national comparison of childhood obesity: The epidemic and the relationship between obesity and socioeconomic status. Int J Epidemiol 30: 1129-1136. doi: 10.1093/ije/30.5.1129
|
| [17] |
Dunton G, Kaplan J, Wolch J, et al. (2009) Physical environmental correlates of childhood obesity: A systematic review. Obes Rev 10: 393-402. doi: 10.1111/j.1467-789X.2009.00572.x
|
| [18] |
Rosenheck R (2008) Fast food consumption and increased caloric intake: A systematic review of a trajectory towards weight gain and obesity risk. Obes Rev 9: 535-547. doi: 10.1111/j.1467-789X.2008.00477.x
|
| [19] | Malik VS, Schulze MB, Hu FB (2006) Intake of sugar-sweetened beverages and weight gain: A systematic review. Am J Clin Nutr 84: 274-288. |
| [20] | Frank L, Andresen M, Schmid T (2004) Obesity relationships with community design, physical activity, and time spent in cars. Am J Prev Med 27 87-96. |
| [21] |
Pucher J, Buehler R, Bassett D, et al. (2010) Walking and cycling to health: A comparative analysis of city, state, and international data. Am J Public Health 100: 1986. doi: 10.2105/AJPH.2009.189324
|
| [22] |
Sallis JF, Floyd MF, Rodriguez DA, et al. (2012) Role of built environments in physical activity, obesity, and cardiovascular disease. Circulation 125: 729-737. doi: 10.1161/CIRCULATIONAHA.110.969022
|
| [23] | Cairns G, Angus K, Hastings G (2009) The extent, nature and effects of food promotion to children: A review of the evidence to December 2008. Geneva: World Health Organization. |
| [24] | Hastings G, McDermott L, Angus K, et al. (2006) The extent, nature and effects of food promotion to children: A review of the evidence. Technical paper prepared for the World Health Organization. World Health Organization. |
| [25] | McGinnis M, Gootman J, Kraak V (2006) Food marketing to children and youth: Threat or opportunity? Washington DC: National Academies Press. |
| [26] |
Veitch J, Timperio A, Crawford D, et al. (2011) Is the neighbourhood environment associated with sedentary behaviour outside of school hours among children? Ann Behav Med 41: 333-341. doi: 10.1007/s12160-011-9260-6
|
| [27] |
Timperio A, Salmon J, Ball K, et al. (2012) Neighborhood characteristics and TV viewing in youth: Nothing to do but watch TV? J Sci Med Sport 15: 122-128. doi: 10.1016/j.jsams.2011.07.010
|
| [28] |
Pabayo R, Spence JC, Cutumisu N, et al. (2012) Sociodemographic, behavioural and environmental correlates of sweetened beverage consumption among pre-school children. Public Health Nutr 15: 1338-1346. doi: 10.1017/S1368980011003557
|
| [29] | Ministry of Health (2008) Portrait of health: Key results of the 2006/07 New Zealand Health Survey. Wellington, New Zealand: Ministry of Health. |
| [30] | Ministry of Health (2008) Methodology Report for the 2006/07 New Zealand Health Survey. Wellington: Ministry of Health. |
| [31] | Ministry of Health (2008) A portrait of health: Key results of the 2006/7 New Zealand Health Survey. Wellington: Ministry of Health. |
| [32] | Pearce J, Blakely T, Witten K, et al. (2007) Neighborhood deprivation and access to fast-food retailing: A national study. Am J Prev Med 32 375-382. |
| [33] | Richardson EA, Pearce J, Mitchell RJ, et al. (2010) The association between green space and cause-specific mortality in urban New Zealand: an ecological analysis of green space utility. BioMed Central Public Health 10: 1. |
| [34] | Salmond C, Crampton P, Atkinson J (2007) NZDep 2006 Index of Deprivation. Wellington: University of Otago. 1-61 p. |
| [35] |
Pearce J, Witten K, Bartie P (2006) Neighbourhoods and health: A GIS approach to measuring community resource accessibility. J Epidemiol Commun H 60: 389-395. doi: 10.1136/jech.2005.043281
|
| [36] |
Ismailov RM, Leatherdale ST (2010) Rural-urban differences in overweight and obesity among a large sample of adolescents in Ontario. Int J Pediatr Obes 5: 351-360. doi: 10.3109/17477160903449994
|
| [37] |
Duncan S, Duncan EK, Fernandes RA, et al. (2011) Modifiable risk factors for overweight and obesity in children and adolescents from Sao Paulo, Brazil. BMC Public Health 11: 585. doi: 10.1186/1471-2458-11-585
|
| [38] | Sullivan C, O'Fallon C (2010) Walking and cycling: Improving combined use of physical activity/health and transport data. NZ Transport Agency research report no. 435. Wellington: NZ Transport Agency. |
| [39] |
Fraser LK, Clarke GP, Cade JE, et al. (2012) Fast food and obesity: A spatial analysis in a large United Kingdom population of children aged 13-15. Am J Prev Med 42: e77-85. doi: 10.1016/j.amepre.2012.02.007
|
| [40] |
Walker RE, Keane CR, Burke JG (2010) Disparities and access to healthy food in the United States: A review of food deserts literature. Health Place 16: 876-884. doi: 10.1016/j.healthplace.2010.04.013
|
| [41] |
Saelens B, Sallis J, Frank L, et al. (2012) Obesogenic Neighborhood Environments, Child and Parent Obesity: The Neighborhood Impact on Kids Study. Am J Prev Med 42: e57-e64. doi: 10.1016/j.amepre.2012.02.008
|
| [42] |
Grafova IB (2008) Overweight children: assessing the contribution of the built environment. Preventive medicine 47: 304-308. doi: 10.1016/j.ypmed.2008.04.012
|
| [43] |
Wolch J, Jerrett M, Reynolds K, et al. (2011) Childhood obesity and proximity to urban parks and recreational resources: a longitudinal cohort study. Health Place 17: 207-214. doi: 10.1016/j.healthplace.2010.10.001
|
| [44] |
Fraser LK, Edwards KL (2010) The association between the geography of fast food outlets and childhood obesity rates in Leeds, UK. Health Place 16: 1124-1128. doi: 10.1016/j.healthplace.2010.07.003
|
| 1. | Seo Yoon Chae, KyoungEun Lee, Hyun Min Lee, Nam Jung, Quang Anh Le, Biseko Juma Mafwele, Tae Ho Lee, Doo Hwan Kim, Jae Woo Lee, Estimation of Infection Rate and Predictions of Disease Spreading Based on Initial Individuals Infected With COVID-19, 2020, 8, 2296-424X, 10.3389/fphy.2020.00311 | |
| 2. | Dipo Aldila, Analyzing the impact of the media campaign and rapid testing for COVID-19 as an optimal control problem in East Java, Indonesia, 2020, 141, 09600779, 110364, 10.1016/j.chaos.2020.110364 | |
| 3. | Xiaoyan Wang, Junyuan Yang, A Bistable Phenomena Induced by a Mean-Field SIS Epidemic Model on Complex Networks: A Geometric Approach, 2021, 9, 2296-424X, 10.3389/fphy.2021.681268 | |
| 4. | Ivan Specht, Kian Sani, Yolanda Botti-Lodovico, Michael Hughes, Kristin Heumann, Amy Bronson, John Marshall, Emily Baron, Eric Parrie, Olivia Glennon, Ben Fry, Andrés Colubri, Pardis C. Sabeti, The case for altruism in institutional diagnostic testing, 2022, 12, 2045-2322, 10.1038/s41598-021-02605-4 | |
| 5. | Junyuan Yang, Xinyi Duan, Xuezhi Li, Dynamical analysis of an immumo-epidemiological coupled system on complex networks, 2023, 119, 10075704, 107116, 10.1016/j.cnsns.2023.107116 | |
| 6. | S. A. Alblowi, M. El Sayed, M. A. El Safty, Decision Making Based on Fuzzy Soft Sets and Its Application in COVID-19, 2021, 30, 1079-8587, 961, 10.32604/iasc.2021.018242 | |
| 7. | Junyuan Yang, Meijia Gong, Zhen Jin, Existence of the backward bifurcation of a non-markovian SIS-network model with saturation treatment function, 2023, 73, 14681218, 103882, 10.1016/j.nonrwa.2023.103882 | |
| 8. | Laura J. Faherty, Pedro Nascimento de Lima, Jing Zhi Lim, Derek Roberts, Sarah Karr, Emily Lawson, Henry H. Willis, Effects of non-pharmaceutical interventions on COVID-19 transmission: rapid review of evidence from Italy, the United States, the United Kingdom, and China, 2024, 12, 2296-2565, 10.3389/fpubh.2024.1426992 |
Gabrielle L. Jenkin, Amber L. Pearson, Graham Bentham, Peter Day, Simon Kingham. Neighbourhood Influences on Children’s Weight-related Behaviours and Body Mass Index[J]. AIMS Public Health, 2015, 2(3): 501-515. doi: 10.3934/publichealth.2015.3.501
| Parameters | Definition | Values | Standard deviation | Source |
| $ \beta $ | Transmission rate by infected individuals | 0.262 | 0.02575 | MCMC |
| $ 1/q $ | Latent period | 5.2 | - | [5,7] |
| $ 1/\gamma $ | Course of the disease | 7 | - | [3,7] |
| $ \lambda $ | Diagnosed rate | 0.5 | 0.00574 | MCMC |
| $ d $ | Death rate | 0.0055 | 0.00571 | MCMC |
| $ \alpha $ | Quarantine rate | 0.3 | 0.00565 | MCMC |
DownLoad:
CSV
| Parameters | Definitions | Values | Standard deviation | Source |
| $ S_k $ | The proportion of susceptible population | $ p(k) $ | - | [16] |
| $ E_k $ | The proportion of latent population | $ 1.0\times10^{-5}p(k) $ | $ 0.000575 $ | MCMC |
| $ I_k $ | The proportion of infected population | $ 9.8\times10^{-6}p(k) $ | $ 0.000576 $ | MCMC |
| $ H_k $ | The proportion of hospitalized population | $ 9.3\times10^{-6}p(k) $ | - | [16] |
| $ D_k $ | The proportion of death population | $ 1.8\times10^{-5}p(k) $ | - | [16] |
| $ S^Q_k $ | The proportion of unsusceptible population | $ 0.3p(k) $ | - | [16] |
DownLoad:
CSV
| Biomasses | Real network | $ 95\% $CI | Scale-free network | $ 95\% $CI |
| Peak values | 29766 | [29743, 29868] | 35925 | [35891, 36272] |
| Peak arrival times | Feb.7th | [Feb.6th, Feb.8th] | Feb.11th | [Feb.9th, Feb.13th] |
| Durations | 101 days | [96,104] days | 99 days | [94,102] days |
| Final sizes | 94055 | [94050, 94059] | 121760 | [121700, 121820] |
DownLoad:
CSV
| Parameters | Definition | Values | Standard deviation | Source |
| $ \beta $ | Transmission rate by infected individuals | 0.262 | 0.02575 | MCMC |
| $ 1/q $ | Latent period | 5.2 | - | [5,7] |
| $ 1/\gamma $ | Course of the disease | 7 | - | [3,7] |
| $ \lambda $ | Diagnosed rate | 0.5 | 0.00574 | MCMC |
| $ d $ | Death rate | 0.0055 | 0.00571 | MCMC |
| $ \alpha $ | Quarantine rate | 0.3 | 0.00565 | MCMC |
| Parameters | Definitions | Values | Standard deviation | Source |
| $ S_k $ | The proportion of susceptible population | $ p(k) $ | - | [16] |
| $ E_k $ | The proportion of latent population | $ 1.0\times10^{-5}p(k) $ | $ 0.000575 $ | MCMC |
| $ I_k $ | The proportion of infected population | $ 9.8\times10^{-6}p(k) $ | $ 0.000576 $ | MCMC |
| $ H_k $ | The proportion of hospitalized population | $ 9.3\times10^{-6}p(k) $ | - | [16] |
| $ D_k $ | The proportion of death population | $ 1.8\times10^{-5}p(k) $ | - | [16] |
| $ S^Q_k $ | The proportion of unsusceptible population | $ 0.3p(k) $ | - | [16] |
| Biomasses | Real network | $ 95\% $CI | Scale-free network | $ 95\% $CI |
| Peak values | 29766 | [29743, 29868] | 35925 | [35891, 36272] |
| Peak arrival times | Feb.7th | [Feb.6th, Feb.8th] | Feb.11th | [Feb.9th, Feb.13th] |
| Durations | 101 days | [96,104] days | 99 days | [94,102] days |
| Final sizes | 94055 | [94050, 94059] | 121760 | [121700, 121820] |
