1. Introduction
Diesel generator sets, which are comprised of an internal combustion engine and coupled electric generator and controller, are commonly used in microgrid applications for backup power and off-grid power in remote locations where utility interconnections are not possible. Hybrid microgrids, which add additional DC energy sources via AC coupling to the AC generator through power electronic converters, offer an attractive alternative. Examples of DC sources include fuel cells, photovoltaic (PV) cells, and wind turbines. This hybrid approach has been shown to be economical in many off-grid applications [1,2,3,4,5,6]. Reducing fuel requirements and providing an alternative to installing uneconomical distribution feeders to remote locations are key components to the economic viability of off-grid hybrid microgrids in comparison to grid-tied system. When grid-tied, hybrid sources of energy can use the grid interface to help balance demand and generation while off-grid hybrid system often require energy storage through batteries or rapid load shedding to maintain system stability.
Energy storage, for example battery banks, can be coupled into the hybrid system through a power electronic converter. Energy storage through batteries provides much flexibility in operation of hybrid microgrids but typically exhibit short lifespan (< 10 years) and must be properly controlled to ensure system operation as detailed in [7]. More specifically, state of charge, depth/rate of discharge, and operational temperature are important factors that dictate the reliability and viability of battery storage systems in microgrids. Studies have shown that “within 6-24 months, 50-70% of solar PV home systems are not working as expected” [8]. The main failure mode in these systems lies within the battery storage system and is the result of improper system design, operation, or maintenance. As a result, it would be advantageous to
reduce or eliminate the need of energy storage in hybrid microgrids. Demand response (DR) is an alternative that can help reduce the need of energy storage.
The concept of DR is to alter the electric usage by user in response to system operation. In grid-tied applications this is often desirable due to economic incentives [9,10,11] and research has shown that coupling DR with PV energy sources can be economically viable in such applications [12,13]. In off-grid applications DR could be a viable alternative, or complimentary technology, to reduce the use of battery storage. More specifically, “mismatch between supply and demand in microgri
ds can be overcome by effectively utilizing distributed energy resources and/or encouraging demand side management” [14]. Some recent work has been developing DR techniques designed to be coupled with intermittent renewable resources for microgrid applications [15,16,17]. The work presented here contributes to these ongoing efforts by providing a detailed analysis of the impacts of DR as applied to an off-grid hybrid photovoltaic-diesel generator microgrid.
This paper examines and quantifies the impacts of leveraging DR in a hybrid microgrid in lieu of energy storage. Two different hybrid diesel generator—PV microgrid topologies for a small residential neighborhood are modeled and simulated with varying levels of demand response. Impacts of DR are quantified through cost of energy, diesel fuel requirements, and utilization of the PV source under varying levels of demand response. The next section discusses the methodology of this work to include hybrid microgrid topologies, demand/DR modeling, PV source and resource modeling, and diesel generator modeling. Additionally, the simulation method and economic analysis are discussed. Results are presented in the next section followed by discussion and conclusion.
2. Methodology
This study was performed by modeling and simulating two different hybrid diesel generator-PV microgrid topologies, one with a single diesel generator and one with multiple paralleled diesel generators, for a small residential neighborhood with varying levels of demand response. Simulations were performed using HOMER Energy software [18]. Various system configurations were considered and the optimal configuration, based on cost of energy, was selected for comparison and analysis at each level of demand response. In particular, the base case was compared to the cases with DR in order to quantify the impacts of DR in these systems.
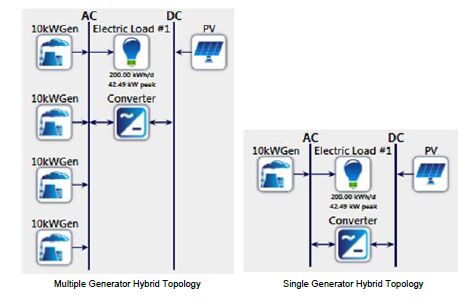
2.1. Hybrid Microgrid Topologies
The hybrid microgrid topologies analyzed in this work are shown in Figure 1. Both systems are comprised of diesel generation, electric load, a power electronic converter, and a PV source tied to the DC bus. The primary difference is that the multiple generator topology consists of multiple generators operating in parallel. It is assumed that these generators feature automatic paralleling and synchronization similar to the Advanced Medium Mobile Power Source (AMMPS) [19]. Such capability yields efficiency improvements by turning on and off generators as they are needed and improves generator loading. The single generator topology consists of one diesel generator. These two topologies were selected for study to compare/contrast the efficiency gains of PV sources and DR incorporation between the scenarios. The design decisions for each topology consist of number or size of generators, size of power electronic converter and size of PV array.
2.2. System Modeling
2.2.1. Demand and Demand Response
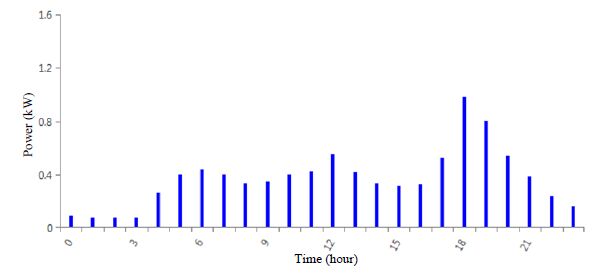
This work focused on analyzing a microgrid as applied to a small residential neighborhood. The demand profile for this was developed based on analysis of prior work and capabilities available within the HOMER software package to develop a realistic residential load profile. This profile was then scaled to approximate a neighborhood of 10-15 residential homes. Prior research has shown that residential load profiles exhibit lowest demand in the early hours of the morning, rise throughout the day with local peaks around hours six and twelve, and peak demand during the evening [20]. Load factors are typically very low for residential homes and approximated at 0.2 for this work. An example of this general residential load profile is shown in Figure 2. Variations from month to month, from day to day, and from time step to time step were modeled to further develop this into a more realistic representation of a small community load profile. More specifically, the data was varied ±10% day-to-day and ±20% from time-step-to-time-step. Additionally, seasonal variation was incorporated. Details on the final load profile
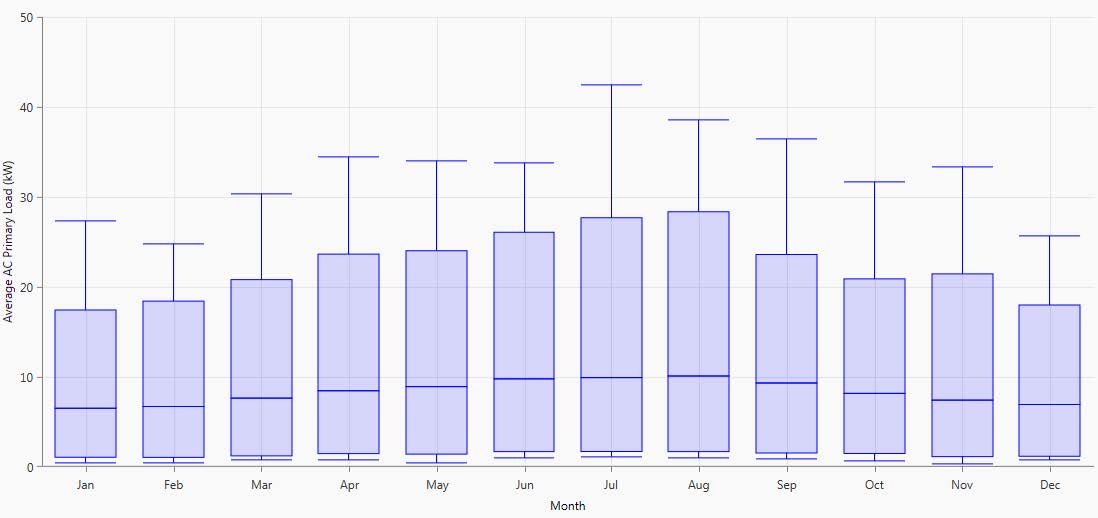
are shown in the box-and-whisker plot in Figure 3 on a month by month basis. Peak loading in the summer is representative of expected air conditioner loads during that time. The final scaled load model for this work had an average energy consumption of 200 kWh/d with a peak load of 42.49 kW. The effects of demand response were simulated by allocating a percentage of this load to be eligible for DR.
Common loads that are candidates for DR, or can be deferred, include water pumps, water heaters, plug-in loads that are non-critical or have internal battery storage, and HVAC systems as discussed in [16]. The DR model used in this work allows for a designated load to be deferred in time. A generalized model for deferrable loads treats each load as a unit of energy that must be met within a certain time period with an associated load profile. For example, a water heater must maintain a certain temperature within the tank. This tank can be viewed as a storage reservoir with a capacity in kWh. Energy can be put into the tank until the maximum temperature is reached (e.g. full capacity) and the load can be deferred until the minimum temperature is reached (e.g. minimum capacity). While this is occurring, the tank is serving the end user based on a specified profile (e.g. providing hot water) which consumes energy. To add energy to the tank a specific load profile, power over time, is modeled. The model used in this work generalizes this concept as a percentage of total load that is available for DR. More specifically, this is modeled based on specifying the daily energy that can be deferred (as a percentage of total daily energy consumption), effective storage capacity of deferred load (in kWh), and the minimum/peak deferred load pr
ofile values (in kW). In simulation, the primary load is provided for at all times. The deferrable load is served within specified guidelines. The strategy used for providing energy to the deferrable load is as follows:
|
PDL,min≤PDL≤PDL,max if(PAC+PDG≥PL,prim)∨(EDL=0)PDL=0 otherwise
|
(1) |
where
PDL:is the deferrable load demand in the current time step (kW)
PDL,min:is the minimum deferrable load demand (kW)
PDL,max:is the maximum deferrable load demand (kW)
PL,prim:is the primary load demand in the current time step (kW)
EDL:is the energy in the deferrable load tank at the end of the prior time step (kWh)
PAC:is the AC power output from the converter in the current time step (kW)
PDG:is the power rating of the diesel generator(s) (kW)
In other words, the deferred load is provided energy when it is available (generation exceeds primary load demand) or if the load can be deferred no longer as the energy in the load tank has reached zero. For this work, the deferrable load available, and peak power of deferrable load, was designated as a percentage of total load. Storage capacity was set to 25% of deferrable load. For example, if DR was set to 10% of the load, then the base load was reduced to 180 kWh/d and 38.24 kW peak while the deferrable load was 20 kWh/d and 4.25 kW peak. Sensitivity analysis was performed on all the deferrable load parameters and minimal change in system performance was observed with the exception of energy available for deferment. As a result, the data presented in this paper focuses on system performance and economics as the quantity of deferrable load increases and holds other parameters fixed.
2.2.2. Solar PV Generation
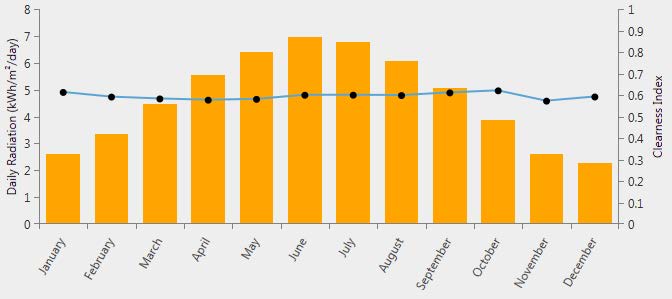
Solar PV generation has two key components to the model: solar resources available and the PV system energy conversion. Solar resource estimation was obtained from the National Solar Radiation Data Base [21] based on the geographical location of the system. A clearness index and solar radiation profile for various locations are available in this database. For this work the solar resources for Denver, Colorado, were used and can be seen in Figure 4. Denver was used as the location because the solar resources are fairly good (~ 5.5 kWh/m2/day average) and exhibits a good location for a hybrid microgrid with PV. The HOMER software used this data and models for the PV panels and inverter to determine how much PV power is generated at every time step of the simulation. More specifically, the AC power output from the PV array/converter combination was calculated at each time step by:
|
PAC=PDC,STCfPV(¯GT¯GT,STC)[1+α(¯Tc−¯Tc,STC)]ηconv
|
(2) |
where
PAC:is the AC power output from the converter in the current time step (kW)
PDC,STC:is the DC power rating of the PV array under standard test conditions (kW)
fPV:is the PV derating factor to account for shading, system losses, soiling, ageing, etc. (%)
¯GT:is the average solar radiation incident on the PV array in the current time step (kW/m2)
¯GT,STC:is the average solar radiation incident on the PV array under STC (kW/m2)
α:is the temperature coefficient of power for the PV array (%/°C)
¯Tc:is average PV cell temperature in the current time step (°C)
¯Tc,STC:is the PV cell temperature under STC (°C)
ηconv:is the power electronic converter efficiency (%)
It is assumed that a maximum power point tracking converter is used. ¯GT was calculated based on panel orientation (latitude tilt, south facing in this work). Temperature data was imported from the surface meteorology and solar energy database [22]. Parameters for the PV panels and converter were chosen based off standard, commercially available, PV panels and converters. PV panel efficiency was 13%, nominal operating cell temperature 47 °C, derating factor 80%, and temperature coefficient −0.5%/°C. The inverter efficiency was 90%.
2.2.3. Diesel Generation
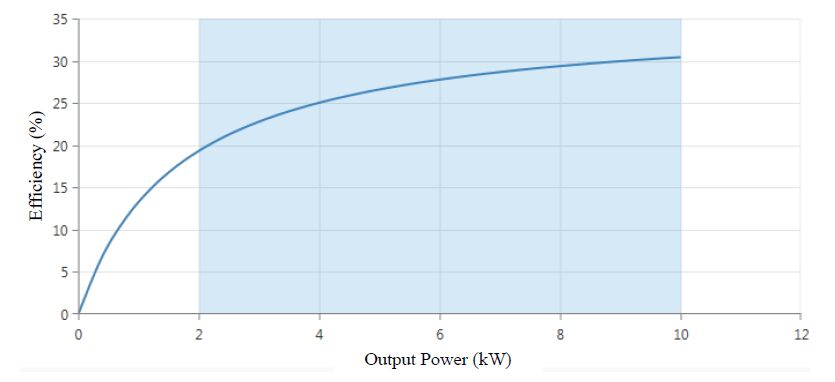
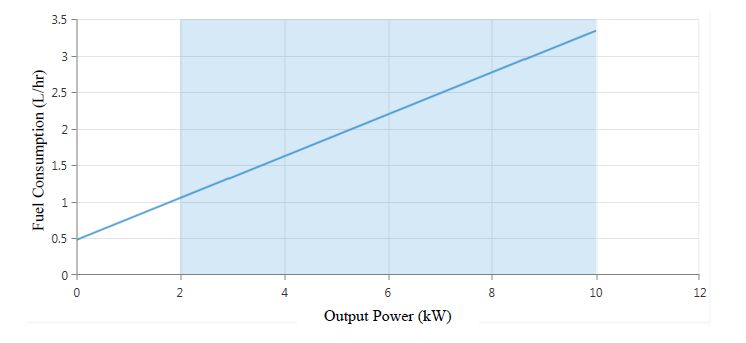
The diesel generator model was developed based on fuel data from commercially available diesel generators [23]. The generators studied in this work varied from 10-40 kW and, based on available data, exhibit very similar fuel/efficiency characteristics within this power range. Actual fuel consumption and efficiency can vary during operation and can also vary based on generator size, or brand/model of generator. However, the data used in this work is representative of commercially available diesel generators. The efficiency and fuel consumptions curves shown in Figure 5 and Figure 6 respectively are approximations of diesel generator performance in the range of 10-40 kW. The operational range of the generators were limited between 20-100% loading, shown by the shaded region in the figures, to increase generator efficiency and prevent wet stacking.
2.3. System Simulation
The systems shown in Figure 1 were constructed in HOMER and simulated for six different cases. More specifically, a base case with no DR, and five subsequent cases with DR increased by 10% each case for a maximum of 50% of the load available for DR. The time step was ten minutes and a simulation of twenty-five years was conducted for each case. For each time step an energy balance calculation is performed and flows of energy to and from each components of the system is determined. Energy production, energy consumption, diesel fuel consumption, system operating and O&M costs, etc. are calculated at each time step. Additionally, specified constraints are held during all time steps. For this work, 100% of load is served, a 10% operating reserve and 20% minimum loading constraints were placed on the generators, and a 0% capacity shortage constraint was set. System configurations that fail to meet these constraints were discarded as infeasible. This ensured that all loads would be met and some excess generation capacity is available at all times. Cost effectiveness of all feasible designs is compared in the simulation. The optimal solution, based on lowest cost of energy, is selected as the design choice for each case and was used to compare to other cases with different DR levels. System component costs, both capital and operation and maintenance costs, are enumerated in Table 1. These costs were estimat
ed based on current installed and operational pricing of generators, converters, and PV panels at the time of this writing. The PV panels are expected to last the duration of the simulation time period, while the converter will need to be replaced after approximately fifteen years, and the generator after approximately 15, 000 hours of operation.
Table 1. System component costs.
| Component |
Capital Cost |
Operation and Maintenance Cost |
| Diesel Generator |
$500/kW |
$0.03/hr + |
|
|
$500/kW/15000hr replacement |
| Diesel Fuel |
--- |
$0.76/L |
| Photovoltaic Source |
$3000/kW |
$10/kW/yr |
| Power Electronic Converter |
$400/kW |
$300/kW/15yr replacement |
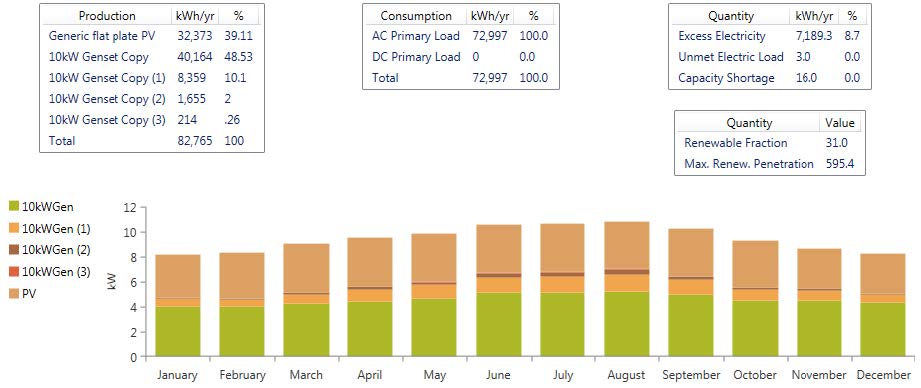
The search space for system configurations included a wide range of PV and converter capacity in 5 kW increments and a wide range of diesel generator capacity in 10 kW increments. Each simulation was checked to ensure the optimal solution did not fall at the edge of the search space. The simulation results include the cost of energy (COE) in $/kWh, capital and operating costs, and diesel generator fuel consumption and hours of operation for each system configuration studied. A summary of these results are shown in Table 2 for the multiple generator base case (no DR). The optimal solution is shown at the top with a COE of $0.371/kWh in this case. A detailed analysis of energy production and consumption was also obtained and is shown in Figure 7. This case had 31% of the load supplied by the PV source and required four 10 kW diesel generators. Note that 7189.3 kWh/yr of excess electricity is generated. The excess generation is due to the minimum loading requirements on diesel generator sets to avoid wet stacking. More specifically, regardless of demand, a certain minimum loading of the diesel generators is required for reliability purposes. As a result, in some cases this minimum loading results in excess energy production. This excess energy can be routed into a dump load to maintain a minimum loading on the generator and/or PV generation can be curtailed to increa
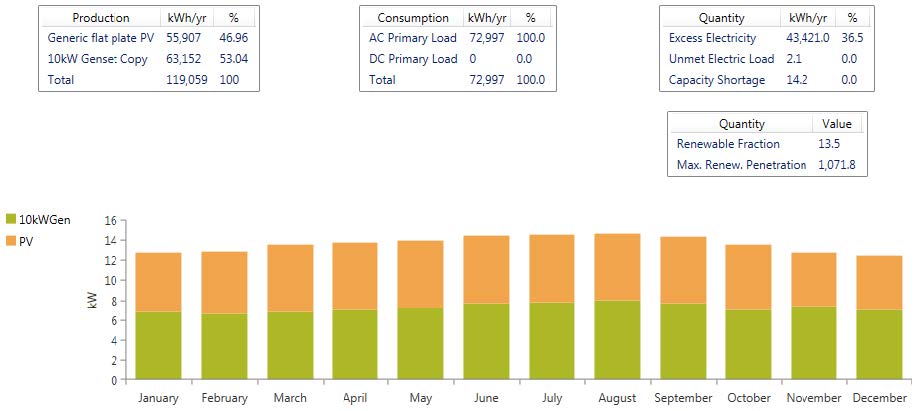
se generator loading. A detailed analysis of energy production and consumption for the base case with a single generator is shown in Figure 8. The next section provides simulation results on DR impacts in the hybrid microgrids shown in Figure 1.
Table 2. Simulation Results for multiple generator base case.
| PV Capacity (kW) |
Generator (kW) |
Converter (kW) |
COE ($) |
Initial Capital ($) |
Renewable Fraction (%) |
10kW Gen1 Fuel (L) |
10kW Gen2 Fuel (L) |
10kW Gen3 Fuel (L) |
10kW Gen4 Fuel (L) |
| 20 |
40 |
15 |
0.371 |
86000 |
31 |
15085 |
3272 |
674 |
97 |
| 25 |
40 |
15 |
0.372 |
101000 |
34 |
14176 |
3189 |
672 |
96 |
| 20 |
40 |
20 |
0.374 |
88000 |
31 |
15078 |
3272 |
674 |
97 |
| 25 |
40 |
20 |
0.374 |
103000 |
35 |
14116 |
3189 |
672 |
96 |
| 15 |
40 |
10 |
0.375 |
69000 |
25 |
16497 |
3394 |
682 |
98 |
| 20 |
40 |
10 |
0.375 |
84000 |
30 |
15484 |
3278 |
674 |
97 |
| 15 |
40 |
15 |
0.377 |
71000 |
26 |
16441 |
3394 |
682 |
98 |
| 15 |
40 |
20 |
0.379 |
73000 |
26 |
16441 |
3394 |
682 |
98 |
| 25 |
40 |
10 |
0.382 |
99000 |
32 |
14883 |
3200 |
672 |
96 |
| 10 |
40 |
10 |
0.383 |
54000 |
18 |
18055 |
3626 |
687 |
99 |
| 10 |
40 |
15 |
0.385 |
56000 |
18 |
18055 |
3626 |
687 |
99 |
| 10 |
40 |
5 |
0.386 |
52000 |
17 |
18405 |
3694 |
687 |
99 |
| 10 |
40 |
20 |
0.388 |
58000 |
18 |
18055 |
3626 |
687 |
99 |
| 15 |
40 |
5 |
0.394 |
67000 |
20 |
17869 |
3547 |
682 |
98 |
| 20 |
40 |
5 |
0.405 |
82000 |
21 |
17568 |
3463 |
674 |
97 |
| 25 |
40 |
5 |
0.419 |
97000 |
22 |
17395 |
3393 |
672 |
96 |
3. Results
The simulation results for the single generator system are shown in Table 3 and Table 3. Table 4shows the optimal system configuration in regards to PV, Converter, and generator capacity over a wide range of DR (0-50%). As more load is available for DR, the capacity of all components is reduced. This effectively reduces system cost and improves the utilization of all system resources. This can be more clearly seen from the data in Table 4. For the base case scenario, there exists much excess electricity production (43, 421 kWh/yr) and only 13.5% of the consumed energy is provided for by the PV source. The COE for this base case is $0.657/kWh. Dramatic improvements are seen at any level of DR as COE, Fuel consumption, excess electricity production all decrease and renewable energy fraction increases as compared to the base case. At modest level of 20% of DR load, COE has been reduced by 21.16%, fuel consumption reduced by 16.74%, and excess electricity reduced by 75.39% as shown in Table 5. Generally speaking, system performance improves as DR increases. The primary impact of incorporating DR is the reduction of generation capacity, both PV and diesel, which is possible due to better utilization of these resources. This can be seen in the large jumps in performance between 10% and 20% DR, and 30% and 40% DR as capacity changes occur for optimal configurations. Simulation results for the multiple generator system are shown in Tables 6 and 7. Table 6 shows the optimal system configuration as DR capability varies. A similar trend in reduction of diesel generator capacity is seen. PV capacity increased as DR is increased as the flexibility of operating four generators allows for better utilization of PV as compared to the single generator case. Also note that the initial starting point is much more economical in comparison to the single generator system. The data in Table 7shows that appreciable reduction in COE and excess electricity production is achieved with DR while the renewable energy fraction and fuel consumption improvements are also seen. These results are significant but not as substantial as compared to the single generator case. The differences between the two cases are due solely to the generation architecture. At a modest level of 20% of DR load, COE has been reduced by 6.20%, fuel consumption reduced by 6.89%, and excess electricity reduced by 57.10% as shown in Table 8. As before, the primary impacts of DR are the reduction of diesel generation capacity, better utilization of all generation resources.
Table 3. Optimal system configurations for singe generator system.
| Percentage of Load Available for DR |
PV Capacity (kW) |
Converter Capacity (kW) |
Diesel Generator Capacity (kW) |
| 0% |
35 |
20 |
40 |
| 10% |
35 |
20 |
40 |
| 20% |
25 |
15 |
30 |
| 30% |
25 |
15 |
30 |
| 40% |
30 |
20 |
20 |
| 50% |
20 |
15 |
20 |
Table 4. System performance metrics for singe generator system.
| Percentage of Load Available for DR |
Cost of Energy |
Fuel Consumption |
Excess Electricity Production |
Renewable Energy Fraction |
| 0% |
$0.657/kWh |
28,601 L |
43,421 kWh/yr |
13.5% |
| 10% |
$0.653/kWh |
28,805 L |
39,230 kWh/yr |
19.0% |
| 20% |
$0.518/kWh |
23,813 L |
14,555 kWh/yr |
31.0% |
| 30% |
$0.499/kWh |
22,487 L |
10,684 kWh/yr |
36.0% |
| 40% |
$0.397/kWh |
17,087 L |
11,169 kWh/yr |
45.4% |
| 50% |
$0.383/kWh |
17,493 L |
4649 kWh/yr |
43.5% |
Table 5. System improvement form base case for single generator system.
| Percentage of Load Available for DR |
Cost of Energy Reduction |
Diesel Fuel Reduction |
Excess Electricity Reduction |
| 10% |
0.61% |
-0.71% |
9.65% |
| 20% |
21.16% |
16.74% |
66.48% |
| 30% |
24.05% |
21.38% |
75.39% |
| 40% |
39.57% |
40.26% |
74.28% |
| 50% |
41.70% |
38.84% |
89.29% |
Table 6. Optimal system configurations for multiple generator system.
| Percentage of Load Available for DR |
PV Capacity (kW) |
Converter Capacity (kW) |
Diesel Generator Capacity (kW) |
| 0% |
20 |
15 |
40 |
| 10% |
20 |
15 |
40 |
| 20% |
20 |
15 |
30 |
| 30% |
25 |
15 |
30 |
| 40% |
25 |
15 |
30 |
| 50% |
25 |
15 |
20 |
Table 7. System performance metrics for multiple generator system.
| Percentage of Load Available for DR |
Cost of Energy |
Fuel Consumption |
Excess Electricity Production |
Renewable Energy Fraction |
| 0% |
$0.371/kWh |
19,128 L |
7189 kWh/yr |
31.0% |
| 10% |
$0.358/kWh |
18,270 L |
6034 kWh/yr |
33.9% |
| 20% |
$0.348/kWh |
17,810 L |
3084 kWh/yr |
35.6% |
| 30% |
$0.341/kWh |
16,241 L |
6626 kWh/yr |
41.1% |
| 40% |
$0.335/kWh |
15,887 L |
5559 kWh/yr |
42.4% |
| 50% |
$0.320/kWh |
15,314 L |
4607 kWh/yr |
43.6% |
Table 8. System improvement form base case for multiple generator system.
| Percentage of Load Available for DR |
Cost of Energy Reduction |
Diesel Fuel Reduction |
Excess Electricity Reduction |
| 10% |
3.50% |
4.49% |
38.46% |
| 20% |
6.20% |
6.89% |
57.10% |
| 30% |
8.09% |
15.09% |
7.84% |
| 40% |
9.70% |
16.94% |
22.68% |
| 50% |
13.75% |
19.94% |
35.92% |
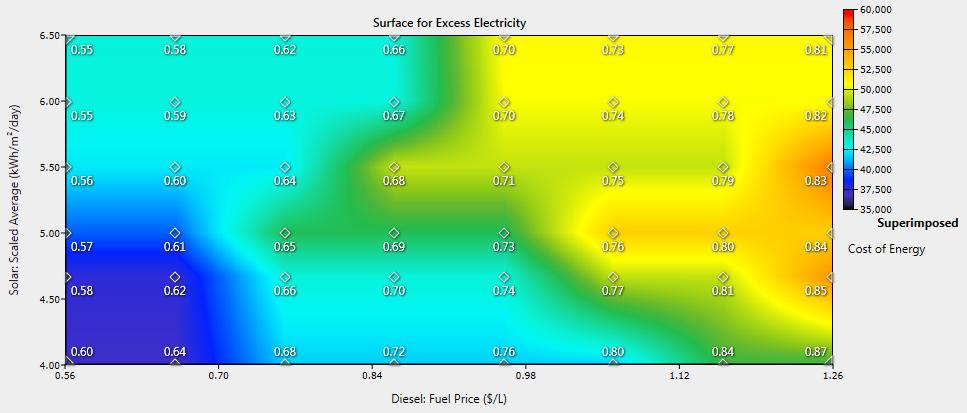
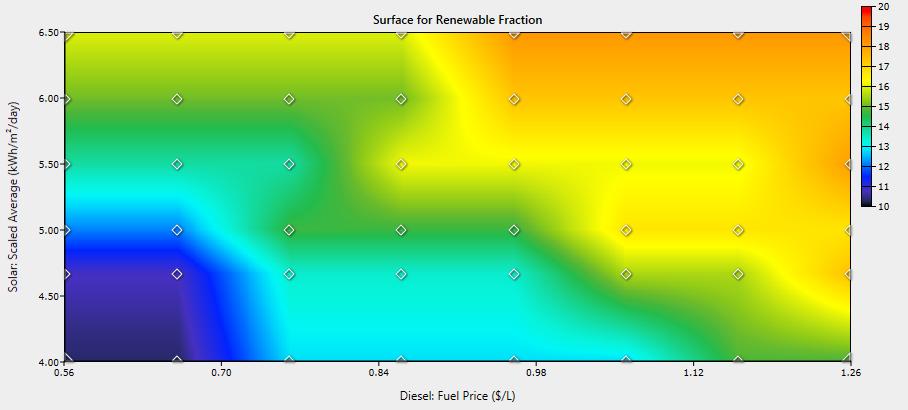
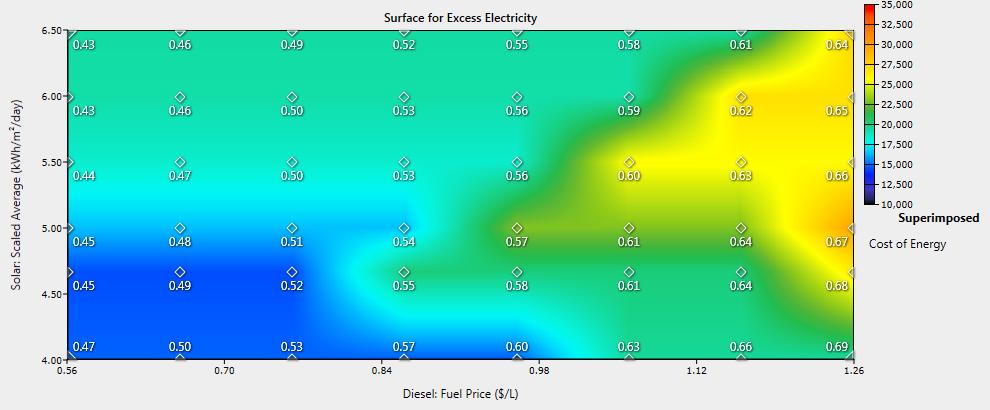
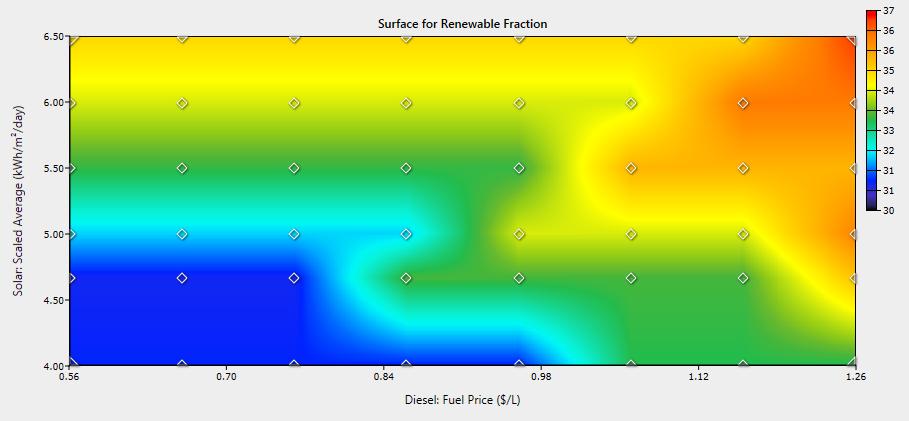
Sensitivity analysis was performed on solar resources and diesel fuel pricing to see how these affected the impacts of DR, energy pricing, and system configuration. Average solar insolation was varied between 4.0 and 6.5 kWh/m2/day and diesel fuel price was varied between $0.56 and $1.26 per liter. Base case results for the single generator system are shown in Figure 9 and Figure 10 while results for the single generator case with 20% DR are shown in Figure 11 and Figure 12. Figure 9 and Figure 11 provide data on excess electricity and COE, while Figure 10 and Figure 12 highlight renewable energy fraction across the range of solar irradiation and diesel fuel prices simulated. The impacts of DR in terms of COE, excess electricity, and renewable energy fraction were very similar over the simulated range of diesel fuel prices and solar resources. In regards to system configuration, the diesel generator sizes remained at 40 kW and 30 kW for the base case and 20% DR case respectively for all simulations. However, the PV/inverter capacities did change inversely proportional to solar insolation and directly proportional to diesel fuel price. In other words, the PV capacity can be decreased with better solar resources and increased in scenarios with higher fuel prices. In summary, these results indicate that the impact of DR will be very positive under a wide range of fuel prices and solar resource levels.
Sensitivity analysis was performed on solar resources and diesel fuel pricing to see how these affected the impacts of DR, energy pricing, and system configuration. Average solar insolation was varied between 4.0 and 6.5 kWh/m2/day and diesel fuel price was varied between $0.56 and $1.26 per liter. Base case results for the single generator system are shown in Figure 9 and Figure 10 while results for the single generator case with 20% DR are shown in Figures 11 and 12. Figure 9 and provide data on excess electricity and COE, while Figures 10 and 12 highlight renewable energy fraction across the range of solar irradiation and diesel fuel prices simulated. The impacts of DR in terms of COE, excess electricity, and renewable energy fraction were very similar over the simulated range of diesel fuel prices and solar resources. In regards to system configuration, the diesel generator sizes remained at 40 kW and 30 kW for the base case and 20% DR case respectively for all simulations. However, the PV/inverter capacities did change inversely proportional to solar insolation and directly proportional to diesel fuel price. In other words, the PV capacity can be decreased with better solar resources and increased in scenarios with higher fuel prices. In summary, these results indicate that the impact of DR will be very positive under a wide range of fuel prices and solar resource levels.
4. Discussion
The analysis in this paper focused on demand response impacts in off-grid hybrid PV-diesel generator microgrids as applied to a small residential community. System topologies with a single diesel generator and multiple diesel generators with parallel operation were studied. The primary objective was to analyze the impacts of DR in the absence of energy storage (e.g. batteries). While elimination of energy storage will not be feasible in all microgrid cases, it simplifies system design and increases system operation and reliability. Additionally, it was advantageous to remove energy storage in this analysis to isolate the impacts of DR. The results shown here indicate that the DR can improve the utilization of energy sources, in particular the intermittent PV source, substantially. As a result, fast acting DR or load shedding can be a valuable tool in designing and implementing efficient hybrid microgrids. Large reductions in the cost of energy, linked to reductions in initial capital and operating costs, are observed in both topologies. The single generator system showed the most improvement as it does not exhibit the advantages of paralleling generators. As a result, aggressive demand response/load shedding schemes could be an alternative to a multiple generator system. Future studies will investigate this further and analyze the feasible limits of DR in this application.
5. Conclusion
This work analyzed the impacts of demand response in an off-grid hybrid microgrid, containing diesel and photovoltaic generation, as applied to a small residential neighborhood. Prior research has shown the hybrid approach to be economical in off-grid applications and this study was performed by simulating two different hybrid diesel generator-PV microgrid topologies, one with a single diesel generator and one with multiple paralleled diesel generators, with varying levels of demand response. A detailed model of each microgrid was developed along with a cost analysis, to include initial capital and O&M costs. HOMER software was used to perform time domain simulations for each case at ten minute intervals over a period of twenty-five years. These simulations determined the optimal system design, defined as lowest cost of energy, for each case and provide data to analyze the impacts of DR in each case. These impacts were quantified through cost of energy reduction, diesel fuel reduction, and increased utilization of the energy sources. The presented results indicate that a moderate level of demand response can have significant positive impacts to the operation of hybrid microgrids as compared to a base case without demand response. For the single generator system and 20% of the load available for demand response, the cost of energy is reduced by 21.16%, fuel consumption reduced by 16.74%, and excess electricity reduced by 75.39%. For the multiple generator system and 20% of the load available for demand response, the cost of energy has been reduced by 6.20%, fuel consumption reduced by 6.89%, and excess electricity reduced by 57.10%. Sensitivity analysis showed that similar results can be expected across a wide range of solar resource levels and diesel fuel prices.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: