Characterization and immobilization of engineered sialidases from Trypanosoma rangeli for transsialylation

1.   Introduction

Lung cancer is one of the common malignancies with the morbidity and mortality ranking top, about more than 1.8 million new cases with lung cancer are diagnosed and near 1.6 million patients die every year ^[1]. Among all cases suffering lung cancer, non-small cell lung cancer (NSCLC) accounts for 85% ^[2], with the main histologic phenotypes of adenocarcinoma, squamous-cell carcinoma and large cell carcinoma ^[3]. Therein, lung adenocarcinoma is the principal pathological pattern, nearly taking up 50% ^[4]. At present, radiotherapy, chemotherapy, surgery, immunotherapy and Chinese medicine are major curative options for patients suffering lung adenocarcinoma, and surgery remains the most effective approach. However, as patients always develop distant metastasis in an early stage with a five-year survival rate less than 15%, surgical is no more a good choice ^[5,6]. Therefore, the exploration on the molecular mechanism of lung adenocarcinoma invasion and metastasis in an early stage is of great importance for the development of novel diagnostic and therapeutic regimens.

Exosome, an extracellular vesicle, was firstly reported by Taylor, et al. in 1979 and then verified in reticulocytes of mature mammals for the first time by Pan, et al. in 1985. Increasing evidence has shown that exosomes are essentially specific subcellular structures with important biological functions and specific bioactive substances like DNA, mRNA, ncRNA, protein, lipid, as well as other specific surface markers, such as CD63, CD81, Alix and Tsg101 ^[7]. Some studies suggested that there were two types of exosome: immune active exosomes involved in antigen presentation and co-stimulation, and the exosomes containing RNA and mediating genetic communication between cells ^[8,9,10]. As exosomes in body fluids originate from the corresponding tissues and organs, the composition of bioactive molecules in exosomes reflects the functional status of the corresponding tissues and organs. In addition, other studies have shown that exosomes, harboring abundant, stable, sensitive and specific biological information, are liquid biopsy specimens of relatively high application value ^[11], and play an important role in the regulation of immune response and tumor metastasis. Tumor-derived exosomes carry a variety of immunosuppressive signals, which can invalidate anti-tumor immune effectors and promote tumors to escape from epidemic control ^[12]. Besides, exogenous exosomes can induce metabolic reprogramming by restoring cancer cell respiration and inhibiting tumor growth ^[13]. With the continuous development of exosome purification, extraction and screening technology, it is promising to develop the application of exosomes in early cancer diagnosis, monitoring and prognosis evaluation ^[14].

The purpose of this study is to investigate the changes on morphology and expression level of exosomes in peripheral blood of mice with lung adenocarcinoma at different stages during the tumorigenesis and development, which helps to the further application of exosomes in lung adenocarcinoma diagnosis and prognosis assessment.

2.   Methods and materials

2.1.   Reagents and instruments

N-methyl-N'-nitro-N-nitrosoguanidine (MNNG) (L/N: EVNGB-RH) was purchased from Tokyo Chemical Industry; Rotary Slicer (Type: RM2235) was from LEICA company; Water Bath-Slide Drier (Type: Tec 2500) was from Changzhou Haosilin Medical Instrument Co., Ltd.; Hematoxylin (Art. No: H9627; L/N: SLBN3249V) and Eosin (Art. No: E6003; L/N: 62R80915X) were both from Sigma; exosome extraction kit (Art. No: E1001) was from Geneseed Biotech Co., Ltd.; primary antibodies CD63, TSG101 and β-actin were all from Abcam, US; secondary antibodies Goat anti-Rabbit IgG and Goat anti-Mouse IgG were from Multi Sciences (Lianke) Biotech Co., Ltd.; enzyme-labeled instrument (SPECTRA max Plus 384) was from Molecular Devices company; electrophoresis system (Mini-Proten Tetra System) was from Bio-RAD company; maintenance feed was provided by Jiangsu Xietong Pharmaceutical Bio-engineering Co., Ltd. Execution Standard Number: GB14924.3-2010 Laboratory Animals-Nutrients for Formula Feeds.

2.2.   Methods

2.2.1.   Animals grouping

Fifty SPF KM mice (4 weeks old, weighing 18-22 g, female) were randomly divided into two groups: control group (n = 10) and lung adenocarcinoma model group (n = 40). Mice in the control group were fed normally with no drug treatment according to SPF requirement. After 28 weeks, the mice were executed and the indices were tested. Mice in the lung adenocarcinoma model group were fed for 28 weeks according to SPF requirement as well. Differently, they were subcutaneously injected (S.C.) with nitrosoguanidine once a week for 4 consecutive weeks from the beginning, 10 mice among which were executed at 4 appointed time points (14^th week, 18^th week, 24^th week, 28^th week), followed by indexes test. According to the literature reports, lung adenocarcinoma can be staged as precancerous (14^th week), early (18^th week), middle (22^nd week) and advanced stages (28^th week) from the first administration.

2.2.2.   Experimental animals modeling

Mice in the model group were allowed to acclimate for one week before model establishment. They were housed in a 65-75% relative humidified environment at 23 ℃ and had free access to food and drink. The establishment of model animals was conducted referring to Luo et al.'s study in 1992 ^[15]: MNNG (0.2 mL, 2.0 mg/mL) were injected into the mice back by S.C. every week for 4 consecutive weeks [A7-im]. Then the samples were collected and tested at the four appointed time points.

2.2.3.   Specimens collection

The mice were anesthetized by intraperitoneal injection of 0.02 mL of ketamine solution (10 mg/mL). Cardiac puncture was performed for blood extraction. The neck skin was cut along the middle line to separate the trachea, which was then ligated at the end of deep inspiration to keep the lungs expanding. Subsequently, the lungs, liver and kidney were separated. Mice of the control group were also treated in the same way. Lung tumor of 0.5 mm was taken as the criterion for judgement of early lung adenocarcinoma in mice. Lung, liver and kidney were immersed in 4% formaldehyde solution for more than 24 hours, respectively. Ten tumor nodules were randomly selected and cut into tissue blocks of 3 mm thick. After dehydration, paraffin immersion, embedding, ultrathin sections (3 μm thick), tissue samples were stained with HE and blocked, followed by observed under a light microscope in many aspects, such as the histological type, location, size and margin of the tumors.

2.2.4.   HE staining

Paraffin sections of mice lung tissues were dewaxed, rehydrated, and stained in hematoxylin dye solution at room temperature for 5 min. Tap water was utilized to wash the sections. Then, the sections were immersed in 1% hydrochloric acid alcohol solution for several seconds and rinsed by tap water until the tissues were back to blue. Subsequently, the sections were stained by Eosin for 3-5 min and washed in tap water again. After dehydration, clearing and sealing, the nuclei presented blue or purple blue, the cytoplasm was pink, and red blood cells showed bright red.

2.2.5.   Exosomes separation

Cardiac puncture was performed in mice in both model and control groups. Blood samples were collected and underwent anticoagulation with heparin. Thereafter, the blood was centrifuged at 4 ℃ for 20 min (2000 r/min). Upper plasma was taken out to 1.5 mL of RNase-free EP tube and stored at -80 ℃ for standby application. For better observation, blood from the 10 mice treated each time point was randomly divided into 5 groups. Exosome extraction reagent, Exoquick precipitation, was used to extract exosomes from the 0.5 mL of standby plasma following the instructions. After extraction, Transmission Electron Microscope (TEM) was applied to observe the morphology and size of exosomes. Western blot was sequentially conducted to detect the specific maker proteins of exosomes, including TSG101 and CD63.

2.2.6.   Transmission electron microscope (TEM) method

The prepared precipitate suspension of exosomes was firstly fixed with 2.5% glutaraldehyde and 1% citric acid, then dropped on a copper-loaded mesh and maintained at room temperature for 2 min. Liquid was absorbed from the side by filter paper, and the exosomes were negatively stained with 4% phosphotungstic acid solution for 2 min at room temperature. Then the dye solution was absorbed and the mesh was dried under incandescent light for about 10 min. Image was observed and photographed under a TEM.

2.2.7.   Western blot

Proteins extracted from exosomes were concentrated by BCA method and quantitated using BCA quantitation kits with loading buffer. Then the proteins were separated by SDS-PAGE (150 g/L) and transferred onto nitrocellulose membrane (NC), which was sequentially blocked in 5% milk powder solution prepared by TBST for 2 hours. TBST was used to wash the membrane. Thereafter, the membrane was incubated with two primary antibodies (anti-mouse TSG101 and CD63, dilution at 1:5000 and 1:1000, respectively) at 4 ℃ for 12 hours, followed by HRP-labeled secondary antibodies (Goat anti-Rabbit IgG and Goat anti-Mouse IgG, both dilution at 1:5000) for 2 hours. Protein bands were visualized using colloidal gold kit according to the manufacturer’s protocols. Quantity One software was utilized to analyze the gray-scale values and the relative expression of proteins were calculated. The experiment was repeated 3 times.

2.2.8.   Statistical analysis

Variance analysis and statistical test were performed to analyze means of multiple groups with GraphPad Prism software. The count data in Table 1 were presented in the form of mean value ± standard deviation. Comparison of measurement data was performed by t test. All experiments were duplicated at least three times. A P-value less than 0.05 was statistically significant.

Table 1.  Statistic number of tumor in lung tissue section of each mouse.

Group	Number
Control Group	0
Model-14w Group	4.20 ± 2.59
Model-18w Group	8.80 ± 6.61
Model-24w Group	6.40 ± 3.21
Model-28w Group	10.00 ± 5.64

---

 | Show Table

DownLoad: CSV

3.   Results

3.1.   HE staining results of mouse lung tissues

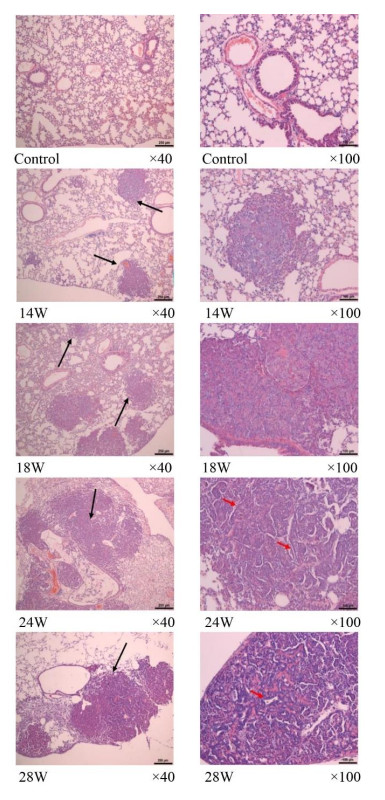
As shown in Figure 1, lung tissues in the control group presented normal structures, with no obvious lesions except local thickening of alveolar wall in individual samples. While in the model groups, pulmonary masses were obvious at 14 W and 18 W and clearly distinguished with the surrounding areas. In addition, masses in some samples showed gland-like growth trend, finally proceeding to lung adenocarcinoma. From the time of 24 W, the adenoid proliferation of cancer cells were more obvious than that at the last 2 time points, showing irregular shapes and unclear boundaries. Moreover, as shown in Table 1, the number of pulmonary masses in each model group was increased significantly relative to that in the control group (P < 0.05). Collectively, the results showed that the lung adenocarcinoma model mice were successfully established.

Figure 1.  HE staining results of lung tissue pathological changes.

DownLoad: Full-Size Img PowerPoint

3.2.   TEM results

TEM was used to observe the morphology and structure of exosomes in the control group and model groups. As exhibited in Figure 2, membranes of exosomes showed clear structures, presenting as saucer or concave hemisphere. Exosomes with 50-200 nm size were considered successfully extracted.

Figure 2.  Morphology and structure of exosomes observed by TEM.

DownLoad: Full-Size Img PowerPoint

3.3.   Western blot results

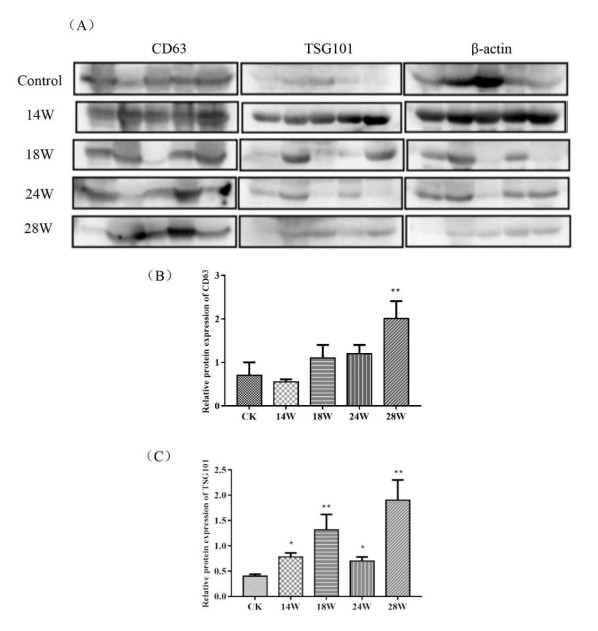
Western blot was conducted to detect the protein levels of CD63 and TSG101 in the control group and model groups. As shown in Figure 3, with the extension of modeling time, the protein levels of CD63 in the model groups were increased gradually relative to that in the control group, and the highest level was found in the model group at 28 W with significant difference (P < 0.01). This finding revealed that there was strong association between the different stages of lung adenocarcinoma and the expression level of exosomes in serum. Similarly, TSG101 in the model groups exhibited remarkedly increased protein level by comparison with that in the control group (P < 0.05). However, there was no significant correlation observed.

Figure 3.  Expression of CD63 and TSG101 detected by Western blot. (A) Electrophoretic band graph of CD63 and TSG101; (B) Expression of CD63; (C) Expression of TSG101. (“*” means P < 0.05, “**” means P < 0.01).

DownLoad: Full-Size Img PowerPoint

4.   Discussion

In recent years, the study on exosomes in disease diagnosis and prognosis evaluation has become a hotspot. So far, exosomes from various tumors have been researched, including colorectal cancer, breast cancer, prostate cancer and pancreatic cancer. Exosomes have been used as potential biomarkers and therapeutic targets for cancer. In 2016, the first exosome-based cancer diagnostic product came into the market ^[16], marking the new progress of exosome-based therapy for cancer. Research based on exosomes and their related components may bring new hope for the treatment of cancer patients.

Some scholars have proposed the mechanism of exosomes involved in tumorigenesis, development and metastasis: tumor exosomes (TEX) contain a large number of active molecules that can promote tumor cell growth, invasion and metastasis, such as proteins, mRNAs and miRNAs. Exosomes can targeted transfer these active substances to mesenchymal cells, endothelial cells, inflammatory cells and immune cells, which were then "domesticated" to produce various factors conducive to the tumor proliferation, invasion and migration, consequently allowing for the formation of "pre-metastasis microenvironment" of tumors ^[17]. The increase of exosomes can promote the proliferation, metastasis and invasion of cancer cells, leading to deterioration of the disease.

In this project, lung adenocarcinoma model mice were constructed by subcutaneous injection of nitrosoguanidine. HE staining was applied to observe the pathological changes of lung tissues, thereby verifying the success of the mouse model establishment. TEM was utilized for the observation of exosomes morphology in serum at different stages of the lung adenocarcinoma in mice (precancerous stage, early stage, middle stage and advanced stage), finding that the exosomes membrane had clear structures and presented as saucer or concave hemisphere. In addition, with the progression of lung cancer in mice, the number of exosomes was increased, which indicated a closely correlation between the exosomes and the tumorigenesis as well as development. Moreover, Western blot was employed to test specific proteins (TSG101 and CD63) of exosome, finding that with the progress of lung cancer, CD63 in the model groups had significantly elevated protein level relative to that in the control group, which again suggested that exosomes might be involved in the regulation of lung cancer progress. However, despite the similar trend of TSG101 expression in the mouse models, the result was not sufficient to reflect the correlation between cancer development stages and exosome level, thus further experimental verification should be carried out. Zhang Y, et al. ^[18] reported that the protein levels of exosome markers, CD62P and CD63, in peripheral blood of lung cancer patients were significantly higher than those of healthy people. Furthermore, Liu F, et al. ^[19] suggested that compared with normal pulmonary epithelial cells, the expression of TSG101 mRNA in lung cancer cell lines was much higher. Taken together, these findings reveal that the up-regulation of exosomes level in lung cancer can be used as a platelet-like diagnostic index so as to provide a new way for the diagnosis of lung cancer.

This study primary verified a strong association between the development of lung adenocarcinoma in mice and the level of exosomes in serum through the detection of exosomes morphology and specific proteins expression levels. However, there are some limitations in this experiment. Although the expression of TSG101 showed increased trend as CD63, it could not reflect such association between tumor and exosome. Therefore, more exosome-related markers should be selected in subsequent experiments for further verification. Although the specific mechanism of exosomes on the occurrence and development of lung adenocarcinoma had not been further studied, this study provides possibility for the diagnosis of pathological staging of lung adenocarcinoma by exosomes.

Acknowledgements

This study was supported by Public Welfare Technology Application on Animal Experiment of Science and Technology Agency in Zhejiang Province (2017C37103).

Conflict of interest

The authors declare they have no conflict of interest.