In this work, we are interested on the study of the Fujita exponent and the meaning of the blow-up for the fractional Cauchy problem with the Hardy potential, namely,
ut+(−Δ)su=λu|x|2s+upinIRN,u(x,0)=u0(x)inIRN,
where \lt i \gt N \lt /i \gt \gt 2 \lt i \gt s \lt /i \gt , 0 \lt \lt i \gt s \lt /i \gt \lt 1, (-∆) \lt sup \gt \lt i \gt s \lt /i \gt \lt /sup \gt is the fractional laplacian of order 2 \lt i \gt s \lt /i \gt , \lt i \gt λ \lt /i \gt \gt 0, \lt i \gt u \lt /i \gt \lt sub \gt 0 \lt /sub \gt ≥ 0, and 1 \lt \lt i \gt p \lt /i \gt \lt \lt i \gt p \lt /i \gt \lt sub \gt + \lt /sub \gt ( \lt i \gt s \lt /i \gt , \lt i \gt λ \lt /i \gt ), where \lt i \gt p \lt /i \gt \lt sub \gt + \lt /sub \gt ( \lt i \gt λ \lt /i \gt , \lt i \gt s \lt /i \gt ) is the critical existence power to be given subsequently.
To Sandro in his 70th birthday with our friendship.
1.
Introduction
In the pioneering work [10], Fujita found a critical exponent for the heat equation with a semilinear term of power type. More precisely, for the problem,
where 1<p<∞, Fujita proved that if 1<p<1+2N, then there exists T>0 such that the solution to problem (1.1) satisfies ||u(⋅,tn)||∞→∞ as tn→T. However, if p>1+2N, then there are both global solutions for small data as well as non-global solutions for large data. The critical value F(0)=1+2N is often called the critical Fujita blow-up exponent for the heat equation. Moreover it is proved that for p=1+2N, a suitable norm of the solution goes to infinity in a finite time. We refer to [24] for a simple proof of this last fact (see also [13]).
Sugitani in [22] studies the same kind of question for the fractional heat equation, that is, the problem,
where N>2s, 0<s<1, p>1 and u0≥0 is in a suitable class of functions.
By (−Δ)s we denote the fractional Laplacian of order 2s introduced by M. Riesz in [20], that is,
where
is the normalization constant to have the identity
for every u∈S(RN), the Schwartz class. See [8,9,14] and Chapter 8 of [17], for technical details and properties of the fractional Laplacian.
In [1], the authors deal with the following problem,
where N>2 and 0∈Ω.
This problem is related to the classical Hardy inequality:
Hardy Inequality. Assume N≥3. For all ϕ∈C∞0(RN) the following inequality holds,
Moreover ΛN:=(N−22)2 is optimal and is not achieved.
The blow-up in the L∞ norm for the solution of problem (1.4) is produced in any time t>0, for any nonnegative data and for all p>1, according with the results by Baras-Goldstein in [3]. Therefore, the Fujita behavior in the presence of the Hardy potential must be understood in a different way.
For λ>0, setting μ1(λ)=N−22−√(N−22)2−λ, then it was proved that if 1<p<1+2N−μ1(λ), there exists T∗>0 that is independents of the nonnegative initial datum, such that the solution u to problem (1.4) satisfies
for any ball Br(0). Moreover for p>1+2N−μ1(λ), if the initial datum is small enough, there exists a global solution to (1.4). According to this behavior the corresponding Fujita type exponent for problem (1.4) is defined by F(λ)=1+2N−μ1(λ) and the blow-up is understood in the sense of local weighted L1 associated to (1.6). The Hardy inequality is an expression of the uncertainty Heisenberg principle, hence we can say that the result in [1], explains the influence of the uncertainty principle on the diffusion problem (1.4).
The following fractional Hardy inequality appears in [9] in order to study the relativistic stability of the matter.
Theorem 1.1. (Fractional Hardy inequality). For all u∈C∞0(IRN) the following inequality holds,
where
The constant ΛN,s is optimal and is not attained. Moreover, ΛN,s→ΛN,1:=(N−22)2, the classical Hardy constant, when s tends to 1.
This inequality was proved in [12]. See also [5,9,23,25]. The reader can find all the details of a direct proof in Section 9.2 of [17].
Recently, in [2] and related to the Hardy inequality stated in (1.7), the authors study the fractional parabolic semilinear problem,
where N>2s, 0<s<1, p>1, c,λ>0, and u0≥0, f≥0 are in a suitable class of functions. By (−Δ)s we denote the fractional Laplacian of order 2s, defined in (1.3). In [2] and [4], the authors prove the existence of a critical power p+(s,λ) such that if p>p+(s,λ), the problem (1.8) has no weak positive supersolutions and a phenomenon of complete and instantaneous blow up happens. If p<p+(s,λ), there exists a positive solution for a suitable class of nonnegative data.
In this note, we deal with the corresponding fractional Cauchy problem,
with 1<p<p+(s,λ) in order to find the value of the corresponding Fujita exponent.
A relevant fact in this work is that the effect of the Hardy potential produces a shift on the right of the Fujita exponent of the fractional heat equation, depending of the spectral parameter λ.
The problem (1.9) with s∈(0,1) and λ=0 was considered in [22]. The author was able to show that F(s):=1+2sN is the associated Fujita exponent. See also [11] for some extensions.
For λ>0, any solution to problem (1.8) is unbounded close to the origin, even for nice data (see [2]). This is the corresponding nonlocal version of the Baras-Goldstein results for the heat equation developed in [3]. Therefore, L∞-blowup is instantaneous and free in problem (1.9) as in the local case and the blowup will be also obtained in a suitable weighted Lebesgue space.
In this work we will treat the case s∈(0,1) and λ>0 that is more involved than the local problem for several reasons, one of them that the kernel of the fractional heat equation has not a closed form with the exception of s=12 and s=1.
The paper is organized as follows. In Section 2 we introduce some tools about the fractional equation. The Fujita exponent F(λ,s) for problem (1.9) in obtained in Section 3. Notice that by the Fujita exponent, we understand that, independently of the initial datum, for 1<p<F(λ,s), any solution to (1.9) blows-up in a certain weighted norm in a finite time. The Fujita exponent verifies F(λ,s)<p+(s,λ), and the effect of the Hardy potential is reflected by the strict inequality, F(0,s)<F(λ,s).
The critical case p=F(λ,s) is analyzed in Subsection 3.1. In this case we are able to show a blowup of a precise norm of u that reflects the critical exponent F(λ,s). In Section 4, for F(λ,s)<p<p+(λ,s), we prove the existence of global solutions for suitable data. This shows in some sense the optimality of our blow up results.
2.
Preliminaries tools
First, we enunciate some Lemmas and notations that we will use along the paper (see [2] for a proof).
Lemma 2.1. Let 0<λ≤ΛN,s. Then v±α=|x|−N−2s2±αλ are solutions to
where αλ is obtained by the identity
Remark 2.2. Notice that λ(αλ)=λ(−αλ)=mαλm−αλ, with mαλ=2sΓ(N+2s+2αλ4)Γ(N−2s−2αλ4).
Lemma 2.3. The following equivalence holds true:
Remark 2.4. Notice that we can explicitly construct two positive solutions to the homogeneous problem (2.1). Henceforth, we denote
with 0<μ(λ)≤N−2s2≤ˉμ(λ)<(N−2s). Since N−2μ(λ)−2s=2αλ>0 and N−2ˉμ(λ)−2s=−2αλ<0, then |x|−μ(λ) is the unique nonnegative solution that is locally in the energy space.
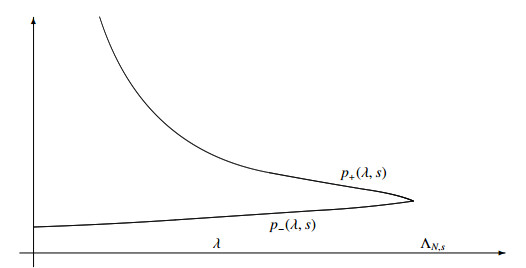
The critical existence power p+(λ,s), found in [2,4], depends on s and λ, and in particular satisfies:
(See Figure 1 below).
Note that if λ=ΛN,s, namely, αλ=0, then p+(λ,s)=N+2sN−2s=2∗s−1, and if λ=0, namely, αλ=N−2s2, then p+(λ,s)=∞. Noting
it follows that for λ=ΛN,s, namely, αλ=0, then p−(λ,s)=2∗s−1 and if λ=0, namely, αλ=N−2s2, then p−(λ,s)=NN−2s. Hence,
3.
Blow up result for the Cauchy problem
It is clear that L∞-blowup is instantaneous and free in problem (1.9) because the solutions are unbounded at the origin.
Before starting the main blowup result we begin by precising the sense for which blow up is considered. As in the case s=1, λ>0, this phenomenon will be analyzed in a suitable weighted Lebesgue space.
Definition 3.1. Consider u(x,t) a positive solution to (1.9), then we say that u blows-up in a finite time if there exists T∗<∞ such that
with μ(λ)=N−2s2−αλ.
The next proposition justifies in some sense the previous definition.
Proposition 3.2. Let λ≤ΛN,s and consider u to be a nonnegative solution to problem (1.9), then
In particular, for all t∈(0,T), we have
The proof follows combining the approximating arguments used in [1,2].
The main blow up result of this section is the following.
Theorem 3.3. Suppose that 1<p<F(λ,s):=1+2sN−μ(λ) and let u be a positive solution to problem (1.9). Then there exists T∗:=T∗(u0) such that
Before proving Theorem 3.3, we need some analysis related to the fractional heat equation.
Let h(x,t) be the fractional Heat Kernel, namely,
There is no known closed form for h(t,x) in real variables. However, in Fourier variables it is simply F(h)(t,ξ)=e−t|2πξ|2s. The properties of the kernel h were studied in [18] for N=1 and in [6] for all dimensions. More precisely, since h(x,t) is defined by
where 0<s<1 and N≥2s, then there exists a constant C>1 such that
There is a direct approach inside of the Real Analysis field and even without using Bessel functions. Such a proof is based on a celebrated result by S. N. Bernstein about the characterization of completely monotone functions via Laplace transform. See Section 12.5 of [17] for a detailed proof.
Notice that h(x,t)=t−N2sH(|x|t12s) and H is a decreasing function that satisfies
with
See for instance [7] and [21]. We set
We also have the elementary formula,
Hence, for t>0, we have
Notice that
Thus
where we have used the fact that H′≤0. Thus
We are now in position to prove Theorem 3.3.
Proof of Theorem 3.3. We follow closely some arguments developed in [1], see also [19]. Let u be a positive solution to (1.9). Fix η>0 to be chosen later and define the function ψη
then by the previous computation it holds that
Notice that
Now, using ψη as a test function in (1.9), we get
Thus
Using Jensen inequality, there results that
Then
Setting
it follows that
Integrating the previous differential inequality, we arrive to
Therefore,
It is clear that, if for some T<∞, we have
then Y(T)=∞.
Since (1−e−(p−1)N2sηT)→1 as T→∞, then condition (3.3) holds if
Hence
and then
It is clear that (3.4) holds for η small if and only if
and then p<F(λ,s).
Since
using the fact that H is bounded, there exists η>0 such that
Hence the result follows.
3.1. The critical case
Notice that the above argument does not hold for the critical case p=F(λ,s). Hence in this case we will use a different argument based on a suitable apriori estimates as in [11,16]. More precisely we have
Theorem 3.4. Assume that p=F(λ,s):=1+2sN−μ(λ). If u is a positive solution to problem (1.9), then there exists T∗:=T∗(u0) such that
Proof. We will perform the ground state transform, i.e., define v(x,t):=|x|μ(λ)u(x,t), then
where
and
See [9,2]. Thus v solves the parabolic equation
It is clear that
Therefore, in order to show the blowup result we will prove that
We argue by contradiction. Assume that ∫IRN|x|−μ(λ)(p+1)vpdx<∞ for all t<∞. We claim that
Let φ∈C∞0(IRN) be such that 0≤φ≤1, φ=1 in B1(0) and φ=0 in IRN∖B2(0). Define ψ(x,t)=φ(t2+|x|4sR2) with R>>1. It is clear that if t>R, then ψ(x,t)=0. Fix T>R, then using ψm as a test function in (3.6), with 1<m<p′, setting QT=IRN×(0,T) and using Kato inequality, it holds that
We begin by estimating I. Define
it is clear that suppψt⊂Q1T and suppψ⊂Q1T. Then we have
In the same way we have
Now, since p=F(λ,s) and setting τ=tR,y=xR12s, we reach that
and
where θ(y,τ)=φ(τ2+|y|4s). Thus
Therefore, using Young inequality, we obtain that
where C is independent of R and T. Letting R,T→∞, we conclude that
and the claim follows.
Recall that by (3.8) we have
with
and
From (3.11) and using the result of the claim we deduce that
Now we deal with J. For κ>0 small enough, We have
Using the same change of variable as above we obtain that
Thus
Thus combining (3.10), (3.13) and (3.14) and letting R→∞, we conclude that
a contradiction and then the result follows.
Remarks 3.5. Notice that the above blow up result holds under the hypothesis that we can choose φ∈C∞0(B2(0)) with 0≤φ≤1, φ=1 in B1(0) and
where θ(y,τ)=φ(τ2+|y|4s).
The above conditions hold choosing m closed to p′ and κ small enough.
4.
Global existence for F(λ,s)<p<p+(λ,s).
In order to show the optimality of F(λ,s) we will prove that, under suitable condition on u0, problem (1.9) has a global solution. To achieve this affirmation, we will show the existence of a family of global supersolutions to problem (1.9) where F(λ,s)<p<p+(λ,s).
Recall that F(λ,s)=1+2sN−μ(λ), since p<p+(λ,s)=1+2sμ(λ), then 2sp−1>μ(λ). Fix γ>0 be such that μ(λ)<γ<2sp−1, then for T>0, we define
where θ=2sp−1 and, as above, β=12s. Notice that
It is clear that
We claim that, under suitable condition on A and T, w satisfies
For simplicity of typing we set
then
By a direct computations we reach that
Since T>0, then
On the other hand we have
Since γ>μ(λ), then λ(γ)>λ.
We deal now with the mixed term
By a direct computations, it follows that
where x1=|x|(T+t)β and y1=|y|(T+t)β. Since H is decreasing then J(x)≥0. Therefore, combining the above estimates it holds that
Hence, w is a supersolution to (1.9) if we can chose A,C>0 such that
hence
The last inequality is equivalent to have
Recall that θ=2p−1, since γ<2sp−1, then
On the other hand we have 2s+γ>(p−1)γ. Thus going back to (4.3), we conclude that, for any T>0, we can choose A small such that w is a supersolution to (1.9) and then the claim follows.
We are now able to state the main global existence result in this section.
Theorem 4.1. Assume that F(λ,s)<p<p+(λ,s). Let u0 be a nonnegative function such that
then the Cauchy problem (1.9) has a global solution u such that u(x,t)≤w(x,t,T) for all (x,t)∈IRN×(0,∞).
Proof. Let u0 be a nonnegative function such that the above condition holds, then u0∈L2(IRN). According to the definition of w given in (4.1), there exist A,T0>0 such that u0(x)≤w(x,0,T0) for all x∈RN. Thus w is a supersolution to problem (1.9). Since v(x,t)=0 is a strict subsolution, we can use the same classical iteration argument as in Theorem 6.2 in [1] for the heat equation and the existence result follows. For the reader convenience we give a schematic idea of the iteration argument. Let Bn be the ball in RN with radius n and centered at the origin. We consider
the weak solutions to the following approximated problems,
with
and ˜vn−1=vn−1 in Bn×(0,T), ˜vn−1=0 in (RN∖Bn)×(0,T). See for instance [15].
Applying the classical comparison principle for finite energy solutions, we conclude that 0<v0≤v1≤⋯≤vn−1≤vn≤w in Bn+1×(0,T1) with T1<T. Hence there exists u∈L2(0,T1,L2loc(RN)) such that vn↑u strongly in L2((0,T1),L2(RN)) and u≤w. Using the monotonicity of vn and the dominated convergence theorem it follows that vn→u strongly Lp(K×(0,T1)) for all compact set K⊂RN. Take ϕ∈C∞0(RN×(0,T1)), then using ϕ as a test function in (4.4) and by letting n→∞ we easily get that u solves problem (1.9) with u(x,0)=u0(x). It is clear that u∈L2(0,T1;Hs(RN)).
Remark 4.2. In the general case 1<p<p+(λ) and under some hypotheses on u0 it is possible to show a complete blowup in a suitable sense.
Suppose that u0(x)≥h where h≥0 satisfies h∈C∞0(RN), supp(h)⊂B0(R) and
Then if u is a positive solution to problem (1.9) we have
We argue by contradiction. Suppose that the above conditions holds and that
Let w be the unique positive solution to the problem
It is clear that w∈L2(0,T(h);Hs0(BR(0)))∩L∞(BR(0)×(0,T(w)). Since u is a supersolution to (4.7), then w≤u and therefore T(w)=∞. Define the energy in time t,
By a direct computations, it follows that ddtE(t)=−⟨wt,wt⟩≤0. Taking into consideration the hypothesis on h, we conclude that E(t)≤0 for all t. Hence
By integration, it holds
a contradiction with (4.6).
Remark 4.3. Notice that
Hence,
See Figure 2.
Acknowledgments
Work partially supported by Project MTM2016-80474-P, MINECO, Spain. The first author is also partially supported by an Erasmus grant from Autonoma University of Madrid and by the DGRSDT, Algeria.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:




