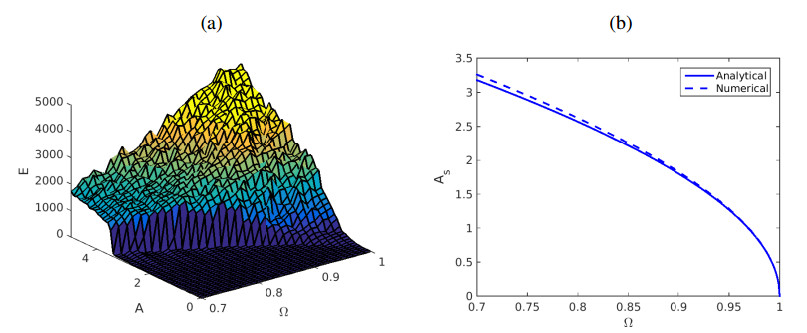
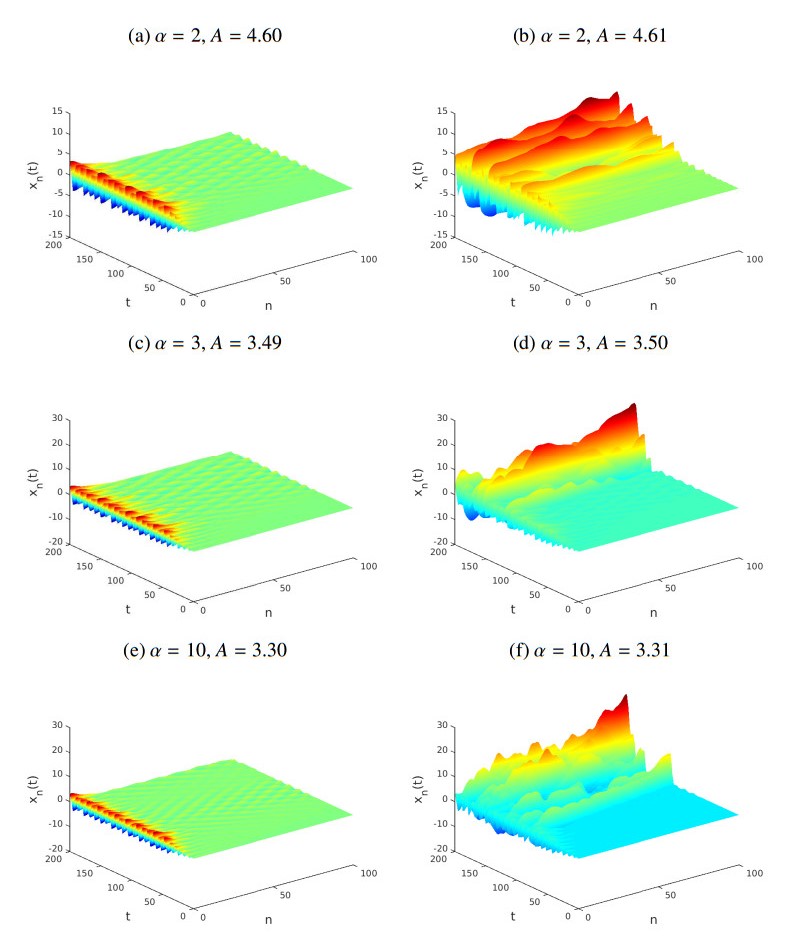
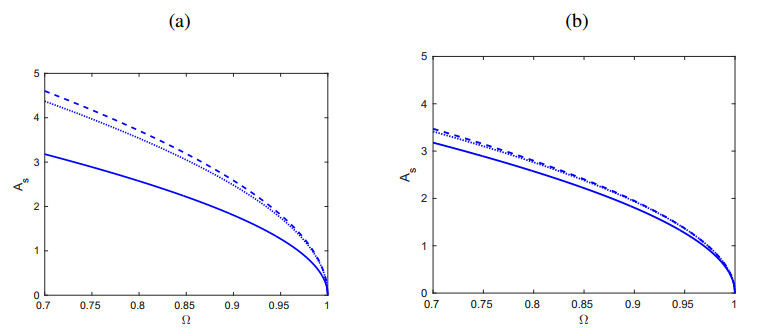
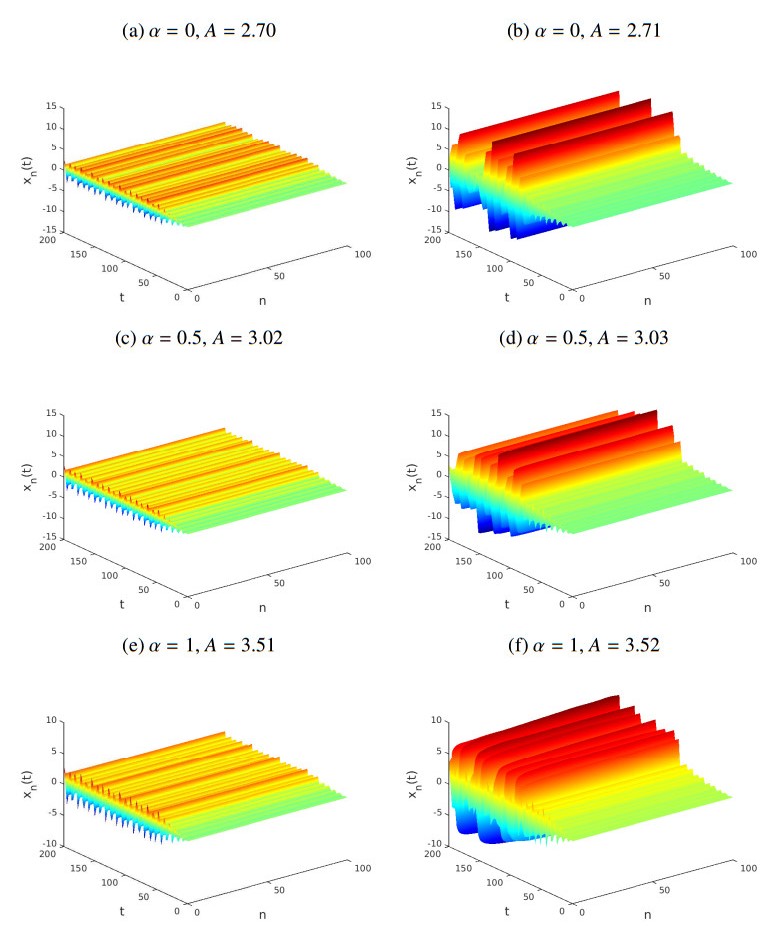
We consider a family of 1-dimensional Hamiltonian systems consisting of a large number of particles with on-site potentials and global (long range) interactions. The particles are initially at rest at the equilibrium position, and are perturbed sinusoidally at one end using Dirichlet data, while at the other end we place an absorbing boundary to simulate a semi-infinite medium. Using such a lattice with quadratic particle interactions and Klein-Gordon type on-site potential, we use a parameter 0≤α<∞ as a measure of the "length" of interactions, and show that there is a sharp threshold above which energy is transmitted in the form of large amplitude nonlinear modes, as long as driving frequencies Ω lie in the forbidden band-gap of the system. This process is called nonlinear supratransmission and is investigated here numerically to show that it occurs at higher amplitudes the longer the range of interactions, reaching a maximum at a value α=αmax≲1.5 that depends on Ω. Below this αmax supratransmission thresholds decrease sharply to values lower than the nearest neighbor α=∞ limit. We give a plausible argument for this phenomenon and conjecture that similar results are present in related systems such as the sine-Gordon, the nonlinear Klein-Gordon and the double sine-Gordon type.
1.
Introduction
A topological index is a numerical representation derived from a graph's structural arrangement, independent of vertex labels. It remains consistent even for isomorphic graphs, indicating robustness. In mathematical chemistry, the focus is on deriving these indices for chemical graphs, correlating with intrinsic physicochemical attributes. This comes from the belief that molecular traits relate to atom valences and positions. Graph-theoretical language effectively conveys these ideas, making chemical graphs rich in real-world molecular information for precise modeling. According to Milan Randić [1], a topological index's acceptance depends on satisfying criteria: positive property correlations, structural interpretation, insightful potential, adaptability, simplicity, non-triviality, effective composition and rooted in structural abstractions. While some molecular attributes align clearly with indices, this is not uniform, leading to doubts about engineered indices and coincidental correlations. Yet, validating indices often involves understanding their relevance to molecular structure components linked to properties. Even when comprehension is elusive, dismissing outcomes hastily is unwise. Meticulous analysis might reveal overlooked physicochemical mechanisms. Given the complexity of ab initio methods for molecular treatment, topological indices remain essential tools in mathematical chemistry's landscape. Numerous distinct topological indices have undergone extensive exploration and application in QSAR/QSPR studies, yielding varying levels of effectiveness. Among the most valuable constants are those that fall into two overarching categories: distance-derived or bond-additive. The former group encompasses indices that find definition in vertex pair distances, while the latter includes indices formed by aggregating contributions across all edges. In the first category, the Wiener index and its various adaptations stand out [2], while the second category features indices such as the Randić index [3] and the Zagreb indices pair [4,5]. The initiation of topological indices dates back to 1947, when chemist Wiener discovered the inaugural Wiener index [6]. This index was devised to predict boiling points of chemical compounds and is defined as
Building upon this initial index, a variety of new topological indices have been introduced to improve the accuracy of boiling point predictions for diverse chemical compounds. Recent advancements in this area are noteworthy. For an in-depth analysis of these developments in boiling point prediction, please consult reference [7], which highlights a pivotal discovery, i.e., the boiling point of benzenoid hydrocarbons shows a stronger correlation with the first Zagreb eccentricity index compared to the second. This crucial finding enhances our comprehension of these compounds' physical characteristics, opening new avenues for both their practical usage and theoretical exploration. In [8], the authors achieved a significant result in their Quantitative Structure-Property Relationship (QSPR) analysis: they were able to accurately predict the boiling points of these compounds using the fifth nearest neighbor (5th NN) entropy method. This finding holds significant importance due to the widespread application of benzene in diverse fields like pharmaceuticals, dyes and lubricants. We encourage interested readers to consult [9,10,11]. In recent scholarly discourse, there has been a notable surge of interest in the broader computational quandaries surrounding the determination of topological indices and their algebraic operations [12] presents a simplicial network model to capture complex higher-order interactions in various systems. It examines the network's structure and derives the Sombor index, revealing key patterns like power-law behavior. The study underscores the model's effectiveness in understanding complex interactions. Also, [13] introduced the variable sum exdeg index was originally used for predicting the octanol-water partition coefficient of certain chemical compounds. It is a unique measure for a graph, calculated by summing up the products of the degree of each vertex raised to the power of a positive real number, with the real number being different from one. This paper, focuses on certain sub groups of tricyclic graphs. Identifying the graph that has the highest variable sum exdeg index from each subgroup ensures that all these graphs have perfect matching. This allows us to compare these graphs and determine which one in the larger collection has the highest value of this index.
In 2015, B. Furtula and I. Gutman [14] defined the forgotten index, or F-index, as follows:
In a seminal study [15], both the forgotten topological index and the first Zagreb index played pivotal roles in computing the total π-electron energy. Acting as indicators, these indices enabled the assessment of the intricate branching intricacies within the molecule's carbon-atom framework. Despite an initial lack of attention, the F-index has emerged as a focus of recent research, attributed to the noteworthy investigation by Furtula and Gutman [15]. This study elucidated the F-index's underlying principles and unveiled its predictive prowess, akin to that of the first Zagreb index. Remarkably, both indices exhibited strong correlation coefficients, exceeding 0.95, when linked with entropy and acetic factor. Notably, [16] accentuated the significance of the F-index by showcasing its accurate prognostication of the logarithm of the octanol-water partition coefficient. Sufficient conditions for a graph to be ℓ-connected, ℓ-deficient, ℓ-Hamiltonian and ℓ-independent in terms of the forgotten topological index is presented in [17]. The forgotten index assumes a crucial role by upholding molecular structure symmetry, while providing a robust mathematical foundation to anticipate the physicochemical attributes of molecules. Recent strides in understanding the forgotten index and its diverse applications have been meticulously documented in contemporary works [18,19,20,21]. Motivated by this backdrop, our current study delves into unearthing a novel iteration of this index. We specifically concentrate on its potential in predicting the boiling points of primary amines. By expanding our understanding of this index's capabilities, we aim to contribute to the advancement of predictive models for molecular properties, enhancing their practical utility in various scientific and industrial contexts.
Throughout this paper, we consider only simple connected graphs. For a graph ζ=(V(ζ),E(ζ)), V(ζ) and E(ζ) denote the set of vertices and edges, respectively. The set ℵ(v) of all neighbors of v is called the open neighborhood of v. Thus, ℵ(v)={u∈V:uv∈E(ζ)}. The degree dζ(u)=d(u) of a vertex u in ζ is defined as d(u)=|ℵ(v)|. The distance dζ(u,v) or d(u,v) [22] between two vertices in a graph ζ is the length of the shortest path joining them. The eccentricity ε(u)=maxv∈V(ζ)d(u,v). The radius of ζ is r(ζ)=minv∈V(ζ)ε(v), and the diameter of ζ is D(ζ)=maxv∈V(ζ)ε(v). For any graph ζ with n vertices, we define Vω(ζ)={v∈V(ζ):ε(v)=1}. In [23], Ahmed et al. introduced new degree-based topological indices known as eccentric neighborhood Zagreb indices which are defined as follows: Let ζ=(V(ζ),E(ζ)) be a connected simple graph and δen(v)=∑u∈ℵ(v)ε(u) be the eccentricity neighborhood degree. Then, the first, second and third eccentric neighborhood Zagreb indices are defined as follows:
Continuing along this research trajectory, our investigation delves into the intricate dynamics of the eccentric neighborhood forgotten index and the eccentric neighborhood modified forgotten index. We systematically analyze their behavior in response to a spectrum of graph operations. Notably, our inquiry extends to the application of these findings within the domain of molecular graphs, with a specific focus on primary amines groups. In recent scholarly discourse, there has been a notable surge of interest in the broader computational quandaries surrounding the determination of topological indices and their algebraic operations [24,25,26,27,28,29,30]. In this intellectual milieu, we make a significant contribution by introducing and rigorously defining the eccentric neighborhood forgotten index and the eccentric neighborhood modified forgotten index. Their precise formulations are as follows:
In this study, our presentation follows a structured and methodical progression.
Section 2 introduces preliminary findings, laying a foundational groundwork for the more intricate discussions that ensue. In Subsection 2.1, we delve into the computational methodologies associated with two distinct indices: the eccentric neighborhood forgotten index (ENFI) and its modified counterpart, the modified eccentric neighborhood forgotten index (MENFI). Our exploration will encompass their applicability across a diverse range of graph structures. An integral component of this subsection will be dedicated to the nuances of graph products, a specialized category within graph operations. As we transition further into Subsection 2.1, we provide an in-depth analysis of how these indices integrate seamlessly into the expansive domain of graph theory. Section 3 pivots our focus towards the pragmatic relevance of topological indices, emphasizing their pivotal role in predicting specific physicochemical attributes. To substantiate our assertions, we employ the robust technique of nonlinear regression analysis. Our choice of primary amines as the subject of study is motivated by their structural heterogeneity, positioning them as ideal candidates for this analytical endeavor. Within this context, we juxtapose the Wiener index with ENFI and MENFI, aiming to discern potential correlations between these indices and the boiling points intrinsic to primary amines. Finally, Section 4 contains our conclusions and reflections on the study.
2.
Preliminaries
In this section, we present a set of preliminary results that will serve as essential foundations for the subsequent segments of the paper. These preliminary findings are integral for establishing the groundwork necessary to advance the discussion further.
Lemma 2.1. [5] Let ζ1 and ζ2 be graphs. Then,
(a) dζ1×ζ2(u,v)=dζ1(u)+dζ2(v),
(b) dζ1[ζ2](u,v)=|V(ζ2)|dζ1(u)+dζ2(v),
(c) dζ1+ζ2(u)={dζ1(u)+|V(ζ2)|,u∈V(ζ1);dζ2(u)+|V(ζ1)|,u∈V(ζ2).
(d) dζ1∨ζ2(u,v)=|V(ζ2)|dζ1(u)+|V(ζ1)|dζ2(v)−dζ1(u)dζ2(v),
(e) dζ1⊕ζ2(u,v)=|V(ζ2)|dζ1(u)+|V(ζ1)|dζ2(v)−2dζ1(u)dζ2(v).
(f) |V(ζ1×ζ2)|=|V(ζ1∨ζ2)|=|V(ζ1[ζ2])| =|V(ζ1⊕ζ2)|=|V(ζ1)||V(ζ2)|,
|E(ζ1×ζ2)|=|E(ζ1)||V(ζ2)|+|V(ζ1)||E(ζ2)|,
|E(ζ1+ζ2)|=|E(ζ1)|+|E(ζ2)|+|V(ζ1)||V(ζ2)|,
|E(ζ1[ζ2])|=|E(ζ1)||V(ζ2)|2+|E(ζ2)||V(ζ1)|,
|E(ζ1∨ζ2)|=|E(ζ1)||V(ζ2)|2+|E(ζ2)||V(ζ1)|2−2|E(ζ1)||E(ζ2)|,
|E(ζ1⊕ζ2)|=|E(ζ1)||V(ζ2)|2+|E(ζ2)||V(ζ1)|−4|E(ζ1)||E(ζ2)|.
Lemma 2.2. [31] Suppose ζ1 and ζ2 be graphs. Then,
(a) εζ1+ζ2(u)={1,ifεζi(u)=1;2,ifεζi(u)≥2, where i∈{1,2}.
(b) εζ1∨ζ2(u,v)={1,ifεζ1(u)=εζ2(v)=1;2,ifεζ1(u)≥2orεζ2(v)≥2.
(c) εζ1[ζ2](u,v)={1,ifεζ1(u)=εζ2(v)=1;2,ifεζ1(u)=2orεζ2(v)≥2;εζ1(u),ifεζ1(u)≥2.
(d) εζ1⊕ζ2(u,v)=2.
Corollary 2.1. [19]
Theorem 2.1. [19]
Theorem 2.2. [19]
Theorem 2.3. [19]
Theorem 2.4. [19]
Lemma 2.3. [23]
(1) If ζ≅Sr is a star graph with r+1 vertices, then
(2) If ζ≅Sr,s is the double star with r+s+2 vertices, then
(3) If ζ≅Cn with n≥4, then
(4) If ζ≅Wn is the wheel graph with n≥5 vertices, then
Proposition 2.1. [23] Let ζ be a graph with D(ζ)=r(ζ)=t. Then,
2.1. Computing ENFI and MENFI of graphs and graph operations
Within this section, we provide explicit formulas detailing the computation of ENFI and MENFI for various graph classes. Additionally, we explore graph operations stemming from binary graph operations, specifically recognized as graph products.
Proposition 2.2. (1) For star graph Sr with r+1 vertices, we have EℵF(Sr)=8r3+r and EℵF∗(Sr)=4r3+r.
(2) If ζ≅Sr,s with r+s+2 vertices, then
(3) Suppose ζ≅Cn, n≥4. Then,
(4) If ζ≅Wn is the wheel graph with n≥5 vertices, then
A banana tree of type (r,s), denoted as Br,s according to the definition by Chan et al. [32], is a graph formed by linking a single leaf from each of r instances of an s-star graph with a unique root vertex that is separate from all the s-stars.
Lemma 2.4. [23] Let ζ≅Br,s with r≥2 and s≥3 and w as the root vertex. Then,
Proposition 2.3. If ζ≅Br,s with r≥2 and s≥3, then
Proof. Suppose ζ≅Br,s with r≥2 and s≥3. One can define the edge partitions of ζ as following: E1={uv∈E(ζ):δen(u)=4r,δen(v)=8}, E2={uv∈E(ζ):δen(u)=8,δen(v)=6s−8} and E3={uv∈E(ζ):δen(u)=6s−8,δen(v)=5}. Note that |E1|=|E2|=r and |E3|=r(s−2). Hence, by applying Eqs (1.6) and (1.7) we get the required result. □
Proposition 2.4. If δen(u)≤Dd(u) and rd(u)≤δen(u), then
2.1.1. Join
A join [5] ζ+F of ζ and F with disjoint vertex sets V(ζ) and V(F) is the graph on the vertex set V(ζ)∪V(F) and the edge set E(ζ)∪E(F)∪{u1u2:u1∈V(ζ),u2∈V(F)}.
Lemma 2.5. [23] Let ζ and F be any two graphs. Then,
(a) If Vω(ζ)=Vω(F)=∅, then δenζ+F(u)=2dζ+F(u);
(b) If |Vω(ζ)|=r and |Vω(F)|=s such that r+s>0, then
We can partition the edge set of E(ζ+F) as follows:
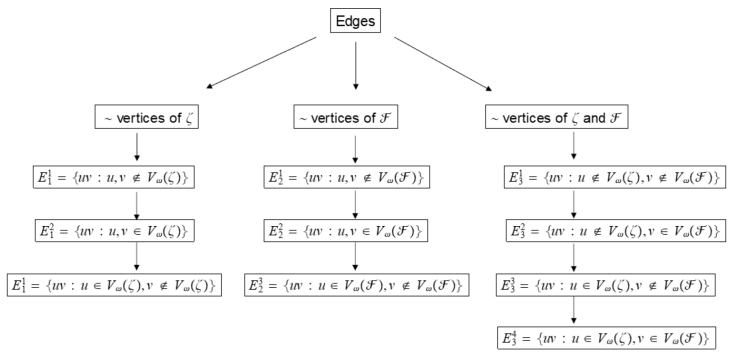
The partition of edges of the graph ζ are: E11 is the set of edges connecting the vertices which are not in Vω(ζ), E21 is the set of edges connecting the vertices of the set Vω(ζ) and E31 be the set of edges connecting vertices of Vω(ζ) to vertices which are not in Vω(ζ). The partition of edges of the graph F are: E12 is the set of edges connecting the vertices not in Vω(F), E22 is the set of edges connecting the vertices of the set Vω(F) and E32 is the set of edges connecting vertices of Vω(F) to vertices which are not in Vω(F). The edge partition connecting vertices of ζ with vertices of F are: E13 is the set of edges connecting the vertices not in Vω(ζ) with the vertices not in Vω(F), E23 is the set of edges connecting the vertices not in Vω(ζ) with the vertices of the set Vω(F), E33 is the set of edges connecting the vertices of the set Vω(ζ) with the vertices not in Vω(F) and E43 is the set of edges connecting the vertices of the set Vω(ζ) with the vertices of the set Vω(F). Figure 1 outlines the procedural steps involved in proving the subsequent theorem.
Theorem 2.5. For any two graphs ζ and F with |Vω(ζ)|=r, |Vω(F)|=s and r+s>0. Then,
and
Proof. We have
For (2.1)(1),
For (2.1)(2),
For (2.1)(3),
For (2.1)(4),
Combining (2.1)(1),(2.1)(2),(2.1)(3) and (2.1)(4), we arrive at the necessary result. For MENI, we have
For (2.2)(5),
Now,
Also,
Furthermore,
Hence,
Now, we initiate the computation process.
First,
Second,
Third,
Hence,
Now,
Following analogous computations, we acquire
Hence,
By incorporating (2.2)(5), (2.2)(6) and (2.2)(7), we arrive at the anticipated outcome. □
Corollary 2.2. If ζ and F be any two graphs such that Vω(ζ)=Vω(F)=∅, then
2.1.2. Disjunction
The disjunction [5] ζ∨F of two graphs ζ and F is the graph with vertex set V(ζ)×V(F) in which (a,b) is adjacent with (c,d) whenever ac∈E(ζ) or bd∈E(F).
Lemma 2.6. [23] Let ζ and F be any two graphs. Then,
(a) If ζ and F are complete graphs, then δenζ∨F(u,v)=dζ∨F(u,v).
(b) If Vω(ζ)=∅ or Vω(F)=∅, then δenζ∨F(u,v)=2dζ∨F(u,v).
(c) If Vω(ζ) and Vω(F) are not empty sets, such that |Vω(ζ)|=r, |Vω(F)|=s, then
Proof.
(a) If ζ and F are complete graphs, then every pair of distinct vertices is connected by an edge. In a complete graph, the distance dζ∨F(u,v) between any two vertices u and v is one because there is exactly one edge connecting them. Similarly, the eccentricity neighborhood degree δenζ∨F(u,v), which reflects the the eccentricity neighborhood degree in a pair of vertices, should also be one since all possible edges exist in a complete graph. Therefore, δenζ∨F(u,v)=dζ∨F(u,v) in complete graphs.
(b) We have εζ∨F(u,v)=1 if εζ(u)=εF(u)=1. Since dζ∨F(u,v)=|V(F)|dζ(u)+|V(ζ)|dF(v)−dζ(u)dF(v), with some direct calculations, we deduce that δenζ∨F(u,v)=2dζ∨F(u,v).
(c) If Vω(ζ) and Vω(F) are not empty sets, such that |Vω(ζ)|=r, |Vω(F)|=s, we have εζ∨F(u,v)=1. If εζ(u)=εF(u)=1, since Vω(ζ) and Vω(F) are non empty, then δenζ∨F(u,v)=2dζ∨F(u,v)+1−rs. Clearly, according to the edge partition of the disjunction we remove 1 from it otherwise.
It is possible to divide the edges of ζ∨F as follows:
The division of edges within E(ζ∨F) forms distinct partitions: E1 encompasses edges linking vertices meeting the criterion ε(u,v)=1, E2 comprises edges connecting vertices where ε(u,v)≠1 holds true and E3 encompasses edges linking vertices with ε(u,v)=1 in tandem with those where ε(u,v)≠1 applies.
Theorem 2.6. Let ζ and F be any two graphs in such that |Vω(ζ)|=r, |Vω(F)|=s with rs≥1. Then,
and
Proof. First, for the ENFI we have
Now, for (2.3)(1),
For (2.3)(2),
By combining (2.3)(1), and (2.3)(2), the desired outcome is achieved. Now, for the MENFI we have
For (2.4)(3),
For (2.5)(4),
For (2.6)(5),
Now, adding (2.4)(3),(2.5)(4) and (2.6)(5), we have our result. □
Corollary 2.3. (a) If Vω(ζ)=∅orVω(F)=∅, then
(b) If ζ and F are two complete graphs, then
2.1.3. Composition
The composition [5] of ζ=(V(ζ),E(ζ)) and F=(V(F),E(F)) is a graph ζ[F] containing vertex set V(ζ)×V(F) and, (a,b) is connected to (c,d) if and only if ac∈E(ζ) or a=c and bd∈E(F).
Lemma 2.7. [23] Let ζ and F be two graphs. Then,
(a) If ζ and F are complete, then
(b) If ζ has at least one vertex with ε(u)=1 and F does not have any vertex with ε(u)=1, then
(c) If Vω(ζ) and Vω(F) are not empty sets, such that |Vω(ζ)|=r, |Vω(F)|=s, then
In the next theorem we will denote ℸ the set of vertices which satisfy ε(u,v)=1. Also, we use the edge partition of E(ζ[F]) which is similar to the edge partition of E(ζ∨F).
Theorem 2.7. Let ζ and F be any two graphs with |Vω(ζ)|=r, |Vω(F)|=s and rs≥1. Then,
and
Proof. Initially, we calculate the ENFI using the following procedure:
Now,
and
Therefore, the result is obtained by summing up (2.7)(1) and (2.7)(2). Transitioning to the computation of the MENFI, we employ the subsequent procedure:
Now,
and
Also,
By combining (2.8)(3),(2.9)(4) and (2.10)(5), we achieve the desired outcome. □
Corollary 2.4. (a) If graphs ζ and F are complete, then
(b) If ζ has at least one vertex with ε(u)=1 and F does not have any vertex with ε(u)=1, then
2.1.4. Symmetric difference
The symmetric deference [5] ζ⊕F is defined by V(ζ⊕F)=V(ζ)×V(F) and E(ζ⊕F)={((a,b),(c,d)):ac∈E(ζ)orbd∈E(F) but not both}.
Lemma 2.8. [23] Let ζ and F be graphs. Then,
Theorem 2.8. Let ζ and F be any two simple connected graphs, then
3.
Methodology and analysis
In this study, the central objective revolved around the primary amines group, strategically chosen as the reference standard to gauge the practical implications of the recently introduced indices within the realm of chemical and physical attributes. Subsequently, leveraging the computational prowess of the R-program analysis tool, we embarked on an advanced non linear regression analysis, thereby enabling precise projection of boiling points tailored exclusively for primary amines. To enhance the accessibility of these projections, the visualization of resultant models was realized through linear amalgamation in Excel. This preliminary phase serves as the bedrock upon which we meticulously structure the primary outcomes distilled from our conscientious research pursuits. Transitioning to the subsequent phase, a methodical expedition into the realm of comprehensive mathematical exploration awaits us. This exploratory journey is geared towards unraveling the innate characteristics and dynamic behavior intrinsic to the newly introduced indices. Furthermore, the scope of this analysis transcends disciplinary boundaries as it traverses through various graph families. Methodically guided by an analytical framework, we minutely deconstruct the attributes that underscore the essence of these indices, all the while meticulously evaluating their practical utility, even in basic operations. This pivotal section stands as the fulcrum of our research endeavor, representing the locus where we venture into the intricate mathematical intricacies, seamlessly interwoven with the tangible applications encapsulated within the indices we have ingeniously formulated.
As we embark on this odyssey to apprehend the intricate nature of chemical entities, the undeniable exigency for rigorous laboratory experiments surfaces, albeit invariably entwined with significant fiscal intricacies. To circumvent this financial conundrum, the domain of theoretical chemistry has ushered forth a diverse spectrum of topological indices. At the heart of conceiving a pioneering topological index lies the essential fulfillment of two paramount criteria. Primarily, the index must exhibit robust correlations with well-defined physical or chemical properties embedded within rigorously standardized datasets. Concurrently, the formulation of the index should exude an aesthetic simplicity, all while bestowing insights that hold theoretical significance. Within the confines of this section, our investigative trajectory diverges into two distinct yet synergistically interlinked subsections. Commencing with the initial subsection, our scholarly gaze is focused on the ENFI and its augmented variant, emblematic components that intricately interlace with the intricate task of predicting boiling points, achieved through intricate non-linear regression analysis. Seamlessly transitioning into the ensuing subsection, a methodical mathematical scrutiny is undertaken, meticulously dissecting these indices. This mathematical exploration engenders a profound understanding of the manifold attributes they embody, resonating across diverse graph families and infusing them with discernible implications.
3.1. Computational details
Gauss view 6.0.16 [33] was used to create the input geometries of the investigated amines for DFT calculations Figure 2. Then, full geometry optimizations were performed within Gaussian 09 package to conduct first principles-based DFT calculations [34] using the B3LYP functional and 6−31+g(d,p) basis set for all atoms. For solvent study, the process was then repeated at the same level of theory using the polarized continuum model (PCM) of solvation and water as a solvent [35]. Water was chosen as the reference solvent because the solvation energies for water are generally larger than for other common solvents, which should thus offer the broadest variety of calculated values [36]. Harmonic frequency calculation was then used to verify that all output geometries as true minima, as well as to estimate the corresponding zero-point energy corrections (ZPE), which were scaled by the empirical factor 0.9806 proposed by Scott and Radom [37]. The implicit solvation energy Esolv is defined as the difference between the gas phase energy and the energy of the molecule in solution, as calculated by PCM. Molecular surface area (MSA) was calculated using the CHEM3D ultra 16.0.0.82 software.
3.1.1. Results and discussion
The optimized structures of the investigated amines are shown in Figure 3. Total energies and ZPEs of all molecules in both media are collected in Table SD1 of the supplementary materials. Boiling point of the chemical compounds depends on several factors such as molecular weight (MW), molecular surface area (MSA), intermolecular hydrogen bonds and shape of the molecule (straight chain or branched). It was reported that the boiling point of the investigated amines is the intermolecular hydrogen bonds. It was pointed out that the attractive forces that hold individual molecules within the bulk liquid should be averaged out, such that calculation of the implicit solvation energy should give an estimate of the strength of the intermolecular interactions [36]. In this state, the implicit solvation energy, Esolv, is given by the difference between the gas phase energy and the energy of the molecule in solution, as calculated by PCM [35].
The investigated amines under probe can be classified into straight chain amines (1−7) and branched amines (8−21). Unfortunately, as a first inspection our results show that the boiling point of the investigated amines (branched and straight chains) does not correlate well with any of the considered descriptors (MW, MSA and Esolv). The molecular weight (MW in g/mol), molecular surface area (MSA in ˚A2), energy of solvation (Esolv in kcal mol−1), boiling point (BP in ˚C) and the Esolv/MSA (in kcal mol−1 ˚A2) are summarized in Table 1.
Considering the n-alkyl amines with straight chain (1−7), the larger the number of the carbon atoms in the chain, the higher the MW, the larger the MSA and the higher the Esolv. Therefore, excellent correlations between the BP and the different properties are obtained with R2 very close to unity (see Figure 4(a–c)). These finding have been theoretically ascribed due to the increase of the molecular surface area (Table 1), leading to increase the van der Waals interactions between molecules [6]. Interestingly, our results show that the boiling of the amines (1−7) nicely exponentially correlate with the amount of Esolv/MSA value with R2=0.996, see Figure 4(d).
For the investigated alkylamines with the same MF and MW, our results show, in general, that the solvation energy (Esolv) of the straight chain amines are larger than those of the branched amines, however, some deviations must be taken into accounts. For example, the Esolv value of the n-propyl amine (1) (3.170 kcal mol−1) is higher than that of the 2-amino propane molecule (12) (3.110 kcal mol−1). Similarly, for molecules with the same MF of C4H11N, the Esolv values are ranged as follows: n-butylamine (3.232) > 2-amino-2-methylpropane (3.136)> 2-aminobutane (3.024)> 2-methylpropylamine (2.748 kcal mol−1). These results can be ascribed in terms of the branching of the molecules. This branching lead to decrease both the intermolecular forces between the molecular surface area of the molecule. All of these factors lead to decrease boiling point of the molecule and deviate from the perfect linear correlation. Similar conclusions can be also noticed when the other amines are taken into account (see Table 1).
Our results show that the Esolv increases as the number of carbon atoms increases in the n-alkylamines. For example, the Esolv of n-propylamine, n-butylamine, n-pentylamine, n-hexylamine are 3.170, 3.232, 3.280 and 3.352 kcal/mol, respectively. The situation is changed when the 2-aminoalkanes, 3-aminoalkanes and/or 4-aminoalkanes were considered. The computed results show that the Esolv value of 2-aminopropane is 0.06 kcal/mol lower than that of n-propylamine. Similarly, the Esolv of 2-aminobutane is lower than that of n-butylamine by 0.208 kcal/mol.
In the context of our initial investigation, it has become evident that there exists a significant gap in our ability to accurately predict the boiling points of chemical compounds. This gap is particularly pronounced when considering the diverse nature of these compounds, which can range from branched to chain structures. Such a disparity underscores the importance of developing robust mathematical models that can cater to this wide spectrum of molecular configurations. To address this, our subsequent subsection delves deeper into the realm of topological indices. We will introduce and employ the newly formulated topological indices ENFI and MENFI, which, when used in tandem with the established Wiener index, promises a more holistic approach to predicting boiling points. By integrating these indices, we aim to provide a comprehensive framework that not only captures the essence of the molecular structures but also offers insights into their physicochemical properties. The overarching goal of this endeavor is twofold. First, to accentuate the significance of these topological indices in the broader context of chemical research. And second, to demonstrate their efficacy and power in predicting physicochemical attributes, irrespective of the inherent structural complexities of the compounds in question. Through this rigorous exploration, we hope to shed light on the potential of these indices as indispensable tools in the realm of chemical analysis and prediction.
3.2. The significance of ENFI and MENFI
In the pursuit of comprehending the diverse attributes inherent in chemical substances, the indispensability of laboratory assays emerges, albeit accompanied by substantial fiscal implications. To circumvent this fiscal challenge, the realm of theoretical chemistry has introduced and defined an array of topological indices. The study by H. Ahmed et al. underscored the utility of eccentric neighborhood Zagreb indices in prognosticating the boiling points of chemical compounds. Within this section, our inquiry is directed toward the exploration of the eccentric neighborhood forgotten index and its modified counterpart, alongside the Wiener index, in consonance with the dataset outlined in Table 2. The interrelations connecting the ENFI, the eccentric neighborhood modified forgotten index, the Wiener index and the boiling points of primary amines are comprehensively delineated in Table 3. Remarkably, as evidenced by Table 4, the eccentric neighborhood forgotten index and its modified variant manifest a robust linear association with the boiling points of primary amines, yielding correlation coefficients of (r=0.958) and (r=0.973) respectively. Moreover, Table 5 imparts a detailed exposition of the statistical analyses encompassing the eccentric neighborhood forgotten index, the eccentric neighborhood modified forgotten index and the Wiener index. These analyses collectively engender a deeper insight into the underlying relationships and implications embedded within these indices. The equations employed for non-linear regression analysis are as follows:
Analyzing the information presented in Figure 5, a compelling conclusion emerges: the boiling point prediction capability of the ENFI and MENFI is nothing short of remarkable. These indices demonstrate an impressive correlation coefficient performance, with values of R=0.894 for ENFI and R=0.946 for MENFI, respectively. Such high correlation coefficients highlight the strong alignment between the predicted boiling points and the actual boiling points of the primary amine derivatives. These results collectively establish the ENFI and MENFI indices as valuable tools in accurately forecasting boiling points across a wide range of chemical compounds derived from primary amines, which can be derived via the eqations: bpexp=1.1297bpENFI+6.2236 and bpexp=1.8446bpMENFI−5.0896. The efficacy of these indices is further fortified by the minimal average percentage deviation observed in their predictions. This outcome underscores the consistency and reliability of ENFI and MENFI in capturing the boiling point trends, reinforcing their suitability for predicting the physical properties of diverse chemical derivatives. In essence, the utilization of ENFI and MENFI indices offers a comprehensive approach to predicting boiling points, enhancing our ability to understand and manipulate the behavior of primary amine derivatives within various chemical contexts. This advancement holds great promise for applications in fields ranging from chemistry research to industrial processes.
Examining the data in Table 6 provides a clear insight into the correlation coefficients among the three indices that are currently under examination. These correlation coefficients exhibit a considerable magnitude, highlighting a robust and statistically significant relationship among these indices. This noteworthy correlation holds crucial implications. In the scientific context, a strong correlation implies that alterations in one index are accompanied by analogous variations in the other indices as well as in the actual boiling points. This consistency in responses underscores the predictive prowess of these indices, indicating their adeptness at approximating boiling points. It is noteworthy that the approach used in the referenced study [38] mirrors similar methodologies. This research advances prior work by developing techniques to calculate the first Zagreb connection index for three varied types of random chain networks: cyclooctatetraene chains, polyphenyl chains and composite chains consisting of octagons, hexagons and pentagons. Crucially, it juxtaposes these calculated values against designated chain models, including meta-chains, ortho-chains and para-chains. This comparison yields a detailed exploration of the range and average values within these diverse random chain configurations, enhancing the understanding of their structural complexities.
3.3. Comparative analysis
To grasp the significance of these new indices, we will compare the results obtained from the FENI and the MFENI with some known indices in the literature. Employing correlation coefficients as a quantitative measure of predictive accuracy, our focus has been initially directed at primary amines, with the corresponding values presented in Table 7. The coefficients range narrowly from 0.972 to 1.00, indicating a high level of precision in prediction.
Although our primary analysis targeted primary amines, the exceptional correlation coefficients observed suggest that the utility of FENI and MFENI may be extended to a broader spectrum of chemical entities. It is conceivable that these indices could be accurately applied to diverse classes of compounds, from simple organic structures such as alcohols to the more intricate molecules prevalent in COVID-19 pharmaceuticals. The established predictive power, as reflected by the correlation coefficients, highlights the potential for these indices to become indispensable tools in comprehensive chemical analysis.
4.
Conculsions
This study has successfully introduced the novel eccentric neighborhood indices, offering a significant leap in the predictive accuracy of boiling points of chemical compounds. Our rigorous assessment demonstrates that these indices outperform established indices like the eccentric connectivity and Wiener indices. Interestingly, the observed correlation coefficients, ranging from 0.958 to 0.973, exceed those achieved by both eccentric connectivity and Wiener indices. The exploration across diverse graphs has not only highlighted the robustness of these indices but also unveiled a rich landscape of inherent traits and behaviors. Notably, we investigate the calculation of these indices within the context of fundamental graph operations, including join, disjunction, composition and symmetric differences.
The pioneering nature of these indices introduces various intriguing facets that warrant subsequent investigation. As we reflect on our findings and look ahead, the journey of these indices is far from over. The path forward is illuminated with several exciting opportunities for future research:
● Developing further iterations: There is immense potential in creating new iterations of these indices, tailored to align with the forgotten topological indices framework.
● Identifying extremal graph behaviors: Future studies should focus on identifying graphs that exhibit maximal and minimal values for these indices, enhancing our understanding of their structural dynamics.
● Exploring mathematical interconnections: Investigating the mathematical relationships between these new indices and their established counterparts remains a promising area, and it is likely to yield deeper insights into their collective utility.
● Analyzing practical applications: The utility of these indices in practical scenarios, especially in analyzing chemically significant compounds, offers a fertile ground for future application-based research.
● Studying associated polynomials: Delving into the polynomials related to these indices can uncover new mathematical patterns and relationships, enriching our theoretical understanding.
● Expanding to broader fields: Venturing beyond chemical graph theory to apply these indices in bioinformatics, network theory and pharmacology could revolutionize our approach in these fields.
This study sets the stage for an exciting journey of discovery and innovation. The eccentric neighborhood indices open up a world of possibilities, and we are committed to exploring these in our continued quest for advancing chemical graph theory and its applications.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
Thanks to Prof. Nuha Wazzan from Department of Chemistry, King Abdulaziz University, Jeddah, Saudi Arabia, for carrying out the DFT calculations. Authors are thankful for King Abdulaziz University's High-Performance Computing Centre (Aziz Supercomputer) for supporting the computation for the work described in this paper.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: