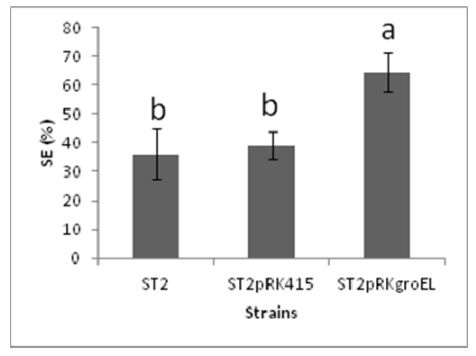
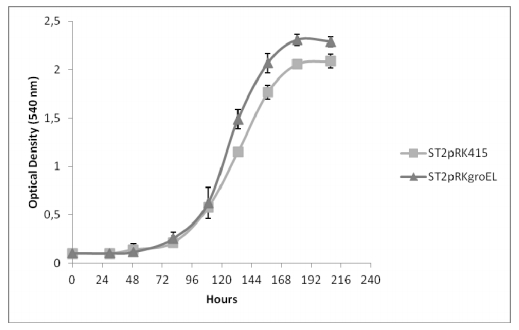
Rhizobia are soil bacteria able to form symbioses with legumes and fix atmospheric nitrogen, converting it into a form that can be assimilated by the plant. The biological nitrogen fixation is a possible strategy to reduce the environmental pollution caused by the use of chemical N-fertilizers in agricultural fields. Successful colonization of the host root by free-living rhizobia requires that these bacteria are able to deal with adverse conditions in the soil, in addition to stresses that may occur in their endosymbiotic life inside the root nodules. Stress response genes, such as otsAB, groEL, clpB, rpoH play an important role in tolerance of free-living rhizobia to different environmental conditions and some of these genes have been shown to be involved in the symbiosis. This review will focus on stress response genes that have been reported to improve the symbiotic performance of rhizobia with their host plants. For example, chickpea plants inoculated with a Mesorhizobium strain modified with extra copies of the groEL gene showed a symbiotic effectiveness approximately 1.5 fold higher than plants inoculated with the wild-type strain. Despite these promising results, more studies are required to obtain highly efficient and tolerant rhizobia strains, suitable for different edaphoclimatic conditions, to be used as field inoculants.
1.
Introduction
The class of Navier-Stokes-Korteweg equations arises in the modelling of capillary fluid flow as it occurs for instance in physical phenomena such as diffuse interfaces [27,40]. Capillarity effects are mathematically described by a dispersive stress tensor depending on the density and its derivatives. In their general form, these systems read
The unknowns are the density ρ and the velocity field u. We consider the isentropic pressure law P(ρ)=1γργ with γ>1. The parameters ν,κ>0 denote the viscosity and capillarity coefficients respectively. The viscous stress tensor S=S(∇u) equals
where μ,λ denote the shear and bulk viscosity coefficients respectively and satisfy μ(ρ)+2λ(ρ)≥0. The capillary term K=K(ρ,∇ρ) amounts to
The capillary tensor is referred to as Korteweg tensor [40], see also [54,55]. The family of Navier-Stokes-Korteweg equations has rigorously been derived in [27] and more recently in [33]. A prominent example of (1.1) are the quantum Navier-Stokes (QNS) equations that will mainly be considered in this paper. The QNS equations are obtained from (1.1) by choosing the shear viscosity to depend linearly on the density, namely μ(ρ)=ρ, vanishing bulk viscosity λ(ρ)=0, and k(ρ)=1/ρ. Its inviscid counterpart (considering λ(ρ)=μ(ρ)=0) is the Quantum Hydrodynamic system (QHD) [7,9,10] which has a strong analogy with Gross-Pitaevskii type equations describing for instance the effective dynamics in terms of a macroscopic order parameter of superfluid helium [39] or Bose-Einstein condensation [50]. This close link to NLS type equations highlights the quantum mechanical nature of the model, see e.g., [7,34]. Beyond that the QHD system also serves as model for semi-conductor devices [30]. In this regard, (1.3) can be interpreted as a viscous regularization, but can also be derived as the moment closure method with a BGK type collision term [23,37], see also [36] for an overview of dissipative quantum fluid models and their utility for numerical simulations. The class of systems (1.1) with capillarity tensor K but with ν=0, namely inviscid systems such as QHD, goes under the name of Euler-Korteweg system [14,20]. The choice k(ρ)=const., μ(ρ)=ρ, λ(ρ)=0 constitutes a second example that is extensively studied in literature and is commonly referred to as Navier-Stokes-Korteweg (NSK) system [13,18,19]. Finally, we mention that for κ=0, namely (1.1) without capillarity term, one recovers the compressible Navier-Stokes equations with density-dependent viscosity [18,45,56].
The aim of this paper is to investigate the low Mach number limit of (1.1) posed on [0,∞)×R2 in the class of weak solutions and for general ill-prepared data. To that end, we focus on the analysis of the (QNS) equations, namely
being complemented with the non-trivial far-field behavior
For (1.3) the capillarity tensor divK, defined in (1.2), can formally be rewritten as
The total energy associated to (1.3) reads
Note that the assumption of finite energy E(ρ,u)<+∞ enforces the far-field behavior (1.4) for the given choice of the internal energy F(ρ).
The motivation to mainly study (1.3) is two-fold. First, our main purpose is to elucidate the relevance of the capillarity tensor K for the developed method. In this regard, the choice k(ρ)=1/ρ allows for a more concise and straightforward exposition. Second, to the best of our knowledge, (1.3) is the only system within the class of (1.1) with density dependent viscosity and non-trivial far-field for which existence of finite energy weak solutions (FEWS) is known [8]. However, postulating existence of weak solutions we discuss how our results can be generalized, to the following set of capillarity and viscosity tensors satisfying the compatibility condition [18,20,21],
see Remark 2.8 below. Assuming (1.7) describes a sufficient condition which leads to suitable a priori estimates required for our method. Note that e.g. NSK, namely k(ρ)=const., μ(ρ)=ρ, λ(ρ)=0 does not satisfy (1.7). Nevertheless, the BD-entropy estimates obtained in [13] enable us to include NSK in our considerations.
For the investigation of the low Mach number limit of (1.3), we consider a highly subsonic regime in which the Mach number Ma=ε=U/c given by the ratio of the characteristic velocity U of the flow and the sound speed c goes to zero. One expects the flow to asymptotically behave like an incompressible one on large time scales and for small velocities. Given the dimensionless system (1.3), we introduce the scaling
The scaled viscosity and capillarity coefficients are such that
The scaled version of (1.3) then reads
For the sake of a concise notation, we suppress the ε-dependence of νε and κε. The scaled energy is given by
We refer to [2,28,35] for details on the scaling analysis. Provided that the energy (1.10) is uniformly bounded, the heuristics suggests that ρε−1 converges to 0 as ε→0. Formally ρεuε→u for which we infer from the continuity equation of (1.9) that divu=0. The limit function u is expected to solve the target system given by the incompressible Navier-Stokes equations
Our main result states the following.
Theorem 1.1. Let T>0, {(ρ0ε,u0ε)}ε>0 be a sequence of general ill-prepared initial data with uniformly bounded energy (1.10) such that √ρ0εu0ε converges weakly to some u0 in L2. Further, let {(ρε,uε)}ε>0 a sequence of (FEWS) to (1.9) with initial data {(ρ0ε,u0ε)}ε>0. Then, ρε−1 converges strongly to zero and √ρεuε converges strongly to u, where u is the unique Leray-Hopf solution of (1.11) with initial data P(u0).
We refer to Theorem 2.6 below for a precise statement. Beyond its analytic scope, we mention that the low Mach number analysis is also motivated by the utility of (1.1) for the numerical purposes, such as investigation of diffuse interfaces [3]. For a general introduction to the mathematical low Mach number theory, we refer to the review papers [2,35] and the monograph [28] and references therein.
In this introduction, we restrict ourselves to point out the key difficulties of the low Mach number theory for weak solutions of (1.9). A key issue in proving convergence towards the target systems consists in controlling the acoustic waves, carried by density fluctuations and the irrotational part of the momentum density. Unless the acoustic waves propagating with speed 1ε are controlled in a suitable way one may only expect weak convergence of the sequence of momentum density ρεuε. The latter is in particular insufficient to obtain compactness of the convective term div(ρεuε⊗uε) and for the passage to the limit in (1.9). The dispersion of acoustic waves can be exploited in order to infer the desired decay. When working on unbounded domains, Strichartz estimates for the wave equation provide an appropriate tool for such an analysis applied to the classical compressible Navier-Stokes equations, see [25] and the survey papers [2,24,35]. The dispersive tensor present in (1.9) alters the dispersion relation of acoustic waves in (1.9) that is no longer linear. We develop a refined dispersive analysis allowing for decay of acoustic waves at explicit improved convergence rates and under arbitrarily small loss of regularity. For that purpose, we adapt the analysis of acoustic oscillations initiated in [6] by the author in collaboration with P. Antonelli and P. Marcati, see Section 4 below. Refined Strichartz estimates taking into account the augmented dispersive relation are also used by the same authors [4] for the study of the low Mach number limit of (1.9) posed on R3. However, as the dispersion turns out to be weaker for d=2 the estimates introduced in [4] do not yield the desired decay properties for d=2. In [6], the authors complement the analysis of [4] for d=3 with suitable refined Strichartz estimates for d=2 and elucidate the link with the Bogoliubov dispersion relation [17] that governs the system of acoustic waves. These estimates can be considered a refinement of the Strichatz estimates in [16] and the ε-dependent version of [32] introduced in the framework of the Gross-Pitaevskii equation, see Section 4. Note, that the ε-dependent estimates do not follow from a direct scaling argument as the Bogoliubov dispersion relation is non-homogeneous.
Second, suitable a priori estimates are required in order to infer the compactness needed for the passage to the limit. At this stage, further difficulties related to the Cauchy Problem of (1.9) and its difference to the one for the classical compressible Navier-Stokes become apparent. The density dependence of the viscosity tensor 2νdiv(ρεDuε) in (1.9) leads to a degeneracy close to vacuum regions. This prevents a suitable control of the velocity field uε which in general can not be defined a.e. on [0,T)×R2. In addition, propagating regularity of ρε is a difficult task due to presence of the highly nonlinear quantum correction term in (1.9). The lack of appropriate uniform estimates is compensated for by the Bresch-Desjardins (BD) entropy estimates [18,19] which are available for (1.9) and more in general for (1.1) under specific conditions on μ,λ and k. While, in the case of (1.9), these provide bounds up to second order derivatives of √ρε, they do not suffice to define uε a.e. on R2, see also (2.4) below. This distinguishes the present analysis from the incompressible limit for the classical compressible Navier-Stokes equations, see e.g., [25], for which only weaker information on the density in Orlicz spaces but on the other hand a uniform Sobolev bound for uε are available. This further motivates the need of an accurate dispersive analysis of the acoustic waves when dealing with weak solutions at low regularity. The presence of the capillarity tensor allows for both refined Strichartz estimates and additional uniform estimates on √ρε (compared to the case κ=0), see also Remark 2.7.
Previously and to the best of our knowledge, the low Mach number limit for (1.9) has only been studied for d=3. In the aforementioned paper [4], see also [5], the low Mach number limit for (1.3) posed on R3 is investigated. As detailed above, the dispersive analysis of the linearized system differs substantially from the present one due to the weaker dispersion for d=2. Moreover, due to the uniqueness and regularity properties of weak solutions to (1.11) for d=2, here we are able to infer additional information on the limit velocity field u, see Theorem 2.6. We also mention [41,57] where the incompressible limit for (1.3) posed on T3 is considered. In these papers, the authors augment (1.3) by additional drag terms that allow for a direct control of the velocity field uε. In addition, [41,57] consider local smooth solutions to the primitive system under further assumptions that are shown to converge to local strong solutions of (1.11) by means of a relative entropy method. In [41], the authors also study the limit of local smooth solutions to (1.3) posed on R3 including again additional drag terms and requiring the initial data to be smooth and well-prepared. Note that the class of weak solutions under consideration in this paper is not suitable for relative entropy methods. Finally, we mention that the low Mach number limit for the (QHD) system, the inviscid counterpart of (1.3), is investigated in [26] on Td for d=2,3. Posed on Rd, it will further be addressed by the author in a forthcoming paper including vortex solutions of infinite energy, see also [34].
The remaining part of this paper is organized as follows. Section 2 reviews the Cauchy Theory for the primitive system (1.3) and the target system (1.11) and provides a precise formulation of the main results of this paper. Subsequently, we collect the needed uniform estimates in Section 3. Strong convergence to zero of acoustic waves is proven in Section 4 while Section 5 completes the proof of the main theorem.
Notations
We list the notations of function spaces and operators used in the following. We denote
● the symmetric part of the gradient by Du=12(∇u+(∇u)T) and the asymmetric part by Au=12(∇u−(∇u)T),
● by D(R+×R2) the space of test functions C∞c(R+×R2) an by D′(R+×R2) the space of distributions. The duality bracket between D and D′ is denoted by ⟨⋅,⋅⟩,
● by Lp(R2) for 1≤p≤∞ the Lebesgue space with norm ‖⋅‖Lp. We denote by p′ the Hölder conjugate exponent of p, i.e. 1=1p+1p′, and for 0<T≤∞ by Lp(0,T;Lq(R2)) the space of functions u:(0,T)×R2→Rn with norm
By Lp−(0,T;Lq(R2)) we indicate the space of functions f∈Lp0(0,T;Lq(R2)) for any 1≤p0<p,
● The sum Lq1(R2)+Lq2(R2) is a Banach space with norm ‖f‖Lq1+Lq2=inf{‖g‖Lq1+‖h‖Lq2:f=g+h,g∈Lq1(R2),h∈Lq2(R2)},
● by Lp2(R2) the Orlicz space defined as
we refer to [1,48] for details.
● for s∈R and p∈[1,∞] the non-homogeneous Sobolev space by Ws,p(R2)=(I−Δ)−s2Lp(R2) and Hs(R2)=Ws,2(R2). Its dual will be denoted by W−s,p′(R2) with p′ being the Hölder conjugate of p. The homogeneous spaces are denoted by ˙Ws,p(R2)=(−Δ)−ksLp(R2) and ˙Ws,2(R2)=˙Hs(R2), and the dual space ˙W−s,p′(R2). For ps<2 we denote the critical Sobolev exponent by p∗=2p2−ps. We refer to Theorem 6.4.5 and Theorem 6.5.1 in [15], see also Chapter 4 in [1], for the classical embedding results for Sobolev and Lebesgue spaces.
● by Q and P the Helmholtz–Leray projectors on irrotational and divergence-free vector fields, respectively:
For f∈Wk,p(R2) with 1<p<∞ and s∈R the operators P,Q can be expressed as composition of Riesz multipliers and are bounded linear operators on Ws,p(R2).
In what follows C will be any constant independent from ε.
For the convenience of the reader, we recall an interpolation result used several times throughout the paper.
Lemma 1.2 (Interpolation). Let T>0, p1,p2,r∈(1,∞) and s0<s1 real numbers. Further, let u∈Lp1(0,T;Ws0,r(R2))∩Lp2(0,T;Ws1,r(R2)). Then, for all (p,s) such that there exists θ∈(0,1) with
it holds u∈Lp(0,T;Ws,r(R2)) with
The Lemma is a simplified statement of Theorem 5.1.2 in [15] and can also be proven by standard interpolation of Sobolev spaces in the space variables, see e.g., Paragraph 7.53 in [1], followed by Hölder's inequality in the time variable.
2.
Preliminary and main results
This section briefly reviews the Cauchy theory for both, the primitive system (1.3) and the target system (1.11). Subsequently, we state the main results of this paper characterising the incompressible limit of (1.9) in the class of weak solutions.
2.1. Cauchy theory
The mathematical analysis of (1.3), and more in general Navier-Stokes-Korteweg systems (1.1), encounters two major difficulties beyond the well-known ones arising in the study of classical compressible Navier-Stokes equations [48]: the density-dependence of the viscosity stress tensor and the presence of the highly non-linear dispersive stress tensor. For compressible fluid flow with constant coefficient viscosity, the energy bound yields √ρu∈L∞tL2x and the energy dissipation provides a L2t,x-bound for ∇u. For the degenerate viscosity stress tensor considered in (1.3), the energy dissipation fails to provide suitable control on u. By consequence, the Lions-Feireisl theory [29,48] which relies on a Sobolev bound for u can not be applied. Without further regularity assumptions, none of the quantities u, ∇u and 1/√ρ is defined a.e. on R2 due to the possible presence of vacuum {ρ=0}. These difficulties are reminiscent of the ones encountered in the analysis of the QHD system [7,10], the inviscid counter-part of (1.3), and also arise in the absence of a capillarity tensor, namely for the barotropic Navier-Stokes equations with density dependent viscosity [19]. It is hence pivotal for the development of the Cauchy Theory to obtain suitable control on the mass density, which turns out to be a difficult task given in particular the presence of the highly non-linear dispersive stress tensor. The lack of uniform bounds for the velocity field u is compensated for by the Bresch-Desjardins (BD)-entropy estimates [18,19]. The mathematical theory for finite energy weak solutions is then developed in terms of the variables (√ρ,Λ:=√ρu) which enjoy suitable bounds in the finite energy framework. Note that the mass is infinite in view of (1.4). Weak solutions are commonly constructed in terms of an approximation procedure [8,11,42]. This does in general not allow one to prove the energy inequality
The energy inequality is replaced by a weaker version by defining the tensor Tν∈L2((0,T)×R2) through
By denoting its symmetric part Sν=Tsymν, we recover the identity √ν√ρSν=νρDu for smooth solutions. The energy inequality for (1.3) then reads
The aforementioned (BD)-entropy estimates provide uniform bounds for the asymmetric part Aν=Tasymν and the second order derivatives of √ρ, see (2.4) below. We refer the reader to [4,8] and references therein for a detailed discussion. Similarly, the capillary tensor given by (1.5) is well-defined in weak sense by virtue of the regularity properties stemming from the energy (2.3) and Bresch-Desjardins entropy inequality (2.4).
Concerning the far-field condition, we mention that the internal energy F(ρ) and the pressure P(ρ) are related through the identity P(ρ)=ρF′(ρ)−F(ρ). The particular choice for F(ρ) in (2.3) enforces the desired far-field behavior.
Following [8] we introduce our notion of weak solutions to (1.3) with far-field behavior (1.4).
Definition 2.1. A pair (ρ,u) with ρ≥0 is said to be a finite energy weak solution (FEWS) of the Cauchy Problem (1.3) posed on [0,T)×R2 with initial data (ρ0,u0) if the following are satisfied
1) Integrability conditions
2) Continuity equation
for any φ∈C∞c([0,T)×R2).
3) Equation for the momentum density
for any ψ∈C∞c([0,T)×R2;R2).
4) Energy inequality. There exists a tensor Tν∈L2((0,T)×R2) satisfying identity (2.2) such that the energy inequality (2.3) holds for a.e. t∈[0,T].
5) BD-entropy inequality. Let
Then for a.e. t∈[0,T],
where Aν=Tasymν, with Tν defined as in the previous point.
Global existence of (FEWS) to (1.3) posed on Td for d=2,3 is proven in [11] and [42] following different approaches. In collaboration with P. Antonelli and S. Spirito [8], the author proves global existence of (FEWS) to (1.3) posed on Rd for d=2,3 with or without non-trivial far-field (1.4) and initial data of finite energy.
Theorem 2.2 ([8]). Let γ>1 and ν,κ>0. Given initial data (ρ0,u0) of finite energy, there exists a global FEWS (ρ,u) to (1.3) with far-field (1.4).
In particular, vacuum regions are included in the weak formulation of the equations. The method of [8] consists in a invading domains approach. More precisely, by a suitable truncation argument a sequence of approximate solutions is constructed. To that end, the authors rely on the existence result [42] on periodic domains. The compactness properties provided by the energy and BD-entropy bounds allow for the passage to the limit in the truncated formulation yielding finally a global (FEWS) to (1.3). Further, the weak solutions constructed in [8] are such that (2.3) and (2.4) are satisfied. The validity of the energy inequality (2.1) for general weak solutions to (1.3) is at present not clear. In addition, the minimal assumptions on weak solutions such that (2.3) and (2.4) are fulfilled remain to determine. For a more detailed discussion of these issues, see e.g., [8], [4,Section 2 and Appendix A] and [49].
Concerning the Cauchy Theory of (1.11), we recall the following well-known result.
Definition 2.3. A vector-field u is a weak solution to (1.11) posed on [0,T)×R2 with initial data u0 if u∈L2loc([0,T)×R2), divu=0 in distributional sense and for all ψ∈C∞c([0,∞)×R2) such that divψ=0 it holds
A weak solution u is called a Leray-Hopf weak solution to (1.11) if the energy equality
is satisfied for a.e. t∈[0,T), where the kinetic energy is defined as
Existence and uniqueness of Leray-Hopf weak solutions to (1.11) for initial data of finite kinetic energy is due to [44].
Theorem 2.4 ([44]).Let ν>0. Given u0∈L2(R2) such that divu0=0, there exists a unique global Leray-Hopf weak solution u∈L∞(0,∞;L2(R2))∩L2(0,∞;˙H1(R2)) to (1.11).
We refer to the monograph [43] for the analysis of (1.11) and we limit ourselves to the following comments. The space L2(R2) corresponds to the energy space of (1.11), namely the space of velocity fields of finite kinetic energy and enjoys scaling invariance. Moreover, due to the Ladyzhenskaya-Prodi-Serrin regularity criterion [43,51,52], see also [46], any weak solution u such that u∈L4(0,T;L4(R2)) satisfies (2.5).
2.2. Main results
We specify the assumptions on the sequence of initial data (ρ0ε,u0ε) that we consider to be general and ill-prepared and without further regularity or smallness assumptions. The assumptions are stated in therms of the hydrodynamic states (√ρ0ε,Λ0ε).
Assumption 2.5. Let (ρ0ε,u0ε) be a sequence of initial data such that
1) there exists C>0 such that E(ρ0ε,u0ε)≤C for all ε>0, where the scaled energy functional is defined in (1.10), $.
2) there exists u0∈L2(R2) such that Λ0ε⇀u0 weakly in L2(R2)
Note that Theorem 2.2 guarantees the global existence of a sequence of (FEWS) to (1.9) with initial data satisfying Assumption 2.5. Our main result then characterises the low Mach number limit of (FEWS) to (1.9) with such initial data.
Theorem 2.6. Let γ>1, κ,ν>0, T>0 and {(ρε,uε)}ε>0 be a sequence of (FEWS) to (1.9) on [0,T)×R2 with initial data {(ρ0ε,u0ε)}ε>0 satisfying Assumption 2.5. Then,
1) ρε−1 converges strongly to 0 in L∞(0,T;L2(R2))∩L4s−(0,T;Hs(R2)) for s∈(0,2),
2) Λε converges weakly-∗ in L∞(0,∞;L2(R2)) and strongly in L2loc([0,T)×R2) to u, where the limit velocity field u is the unique global Leray-Hopf weak solution to (1.11) with initial data u|t=0=P(u0), in particular u∈L∞(0,T;L2(R2))∩L2(0,T;˙H1(R2)),
3) the irrotational part of the momentum density Q(ρεuε) converges strongly to 0 in L2(0,T;Lr(R2)) for any r∈(2,∞).
Even though only the weak form of the energy inequality (2.3) is available for ε>0, we recover unique Leray-Hopf weak solutions in the limit. Note that for the general ill-prepared data for the primitive system, the possible formation of an initial layer can not be ruled out. In particular, E(ρ0ε,u0ε) does not converge to EINS(P(u0)) and one may not infer the energy inequality for u by passing to the limit in (2.3). However, the validity of the energy equality follows from Ladyzenskaya-Prodi-Serrin regularity criterion [43,51,52] as we prove that u∈L4(0,T;L4(R2)). Moreover, by virtue of the uniqueness of Leray-Hopf weak solutions, we conclude that the sequence Λε converges without requiring any extraction of a subsequences. The regularity properties stemming from the energy and BD-entropy estimates are essential for that purpose.
This is in contrast to the low Mach number limit for (1.3) posed on R3 considered in [4]. In 3D, the regularity properties of the limit velocity field u do not suffice in order to infer the validity of the energy inequality in the limit, see [4,Theorem 2.4 and Remark 2.5]. By consequence, one recovers a global weak Leray-Hopf solution only for well prepared initial data, namely data such that E(ρ0ε,u0ε) does converge to EINS(P(u0)). In addition, for d=3 convergence does hold up to subsequences only.
On the other hand, we can not rely on the dispersive estimates providing suitable decay of the acoustic waves for d=3, see [4,Proposition 4.2] due to the weaker dispersion for d=2, see Section 4 below.
Remark 2.7. The presence of the capillarity tensor K in (1.9) is essential for both the uniform estimates (Section 3) and the acoustic analysis (Section 4). Regarding the former, the respective BD-entropy inequality (2.4) allows for uniform bounds of second order derivatives of √ρε−1 which enable us to infer a suitable Sobolev bound on ρεuε, see Lemma 3.3 and Remark 3.4 below. For the latter, it leads to improved decay rates for the acoustic waves through an alteration of the dispersion relation, see (4.1). Both are in general no longer available without capillarity tensor, namely for κ=0 corresponding to the degenerate compressible Navier–Stokes equations; the low Mach number limit of which will be subject of future investigation.
Remark 2.8. The presented theory generalizes to systems (1.1) provided that the capillarity tensor is chosen in a suitable way so that the respective BD-entropy inequality (2.4) entails bounds on second order derivatives of √ρε. This is in particular the case provided that the BD relation (1.7) is satisfied [20,21], see also Remark 3.4. We stress that even though the NSK equations do not satisfy (1.7) suitable estimate can be shown, see [12,13]. In addition, the linearized system for acoustic waves turns out to be still governed by the dispersion relation obtained for (1.9), see Remark 4.10. Finally, this allows one to infer the required compactness properties for {(ρε,√ρεuε)}ε>0 and to prove convergence of FEWS towards Leray-Hopf weak solutions of (1.11).
3.
Uniform estimates
We collect the necessary a priori estimates for finite energy weak solutions (FEWS) to (1.3) with uniformly bounded (in ε) energy and BD-entropy functionals. We denote the sequence of momenta mε:=√ρεΛε and m0ε:=√ρε0Λ0ε. The next Lemma only relies on uniform bounds implied by (2.3).
Lemma 3.1. Let T>0 and the initial data (ρ0ε,u0ε) such that there exists C>0 (independent of ε) and E(ρ0ε,u0ε)≤C, then
1) √ρ0ε−1∈H1(R2) is uniformly bounded with ‖√ρ0ε−1‖L2≤Cε,
2) ρ0ε−1∈Lγ2(R2) and ρ0ε−1∈L2(R2) are uniformly bounded with ‖ρ0ε−1‖L2≤Cε for γ≥2 and ‖ρ0ε−1‖L2≤C√ε for γ∈(1,2),
3) Λ0ε∈L2(R2) is uniformly bounded,
4) m0ε∈H−δ(R2) is uniformly bounded for δ>0 arbitrarily small.
If further (ρε,uε) is a sequence of FEWS to (1.3) with initial data (ρ0ε,u0ε), then
5) √ρε−1∈L∞(0,∞;H1(R2)) is uniformly bounded with ‖√ρε−1‖L∞L2≤Cε,
6) ρε−1∈L∞(0,∞;Lγ2(R2)) and ρε−1∈L∞(0,∞;L2(R2)) are uniformly bounded with ‖ρε−1‖L∞L2≤Cε for γ≥2 and ‖ρε−1‖L∞L2≤C√ε for γ∈(1,2).
7) Λε∈L∞(0,∞;L2(R2)) is uniformly bounded,
8) mε∈L∞(0,T;L2(R2)+Lr(R2)) is uniformly bounded for all r∈[1,2). In particular, m0ε∈L∞(0,T;H−δ(R2)) is uniformly bounded for δ>0 arbitrarily small,
9) Sν,ε∈L2(0,T;L2(R2)) is uniformly bounded.
Proof. It follows from the energy inequality (2.3) and the fact that F is non-negative that the internal energy F(ρε)∈L∞(0,∞;L1(R2)) is uniformly bounded. Exploiting the convexity of F, see e.g., [47,p. 590] or [4,Lemma 3.2], we obtain ρε−1∈L∞(0,∞;Lγ2(R2)), where Lγ2 denotes the Orlicz space. More precisely,
for a.e. t∈R+. If γ≥2, then (3.1) yields
which proves (6) for γ≥2. We postpone the proof of (6) for general γ>1 and proceed to show (5). We observe that ∇√ρε∈L∞(0,∞;L2(R2)) bounded uniformly from (2.3) and since |√ρε−1|≤|ρε−1|, it holds
for a.e. t∈R+. Hence, in order to conclude that √ρε−1∈L∞(0,∞;H1(R2)) uniformly bounded it remains to show that
For γ≥2, it follows from (3.2) that
For all γ>1, it follows from (3.1) and the Chebychev inequality that
where L2 denotes the Lebesgue measure. Note that if f is a measurable function such that ∇f∈L2(R2) and supp(f) is of finite Lebesgue measure then
For a proof of (3.3) see for instance [22,Inequality (3.10)]. Let χ∈C∞c(R) such that 1[3/4,5/4](r)≤χ(r)≤1[1/2,3/2](r). Applying inequality to (√ρε−1)(1−χ(ρε)) yields
We obtain that
which completes the proof of (5). The proof of (1) follows verbatim the one of (5) and is omitted. The first statement of (6) has already been shown for γ≥2. For γ∈(1,2), we observe that |ρε−1|≤C|√ρε−1|2 on the set {|ρε−1|>12} so that
statement (6) then follows together with (3.1). Statement (2) is proven analogously to (6). Note that (3) and (7) and (9) are immediate consequences of (2.3). Finally, we show (8), statement (4) following verbatim. It suffices to decompose mε=Λε+(√ρε−1)Λε and to exploit (5). Indeed, one has
for all p∈[1,2).
Remark 3.2. Note that in contrast to compressible fluid flow with constant viscosity coefficients [47] the assumption for the initial data to be of uniformly bounded energy and (2.3) only yield a bound on the symmetric part Sν,ε of Tν,ε, see (6) of Lemma 3.1. In particular, no L2 or Sobolev bound for uε is available. On the other hand, the control of ∇√ρε allows one to prove that √ρε−1 converges to 0 in L∞(0,∞;Hs(R2)) for any s∈[0,1) by virtue of (1) Lemma 3.1 while in the constant viscosity coefficient case such bounds are available in Orlicz spaces only [25,47].
Additional uniform bounds can be obtained from (2.4). Note that the scaled BD-entropy functional reads
As the initial data (ρ0ε,u0ε) is of uniformly bounded energy it follows that B(ρ0ε,u0ε)≤C for some C>0. In particular, this allows one to infer a L2-bound on Tν,ε. Similarly, it provides Sobolev bounds of second order for √ρε−1.
Lemma 3.3. Under the assumptions of Lemma 3.1, the following hold true,
1) √ρε−1∈L2s−1(0,T;Hs(R2)) is uniformly bounded for all s∈[1,2] with √ρε−1∈Lp(0,T;L∞(R2)) uniformly bounded for all p∈[2,∞). Moreover,
2) mε∈Lp(0,T;L2(R2)) is uniformly bounded for all p∈[2,∞) and mε∈L2s−(0,T;Hs(R2)) is uniformly bounded for s∈(0,1).
Proof. To prove (1), we note that √ρε−1∈L2(0,T;H2(R2)) is uniformly bounded for any T>0 by combining ∇2√ρε∈L2(0,T;L2(R2)) from (2.4) and √ρε−1∈L∞(0,∞;H1(R2)) from (5) Lemma 3.1. Applying the interpolation Lemma 1.2 leads to
where θ∈(0,1], s=1+θ and p=2/θ. In particular, the Sobolev embedding Hs(R2)↪L∞(R2) for any s>1 yields that √ρε−1∈Lp(0,T;L∞(R2)) for all p∈[2,∞). Again by interpolation, one has
In particular, it follows from the Gagliardo-Nirenberg-Sobolev inequality that √ρε−1 converges strongly to 0 in L4(0,T;L∞(R2)) at convergence rate √ε. Inequalities (3.5) follow.
We show (2). It suffices to decompose mε=Λε+(√ρε−1)Λε and to exploit (1) of Lemma 3.3 in order to verify that for any T>0 it holds mε∈L∞(0,T;L2(R2))+Lp(0,T;L2(R2))⊂Lp(0,T;L2(R2)) uniformly bounded for any p∈[2,∞). By definition of Tν,ε, see (2.2), it holds
One has Tν,ε∈L2(0,T;L2(R2)) uniformly bounded and (√ρε−1)Tν,ε∈L2(0,T;Lr1(R2)) uniformly bounded for all r1∈[1,2) upon using (5) of Lemma 3.1. Further, as ∇√ρε∈L2(0,T;Lr2(R2)) for any r2∈[2,∞) from ∇2√ρε∈L2(0,T;L2(R2)), we recover that 2Λε⊗∇√ρε∈L2(0,T;Lr(R2)) uniformly bounded for all r∈[1,2). Hence,
for arbitrary small δ>0. Thus,
with p∈[2,∞). Finally, mε∈L2(0,T;H1−δ(R2)) uniformly bounded for arbitrary small δ>0. Interpolating with the bound mε∈Lp(0,T;L2(R2)) yields that
where
As p∈[2,∞) can be chosen arbitrarily large but finite and θ>0 arbitrarily close to 1, it follows that for s∈(0,1) it holds mε∈L2s−(0,T;Hs(R2)) uniformly bounded.
Remark 3.4. We emphasize that both statements of Lemma 3.3 rely on the uniform bound for ∇2√ρε stemming from (2.4) which is not available for κ=0. In particular, if κ=0 then the third term on the right-hand side of (3.6) is merely bounded in L∞(0,T;L1(R2)). In turn, we are no longer able to state that mε∈Lp(0,T;Ws,r(R2)) for some s>0, r≥2 and p∈[1,∞).
On the other hand, for κ>0 and different choices of viscosity μ(ρ),λ(ρ) and capillarity coefficients k(ρ) the essential uniform bound for ∇2√ρε can be inferred provided that (1.7) is satisfied [21] or k(ρ)=const., μ(ρ)=ρ, λ(ρ)=0 see [12,13].
4.
Control of acoustic oscillations
The aim of this section is to provide suitable control of fast-propagating acoustic waves, namely the density fluctuations σε:=ε−1(ρε−1) and the irrotational part of the momentum density Q(mε). In general, for ill-prepared data these fast oscillations may prevent the sequence Q(mε) from converging strongly to the incompressible limit velocity field u and only allow for weak convergence. However, when the problem is posed on the whole space, the dispersion at infinity can be exploited to prove strong convergence to zero of the acoustic waves as ε→0 in suitable space-time norms at an explicit convergence rate. We refer to the monograph [28,Chapter 7] and the survey paper [24] for the analysis on bounded domains. The acoustic equations are obtained by linearizing (1.9) around the constant solution (ρε=1,uε=0), see also the scaling in (1.9), and applying the Leray-Helmholtz projection onto curl-free vector fields to the moment equation. More precisely,
where the Leray-Helmholtz projections are defined by Q:=∇Δ−1div and P:=Id−Q respectively and
Formally, the density fluctuations σε satisfy the Boussinesq-type equation
The fourth-order term stems from the dispersive stress tensor divK in the equation for the momentum density upon using identity (1.5) and alters the dispersion relation for the acoustic equations. In the absence of capillary effects, namely for κ=0, (4.3) reduces to the wave equation with sound speed 1/ε which is known to govern the evolution of acoustic waves for a classical compressible fluid. For κ>0, the dispersion relation for high frequencies (above the threshold 1/ε) is no longer linear but quadratic. For a discussion of the physical background and the link to the Bogoliubov dispersion relation [17] appearing in the microscopic theory for Bose-Einstein condensation we refer to [6]. Moreover, by an accurate dispersive analysis of (4.1) it is proven in [6], see also [4,16], that the presence of the quantum correction term leads to improved decay rates of acoustic waves on Rd with d≥2 compared to compressible fluids without capillarity effects. For that purpose, (4.1) is symmetrized by means of the transformation
so that the system reads
where ˜Gε=(−Δ)−12divGε. Upon controlling (σε,Q(mε)) in terms of (˜σε,˜mε), it suffices to investigate (4.5). System (4.5) can be characterised by means of the linear semigroup operator eitHε where Hε is defined via the Fourier multiplier
A stationary phase argument leads to the following dispersive estimate for the semigroup operator eitHε, see [4,Corollary B.6] and also [6,Corollary 4.3].
Lemma 4.1. Let d≥2, ϕε as in (4.6), R>0 and let χ(r)∈Cc(0,∞) be a smooth cut-off frequency cut-off localizing in frequencies of order R. Then there exists a constant C>0 such that
for any δ∈[0,d−22].
For ε=1, the dispersive estimate (4.7) is proven in [32] to investigate the large time behavior of solution to the Gross-Pitaevskii (GP) equation. Here, we only mention that the (GP) equation is formally equivalent to the QHD system, the inviscid counter part of (1.3), see [6]. Note that the right-hand side of (4.7) blows up for κ→0. Indeed, the acoustic dispersion is then governed by the wave equation while (4.7) is a Schrödinger-like dispersive estimate. Here, we consider κ>0 to be fixed.
The symbol ϕε is non-homogeneous and does not allow for a separation of scales. Hence the ε-dependent version can not be obtained by a simple scaling argument. For δ=0, the dispersive estimate (4.7) reduces to the one for the free Schrödinger propagator eitΔ. In addition, (4.7) yields a regularizing effect for low frequencies for d>2 that provides decay of order εδ at the expense of a factor Rδ for δ>0 arbitrarily small. This is related to the curvature of the hypersurface τ=ϕε(|ξ|) which depends on the spatial dimension d. For d=2, (4.7) does not yield any decay in ε. It is shown in [6,Proposition 3.8] that the desired decay for d=2 can be obtained by separating the regimes of frequencies above and below the threshold 1/ε. The symbol ϕε is well approximated by |ξ|ε, namely the wave operator with speed 1/ε for frequencies below the threshold 1/ε and by |ξ|2, i.e., the free Schrödinger operator for frequencies larger than 1/ε. The desired decay then follows from the wave-like estimate for low frequencies and Sobolev embedding for high frequencies. However, this leads to a loss of the aforementioned regularizing effect. Interpolating in the low frequency regime between the wave-type estimate and (4.7) allows one to obtain Strichartz estimates with arbitrarily small loss of regularity.
Definition 4.2. The exponents (q,r) are said to be μ-admissible if 2≤q,r≤∞, (q,r,μ)≠(2,∞,1) and
We say that a pair is Schrödinger or wave admissible if μ=d2 or μ=d−12 respectively. Further, we denote β=β(r):=12−1r.
Proposition 4.3 ([6]). Let ε>0 and θ∈[0,1). Then, for any 2−θ2-admissible pair (q,r) and s0=3β(r)θ, it holds
For θ=0, the Strichartz estimate reduces to the one for the Schrödinger group and does not provide any decay in ε. For θ=1, we recover a wave-like estimate with sound speed 1/ε. In [16,Corollary B.1], the authors prove estimate (4.8) for θ=1 and d≥2 and low frequencies in the framework of the (GP)-equation. For high frequencies, a Schrödinger type estimate is obtained. In this regard, (4.8) can be considered as a refinement of [16,Corollary B.1 ].
Remark 4.4. In [6], Corollary 4.3 is stated in terms of Besov spaces which is slightly more precise but not needed for our purpose.
Abstract arguments [31,38] then also yield the non-homogeneous Strichartz estimate for eitHε.
Corollary 4.5. Let ε>0 and θ∈[0,1). Then, for any 2−θ2-admissible pair (q,r) and s0=3β(r)θ, it holds
Further, for any 2−θ2-admissible pairs (q,r) and (q1,r1) it holds
with s1=3θβ(r1).
In order to obtain suitable bounds on (˜σε,˜mε) by means of the Strichartz estimates, we start by proving uniform bounds for (σ0ε,m0ε).
Lemma 4.6. Under the Assumptions 2.5, the initial data (σ0ε,m0ε) satisfy the following bounds:
1) σ0ε∈L2(R2) uniformly bounded,
2) ε∇σ0ε∈H−δ(R2) uniformly bounded for δ>0 arbitrarily small,
3) m0ε∈H−δ(R2) uniformly bounded for δ>0 arbitrarily small.
Proof. It follows from (2) Lemma 3.1 that σ0ε=ε−1(ρ0ε−1)∈L2(R2) uniformly bounded. Statement (2) follows from the identity
and the uniform bound for √ρ0ε−1∈H1(R2)↪Lr(R2) for r∈[2,∞) provided by (1) Lemma 3.1. To prove statement (3), we recall that Λ0ε∈L2(R2) uniformly bounded and √ρε−1∈H1(R2)↪Lr1 with r1∈[2,∞) uniformly bounded. It follows mε=Λε+(√ρ0ε−1)Λε∈L2(R2)+Lr(R2)↪H−δ(R2) uniformly bounded with δ>0 arbitrarily small.
To infer a bound on the nonlinearity Gε defined in (4.2), Gε is decomposed as Gε=−G1ε+G2ε where
Exploiting the a priori estimates stemming from inequalities (2.3) and (2.4) we obtain the following uniform bounds.
Lemma 4.7. Let T>0, (ρ0ε,u0ε) be initial data satisfying Assumptions 2.5 and (ρε,uε) a FEWS with initial data (ρ0ε,u0ε). Then,
1) G1ε∈L∞(0,T;W−2,r′(R2)) uniformly bounded for all r′∈[1,2);
2) G2ε∈Lp(0,T;H−1(R2)) uniformly bounded for all p∈[1,2).
Proof. It follows from (2.3) and Lemma 3.1 that
uniformly bounded. As W1,r(R2)↪L∞(R2) for all r>2 and by duality L1↪W−1,r′(R2), one obtains,
uniformly bounded for all r′∈[1,2). To bound G2ε, we observe that
uniformly bounded for all p∈[1,2). Indeed, (9) Lemma 3.1 yields that Sν,ε∈L2(0,T;L2(R2)) uniformly bounded and √ρε−1∈Lp1(0,T;L∞(R2)) uniformly bounded for all p1∈[2,∞) from (1) Lemma 3.3. Hence,
uniformly bounded for all p∈[1,2).
The uniform estimates for (σ0ε,m0ε) and Gε together with the Strichartz estimates allow one to infer strong convergence of (˜σε,˜mε) to 0 as ε→0 in space-time norms.
Proposition 4.8. Let T>0, (ρ0ε,u0ε) be initial data satisfying Assumptions 2.5 and (ρε,uε) a FEWS with initial data (ρ0ε,u0ε). Further, let θ∈(0,1) and (q,r) be a 2−θ2-admissible pair, then,
where s=3β(r)θ with β(r) as in Definition 4.2.
Note that s>0 provided that r>2 and that s can be made arbitrarily small by choosing θ>0 sufficiently small.
Proof. First, we show that the initial data satisfy ˜σ0ε,˜m0ε∈H−12(R2) uniformly bounded. Lemma 4.6 states that σ0ε,m0ε∈H−12(R2) uniformly bounded. The transformation T1:σ0ε↦˜σ0ε is defined through the Fourier-multiplier φε(|ξ|):=(1+ε2κ2|ξ|2)12 which entails a loss of derivatives for high frequencies only, namely
It then follows from (1) and (2) of Lemma 4.6 that
where P≤ε−1 and P>ε−1 denote the projections on frequencies of order below or above ε−1 respectively. Similarly, the transformation T2:Q(m0ε)↦˜m0ε=Δ−12divQ(mε) is given by the Riesz transform which is bounded on L2(R2). One has
Analogously, it follows that for any r′1,q′2∈[1,2) that
from Lemma 4.7. Second, for θ∈(0,1) and any 2−θ2 admissible pair (q,r), the Strichartz estimate (4.8) applied to (1−Δ)−12−s˜σ0ε with s=3θβ(r) yields
where we exploited (4.10) and (4.11) respectively. Similarly, for any θ∈(0,1) and any 2−θ2 admissible pair (q,r), the non-homogeneous Strichartz estimate (4.9) applied to (1−Δ)−2−(s+s1)˜G1ε yields
where we used the first inequality of (4.12) and (1) Lemma 4.7 in the last step. Similarly, for any θ∈(0,1) and any 2−θ2 admissible pair (q,r) and q′2∈[1,2) it holds that
upon using the second inequality of (4.12) and (2) Lemma 4.7. We are now in position to infer the desired decay of (~σε,~mε). The Duhamel formula associated to (4.5) is given by
Summarizing it follows that for any θ∈(0,1) and 2−θ2 admissible pairs (q,r) and (q1,r1) one has
Note that s>0 provided that r>2.
The desired decay of Q(mε) follows upon observing that Q(mε) can be controlled in terms of ~mε and interpolation with the uniform bound of mε at Sobolev regularity from (2) Lemma 3.3.
Corollary 4.9. Let T>0, (ρ0ε,u0ε) be initial data satisfying Assumptions 2.5 and (ρε,uε) a FEWS with initial data (ρ0ε,u0ε). Then, for all r∈(2,∞), there exists α>0 such that
Proof. First, from the uniform bound mε∈L2s1−(0,T;Hs1(R2)) for all s1∈(0,1) provided by (2) Lemma 3.3, we conclude that
for any r∈[2,∞) from the Sobolev embedding. In particular, given r∈[2,∞) one may choose s1 sufficiently close to 1 such that s1−2β(r)>0. Second, it follows from Proposition 4.8 that for any θ∈[0,1) and 2−θ2-admissible pair (q,r) one has
where s2=3θβ(r) with β(r) as in Definition 4.2. For θ∈(0,1) to be fixed later, let (q,r) be a 2−θ2-admissible pair. Then, the interpolation Lemma 1.2 yields that
where
For θ∈(0,1) sufficiently small, s1 sufficiently close to 1 and any r∈(2,∞) one may choose θ′∈(0,1) sufficiently close to 1 so that s0>0. Moreover, since (q,r) is 2−θ2-admissible with r>2 one has that q∈(2,∞) and therefore q0∈[2,∞). It follows that for any r∈(2,∞) there exists α>0 such that
Remark 4.10 If (1.1) is considered with a general capillarity tensor K, as defined in (1.2), and in the scaling (1.8), then the respective linearized system amounts to (4.1) at leading order. More precisely, we wish to linearize (1.2) for ρε=1+εσε and note that only the first term ρdiv(k(ρ)∇ρ)I of K yields a contribution of order O(ε) while the second and third term contribute with terms of order at least O(ε2). Those may be discharged into Gε on the right-hand side of (4.1) and bounded in appropriate Sobolev spaces at negative regularity. We recover the Bogoliubov dispersion relation as in (4.3) and the dispersive analysis then follows the same lines.
Note that if κ=0, one may still prove that Q(mε) strongly converges to zero in Lq(0,T;W−s,r(R2)) for some s>2 and wave-admissible exponents (q,r), though with increased loss of regularity and worse decay rate as (4.7) is no longer available. However, under the light of Remarks 2.7 and 3.4 we lack an appropriate uniform estimate to perform the interpolation argument of Corollary 4.9.
5.
Proof of the main theorem
This section provides the proof of Theorem 2.6. First, we show strong convergence of Λε and mε in L2loc((0,∞)×R2). Second, we pass to the limit in (1.9) to show that the limit function is the unique Leray weak solution of (1.11).
In order to show strong convergence of the momentum density {mε}ε>0, it remains to prove compactness of the solenoidal part {P(mε)}ε>0 of the momentum density mε.
Lemma 5.1. Under the assumptions of Theorem 2.6, there exists u∈L∞(0,∞;L2(R2)) such that up to extracting a subsequence (not relabeled)
1) the sequence of momentum density {mε}ε>0 converges strongly to u in L2loc([0,∞)×R2),
2) {Λε}ε>0 converges weakly-∗ in L∞(0,∞;L2(R2)) and strongly in L2loc([0,∞)×R2) to u.
Proof. The momentum density is decomposed in the irrotational and the solenoidal part mε=Q(mε)+P(mε) by applying the Leray-Helmholtz projections. It follows from Corollary 4.9 that for all q∈[2,∞) there exists α>0 such that Q(mε) converges strongly to 0 in L2(0,T;Wα,r(R2)). In particular, Q(mε)→0 in L2(0,T;Lr(R2)) for all r∈[2,∞). By consequence, one also has Q(mε)→0 in L2loc([0,∞)×R2). Note that no extraction of subsequences is required. Second, since Λε∈L∞(0,∞;L2(R2)) uniformly bounded, there exists u∈L∞(0,∞;L2(R2)) such that Λε⇀u in L∞(0,∞;L2(R2)) up to extraction of a subsequence (not relabeled). We conclude that also mε⇀u in L2s−(0,T;Hs(R2)) for any T>0 und s∈(0,1) up to extraction of a further subsequence (not relabeled) by virtue of (2) Lemma 3.3. We show that P(mε) converges strongly to u in L2(0,T;L2loc(R2)). We recall that P(mε)∈L2s−(0,T;Hs(R2)) uniformly bounded for all s∈(0,1) from Lemma 3.3. Further, by projecting the moment equation of (1.3) on solenoidal vector fields we obtain
where Sν,ε denotes the symmetric part of Tν,ε defined by (2.2). Exploiting the uniform bounds of Lemma 3.1 and Lemma 3.3 and arguing as in the proof of Lemma 4.7, we conclude that ∂tP(mε)∈L2(0,T;H−s1(R2)) uniformly bounded for all s1>2. Hence,
with s∈(0,1) and s1>2. The Aubin-Lions Lemma, see e.g., [53], then implies that P(mε) converges strongly to u in L2(0,T;L2loc(R2)). By consequence,
As Λε in L∞(0,T;L2(R2)) uniformly bounded and √ρε−1 converges strongly to 0 in L2(0,T;L∞(R2)) by virtue of Lemma 3.3, it follows from Corollary 4.9 that there exists α>0 such that
Therefore, Λε converges strongly to u in L2loc([0,∞)×R2).
We are now in position to prove the main result Theorem 2.6.
Proof of Theorem 2.6. To show the first statement, we note that (6) Lemma 3.1 yields ‖ρε−1‖L∞L2≤C√ε. On the other hand,
As √ρε−1∈Lp(0,T;L∞(R2)) and ∇√ρε∈L4(0,∞;L4(R2)), it follows that ∇2(ρε−1)∈Lp2(0,T;L2(R2)) for all p2∈[1,2). Upon applying Lemma 1.2 we infer that for all θ∈(0,1)
where s=2θ and p=2/θ. Statement (3) follows from Corollary 4.9. To show (2), we first prove that u∈L∞(0,∞;L2(R2)∩L2(0,T;˙H1(R2)) for arbitrary T>0. To that end, we identify the weak limit of Tν,ε. By Definition, see (2.2), it holds
in distributional sense. One has that ∇mε converges to ∇u in the sense of distributions as mε→u in L2loc([0,∞)×R2)) from Lemma 5.1. Further, Tν,ε∈L2(0,T;L2(R2)) is uniformly bounded. Thus, there exists T∈L2(0,T;L2(R2)) such that Tν,ε⇀T in L2(0,T;L2(R2)) up to passing to a subsequence. The term ν(√ρε−1)Tν,ε converges to 0 in the sense of distributions as √ρε−1 converges strongly to 0 in L∞(0,∞;Lr(R2)) for all r∈[2,∞). The third term 2νΛε⊗∇√ρε converges to 0 in D′([0,∞)×R2) as ∇√ρε converges strongly to 0 in L4(0,T;L2(R2)) from Lemma 3.3 and Λε∈L∞(0,∞;L2(R2)) is uniformly bounded. Hence, by uniqueness of weak limits, it holds ν∇u=√vT in D′([0,∞)×R2). Moreover, νDu=√νS where S:=Tsym. It follows that
It is straightforward to check that for u∈L2(0,T;H1(R2)) such that divu=0 it holds
One may hence pass to the limit in (2.3) in order to obtain
As the initial data (ρ0ε,u0ε) are ill-prepared, the right-hand side of the previous inequality does in general not converge to ∫R212|u0|2dx. However, note that u∈L4(0,T;L4(R2)) by interpolation and the validity of the energy equality (2.5) will follow from the Ladyzhenskaya-Prodi-Serrin regularity criterion, see e.g., [43,Chapter 6] and also [51,52] once we have shown that u is indeed a weak solution to (1.11) with initial data P(u0)∈L2(R2).
Second, we show that u∈L∞(0,∞;L2(R2))∩L2(0,T;˙H1(R2)) is a weak solution to the incompressible Navier-Stokes equations (1.11) with initial data P(u0). Note that the strong convergence of √ρε−1 to 0 in L∞(0,∞;L2(R2)) from (5) Lemma 3.1, the analogue statement for √ρ0ε−1 from (1) Lemma 3.1 and the weak-∗ convergence of Λε to u in L∞(0,∞;L2(R2)) suffice to pass to the limit in the continuity equation of (1.3). Namely, let φ∈C∞c([0,∞)×R2), then the weak formulation reads
and it follows that divu=0 as ε→0. Next, we pass to the limit in the equation for the momentum density. Let ψ∈C∞c([0,T)×R2) such that divψ=0, then for all ε>0 it holds
Note that the weak L2-convergence of Λ0ε by Assumption 2.5 and the strong L2-convergence of √ρ0ε−1 to 0 from (2) Lemma 3.1 yield
Since Λε→u in L2loc([0,∞)×R2) strongly and √ρε−1→0 in L∞(0,∞;Lr(R2)) strongly for all r∈[2,∞), we may pass to the limit on the left-hand-side of (5.1) to obtain
In order to pass to the limit on the right-hand side of (5.1) we note that (3.5) yields strong convergence of ∇√ρε to 0 in L4(0,T;L2(R2)). It follows
as ε→0. Taking into account the aforementioned convergence properties of Λε and ∇√ρε we conclude that
Summarizing, we have shown that u∈L∞(0,∞;L2(R2))∩L2(0,T;˙H1(R2)) is a weak solution to (1.11). By virtue of the Ladyzhenskaya-Prodi-Serrin [43,51,52] regularity criteria, the velocity field u is the unique Leray-Hopf weak solution to (1.11) with initial data P(u0). The uniqueness result then implies convergence of the whole sequence Λε.
Remark 5.2. Note that Lemma 5.1 and the proof of Theorem 2.6 can be developed along the same lines when dealing with general viscosity and capillarity coefficients satisfying (1.7) or for NSK by adapting carefully the respective uniform estimates stemming from the energy and BD-entropy estimates, see Remark 3.4. In particular, the compactness of P(mε) can be inferred in the same manner.
Acknowledgments
The author would like to thank P. Antonelli for fruitful discussions. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1283/2 2021 – 317210226. This project was initiated while the author was a post-doc fellow at the Institut Fourier, University Grenoble Alpes, France, where he was supported by the French National Research Agency in the framework of the "Investissements d'avenir" program (ANR-15-IDEX-02) and the project "SINGFLOWS" (ANR-18-CE40-0027-01).
Conflict of interest
The author declares no conflict of interest.













 DownLoad:
DownLoad: