1. Staphylococcus aureus as a Pathogen
In humans, Staphylococcus aureus (S. aureus), is a commensal bacterium residing mainly in the anterior nares [1,2]. Depending upon which part of the human population is tested, 15 to 30% carry these bacteria permanently (persistent carriers), another 30 to 55% are periodically colonized (intermittent carriers), while the others are non-carriers [3,4]. Several staphylococcal adhesion factors are known as well as their molecular targets in the host [5]. Certain components of the bacterial cell wall, such as clumping factors [6,7], fibronectin-binding proteins [8,9,10] or wall teichoic acids [11], may serve as adhesins (microbial surface components recognizing adhesive matrix molecules, MSCRAMMs [12,13]) and facilitate attachment of the bacteria to the extracellular matrix, to cell surfaces or to docking molecules in host tissues. It is, however, still largely unknown which factors determine the individual carrier status in human hosts. Different combinations of bacterial MSCRAMMs with docking molecules in host tissues, which may vary due to individual genetic differences in humans [1,14], may determine whether an individual is a carrier, a potential carrier or a non-carrier. Another factor may be whether there are other (competing) microbes present or not [1]. Moreover, the status of the host’s immune system may also affect bacterial colonization as indicated by the facts that the relative number of persistent carriers is higher in children than in young adults [15], that the rate of carriers is higher among patients undergoing allergen-injection immunotherapy than in the respective control groups [16], and that S. aureus carriers were more abundant among individuals carrying the human immunodeficiency virus(HIV) than among individuals of the control group without HIV infection [17].
A carrier of staphylococci is at higher risk to acquire acute staphylococcal infections compared with non-carriers as most infections in carriers occur with the same bacterial strain that had been already associated with the carrier [18]. As the immune system of carriers has already had a chance to get in touch with the colonizing bacteria, acute infections with the colonizing strains of bacteria are generally less severe and have better prognoses than spontaneous infections in hosts that previously had been non-carriers [19]. Although there are strains of S. aureus that are more often involved in acute infections than others [20,21], it seems likely that the nature of staphylococcal infections is more or less opportunistic [14]. Open wounds, viral infections of the host or defects in host immune functions are conditions, which favor the transition of S. aureus from a commensal to a pathogen [22,23]. Staphylococcal infections occur in urinary and gastrointestinal tracts, in bone, and in the heart, but mostly on the skin (abscesses, furunculosis, scalded skin syndrome [24,25]) or in the respiratory tract causing rhinosinusitis [26] or pneumonia [27]. In some cases, sepsis may result from S. aureus infections and fatalities may occur from very extreme reactions of the host’s immune system [28,29]. S. aureus infections, however, are not always eliminated by the host immune system as the bacteria have evolutionarily developed many strategies to evade the host’s immune responses [30]. Another major problem in treating these ailments is that many staphylococcal strains are resistant to antibiotics. Infections caused by methicillin-resistant S. aureus (MRSA) [31,32] may occur within the community (community-acquired infection) or during hospitalization of patients (nosocomial or hospital-acquired infection) [33]
.
2. Host Responses to Staphylococcus aureus
The barriers separating the internal space of a multicellular organism from the environment are comprised of epithelia. Thus, epithelial cells are generally the first cells in the body, which are engaged with bacteria or bacterial products when pro- and eukaryotic organisms interact. Respiratory epithelia are generally exposed to the external medium and confronted with inhaled bacteria on a regular basis. This is one reason why respiratory epithelia are well studied with respect to their ability to perform routine airway clearance [34,35,36] and to activate innate or adaptive immune responses upon exposure to microorganisms [37,38,39,40,41,42,43].
To install an adequate immunological defense reaction to airborne foreign objects, the surface cells of the respiratory tract have to have the ability to recognize the quality of the inhaled material. The composition of all microbial factors, comprised of bacterial surface molecules as well as secreted factors, is highly specific for certain types of bacteria and has therefore been termed pathogen-associated molecular pattern (PAMP) or, as not all microbes are actually pathogens, microbe-associated molecular pattern (MAMP) [44]. Host cells are able to discriminate between different MAMPs/PAMPs by activation of a subset of pattern recognition receptors (PRRs) present at the cell surface or within the cytoplasm [45]. There are two types of membrane-bound PRRs in eukaryotic cells, the C-type lectin receptors differentiating sugar residues (mannose, fucoseor glucans) in carbohydrates exposed at the surface of viruses, fungi or bacteria from those in host cells [46,47], and the Toll-like receptors (TLRs) [47,48] which may recognize bacterial lipopolysaccharides (LPS), lipopeptides, proteins or nucleic acids [49]. Cytoplasmic NOD proteins (nucleotide-binding oligomerization domain proteins) [50] recognize bacterial peptidoglycans. Intracellular signaling activated by these receptor systems results in activation of enzymes involved in defensive cellular responses (e.g. phospholipase A2, lysozyme), production and secretion of antimicrobialpeptides or generation of reactive oxygen and nitrogen species to directly kill bacteria or infected host cells. In addition, the production and secretion of cytokines and chemokines is induced, which may mediate chemotaxis of immune cells (e.g. neutrophils) to the site of signal origin or may additionally activate the adaptive immune system [29,43].
With respect to the defense of airway epithelia against S. aureus, activation of TLR-2 and NOD2 signaling pathways seem to be especially relevant. Bacterial surface molecules like wall teichoic acids (WTA), lipoteichoic acids (LTA) or peptidoglycan have been identified as potential activators of TLR-2 signaling in epithelial cells [51,52,53,54]. In addition, staphylococcal peptidoglycan has been shown to induce NOD2 signaling [55]. Another surface bound component of S. aureus, the immunoglobulin-binding protein A, also activates defensive signaling in airway epithelial cells by binding to the TNF-α receptor [56,57,58]. The signaling pathways activated by these bacterial surface molecules coincide on the production and secretion of pro-inflammatory cytokines, the interleukins 1α, -6 and -8 as well as TNF-α in different cell types [29,59]. The chemokine IL-8 (CXCL8) is chemotactic for neutrophils, which are lured to the site of infection to fight the bacteria by endocytosis and oxidative processes [60], while IL-6 enhances immunoglobulin secretion by B cells [61] and stimulates hepatocytes to produce acute-phase proteins [62,63]. TNF-α functions as a cytotoxic cytokine [64] that may induce death of overly stressed cells (e.g. from internalized bacteria). Interestingly, accumulation of IL-6 and IL-8 in supernatants of airway epithelial cells did not require contact of the cells with bacterial surface molecules, but was elicited by exposing cells to bacterial supernatants [65] or just one of the important virulence factors ofS. aureus strains, alpha-toxin (hemolysin A, Hla) [66,67,68]. Furthermore, inoculation of mice with Hla-secreting strains of S. aureus accelerated IL-8 accumulation in the bronchoalveolar lavage fluid in contrast to inoculation using hla-negative strains as controls [69]. Incubation of airway epithelial cells with Hla resulted in release of the cytotoxic cytokine TNF-α [70]. This indicates that secretion of Hla by bacteria is sufficient to mount an inflammatory response in host epithelial cells and that direct physical interaction of host cells with bacteria is not essential.
Proteomic studies have shown that the pattern of proteins released into the bronchoalveolar lavage fluid by cells of the airways in mice changed substantially in response to nasal inoculation with S. aureus [71,72]. The authors observed dramatic increases inextracellular proteins within 6 h after inoculation. Pro-inflammatory cytokines (IL-1β, IL-8, IL-6 as well as TNF-α), complement factors, pulmonarysurfactant protein A (SP-A), extracellular matrix components, protease inhibitors, cathelicidin, an anti-microbial peptide, lectins binding bacterial sugar moieties, and the coagulation factors V, X and XIII were much more abundant in the airway fluid in infected than in control mice. Many of these host proteins have been shown to interact with bacterial cells or their secretory products directly. Complement factors, immunoglobulins and SP-Aare opsonins that bind to S. aureus topromote phagocytosis of the bacteria by macrophages and neutrophils, generally a way to dispose of pathogens. Extracellular matrix (ECM) components as fibronectin and vitronectinare potential attachment sites for surface-bound S. aureus binding proteins, and coupling of bacteria to these ECM molecules facilitates internalization of bacteria by alveolar epithelial cells [8,73,74]. As non-professional phagocytes, these cells may or may not digest the ingested bacteria. In the latter case, the intracellular space may function as a refuge for the bacteria which may either protect them from being attacked by the host immune system resulting in long-term persistence or may be used as a reaction vessel to generate toxins and destructive enzymes to kill the cell and cause tissue disruption [75,76,77,78,79,80,81]. Loss of cells from epithelia may be associated with loss in barrier function [82], which enables external bacteria to enter the interior of the body.
Proteomic and phosphoproteomic analyses using immortalized human airway epithelial cells treated with Hla revealed that substantial changes in protein expression and, even more pronounced, protein phosphorylation, occurred in signaling pathways and housekeeping proteins associated with cell-cell- and cell-matrix contacts, re-organization of the actin cytoskeleton and epidermal growth factor (EGF) signaling [83]. These findings correspond well to results of analyses of individual signaling pathways in these cells affecting cell-matrix interaction [84], Erk-type MAP kinase signaling and immediate early gene expression [66], or p38 MAP kinase signaling and secretion of pro-inflammatory cyto- and chemokines [67,85].
From the perspective of the host, a moderate cytokine-mediated inflammation is a suitable response to contact with bacteria or the secretory products of bacteria and helps the host to defend itself against potential pathogens. However, exaggerated pro-inflammatory signaling may induce severe tissue damage in the host. This insight has primed the search for mediators of Hla-induced pro-inflammatory signaling in epithelial cells [86]. Taken together, these examples show that interactions between bacterial and host molecules may be ambivalent with respect to costs and benefits for each of the interacting organisms. Depending on the specific conditions (concentrations, exposure time, status of the host immune system etc.), such interactions may provide protection of the host against bacterial attack or may benefit the bacteria to successfully establish an infection.
3. S. aureus Virulence Factors
Whether a strain of S. aureus is pathogenic or not depends on its ability to express different virulence factors. These factors may either remain attached to the bacterial cell surface and act on host tissues by direct host-pathogen interaction or may be secreted to the external medium and affect host cells even if bacteria do not physically interact with host cell surfaces [87]. Generally, virulence factors mediate pathogenesis in the host. Virulence factors may fulfill several functions for the bacteria in the host: They may (i) assist the bacteria in colonizing a niche in the host and may also be involved in mediating internalization of the bacteria by host cells, which is, if actively induced by bacterial factors, termed invasion, (ii)mediate suppression of the host’s immune systemor immune evasion of the bacteria, or (iii) may assist the bacteria in degrading host cells or tissues to obtain space for spreading or to acquire nutrients.
Genome analyses have shown that very different sets of genes coding for virulence factors are present in different S. aureus strains. This heterogeneity is due to the fact that many of these genes are not part of the bacterial core genome, but are encoded in pathogenicity islands (e.g. toxic shock syndrome toxin-1 and some enterotoxins) originating from horizontal gene transfer, or in phages (e.g. Panton-Valentine leukocidine, PVL) or in plasmids [88,89,90,91,92,93]. These genes are controlled by a complex regulatory network, which includes several two-component systems, alternative sigma factors, and various transcription factors [94,95,96]. The regulatory network integrates signals from the external environment and those from the internal metabolic machinery of the bacterial cell to generate particular subsets of virulence factor combinations at proper times and in amounts required for covering the momentary needs of the bacterial population. Depending on the actual density of bacterial cells (quorum sensing [97,98]), the composition of the medium, the presence of competitors, the quality of the host tissue or reactions of the host immune system, bacteria may undergo genetic adaptation [92] or show physiological acclimation by optimizing functions of the regulatory network to achieve expression of appropriate cocktails of virulence factors [99,100,101,102,103]. Proteome analyses [104,105], especially of the proteins that are secreted to the external medium by the bacteria, the secretome or exoproteome, have revealed [87,106,107] that the accessory gene regulator (agr)- [108,109] and the staphylococcal accessory regulator (sar)-systems [95,110] are involved in the expression of genes encoding either adhesion factors (at low densities of bacterial cells in the growth medium, i.e. during early exponential growth phase) or toxins (at high densities of bacterial cells in the growth medium, i.e. during late exponential growth phase and stationary phase). Adhesion factors mediate initial contact between the bacterium and host molecules in the extracellular matrix or at cell surfaces and are essential for commensal or pathogenic bacteria to extend their stay at their respective host niche to form colonies or biofilms [111] and, occasionally, to be internalized by host cells [112]. In some cell systems, internalized bacteria may even survive prolonged periods in a metabolically depressed condition as so-called small colony variants [81]. When extracellular bacteria reach critical densities in the host, they initiate the expression of bacterial modulators, toxins or enzymes that may attenuate responses of the host’s immune system [113,114,115,116] or assist the bacteria in degrading host cells or tissues to obtain space for spreading or to acquire nutrients from the host [117,118]. Recent comparative proteomic studies using the S. aureus RN1HG/HG001 strain [119] cultured either in tryptic soy broth (TSB, full medium) or in a modified culture medium for eukaryotic cells (pMEM) indicated that Hla production may occur already in the exponential growth phase in pMEM-cultured bacteria while it was still absent during this phase in bacteria cultured in tryptic soy broth (TSB) (Gutjahr 2010, http://ub-ed.ub.uni-greifswald.de/opus/volltexte/2011/915/). These preliminary data indicate that it may be worth to study effects of medium composition on virulence factor expression in these bacteria more thoroughly.
S. aureusreleases many different exoproteins (up to several hundred [87,106,107,120,121]) with entirely different functions into the extracellular medium. As S. aureus resides in human nares, it is often the first bacterium, which contributes to the genesis of lung infections (pneumonia) [122]. When focusing on S. aureus and the human lung, the pore-forming toxins Panton-Valentine leukocidin (PVL) and hemolysin A (Hla) appear to be important virulence factors determining morbidity as well as mortality associated with pneumonia [123,124,125]. This notion is based on the observation that patients infected with S. aureus strains carrying the phage-encoded genes for the two components of PVL are at risk to develop necrotizing pneumonia, often a lethal condition [126,127]. As for the pore-forming hemolysin A (Hla), it has been shown in animal models that antibodies against Hla or blockers of the Hla-transmembrane pore like cyclodextrins mediate protection against S. aureus pneumonia [128,129,130], which may otherwise be induced by Hla-secreting strains of S. aureus [131]. Progressive tissue destruction associated with necrotizing pneumonia is mainly due to the PVL-mediated plasma membrane damage in leukocytes (especially neutrophils [132,133] resulting in the induction of indirect necrotic processes in human lung tissue. The prevalence of genes encoding the PVL components, however, is relatively rare among invasive S. aureus strains compared with almost ubiquitous presence of hla genes in such strains [124,134]. These data indicate that S. aureus strains, which produce hemolysin A, may be quantitatively more relevant as potential inducers of pneumonia than are those generating PVL. Such a notion is supported by the observations that hemolysin A affects the barrier-forming epithelial cells in the airways directly [135] and does this in a dose-dependent fashion [136]. Low concentrations of Hla induce cell-type specific changes in ion permeability of the plasma membrane, ATP release, activation of intracellular signaling cascades, re-arrangement of the actin cytoskeleton and changes in the barrier function of epithelial cell layers, whereas high concentrations seem to induce plasma membrane damage and cell death.
Considering its high importance for potential disturbances of the integrity of airway epithelia, this review focuses on S. aureus hemolysin A and its sub-lethal effects on airway epithelial cells. A hypothesis is developed that Hla may not just be a tissue-destructive agent providing the bacteria with host-derived nutrients, but may also play complex roles in the very early stages of interactions of bacteria with healthy airways, possibly paving the way for establishing acute infections.
4. S. aureus Hemolysin A (Hla)
The hla gene of S. aureus codes for a precursor protein, which is post-translationally processed by proteolysis [137]. The soluble product is secreted to the extracellular space as a 33.4 kDa protein (alpha-toxin, hemolysin A, Hla) comprised of 293 amino acid residues (no cysteins), and a pI of 8.5 to 8.6. It folds spontaneously into its final conformation in aqueous solutions [138]. Upon contact with cell surfaces of eukaryotic cells (Figure 1A-B), Hla monomers may interact with certain lipid domains enriched in surface-exposed phosphocholine headgroups (lipid rafts containing sphingomyelin and phosphatidylcholine) [139,140,141]. In addition or alternatively to lipid binding, certain membrane-associated cell surface proteins may provide docking sites for Hla. Experimental evidence indicates that metalloproteinases, in particular ADAM10, are Hla receptor molecules on eukaryotic cell surfaces, as Hla has been shown to directly interact with ADAM10, and this interaction was diminished upon siRNA-mediated knockdown of ADAM10 [142]. Moreover, transgenic mice with a conditional disruption of the ADAM10 gene in their lung epithelium were reported to be resistant to lethal pneumonia induced by nasal inoculation using pathogenic S. aureus strains [143]. The interaction of Hla with ADAM10 results in redistribution of the complexes to plasma membrane areas enriched in caveolin-1 [142,144] and activation of the proteolytic activity of ADAM10. It is, however, still unclear whether ADAM10 activation occurs just by interaction with Hla or only after formation of a functional Hla-pore in the plasma membrane of the affected cell [142,143,145].
Obviously, the mechanism of interaction of Hla with host cells is concentration-dependent. Low concentrations may result in binding of monomers to specific binding sites with half-maximal binding (to rabbit erythrocytes) of 1-2 nmol/L (33-66 ng/mL) [136]. Such binding sites, however, seem to be absent in human erythrocytes as significant rates of Hla monomer binding, pore-formation and subsequent cell lysis does not occur at concentrations below 1 μmol/L (33, 000 ng/mL) [136]. Pore-formation by Hla in lipid bilayer or vesicle experiments in vitro has been studied at very different concentrations (1 ng/mL up to 16.5 μg/mL) [139,146,147].
These data indicate that pore formation may actually occur at any given Hla concentration, but that high concentrations of Hla monomers in the medium or the presence of receptors in intact cells may strongly accelerate pore formation. Unfortunately, experimental data about the Hla concentrations actually reached in infected host tissues are missing. Moreover, we know as yet only one or two potential receptor molecules for Hla monomers in mammalian cells, ADAM10 [142] and, potentially, alpha5beta1-integrin [70], and it is not known whether there are others or not. The relative abundances of ADAM10 are known for only very few cell types. As the cellular effects of pore formation are dependent on the actual number of pores present at a given time in a given cell, the rate of monomer binding, assembly and pore-formation is equally important as the rate of removal of pores from the plasma membrane by endocytosis and degradation or exosome formation. Given the lack in experimental data described above, it is virtually impossible to exactly predict which cell type in the host is affected by Hla in which way.
Formation of a functional transmembrane pore is a multi-step process requiring that Hla monomers attached to the surface of the host cell plasma membrane (Figure 1B) assemble into ahomoheptameric complex (Figure 1C), the prepore [147,148,149]. Each of the monomers contains two six-strand anti-parallel β-sheets, a β-sandwich, in those domains of the Hla monomers, which are exposed to the extracellular medium. These regions of all seven monomers together form the cap region of the prepore, while another array of β-sheets close to the cell surface form the rim region of the prepore [150,151]. Charged amino acid residues at the lateral surfaces of the rim region may provide contact sites with polar headgroups of lipids in host cell membranes. Several amino acids with aromatic side chains (tryptophane, tyrosine) at the base of the rim domain, however, may provide the contact sites for interaction of the prepore with the hydrophobic lipid environment of the plasma membrane [150]. The residues 118-140 in the sequence of the Hla monomer form the main portion of the pre-stem domain. If the prepore is fully assembled, all seven subunits simultaneously unfold their pre-stem domains, which are then inserted into the lipid bilayer. In the central regions of these domains, polar and hydrophobic amino acid side chains alternate, which fits to the model that these domains of all seven monomers form a transmembrane pore (Figure 1D,stem) with a hydrophobic surface interacting with the surrounding membrane lipids and a polar surface lining the central aqueous pore [152]. The histidine residue at position 35 in each of the monomers has a central function in the conformational change that results in the formation of the stem. Replacement of this amino acid by leucine completely abolished the transition of the Hla-heptamer from the prepore- (Figure 1C) to the pore stage (Figure 1D) [153]. Therefore, the H35L-mutant of Hla is often used to discriminate host cell effects depending on Hla plasma membrane attachment and prepore formation from those requiring formation of a functional transmembrane pore.
The Hla transmembrane pore is relatively resistant against proteolysis, and detergents are needed to extract the pore from the host cell membrane. This indicates that the insertion of the pore does not disturb the surrounding lipid layer in a way that it induces non-specific leakiness [154]. In turn, this means that all compounds that are exchanged between extra- and intracellular spaces of Hla-treated eukaryotic cells either utilize the pore itself for membrane passage or permeate by other pathways secondarily activated by pore formation.
The inner diameter of the pore at its narrowest site is approximately 1.4 nm [155,156,157]. Nominally, this diameter is large enough for the permeation of ions and small organic molecules up to molecular masses of 2 kDa [155]. Even single stranded RNA or DNA may be able to pass through the pore when electrical driving forces are provided. There are suggestions to use such systems for the development of new DNA sequencing techniques [158,159]. The ion selectivity of the Hla pore is not be very pronounced [118] so that cations as well as anions may pass the pore depending on their electrochemical gradients across the plasma membrane of the affected cell. Potassium ions (K+) [152,159,160,161]as well as chloride ions (Cl-) [159] have been shown to pass the Hla pore.
The question, however, which substances are actually able to permeate through the cell membrane-inserted Hla pore under physiologically relevant conditions is not entirely clear as illustrated by differences in the conclusions concerning the calcium permeability of the pore in studies using recombinant Hla preparations on lymphocytes [162], keratinocytes [160], or fibroblasts [163,164] on one hand showing that the pore is not calcium-permeable, and, on the other hand, pheochromocytoma [165], endothelial [166] or epithelial cells [67,167] indicating that the pore is calcium-permeable. Several researchers have observed substantial losses of ATP from various types of Hla-treated cells [152,160,164,168,169,170,171,172], which indicates that Hla pores are directly permeable to ATP and other molecules of similar sizes. However, eukaryotic cells may use the release of ATP from the cytosol to the extracellular space as some kind of a danger signal in response to potentially cell damaging stimuli [173,174] which initiates immunological and other cellular responses in neighboring cells. Pannexins have been implicated in mediating such ATP release from cells of various tissues by forming open pores resembling gap junction hemi-channels spanning through the plasma membrane of just one cell connecting intra- and extracellular spaces [175]. As there are controversial reports about entry or release of other molecules of similar molecular dimensions in Hla-treated fibroblasts or epithelial cells [167,176], it is not quite clear whether ATP is actually released through the Hla pore or by other pathways activated by Hla pore formation in the plasma membrane.
Under normal physiological conditions of a cell, the Hla pore inserted into the plasma membrane is constitutively open. However, changes in extra- or intracellular concentrations of protons (pH) or divalent cations (Ca2+, Zn2+) or changes in membrane potential [146,157] may modify the conductive properties of the pore.
5. Effects of S. aureus Hla in Airway Epithelial Cells
Using the non-pore forming H35L-variant of S. aureus hemolysin A [153], researchers obtained experimental evidence indicating that virtually all of the as yet observed Hla effects on eukaryotic epithelial cells are due to the formation of functional pores through the plasma membranes of the host cells. Attachment of Hla monomers to the outer surface of the cell membrane or formation of prepores does not seem to affect the host cells substantially.
The sensitivities of cells toward Hla is very different, even in cells originating from the same kind of tissue. As examples, two types of immortalized human bronchial epithelial cells and a lung cancer cell line have been compared in this respect. In different assays (live-dead cell staining, time lapse-microscopy of confluent cell layers, cell impedance, activation of intracellular signaling pathways etc.) S9 cells were much less sensitive to Hla-treatment compared with 16HBE14o- cells or A549 cells [67,84]. This points to a common basis for these differences which may lie in the different ways the cells accept Hla monomers at their surfaces or in differences in the half-life of Hla pores in the plasma membranes. The kinetics of Hla monomer association with the cell membrane may be affected by the abundance of potential receptor molecules. It has been shown that the amount of ADAM10 in airway epithelial cells determines the membrane-bound amount of Hla at a given time [142] and roughly correlates with the sensitivity of the respective cells to Hla [83], a finding that becomes even more obvious if cell types other than airway epithelial cells are considered, e.g. erythrocytes from different mammalian species [177]. On the other hand, it has been shown that the ability of cells to process plasma membrane areas containing Hla pores may also be an important determinant for their sensitivity toward Hla. Endocytosis and autophagy [178,179] or exosome production [180] may remove Hla pores from the plasma membrane and render them biologically inactive. We hypothesize that cells less sensitive toward Hla may have less receptor molecules on the their cell surfaces and/or may be able to more rapidly dispose of plasma membrane domains containing Hla pores than cells with high sensitivity toward Hla.
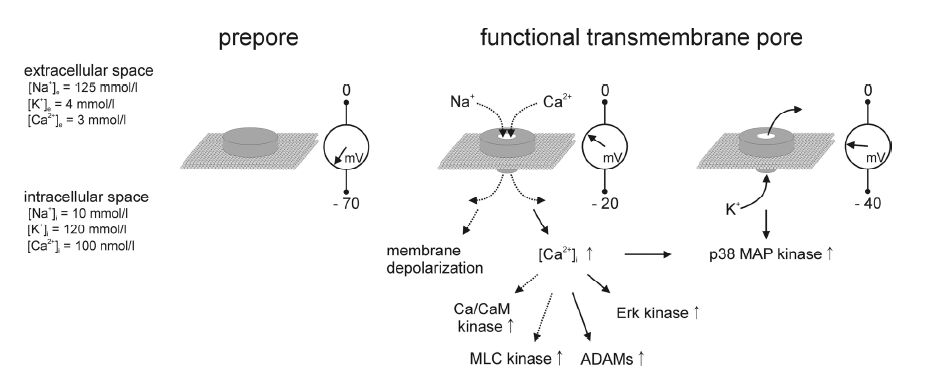
Hla pore formation in eukaryotic cells results in permeabilization of the plasma membrane for monovalent cations (Figure 2) as has been directly shown for potassium (K+) ions [160,161,162,164] and suggested for sodium ions (Na+). As there is usually no driving force for the net exit of potassium ions from the cytosol to the extracellular space in quiescent cells, the observed efflux of K+ from Hla-treated cells must be preceded by depolarization of the cell membrane [160,164], which has, unfortunately, not experimentally been shown yet. However, depolarization of the plasma membranemay mediate, through the exit of potassium ions from the cells [161], the activation of p38 MAP kinase which has been previously characterized as a typical signaling process in Hla-treated cells [67,161,169] that may mediate cell protective processes and the activation of innate immune responses in the host (169). At least in airway epithelial cells, activation of p38 MAP kinase also depends on an elevation in the cytosolic concentration of free calcium ions ( [Ca2+]i) [67]. As already known for some time, addition of Hla to the extracellular medium of epithelial cells actually results in a substantial rise in [Ca2+]i [166,167,181]. In the airways, these alterations may affect ciliary beat frequency, fluid and mucus secretion or release of pro-inflammatory cytokines and chemokines [65,67,135,182,183,184,185,186]. Such functional changes are supposed to represent defensive actions of the epithelial cells against the bacteria [35]. On the other hand, exposure of epithelial cells to Hla may modulate or even disrupt intracellular signal transduction [66,83,84,143] and induce cell shape changes [67,187,188] driven by actin-myosin interactions [189].
It has been postulated [154], but never been experimentally shown, that calcium ions can pass through the Hla pores. The data strongly support this hypothesis (Figure 2) because [Ca2+]i starts to increase with a short time lag upon addition of Hla to experimental cells [167] which may be explained by the time needed for Hla to form functional pores in the membrane, and for the resulting calcium influx to outperform cellular mechanisms that buffer or extrude calcium ions. Moreover, it has been shown that the presence of extracellular calcium is required for the Hla-mediated activation of the metalloproteinase ADAM10 [143] and that ADAM10 activation can be mimicked using calcium ionophores [190,191].
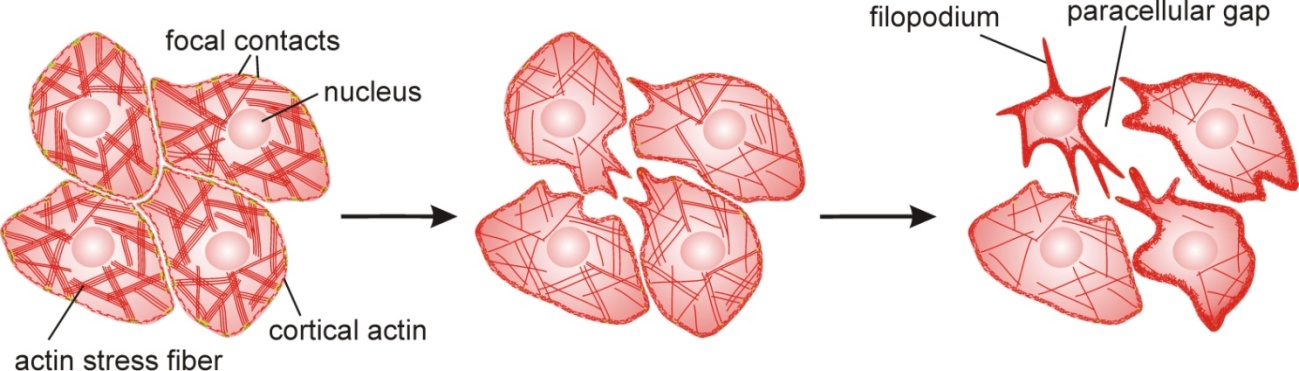
Activation of ADAM10 in Hla-treated cells, in turn, mediated cleavage of E-cadherins [143], which are important coupling proteins in cell-cell adhesion complexes (adherens junctions) [192]. We have recently shown that treatment of airway epithelial cells with recombinant Hla (rHla) results in changes in paxillin phosphorylation and acceleration in the formation as well as in disassembly of focal adhesion complexes [84], which attach the cells to the underlying matrix [193]. This results in a net loss of peripheral focal contacts located mainly in newly formed lamellipodia [84] and in massive changes in the architecture of the actin cytoskeleton (Figure 3). Such cells are not able anymore to stabilize and adequately adjust their cell shapes to movements of neighboring cells resulting in the appearance of paracellular gaps in the cell layer [67,84] (Figure 3). This correlates with epithelial injury and loss of epithelial barrier function observed during S. aureus infections in intact airways [145].
Attempts to dissect the cellular and molecular mechanisms underlying these cellular changes have not yet resulted in a conclusive picture. Several researchers have obtained evidence that Hla-treatment of cells results in activation of the protein kinases Src and Fak as well as Erk-type MAP kinases [67,84,142], but the modes of their activation are still elusive. The activation of metalloproteinases of the ADAM family, especially ADAM10, may result in ectodomain shedding of precursors of important signaling molecules like the epidermal growth factor (EGF) [194,195]. However, as members of the ADAM family, especially ADAM17, have been also implicated in shedding the ectodomains of receptors for TNF-α, EGF and IL-6 [56,57], the soluble portions of these receptors may mop up free ligand molecules from the airway lumen and terminate signaling. Hla-secreting strains of S. aureus were implicated in the activation of shedding of the ectodomain of syndecan-1, the major heparan sulfate proteoglycan of epithelial cells [196]. It is known that the shedding products of syndecan-1 elicit pro-inflammatory and tissue destructive actions in airways [197]. Depending on the mode of action of the Hla-activated sheddases and on the quality of their substrates, the resulting soluble shedding products may activate or inactivate autocrine or paracrine signaling providing either protective or deleterious signals for the respective target cells.
The decrease in the cellular ATP level induced by Hla-treatment [152,160,164,168,169,170,171,172] may affect the activities of energy-requiring molecules such as ATPases (potentially followed by dissipation of ion gradients) or protein kinases (potentially followed by hypophosphorylation and functional impairment of important regulatory or housekeeping proteins). It is, however, questionable whether the loss of ATP from the cytosol actually inhibits ion pump activities as experiments have shown that intracellular Ca2+-ATPases are still active at full pace when cellular ATP-levels drop to 10% of the control levels [198]. Another effect of ATP depletion in cells may be the accelerated chronophin-dependent dephosphorylation of the slingshot phosphatase followed by activation of the actin depolymerizating factor cofilin [199], a process which would result in degradation of actin stress fibers and accumulation of short actin filaments as actually observed (Figure 3). Such a mechanism could well explain the Hla-mediated changes in actin organization observed in Hla-treated airway epithelial cells [84]. Extracellular ATP, on the other hand, may function as a danger signal by activating purinergic receptors on airway epithelial cells [200,201,202] which may increase the ciliary beat frequency [203,204] and inhibit the apical uptake of sodium ions through the epithelial sodium channel (ENaC) [183] which results in an increase in luminal fluid volume. Both mechanisms may accelerate the removal of pathogens from the airways.
6. Potential Roles of Sub-lytic Concentrations of Hla in the Airways
Bacterial pore-forming toxins are generally considered to be agents used by the bacteria for the destruction of host cells aiming at the acquisition of nutrients (iron, amino acids, carbohydrates etc.), for providing space for bacterial growth and for compromising immune defense functions of the host. If this would be the sole function, however, it would be surprising that such complicated mechanisms of regulation of the expression of pore-forming toxins have evolved, that redundancy of pore-forming toxins in the same bacterial strain occurs, that the assembly of toxin monomers and pore formation in host cells is such a complex process, and that the cell physiological effects of sub-lytic concentrations of pore-forming toxins on eukaryotic host cells are so discrete and delicate as described above.
Moreover, all living cells show a certain degree of resilience against different types of adverse environmental conditions. If, as an example, presence of a small amount of Hla pores in an epithelial cell allows calcium influx along the electrochemical gradient from the extracellular space to the cytosol, all of this calcium will be readily extruded by Ca2+-ATPases in the plasma membrane (PMCA) or in the endoplasmic reticulum membrane (SERCA) without any net effect on the intracellular calcium concentration. If the number of pores, however, gets larger the resulting calcium influx may outperform the pump rates of these ATPases. In that case, [Ca2+]i will rise and affect cellular signaling. Even then, this does not mean immediate death for the cell, but induction of different cell behavior or altered gene expression. Such mechanisms may provide potential explanations for differences in the individual responses of (even clonal) cells to uniform Hla incubation conditions as observed in experiments with immortalized airway epithelial cells [67].
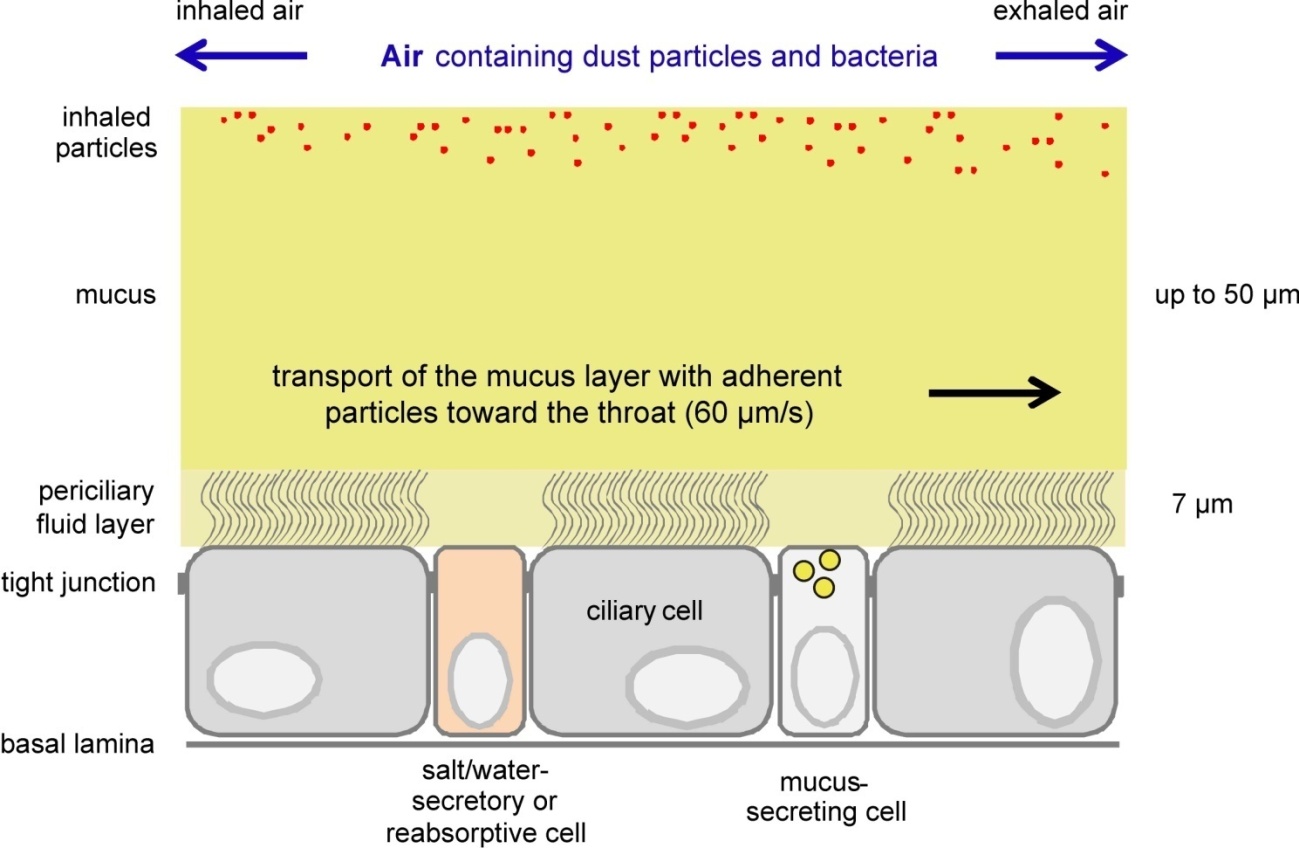
In healthy mammalian airways, mucociliary clearance (Figure 4) will limit the number of bacteria residing in the lumen of an individual at any given time. The number of bacteria (quorum sensing), however, somehow determines the genetic programs currently realized in bacteria, and it is known that toxin production by S. aureus seems to be activated only if bacterial densities are high [107]. However, these genetic programs may also be affected by the medium conditions of the bacteria, and it would be interesting to study virulence factor expression at those conditions that actually exist in the human airways [205].
Even mild disturbances of the mucociliary clearance, e.g. in hospitalized elderly people or humans suffering from viral infection, or in cystic fibrosis patients [182], may enable bacteria to stay long enough at the surface of the airway mucus layer to produce virulence factors. While the bacteria themselves are not able to cross the mucus layer and getting in physical contact with surfaces of epithelial cells, the soluble virulence factors may actually reach the cells by diffusion through the mucus layer. If, as described above, exposure of cells just to Hla elicits substantial changes in ion homeostasis, cell signaling and structural changes in the epithelial cell layers, we assume that bacteria actually utilize pore-forming toxins in sub-lytic concentrations to interfere with normal airway barrier and clearance functions and to compromise these.
In summary, the staphylococcal pore-forming virulence factor alpha-toxin (hemolysin A, Hla) is one of the important determinants for pathogenesis in host organisms. During fulminant infections, Hla may primarily serve the bacteria to induce host tissue destruction and to acquire host-borne nutrients for bacterial growth. However, there are many indications that Hla may have additional functions in the early stages of infection, especially in the lung, where the diffusion barrier of the airway mucus lining prevent bacteria from getting in direct contact with epithelial cells, while soluble virulence factors like Hla may pass the mucus layer by diffusion and negatively affect the barrier functions of the airway epithelia. These initial actions of pore-forming toxins may enable bacteria to establish infections in principally healthy individuals.
Acknowledgments
Part of our work on Hla has been financially supported by supported by HWP funding from the state government of Mecklenburg-Vorpommern and the Ernst Moritz Arndt-University and by start-up funds from SFB-TR34 (Deutsche Forschungsgemeinschaft). I thank Michael Hecker for his support of our work. Many thanks to Petra Hildebrandt for critically reading the manuscript and to four anonymous reviewers for their constructive suggestions for improvements of text and figures.
Conflict of Interest
I declare no conflicts of interest in this paper.
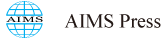








 DownLoad:
DownLoad: