Chronic pelvic pain (CPP) can cause extreme physical distress in women and has widespread socio-economic consequences. Nerve root blocks have become a safe and effective treatment modality in multiple specialties in both the diagnosis and treatment of pain. We describe a novel technique of a laparoscopic uterosacral nerve block (USNB) and demonstrate its effectiveness in the treatment of a complex case of CPP. USNB has potential diagnostic, prognostic and therapeutic implications. It should therefore be considered as part of the multi-disciplinary management of women with CPP of suspected uterine origin such as adenomyosis, degenerating fibroids or following myomectomy.
1.
Introduction
Chronic pelvic pain (CPP) is very common amongst women with a reported prevalence of 5.7%–26.6% [1],[2]. Not only can it cause extreme physical distress, but it is closely related with psychological well-being and frequently coexists with social and economic problems [3]. Endometriosis, adenomyosis, fibroids, adhesions, chronic pelvic inflammatory disease, pelvic organ prolapse and pelvic congestion are potential gynaecological aetiologies of CPP. However up to 70% are attributed to non-gynaecological aetiologies [4], such as inflammatory bowel syndrome (IBS), bladder pain syndrome (BPS), musculoskeletal causes and nerve damage. This overlap between specialities often causes diagnostic difficulty and often results in unsatisfactory treatment [5].
Management of CPP should be multi-disciplinary in nature and tailored towards the underlying aetiology utilising conservative, hormonal and surgical strategies. However, in cases where the cause remains unidentified, strategies including analgesia, antidepressants, anticonvulsants and transcutaneous electrical nerve stimulation can all be used to alleviate symptoms [6]. Whilst effective in the management of faecal incontinence and overactive bladder, the role of interventional neuromodulatory techniques, such as percutaenous tibial nerve stimulation or sacral neuromodulation, in the context of CPP remains unclear [6].
Where conservative treatment is unsuccessful, current surgical options include laparoscopic uterine nerve ablation (LUNA) or presacral neurectomy (PSN). Understanding of the nerve supply to the pelvis is essential to enable patient selection for such procedures. LUNA involves transection or excision of the uterosacral ligament which contain the afferent nerve plexuses and parasympathetic ganglia that carry pain signals from the uterus, cervix, and proximal part of the Fallopian tube [7]. The afferent nerve tissue that runs through the uterosacral ligament joins the inferior hypogastric plexus, which contributes to the superior hypogastric plexus, along with afferent and autonomic efferent nerve fibres from both the rectum and bladder. PSN involves the transection of the superior hypogastric plexus, which entails the denervation of additional pelvic viscera when compared to LUNA. It is therefore open to greater post-operative complications involving both bowel and bladder [8], with post-operative constipation reported in up to 74% of cases [9]. Regarding efficacy, whilst early results suggested potential benefit of LUNA in primary dysmenorrhea [10], it is currently of debated clinical benefit in CPP [11]–[13]. PSN appears to be more effective [14], but along with the aforementioned potential bowel and bladder side effects, it also requires significant surgical expertise and risks intraoperative complication owing to the close proximity of the great vessels and major lymphatic channels.
Nerve blocks have become a safe, successful and practical treatment modality in a variety of specialties in the diagnosis and treatment of both acute and chronic pain. In gynecology, nerve blocks have been used in a number of scenarios including pudendal nerve block for post-operative pelvic floor repair analgesia [15], paracervical block for uterine curettage [16], iliohypogastric pain for pain control after Caesarean section [17], and superior hypogastric nerve block for analgesia following uterine artery embolisation and total abdominal hysterectomy [18],[19]. We describe the novel technique of laparoscopic uterosacral nerve block (USNB) in the treatment of refractory CPP.
2.
Surgical technique
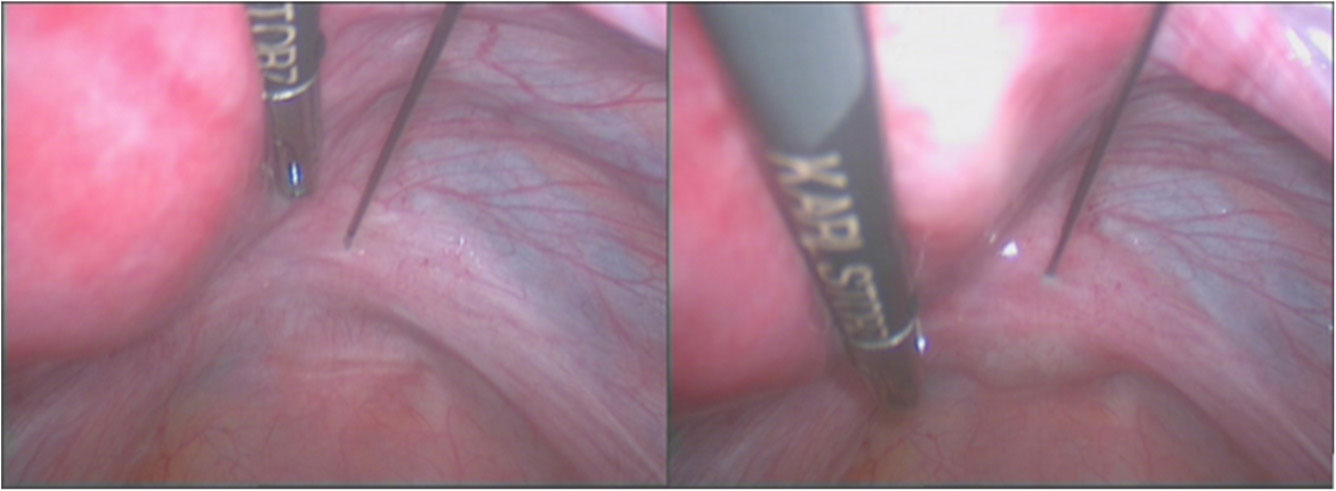
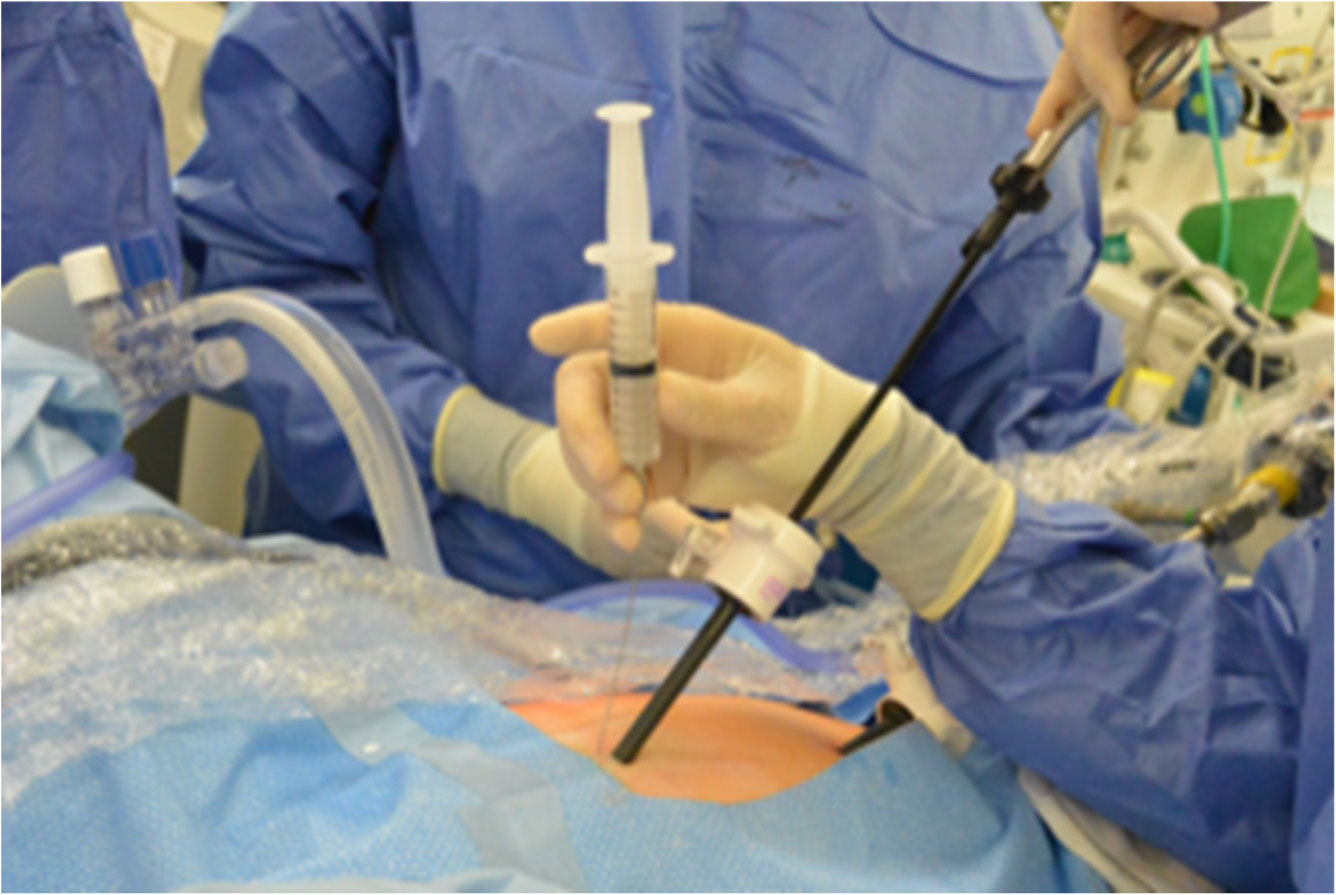
Routine laparoscopic entry and CO2 insufflation is undertaken to achieve a pneumoperitoineum. A 20 G, 130 mm pudendal needle (Rocket Medical plc, Washington, Tyne & Wear, UK) attached to a syringe containing local anaesthetic and steroid is then inserted suprapubically (Figure 1). The uterus should be instrumented and anteverted, so the uterosacral ligaments are under slight tension. The ureters can then be identified and mapped. The needle is then inserted, 2 cm distal to the insertion of the uterosacral ligament into the cervix to a depth of 3–5 mm (Figure 2). Following aspiration to ensure the needle is not placed intravascularly, the local anaesthetic and steroid mixture is instilled, divided equally between both uterosacral ligaments, until a surface bleb is visualized (Figure 2). Care should be made to avoid underlying vessels and the ureters.
3.
Case report
A 24-year-old nulliparous woman presented with a three-year history of severe pelvic pain following uterine artery embolisation for treatment of abnormal bleeding secondary to gestational trophoblastic disease. The pain was constant, with intermittent random sharp exacerbations, and associated with dyspareunia but in absence of bowel or bladder symptoms. She had previously been extensively investigated including pelvic MRI and ultrasound scans, hysteroscopy and three laparoscopies, none of which identified pathology. The diagnostic laparoscopies did not lead to any alleviation of pain. Multidisciplinary input was sought involving specialists in gynecology, gastroenterology, pain management and hypnotherapy. Conservative management with analgesia including paracetamol, ibuprofen, tramadol and buprenorphine patches provided limited relief. A variety of hormonal treatments were ineffective or poorly tolerated. Low dose sertraline and nortriptyline provided slight benefit, but cetirizine was ineffective, and gabapentin caused intolerable side effects. Her symptoms were so severe she presented requesting hysterectomy. In light of her age and nulliparity, fertility sparing surgical intervention was discussed and she was offered a laparoscopic uterosacral nerve block.
The laparoscopy findings were unremarkable with no pathology identified in the uterus, Fallopian tubes, ovaries or pelvic peritoneum. She underwent an uncomplicated USNB using 6 mls of 1% lidocaine and 1.5 mg of dexamethasone and was discharged home the same day. Within days post-operatively she was pain free, had stopped all medications and described herself as having finally ‘got her life back’. Seven months post-operatively the pain returned. She underwent a further uncomplicated USNB, this time using 6 mls 0.25% bupivacaine and 1.5 mg dexamethasone. She remains pain free nine months post-operatively.
4.
Discussion
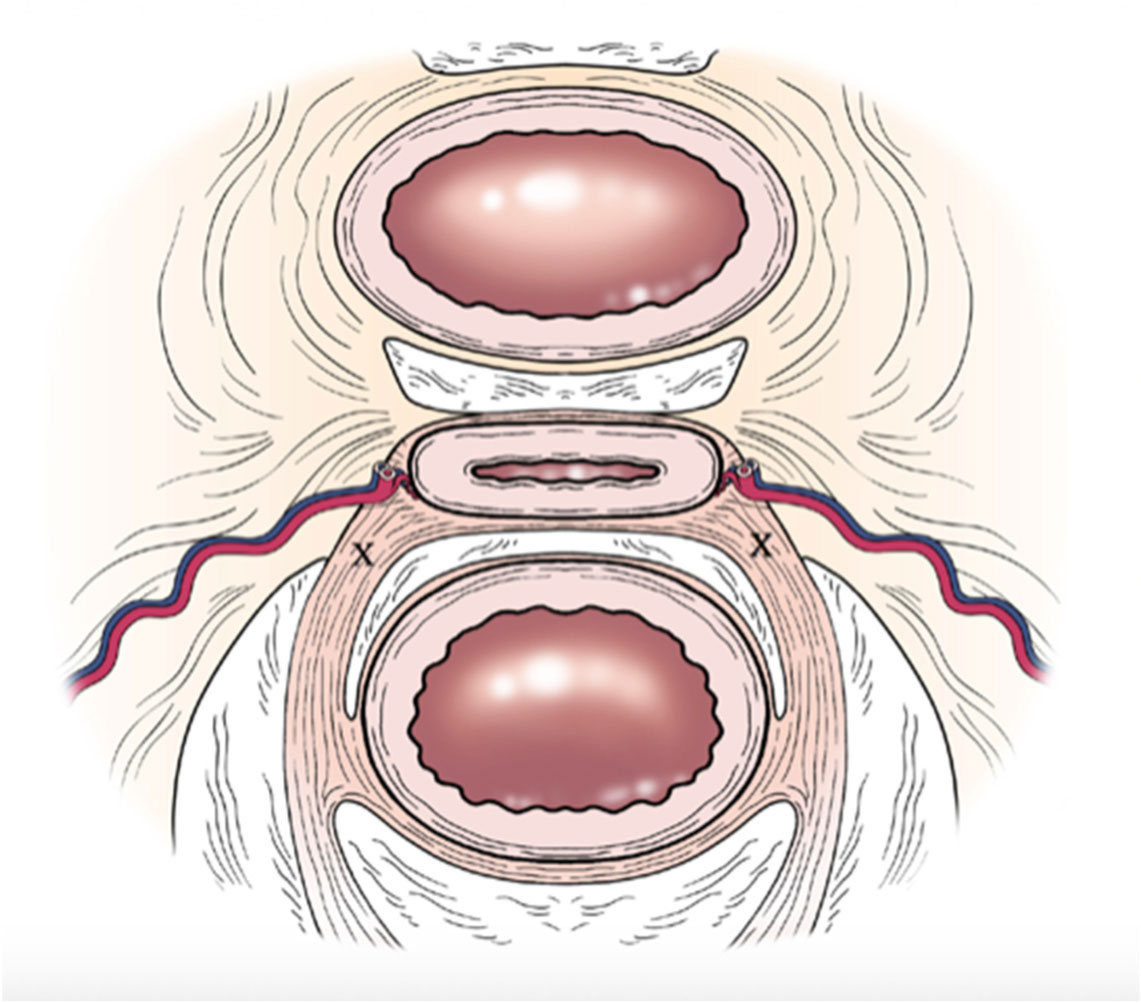
The concept of USNB is centralized around the principle of ‘blocking’ the afferent pain nerve fibres that travel within the uterosacral ligament using an atraumatic method. The nerve fibers that run in the ligament, including the parasympathetic and sympathetic nerve bundles, are therefore preserved. The decision to infiltrate the block 2 cm from the insertion of the ligament into the cervix is based on a study by Fujii et al which revealed the greatest number of nerve fibers are 16.5–33 mm distal to the site of attachment into the cervix [20]. The majority of nerve fibres were also found at a depth of 3–15 mm. The decision to infiltrate at the superficial end of this spectrum, between 3–5 mm, was to minimize potential damage to the uterine arteriovenous plexus. Figure 3 demonstrates the close proximity of the uterine vasculature to the optimal site of infiltration.
USNB is a simple procedure which requires universally available medications and equipment, and requires little technical expertise. It can easily be performed at the same time as a diagnostic laparoscopy, particularly in cases where no pathology is identified. A pain-free outcome indicates the origin of the pain is from the uterus, cervix or proximal Fallopian tube. It can therefore assist in the diagnosis of various gynaecological conditions such as adenomyosis, a condition traditionally difficult to diagnose because of the lack of pathognomonic signs or clinical findings [21]. Whilst magnetic resonance imaging (MRI) and ultrasound can be useful, the diagnosis is only confirmed histologically following hysterectomy.
USNB may also provide important prognostic information to help identify those patients who may benefit from LUNA. Whilst, the evidence on LUNA is currently inconclusive, it has been proposed that it may be effective in ‘well selected’ patients [12]. This is based on Daniels et al suggestion that because of the presence of at least five pathways within the pelvis that transmit noxious stimuli, potential for ‘neuronal cross talk’ exists [13]. As such LUNA may not obliterate enough afferent fibres to produce complete pain relief. The same principle can be extrapolated to USNB, and therefore a positive response may be prognostic of LUNA success. However, it may be ongoing pain following LUNA may be due to neuralgia following transection of nerve fibres, as can happen with any denervation procedure.
As demonstrated in this case, the effect of USNB is likely transient. The initial USNB used lignocaine, a short acting local anaesthetic, and provided seven months relief. It is anticipated that the use of a longer acting local anaesthetic may provide longer term analgesia, but numerous blocks may still be required. Whilst multiple treatments could be undertaken laparoscopically, repeated laparoscopies pose cumulative surgical and anaesthetic risk. A potential repeated treatment could instead be undertaken transvaginally in an outpatient setting. Such a technique was previously demonstrated over 50 years ago, referring to a paracervical block infiltrated between 4–5 o'clock and 7–8 o'clock [22]. One author however strongly insisted on using a more accurate technique involving immobilisation and palpation of the uterosacral ligaments using rectovaginal examination [22]. It is our opinion that a paracervical block would not block the area of the uterosacral ligament containing the most neural tissue and as such, would not provide the accuracy associated with laparoscopic USNB. Morevoer, performing a rectovaginal examination in an outpatients clinic may be unacceptable to women and clinicians may not be able to identify the uterosacral ligaments with certainty. Furthermore, undertaking the procedure blind potentially increases the risk of iatrogenic damage to underlying structures including the rectum, bladder, ureters and blood vessels. To overcome these risks, and improve accuracy, the area can be marked vaginally intra-operatively during laparoscopic USNB. This would be accomplished by palpating the uterosacral ligaments under direct vision and using a permanent tattoo, as used in radiotherapy treatment, for future reference. Alternatively, it would also be feasible to undertake USNB transvaginally under ultrasound guidance, although this would require significant technical expertise.
An alternative future consideration, in women who experience transient symptomatic relief following USNB, could be to perform a longer term ‘neurolytic’ block using alcohol, phenol or radio frequency ablation. Such techniques have been used in celiac plexus blocks with success in chronic abdominal pain of both malignant and benign aetiologies [23]. Laparoscopic presacral neurolysis, has previously been demonstrated as an alternative to PSN in patients with endometriosis, using the same concept at the superior hypogastric plexus [23]. However whilst good symptomatic relief was achieved, 73% of women suffered from constipation post-operatively [24]. Special consideration should be given prior to the use of alcohol or phenol due to the risks of local spread or intra vascular administration. Radiofrequency ablation however uses high-frequency alternating current to induce coagulative necrosis at the intended site, and as the tissue heating dissipates rapidly with distance from the electrode tip, the site ablated is more focused when compared to the chemical neurolytic techniques [25]. The concept of pulsed radiofrequency could also be considered as a less invasive option. The use of neurolytic techniques require further studies to assess safety and efficacy, and should be performed in a multi-disciplinary setting, under the guidance of pain team specialists.
5.
Conclusion
CPP is a common presenting complaint in women and is associated with negative cognitive, psychological, social and economic connotations. The overlap of diagnoses across a range of specialties creates clinical uncertainty and often results in diagnostic delay and suboptimal management. The current surgical options, LUNA and PSN, are limited by unproven efficacy or are associated with significant side effects. We demonstrate the effective utilization of laparoscopic USNB in a woman with chronic pelvic neuropathic pain of uterine origin, refractory to traditional treatment for chronic pelvic pain. USNB can have important diagnostic and prognostic roles in the management of CPP and has an excellent, albeit temporary therapeutic effect in carefully selected women with related to the cervix, uterus or proximal Fallopian tubes. Whilst this case report demonstrates promise, further prospective studies are essential to assess the role of USNB in CPP and determine its value in the clinical applications outlined in this manuscript.









 DownLoad:
DownLoad: