1. Introduction
Today, in addition to chemical compounds, many biologics have been developed for clinical application. For both categories of drug, validation of pharmacological efficacy by pharmacokinetics (PK) and pharmacodynamics (PD) studies is important for successful development of safe and effective therapeutics [1,2]. In conventional PK/PD analysis, drug concentrations are examined in a blood or tumor sample. The profile of a small-molecule chemical compound can be predicted based on the profiles of similar compounds, or by using any of several pharmacological compartment models [2,3,4].
Unlike chemical compounds, biologics (especially antibodies) have unique PK/PD profiles and multiple mechanisms of action, including neutralizing effects, induction of apoptosis, and immunoreactions such as ADCC (antibody-dependent cellular cytotoxicity), CDC (complement dependent cytotoxicity), and ADPC (antibody-dependent cellular phagocytosis) [5,6]. Moreover, the PK profile of an antibody has distinct features that depend on the structure of the antibody itself or the biology of the targeted antigen [5,7,8,9,10]. In regard to PD, efficient drug delivery into the targeted site and accumulation in normal tissues should be checked carefully. Traditionally, however, such PK/PD studies are usually conducted in the middle or late stage of drug discovery and development.
A more convenient evaluation method for visualizing drug distribution in the early stage of development would improve the success rate. Mass spectrometry imaging (MSI) is a method for viewing a biomolecule or metabolite in a tissue sample using MS analysis [11,12,13,14,15,16,17,18,19,20]. We applied this approach to drug imaging as a form of in situ PK/PD analysis. Although in situ evaluations usually employ autoradiograms with radiolabeled drugs, the associated techniques are complicated and expensive [14,21,22]. By contrast, MSI is convenient, and (excluding the cost of the analytical device itself) the running cost is low.
Here, we review advances in the use of MSI for early drug discovery and development, and describe our recent relevant work.
2. PK/PD and drug development
Chemical compounds have linear PK profiles, and their biodistribution can be predicted using pharmacological compartment models [2,3,4]. By contrast, antibodies have complex non-linear PK profiles with substantial between- and within-patient variability. In particular, the target-binding activity and immunogenicity of the antibody strongly influence the PK profile. The former phenomenon is referred to as target-mediated drug disposition (TMDD). High-affinity target binding or high levels of target will strongly influence the PK profile, typically resulting in non-linear PK characteristics [5,8,23]. The immunogenicity of an antibody is another important factor influencing the PK profile [9,24].
Several factors are involved in forming an anti-drug antibody (ADA) against a therapeutic antibody. ADAs are classified into two types, binding antibody (Bab) and neutralizing antibody (NAb). ADA-Babs are produced even against fully human therapeutic antibodies that avoid immunogenicity based on species differences. Babs react to allotypes that vary based on genetic differences between populations. On the other hand, NAbs react to the epitope that determines the specificity of the antibody. In immunology, this phenomenon is referred to as an idiotype network. Both B and T lymphocytes recognize antigens specifically, either via antibodies (B cells) or T-cell receptors. Idiotype networks enable the host to avoid the expansion of autoreactive B or T cells [7,9,24,25].
ADAs can be produced not only against antibodies, but also against chemical compounds. Because it is still difficult to abolish the immunogenicity of a drug, especially an antibody drug, the detection, characterization, and control of ADAs have become more and more important. These factors, which influence drug development, can be predicted using molecular imaging and DDS technologies. Genetically engineered mice with targets derived from humans or monkeys would be helpful for such predictions [7,9].
In the drug discovery, determination of the mode of action (MOA) and its uniqueness in comparison with conventional drugs are also important factors influencing the success rate of drug development. Chemical compounds, especially molecular targeting drugs such as kinase inhibitors, have simple straightforward MOAs. By contrast, antibodies have multiple functions: (1) neutralizing effect; (2) apoptosis-inducing effect; (3) ADCC (antibody-dependent cellular cytotoxicity); (4) CDC (complement dependent cytotoxicity); (5) ADPC (antibody-dependent cellular phagocytosis) [5,6]. Furthermore, next-generation antibody therapeutics have additional distinctive actions. An antibody-drug conjugate (ADC), a combination of an antibody and chemical compound connected via a specialized linker, has a chemotherapeutic effect as an additional action [14,26,27,28,29,30,31]. In radioimmunotherapy (RIT) and photoimmunotherapy (PIT), the new properties are radiotherapeutic and phototherapeutic, respectively [32,33]. The recently approved anti-PD-1, anti-PD-L1, and anti-CTLA-4 antibodies have a unique MOA; they block the immune checkpoint to enhance the anti-tumor immunoreaction [34,35,36].
3. EPR effect and DDS drug
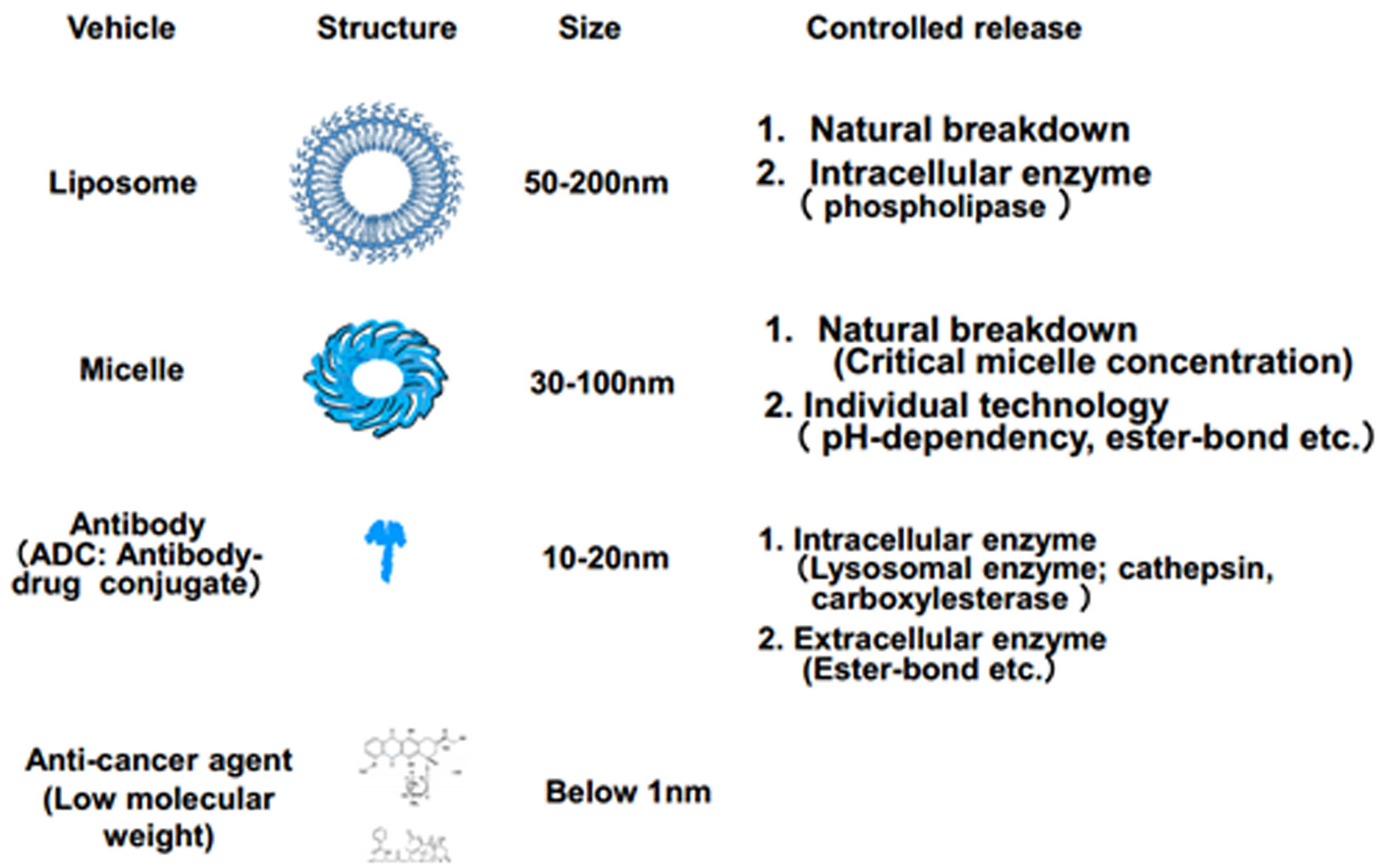
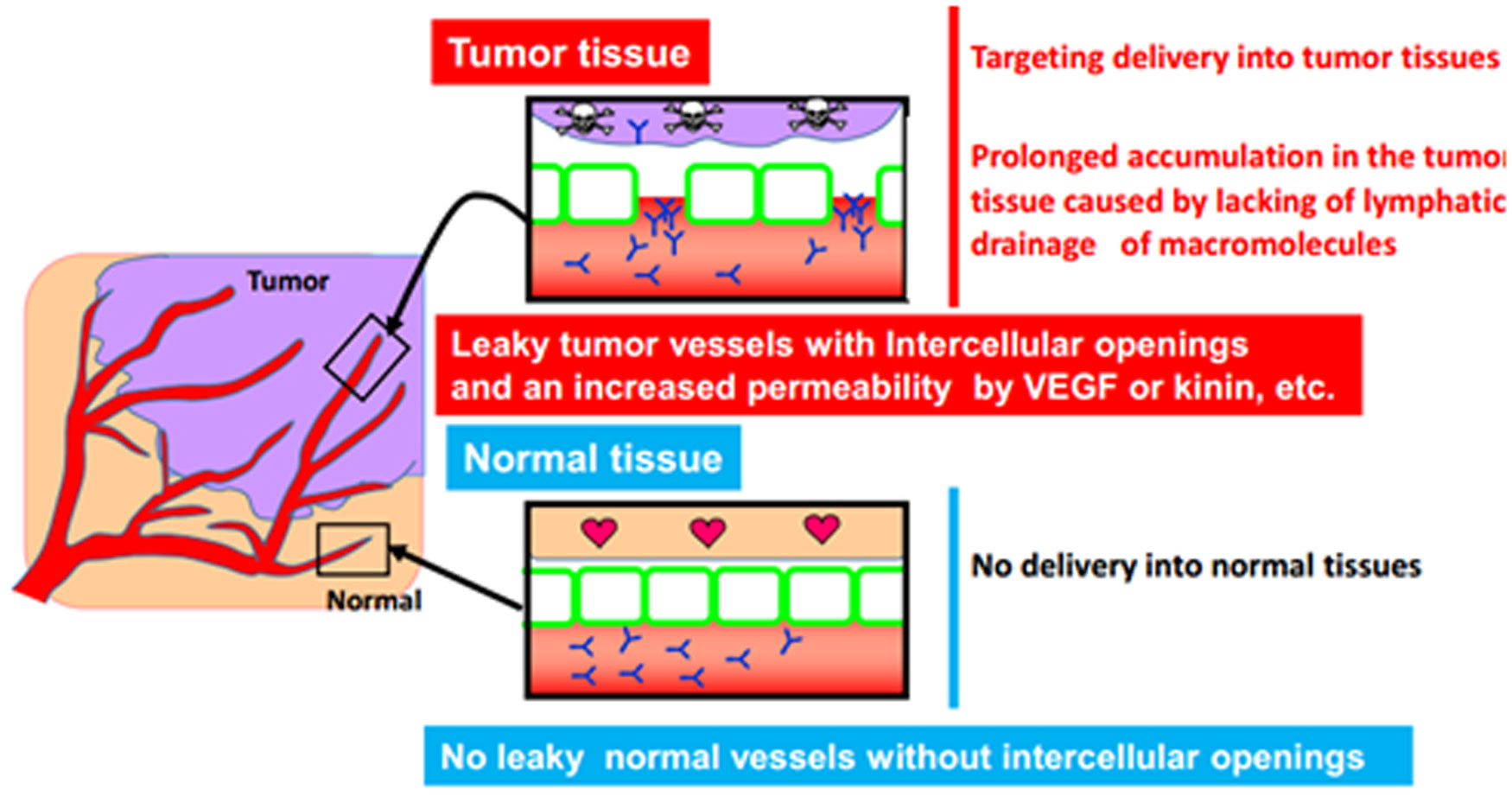
A drug delivery system (DDS) is a method that delivers a required dose of drug into a specified area in the body when needed. Anticancer agents (ACAs) are distributed throughout the body, leading to adverse side effects. On the other hand, a DDS can target tumors, thereby enhancing the action of the drug and minimizing toxicity [14,37,38]. The EPR (enhanced permeability and retention) effect is a very important concept for DDSs. In normal tissues, low-molecular weight (MW) agents can extravasate easily, whereas high-MW (HMW) agents cannot. By contrast, in tumors, HMW agents can extravasate due to leaky tumor vessels and increased permeability [37,39]. HMW agents from 10 to 200 nm in size can extravasate into the tumor selectively, dependent on the EPR effect (Figure 1).
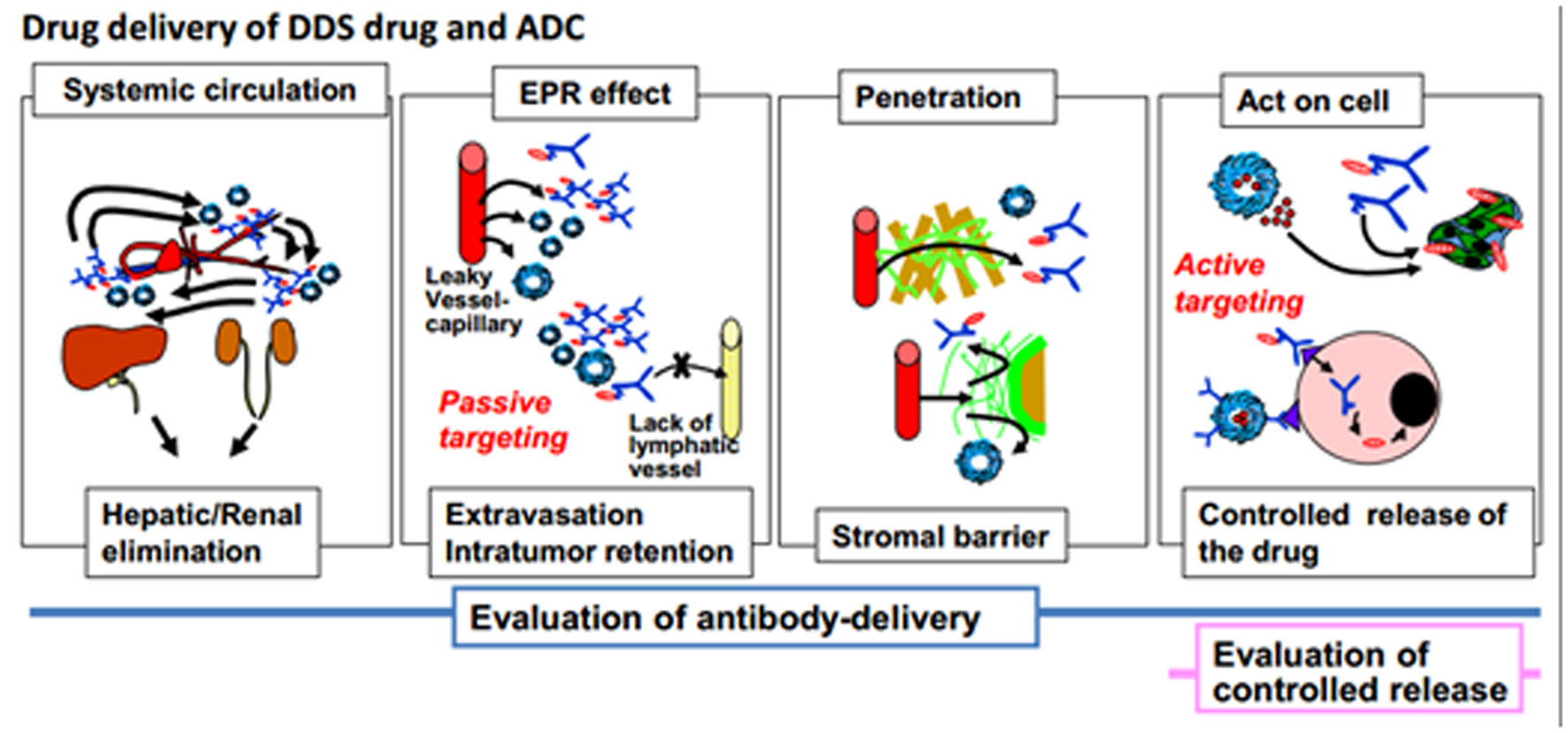
Accordingly, many DDS drugs, such as liposome or micelles, have been developed [37,38,40,41,42,43,44,45,46,47]. We consider antibody-drug conjugates (ADCs) to be DDS drugs because the antibody ranges in size from 10 to 20 nm and can extravasate via the EPR effect [14,39]. Figure 2 shows a comparison among liposomes, micelles, and ADCs. Liposomes range in size from 50 to 200 nm, and the drugs they contain are released by natural breakdown or enzymatic cleavage [41,42,48]. Micelles range in size from 30 to 100 nm, and the drugs they contain are released by natural breakdown or unique technologies such as pH-dependent cleavage [38,40,47]. ADCs range in size from 10 to 20 nm. In an ADC, a specialized linker is used for the control of drug release. Importantly, ACAs are very small size, below 1 nm; consequently, they can distribute into both tumor and normal tissues, often causing adverse effects. By contrast, DDS drugs cannot distribute in this fashion, and the frequency of adverse effects is correspondingly reduced. DDS drugs and ADCs act via four steps: (1) systemic circulation; (2) EPR effect (passive targeting); (3) penetration within tumor tissue; (4) action on cells [14]. To evaluate these four steps, delivery of the drug carrier or antibody should be examined. In addition, to evaluate the final step, controlled release should be examined. In regard to the final step, our strategy of using MSI to visualize the drug released from a DDS drug or ADC is very useful (Figure 3).
4. MSI
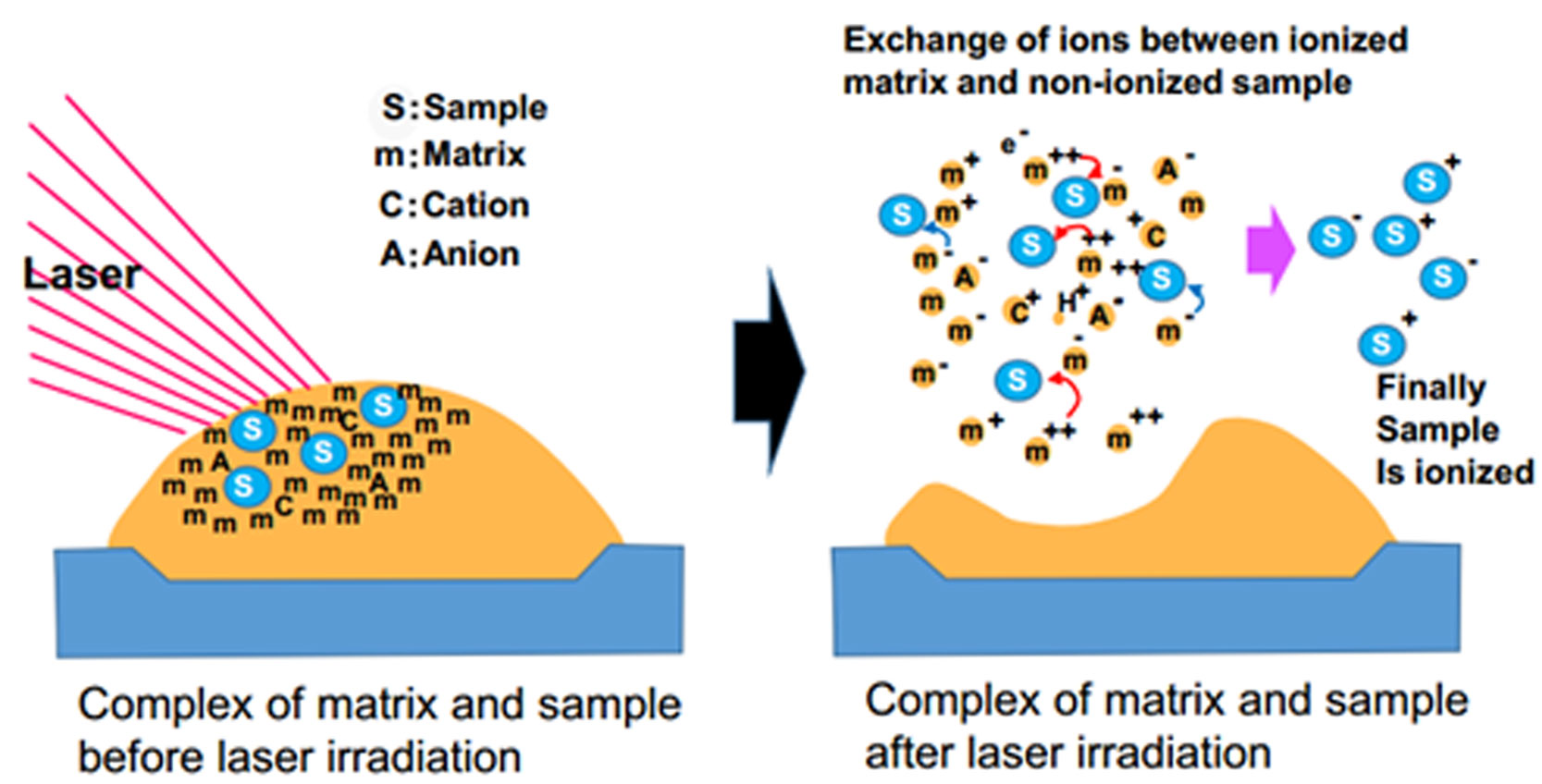
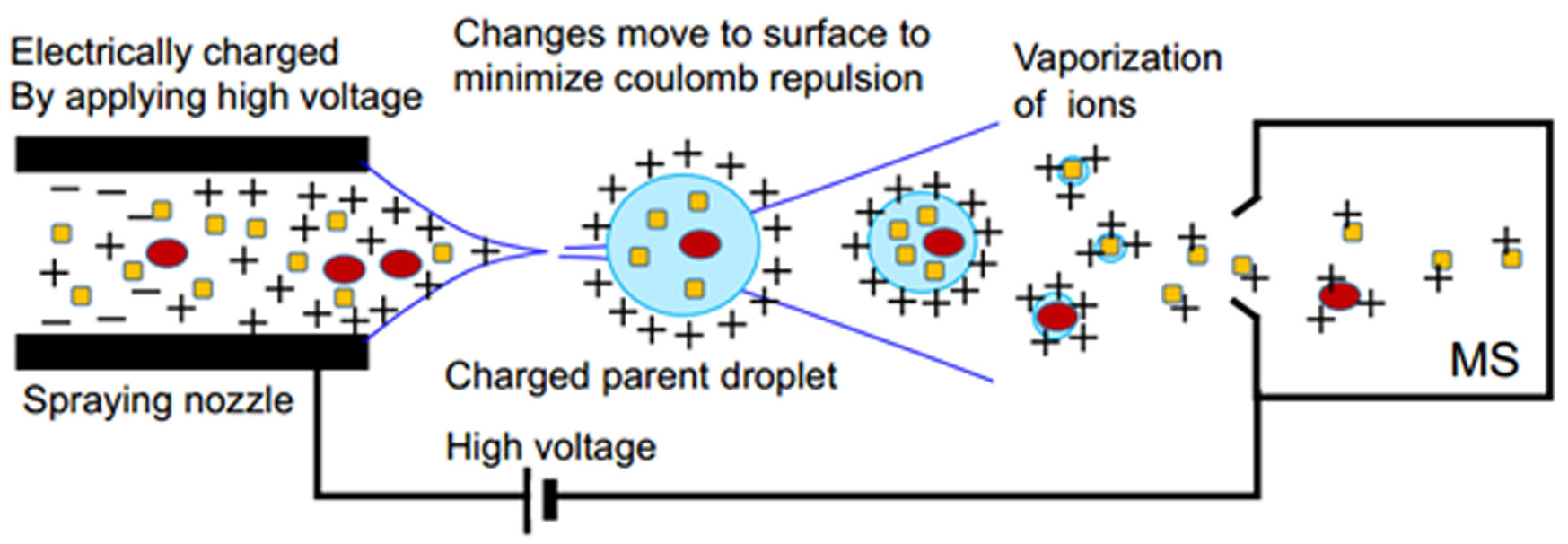
MSI is a method for directly visualizing biomolecules or metabolites in tissue samples [11,12,13,14,15,16,17,18,19]. In MS, it is important to ionize the targeted molecule. Methods for ionization include MALDI (matrix-assisted laser desorption ionization), ESI (electrospray ionization), and SIMS (secondary-ion mass spectrometry). In MALDI, the matrix must be sprayed on the tissue sample. After the treated sample is laser-irradiated, ion exchange occurs between ionized matrix transfer protons and the analyte molecules (i.e., biomolecules and metabolites). Finally, the molecules become ionized [11,12,18]. ESI uses an electrospray in which a high voltage is applied to a liquid to create charged aerosol droplets. A wide range of molecules, including chemical compounds, can be ionized without any addition of matrix under ambient conditions [12,13,15,49,50,51]. DESI (desorption electrospray ionization) is a specialized ambient molecular imaging technology, performed without pretreatment, that allows visualization of the spatial localization of targeted molecules, including chemical compounds [52,53,54].
In SIMS, the molecules are secondarily ionized from the surface of the sample, which is bombarded by an energetic primary ion beam (e.g., metal ions such as Au or Bi). This method can provide detailed chemical information about a material of interest, and is therefore useful for identification and localization of metal composites such as gold, magnetic, and semiconducting nanoparticles. Ionized molecules are analyzed by transmission quadrupole, time-of-flight (TOF) or Fourier transform MS [12,16,18,55]. MALDI-TOF-MS and ESI with LC-MS are described in later sections.
5. MALDI-MSI and mass microscopy
The principles underlying MALDI are shown in Figure 4. Tissue samples are prepared with a sprayed matrix. After the matrix is irradiated by the laser, it absorbs energy, causing it to be desorbed and ionized. Biomolecules are not ionized directly, but are instead desorbed with the matrix around the irradiated site. Subsequently, protons are exchanged between the ionized matrix and the biomolecules, and the biomolecules are ultimately ionized. Matrices used for MALDI include sinapinic acid (SA), α-cyano-4-hydroxycinnamic acid (CHCA), and 2,5-dihydroxybenzoic acid (DHBA). SA is commonly used for protein analysis. Both CHCA and DHBA are used for analysis of peptides or tryptic peptides. Low-MW metabolites, lipids, or compounds are often measured as a matrix in MALDI [11,12,18,56].
Recently, other matrices (e.g., graphene, 2-amino-4,5-diphenylfuran-3-carboxylic acid, and graphene oxide (GO)-modified sinapinic acid) or the integration of nanotechnology with mass spectrometry have been used to measure ionized molecules with high sensitivity and selectivity [57,58,59,60,61,62].
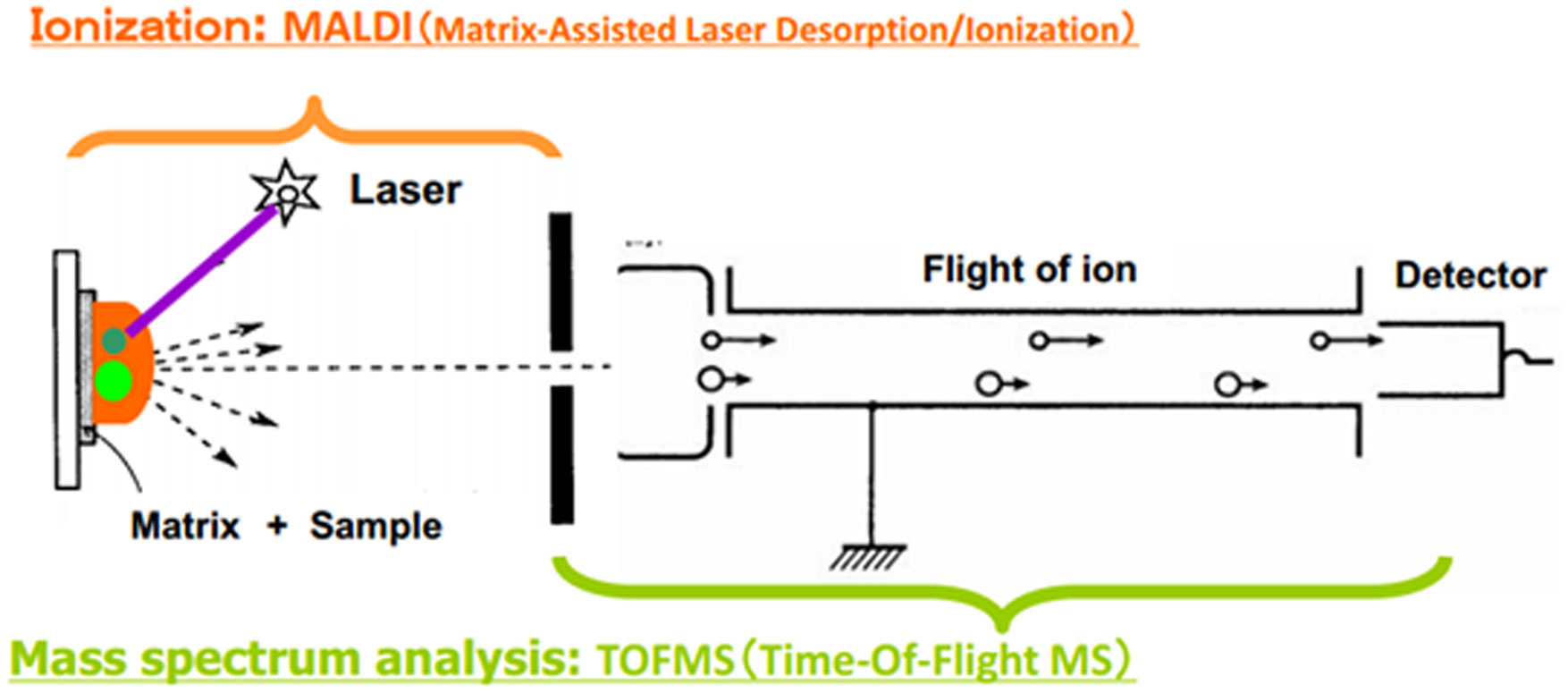
In TOF-MS, the ionized sample reaches the detector (Figure 5). Light ions arrive faster than heavy ions, and molecular size is determined by the velocity. A doubly charged ion arrives twice as fast as a singly charged ion. Therefore, to state it more precisely, the mass-to-charge ratio (m/z) can be measured. The tissue distribution of a targeted molecule can be acquired as a picture after the measurement of multiple small areas by MALDI-TOF-MS. In some cases, MS/MS analysis can be used to verify the identity of drugs and drug metabolites.
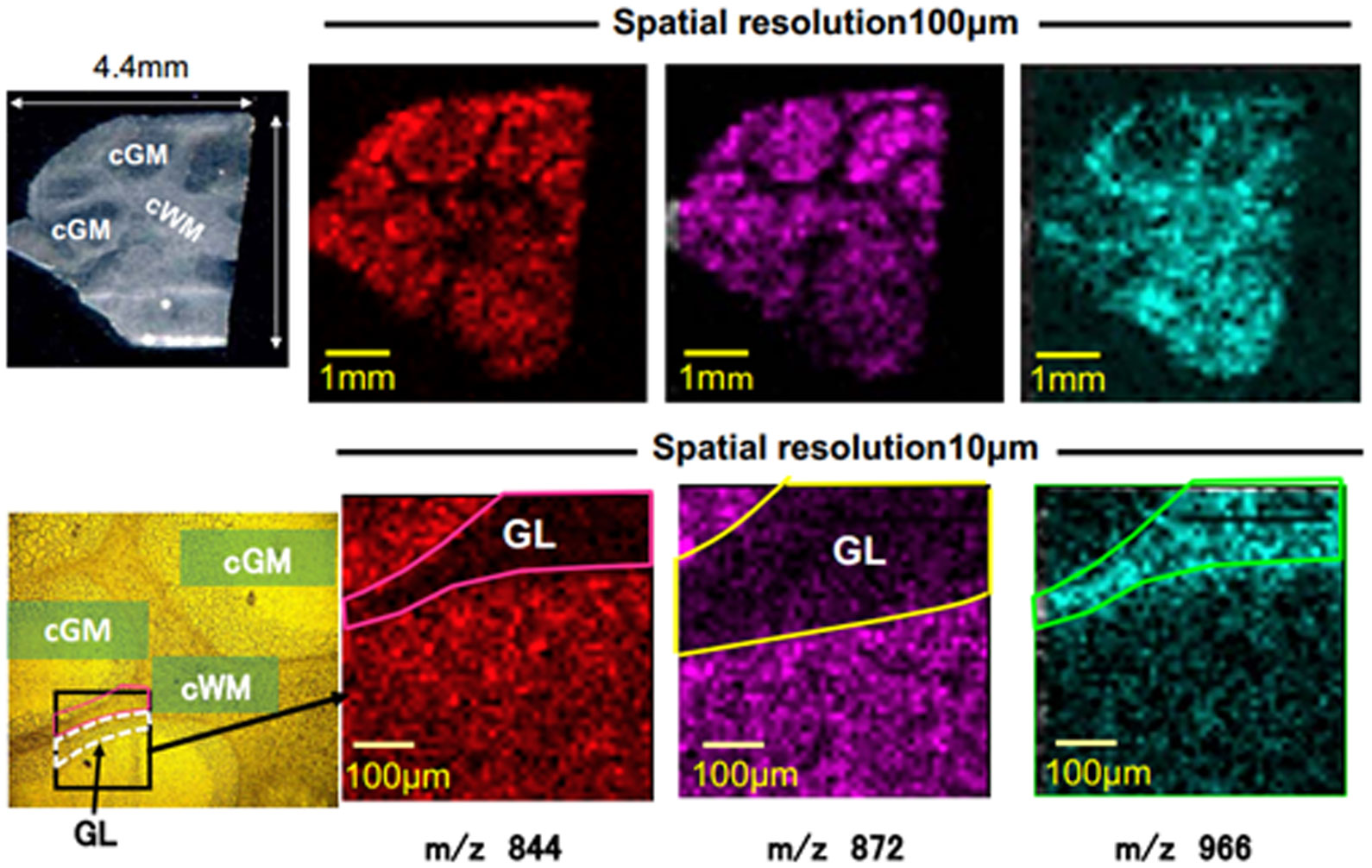
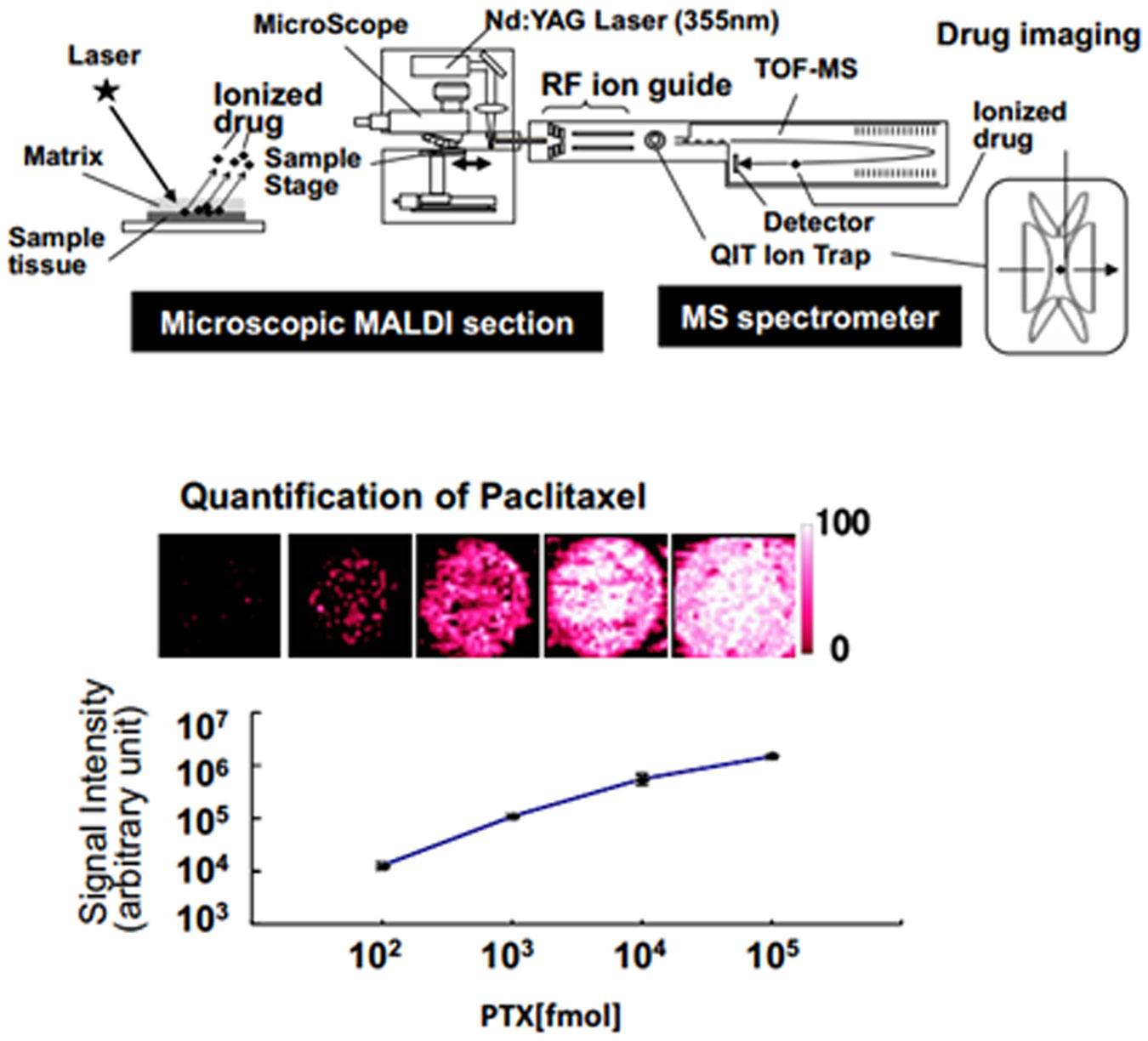
The MSI device we used for drug imaging is called a mass microscope [21,22,63,64,65,66]. This instrument is a conceptually new imaging device that combines an optical microscope system with a high resolution (≤ 10 µm) with atmospheric-pressure MALDI, which is distinct from conventional MALDI-TOF-MS. A transmitted light image of a target tissue can be obtained directly via the dedicated microscope apparatus, making comparison with the MSI image easy. Figure 6 shows the difference in resolution between 100 µm and 10 µm. At a resolution of 100 µm, gray matter and white matter can be discriminated, but it is difficult to obtain more detail. On the other hand, at a resolution of 10 µm, the distribution of the granule layer in white matter can be easily distinguished. Thus, the use of a high-resolution mass microscope is advantageous for observing finer tissue distributions.
Figure 7 shows a schematic of drug imaging using a mass microscope. The results of this analysis, which used a dilution series of paclitaxel as a standard, revealed that the imaging intensity of the drug was correlated with the amount of the drug. It was able to be used as a semi-quantitative measurement (Figure 7).
6. Visualization of DDS drug and EPR effect
As mentioned above, many DDS drugs have been developed to take advantage of the EPR effect. To date, SMANCS (polymer conjugate neocarzinostatin), Doxil (doxorubicin-enclosing liposome), and abraxane (paclitaxel/albumin suspension) have already been clinically applied [67,68,69]. In Japan, which leads the world in DDS research based on nanotechnology, excellent nanocarriers such as micelles, MENDs (multifunctional envelope-type nano devices) and improved liposomes have been successfully developed [40,41,47,70]. In addition, many technologies, including antibody or ligand conjugation, size reduction or pH-dependent dissociation to improve cancer targeting, tumor penetration, and controlled release of drug, have been exploited [38,40,47,71,72].
Another representative DDS drug is paclitaxel (PTX)-encapsulated micelles [73]. In preclinical settings, PTX-micelles exerted stronger anti-tumor effects than free PTX. Peripheral neuropathy is a major adverse effect of PTX, but in a mouse model of mechanical sensory threshold testing, free PTX caused peripheral neuropathy whereas PTX-micelle did not.
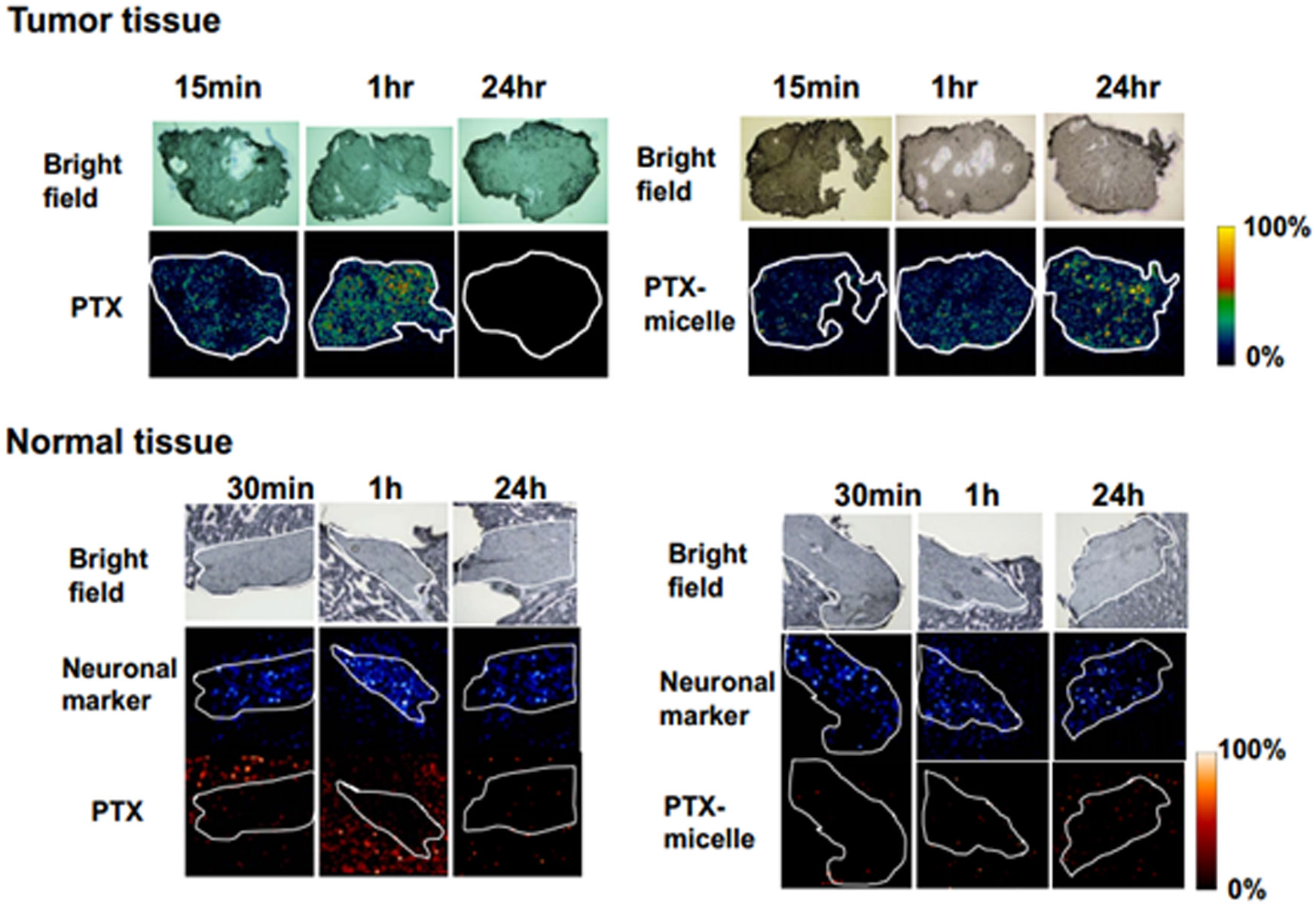
We evaluated the drug distribution in both tumor and peripheral neuronal tissue using a mass microscope. In the tumor, free PTX and PTX released from micelles were detected. A free-PTX signal was detected 15 min and 1 hr after administration, but decreased gradually and disappeared by 24 hr. In contrast to free PTX, released PTX was detected more than 24 hr after the administration, and the signal intensity was greater at 24 hr than at 15 min or 1 hr (Figure 8) [22].
Next, we conducted drug imaging in normal neuronal tissue. A strong free-PTX signal was detected in perineuronal lesions 30 min and 1 h after administration. By contrast, the released PTX signal from PTX micelles was extremely weak around the neuron (Figure 8). This significant difference in distribution may explain why PTX micelles do not cause neurotoxicity. Thus, we succeeded in visualizing the EPR effect for the first time [22].
7. ADC and visualization of controlled release
Several ADCs have been used in the clinic already, and more than 40 ADCs have been studied in clinical trials worldwide [26,27,30]. One important application of ADCs is in treating relapsed or refractory malignant diseases. For example, SGN-35 is effective for patients with CD30-positive relapsed or refractory malignant lymphoma, and T-DM1 is also effective for patients with HER2-positive advanced or remnant breast cancer previously treated with standard drugs, including naked anti-HER2 antibody [34,74,75,76]. An ADC has three parts: Antibody, linker, and drug. The drug is conjugated to the antibody via the specialized linker.
As described above, ADCs act via steps, and evaluation of antibody delivery and controlled release throughout these steps is very important. ADCs are also capable of active targeting, depending on specific recognition of and binding to the target antigen [10,28]. The linker is stable in the bloodstream, but should efficiently release the drug in the tumor cells or within their microenvironment [27,77,78]. The total number of drug molecules that can be conjugated with a single antibody molecule is usually about four, but can be up to eight. Therefore, highly toxic agents must be used [26,27,77,78].
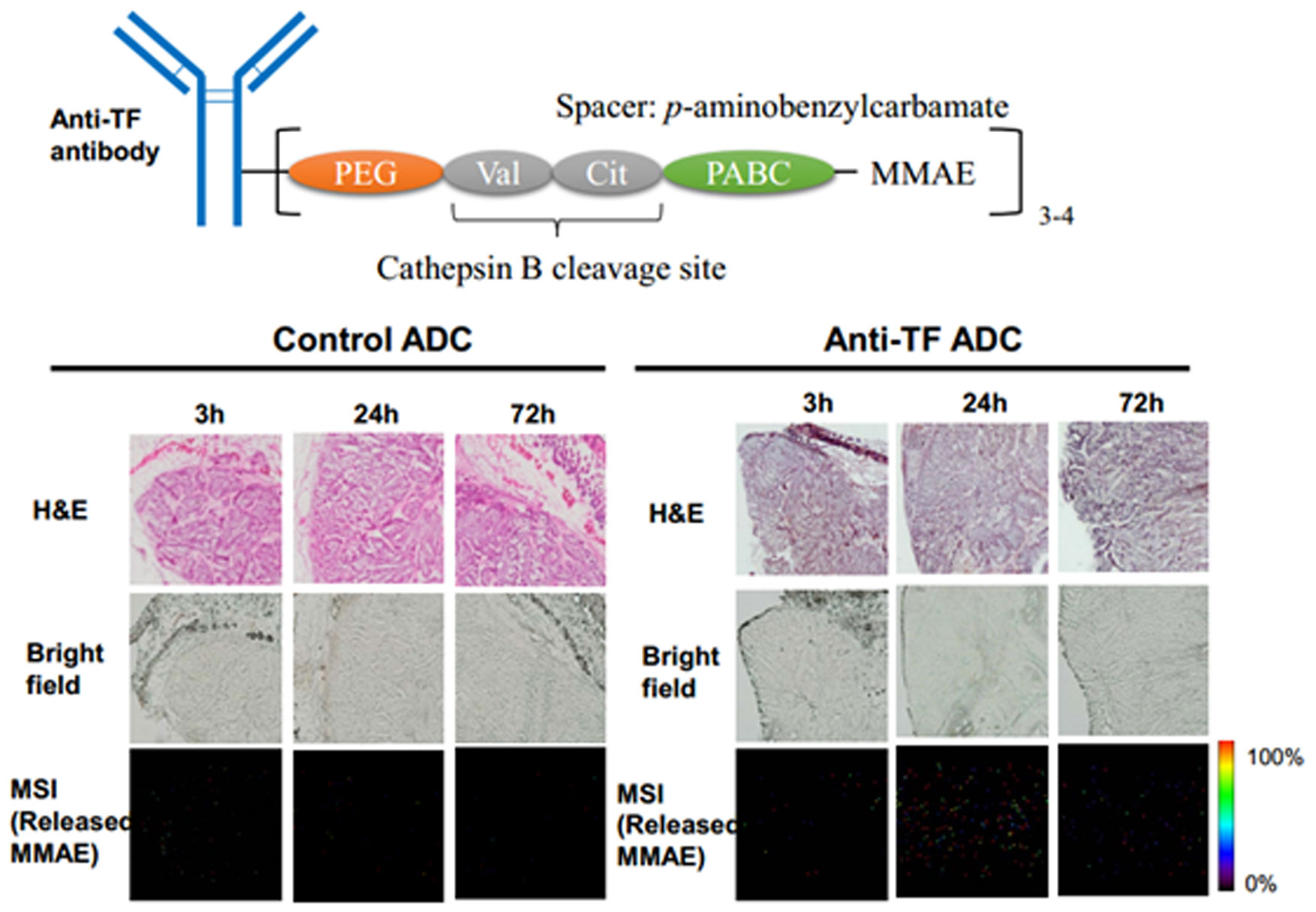
Linker technology is a typical controlled-release technology in DDS. Therefore, it is clear that ADC should be considered to belong to the DDS drug category. We previously succeeded in visualizing the four steps of antibody delivery using molecular imaging modalities such as fluorescence or PET (positron emission tomography)/SPECT (single photon emission computed tomography) [79,80]. We succeeded in developing an anti-tissue factor (TF)-ADC, which had a significant anti-tumor effect in a xenograft model of PC [81]. We sought to visualize the controlled release of anti-TF-ADC in the final step.
The MW of monomethyl auristatin E (MMAE) is 717.5. In MS analysis, three positive-ion peaks are derived from MMAE: m/z 718.4, 740.4, and 756.4, representing singly charged hydrogen [M + H]+, sodium [M + Na]+, and potassium [M + K]+ ions, respectively. Finally, we selected and confirmed the prominent fragment m/z 496.3 as a MMAE-specific fragment peak, detected when m/z 740.4 was used as a precursor ion. Thus, we succeeded in visualizing and quantifying MMAE separately from other biomolecules. We also found that most MMAE was not released from the ADC during the MALDI process. Therefore, we concluded that controlled release of ADC can be visualized and quantified by MSI [21].
Control ADC or anti-TF-ADC was administered into a mouse bearing a human pancreatic cancer tumor. When the tumor samples were examined by MSI, a stronger released MMAE signal was detected from anti-TF-ADC than from control ADC. The signal was strongest at 24 hr after the administration (Figure 9). We concluded that ADC distribution and controlled drug release in the tumor area were successful [21].
8. ESI-MSI
MALDI-MSI, including mass microscopy, is widely used worldwide. Some drugs cannot be visualized because of low ionization efficiency due to matrix dependency. Moreover, matrix preparation makes it difficult to visualize living cells. However, essentially all drugs can be ionized using the ESI method [12,13,15,16,50]. Moreover, ESI can generate multiply charged ion species, thereby effectively extending the dynamic range. Even if a molecule has a MW of 10,000, the 20-valent ions would be m/z 500 and the 40-valent ions m/z 250, which could be identified by MS (Figure 10).
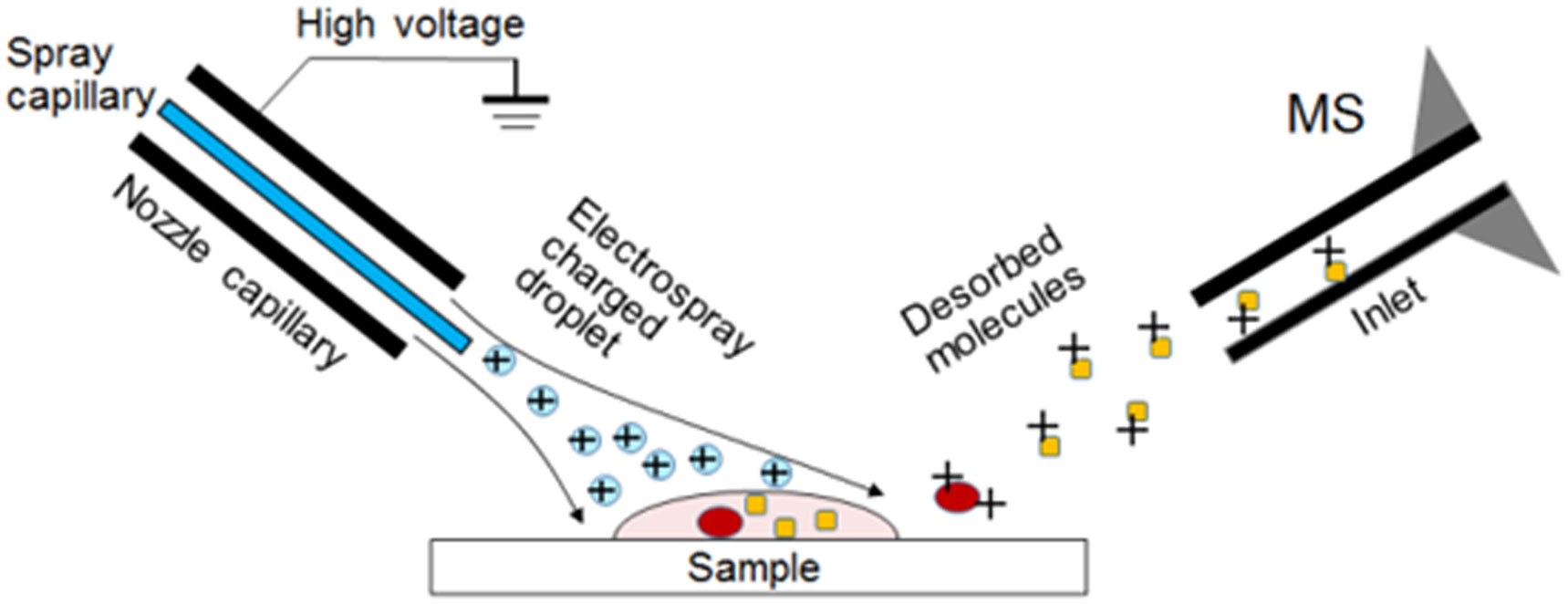
Molecular weight is determined by computer analysis by calculating each multiply charged ion. Indeed, ESI has been widely used for analysis of not only drugs but also other materials, such as natural products and biopolymers [11,12,15]. Because of the very soft ionization process in the ESI method, it is suitable for visualization of high polarity, barely volatile, and thermally unstable drugs. DESI, derived from ESI, is an ambient ionization technique performed without pretreatment that can be coupled to mass spectrometry to visualize analyte molecules at atmospheric conditions (Figure 11) [52,53,54]. However, ionized molecules must be transferred to the mass analyzer via the same inlet, posing the risk of contamination caused by carryover of sequential samples [82].
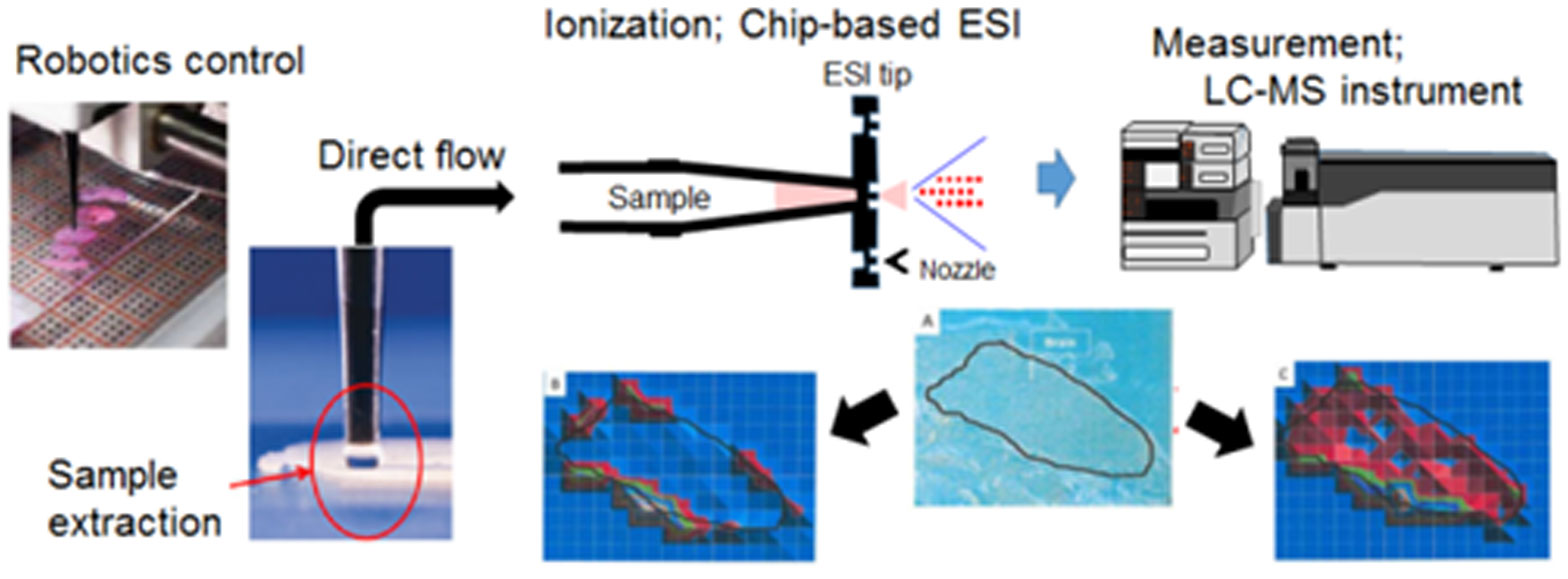
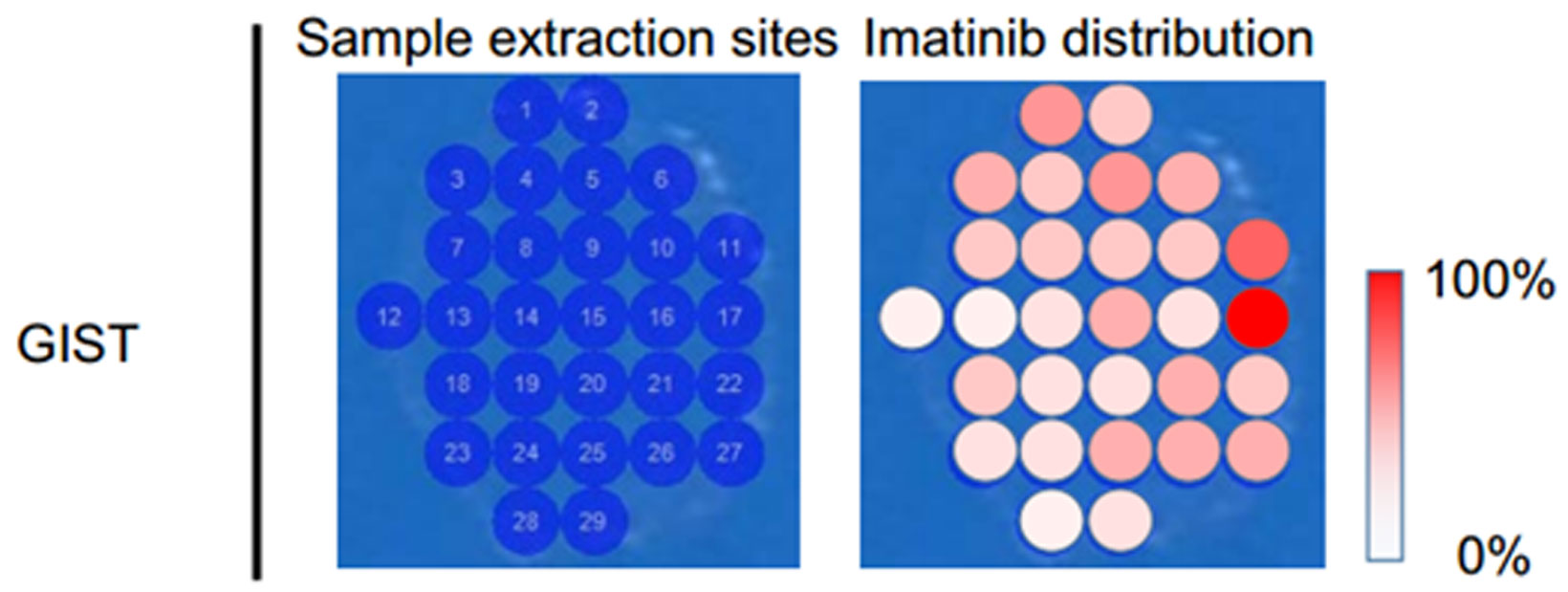
Therefore, we have focused on ESI-MSI using liquid extraction surface analysis (LESA) as another type of ambient ionization technique performed without pretreatment. This method has the advantage of fully automated liquid extraction—based surface sampling, and can provide information about drug distribution (Figure 12). Because the tips and nanospray nozzles for ESI-MSI with LESA are single-use, there is no carryover-dependent contamination [82]. We injected imatinib, a small compound, into mice bearing gastrointestinal tumors (GISTs), and observed strong imatinib signals in the tumor (Figure 13) [83]. Next, we visualized controlled release of MMAE from the ADC in a mouse model of brain tumor. Unlike the skin xenograft model, we hardly detected the released MMAE signal in the brain tumor samples. We speculated that antibody distribution was suppressed by low blood supply or the blood-brain barrier. Subsequently, we attempted to use LISA-ESI-MSI for the visualization of controlled released of MMAE. As expected, we observed a strong signal of released MMAE (our unpublished data).
The measurement sensitivity of ESI-MSI is higher than that of MALDI-MSI, although the spatial resolution of mass microscopy (5-10 µm) is still superior to that of LISA-ESI-MSI (0.5-1 mm). Recently, however, technologies for single-cell ESI-MSI analysis have progressed considerably. For example, a nano-ESI tip robotically controlled under a TV monitor enables the evaluation of single-organelle proteomics from living cells [72,84]. These technologies will be useful to improve the spatial resolution of ESI-MSI.
9. Conclusion
We emphasize the usefulness of MSI, which can provide information about not only drug delivery but also controlled release of the drug. Moreover, with drugs and their metabolites, many biomolecules can be visualized at the same time. Markers involved in the efficacy and toxicity of drugs should be evaluated, and it should be possible to discover a new biomarker to predict or monitor drug efficacy and toxicity. We developed several ADCs such as stroma-targeting ADC (CAST therapy), anti-TF-ADC, and anti-IL-7R ADC [81,85,86,87,88]. We used fluorescence and PET/SPECT for the evaluation of antibody delivery [21,80].
We also conducted general PK analysis using homogenized tissue samples; however, this approach provided only average drug concentration, but no information about drug delivery, controlled release, or action on cells within tumor tissue. Visual observation of these aspects is necessary to determine the MOA of CAST therapy. To address this need, we introduced MSI into our approach to early drug discovery and development. Although the spatial resolution and measurement sensitivity are not sufficient for wide use, technological advances (including single-cell analysis) will make more general application possible in the near future [84].
Single-cell MS analysis will also provide molecular-level insight into cancer cell heterogeneity and complex microenvironments consisting of multiple varieties of cells. In addition, it would be helpful for finding or validating druggable targets and biomarkers of drug efficacy and toxicity. Therefore, MSI is a very attractive and beneficial method for early drug discovery and development.
Acknowledgements
The authors thank S. Saijou, S. Hanaoka, and R. Tsumura for assistance in producing antibodies. We also thank Y. Fujiwara for assistance with the study of MS imaging, and M. Nakayama and M. Shimada for secretarial support. This work was financially supported by grants from the National Cancer Center Research and Development Fund (27-S-5 and 29-S-1 to Masahiro Yasunaga and 26-A-14 to Yasuhiro Matsumura); a Grant-in-Aid for Scientific Research on Priority Areas from the Ministry of Education, Culture, Sports and Science of Japan (Yasuhiro Matsumura); JSPS KAKENHI Grant (15H04316 to Masahiro Yasunaga, 16K15600 to Toshirou Nishida and Masahiro Yasunaga and 16H05419 to Toshirou Nishida and Masahiro Yasunaga); Number 15H04316 (Masahiro Yasunaga); Practical Research for Innovative Cancer Control (16ck0106114h0003) from the Japan Agency for Medical Research and Development, AMED (Masahiro Yasunaga); Project Mirai Cancer Research Grants (Masahiro Yasunaga); the Princess Takamatsu Cancer Research Fund (Masahiro Yasunaga); Japan Leukemia Research Fund (Masahiro Yasunaga); Kawano Masanori Memorial Public Interest Incorporated Foundation for Promotion of Pediatrics (Masahiro Yasunaga).
Conflicts of interest
The authors declare no competing financial interests.









 DownLoad:
DownLoad: