Multi-layer Attribute Selection and Classification Algorithm for the Diagnosis of Cardiac Autonomic Neuropathy Based on HRV Attributes

Herbert F. Jelinek; Jemal H. Abawajy; David J. Cornforth; Adam Kowalczyk; Michael Negnevitsky; Morshed U. Chowdhury; Robert Krones; Andrei V. Kelarev; Herbert F. Jelinek; Jemal H. Abawajy; David J. Cornforth; Adam Kowalczyk; Michael Negnevitsky; Morshed U. Chowdhury; Robert Krones; Andrei V. Kelarev

doi:10.3934/medsci.2015.4.396

AIMS Medical Science

2015, Volume 2, Issue 4: 396-409. doi: 10.3934/medsci.2015.4.396

Previous Article Next Article

Research article

Multi-layer Attribute Selection and Classification Algorithm for the Diagnosis of Cardiac Autonomic Neuropathy Based on HRV Attributes

1.
Centre for Research in Complex Systems and School of Community Health, Charles Sturt University, Albury, NSW, Australia;
2.
School of Information Technology, Deakin University, 221 Burwood Hwy, Melbourne, Victoria 3125, Australia;
3.
School of Design Communication and IT, University of Newcastle, University Drive, Callaghan, NSW 2308, Australia;
4.
Department of Computer Science and Software Engineering, University of Melbourne, Parkville, Victoria 3010, Australia;
5.
School of Engineering & ICT, University of Tasmania, Private Bag 65, Hobart 7001, Australia;
6.
Rural Medical School, University of Melbourne, Wangaratta, Victoria, Australia

Received: 18 August 2015 Accepted: 25 November 2015 Published: 02 December 2015

Cardiac autonomic neuropathy (CAN) poses an important clinical problem, which often remains undetected due difficulty of conducting the current tests and their lack of sensitivity. CAN has been associated with growth in the risk of unexpected death in cardiac patients with diabetes mellitus. Heart rate variability (HRV) attributes have been actively investigated, since they are important for diagnostics in diabetes, Parkinson's disease, cardiac and renal disease. Due to the adverse effects of CAN it is important to obtain a robust and highly accurate diagnostic tool for identification of early CAN, when treatment has the best outcome. Use of HRV attributes to enhance the effectiveness of diagnosis of CAN progression may provide such a tool. In the present paper we propose a new machine learning algorithm, the Multi-Layer Attribute Selection and Classification (MLASC), for the diagnosis of CAN progression based on HRV attributes. It incorporates our new automated attribute selection procedure, Double Wrapper Subset Evaluator with Particle Swarm Optimization (DWSE-PSO). We present the results of experiments, which compare MLASC with other simpler versions and counterpart methods. The experiments used our large and well-known diabetes complications database. The results of experiments demonstrate that MLASC has significantly outperformed other simpler techniques.

Keywords:

Citation: Herbert F. Jelinek, Jemal H. Abawajy, David J. Cornforth, Adam Kowalczyk, Michael Negnevitsky, Morshed U. Chowdhury, Robert Krones, Andrei V. Kelarev. Multi-layer Attribute Selection and Classification Algorithm for the Diagnosis of Cardiac Autonomic Neuropathy Based on HRV Attributes[J]. AIMS Medical Science, 2015, 2(4): 396-409. doi: 10.3934/medsci.2015.4.396

Related Papers:

[1]	Fang Wang, Lianying Cao, Xiaoji Song . Mathematical modeling of mutated COVID-19 transmission with quarantine, isolation and vaccination. Mathematical Biosciences and Engineering, 2022, 19(8): 8035-8056. doi: 10.3934/mbe.2022376
[2]	Xiaojing Wang, Yu Liang, Jiahui Li, Maoxing Liu . Modeling COVID-19 transmission dynamics incorporating media coverage and vaccination. Mathematical Biosciences and Engineering, 2023, 20(6): 10392-10403. doi: 10.3934/mbe.2023456
[3]	Quentin Griette, Jacques Demongeot, Pierre Magal . What can we learn from COVID-19 data by using epidemic models with unidentified infectious cases?. Mathematical Biosciences and Engineering, 2022, 19(1): 537-594. doi: 10.3934/mbe.2022025
[4]	Weike Zhou, Aili Wang, Fan Xia, Yanni Xiao, Sanyi Tang . Effects of media reporting on mitigating spread of COVID-19 in the early phase of the outbreak. Mathematical Biosciences and Engineering, 2020, 17(3): 2693-2707. doi: 10.3934/mbe.2020147
[5]	Pannathon Kreabkhontho, Watchara Teparos, Thitiya Theparod . Potential for eliminating COVID-19 in Thailand through third-dose vaccination: A modeling approach. Mathematical Biosciences and Engineering, 2024, 21(8): 6807-6828. doi: 10.3934/mbe.2024298
[6]	Abdallah Alsammani, Calistus N. Ngonghala, Maia Martcheva . Impact of vaccination behavior on COVID-19 dynamics and economic outcomes. Mathematical Biosciences and Engineering, 2025, 22(9): 2300-2338. doi: 10.3934/mbe.2025084
[7]	Yujie Sheng, Jing-An Cui, Songbai Guo . The modeling and analysis of the COVID-19 pandemic with vaccination and isolation: a case study of Italy. Mathematical Biosciences and Engineering, 2023, 20(3): 5966-5992. doi: 10.3934/mbe.2023258
[8]	Aili Wang, Xueying Zhang, Rong Yan, Duo Bai, Jingmin He . Evaluating the impact of multiple factors on the control of COVID-19 epidemic: A modelling analysis using India as a case study. Mathematical Biosciences and Engineering, 2023, 20(4): 6237-6272. doi: 10.3934/mbe.2023269
[9]	Luyu Zhang, Zhaohua Zhang, Sen Pei, Qing Gao, Wei Chen . Quantifying the presymptomatic transmission of COVID-19 in the USA. Mathematical Biosciences and Engineering, 2024, 21(1): 861-883. doi: 10.3934/mbe.2024036
[10]	Yuto Omae, Yohei Kakimoto, Makoto Sasaki, Jun Toyotani, Kazuyuki Hara, Yasuhiro Gon, Hirotaka Takahashi . SIRVVD model-based verification of the effect of first and second doses of COVID-19/SARS-CoV-2 vaccination in Japan. Mathematical Biosciences and Engineering, 2022, 19(1): 1026-1040. doi: 10.3934/mbe.2022047

Abstract

1. Introduction

A disease outbreak (COVID-19) of an uncommon pneumonia triggered by a new coronavirus, SARS-CoV-2, appeared in Wuhan, China, in December 2019 ^[1], has instigated at least 631, 989, 826 confirmed cases, with 6, 578, 767 deaths in nearly 230 nations and territories by October 21, 2022 ^[2]. The COVID-19 crisis was acknowledged as a pandemic by the World Health Organization (WHO) on March 11, 2020. The earliest case and death in India were reported on January 30, 2020 and March 13, 2020, respectively ^[3]. In the early outbreak, pharmaceutical interventions, for instance, drugs and vaccination, were unavailable, thereafter controlling the pandemic greatly depends only on non-pharmaceutical interventions, such as lockdown, maintaining social distancing, contact tracing, testing, using face masks, etc ^[4,5,6,7]. However, in India, the vaccination campaign with a single and double dose was started on January 15, 2021 and February 13, 2021, respectively. The double-dose vaccination campaign started on December 13, 2020 in the USA ^[8].

The estimation of the reproduction number of a disease is particularly important in modeling the transmission of infection as well as notifying and assessing control policies ^[9,10]. On the other hand, the instantaneous (or effective) reproduction number $ R_t $ exposes the limit of disease spread with the impact of an intervention or population immunity. Public health officials and policymakers use $ R_t $ to evaluate the efficacy of control measures and several other factors that influenced the disease transmission at certain points of time and to update policy accordingly. $ R_t $ estimates could be exercised to evaluate the effectiveness of control measures or as a near real-time indicator of epidemic progress. For these intents, estimates need to be precise and accurately signify uncertainties, and for near real-time scrutinizing, they also need to be timely. Consequently, $ R_t $ estimation is crucial for assessing the achievement of public measures. However, $ R_t $ estimation from available data offers numerous challenges, with crucial inferences for the interpretation of the course of the epidemic ^[11,12]. Though, the parameter assumptions and model structure makes the estimation of $ R_t $ sensitive ^[11]. Poor quality or unavailability of data, on the other hand, often impedes the utilization of several estimation methods, for instance, serial intervals of a disease that are typically required for the estimation of $ R_t $ ^{[12,13,14,15]}.

Specific hypotheses and data estimates are required for computing the exact value of $ R_t $. Several methods are used to estimate the effective reproduction number and time-dependent rate in the literature. Cazelles et al. ^[16] utilized stochastic models for the transmission dynamics of a disease coupled with particle Markov Chain Monte Carlo Algorithm and estimated the time-dependent transmission rate. Nishiura et al. ^[17] discussed a likelihood-based method for the estimation of $ R_t $ from the data of early epidemic growth. Bettencourt and Ribeiro ^[18] estimated $ R_0 $ and $ R_t $ by using the compartmental Susceptible-Infectious-Recovered (SIR) model and incidence data of H5N1 influenza in humans. Pollicott et al. ^[19] and Kong et al. ^[20] introduced an inverse method for epidemic models that extract the time-dependent transmission rate from the incidence or prevalence data. Wang et al. ^[21,22] developed an inverse method and estimated the time-dependent transmission rate and death rate using a generalized boosting model (GBM) and a mechanistic ordinary differential equation (ODE) model. Hasan et al. ^[23] developed a novel method to estimate the effective reproduction number based on the Kalman filter and a low pass filter method. The authors used a simple SIRD (Susceptible-Infectious-Recovered-Dead) model and augmented the model into a discrete-time stochastic model. This method is quite beneficial since it does not require serial intervals, which forms the process easier without falling the estimation quality.

In this paper, we estimate the time-dependent effective reproduction number and vaccination rate using the method developed by Hasan et al. ^[23] for COVID-19 in the USA and India. We use an augmented SVEIR model and the data of daily new cases, cumulative cases, daily new deaths, cumulative deaths, and fully vaccinated individuals concerning COVID-19.

2. A discrete-time stochastic augmented SVEIR model

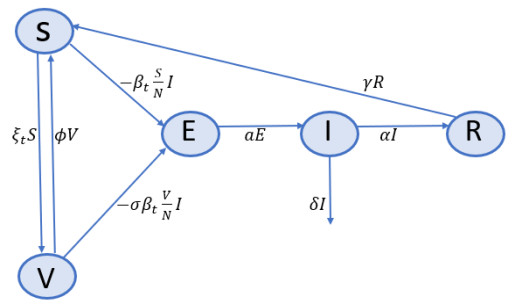
We estimate the effective reproduction number, $ R_t $, and time-dependent vaccination rate, denoted by $ \xi_t $, by using a simple compartmental SVEIR model. Figure 1 shows the scheme of the model. Let us denote $ S, V, E, I, $ and $ R $ respectively as susceptible, vaccinated, exposed (not yet infectious), active/confirmed, and recovered compartment. Let $ N = S+V+E+I+R $, where $ N $ denotes the total population.

Figure 1. Scheme of the SVEIR model (2.1).

DownLoad: Full-Size Img PowerPoint

In the model (2.1), the susceptible individuals are vaccinated at rate $ \xi_t $, which is time-dependent. $ \beta_t $ signifies the average number of contacts per individual per unit time and is time-dependent due to interventions. Since the vaccine is imperfect, vaccinated individuals can also get the infection, but at a reduced rate, $ \sigma \beta_t $, where $ 1-\sigma $ characterizes the vaccine efficacy. The immunity acquired by vaccination wanes with time, and vaccinated individuals can become susceptible again at a rate $ \phi $. $ a $ stands for the transition rate of exposed individuals becoming infectious, $ \alpha $ denotes the recovery rate of infectious individuals, and $ \delta $ is the disease-induced death rate. $ \gamma $ represents the antibody waning rate since the immunity acquired by infection also wanes with time. Hence, the model is written in the following non-linear ordinary differential equations:

$\begin{equation} \begin{aligned} \frac{dS}{dt} & = - \frac{S}{N} \beta_t I + \gamma R - \xi_t S + \phi V, \\ \frac{dV}{dt} & = - \frac{V}{N} \sigma \beta_t I + \xi_t S - \phi V, \\ \frac{dE}{dt} & = \beta_t I \Big(\frac{S}{N} + \sigma \frac{V}{N}\Big) - a E, \\ \frac{dI}{dt} & = a E - (\alpha + \delta) I, \\ \frac{dR}{dt} & = \alpha I - \gamma R. \\ \end{aligned} \end{equation}$ $

(2.1)

To use the method ^[23], we also need some more information about the Case Fatality Rate (CFR) and the average infectious time, $ T_i $, and

$\begin{align} \alpha = \frac{1-CFR}{T_i}, \quad \delta = \frac{CFR}{T_i}. \end{align}$ $

(2.2)

For COVID-19, we consider $ T_i = 14 $ ^[21], however it may vary from 1.5 to 30 days amongst distinct diseased persons ^[24]. CFR is assumed to be 1%.

Covaxin and Covishield, two COVID-19 vaccines were advanced and being utilized in India. Bhatnagar et al. ^[25] studied that the vaccine efficacy of full (two doses) vaccination was 71% (95% CI: 57-81%) with Covaxin/BBV152 and with covishield/AZD1222, it was 85% (95% CI: 79-89%). The vaccine efficacy was highest at 94% (95% CI: 86-97%) for 6-8 weeks between two doses of Covishield and 93% (95% CI: 34-99%) of Covaxin. In the USA, the COVID-19 mRNA vaccines BNT162b2 (Pfizer-BioNTech) and mRNA-1273 (Moderna) COVID-19 vaccines have been completely permitted by the Food and Drug Administration (FDA) for individuals aged 18 years and older and individuals aged 16 years and older, respectively ^[26]. In clinical trials, mRNA based COVID-19 vaccines, BNT162b2 (Pfizer Inc, New York, USA; BioNTech Manufacturing GmbH, Mainz, Germany; Comirnaty) and mRNA-1273 (Moderna Inc, Cambridge, USA; Spikevax) were greatly effectual (95% and 94%, respectively) against symptomatic COVID-19 infection ^[27]. In our estimation, vaccine efficacy is to be assumed 95% and 85% for the USA and India, respectively.

To compute the effective reproduction number, $ R_t $, we can still apply the next generation matrix method ^[28,29]. According to Lemma 1 in ^[30], we define

$\begin{align*} F = \left( \begin{array}{cc} 0 & \beta_t (\frac{S}{N} + \sigma \frac{V}{N}) \\ 0 & 0 \end{array} \right), \quad V = \left(\begin{array}{cc} a & 0 \\ -a & a+\delta \end{array} \right). \end{align*}$ $

Following ^[28,29], the effective reproduction number is defined as the spectral radius of the next generation matrix ($ FV^{-1} $), i.e.,

$\begin{equation} R_t = \rho(FV^{-1}) = \frac{\beta_t}{\alpha + \delta}\Big(\frac{S(t)}{N} + \sigma \frac{V(t)}{N}\Big) \approx \frac{\beta_t}{\alpha + \delta}. \end{equation}$ $

(2.3)

The approximation is under the assumption that government intervention is taken at an early stage so that $ S(t)+\sigma V(t) \approx N $. This is the case especially for the emerging diseases.

We further augment the SVEIR model (2.1) by considering the following seven equations:

$\begin{align} \frac{dC}{dt}& = aE, \end{align}$ $

(2.4)

$\begin{align} \frac{dD}{dt}& = aE - D, \end{align}$ $

(2.5)

$\begin{align} \frac{dCD}{dt}& = \delta I, \end{align}$ $

(2.6)

$\begin{align} \frac{dDD}{dt}& = \delta I - DD, \end{align}$ $

(2.7)

$\begin{align} \frac{dP}{dt}& = \xi_t S, \end{align}$ $

(2.8)

$\begin{align} \frac{dR_t}{dt}& = 0, \end{align}$ $

(2.9)

$\begin{align} \frac{d\xi_t}{dt}& = 0, \end{align}$ $

(2.10)

where the first equation takes into account the cumulative cases ($ C $), second equation provides the daily number of new cases ($ D $), third equation gives cumulative deaths ($ CD $), fourth equation offers the daily number of new deaths ($ DD $), fifth equation produces the cumulative number of vaccinated individuals ($ P $), the sixth and seventh equations say that the effective reproduction number ($ R_t $) and vaccination rate ($ \xi_t $) are assumed to be piecewise constant functions with one day time interval jump.

Further, by discretization and applying the forward Euler method, the discrete-time augmented SVEIR model is given as follows:

$\begin{equation} \begin{aligned} S(l+1) & = S(l)\Big(1-\Delta t \xi_t(l)-\frac{(a+\delta)\Delta t}{N} R_t(l)I(l)\Big) + \gamma \Delta t R(l) + \phi \Delta t V(l), \\ V(l+1) & = V(l)\Big(1- \phi \Delta t -\frac{(a+\delta)\sigma \Delta t}{N} R_t(l)I(l) \Big) + \Delta t \xi_t(l) S(l), \\ E(l+1) & = E(l)(1-a\Delta t) + \frac{(a+\delta)\Delta t}{N}R_t(l)I(l)(S(l)+\sigma V(l), \\ I(l+1) & = I(l)(1-(a+\delta) \Delta t) + a \Delta E(l), \\ R(l+1) & = R(l)(1-\gamma \Delta t) + \alpha \Delta t I(l), \\ C(l+1) & = C(l)+a \Delta t E(l), \\ D(l+1) & = D(l)(1-\Delta t)+a \Delta t E(l), \\ CD(l+1) & = CD(l)+\delta \Delta t I(l), \\ DD(l+1) & = DD(l)(1-\Delta t)+\delta \Delta t I(l), \\ P(l+1) & = P(l)+\Delta t \xi_t(l) S(l), \\ R_t(l+1) & = R_t(l), \\ \xi_t(l+1) & = \xi_t(l). \end{aligned} \end{equation}$ $

(2.11)

We estimate the basic reproduction number, $ R_t $, by using the cumulative cases, new daily cases, cumulative deaths and new daily deaths, and vaccination rate, $ \xi_t $, by using the full (with two doses) vaccination data. The data has been collected from the World Health Organization (WHO) website https://covid19.who.int/ and https://ourworldindata.org/coronavirus on a daily basis. Since the frequency of the data could be once a day which is low, then by utilizing a modified Akima cubic Hermite interpolation, the new reported data could be interpolated and it fits with $ \Delta t $ time steps. The $ \Delta t $ time step is taken as $ 0.01 $ in our simulation, i.e., 100 times discretization within one day time interval. For simplicity, we outline the augmented state vector as follows:

$\begin{equation} y(l+1) = \left(\begin{array}{c} S(l+1)\\ V(l+1)\\ E(l+1)\\ I(l+1)\\ R(l+1)\\ C(l+1)\\ D(l+1)\\ CD(l+1)\\ DD(l+1)\\ P(l+1)\\ R_t(l+1)\\ \xi_t(l+1)\\ \end{array} \right), \end{equation}$ $

(2.12)

and the discrete time augmented SVEIR model (2.11) can be rewritten in the following form:

$\begin{equation} y(l+1) = g(y(l)) + v(l), \end{equation}$ $

(2.13)

where $ g $ is the nonlinear expression of the equations in the right-hand side of the augmented SVEIR model (2.11) and $ v $ denotes the uncertainty to the inaccuracies in the model owing to interpretation in the modeling. The uncertainty is supposed to be a zero mean Gaussian white noise with known covariance $ Q_F $. It is to make the computation simple since the real epidemic data generally follow Gamma distribution. $ Q_F $, in practice, could be taken as a tuning parameter for the EKF. Hence, the model becomes in the form of a discrete-time stochastic augmented SVEIR model.

New daily cases, cumulative cases, new daily deaths, cumulative deaths, and cumulative vaccinated individuals can be incorporated into the model including the ensuing output vector

$\begin{equation} x(l+1) = C y(l) + z(l), \end{equation}$ $

(2.14)

where $ z $ signifies uncertainties owing to the incorrect testing outcomes. It is also supposed the uncertainties to be a zero mean Gaussian white noise with known covariance $ R_F $. Similar to $ Q_F $, $ R_F $ could also be taken as a tuning parameter. Ensuing the convenient data, the measurement/data matrix $ C $ is considered to be

$\begin{equation} C = \left( \begin{array}{cccccccccccc} 0& 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0& 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{array} \right). \end{equation}$ $

(2.15)

A two-stage filtering approach: We use a two-stage filtering approach for the estimation of the time-dependent effective reproduction number, $ R_t $, and vaccination rate, $ \xi_t $. This method consists a low-pass filter and the EKF. The EKF is an expansion of Kalman filter (KF) for nonlinear systems. The KF is centered on Bayesian estimation and is an optimal linear filter. The EKF is established based on the linearization of the non-linear system around its estimate. Because of this linearization, the stability and optimality of the EKF cannot be ensured. However, the EKF may provide a fairly good estimation if the non-linearity is not very extreme. In the estimation process, the state variables, $ R_t $ and $ \xi_t $ are estimated by using the EKF under uncertainties in the number of new reported cases which could be a consequence of the delays in reporting.

Let $ \hat{y}(l) $ be a vector state, estimated by the EKF. Operating the first-order Taylor series expansion to $ g $ at $ \hat{y}(l) $, which yields

$\begin{equation} g(y(l)) = g(\hat{y}(l)) + J_g (\hat{y}(l))(y(l)-\hat{y}(l)). \end{equation}$ $

(2.16)

Here $ J_g (\hat{y}(l)) $ denotes the Jacobian matrix of $ g $, specified by

$\begin{equation} J_g (\hat{y}(l)) = \\\left(\begin{array}{c} J_{11}(\hat{y}(l))& \phi \Delta t & 0 & J_{14}(\hat{y}(l)) & \gamma \Delta t & 0 & 0 & 0 & 0 & 0 & J_{111}(\hat{y}(l)) & - \hat{S}(l) \Delta t \\ \hat{\xi}_t(l)\Delta t& J_{22}(\hat{y}(l)) & 0 & J_{24}(\hat{y}(l)) & 0 & 0 & 0 & 0 & 0 & 0 & J_{211}(\hat{y}(l)) & \hat{S}(l) \Delta t \\ J_{31}(\hat{y}(l))& J_{32}(\hat{y}(l)) & 1-a \Delta t & J_{34}(\hat{y}(l)) & 0 & 0 & 0 & 0 & 0 & 0 & J_{311}(\hat{y}(l)) & 0 \\ 0& 0 & a \Delta t & 1 - (a+\delta) \Delta t & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0& 0 &0 & \alpha \Delta t & 1- \gamma \Delta t & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0& 0 & a \Delta t & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0& 0 & a \Delta t & 0 & 0 & 0 & 1-\Delta t & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \delta \Delta t & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \delta \Delta t & 0 & 0 & 0 & 0 & 1- \Delta t & 0 & 0 & 0 \\ \hat{\xi}_t(l) \Delta t & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & \hat{S}(l) \Delta t \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right), \end{equation}$ $

(2.17)

with

$\begin{align*} J_{11}(\hat{y}(l))& = 1- \hat{\xi}(l)\Delta t - \frac{(a+\delta)\Delta t}{N}\hat{I}(l)\hat{R}_t(l), \\ J_{14}(\hat{y}(l))& = - \frac{(a+\delta)\Delta t}{N}\hat{S}(l)\hat{R}_t(l), \\ J_{111}(\hat{y}(l))& = - \frac{(a+\delta)\Delta t}{N}\hat{S}(l)\hat{I}(l), \\ J_{22}(\hat{y}(l))& = 1- \phi \Delta t - \frac{(a+\delta)\sigma \Delta t}{N}\hat{I}(l)\hat{R}_t(l), \\ J_{24}(\hat{y}(l))& = - \frac{(a+\delta)\sigma \Delta t}{N}\hat{V}(l)\hat{R}_t(l), \\ J_{211}(\hat{y}(l))& = - \frac{(a+\delta)\sigma \Delta t}{N}\hat{V}(l)\hat{I}(l), \\ J_{31}(\hat{y}(l))& = \frac{(a+\delta) \Delta t}{N}\hat{I}(l)\hat{R}_t(l), \\ J_{32}(\hat{y}(l))& = \frac{(a+\delta)\sigma \Delta t}{N}\hat{I}(l)\hat{R}_t(l), \\ J_{34}(\hat{y}(l))& = \frac{(a+\delta) \Delta t}{N}(\hat{S}(l) + \sigma \hat{V}(l))\hat{R}_t(l), \\ J_{311}(\hat{y}(l))& = \frac{(a+\delta) \Delta t}{N}(\hat{S}(l) + \sigma \hat{V}(l))\hat{I}(l). \end{align*}$ $

The EKF contains two stages: forecast and update. The model (2.11) is utilized to forecast the upcoming state and covariance and upgrade them after attaining measurement/new data. The EKF could be pondered as one of the straightforward dynamic Bayesian networks. EKF recursively computes the estimate of correct state values over time utilizing a mathematical process model and next measurements while recursive Bayesian estimation computes estimates of an unidentified probability density function over time utilizing a mathematical process model and incoming new data ^[31]. Let $ \hat{y}(m|n) $ signifies the estimation of $ y $ at time $ m $ considering observations up to and together with the time $ n \leq m $. The Kalman filter algorithm is given as follows.

Forecast:

$\begin{align*} \hat{y}(l+1|l) & = g(\hat{y}(l|l)), \\ p(l+1|l) & = J_g (\hat{y}(l|l))p(l|l) J_g (\hat{y}(l|l))^T + Q_F(l). \end{align*}$ $

Update:

$\begin{align*} \hat{x}(l+1) & = x(l+1) - C \hat{y}(l+1|l), \\ K(l+1) & = p(l+1|l)C^T (Cp(l+1|l)C^T + R_F(l))^{-1}, \\ \hat{y}(l+1|l+1) & = \hat{y}(l+1|l) + K(l+1)\hat{x}(l+1), \\ p(l+1|l+1) & = (I-K(l+1)C)p(l+1|l), \end{align*}$ $

where $ p(l|l) $ signifies a posteriori estimate covariance matrix. In the step, "update", a low pass filter approach concerning a rational transfer function is utilized to detach short term fluctuation at time step $ l $, and is specified by

$\begin{equation} \hat{x}(l) = \frac{1}{x_n}(\hat{y}(l)+\hat{y}(l-1)+\cdots + \hat{y}(l -x_n+1)), \end{equation}$ $

(2.18)

where $ x_n $ is a window length along the data. We take $ x_n = 3/\Delta t $ for our case.

To ensure the estimation quality, we compute a Relative Root Mean Square Error (RRMSE) between the reported and estimated cases. The RRMSE is expressed by

$\begin{equation} RRMSE = \frac{1}{O_d} \sum\limits_{i = 1}^{O_d}\frac{||Y_i - \hat{Y}_i ||^2}{||Y_i||^2}, \end{equation}$ $

(2.19)

where $ O_d $ denotes the total number of observed time in days and $ Y \in \left\lbrace C, D, CD, DD, P \right\rbrace $.

We illustrate the observed and estimated numbers of COVID-19 cases in India in Figure 2 and obtained a good agreement between the data and estimated numbers. We also plot the reported and estimated number of fully vaccinated individuals in Figure 3. In the estimation procedure, the observation and process covariance matrices are chosen as tuning parameters and are taken as $ R_F = diag(100\; 10\; 5\; 1\; 1) $ and $ Q_F = diag(100\; 10\; 10\; 10\; 5\; 5\; 5\; 5\; 5\; 0.5\; 0.5\; 0.5) $, respectively. These tuning parameters are attained from error and trial and adopted such that RRMSE between the reported and estimated data are adequately small. For our case, the RRMSEs are given in Table 2. Here, we notice that the obtained RRMSEs are sufficiently small. The error could be reduced more by choosing distinct values of $ R_F $ and $ Q_F $.

Figure 2. Comparison between estimated and reported cases of cumulative cases ($ C $), daily new cases ($ D $), cumulative deaths ($ CD $), and daily new deaths ($ DD $) of COVID-19 during February 15, 2021 to August 22, 2022 in India. The green colored curve shows the prediction from August 23, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

Figure 3. Comparison between estimated and reported cases of full vaccinated individuals ($ P $) of COVID-19 during February 15, 2021 to August 22, 2022 in India. The green colored curve shows the prediction from August 23, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

Table 1. Numerical values of model parameters.

Parameters	Numerical values for India	Source	Numerical values for the USA	Source
$ 1-\sigma $	0.85	^[25]	0.95	^[27]
$ \xi_t $	Figure 5	Estimated	Figure 9	Estimated
$ \phi $	1/180 day$ ^{-1} $	^[32]	1/180 day$ ^{-1} $	^[32]
$ a $	1/2 day$ ^{-1} $	^[21]	1/2 day$ ^{-1} $	^[21]
$ \alpha $	0.0627	$ \frac{1-CFR}{T_i} $	0.0627	$ \frac{1-CFR}{T_i} $
$ \gamma $	1/180 day$ ^{-1} $	^[32]	1/180 day$ ^{-1} $	^[32]
$ \delta $	1.8534e-06	$ \frac{CFR}{T_i} $	9.2978e-06	$ \frac{CFR}{T_i} $
$ R_t $	Figure 4	Estimated	Figure 8	Estimated

| Show Table

DownLoad: CSV

Figure 4. Estimated time-dependent effective reproduction number ($ R_t $) for COVID-19 in India. The green colored curve shows the prediction from August 23, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

Figure 5. Estimated time-dependent vaccination rate ($ \xi_t $) for COVID-19 in India. The green colored curve shows the prediction from August 23, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

Table 2. RRMSE between the reported and estimated data for the USA and India.

Cases	RRMSE for the USA	RRMSE for India
Cumulative cases (C)	1.0876e-05	7.0211e-08
Daily new cases (D)	1.9846e-04	8.5272e-05
Cumulative deaths (CD)	4.5707e-06	2.5711e-08
Daily deaths (DD)	0.0012	0.0125
Vaccinated individuals (P)	6.1981e-04	0.1259
Total RRMSE	0.0021	0.1385

| Show Table

DownLoad: CSV

For the USA, the observed and estimated COVID-19 and vaccinated cases are plotted in Figure 6 and 7, respectively. The observation and process covariance matrices are chosen as $ R_F = diag(1000\; 100\; 50\; 10\; 10) $ and $ Q_F = diag(100\; 10\; 10\; 10\; 5\; 5\; 5\; 5\; 5\; 0.5\; 0.5\; 0.5) $, respectively. The RRMSEs for the USA are also given in Table 2, which are relatively smaller than India.

Figure 6. Comparison between estimated and reported cases of cumulative cases ($ C $), daily new cases ($ D $), cumulative deaths ($ CD $), and daily new deaths ($ DD $) of COVID-19 during December 13, 2020 to August 16, 2022 in the USA. The green colored curve shows the prediction from August 17, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

Figure 7. Comparison between estimated and reported cases of full vaccinated individuals ($ P $) of COVID-19 during December 13, 2020 to August 16, 2022 in the USA. The green colored curve shows the prediction from August 17, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

We finally plot the time-dependent effective reproduction number $ R_t $ and vaccination rate $ \xi_t $ for India in Figure 4 and 5, respectively, and for the USA in Figure 8 and 9, respectively. We do not take average out of the new cases data, but consider the likelihood estimation of a new case at one day to depend also on the estimation of the previous three days. The estimated curves of $ R_t $ and $ \xi_t $ for the USA and India are also showing spikes and serrations with data.

Figure 8. Estimated time-dependent effective reproduction number ($ R_t $) for COVID-19 in the USA. The green colored curve shows the prediction from August 17, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

Figure 9. Estimated time-dependent vaccination rate ($ \xi_t $) for COVID-19 in the USA. The green colored curve shows the prediction from August 17, 2022 to December 31, 2022.

DownLoad: Full-Size Img PowerPoint

We also provide the short-term forecast for India from August 23, 2022 to December 31, 2022. The forecasting scenario is shown in Figures 2, 3, 4, and 5 in green colored curves. With the current scenario, the prediction shows that the new daily cases and deaths are steadily decreasing in India. However, the effective reproduction number will be greater than one by December 31, 2022.

The predictions for the USA from August 17, 2022 to December 31, 2022 are also provided in Figures 6, 7, 8 and 9 in green colored curves. These results also show that the number of new daily cases and deaths is decreasing. From Figure 8, we observe that the effective reproduction number will be greater than one by December 31, 2022.

3. Discussion

Several mathematical models and approaches have been evolved and utilized to estimate various types of time-dependent rates and reproduction numbers. Estimating the time-dependent vaccination rate with the effective reproduction number for COVID-19 progress is essential for making public health decisions to regulate the pandemic. We here estimate the time-dependent effective reproduction number $ R_t $ and vaccination rate $ \xi_t $ based on model (2.11) with respect to the COVID-19 data in the USA and India by using a low pass filter approach and EKF developed by Hasan et al. ^[23]. Our estimated $ R_t $ and $ \xi_t $ chase the dynamics of the model, showing the spikes and serrations with data. The prediction results show that the new daily cases and deaths are decreasing in the USA and India. We observed that the effective reproduction number would be greater than one by December 31, 2022 in both countries. Which implies that it is still necessary to maintain safety and preventive measures to control COVID-19. Our results are beneficial for the policy/health makers to track the status of the effective reproduction number that whether it is greater or less than one.

The inverse method, given by Pollicott et al. ^[19] and Kong et al. ^[20], needs an explicit formula to estimate the time-dependent rates. In comparison, the method we used in this work is more straightforward and has various advantages. From the modeling perspective, the time-dependent effective reproduction number and vaccination rate follow the dynamics according to the data. This method does not need serial intervals' information. In this case, the provided time series data have drastic changes or instead do not have many changes. The resulting time-dependent rates show the same serrations and spikes. Consequently, the latest information could be elaborated from the data dynamics.

Various rates in epidemiological models for contagious diseases vary significantly over time. It is further feasible to estimate other time-dependent rates, such as immunity waning rate and vaccine efficacy, that decrease over time. The model we utilized in this work could also be applied to COVID-19 transmission dynamics in any other country, specifically when vaccination is employed. We have not considered reporting ratio in our model, however, by considering it, time-varying estimates of COVID-19 infection will be observed in future. Using an extended multi-strain SVEIR model (including multiple infectious compartments with different strains), estimation of the strain-specific effective reproduction number will be addressed in the future.

Acknowledgments

The research work of Sarita Bugalia is supported by the Council of Scientific & Industrial Research (CSIR), India [File No. 09/1131(0025)/2018-EMR-I]. The research work of Jai Prakash Tripathi is supported by the Science and Engineering Research Board (SERB), India [File No. ECR/2017/002786]. The research work of Hao Wang is partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC). We are highly thankful to all the anonymous reviewers and editor for their insightful comments and suggestions, which helped us to improve the manuscript considerably.

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	Colagiuri S, Colagiuri R, Ward J (1998) National diabetes strategy and implementation plan. Canberra: Paragon Printers.
[2]	Pop-Busui R, Evans GW, Gerstein HC, et al. (2010) The ACCORD Study Group. Effects of cardiac autonomic dysfunction on mortality risk in the Action to Control Cardiovascular Risk in Diabetes (ACCORD) Trial. Diab Care 33: 1578-1584.
[3]	Spallone V, Ziegler D, Freeman R, et al. (2011) Cardiovascular autonomic neuropathy in diabetes: clinical impact, assessment, diagnosis, and management. Diab Metab Res Rev 27: 639-653.
[4]	Dimitropoulos G, Tahrani AA, Stevens MJ (2014) Cardiac autonomic neuropathy in patients with diabetes mellitus. World J Diab 5: 17-39. doi: 10.4239/wjd.v5.i1.17
[5]	Vinik AI, Erbas T, Casellini CM (2013) Diabetic cardiac autonomic neuropathy, inflammation and cardiovascular disease. J Diabetes Investig 4: 4-18. doi: 10.1111/jdi.12042
[6]	Task Force of The European Society of Cardiology and The North American Society of Pacing and Electrophysiology (1996) Special report: heart rate variability standards of measurement, physiological interpretation, and clinical use. Circulation 93: 1043-1065. doi: 10.1161/01.CIR.93.5.1043
[7]	Jelinek HF, Abawajy JH, Kelarev AV, et al. (2014) Decision trees and multi-level ensemble classifiers for neurological diagnostics. AIMS Med Sci 1: 1-12.
[8]	Dietrich DF, Schindler C, Schwartz J, et al. (2006) Heart rate variability in an ageing population and its association with lifestyle and cardiovascular risk factors: results of the SAPALDIA study. Europace 8: 521-529.
[9]	Lake DE, Richman JS, Griffin MP, et al. (2002) Sample entropy analysis of neonatal heart rate variability. Am J Physiol 283: 789-797.
[10]	La Rovere MT, Pinna GD, Maestri R, et al. (2003) Short-term heart rate variability strongly predicts sudden cardiac death in chronic heart failure patients. Circulation 107: 565-570. doi: 10.1161/01.CIR.0000047275.25795.17
[11]	Huikuri HV, Linnaluoto MK, Seppänen T, et al. (1992) Circadian rhythm of heart rate variability in survivors of cardiac arrest. Am J Cardiol 70: 610-615. doi: 10.1016/0002-9149(92)90200-I
[12]	Cornforth DJ, Tarvainen MP, Jelinek HF (2014) Visualization methods for assisting detection of cardiovascular neuropathy. Engineering in Medicine and Biology Society (EMBC2014) 36th Annual International Conference of the IEEE, 26-30 Aug. 2014, 6675-6678.
[13]	Tarvainen MP, Cornforth DJ, Jelinek HF (2014) Principal component analysis of heart rate variability data in assessing cardiac autonomic neuropathy. Engineering in Medicine and Biology Society (EMBC2014), 36th Annual International Conference of the IEEE, 26-30 Aug. 2014, 6667-6670.
[14]	Abawajy J, Kelarev A, Chowdhury M (2013) Multistage approach for clustering and classification of ECG data. Comp Meth Pro Biomed 112: 720-730.
[15]	Abawajy J, Kelarev A, Chowdhury M, et al. (2013) Predicting cardiac autonomic neuropathy category for diabetic data with missing values, Comp Bio Med 43: 1328-1333.
[16]	Stranieri A, Abawajy J, Kelarev A, et al. (2013) An approach for Ewing test selection to support the clinical assessment of cardiac autonomic neuropathy. Art Intel Med 58: 185-193. doi: 10.1016/j.artmed.2013.04.007
[17]	Jelinek HF, Yatsko A, Stranieri A, et al. (2015) Diagnostic with incomplete nominal/discrete data. Art Intel Med 4: 22-35.
[18]	Cornforth D, Jelinek HF (2007) Automated classification reveals morphological factors associated with dementia, App Soft Compu 8: 182-190.
[19]	Ewing DJ, Campbell JW, Clarke BF (1980) The natural history of diabetic autonomic neuropathy. Q J Med 49: 95-100.
[20]	Ewing DJ, Martyn CN, Young RJ, et al. (1985) The value of cardiovascular autonomic functions tests: 10 years experience in diabetes. Diab Care 8: 491-498. doi: 10.2337/diacare.8.5.491
[21]	Khandoker AH, Jelinek HF, Palaniswami M (2009) Identifying diabetic patients with cardiac autonomic neuropathy by heart rate complexity analysis. BioMed Engine Online 8: 1-12. doi: 10.1186/1475-925X-8-1
[22]	Thayer JF, Yamamoto SS, Brosschot JF (2010) The relationship of autonomic imbalance, heart rate variability and cardiovascular disease risk factors, Int J Cardiol 141: 122-131.
[23]	Karmakar CK, Khandoker AH, Jelinek HF, et al. (2013) Risk stratification of cardiac autonomic neuropathy based on multi-lag Tone-Entropy. Med Bio Engine Comp 51: 537-546. doi: 10.1007/s11517-012-1022-5
[24]	Tan CO (2013) Heart rate variability: are there complex patterns? Front Physiol 4: 1-3.
[25]	Imam MH, Karmakar C, Khandoker AH, et al. (2014) Analysing cardiac autonomic neuropathy in diabetes using electrocardiogram derived systolic-diastolic interval interactions. Compu Cardiol 41: 85-88.
[26]	Spallone V, Menzinger G (1997) Diagnosis of cardiovascular autonomic neuropathy in diabetes. Diabetes 46: 67-76. doi: 10.2337/diab.46.2.S67
[27]	Jelinek HF, Pham P, Struzik ZR, et al. (2007) Short term ECG recording for the identification of cardiac autonomic neuropathy in people with diabetes mellitus. Proceedings of the 19th International Conference on Noise and Fluctuations, Tokyo, Japan, pp. 683-686.
[28]	Khandoker AH, Weiss DN, Skinner JE, et al. (2011) PD2i heart rate complexity measure can detect cardiac autonomic neuropathy: an alternative test to Ewing battery. Compu Cardiol 38: 525-528.
[29]	TFESC/NASPE (1996) Heart rate variability. Standards of measurement, physiological interpretation, and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Euro Heart J 17: 354-381.
[30]	Goldberger AL, Amaral LAN, Hausdorff JM, et al. (2002) Fractal dynamics in physiology: Alterations with disease and aging. Pro Nat Aca Sci USA 99: 2466-2472. doi: 10.1073/pnas.012579499
[31]	Peng CK, Havlin S, Stanley HE, et al. (1995) Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5: 82-87. doi: 10.1063/1.166141
[32]	Ho YL, Lin C, Lin YH, et al. (2011). The prognostic value of non-linear analysis of heart rate variability in patients with congestive heart failure—a pilot study of multiscale entropy. PLoS ONE 6: 1-6.
[33]	Sturmberg JP, Bennett JM, Picard M, et al. (2015) The trajectory of life. Decreasing physiological network complexity through changing fractal patterns. Front Physiol 6: 1-11.
[34]	Oida ET, Moritani KT, Yamori Y (1999) Diabetic alteration of cardiac vago-sympathetic modulation assessed with tone-entropy analysis. Acta Physiol Scandi 165: 129-135. doi: 10.1046/j.1365-201x.1999.00494.x
[35]	Lake DE, Moorman JR (2011) Accurate estimation of entropy in very short physiological time series: the problem of atrial fibrillation detection in implanted ventricular devices. Am J Physiol Heart Cicul Physiol 300: H319-325. doi: 10.1152/ajpheart.00561.2010
[36]	Jelinek HF, Khandoker A, Palaniswami M, et al. (2010) Tone-entropy analysis as a cardiac risk stratification tool. Compu Cardiol 37: 955-958.
[37]	Quinlan R (1993) C4.5: Programs for Machine Learning. San Mateo, CA: Morgan Kaufmann Publishers.
[38]	Breiman L (2001) Random Forests. Machine Learning 45:5-32. doi: 10.1023/A:1010933404324
[39]	Williams G (2011) Data mining with Rattle and R: the art of excavating data for knowledge discovery (use R!). New York, Dordrecht, Heidelberg, London: Springer.
[40]	Platt J (1998) Fast training of support vector machines using sequential minimal optimization. In: Schoelkopf B, Burges C, Smola A, editors, Advances in Kernel Methods—Support Vector Learning 41-64.
[41]	Witten H, Frank E, Hall MA (2011) Data mining: practical machine learning tools and techniques with java implementations. 3ed, New York, Sydney: Morgan Kaufmann, 2011.
[42]	Bouckaert, RR, Frank E, Hall M, et al. WEKA manual for version 3-7-13, http://www.cs.waikato.ac.nz/ml/weka/, viewed 15 July 2015.
[43]	Hall M, Frank E, Holmes G, et al. (2009) The WEKA data mining software: an update. SIGKDD Explor 11: 10-18.
[44]	Negnevitsky M (2011) Artificial intelligence: a guide to intelligent systems. 3rd eds., New York: Addison Wesley.
[45]	Williams GJ (2009) Rattle: a data mining GUI for R, The R J 1: 45-55.
[46]	Kohavi R, John GH (1997) Wrappers for feature subset selection. Art Intell 97:273-324. doi: 10.1016/S0004-3702(97)00043-X
[47]	Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. New York: Addison-Wesley.
[48]	Cornforth DJ, Jelinek HF, Teich MC, et al. (2004) Wrapper subset evaluation facilitates the automated detection of diabetes from heart rate variability measures. Proceedings of the International Conference on Computational Intelligence for Modelling Control and Automation (CIMCA'2004), University of Canberra, Australia, pp. 446-455.
[49]	Moraglio A, Di Chio C, Poli R (2007) Geometric Particle Swarm Optimisation. Proceedings of the 10th European Conference on Genetic Programming, Berlin, Heidelberg, 125-136.
[50]	Demsar J (2006) Statistical comparisons of classifiers over multiple data sets. J Machine Learning Res 7: 1-30.
[51]	Dietterich TG (1998) Approximate statistical tests for comparing supervised classification learning algorithms. Neural Compu 10: 1895-1924. doi: 10.1162/089976698300017197
[52]	Cornforth D, Tarvainen M, Jelinek HF (2014) How to calculate Rényi entropy from Heart Rate Variability, and why it matters for detecting cardiac autonomic neuropathy. Front Bioeng Biotecho 2: 1-7.
[53]	Ziegler DA, Rathmann VW, Strom A, et al. (2015) Increased prevalence of cardiac autonomic dysfunction at different degrees of glucose intolerance in the general population: the KORA S4 survey. Diabetologia 58:1118-1128. doi: 10.1007/s00125-015-3534-7

This article has been cited by:

1.	Zuo‐jing Yin, Han Xiao, Stuart McDonald, Vladimir Brusic, Tian‐yi Qiu, Dynamically adjustable SVEIR(MH) model of multiwave epidemics: Estimating the effects of public health measures against COVID‐19, 2023, 95, 0146-6615, 10.1002/jmv.29301
2.	Liaofu Luo, Jun Lv, Mathematical Modelling of Virus Spreading in COVID-19, 2023, 15, 1999-4915, 1788, 10.3390/v15091788
3.	Yunbo Tu, Xinzhu Meng, A reaction–diffusion epidemic model with virus mutation and media coverage: Theoretical analysis and numerical simulation, 2023, 214, 03784754, 28, 10.1016/j.matcom.2023.06.023
4.	Arjun Kumar, Uma S. Dubey, Balram Dubey, Modeling the effect of vaccinations, hospital beds, and treatments on the dynamics of infectious disease with delayed optimal control and sensitivity analysis, 2024, 139, 2190-5444, 10.1140/epjp/s13360-024-05508-1
5.	Toshiaki Takayanagi, Estimating parameter values and initial states of variables in a mathematical model of coronavirus disease 2019 epidemic wave using the least squares method, Visual Basic for Applications, and Solver in Microsoft Excel, 2023, 4, 26669900, 100111, 10.1016/j.cmpbup.2023.100111
6.	Sarita Bugalia, Jai Prakash Tripathi, Hao Wang, Mutations make pandemics worse or better: modeling SARS-CoV-2 variants and imperfect vaccination, 2024, 88, 0303-6812, 10.1007/s00285-024-02068-x
7.	May Anne E. Mata, Rey Audie S. Escosio, El Veena Grace A. Rosero, Jhunas Paul T. Viernes, Loreniel E. Anonuevo, Bryan S. Hernandez, Joel M. Addawe, Rizavel C. Addawe, Carlene P.C. Pilar-Arceo, Victoria May P. Mendoza, Aurelio A. de los Reyes, Analyzing the dynamics of COVID-19 transmission in select regions of the Philippines: A modeling approach to assess the impact of various tiers of community quarantines, 2024, 10, 24058440, e39330, 10.1016/j.heliyon.2024.e39330
8.	Abu Zobayer, Mohammad Sharif Ullah, K. M. Ariful Kabir, A cyclic behavioral modeling aspect to understand the effects of vaccination and treatment on epidemic transmission dynamics, 2023, 13, 2045-2322, 10.1038/s41598-023-35188-3
9.	Shimelis Bekele Zerefe, Tigabu Kasie Ayele, Surafel Luleseged Tilahun, Mehmet Ünver, Mathematical Modeling of COVID‐19 Disease Dynamics With Contact Tracing: A Case Study in Ethiopia, 2024, 2024, 1110-757X, 10.1155/2024/5556734
10.	Jayashree Anandakumar, Kuralayanapalya Puttahonnappa Suresh, Archana Veeranagouda Patil, Chethan A. Jagadeesh, Sushma Bylaiah, Sharanagouda S. Patil, Divakar Hemadri, Comprehensive Spatial-Temporal and Risk Factor Insights for Optimizing Livestock Anthrax Vaccination Strategies in Karnataka, India, 2024, 12, 2076-393X, 1081, 10.3390/vaccines12091081
11.	Sarita Bugalia, Jai Prakash Tripathi, Assessing potential insights of an imperfect testing strategy: Parameter estimation and practical identifiability using early COVID-19 data in India, 2023, 123, 10075704, 107280, 10.1016/j.cnsns.2023.107280
12.	Gaurang Sharma, Amit Sharma, Nishant Parmar, A delay differential equation model on covid-19 with vaccination strategy, 2024, 58, 0399-0559, 4093, 10.1051/ro/2024147
13.	Zafer Bekiryazici, Ayhan Önen, Analyzing the stochastic dynamics of COVID-19 waves in Turkey using real data and piecewise sinusoidal functions, 2024, 12, 2195-268X, 2830, 10.1007/s40435-024-01420-9
14.	François M. Castonguay, Brian F. Borah, Seonghye Jeon, Gabriel Rainisch, Patsy Kelso, Bishwa B. Adhikari, Daniel J. Daltry, Leah S. Fischer, Bradford Greening, Emily B. Kahn, Gloria J. Kang, Martin I. Meltzer, The public health impact of COVID-19 variants of concern on the effectiveness of contact tracing in Vermont, United States, 2024, 14, 2045-2322, 10.1038/s41598-024-68634-x
15.	S. Swetha, S. Sindu Devi, K. Kannan, Optimal Control Strategies for COVID-19 Using SEIQR Mathematical Model, 2024, 0369-8203, 10.1007/s40010-024-00898-4
16.	Vikram Singh, Shikha Kapoor, Sandeep kumar Gupta, Sandeep Sharma, Modelling the leadership role of police in controlling COVID-19, 2024, 12, 2544-7297, 10.1515/cmb-2024-0010
17.	Svetozar Margenov, Nedyu Popivanov, Tsvetan Hristov, Veneta Koleva, Computing the COVID-19 Basic and Effective Reproduction Numbers Using Actual Data: SEIRS Model with Vaccination and Hospitalization, 2024, 12, 2227-7390, 3998, 10.3390/math12243998
18.	Yutao Yan, Shuzhen Yu, Zhiyong Yu, Haijun Jiang, Hui Wang, Global dynamics of delayed discrete-time SEIR negative information propagation model with multi-platform and cross-transmission mechanism, 2025, 10075704, 108591, 10.1016/j.cnsns.2025.108591

Reader Comments

Your name:*

Email:*
© 2015 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Medical Science

0.7

Metrics

Article views(6432) PDF downloads(1154) Cited by(11)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(2) / Tables(2)

AIMS Medical Science

Multi-layer Attribute Selection and Classification Algorithm for the Diagnosis of Cardiac Autonomic Neuropathy Based on HRV Attributes

Related Papers:

Abstract

1. Introduction

2. A discrete-time stochastic augmented SVEIR model

3. Discussion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Medical Science

Multi-layer Attribute Selection and Classification Algorithm for the Diagnosis of Cardiac Autonomic Neuropathy Based on HRV Attributes

Related Papers:

Abstract

1. Introduction

2. A discrete-time stochastic augmented SVEIR model

3. Discussion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog