1. Introduction
Environmental chemicals and contaminants are ubiquitous and can be found everywhere: in water, air, food, soil, etc. While some chemicals are short-lived in the environment and may elicit no harmful effects in humans, other chemicals bioaccumulate in the environment or persist for a long time in the human body due to frequent exposure, potentially leading to adverse health effects. In order to determine whether the general population is exposed to specific and potentially deleterious chemicals, national human biomonitoring (HBM) survey programs have been developed in several countries worldwide. Such programs allow monitoring of the exposure of the general population to environmental contaminants, and most programs develop national reference values for selected chemicals. As one of the outcomes from an European Food Safety Authority (EFSA)-commissioned project to review the state of the art of human biomonitoring for chemical substances and its application to human exposure assessment for food safety [1], a comparative analysis among national HBM survey programs facilitated the identification of vulnerable populations (e.g., by age, sex, socioeconomic status, etc.) as well as chemical exposure associated with food intake. Such analysis can be useful for the design of future HBM programs especially for international cooperative efforts. In particular, the upcoming European Human Biomonitoring Initiative (EHBMI), which is based on the harmonization work done by the European Union (EU)-funded pilot program Consortium to Perform Human Biomonitoring on a European Scale (COPHES) and its feasibility study (Demonstration of a Study to Coordinate and Perform Human Biomonitoring on a European Scale; DEMOCOPHES) and aims to set up the frame of European survey programs, may be inspired from the major programs surveyed in the EFSA project.
The objective of this review is twofold: (1) to provide a brief description and a comparative analysis of nine national HBM survey programs: NHANES (USA), CHMS (Canada), GerES (Germany), FLEHS (Flanders in Belgium), ENNS (France), BIOAMBIENT.ES (Spain), PROBE (Italy), CZ-HBM (Czech Republic), and KorSEP (South Korea) and (2) to elaborate on key observations from the comparative analysis, namely the identification of vulnerable populations and of chemicals that might be associated with food intake. These nine programs are particularly chosen because they are well-established programs that have published large-scale HBM data with considerable impact of the general population (i.e., more than 1, 000 participants) of their respective countries.
2. Background to human biomonitoring
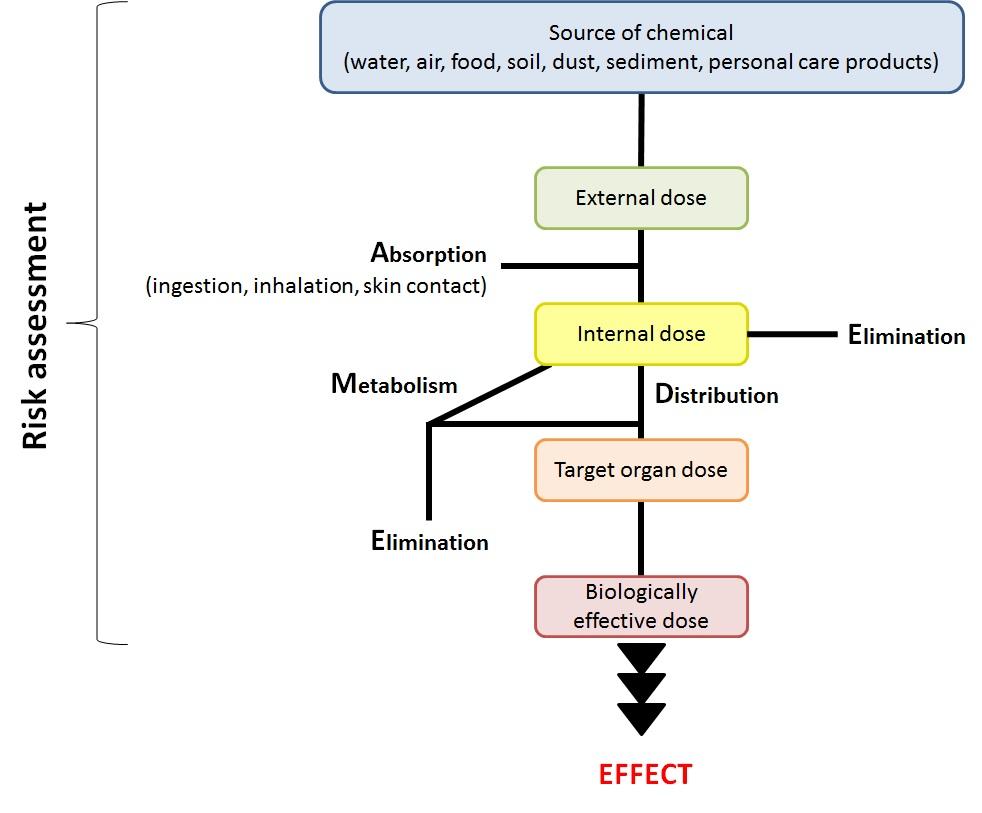
HBM is a scientifically-developed approach for assessing human exposures to natural and synthetic compounds from the environment, occupation, and lifestyle. It relies on the analyses of human tissues and fluids and provides the only direct method of determining whether people have been exposed to particular substances, the magnitudes of such exposures, and how the exposures may change over time. HBM is a growing discipline used for exposure and risk assessment in environmental and occupational health and has become a more useful tool in recent years as the result of advancements in the capability to measure more minute amounts of chemicals in the human body. HBM focuses on the use of biomarkers as measurable indicators of changes or events in biological systems. Biomarkers are measurements of the concentrations of chemical substances, their metabolites, or reaction products in human tissues or specimens such as blood, urine, hair, adipose tissue, teeth, saliva, breast milk, and semen. The main advantage of using biomarkers is that they are intrinsic in their nature, representing an integrative measurement of exposure to a given agent (i.e., the internal dose), that results from complex pathways of human exposure and also incorporates toxicokinetic information and individual characteristics such as a genetically-based susceptibility. Through the use of biomarkers, it is not only possible to monitor exposure but also to detect early health effects. For population studies, biomarkers should be sensitive, specific, biologically relevant, feasible, practical, and inexpensive [2,3,4,5,6]. Figure 1 adapted from [4,5] shows the relationships among exposures, biomarkers, and adverse health outcomes. For risk assessment, exposure to chemicals from different sources in the environment leading to the absorption, distribution, metabolism, and excretion of chemicals in the human body can be followed with biomarkers of exposure. Biomarkers of early effect are considered more closely related to adverse health effects. The development of a HBM program requires several parameters to be established, tested, and optimized before the program can be implemented. A study population should be defined, considering various factors such as age, sex, habitation, occupation, and socioeconomic status as outcomes of HBM program can often be stratified using these factors. The design can be a representative sample of a general or specific population (e.g., vulnerable populations) of a specific region or an entire country. The feasible sample size of the population (i.e., number of study participants) should be considered, depending on the hypotheses to be tested, the capacities of the responsible members of the HBM program, and possible duration of the program. If specific subpopulations are of interests for the program, the calculations of the power of the study to detect differences within specified subpopulations should be included for proper numbers of participants to be enrolled. Recruitment of study participants can be conducted with various approaches such as census registries, advertisement on local newspapers or organizations, workplaces, hospitals, etc. Questionnaires should be developed to obtain information on a number of individual issues related to the participant such as demographic data, socioeconomic data, lifestyle, and specific exposures in the environment (e.g., from traffic and/or from occupation) [1].
Field work for sampling is often developed from a pilot study, setting the optimal program for collection and processing of biological samples. For example, urine samples are normally provided as the first morning void or collection of urine from a 24-hour period. The samples must be handled in a uniform manner (e.g., proper cooling procedure and storage time before analysis) in order to secure reproducible and reliable results. Chemical analysis of the samples should follow well-defined standard operation procedures to ensure validity of the results [1]. Results can be evaluated and interpreted for different purposes. For example, reference values of a general population can be established using the upper limit values such as 90th or 95th percentile of chemical levels among the population. HBM programs in Germany and Italy have both used this criterion for the development of reference values (further elaborated in [7,8]). Such reference values can then be compared with established health-based guidance values such as HBM-values or biological equivalent (BE) values, which translate the measured dose to health risks. The concepts behind HBM-values and biological equivalent values have been previously reviewed [8,9]. Also, interpretation of HBM results can combine HBM data and the use of external monitoring data or pharmacokinetic modeling in order to better understand of exposure sources of chemicals or the metabolism of chemicals, respectively. Also, time trends in human exposure may be tested. With this said, harmonization of data treatment and evaluation is absolutely crucial when comparing measurements and for publication purposes.
Feedback of results to participants at an individual level should be provided if possible. Also, grouped results can be provided to sponsoring institutions for further data interpretation as long as the personal data protection policies are respected. Grouped results can be further analyzed and are often reported in scientific or technical journals. The implications of HBM results can then be translated to policy makers and the general public at various levels. Communication of HBM program and findings should be based on a communication plan with targeted information tools from the start of the fieldwork to the dissemination of individual and aggregate levels results [1]. Lastly, quality control during all steps of the HBM program (e.g., from obtaining informed consent from participants to performing proper chemical measurements) is expected. The process of conducting HBM involves the following stakeholders: researchers, statisticians, participants, communities, participant representatives, research ethics committees, (regional or national) regulators, politicians, sponsors, industry, and the media [10]. Currently, HBM is the only available tool that integrates exposures from all sources and provides data for epidemiological studies of strengths of associations, dose response relationships, etc.; however, it does not differentiate the exposure by source. Furthermore, HBM alone cannot provide information on how long a chemical has been in the body. However, in combination with additional data collected (e.g., from questionnaires, interviews, etc.), HBM data may provide information about sources through knowledge (e.g., from patterns of dietary habits). For example, higher levels of acrylamide adducts in hemoglobin have been observed in populations with high intake of fried food [11], and a clear association between hair concentrations of Hg in adults and intake of fish has also been found in Europe from the COPHES/DEMOCOPHES study [12,13].
3. Description of the established national HBM survey programs
This section provides an overview of nine well-established national HBM survey programs, i.e., target population has been identified, questionnaires have been developed, and sample collections as well as analytical methods for chemical measurements have been optimized, etc. As mentioned earlier, these programs have been selected for this review as they have published large-scaled HBM data with a considerable impact in the country of origin.
3.1. United States of America: National Health and Nutrition Examination Survey (NHANES)
NHANES is an ongoing cross-sectional program aimed to assess the health and nutritional status of adults and children in the United States. Developed in the early 1960s, NHANES is a major program of the National Center for Health Statistics and a part of the Centers for Disease Control and Prevention (CDC). Since 1999, NHANES has been a continuous yearly program. For recruitment of participants, sampling is performed to represent the American population (non-institutionalized civilians) of all ages. Self-reported information on demographics, socioeconomic status, and health is supplemented with physical examination to collect medical, dental and physiological measurements as well as laboratory tests (e.g., for chemical analyses) [14]. Since 2002, NHANES collects dietary intake data with the “What We Eat in America” survey that uses the “Automated Multiple-Pass Method”, a 5-step dietary interview involving 24-hr recalls (further described in [15,16]).
As one of the components of NHANES, analysis of chemical exposure in the general American population is performed using blood and urine samples collected from the participants. The chemicals or classes of chemicals analyzed in the recent NHANES include acrylamide and its metabolite glycidamide, dioxins (polychlorinated dibenzo-p-dioxins; PCDDs), furans (polychlorinated dibenzofurans; PCDFs), polychlorinated biphenyls (PCBs), polybrominated diphenyl ethers (PBDEs), pesticides (e.g., carbamates, organophosphorus, pyrethroids) and metabolites, metals (e.g., As, Cd, Co, Cu, Pb, Hg, Se, Tl, W, U, Zn), phenols such as bisphenol A (BPA) and parabens, trihalomethanes, tobacco smoke (e.g., cotinine as a metabolite of nicotine), perchlorate, perfluorinated compounds (PFCs), phthalate metabolites, polycyclic aromatic hydrocarbons(PAHs) metabolites, phytoestrogens and metabolites, and volatile organic compounds (VOCs) and metabolites. These chemicals have been selected based on several factors including scientific data suggesting exposure in the general American population, potential adverse effects associated with the exposure of these chemicals and the availability of analytical methods (i.e., accuracy, sensitivity, speed) to specifically measure these chemicals. Many of these chemicals are considered as commonly used industrial chemicals(e.g., PBDEs, PFCs, BPA), by-products of chemical reactions such as acrylamide formation from cooking carbohydrates at high temperature, or contaminants in the environment [17]. NHANES is considered the most extensive HBM program with much emphasis devoted to the development of sensitive and specific analytical methods and the refinement of all of the tools serving as references for other HBM programs.
3.2. Canada: Canada Health Measures Survey (CHMS)
CHMS is an ongoing cross-sectional survey carried out in 2-year cycles including study participants aged 3 to 79 and living in Canada. CHMS was launched in 2007 by Statistics Canada in partnership with Health Canada and the Public Health Agency of Canada, and 4 cycles have already been performed. Information regarding lifestyle habits, medical history, demographics, socioeconomic status, etc. of the recruited participants is collected during home interviews and questionnaires. For food intake data collection, a semi-quantitative food frequency questionnaire (FFQ) is administered, particularly collecting data on the consumption frequency of various food groups (e.g., meat, dairy, vegetables consumed per day, week, month, or year). The participants also report to one of the CHMS collection sites for direct health measures, and blood and urine samples from the participants will be collected for testing health and nutritional markers as well as chemical levels from environmental exposure. Small amounts of blood and urine from consenting participants are also frozen and stored anonymously in a biobank at the National Microbiology Laboratory in Winnipeg for use in future health studies [18,19].
As of July 2015, chemical analyses from CHMS cycles 1-3 have been published. In particular, 48 substances including acrylamide and its metabolite glycidamide, environmental phenols such as BPA and triclosan, metals (e.g., As, Cd, Fl, Pb, Hg), cotinine, PAH metabolites, VOCs such as benzene have been analyzed in blood and urine in CHMS cycle 3 (2012-2013), and the results are published in the Third Report on Human Biomonitoring of Environmental Chemicals in Canada. Additionally, other classes of chemicals such as PBDEs, PCBs, chlorophenols, PFCs, phthalate metabolites, and pesticides such as carbamate, organochlorines, organophosphates, and pyrethroids had been analyzed in previous CHMS cycles [20]. CHMS aims to achieve the following objectives: (1) establish nationally-representative blood and urine concentrations for environmental chemicals, (2) provide baseline data to track temporal trends, (3) facilitate data comparisons among sub-populations in Canada and with other countries, and (4) provide data to explore relationships between environmental chemicals, other physical measures, and self-reported information (Doug Haines, personal communication). A strategy has been developed to communicate results to survey participants with the expert opinion of CHMS Laboratory Advisory Committee, the Physician Advisory Committee, l'Institut national de santé publique du Québec, and Health Canada's Research Ethics Board [20].
3.3. Germany: German Environmental Survey (GerES)
GerES is an ongoing nationwide cross-sectional human biomonitoring program that has been periodically conducted in Germany since the mid-1980s. The survey is conducted by the German Federal Environmental Agency (Umweltbundesamt; UBA) in close collaboration with the Robert Koch Institute, who is responsible for the health examination part of the survey. Each survey focuses on specific population of people living in Germany such as residents of East or West Germany and children, and the study populations are recruited from resident registries to represent age, sex, community size, and locations [21]. There are three key features to the GerES: (1) human biomonitoring, (2) environmental biomonitoring, and (3) standardized interview-based questionnaires. Multiple questionnaires are administered to the study participants during home visits to retrieve information on exposure conditions (e.g., lifestyles/hobbies, housing conditions, quality of the residential environment, exposure-relevant behavior). For dietary data (namely the food selection of the participants), a specialized FFQ is given to collect consumption data of 50 food groups. Blood and urine specimens are taken from the participants, and extended monitoring of the subjects‘ environment (e.g., analyses of tap water, house dust, and indoor air) is conducted [22]. For the ongoing GerES V (2014-2017), children and adolescents aged 3-17 are the target population, and the following substance classes are measured in urine samples: cotinine, metals (namely As and Hg), mercaptobenzothiazole (MBT), organophosphate metabolites, PAH metabolites, parabens, phthalate metabolites, and pyrrolidones. These chemicals are selected because of the likelihood of exposure of these chemicals from the environment in children and adolescent. For example, phthalates and their substitutes are measured because of the use as plasticizers in food packaging, toys, etc., and MBT is measured because of its use in the manufacturing of rubber and can be found in toys. The previous cycles of GerES had analyzed other substances in urine, blood, or hair such as several classes of pesticides (e.g., organochlorines and pyrethroids), BPA, chlorophenols, and PCBs. Every participant is informed about the concentrations of the analyzed substances in his/her biological (e.g., blood and urine), drinking water, and indoor air samples. Additionally, an environmental-medical assessment of these data is supplied [21]. GerES has major impact on the environmental health in Germany with much focus on consumer safety and establishment of reference values. GerES has demonstrated temporal trends (e.g., decline in blood lead levels over time, decline in prohibited phthalates after regulation, rise in alternatives to prohibited substances) and regional differences with lower exposure levels to some industrial chemicals in the former East Germany compared with West Germany. Also, age and sex differences have been found providing data for more targeted concepts of intervention, reduction and prevention. GerES is considered the most extensive HBM program in Europe and served as the basis for the protocols developed [23] and the reference values used for the COPHES/DEMOCOPHES study [24].
3.4. Belgium (Flanders): The Flemish Environment and Health Study (FLEHS)
FLEHS is a cross-sectional survey initiated in 2003 that measures selected pollutants and certain health effects in humans (mainly via the detection of biomarkers) living in Flanders. The FLEHS is implemented by the Flemish Centre of Expertise for Environment and Health and is funded and steered by the Flemish government [25]. Study participants are categorized into groups: mothers and newborns, adolescents (aged 14-15), adults (aged 20-40), and older adults (aged 50-65). They are selected in urban, rural, and industrial areas and only qualify if they have resided for at least 10 years in Flanders. Recruited participants (and parents if the participants were children or adolescents) are asked to fill out extensive questionnaires regarding personal background, lifestyle factors, and food intake. Blood (including cord and maternal blood from mothers and their newborns), urine, and hair (only from mothers and adolescents) samples are also collected from the participants [25]. The following substances were analyzed in FLEHS I (2002-2006) and FLEHS II (2007-2009): chlorophenols, cotinine, dioxins, fluorocarbons, furans, the herbicide 2, 4-dichlorophenoxyacetic acid (2, 4-D), metals (e.g., As, Cd, Cu, Pb, Mn, Hg, and Tl), organochlorine pesticides, organophosphate metabolites, PAH metabolites, PBDEs, PCBs, phenols such as BPA, phthalate metabolites, and pyrethroid metabolites. Also, measurements of 8-hydroxydeoxyguanosine (8-OHdG; a biomarker of oxidative DNA damage) and the single cell gel electrophoresis were conducted in FLEHS I/II to determine the amount of DNA damage [26]. The ongoing FLEHS III survey (2012-2015) is further exploring the Flemish exposure levels to improve risk assessment and communication, and reference values will be established. High-throughput measurements such as transcriptomics have been included in the program. The Flemish program has currently engaged sociologists in developing a dissemination and communication strategy targeting the population [26].
3.5. France: The French National Survey on Nutrition and Health (ENNS)
ENNS is an ongoing cross-sectional survey aimed to describe the patterns of food consumption, nutritional status, and physical activity and to measure nutritional and environmental biomarkers in the general population (aged 3-74) in France. The French National Institute for Public Health Surveillance, along with the French National Program on Health and Nutrition, is responsible for carrying out the ENNS study. ENNS comprises 3 parts: (1) data collection (e.g., of socioeconomic and demographic information) of the participants using both face-to-face interview and self-administered questionnaires, (2) a food consumption survey using 24-h dietary recalls, and (3) a clinical examination including urine, blood, and hair samples [27,28]. A total of 42 substances including chlorophenols, metals (e.g., As, Cd, Co, Pb, Hg, Ni, U), PCBs, and several classes of pesticides (e.g., organochlorines, organophosphates, and pyrethroids) have been measured [28]. The findings from the first survey have generated reference values of exposure to various metals and chemicals in the French adult population. The clinical results are communicated to participants within two months after the examination with a letter to his/her own usual physician if results are abnormal. A comparison of the food consumption with the French nutritional recommendations is conducted and sent to the participants, who also receive information on how to eat well [27,28].
3.6. Spain: BIOAMBIENT.ES
BIOAMBIENT.ES was the first nationwide cross-sectional study with a stratified cluster sampling designed to cover all geographical areas, sex, and occupational sectors in order to obtain a representative sample of the Spanish workforce. The recruitment of the participants of the cross sectional study took place through the annual occupational medical check-ups in various health facilities. Study persons aged 16 or older were recruited and successfully participated in the study between March 2009 and July 2010 [29]. A short self-administered epidemiological questionnaire was given to selected participants to collect basic individual information on socio-demographic data and environmental- and lifestyle-related exposure. A health exam was provided for each participant, who agreed to provide the results for the BIOAMBIENT.ES study, and blood and urine specimens were collected for analyses of pollutants. BIOAMBIENT.ES analyzed the levels of the following substances: PBDEs, cotinine, metals (Cd, Pb, and Hg), organochlorine pesticides, PAH metabolites, and PCBs [29]. This survey was conducted to generate reference values of chemical exposure (namely PCBs, Pb, and Hg) and confirmed high mercury levels attributable to fish intake. An information leaflet including individual levels of the results for each participant as well as general information on each toxicant was provided to the participants [29,30].
3.7. Italy: Program for Biomonitoring the Italian Population Exposure (PROBE)
PROBE was a cross-sectional population study to determine the exposure to metals of the healthy general population in Italy. It was commissioned and funded by the Italian National Institute of Health (Istituto Superiore di Sanità; ISS) and ran from 2008 to 2010. The recruited participants (aged 18-65) were residents of one of the five urban regions which were selected to establish representative data for South, Central, and North Italy without medical conditions (e.g., cancer). Questionnaire was given to the participants to collect information regarding participant‘s general characteristics (i.e., sex, age, height, weight, etc.), medical history, lifestyle, food intake, and environmental exposure, and morning blood samples were collected from the participants who had fasted overnight [31,32]. A total of 20 metals (i.e., Sb, As, Be, Cd, Cr, Co, Ir, Pb, Mn, Hg, Mo, Ni, Pd, Pt, Rh, Tl, Sn, W, U, and V) were analyzed directly in the blood and serum samples. The 95th percentile values from this study were established as the reference values that can be used for comparisons with higher exposure scenarios in Italy. PROBE further analyzed the data with the stratification of sub-groups of multiple variables (such as sex, age, place of residence, etc.) to find and launch new environment and health measures to reduce the exposure to environmental metals of the Italian population [32].
3.8. Czech Republic: Human Biomonitoring Project (CZ-HBM)
CZ-HBM was carried out as a limited representative cross-sectional study of the urban/suburban population in the Czech Republic and covered two time periods: (1) 1994-2003 and (2) 2005-2009. It was a part of the nationwide environmental health monitoring system funded by the Czech Ministry of Health. The purpose of CZ-HBM was (1) to document the extent, distribution, and determinants of population exposure to environmental pollutants, (2) to follow up long-term time trends and their possible changes as a result of preventive measures, (3) to establish a database from which to derive the reference values important for the characterization of the exposure of the general population, and (4) to use the available data for health risk assessment and management [33].
Three population groups were included in the CZ-HBM: adults aged 18-58, children aged 8-10, and breastfeeding primiparas. Information of each participant and biological specimens from the participants such as blood, urine, breast milk, hair, and teeth were collected [33]. For food intake, data was collected via two 24-hour recall processes [34]. Three groups of biomarkers were analyzed: (1) selected heavy metals (Cd, Pb, and Hg) and essential elements (Cu, Se, and Zn), (2) indicator PCBs and organochlorine pesticides, and (3) cytogenetic changes in peripheral lymphocytes in blood [33].The reference values for Cd, Hg, and Pb levels as well as for PCBs and organochlorine pesticides in breast milk samples have been published in scientific journals [35,36].
3.9. South Korea: Korea National Survey for Environmental Pollutants in the Human Body (KorSEP)
KorSEP was a cross-sectional HBM survey initiated as a part of The Korea National Health and Nutrition Examination Survey (KNHANES) in 2005 and designed to measure the levels of environmental pollutants in the human body across the general population in South Korea and to identify human exposure to toxic substances from the environment. Three cycles had been conducted: KorSEP I (2005), KorSEP II (2007), and KorSEP III (2008) [37]. For KorSEP III, the participants comprised non-institutionalized citizens aged 20 or older. The study entailed questionnaire-based interviews (for data collection regarding sociodemographic information, socioeconomic data, family history, indoor and outdoor environments, lifestyle (i.e., exposure to smoking, alcohol and drug consumption, and physical activity), occupational history and dietary information) and sample collection. Blood and urine specimens were collected, and the following substances were measured: BPA, cotinine, metals (As, Cd, Pb, Mn, and Hg), and metabolites of PAHs, phthalates, and pyrethroids. Some findings from the KorSEP III study have been published as scientific articles [37,38,39].
4. Observations of the features among the HBM programs
Several similarities and differences of the HBM parameters are seen among the reviewed HBM programs. For instance, all the national HBM programs are initiated by their respective governments and are cross-sectional in nature. Of these reviewed programs, NHANES, CHMS, GerES, FLEHS, and ENNS are still ongoing as of July 2015 while other European countries are preparing for the EHBMI. This initiative is based on national activities organized in national hubs with common protocols and associated research (unpublished).
The participants of the reviewed HBM programs mainly consist of randomly selected and voluntary adults (i.e., aged 18 and over) living in the respective countries. Besides PROBE and KorSEP, children and adolescents (i.e., aged 3-12 and 13-17, respectively) have also participated in the programs. In addition, pregnant women and their newborns were recruited in FLEHS and CZ-HBM. Table 1 shows an overview of the study populations among the reviewed HBM programs.
Table 1. Summary of the target populations in the national HBM programs.
|
NHANES |
CHMS |
GerES |
FLEHS |
ENNS |
BIOAMBIENT:ES |
PROBE |
CZ-HBM |
KorSEP |
| Adults |
x |
x |
x |
x |
x |
x |
x |
x |
x |
| (age ≥ 18) |
|
|
|
|
|
|
|
|
|
| Adolescents |
x |
x |
x |
x |
x |
x |
|
|
|
| (age 13–17) |
|
|
|
|
|
|
|
|
|
| Children |
x |
x |
x |
|
x |
|
|
x |
|
| (age 3–12) |
|
|
|
|
|
|
|
|
|
| Mother-newborns |
|
|
|
x |
|
|
|
x |
|
For biological matrices used for analysis of chemical exposure within the general population, it is observed that all the HBM programs have collected blood samples from participants. Urine samples have also been collected by all HBM programs except for PROBE. The latest GerES V survey collects only urine samples from the participants (i.e., children and adolescents), but blood and hair samples had been collected from previous GerES surveys. Other tested biological matrices include breast milk and teeth samples. Table 2 shows the biological matrices used in the HBM national programs.
Table 2. Biological matrices used for chemical measurements in national HBM programs.
| Blood |
Urine |
Hair |
Breast milk |
Teeth |
| (n = 9) |
(n = 8) |
(n = 4) |
(n = 3) |
(n = 1) |
| NHANES |
NHANES |
GerES |
FLEHS |
CZ-HBM |
| CHMS |
CHMS |
FLEHS |
ENNS |
|
| GerES |
GerES |
ENNS |
CZ-HBM |
|
| FLEHS |
FLEHS |
CZ-HBM |
|
|
| ENNS |
ENNS |
|
|
|
| BIOAMBIENT.ES |
BIOAMBIENT.ES |
|
|
|
| PROBE |
CZ-HBM |
|
|
|
| CZ-HBM |
KorSEP |
|
|
|
| KorSEP |
|
|
|
|
The number of chemicals analyzed among HBM programs varies significantly. The latest cycle of NHANES analyzed the highest number of substances (212 chemicals reported from The Fourth National Report on Human Exposure to Environmental Chemicals in 2009 while an updated report published in 2015 included 265 chemicals) [17], whereas PROBE only analyzed metals. However, it should be mentioned that the Italian ISS conducted a small-scale HBM study (SEBIOREC) from 2008 to 2009 specifically in Caserta and Naples provinces to investigate the levels of persistent organic pollutants (POPs) such as dioxins, furans, PCBs, etc. and metals in blood and milk samples of healthy volunteers [40]. However, the classes of chemicals analyzed in HBM programs are similar. Table 3 shows the classes of chemicals analyzed by at least two HBM programs.
Table 3. Classes of chemicals analyzed in at least two national HBM programs.
|
NHANES |
CHMS |
GerES |
FLEHS |
ENNS |
BIOAMBIENT:ES |
PROBE |
CZ-HBM |
KorSEP |
COUNT |
| Metals |
x |
x |
x |
x |
x |
x |
x |
x |
x |
9 |
| PCBs |
x |
x |
x |
x |
x |
x |
|
x |
|
7 |
| Cotinine |
x |
x |
x |
x |
|
x |
|
x |
x |
7 |
| Organochlorines (insecticides) |
x |
x |
x |
x |
x |
x |
|
x |
|
7 |
| PAHs |
x |
x |
x |
x |
|
x |
|
|
x |
6 |
| Pyrethroids (insecticides) |
x |
x |
x |
x |
x |
|
|
|
x |
6 |
| Environmental phenols (e.g., BPA) |
x |
x |
x |
x |
|
|
|
|
x |
5 |
| Organophosphates (insecticides) |
x |
x |
x |
x |
x |
|
|
|
|
5 |
| Chlorinated Phenols |
x |
x |
x |
x |
x |
|
|
|
|
5 |
| PBDEs |
x |
x |
|
x |
|
x |
|
|
|
4 |
| Phthalates |
x |
x |
|
x |
|
|
|
|
x |
4 |
| PFCs |
x |
x |
|
x |
|
|
|
|
|
3 |
| Acrylamide |
x |
x |
|
|
|
|
|
|
|
2 |
| Carbamates (insecticides) |
x |
x |
|
|
|
|
|
|
|
2 |
| VOCs |
x |
x |
|
|
|
|
|
|
|
2 |
| Dioxins (PCDDs) |
x |
|
|
x |
|
|
|
|
|
2 |
| Furans (PCDFs) |
x |
|
|
x |
|
|
|
|
|
2 |
Metals have been measured by all the reviewed HBM programs with arsenic, lead, cadmium, and mercury being the most frequently analyzed metals. Other frequently analyzed classes of chemicals include PCBs, cotinine, organochlorine pesticides, etc. However, it should be mentioned that several classes of chemicals such as parabens and PFCs have been added to recent HBM surveys or have been brought up as chemicals of concerns. For example, in December 2013, high levels of multiple PFCs were found in serum samples of Swedish children who might be exposed to such PFCs via contaminated drinking water coming from a municipal waterworks situated near a fire drill site [41]. On the other hand, there are several chemicals that have only been analyzed by one HBM program. In particular, phytoestrogens have been analyzed only by NHANES, and pyrrolidones and MBT have been analyzed only by GerES.
Results of the HBM surveys have been published mainly as respective governmental reports (e.g., NHANES, CHMS, GerES, PROBE) or in scientific journals. Most of the HBM programs have indicated that the individual results are provided to the participants. The results of the reviewed HBM programs can be compared to each other in order to differentiate potential population risks, e.g., due to lifestyle, environmental exposures, etc. For example, mercury levels in hair samples from the ENNS participants were reported to be higher than those observed in Germany and the United States but lower than the levels in Spain and were most likely the effect of the differences in the consumption of fish in these countries. The ENNS study also observed that the levels of 2, 5-dichlorophenol (2, 5-DCP; a metabolite of para-dichlorobenzene, which is used as moth-killers, air-fresheners, and disinfectant) was approximately 10 times higher than the levels in Germany, raising concern of the exposure source of this chemical within the general French population [28]. The Spanish population studied in the BIOAMBIENT.ES program showed Pb levels similar to populations in France and in Belgium but slightly lower levels than the Italian, Czech, German, or UK populations [29]. In the CZ-HBM study, increased urinary cadmium levels were observed in Czech children compared to German children [42], and it was also observed that the levels of phthalate metabolites within the KorSEP participants tended to be higher than the levels found in the NHANES but lower than the levels found in the GerES IV [37].
5. Identification of the vulnerable populations upon chemical exposure using HBM
Even though national HBM surveys have differences among the study design and approaches, the results generated from these surveys can often be stratified by various factors such as age, sex, and socioeconomic status (SES). Among these factors, age is observed to be one of the key determinants in identifying vulnerable populations upon chemical exposure in HBM programs, particularly children and the older adults. Children are regarded as a population of high risk for health impairment due to behavior (e.g., hand-to-mouth contact, crawling, chewing toys), making them more vulnerable to chemical exposure, and interest in children‘s environmental health is increased by rapidly rising rates of chronic disease in children of asthma, cancer, autism, attention-deficit/hyperactivity disorder, birth defects, obesity, and diabetes [43]. Children are not only exposed to higher amounts of chemicals due to behaviors, but they also have proportionately greater exposures than adults to toxic chemicals on a body weight basis as children have a larger surface to volume ratio and more permeable skin. Furthermore, chemicals may also have different effects on children than adults because of the ongoing body development in children, e.g., endocrine disruption from hormones [44] and the impairment in neurodevelopment from childhood lead exposure [45]. Children's extremely rapid but exquisitely delicate developmental processes can be easily disrupted, which is associated with windows of vulnerability most frequently reported to be related to fetal development but persists throughout childhood [46,47]. Cancer is a unique risk to children (compared to adults) because of their anticipated life span, and children also have more time than adults to develop chronic diseases that may be triggered by environmental exposures in early life related to diabetes and cardiovascular risk [47]. Lastly, as metabolic pathways in children are immature, it is possible that half-lives of environmental chemicals in children‘s bodies are longer as observed by [48].
Phthalates have been observed to be a major concern for children based on HBM findings as both the GerES and NHANES previously showed that children appeared to have higher body burdens of phthalates and PAH metabolites than adults [49,50]. In addition, GerES IV found that levels of organochlorine pesticides such as hexachlorobenzene (HCB), hexachlorocyclohexane (HCH), and dichlorodiphenyldichloroethylene (DDE) in children decreased with increasing age [51], and data analysis from the NHANES showed that children aged 6-11 had the highest urinary level of the PAH metabolite 1-hydroxypyrene compared to adolescents and adults [52,53]. Other scientific HBM studies also indicated higher levels of PBDEs and PFCs in children aged 1.5-9 than other subjects aged 9 or older [54,55,56]. These findings emphasize the need of HBM in children in order to generate the data appropriate for accurate risk assessment and management regarding children‘s exposure to chemicals.
On the other hand, older adults are also more vulnerable to health effects from chemical exposure than their younger counterparts. The ability of the body to respond to physiological challenge posed by environmental chemicals is dependent upon the health of the organ systems responsible for the elimination of such substances from the body. With aging, the body as well as the organ systems gradually diminish capacities, e.g., as a result of decrease in skeletal muscle mass. This normal change with life can affect the volume of chemical distribution in the body, resulting in physiologic and metabolic limitations and a decrease in the body's ability to protect itself from the adverse effects of xenobiotics. With increasing life expectancy, more people will confront the problems where age is a risk factor (e.g., neurodegenerative diseases). While proper diet and exercise may lessen the immediate severity of some aspects of aging, the process will continue to gradually degrade the ability to cope with a variety of injuries and diseases. Thus, the adverse effects of long-term, low-level exposure to environmental substances will have a longer time to be manifested in a physiologically weakened older population [57]. From the reviewed HBM programs, it is observed that several metals accumulate in the older adult population. FLEHS findings showed that the highest levels of total Hg in blood were found in older adults (aged 50-65) [58], and the PROBE study also showed that both blood Pb and Pd concentrations increased with age [31]. Aside from metals, urinary levels of phthalates appeared to be higher among subjects with older age in the KorSEP study [38], and a scientific HBM study from Australia observed the highest level of the PFC perfluorooctane sulfonate (PFOS) in the serum of subjects aged 60 or older [55]. These findings suggest slower clearance of these chemicals out of the body. Therefore, it is likely that the older adults are at a higher risk of developing adverse effects from exposure to chemicals, making it important to monitor the chemical levels in older adults within a HBM program.
Factors other than age such as sex, SES, region of residence, and lifestyle habits such as smoking can also lead to increased health risk from chemical exposure, and HBM data can be used to identify such vulnerable populations. Table 4 shows the overview of vulnerable populations due to other risk factors than age identified from HBM. This table not only provides information on the risk factors identified from individual HBM programs but also information that can serve as a reference for the design of future HBM programs. For example, in addition to increasing age, body burden of lead is higher in males (observed in both Europe and North America), people with low household income, and smokers. Future studies can be designed to investigate the association between these factors and lead exposure.
Table 4. Other factors associated with increased body burdens observed in national HBM programs.
| Factors |
HBM findings |
| Sex |
NHANES: Women had higher urinary parabens levels than men. |
|
CHMS: Men had higher levels of PFOS than women, whereas women had higher levels of DDE than men. |
|
GerES IV: Boys had higher levels of As, Hg, and PCBs (except for PCB 138) than girls. |
|
ENNS/NHANES: Women had higher Cd levels than men. |
|
BIOAMBIENT.ES/PROBE/CHMS: Males had higher blood Pb level than females. |
|
PROBE: Men had higher blood Hg, Pd, and W levels than women while women had higher blood Co, Rh, and V
levels than men. |
|
CZ-HBM: Women had higher blood and urinary Hg levels than men. |
|
KorSEP: Women had higher levels of urinary phthalate metabolites than men. |
| SES |
NHANES: People with high household income had higher triclosan levels than people with low household
income. |
|
CHMS: People with low household income had higher blood Pb levels than people with high household
income. |
|
GerES IV: Children with high SES had higher levels of PCBs, DDE, HCB, and β-HCH than children with low
SES. |
|
KorSEP: Subjects with lower income had higher levels of urinary phthalate metabolites. |
| Region |
GerES: Children from large communities had higher As and DDE levels than children from small
communities. |
|
FLEHS: People living in rural areas or near industrial hot-spots (i.e., waste incinerators, smelt plant)
had higher exposure to persistent chlorinated compounds or metals such as Cd and Cu, respectively, compared to their
respective control populations. |
|
CZ-HBM: Levels of indicator PCB congeners in breast milk samples in PCB hot-spots area of
UherskéHradi?tě were reported. |
| Smoking |
NHANES: Increased urinary PAH and hemoglobin acrylamide adduct levels |
|
GerES/ENNS/PROBE/CZ-HBM: Increased Cd levels |
|
PROBE/CHMS: Increased Pb level |
6. Identification of chemical exposure associated with food intake
One of the specific tasks from the EFSA-commissioned project mentioned earlier was to assess the feasibility of HBM and its application to human exposure assessment for food safety [1]. This task stems from a specific challenge related to risk assessments of chemicals stemming from contaminants in food and feed. The presence of such chemical contaminants or other unwanted substances in food and feed is often unavoidable as some of these substances are ubiquitous in the environment. However, it has been observed that the data collection of dietary intake along with chemical analyses of biological samples allows HBM programs to identify chemical exposures that might be associated with dietary intake. For example, the GerES study reported that food is a major exposure source of organochlorines, biocides, and phthalates, and the exposure to organophosphate pesticides is mainly influenced by age, consumption of fresh fruit and fruit juice [51]. Table 5 shows the list of chemicals identified from the reviewed HBM programs that are associated with intake of particular food populations.
Table 5. Chemicals associated with dietary intake identified in national HBM programs.
| Chemical class |
Chemical |
Associated food |
HBM program |
| Metals |
Arsenic |
Seafood/Fish |
FLEHS (Flanders) |
|
|
|
ENNS (France) |
|
|
|
KorSEP (South Korea) |
|
|
Rice |
NHANES (USA) |
|
Mercury |
Seafood/Fish |
NHANES (USA) |
|
|
|
CHMS (Canada) |
|
|
|
GerES (Germany) |
|
|
|
FLEHS (Flanders) |
|
|
|
KorSEP (South Korea) |
|
|
Alcohol |
CHMS (Canada) |
|
Lead |
Alcohol |
PROBE (Italy) |
|
Manganese |
Alcohol |
PROBE (Italy) |
| PCBs |
PCBs in general |
Seafood/Fish |
BIOAMBIENT.ES (Spain) |
|
Non-dioxin-like-PCBs |
Food of animal origin/Seafood |
ENNS (France) |
| Organophosphates |
|
Fresh fruits & Fruit juice |
GerES (Germany) |
These associations have been mostly made based on chemical analysis of human samples and questionnaire data from the participants. There are currently very few efforts in national HBM programs to perform direct chemical measurements in food, and subsequently, there is a lack of direct correlation between measured chemical levels in food and body burden in the general population. CHMS, GerES, and CZ-HBM have analyzed water samples (e.g., tap water) for chemical measurements, and only CZ-HBM measured various food groups and drinking water for mercury levels in the population [34]. A drawback among these programs is the lack of standardization in food intake data collection, which might decrease the reliability of the conclusions on food source taken from the HBM programs and increase the uncertainty regarding comparability of results obtained from food questionnaire within countries and between countries. When it comes to food intake data collection, the customized 24-hour food recall method, which the participants recall the food and the amount consumed the day before, has been recommended by EFSA, yet only three HBM programs (NHANES, ENNS, and CZ-HBM) use this method. Food frequency questionnaires, where the participants report the frequency consumption of multiple food groups, have been used by CHMS, GerES, and BIOAMBIENT.ES. The remaining three programs (FLEHS, PROBE, and KorSEP) collected food intake data only using personal questionnaires.
Altogether, while HBM programs can identify associations between chemical exposure and certain food intake, additional initiatives to investigate exposure source especially in food and a better harmonization in food intake data collection can be extremely useful in establishing clearer relationships between body burden and chemical exposure via food.
7. Conclusion colspan
Human biomonitoring can be a very useful tool of identifying not only the risks of chemical exposures in the general population but also vulnerable populations and associations between chemical exposure and food intake. There are many similarities among the existing national HBM programs such as governmental funding, target population/recruitment, biological matrices (e.g., blood and urine), communication of results, and classes of chemicals such as metals and PCBs have been analyzed in most of the programs. Trends such as levels of chemical exposure from different countries can be observed and compared using HBM data in order to identify any country-specific risks. Furthermore, existing HBM programs readily stratify results by age, sex, lifestyle, etc. Children and older adults are identified in various contexts as potentially higher exposed sub-populations or as vulnerable groups of exposure to specific classes of chemicals. Other factors, such as socioeconomic status and region, can also affect chemical exposure levels within a population. While HBM data can provide additional evidence in the link between chemical exposure and food intake, there are some limitations such as the paucity of chemical measurements directly in food and the lack of standardization in data collection of dietary intake. Chemical measurements in food as well as harmonization of data collection of dietary intake can potentially strengthen associations between chemical exposure and food intake. Overall, although there are some discrepancies in the study designs among the reviewed national HBM programs, results from the programs can provide useful information such as chemical levels found within the general population of a country that can be compared that of another country. Furthermore, the results can be used by regulatory authorities or the government to enforce legislations in order to reduce the exposure of chemicals into the human body.
Acknowledgments
The project that this review was based on was financed by the EFSA through a public procurement procedure on ‘Review of the state of the art of human biomonitoring for chemical substances and its application to human exposure assessment for food safety (OC/EFSA/EMRISK/2013/01). The opinions expressed are those of the authors only and do not represent the EFSA’s official position.
Conflicts of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: 

