Citation: Herbert F. Jelinek, Jemal H. Abawajy, Andrei V. Kelarev, Morshed U. Chowdhury, Andrew Stranieri. Decision trees and multi-level ensemble classifiers for neurological diagnostics[J]. AIMS Medical Science, 2014, 1(1): 1-12. doi: 10.3934/medsci.2014.1.1
| [1] | Herbert F. Jelinek, Jemal H. Abawajy, David J. Cornforth, Adam Kowalczyk, Michael Negnevitsky, Morshed U. Chowdhury, Robert Krones, Andrei V. Kelarev . Multi-layer Attribute Selection and Classification Algorithm for the Diagnosis of Cardiac Autonomic Neuropathy Based on HRV Attributes. AIMS Medical Science, 2015, 2(4): 396-409. doi: 10.3934/medsci.2015.4.396 |
| [2] | Herbert F. Jelinek, Andrei V. Kelarev . A Survey of Data Mining Methods for Automated Diagnosis of Cardiac Autonomic Neuropathy Progression. AIMS Medical Science, 2016, 3(2): 217-233. doi: 10.3934/medsci.2016.2.217 |
| [3] | XinQi Dong, Manrui Zhang . The Prevalence of Neurological Symptoms among Chinese Older Adults in the Greater Chicago Area. AIMS Medical Science, 2015, 2(1): 35-50. doi: 10.3934/medsci.2015.1.35 |
| [4] | Segun Akinola, Reddy Leelakrishna, Vijayakumar Varadarajan . Enhancing cardiovascular disease prediction: A hybrid machine learning approach integrating oversampling and adaptive boosting techniques. AIMS Medical Science, 2024, 11(2): 58-71. doi: 10.3934/medsci.2024005 |
| [5] | Paula Barrett-Brown, Donovan McGrowder, Dalip Ragoobirsingh . Diabetes education—Cornerstone in management of diabetes mellitus in Jamaica. AIMS Medical Science, 2021, 8(3): 189-202. doi: 10.3934/medsci.2021017 |
| [6] | Mujeeb Ur Rehman Parrey, Hanaa El-Sayed Bayomy, Fawaz Salah M Alanazi, Asseel Farhan K Alanazi, Abdullah Hamoud M Alanazi, Abdulelah Raka A Alanazi . Diabetic retinopathy: knowledge, attitudes, and practices among diabetic patients. AIMS Medical Science, 2025, 12(2): 210-222. doi: 10.3934/medsci.2025013 |
| [7] | Ayomide Abe, Mpumelelo Nyathi, Akintunde Okunade . Lung cancer diagnosis from computed tomography scans using convolutional neural network architecture with Mavage pooling technique. AIMS Medical Science, 2025, 12(1): 13-27. doi: 10.3934/medsci.2025002 |
| [8] | Fotios Kounelis, Christos Makris . Space Efficient Data Structures for N-gram Retrieval. AIMS Medical Science, 2017, 4(4): 426-440. doi: 10.3934/medsci.2017.4.426 |
| [9] | Brandon M. Jones, E. Murat Tuzcu, Amar Krishnaswamy, Samir R. Kapadia . Incidence and Prevention of Strokes in TAVI. AIMS Medical Science, 2015, 2(1): 51-64. doi: 10.3934/medsci.2015.1.51 |
| [10] | Fatemeh keshavarzi, Mohsen Askarishahi, Maryam Gholamniya Foumani, Hossein Falahzadeh . Parametric and the Cox risk model in the analysis of factors affecting the time of diagnosis of retinopathy with patients type 2 diabetes. AIMS Medical Science, 2019, 6(2): 170-178. doi: 10.3934/medsci.2019.2.170 |
Neurological disorders often span multiple chronic disease entities such as diabetes, kidney and cardiovascular disease and present an area of medical practice where data mining can provide assistance in clinical decision making. Decision making and diagnosis in medical practice is most often based on incomplete data due to either unavailability of diagnostic laboratory services, technical issues or lack of patient cooperation as well as counter-indications for undertaking certain diagnostic tests. Utilizing data mining methods, powerful decision rules can be determined, which enhance the diagnostic accuracy when an incomplete patient profile is available or multiclass presentations are possible. In order to reduce the cost of performing medical tests required to collect the attributes yet maintain diagnostic accuracy, it is essential to optimize the features used for classification and to keep the number of features as small as possible.
Diabetes mellitus is a major world-wide health issue. Cardiovascular complications associated with diabetes account for 65% of all diabetic deaths. The large impact of cardiovascular disease on people with diabetes has brought about that the National Diabetes Strategy and ACCORD Study Group recommended that people with diabetes be regularly screened for the presence of comorbidities including autonomic nervous system dysfunction with the aim to decrease the incidence of cardiovascular related mortality [1,2,3]. The increased risk of cardiac mortality due to arrhythmias makes screening of people with diabetes for autonomic neuropathy vital so that early detection, intervention and monitoring can occur [4].
People with diabetes and autonomic neuropathy have increased mortality rates (29%) compared to people with diabetes without autonomic neuropathy (6%) [5,6]. As many as 22% of people with type 2 diabetes suffer from cardiovascular autonomic neuropathy (CAN) which leads to impaired regulation of blood pressure, heart rate and heart rate variability (HRV). Silent ischemia is significantly more frequent in patients with CAN than in those without CAN [7]. Significantly more people with diabetes die from cardiovascular disease such as heart attack and stroke, which can be attributed to CAN [8]. Early subclinical detection of CAN and intervention are of prime importance for risk stratification in preventing the potentially serious consequences of CAN.
Autonomic neuropathy in diabetics is traditionally detected by performing the Ewing battery of tests, which was recommended by the American Diabetes Association and the American Academy of Neurology and evaluates heart rate and blood pressure changes evoked by stimulation of cardiovascular reflexes [9,10,11]. The five different tests/categories in the Ewing battery are shown in Table 1 below following [10].
| Test | Normal | Borderline | Abnormal |
| 1. Heart rate response to standing (BPM) | ≥ 1.04 | 1.01–1.03 | ≤ 1.00 |
| 2. Blood pressure response to standing (mmHg) | ≤ 10 | 11–29 | ≥ 30 |
| 3. Heart rate response to deep breathing (mmHg) | ≥ 15 | 11–14 | ≤ 10 |
| 4. Valsalva maneuver and heart rate response (BPM) | ≥ 1.21 | 1.11–1.20 | ≤ 1.10 |
| 5. Blood pressure response to sustained handgrip (mmHg) | ≥ 16 | 11–15 | ≤ 10 |
DownLoad: CSVSeveral studies have shown that abnormalities in reflex testing give a good assessment of advanced diabetic autonomic neuropathy and aid in its objective diagnosis rather than relying on clinical signs such as gustatory sweating, reflux, and incontinence as self-reported by individuals. The response of subjects to each of the Ewing tests is defined as normal, borderline or abnormal. From this grading CAN risk assessment can be divided into a normal and no CAN evident category and four CAN categories comprising: early, definite, severe and atypical (Table 2).
| Category | Decision Paradigm |
| Normal | All tests normal or one borderline |
| Early | One of the three heart rate tests abnormal or two borderline |
| Definite | Two or more of the heart rate tests abnormal |
| Severe | Two or more of the heart rate tests abnormal plus one or both of the blood pressure tests abnormal or both borderline |
| Atypical | Any other combination of tests with abnormal results |
DownLoad: CSVElectrocardiogram (ECG) is a recording of the electrical activity of the heart using surface electrodes [12,13]. The most commonly used configuration is a 12-lead ECG, which consists of a number of specific characteristics defined as waves or intervals. These included the P, QRS, T and u-waves and the QT, QTd and PQ intervals. The QRS complex represents the depolarization of the ventricles of the heart. The duration of the QRS complex is also often used in diagnostics. The time from the beginning of the P wave until the start of the next QRS complex is called the PQ interval and represents electrical activity in the atria of the heart. Whereas the distance from the Q wave to the start of the T wave is the QT interval, depicting the re-polarization of the ventricles, which if corrected for heart rate becomes the QTc. The difference of the maximum QT interval and the minimum QT interval over all 12 leads is known as the QT dispersion (QTd). The electrical axis of the heart is determined from the QRS wave and can indicate cardiac myopathy. ECG features have also been shown to indicate CAN [14,15]. Sympathetic nervous system activity has been shown to be associated with changes in QT interval length and as a predictor of ventricular arrhythmia [14,16]. Our own work has also identified ECG components to be associated with CAN [17].
This section contains brief background material and describes the methodology used in this work.
The Diabetes Screening Complications Research Initiative (DiScRi) is a research initiative in Australia that has made it possible to collect a large dataset consisting of over 2500 entries and several hundred features. Therefore, a priority of any machine learning classification is to reduce the data to a manageable set. A hybrid of Maximum Relevance filter (MR) and Artificial Neural Net Input Gain Measurement Approximation (ANNIGMA) wrapper approaches were used to reduce the number of features necessary for optimal classification. The combined heuristic MR-ANNIGMA exploits the complimentary advantages of both the filter and wrapper heuristics to find significant features [17].
We investigated six efficient decision tree classifiers, namely ADTree, J48, NBTree, RandomTree, REPTree and SimpleCart [18]. Of these ADTree generates smaller rules compared to the other decision trees and the results are therefore easier to interpret [20]. J48 is based on the C4.5 algorithm and uses information entropy to build decision trees from the set of training data. Each node of the tree represents the most effective split of the samples determined by the highest normalized information gain [21]. NBTree is a Na?ve-Bayes/Decision Tree hybrid and contains Na?ve-Bayes classifiers at the leaves to create the decision tree [22]. RandomTree employs a simple pre-pruning step to stops at a fixed depth for randomly chosen attributes at each node [18]. REPTree considers all attributes to build a decision tree based on information gain [18]. Finally SimpleCart (classification and regression trees) creates a binary split by applying minimal cost-complexity pruning. This procedure is continued on each subgroup until some minimum subgroup size is reached [23].
Ensemble methods have been extensively used in data mining and artificial intelligence [24,25,26]. Here we describe the following methods implemented in WEKA: AdaBoost, Bagging, Dagging, Decorate, Grading, MultiBoost and Stacking.
· AdaBoost, boosting trains several classifiers in succession. Each classifier is trained on the instances that have turned out more difficult for the preceding classifier. To this end all instances are assigned weights, and if an instance turns out difficult to classify, then its weight increases [28].
· Bagging (bootstrap aggregating), generates a collection of new sets by resampling the given training set at random and with replacement. New classifiers are then trained, one for each of these new training sets. They are amalgamated via a majority vote [27].
· MultiBoosting extends the approach of AdaBoost with the wagging technique, which is a variant 5 AIMS Medical Science Volume 1, Issue 1, 1-12. of bagging but where the training weights generated during boosting are utilized in the selection of the bootstrap samples [29].
· Stacking is a generalization of voting, where a meta learner aggregates the outputs of several base classifiers [30].
· Decorate is based on constructing special artificial training examples to build diverse ensembles of classifiers [31].
· Dagging is useful in situations where the base classifiers are slow. It divides the training set into a collection of disjoint (and therefore smaller) stratified samples, trains copies of the same base classifier and averages their outputs using vote [32].
· Grading is a meta-classifier, which grades the output of base classifiers as correct or wrong labels, and these graded outcomes are then combined [33].
All experiments presented in this paper used WEKA software environment described in the monograph [18] and article [19]. WEKA includes ADTree, J48, NBTree, RandomTree, REPTree, SimpleCart, Decision Table, FURIA, J48, NBTree, Random Forest, SMO and ensemble meta classifiers AdaBoost, Bagging, Dagging, Decorate, Grading, MultiBoost and Stacking. We used WEKA Explorer to run each of these classifiers and meta-classifiers. The monograph [18] provides excellent explanations of how to run each of these classifiers and meta-classifiers in WEKA Explorer. There are also pdf files of the WEKA manual and tutorial available with every installation.
To prevent overfitting, we used 10-fold cross validation in assessing the performance of the classification schemes for all our experiments. It is a standard method for preventing overfitting, which is also available in WEKA Explorer and calculates outcomes for any number of classes among other performance metrics. The standard output produced by WEKA Explorer contains ROC area (as well as several other measures), obtained using 10-fold cross validation (refer to [18] for a detailed explanation of 10-fold cross validation and how to use these classifiers in WEKA Explorer).
To prepare data for WEKA Explorer, all instances of data were collected in one csv file and pre-processed. Pre-processing included the reduction of the number of missing values. To this end, more than 50 expert editing rules were collected and applied. Most of these rules rely on the fact that several medical parameters usually change only gradually with time, and so their values behave as a monotonic mathematical function. Therefore, for the purposes of data mining, it is safe to assume that a missing value of an attribute is approximately equal to the average of the preceding and following values of the same attribute. For other features, it is known that some clinical values indicating pathology very seldom improve. For example, if a person has been diagnosed with diabetes, then this diagnosis can be recorded in all subsequent instances of data for the same patient. Finally, some of the expert editing rules checked data for consistency and deduced missing values of certain attributes from other closely related features. For example, the “Diagnostic DM (years)” feature in DiScRi refers to the number of years since the patient has been diagnosed with diabetes. If this number is greater than zero in an instance, then the value of another related feature, the “Diabetic Status”, must be set as “yes”. These editing rules were collected in consultation with the experts managing the database. A Python script was written by the third author to automate the application of these rules. Pre-processing of the data utilizing the expert editing rules reduced the data to 1299 complete rows with complete values and 200 features included in the csv file.
We created 3 copies of this file to address the progression of cardiac autonomic neuropathy (CAN) indicated in the DiScRi database as “no CAN”,“early CAN” and “definite CAN”. In the first copy, a two-class paradigm was investigated with the last column containing the class value for classification including “definite CAN” and “no CAN”. In the second copy, we added three CAN classes as “no CAN”,“early CAN” or “definite CAN”. In the third copy, as the last column we added one of four CAN classes including “no CAN”,“early CAN”,“definite CAN” or “severe CAN”. In order to enable all classifiers available in WEKA Explorer to process these three files, the files were reformatted into ARFF format, which is the standard format used by all classifiers in WEKA. These three files were used in all experiments presented in the paper.
In medical applications it is important to consider models produced by the classifiers that can be expressed in a clear form and facilitate their application in clinical practice. Therefore various versions of the decision trees deserve special attention, since they satisfy this requirement.
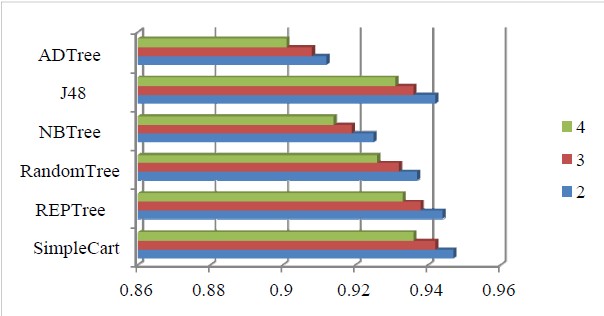
Figure 1 presents the results of our experiments comparing the performance of the current decision trees available in WEKA for the neurological diagnosis of CAN progression. We refer to Section 3.4 for complete simulation details and WEKA Explorer results.
Figure 1. ROC of decision trees for the neurological diagnostics of CAN progression.
The best result was obtained using SimpleCart with an area under the curve (ROC) of 0.947 for classification of two CAN classes with classification of four CAN classes having an AUC of 0.936 (normal, early, definite and severe), which is still the best result for the four class paradigm.
Further, we investigated several other base classifiers: Decision Table, FURIA, J48, NBTree, Random Forest and SMO. Random Forest constructs a multitude of decision trees during training and has as an output the mode of the classes output by individual trees [27]. Random Forest is hard wired to RandomTree and cannot use other base classifiers as an input parameter. This is why it is appropriate to regard it as a base classifier in our experiments. Recall that FURIA is a fuzzy unordered rule induction algorithm [35].
We introduce Random Forest into this setting as an additional base classifier. Random Forest cannot be used as a meta-classifier that accepts another base classifier as a parameter. All ensemble classifiers are in fact meta-classifiers that accept any base classifier as a parameter.
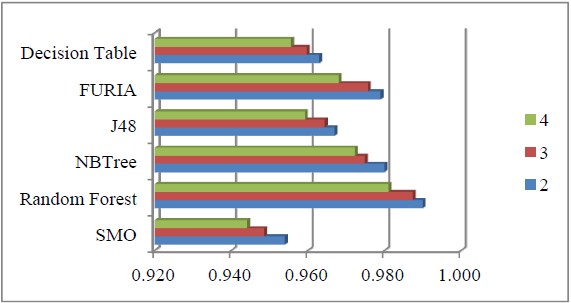
Figure 2 presents the results of experiments comparing the outcomes of these base classifiers for 2, 3 and 4 classes of the neurological classification of CAN progression based on the DiScRi dataset. The results show that Random Forest outperformed all other base classifiers.
Figure 2. Base classifiers for 2, 3 and 4 classes of the neurological diagnostics of CAN progression.
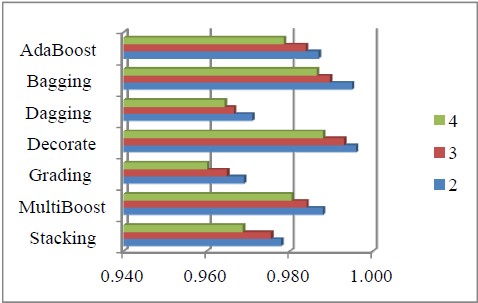
Since Random Forest performed best, we investigated further ways of enhancing its performance using meta-classifiers. The ensemble methods listed in Section 3 were used with Random Forest as their base classifier. The resulting combined ensembles were created in WEKA Explorer. Figure 3 displays the results obtained using WEKA Explorer for AdaBoost, Bagging, Dagging, Decorate, Grading, MultiBoost and Stacking set up with Random Forest as the base classifier.
Figure 3. Meta classifiers for 2, 3 and 4 classes of the neurological diagnostics of CAN progression.
The outcomes show that the overall best performance was obtained when combining Random Forest with Decorate for the 2, 3 and 4-class problem.
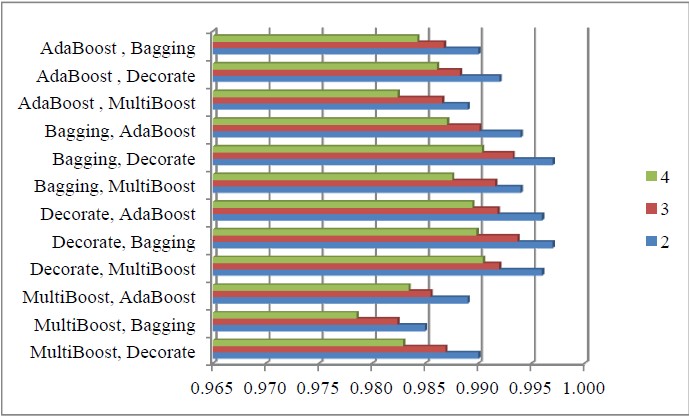
A different method of enhancing base classifiers is to include them into a multi-level scheme generated by several ensemble classifiers combined on two levels. In this scheme, a second ensemble meta-classifier is used as a base classifier for the first meta-classifier in WEKA Explorer. After that a base classifier is connected to the second ensemble meta-classifier. This creates an ensemble with three levels. We investigated all options of combining the best ensemble methods to create all possible pairs of different meta-classifiers and produce a three level ensemble classifier based on Random Forest. In this way we applied the best meta-classifiers via the multi-level classification paradigm.
The best outcome was obtained by two options combining Bagging and Decorate into one multi-level ensemble classifier. The first option was Bagging in the second level after applications of Decorate based on Random Forest in the first level. The other optimal result was using Decorate in the second level to combine the results of Bagging applied to Random Forest as a base classifier (Figure 4).
Figure 4. Meta-classifiers with two levels for 2, 3 and 4 classes of the neurological diagnostics of CAN progression.
Among the standard decision tree base classifiers considered in this paper, the best result was obtained using SimpleCart with an area under the curve (ROC) of 0.947 for classification of two CAN classes and for the four-class classification with an AUC of 0.936. The best base classifier was Random Forest regardless of the number of classes of CAN.
Looking at ensemble classifiers based on decision trees the best performance was obtained bycombining RandomTree with Decorate as the ensemble method with a ROC = 0.984.
Comparing ensemble classifiers based on RDR, we see that bagging and boosting outperformed other ensemble methods. Dagging produced worse results because usually it benefits classifiers with high complexity and in the current case RDR is fast enough. Stacking and grading use a meta-classifier to combine outcomes of base classifiers and in the current experiments we only considered Ripple Down Rules as base classifiers and thus stacking performed worse compared to bagging and boosting. The good performance of AdaBoost of bagging indicates that the diversity of ensemble classifiers used in the two levels is crucial for success of the combined multi-level ensemble classifier.
Further experiments have shown that Random Forest also performed best when combined with AdaBoost, Bagging, Decorate and MultiBoost for 2, 3, and 4 classes of the neurological diagnostics of CAN progression, and within the framework of the multi-level paradigm. The experiments show that the multi-level scheme performed best when Bagging and Decorate were combined in the construction of a multi-level ensemble classifier based on Random Forest.
The results of experiments investigating the applications of data mining methods to a large diabetes screening dataset with emphasis on classification of cardiac autonomic neuropathy indicates that Random Forest is the best classifier to apply either on its own or in combination with ensemble classifiers and multi-level applications.
The experimental results presented in Figures 1 through to 4 determine the best options that may be recommended for the neurological diagnostics of CAN progression with regard to using decision tree classifiers, meta classifiers based on RDRs, and multi-level ensemble meta classifiers based on Random Forest.
The multi-level paradigm achieved best outcomes when Bagging and Decorate were combined in the construction of a multi-level ensemble classifier. The first option was to use Bagging in the second level after applications of Decorate based on Random Forest in the first level. The other optimal result was achieved by using Decorate in the second level to combine the results of Bagging applied to Random Forest acting as a base classifier to produce input for Decorate.
The authors are grateful to two referees for comments and recommendations that have helped to improve the text of this article.
The authors wish to acknowledge the many students that have contributed to data analyzed and reported in this paper. Part of the research presented was funded by the Diabetes Australia Research Trust, Albury and Tallangatta Council Funding, Deakin-Ballarat Collaboration Funding and Charles Sturt University Research Compacts grants. Roche Australia Pty is gratefully acknowledged for provided glucose meters and test strips.
All authors declare no conflicts of interest in this paper.
| [1] | Colagiuri S, Colagiuri R, Ward J (1998) National diabetes strategy and implementation plan. Canberra: Paragon Printers. |
| [2] | Pop-Busui R, Evans GW, Gerstein HC, et al. (2010) The ACCORD Study Group. Effects of cardiac autonomic dysfunction on mortality risk in the Action to Control Cardiovascular Risk in Diabetes (ACCORD) Trial. Diab Care 33: 1578-84. |
| [3] |
Spallone V, Ziegler D, Freeman R, et al. (2011) Cardiovascular autonomic neuropathy in diabetes: clinical impact, assessment, diagnosis, and management. Diab Metab Res Rev 27:639-53. doi: 10.1002/dmrr.1239
|
| [4] | Jelinek HF, Imam HM, Al-Aubaidy H, et al. (2013) Association of cardiovascular risk using nonlinear heart rate variability measures with the Framingham risk score in a rural population. Front Physiol 4: 186. |
| [5] |
Ziegler D (1994) Diabetic cardiovascular autonomic neuropathy: prognosis, diagnosis and treatment. Diab Metabol Rev 10: 339-83. doi: 10.1002/dmr.5610100403
|
| [6] |
Gerritsen J, Dekker JM, TenVoorde BJ, et al. (2001) Impaired autonomic function is associated with increased mortality, especially in subjects with diabetes, hypertension or a history of cardiovascular disease. Diab Care 24: 1793-8. doi: 10.2337/diacare.24.10.1793
|
| [7] | Johnston SC, Easton JD (2003) Are patients with acutely recovered cerebral ischemia more unstable? Stroke 4: 24-46. |
| [8] |
Ko SH, Kwon HS, Lee JM, et al. (2006) Cardiovascular autonomic neuropathy in patients with type 2 diabetes mellitus. J Korean Diab Assoc 30: 226-35. doi: 10.4093/jkda.2006.30.3.226
|
| [9] |
Agelink MW, Malessa R, Baumann B, et al. (2001) Standardized tests of heart rate variability: normal ranges obtained from 309 healthy humans, and effects of age, gender and heart rate. Clin Auton Res 11: 99-108. doi: 10.1007/BF02322053
|
| [10] |
Ewing DJ, Martyn CN, Young RJ, et al. (1985) The value of cardiovascular autonomic functions tests: 10 years experience in diabetes. Diab Care 8: 491-8. doi: 10.2337/diacare.8.5.491
|
| [11] |
Pumprla J, Howorka K, Groves D, et al. (2002) Functional assessment of HRV variability: physiological basis and practical applications. Int J Cardiol 84: 1-14. doi: 10.1016/S0167-5273(02)00057-8
|
| [12] |
Stern S, Sclarowsky S (2009) The ECG in diabetes mellitus. Circulation 120: 1633-6. doi: 10.1161/CIRCULATIONAHA.109.897496
|
| [13] | Reilly RB, Lee TC (2010) Electrograms (ECG, EEG, EMG, EOG). Technol Heal Care 18:443-58. |
| [14] |
Baumert M, Schlaich MP, Nalivaiko E, et al. (2011) Relation between QT interval variability and cardiac sympathetic activity in hypertension. Am J Physiol Heart Circ Physiol 300: H1412-7. doi: 10.1152/ajpheart.01184.2010
|
| [15] | Kelarev AV, Dazeley R, Stranieri A, et al. (2012) Detection of CAN by ensemble classifiers based on ripple down rules. Lect Notes Artif Int 7457: 147-59. |
| [16] |
Fang ZY, Prins JB, Marwick TH (2004) Diabetic cardiomyopathy: evidence, mechanisms, and therapeutic implications. Endocrinol Rev 25: 543-67. doi: 10.1210/er.2003-0012
|
| [17] | Huda S, Jelinek HF, Ray B, et al. (2010) Exploring novel features and decision rules to identify cardiovascular autonomic neuropathy using a Hybrid of Wrapper-Filter based feature selection. Marusic S, Palaniswami M, Gubbi J, et al, editors. Intelligent sensors, sensor networks and information processing, ISSNIP 2010. Sydney: IEEE Press, 297-302. |
| [18] | Witten H, Frank E (2011) Data mining: practical machine learning tools and techniques with java implementations. 3Eds, Sydney: Morgan Kaufmann, 2011. |
| [19] |
Hall M, Frank E, Holmes G, et al. (2009). The WEKA data mining software: an update. SIGKDD Explor 11(1): 10-8. doi: 10.1145/1656274.1656278
|
| [20] | Freund Y, Mason L (1999) The alternating decision tree learning algorithm. Proceedings of the sixteenth international conference on machine learning, 124-33. |
| [21] | Kotsiantis SB (2007) Supervised machine learning: A review of classification techniques. Informatica 31: 249-68. |
| [22] | Kohavi R (1996) Scaling up the accuracy of Naive-Bayes classifiers: a decision-tree hybrid. Proceedings of the 2nd international conference on knowledge discovery and data mining,202-7. |
| [23] | Breiman L, Friedman JH, Olshen RA, et al. (1984) Classification and regression trees. California: Wadsworth International Group. |
| [24] | Dazeley R, Yearwood J, Kang B, et al. (2010) Consensus clustering and supervised classification for profiling phishing emails in internet commerce secu+rity. In: Kang BH, Richards D, editors. Knowledge management and acquisition for smart systems and services, PKAW 2010. Daegu: Springer Verlag, 235-46. |
| [25] | Yearwood J, Webb D, Ma L, et al. (2009) Applying clustering and ensemble clustering approaches to phishing profiling. Proceedings of the 8th Australasian data mining conference, AusDM 2009. Curr Res Prac Inf Technol 101: 25-34. |
| [26] | Kang B, Kelarev A, Sale A, et al. (2006) A new model for classifying DNA code inspired by neural networks and FSA. Advances in Knowledge Acquisition and Management, 19th Australian Joint Conference on Artificial Intelligence, AI06. Lect Notes Comp Sci 4303:187-98. |
| [27] | Breiman L (1996) Bagging predictors. Mach Learn 24: 123-40. |
| [28] | Freund Y, Schapire R (1996) Experiments with a new boosting algorithm. Proceedings of 13th International Conference of Machince Learning 148-56. |
| [29] |
Webb G (2000) Multiboosting: A technique for combining boosting and wagging. Mach Learn 40: 159-96. doi: 10.1023/A:1007659514849
|
| [30] |
Wolpert D (1992) Stacked generalization. Neural Networks 5: 241-59. doi: 10.1016/S0893-6080(05)80023-1
|
| [31] | Melville P, Mooney R (2005) Creating diversity in ensembles using artificial data. Inf Fusion6: 99-111. |
| [32] | Ting K, Witten I (1997) Stacking bagged and dagged models. Fourteenth International Conference Machine Learning, 367-75. |
| [33] | Seewald AK, Furnkranz J (2001) An evaluation of grading classifiers. Hoffmann F, Adams N, Fisher D, et al, editors. Advances in intelligent data analysis, IDA 2001. Heidelberg: Springer,115-24. |
| [34] | Kelarev A, Stranieri A, Yearwood J, et al. (2012) Empirical study of decision trees and ensemble classifiers for monitoring of diabetes patients in pervasive healthcare, 15th International Conference on Networked-Based Information System, NBiS-2012. Melbourne: CPS, 441-6. |
| [35] | Huehn J, Huellermeier E (2009) FURIA: An algorithm for unordered fuzzy rule induction. DMKD 19: 293-319. |
| [36] | Kelarev A, Stranieri A, Yearwood J, et al. (2012) Improving classifications for cardiac autonomic neuropathy using multi-level ensemble classifiers and feature selection based on random forest. In: Zhao Y, Li J, Kennedy PJ, et al, editors. Data mining and analytics, 11th Australasian Data Mining Conference, AusDM 2012. Sydney: CRPIT, 134: 93-102. |
| 1. | J. Abawajy, A. V. Kelarev, M. Miller, J. Ryan, Rees semigroups of digraphs for classification of data, 2016, 92, 0037-1912, 121, 10.1007/s00233-014-9685-x | |
| 2. | Andrei V. Kelarev, Willy Susilo, Mirka Miller, Joe Ryan, Ideals of Largest Weight in Constructions Based on Directed Graphs, 2016, 15, 2278-9634, 8, 10.18052/www.scipress.com/BMSA.15.8 | |
| 3. | Karim Ennouri, Abdelaziz Kallel, Remote Sensing: An Advanced Technique for Crop Condition Assessment, 2019, 2019, 1024-123X, 1, 10.1155/2019/9404565 | |
| 4. | Morshed Chowdhury, Jemal Abawajy, Andrei Kelarev, Kouichi Sakurai, 2014, Chapter 3, 978-3-662-45669-9, 25, 10.1007/978-3-662-45670-5_3 | |
| 5. | Morshed U. Chowdhury, Jemal H. Abawajy, Andrei Kelarev, Herbert F. Jelinek, A Clustering-Based Multi-Layer Distributed Ensemble for Neurological Diagnostics in Cloud Services, 2020, 8, 2168-7161, 473, 10.1109/TCC.2016.2567389 | |
| 6. | Jemal Abawajy, Andrei Kelarev, Xun Yi, Herbert F. Jelinek, Minimal ensemble based on subset selection using ECG to diagnose categories of CAN, 2018, 160, 01692607, 85, 10.1016/j.cmpb.2018.01.019 | |
| 7. | Mohanad Alkhodari, Mamunur Rashid, Mohammad Abdul Mukit, Khawza I. Ahmed, Raqibul Mostafa, Sharmin Parveen, Ahsan H. Khandoker, Screening Cardiovascular Autonomic Neuropathy in Diabetic Patients With Microvascular Complications Using Machine Learning: A 24-Hour Heart Rate Variability Study, 2021, 9, 2169-3536, 119171, 10.1109/ACCESS.2021.3107687 | |
| 8. | Mayura Nagar, Pooja Raundale, Ahsan Khandoker, Herbert Jelinek, 2022, A Systematic Literature Review: Role of AI Algorithms for Automated Diagnosis of Diabetic Cardiac Autonomic Neuropathy [DCAN], 978-93-80544-44-1, 669, 10.23919/INDIACom54597.2022.9763159 | |
| 9. | S. Ramya, T. Vijayaraghavan, D. Kalaivani, 2023, Diabetic Prediction using Feature Selection based Random Forest and Fine Tuned K-Nearest Neighbor Classifier Algorithm-A Design Thinking Approach, 979-8-3503-0009-3, 1303, 10.1109/ICESC57686.2023.10193333 |
Figures(4) / Tables(2)
Herbert F. Jelinek, Jemal H. Abawajy, Andrei V. Kelarev, Morshed U. Chowdhury, Andrew Stranieri. Decision trees and multi-level ensemble classifiers for neurological diagnostics[J]. AIMS Medical Science, 2014, 1(1): 1-12. doi: 10.3934/medsci.2014.1.1
| Test | Normal | Borderline | Abnormal |
| 1. Heart rate response to standing (BPM) | ≥ 1.04 | 1.01–1.03 | ≤ 1.00 |
| 2. Blood pressure response to standing (mmHg) | ≤ 10 | 11–29 | ≥ 30 |
| 3. Heart rate response to deep breathing (mmHg) | ≥ 15 | 11–14 | ≤ 10 |
| 4. Valsalva maneuver and heart rate response (BPM) | ≥ 1.21 | 1.11–1.20 | ≤ 1.10 |
| 5. Blood pressure response to sustained handgrip (mmHg) | ≥ 16 | 11–15 | ≤ 10 |
DownLoad: CSV| Category | Decision Paradigm |
| Normal | All tests normal or one borderline |
| Early | One of the three heart rate tests abnormal or two borderline |
| Definite | Two or more of the heart rate tests abnormal |
| Severe | Two or more of the heart rate tests abnormal plus one or both of the blood pressure tests abnormal or both borderline |
| Atypical | Any other combination of tests with abnormal results |
DownLoad: CSV| Test | Normal | Borderline | Abnormal |
| 1. Heart rate response to standing (BPM) | ≥ 1.04 | 1.01–1.03 | ≤ 1.00 |
| 2. Blood pressure response to standing (mmHg) | ≤ 10 | 11–29 | ≥ 30 |
| 3. Heart rate response to deep breathing (mmHg) | ≥ 15 | 11–14 | ≤ 10 |
| 4. Valsalva maneuver and heart rate response (BPM) | ≥ 1.21 | 1.11–1.20 | ≤ 1.10 |
| 5. Blood pressure response to sustained handgrip (mmHg) | ≥ 16 | 11–15 | ≤ 10 |
| Category | Decision Paradigm |
| Normal | All tests normal or one borderline |
| Early | One of the three heart rate tests abnormal or two borderline |
| Definite | Two or more of the heart rate tests abnormal |
| Severe | Two or more of the heart rate tests abnormal plus one or both of the blood pressure tests abnormal or both borderline |
| Atypical | Any other combination of tests with abnormal results |
