Stochastic invariance for hybrid stochastic differential equation with non-Lipschitz coefficients

1.   Introduction

The study of a hyperplane arrangement typically goes along with the study of its characteristic polynomial as the polynomial carries combinatorial and topological information of the arrangement (e.g., ^[10,16,17]). Terao's factorization theorem shows that if an arrangement is free, then its characteristic polynomial factors into the product of linear polynomials over the integer ring. Many attempts have been made in order to compute and to make a broader understanding the characteristic polynomials (e.g., ^{[1,2,6,7,9,12,13,15,23,24]}). It is well-known that the characteristic polynomial of any hyperplane arrangement gets generalized to the Tutte polynomial ^[22]. More recently, the generalizations of the polynomials, the arithmetic Tutte polynomial, the characteristic quasi-polynomial and the chromatic quasi-polynomials were introduced (e.g., ^{[12,14,15,21]}).

The braid arrangement (or type $A$ Coxeter arrangement) is the hyperplane arrangement in $\mathbb{R}^{n}$ defined by

Deformations of the braid arrangement are often studied in the literature, among these deformations are the Linial arrangement, Shi arrangement, Catalan arrangement, semiorder arrangement, generic braid arrangement, and semigeneric braid arrangement, etc, see ^{[3,4,5,8,11,19,20,23]} for a discussion of the combinatorics and freeness of these arrangements. The semigeneric braid arrangement is the hyperplane arrangement in $\mathbb{R}^{n}$ defined by

where $a_i{\rm{'s}}$ are generic. Stanley asked to find the characteristic polynomial of this arrangement. In this paper, we give a formula for the characteristic polynomials of the semigeneric braid arrangement and its subarrangements, which we call the semigeneric graphical arrangements.

The remainder of the paper is organized as follows. In Section 2, we recall definitions and basic facts of arrangements. In Section 3, we prove our main results which provide the characterizations of a central semigeneric graphical arrangement, and induce a formula for the characteristic polynomial of a semigeneric graphical arrangement. In Section 4, we show some applications of our main results.

2.   Preliminaries

We first review some basic concepts and preliminary results on arrangements. Our standard reference is ^[17,18]. Let $\mathbb{K}$ be a field, $n$ be a positive integer and $V = \mathbb{K}^{n}$ be the $n$-dimensional vector space over $\mathbb{K}$. A hyperplane in $V$ is a affine subspace of codimension one of $V$. An arrangement $\mathcal{A}$ is a finite set of hyperplanes in $V$. An intersection lattice $L(\mathcal{A})$ of $\mathcal{A}$ is defined by

with an order by reverse inclusion $X \leq Y \Leftrightarrow Y \subseteq X$ for $X, Y \in L(\mathcal{A})$. The characteristic polynomial $\chi_{\mathcal{A}}(t) \in \mathbb{Z}[t]$ of $\mathcal{A}$ is defined by

where $\mu$ denotes the Möbius function $\mu: L(\mathcal{A}) \rightarrow \mathbb{Z}$ defined recursively by

Let $G$ be a simple graph with vertex set $V(G) = [n] = \{1, \ldots, n\}$ and edge set $E(G)$. The graphical arrangement $\mathcal{A}_{G}$ in $\mathbb{K}^{n}$ is defined by

A simple graph is chordal if it does not contain an induced cycle of length greater than three, or $C_{n}$-free for all $n > 3$ in shorthand notation. The freeness of graphical arrangements is completely characterized by chordality. If $G = K_n$, the complete graph on $[n]$, then $\mathcal{A}_G = \mathcal{A}_{n-1}$.

A natural deformation of the graphical arrangement turns up if we use generic elements $a_i{\rm{'s}}$ to replace $0{\rm{'s}}$ in the equations of hyperplanes. Stanley explained the meaning of generic elements in ^[18] as follows.

Let $\mathcal{A}$ be an arrangement in an $n$-dimensional vector space $V$ and $L_1(x), \ldots, L_m(x)$ be linear forms, not necessarily distinct, in the variables $x = (x_1, \ldots, x_n)$ over the field $\mathbb{K}$. Let $\mathcal{A}$ be defined by $L_1(x) = a_1, \ldots, L_m(x) = a_m$, where $a_1, \ldots, a_m$ are generic elements of $\mathbb{K}$. This means if $H_i = \ker(L_i(x)- a_i)$, then

Definition 2.1. Let $G$ be a simple graph with vertex set $V(G) = [n]$ and edge set $E(G)$. The semigeneric graphical arrangement in $\mathbb{R}^n$ is defined by

where $a_i{\rm{'s}}$ are generic. $\mathcal{S}_G$ is simply a subarrangement of the semigeneric braid arrangement $\mathcal{S}_n$. In particular, if $G = K_n$, then $\mathcal{S}_G = \mathcal{S}_n$.

According to the definitions of generic elements and $\mathcal{S}_G$, the genericity of $a_i{\rm{'s}}$ can be sure when they take any numbers in $\mathbb{R}$. We do not emphasize that $a_i{\rm{'s}}$ are generic in later section.

Clearer comprehending can be achieved by a simple example.

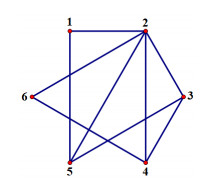
Example 2.2. Figure 1 shows a simple graph $G$, a subgraph of $K_6$, the semigeneric graphical arrangement $\mathcal{S}_G$ consists of the following hyperplanes:

3.   Main results

There are a few powerful methods for computing the characteristic polynomials of hyperplane arrangements. In ^[7], Athanasiadis showed that simply by computing the number of points missing the hyperplanes (over finite fields) and by using the Möbius formula, the characteristic polynomials of many hyperplane arrangements can be computed. Our method is closer in spirit to ^[18] in which Stanley gives an interpretation of linearly independent subarrangement $\mathcal{B}$ of the generic braid arrangement in terms of the graph $G_{\mathcal{B}}$. We will provide a necessary and sufficient condition for a central semigeneric graphical arrangement $\mathcal{S}_G$ from the point of graph $G$ (i.e., Theorem 3.4).

Lemma 3.1. The semigeneric graphical arrangement $\mathcal{S}_G$ is central (i.e. $\cap_{H\in\mathcal{S}_G} H\neq\emptyset$) if the graph $G$ is an acyclic graph.

Proof. $\mathcal{S}_G$ is central if the intersection of all the hyperplanes contains at least one point $(x_1, \ldots, x_n)$. We can find such an assignment $(x_1, \ldots, x_n)$ satisfying $x_i - x_j = a_i(ij\in E(G))$. That can be done by just picking one from $x_i{\rm{'s}}$ at a time since the graph $G$ is acyclic and $a_i$'s are generic.

Owing to Lemma 3.1, we consider the centrality of $\mathcal{S}_G$ where $G$ is a cycle.

Lemma 3.2. If the arrangement $\mathcal{S} : = \left\{x_{i_j}-x_{i_{j+1}} = b_j: 1\leq i_j\leq n, j = 1, \ldots, k, i_{k+1} = i_1\right\}$, then $\mathcal{S}$ is central if and only if $\sum_{j = 1}^{k} b_j = 0$.

Proof. The arrangment $\mathcal S$ is central means there exists at least one point on all the hyperplanes, that is, at least a solution to the system of the equations of all the hyperplanes in $\mathcal S$. That means $\mathrm{rank} (M(\mathcal S)) = \mathrm{rank}((\overline{ M}(\mathcal S))$, where $M(\mathcal S)$ and $\overline{ M}(\mathcal S)$ are the coefficient matrix and augmented matrix of the system of the equations, respectively.

Perform the following series of elementary row operations on $M(\mathcal S)$ and $\overline{ M}(\mathcal S)$, we have

and

where $B$ is a $(k-1)\times k$ matrix, $\beta^T = (b_1, \ldots, b_{k-1})$, vector ${\bf{0}} = (0, \ldots, 0) \in \mathbb{R}^k$, and $P(i, j(m))$ denotes the elementary matrix by adding $m$ multiple of $j$-th row of the identity matrix to $i$-th row of the identity matrix. Distinctly, $\sum_{j = 1}^{k}b_j = 0$ if and only if $\mathrm{rank}(\overline{ M}(\mathcal S)) = \mathrm{rank}(B) = \mathrm{rank}(M(\mathcal S))$, that is, the arrangement $\mathcal{S}$ is central.

Applying Lemma 3.2 to a semigeneric graphical arrangement, we get the following theorem.

Theorem 3.3. Let $G$ be a $k$-cycle with $V(G) = \{i_1, \ldots, i_{k}\}\subseteq\{1, \ldots, n\}$, the semigeneric graphical arrangement $\mathcal{S}_G$ consists of the following hyperplanes:

The arrangement $\mathcal{S}_G$ is central if and only if $\sum_{j = 1}^{k} (-1)^{\delta_j}a_{i_{j+\delta_j}} = 0$, where $\delta_j = \begin{cases} 0, & {{if}} i_j < i_{j+1} \\ 1, & {{if}} i_j > i_{j+1} \end{cases}$.

In the theorem below, we will characterize the central semigeneric graphical arrangement $\mathcal{S}_G$ in terms of $G$.

Theorem 3.4. The semigeneric graphical arrangement $\mathcal{S}_G$ is central if and only if graph $G$ satisfies one of the following two conditions:

(1) $G$ is an acyclic graph;

(2) the semigeneric graphical arrangements of all cycles in $G$ are central.

Proof. Suppose $C_1, \ldots, C_p$ are $p$ connected components of $G$ which are not the isolated vertices. If all the subarrangements corresponding to $C_1, \ldots, C_p$ are central, then $\mathcal{S}_G$ is central. Therefore, it suffices to prove $\mathcal{S}_C$ is central, where $C$ is a connected component of $G$ containing cycles.

Assume $|E(C)| = t$ and $\mathcal{S}_C: = \left\{\ker(\alpha_i\cdot x- a_i)|1\leq i\leq t\right\}$. Let $T$ be a spanning tree of $C$ which is a tree that contains every vertex of $C$, then $\overline{T} = C-E(T)$ is the cotree of $T$ in $C$. Assume $|V(C)| = s$, then $|V(T)| = s$. Since a connected graph with $s$ vertices is a tree if and only if it has $s-1$ edges, let the normal vectors of the hyperplanes of $\mathcal{S}_T$ be $\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}$. Firstly, we will prove the vectors $\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}$ form a basis of $\mathrm{span}(\alpha_{1}, \ldots, \alpha_{t})$, a space spanned by $\alpha_{1}, \ldots, \alpha_{t}$. By Lemma 3.1, the vectors $\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}$ are linearly independent, i.e., $\mathrm{rank}(\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}) = s-1$. Moreover, by the definition of spanning tree, we know that $T+e$ will generate a cycle $D$ satisfying $e\in E(D)$ for all $e\in E(\overline{T})$. Assume $|E(D)| = k$ and $\alpha_{v_1}, \ldots, \alpha_{v_{k-1}}$ are the normal vectors of hyperplanes of $\mathcal{S}_{D-e}$, it follows that

and the normal vector of hyperplane corresponding to $e$ is $\alpha_{v_k}\in\left\{\alpha_1, \ldots, \alpha_t\right\}-\left\{\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}\right\}$. Since $D$ is a cycle, $\alpha_{v_k}$ is a linear combination of $\alpha_{v_1}, \ldots, \alpha_{v_{k-1}}$, i.e.,

Since $\alpha_{v_k}$ is the normal vector of hyperplane for any $e\in E(\overline{T})$, hence $\alpha_{1}, \ldots, \alpha_{t}\in \mathrm{span}(\alpha_{u_1}, \ldots, \alpha_{u_{s-1}})$, and the vectors $\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}$ form a basis of $\mathrm{span}(\alpha_{1}, \ldots, \alpha_{t})$.

Let $M(\mathcal{S}_C)$ and $\overline{M}(\mathcal{S}_C)$ be the coefficient matrix and the augmented matrix of the linear system of the hyperplane equations of $\mathcal{S}_C$, respectively, that is,

Since $\alpha_{u_1}, \ldots, \alpha_{u_{s-1}}$ form a basis of $\mathrm{span}(\alpha_{1}, \ldots, \alpha_{t})$ and the semigeneric graphical arrangements of all cycles in $G$ are central, according to Lemma 3.2, $\overline{M}(\mathcal{S}_C)$ can be changed as follows by performing the same series of elementary row operations :

So $\mathrm{rank}({M}(\mathcal{S}_C)) = \mathrm{rank}(\overline{M}(\mathcal{S}_C)) = s-1$, i.e., $\mathcal{S}_C$ is central.

We complete the proof.

For the characteristic polynomial of an arrangement $\mathcal{A}$ in $n$-dimensional vector space, we adopt Whitney's theorem ^[18] which gives a basic formula,

Combining Whitney's theorem and Theorem 3.4, we will give a formula for the characteristic polynomial of the semigeneric graphical arrangement $\mathcal{S}_G$.

Corollary 3.5. Let $G$ be a simple graph with $V(G) = [n]$, then the characteristic polynomial of $\mathcal{S}_G$ is

where $D$ ranges over all spanning subgraphs of $G$, and $D$ is an acyclic graph or semigeneric graphical arrangements of all cycles in $D$ are central. $|E(D)|$ denotes the number of the edges, and $p(D)$ denotes the number of the connected components of $D$.

Proof. Assume $D$ is the spanning subgraph of $G$ corresponding to the subarrangement $\mathcal{B}$ of $\mathcal{S}_G$. It is clear that $\#\mathcal{B} = |E(D)|$. The rank of $\mathcal{B}$ is the number of the edges of a spanning forest of $D$. Since a connected graph with $n$ vertices is a tree if and only if it has $n-1$ edges, the number of the edges of a spanning forest of a graph $D$ is the number of vertices minus the number of connected components, that is $\mathrm{rank}(\mathcal{B}) = n-p(D)$.

4.   Applications

In this section, we will give some applications of Theorem 3.4 and Corollary 3.5.

Example 4.1. The defining polynomial of $\mathcal{S}_{4}$ (i.e., 4-dimensional semigeneric braid arrangement) is

where $a_1, a_2, a_3$ are generic elements. Table 1 illustrates all types of characteristic polynomials for $\mathcal{S}_{4}$, which depend on the values of $a_2, a_3, a_2+a_3, a_2-a_3$. The symbol "T" in Table 1 indicates that the condition is met, and "F" indicates that the condition is not met.

Example 4.2. For the semigeneric graphical arrangement $\mathcal{S}_G$ of Example 2.2, we take $a_1 = 1, a_2 = 3, a_3 = 0, a_4 = 2$. Compute the characteristic polynomial $\chi_{\mathcal{S}_G}(t)$.

According to Theorem 3.4, we need to figure out the central subarrangements of cycles in $G$, which depend on the values of the generic elements $a_{i}{\rm{'s}}$. In Figure 2, it is not difficult to see the semigeneric graphical arrangements corresponding to cycles (a)–(c) are central, the others are non-central.

Obviously, a subarrangement of $\mathcal{S}_G$ is central if and only if the corresponding subgraph $D$ is an acyclic graph or only contains cycles (a), (b) or (c) in Figure 2. The isomorphism types of spanning subgraph $D$ (with the number of distinct labelings written below $D$) are given by Figure 3.

For all the subgraphs $D$ in Figure 3, we will list the number of connected components $p(D)$, the number of edges $|E(D)|$, and the number of distinct labelings of $D$ in Table 2.

Hence, from Corollary 3.5, we get

5.   Conclusions

In this paper, we study the characteristic polynomial of the semigeneric graphical arrangement $\mathcal{S}_{G}$, which is a deformation of the graphical arrangement. The formula of the characteristic polynomial is obtained by characterizing central subarrangements of $\mathcal{S}_{G}$ via the corresponding graph ${G}$. The semigeneric graphical arrangement $\mathcal{S}_{G}$ is a subarrangement of the semigeneric braid arrangement (or type $A$ semigeneric arrangement). It would be interesting to develop a new method for computing the characteristic polynomials of others types (e.g., type $B$ and type $D$) of semigeneric arrangements in the future.

Acknowledgments

The work was partially supported by Science and Technology Research Project of Jilin Province (No. JJKH20220719KJ) and NSF of China (No. 11501051).

Conflict of interest

The authors declare no conflict of interest in this paper.