The zero-energy limit and quasi-neutral limit of scaled Euler-Maxwell system and its corresponding limiting models

1.   Introduction

Atoms decompose into anions and cations when their thermal energy is higher than ionization energy. The state in which the ionized gaseous substance becomes highly electrically conductive, such that particles interact with each other dramatically by their self-consistence electromagnetic field, is called plasma ^[1,17]. In order to understand the dynamics of plasma on macroscopic scale, Maxwell laws of magnetism are coupled with the Euler system of fluid flows, which is the so-called Euler-Maxwell system.

In this paper, we consider a unipolar compressible Euler-Maxwell system for electrons, see ^[5],

with the initial data

Here the unknown variables $(n, u, E, B)(t, x)$ are number density, velocity vector field, electric and magnetic fields of electrons respectively, $x = (x_1, x_2, x_3)\in \mathbb{T}^{3}$ is three-dimensional position vector in torus and $t > 0$ denotes the regular time. The parameters $m_e$ and $e$ are the mass and charge of the electron, whereas $j, \kappa$ are the current density and specific resistivity respectively. The physical constants parameters $\mathbb{\varepsilon}_{0}, \mu_{0}$ and $c$ are permittivity, permeability of free space and the speed of light respectively, which are connected by the relation

In the paper, we assume that the fluid is isothermal, so that the pressure function $p(n)$ are of the form

where $k > 0$ is Boltzmann constant, and $T > 0$ is the constant temperature.

Under usual scaling, Euler-Maxwell system is usually of the form (for simplicity, we still denote as $(n, u, E, B)$,

in which $\lambda$ is the scaled debye length, $\beta$ is the reciprocal of the relaxation time and $\nu$ is the reciprocal of the speed of light. The meaning of the unknown variables $(n, u, E, B)$ are the same as those in (1.1).

The asymptotic analysis of the (1.3) for smooth solutions is a well-known problem. The local-in-time convergence is studied in ^[19,20]. The non-relativistic limit $\nu\rightarrow 0$ and the quasi-neutral limit $\lambda\rightarrow 0$ are justified in ^[13] and ^[14], and the limit systems are compressible Euler-Poisson system and the e-MHD system, respectively. The combined non-relativistic quasi-neutral limit $\mathbb{\varepsilon}\rightarrow 0$ with a special relation $\nu = \lambda^2$ is justified in ^[15]. The resulting limit system is the incompressible Euler equations. The zero-relaxation limit $\beta\rightarrow \infty$ is studied in ^[6,16,21] and the limit system is the drift-diffusion equations. The results in the above papers are valid on uniform time intervals independent of the parameters. We refer to ^[3,18] for more information. In the paper, we introduce the following scaling,

whereas $x_{c}, t_{c}, j_{c}, n_{c}, u_{c}, E_{c}, B_{c}$ are the characteristic scale units for space, time, current density, number density, velocity, electric field and magnetic field respectively. These characteristic scaling units can be expressed by the following relations:

$x_{c} = u_{c}t_{c}$ : The system of charged particles is observed at characteristic time scale.

$u_{c} = \sqrt{\frac{kT}{m_e}}$ : Characteristic velocity is expressed as electron thermal speed.

$E_{c} = u_{c} B_{c}$ : The electric field is induced due to the motion of plasma in magnetic field.

By using the above scaling units dimensionless system with new variables is given as,

in which the five dimensionless parameters are defined as follows

Here $\alpha^{2}$ is the ratio electric energy to thermal energy, $\gamma$ is the ratio of characteristics velocity of plasma to the speed of light, $\lambda$ is the scaled Debye length, $\beta$ is the relaxation electron frequency and $\eta$ is the ratio charge density of electrons moving with velocity $u_{c}$ to current density. Replacing $\alpha^{2}\hat{E} = \dot{E}$ and keeping $\frac{\gamma^{2}}{\lambda^{2}\alpha^{2}\eta} = 1$, we get the system (keeping the new variables with same physical variables) as follows,

with the initial data

In order to simplify the later proof, we introduce the enthalpy function

the constant $R = kT,$ then the momentum conservation equation of (1.4) is equivalent to

Now we want to tell the main difference of our scaled system (1.4)–(1.5) from (1.3). Firstly, the singular parameters have different physical interpretations. Secondly, the main observation is that the limiting regimes for singular parameters satisfy curl divergence equation for magnetic field which shows consistency with conservation of mass for all profiles of asymptotic expansion. In particular, magnetic curl is a measure of current density and thus cannot be ignore in moving plasma. But curl of $B$ can possibly be very small for $\eta < < 1$. The limiting regimes of system (1.3) can be obtained by choosing $\eta < < 1$ along with other small parameters from (1.4)–(1.5). Starting at (1.4)–(1.5), the main objective of this paper is to derive formally the limiting models concerning the following two kinds of singular limits and their combined limit. We state their physical understanding here.

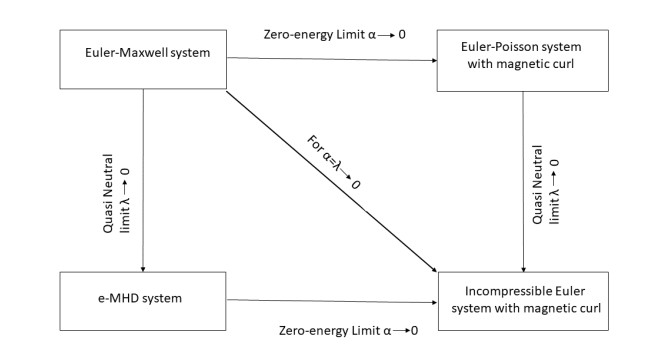
(1) The zero-energy limit $\alpha^2\rightarrow 0$. By defining dimensionless number $\alpha$ for energies we may assume that for thermal energy higher than electric energy, the pressure gradient and electric force dominates over magnetic forces and rate change of magnetic field remains uniform. In particular we approximate Euler-Maxwell system and e-MHD by limiting regimes for $\alpha \rightarrow 0$ as shown in figure below.

(2) The quasi-neutral limit $\lambda\rightarrow 0$. The Debye length $\lambda$ is the measure of a charge carrier's net electrostatic effect in solution, and how far those electrostatic effects persist. One of the significant properties of plasma is bulk interaction, namely the Debye length is small compared to the physical size of the plasma ^[4,5]. So usually in plasma physics, we study the limit $\lambda\rightarrow 0$. Since zero Debye length means quasi-neutrality, the limit is also called quasi-neutral limit.

The paper is organized as follows. In the next section, we state some preliminaries. Section 3 is devoted to the formal derivation of limiting models starting at (1.4). In detail, the quasi-neutral limit $\lambda\rightarrow 0$ of (1.4) is the following e-MHD (See Subsection 3.1)

and the zero-energy limit of the above e-MHD is the following incompressible Euler equation with magnetic curl (See Subsection 3.2 and the rigorous proof in Section 4)

The curl of a magnetic field at any point is equal to the current density at that point. This is the simplest statement relating the magnetic field and moving charges. The divergence of curl of magnetic implies conservation of current density

The curl of curl of magnetic field implies

The above equation is elliptic equation. It is important to see that magnetic field in limiting regimes is identified by the distribution of velocity of electrons flow in the domain of plasma confinement. Also, one can see that for $\eta \rightarrow 0$ in curl divergence equation, $B$ can be zero, constant or time varying. For existence and uniqueness of curl divergence equation see Lemma 2.2. Going the other path, the zero-energy limit of (1.4) is the following Euler-Poisson system with magnetic curl (See Subsection 3.4)

and the quasi-neutral limit of the above system is the incompressible Euler equation with magnetic curl, which is the same as first taking the quasi-neutral limit and then the zero-energy limit (See subsection 3.5).The combined zero-energy, quasi-neutral of Euler-Maxwell system, limiting model is also the incompressible Euler equation with magnetic curl (See Subsection 3.3). We summarize the limiting models by Figure 1 as follows.

2.   Notations and preliminaries

In the following, we denote by $C$ a generic positive constant independent of any small parameters. For a multi-index $l = (l_1, l_2, l_3)\in \mathbb{N}^3$, we introduce the operator

We denote by $\|\cdot\|_s$, $\|\cdot\|$ and $\|\cdot\|_\infty$ the norm of the usual Sobolev spaces $H^s\left(\mathbb{R}^d\right)$, $L^2\left(\mathbb{R}^d\right)$ and $L^\infty\left(\mathbb{R}^d\right)$, respectively. The inner product in $L^2\left(\mathbb{R}^d\right)$ is denoted by $(\cdot, \, \cdot).$

Lemma 2.1. (Moser-type calculus inequalities, see ^[9,11]). Let $s \geq 1$ be an integer. Suppose $u\in H^s\left(\mathbb{R}^d\right), \, \nabla u\in L^\infty\left(\mathbb{R}^d\right)$ and $v\in H^{s-1}\left(\mathbb{R}^d\right)\cap L^\infty\left(\mathbb{R}^d\right)$. Then for all $\alpha\in\mathbb{N}^d$ with $1\leq|\alpha|\leq s$ and all smooth function $f$, we have $\partial^\alpha_x(uv)-u\partial^\alpha_xv\in L^2\left(\mathbb{R}^d\right)$, $\partial^\alpha_xf(u)\in L^2\left(\mathbb{R}^d\right)$ and

where the constant $C_\infty > 0$ depends on $\| u\|_{\infty}$ and $s$, and $C_s > 0$ depends only on $s$. Moreover, if $s > \frac{d}{2}+1$, then the embedding $u\in H^s\left(\mathbb{R}^d\right)\hookrightarrow W^{1, \infty}\left(\mathbb{R}^d\right)$ is continuous and we have

The result about linear curl-div equations from ^[13] is as follows.

Lemma 2.2. Let $s \geq 0$ be an integer, $(g, h)$ $\in H^{s}(\mathbb{T}^{3})$ with $\operatorname{div} g(x, t) = 0$ and $\boldsymbol{m}(h): = \int_{ \mathbb{T}^3}hdx = 0$. Then the linear problem

has a unique solution $A(x, t) \in H^{s + 1}(\mathbb{T}^{3})$, in the class $\boldsymbol{m}(A) = 0$. Furthermore, we have

The next result concerns the local existence of smooth solutions which can be easily obtained by employing the theory of Kato ^[8] for the symmetrizable hyperbolic system.

Proposition 2.1. Let $s \geq 3$ be an integer and $\left(n_{0}, \, u_{0}, \, E_0, \, B_0\right)\in H^s\left(\mathbb{T}^3 \right)$ with $n_{0}\geq 2\underline{n}$ for some given constant $\underline{n} > 0$, independent of any small parameters. Then there exists $T_1 > 0$ such that the Cauchy problem (1.4) has a unique smooth solution $\left(n, \, u, \, E, \, B\right)$ defined in time interval $[0, T_1]$, satisfying $n \geq \underline{n}$ and

For the local existence of (1.6) is similar to the incompressible Euler equations, thus we have ^[10]

Proposition 2.2. Assume $(\bar{u}_{0}, \bar{B}_{0})\in C^{\infty}(\mathbb{T}^{3})$ is sufficient smooth initial data satisfy the compatibility condition

then there exists $0\leq T_*\leq \infty$, the maximum existence time and a unique smooth solution, $(u^{0}, E^{0}, B^{0})\in C^{\infty}([0, T_*]\times\mathbb{T}^{3})$ of (1.6).

3.   The formal derivations of limiting models

3.1.   The quasi-neutral limit of Euler-Maxwell system

We consider the quasi-neutral limit by letting $\lambda\rightarrow 0$ in (1.4), while letting all the other small parameters be $O(1)$. By Proposition 2.1, let $(n^\lambda, u^\lambda, E^\lambda, B^\lambda)$ be the unique local smooth solution to (1.4)–(1.5) satisfying

with the initial data,

Formally, the leading profile when $\lambda\rightarrow 0$ is the following e-MHD,

with the initial data

Following the idea of ^[2], we introduce the general vorticity

then (3.3) becomes

where the electric field $E^{0}$ and magnetic field $B^{0}$ are represented explicitly as

By Proposition 2.2, the local existence of classical smooth solution is obtained. The rigorous proof of the quasi-neutral limit from (3.1) to (3.3) is based on the weighted energy method, which is similar to that in ^[14]. That is to say, we denote

which satisfies the following problem

Then the classical energy method is applied. The details of the proof are similar to those in ^[14], but with higher convergence rate (See Theorem 2.1 in ^[14]).

Remark 3.1. The e-MHD can also be derived for dielectric constant limit $\mathbb{\varepsilon} \rightarrow 0$ with fixed non relativistic parameter $\gamma$ from Vlasov-Maxwell system ^[2]. In our case the Debye length tend to zero when speed of light $c\rightarrow \infty$, and can also be varied by choosing suitable characteristic velocity $u_{c}$.

3.2.   The zero-energy limit of e-MHD

We consider the zero-energy limit of e-MHD. We let $\alpha\rightarrow 0$ while letting other parameters be $O(1)$, which yields

with initial data

Similarly, the local existence of the above system is due to Proposition 2.1. By setting $\alpha = 0$, we formally get the limiting system

with initial data

We will rigorously prove the limit from (3.5) to (3.7) in Section 4.

3.3.   The combined zero-energy and quasi-neutral limit of Euler-Maxwell system

In this subsection, we study the combined limit $\lambda = \alpha\rightarrow 0$ while letting other parameters be $O(1)$. This yields

and the initial data

By Proposition 2.1, let $(n^{\lambda}, u^{\lambda}, E^{\lambda}, B^{\lambda})$ be the local smooth solution of (3.9)–(3.10) for $\lambda > 0$. We now wish to look for an approximation of solution under the form of a power series with respect to $\lambda$. We assume the initial data $(n_{0}^{\lambda}, u_{0}^{\lambda}, E_{0}^{\lambda}, B_{0}^{\lambda})$ admit the following asymptotic expansion in $\lambda$:

where $\left(\bar{n}^j, \bar{u}^j, \bar{E}^j, \bar{B}^j\right)_{j\geq 0}$ are sufficiently smooth. Then we make the following ansatz:

By substitution of expansion (3.11) in (3.9), we obtain

(1) The leading profile satisfy the following system incompressible Euler equations with magnetic curl

with initial data

Since $\nabla\times E = 0$, there exists a potential function $\phi^0$ such that $E^0 = -\nabla\phi^0$. The proof of the existence for (3.12)–(3.13) is similar to that of an incompressible Euler system in ^[10]. Namely there is a unique local smooth solution $(u^0, E^0, B^0)$ satisfying the following compatibility condition

(2) For $j\geq 1$, the profiles $(n^j, u^j, E^j, B^j)$ are obtained by induction. We assume that $(n^k, u^k, E^k, B^k)_{0\leq k\leq j-1}$ are smooth and already determined in previous steps. Then $(n^j, u^j, E^j, B^j)$ satisfy the linear system

with initial data

The enthalpy function $h^{0} = 0$ and $h^{j-1}$ depend only on $(n^{k})_{0\leq k \leq j-1}$ and are given as

Since $\mathrm{div} B^{j} = 0$, there exists a vector function $\psi^{j}$ such that $B^{j} = -\nabla \times \psi^{j}$. The equation $\nabla\times E^j = - \partial_t B^{j-1}$ in (3.15) becomes $\nabla\times(E^{j} - \partial_{t}\psi^{j-1}) = 0$. It follows that there exists a potential function $\phi^{j}$ such that $E^{j}$ is obtained as

The last two equations of (3.15) imply that $B^{j}$ satisfies linear curl-div system. Then, due to Lemma 2.2 and Proposition 2.2, (3.15) is solved if the following compatibility conditions are satisfied.

Here we summarize the above analysis as follows.

Proposition 3.1. Assume $(\bar{n}^j, \bar{u}^j, \bar{E}^j, \bar{B}^j)_{j\geq 0}\in C^{\infty}(\mathbb{T}^{3})$ be the smooth initial data satisfying the compatibility conditions (3.14) and (3.17), $\bar{n}^0 > \underline{n}$ for some $\underline{n} > 0$. Then there exists a time $T_* > 0$, such that the problem (3.12)–(3.13) and (3.15)–(3.16) have a unique smooth solutions $(n^{j}, u^{j}, E^{j}, B^{j})_{j \geq 0}$ defined on $[0, T_*]\times \mathbb{T}^{3}$. In particular, the formal limiting system of combined zero-energy quasi-neutral limit $\lambda = \alpha \rightarrow 0$ in (3.9) is the incompressible Euler system with magnetic curl (3.12)–(3.13).

3.4.   The zero-energy limit of Euler-Maxwell system

We now treat the zero-electric-energy limit $\alpha\rightarrow 0$ in (1.4) while letting all the other parameters be $O(1)$. This yields

and the initial data

By Proposition 2.1, let $(n^{\alpha}, u^{\alpha}, E^{\alpha}, B^{\alpha})$ be the unique local smooth solution of (3.18) for $\alpha > 0$. We wish to look for an approximate solution under the form of a power series. We assume that the initial data admit the following asymptotic expansion with respect to $\alpha$.

where $\left(\bar{n}^j, \bar{u}^j, \bar{E}^j, \bar{B}^j\right)_{j\geq 0}$ are sufficiently smooth. Then we make the following ansatz:

By substitution of expansion (3.20) in (3.18), we obtain

(1) The leading profile satisfies the following

with initial data

Since $E^0$ is irrotational, there exists a potential function $\phi^0$, such that $E^{0} = -\nabla \phi^{0}$. Then the above system becomes the following Euler-Poisson system

with the initial data

Due to ^[7], (3.21) is solvable at least locally. The electric and magnetic fields are obtained from the following equations,

in which the following compatibility conditions should be satisfied.

(2) For $j\geq 1$, the profiles $(n^{j}, u^{j}, E^{j}, B^{j})$ are determined by induction. Assume that solution $(n^{k}, u^{k}, B^{k}, E^{k})$ for $0 \leq k \leq j - 1$ are smooth and already determined in previous steps. Then the solution $(n^{j}, u^{j}, B^{j}, E^{j})$ satisfy the following linear system

together with initial data

The enthalpy function $h^{0} = 0$ and $h^{j-1}$ depend only on $(n^{k})_{0\leq k \leq j-1}$ and are given as

As we have done to (3.15), electric and magnetic field can be given as follows, namely there exist $\phi^j$ and $\psi^j$, satisfying

then (3.24)–(3.25) can be solved if the following compatibility conditions are satisfied.

We summarize the above analysis as follows

Proposition 3.2. Assume $(\bar{n}^j, \bar{u}^j, \bar{E}^j, \bar{B}^j)_{j\geq 0}\in C^{\infty}(\mathbb{T}^{3})$ be the smooth initial data satisfying the compatibility conditions (3.23) and (3.26), $\bar{n}^0 > \underline{n}$ for some $\underline{n} > 0$. Then there exists a time $T_* > 0$, such that the problem (3.21)–(3.22) and (3.24)–(3.25) have a unique smooth solutions $(n^{j}, u^{j}, E^{j}, B^{j})_{j \geq 0}$ defined on $[0, T_*]\times \mathbb{T}^{3}$. In particular the limiting system when $\alpha \rightarrow 0$ in (3.18) is the Euler Poisson system with magnetic curl (3.21).

3.5.   The quasi-neutral limit of Euler-Poisson system

We now treat the quasi-neutral limit $\lambda\rightarrow 0$ of Euler-Poisson system with magnetic curl, while letting all the other parameters be $O(1)$. This yields

with the initial data

Setting $\lambda = 0$ in (3.27), we have the following incompressible Euler equation with magnetic curl

with the initial data

The local existence of (3.27)–(3.28) and (3.29)–(3.30) is due to ^[7] and Proposition 2.2. The asymptotic expansion is similar to that in ^[12] except for a linear div-curl equation with respect to the magnetic field $B$, which one can use the same procedure to get through previous subsections.

4.   Rigorous justification of incompressible Euler system with magnetic curl as a limit of e-MHD

This section is devoted for rigorous derivation of incompressible Euler system with magnetic curl as a limit of e-MHD system (1.6). The singular parameter $\alpha \rightarrow 0$ in e-MHD when thermal energy is much greater than electric energy. The justification is based on the asymptotic analysis and $\alpha$-weighted magnetic energy. By using asymptotic expansion of solution, we get system of equations for different order of singular parameter $\alpha$. It is remarked that higher order asymptotic expansion are crucial for energy bound otherwise by zero order profile of asymptotic expansion, we obtain the boundedness of norm $\|(B^{\alpha}-B^{0})\|_{H^{s}}$ only as $\alpha \rightarrow 0$.

4.1.   Formal expansion

The local existence of (1.6) is due to Lemma 2.2, the introduction of the general vorticity and Proposition 2.2. To this end, we want to look for an approximate solution $(u^\alpha, B^\alpha)$ to (1.6). Assume the initial data admit an asymptotic expansion with respect to $\alpha$,

where $(\bar{u}^j, \bar{E}^j, \bar{B}^j)_{j\geq 0}$ are sufficiently smooth, and the following ansatz:

Substituting the above into (1.6), we obtain

(1) The leading profile $(u^0, B^0, E^0)$ satisfy the following incompressible Euler equation with magnetic curl

with initial data

in which $\bar{B}^0$ satisfies

Since $\nabla \times E^{0} = 0$, there exists a potential function such that $E^{0} = -\nabla \phi^{0}$. Then the local existence of (4.2) is obtained due to Proposition 2.2.

(2) For $j \geq 1$, the profiles $(u^{j}, B^{j}, E^{j})$ are obtained by induction. Assume that $(u^k, B^k, E^k)_{0\leq k\leq j-1}$ are smooth and already determined in previous steps. Then $(u^j, B^j, E^j)$ satisfy the following linear system

with the initial data

Since $B^j$ is divergence-free, then there exists a vector potential function such that $B^{j} = -\nabla \times \psi^{j}$. By the third equation in (4.5), we have

This implies there exists a potential function $\phi^{j}$ such that $E^{j}$ is given as,

where $(E^j, B^j)$ satisfy the following compatibility conditions,

Proposition 4.1. Assume that the initial data $(\bar{u}^j, \bar{B}^j, \bar{E}^j)$ are sufficiently smooth, then there exist the unique smooth profiles $(u^j, B^j, E^j)_{j\geq 0}$ to the problem (4.2)–(4.3) and (4.5)–(4.6) in the time interval $[0, T_*]$. In other words, there exists a unique asymptotic expansion up to any order of the form (4.1).

4.2.   Error estimates and main result

Let $m\in \mathbb{N}$ be a fixed integer and $(u^\alpha, B^\alpha, E^\alpha)$ be the exact solution to (1.6) defined on $[0, T_1^\alpha]$. We set

where $(u^j, B^j, E^j)_{0\leq j\leq m}$ are constructed through the previous steps. When $\alpha\rightarrow 0$, we wish to establish the limit

The remainders $(R_u^\alpha, R_B^\alpha)$ are defined as follows.

It is clear that the convergence rate depends strongly on the order of the remainders with respect to $\alpha$. Since the profiles $(u^j, B^j, E^j)$ are sufficiently smooth, a straightforward computation gives

whereas $\bar{R_{B}^{\alpha}} = \alpha^{2}R_{B}^{\alpha}$.

Our main result is stated as

Theorem 4.1. Let $s\geq 3$ and $m\in \mathbb{N}$ be integers. Assume

where $C_1$ is a constant independent of $\alpha$. Then there exists a constant $C_2 > 0$, which depends on $T_1^\alpha$ but not on $\alpha$, such that as $\alpha\rightarrow 0$ we have $T_1^\alpha\geq T_*$ and the solution $(u^\alpha, E^\alpha, B^\alpha)$ to the periodic problem (1.6) satisfies

4.3.   Rigorous justification of limit

Let

then the exact solution $(u^{\alpha}, E^{\alpha}, B^{\alpha})$ and the approximate solution $(u_{m}^{\alpha}, E_{m}^{\alpha}, B_{m}^{\alpha})$ are both defined in time interval $[0, T_2^\alpha]$. In the interval, we denote

which satisfy

with the initial data

Furthermore, $U^{\alpha}$ and $G^{\alpha}$ satisfy the following relation

From now on for simplicity, we denote

Lemma 4.1. ($L^2$-estimate) For all $0 < T\leq T_2^\alpha$, it holds

Proof. Taking the inner product of the first equation in (4.11) with $U^{\alpha}$, and using integration by parts, we get

We will treat the four terms on the right hand side term by term. First by using vector identity we get,

and the rest three terms have the following estimates

Combining the above two estimates and using (4.14), one obtains

Similarly, taking the inner product of the second equation in (4.11) with $G^{\alpha}$, using Cauchy-Schwarz inequality, we have

Adding the above two inequalities, and integrating over $[0, T]$ yield (4.13).

Lemma 4.2. (Higher order estimates) For all $0 < T \leq T_2^\alpha$, it holds

where $W_l^\alpha = (U_l^\alpha, \alpha G_l^\alpha)$.

Proof. Apply $\partial_{x}^{l}$ to (4.11), we obtain

whereas,

Taking $L^{2}$ inner product with $U^{\alpha}_{l}$ of first equation in the system above, we have

We will treat the right hand side of the above inequality term by term. First, using the second equation in (4.16), we have

in which

Then using Cauchy-Schwarz inequality, Moser-Type calculus inequalities in Lemma 2.1, we have

Combining the four estimates above and using (4.17), we have

Integrating over $[0, T]$ and adding for all $0\leq l\leq s$ yields (4.15).

4.4.   Proof of Theorem 4.1

We introduce an energy functional,

Then it follows from (4.15) that there exists a $\alpha^{0} > 0$ depending only upon $T_2^\alpha$, such that for any $0 < \alpha \leq \alpha^0$ and any $0 < t \leq T_2^\alpha$,

Then Gronwall's inequality and the fact $\Gamma(0) \leq C\alpha^{4(m+1)}$ imply there exists a sufficiently small $\tilde{\alpha^0} > 0$ such that for all $0 < \alpha \leq \tilde{\alpha^0}$ and $0 < t \leq T_2^\alpha$,

which completes the proof.

Acknowledgments

The author would like to thank Professor Yachun Li for her fruitful discussion. The author's research was supported in part by Chinese National Natural Science Foundation under grant 11571232 and 11831011.

Conflict of interest

The author declares no conflict of interest.