A multiple objective programming approach to linear bilevel multi-follower programming

1.   Introduction

Multilevel programming (MLP) is developed to model the decentralized decision-making situations wherein decision makers are arranged within a hierarchical structure. In a MLP problem, when only two levels exist, the problem is referred to as the bilevel programming (BLP) problem. In actual, BLP problems involve two nested optimization problems where the constraint region of first-level problem contains the second-level optimization problem. In this model, a decision maker at the first-level is termed as a leader, and at the second-level, a follower. BLP problems have many applications in the real world, such as those in supply chain management ^[14], planning ^[16], and logistics ^[19]. Most of the research concerning MLP have focused on bilevel programming (BLP) ^[1,5]. In this paper, we consider linear bilevel problems with one leader and multiple followers. This model is called linear bilevel multi-follower programming (LBLMFP) problem. Shi et al. extended the Kth-Best algorithm to solve LBLMFP problems ^[21]. Several researchers developed heuristic algorithms to the BLP problems, for instance, see ^[10]. Lu et al, applied the extended Kuhn-Tucker approach to solve LBLMFP problem ^[13]. Also, one approach is developed to solve the LBLMFP problems based on multi-parametric programming ^[7]. In addition, some researchers have exploited multiple objective programming techniques to solve BLP problems ^[9,18]. These kinds of solution approaches are developed based on some relationships between BLP and multiple objective programming that were first presented by F$\ddot u$l$\ddot o$p ^[8]. For example, Glackin et al. presented an algorithm to solve linear bilevel programming (LBLP) problems based on multiple objective linear programming (MOLP) techniques ^[9].

In this paper, Motivated by the relationship between LBLP and MOLP, a relationship between a class of LBLMFP problems and MOLP problems is introduced for the first time. Moreover, we present an algorithm for solving LBLMFP problems based on the proposed relation.

The paper is organized as follows: In the next section, we present the basic definitions, and some notions about LBLMFP problems and MOLP problems. In Section 3, we introduce two MOLP problems such that each feasible solution for the LBLMFP problem is efficient for both of the two MOLP problems. Next, we obtain results, based on which the LBLMFP problem can be reduced to optimize the first-level objective function over a certain efficient set. Based on this result, a new algorithm is developed in Section 4 for solving the LBLMFP problem. Furthermore, we obtain some results for special cases. Section 5 presents a number of numerical examples to illustrate the proposed algorithm. Finally, in Section 6, we present the conclusions.

2.   Preliminaries

In this section, we present the formulation of LBLMFP problem which we shall investigate, accompanied by basic definitions. In addition, we recall some notions and theoretical properties about MOLP problems.

2.1.   Linear bilevel multi-follower programming problem

In this article, we consider a linear bilevel programming (LBLP) problem with two followers. There are individual decision variables in separate objective functions and constraints between the followers. Each follower takes other followers' decision variables as a reference. This is called a reference-uncooperative LBLMFP problem ^[23]. This model can be formulated as follows:

where $x^i \in X^i \subset \mathbb{R}_+^{n_i}, \; i = 1, 2, 3$, $F: X^1 \times X^2 \times X^3 \to \mathbb{R}$, and $f_k: X^2 \times X^3 \to \mathbb{R}, \; k = 1, 2$, $c^{ij},$ for $i, j\in \{1, 2, 3\}$, are the vectors of conformal dimension, and for each $i \in \{1, 2, 3 \}$, $A_i$ is a $m \times n_i$ matrix, $B_i$ is a $q \times n_i$ matrix, $b_1 \in \mathbb{R}^m$, and $b_2 \in \mathbb{R}^q$. Also, although $x^i \geq 0,$ for $i = 1, 2, 3,$ do not explicitly appear in this problem, we assume that they exist in the set of constraints.

Notice that, the followers' objective functions are linear in $x^2$ and $x^3$ and for each follower, the value for the variable $x^1$ is given. Thus, a problem equivalent to the LBLMFP problem is obtained if the followers' objective functions are replaced by $\sum \limits_{\substack{j = 1}}^3 (c^{ij})^Tx^j$, for i = 2, 3.

We need to introduce the following definitions that can be found in ^[23].

(1) Constraint region of the LBLMFP problem:

We suppose that $S$ is non-empty and compact.

(2) Projection of $S$ onto the leader's decision space:

(3) Feasible sets for the first and second followers, respectively:

The feasible region of each follower is affected by the leader's choice of $x^1$, and the other followers' decisions.

(4) The first and second followers' rational reaction sets, respectively:

where

and

where

(5) Inducible region ($IR$):

In actual, the inducible region is the set of feasible solutions of the LBLMFP problem. Therefore, determining the solution for the LBLMFP problem is equivalent to solving the following problem:

In order to assure that (2.1) has an optimal solution ^[23], we supposed that the following assumptions hold:

(1) $IR$ is non-empty.

(2) $P_1(x^1, x^3)$ and $P_2(x^1, x^2)$ are point-to-point mappings with respect to $(x^1, x^3)$ and $(x^1, x^2)$, respectively. In other words, for each leader's choice of $x^1$, there will be a unique solution to each follower.

2.1.1.   Multiple objective linear programming problem

Assume that $p\geq2$ is an integer and $c_i \in \mathbb{R}^n, \; i = 1, 2, \cdots, p$ are row vectors. Let $C$ be a $p \times n$ matrix whose $i$-th row is given by $c_i, \; i = 1, 2, \cdots, p$, and $U$ is a non-empty, compact and convex polyhedral set in $\mathbb{R}^n$. A multiple objective linear programming (MOLP) problem is formulated in general as follows:

where $U$ is called feasible region.

Definition 1. ^[22] A feasible point, $\bar{x}\in U$, is called an efficient solution if there exists no $x \in U$ such that $Cx\leqslant C \bar{x}$ and $Cx \not = C \bar{x}$.

An efficient solution is also called a Pareto-optimal solution.

Let $E$ denote the set of all efficient solutions of the MOLP problem. Note that $E \not = \emptyset$ [^[6], Theorem $2.19$].

Let $d \in \mathbb{R}^n$. Consider the following mathematical programming problem:

This problem is a non-convex linear optimization problem over the efficient set $E$ of the MOLP problem. Let $E^*$ denote the set of optimal solutions to the problem (2.2) and $U_{ex}$ denote the set of extreme points of the polyhedron $U$. Because $U$ is a non-empty, compact and convex polyhedron in $\mathbb{R}^n$, $U_{ex}$ is non-empty [^[3], Theorem $2.6.5$]. So, the following result holds:

Theorem 1. Let $U$ be a non-empty, compact, and convex polyhedral set, and let $E^*$ be non-empty. Then, at least one element of $E^*$ is an extreme point of $U$ [^[4], Theorem $4.5$].

By considering the relation $E \subseteq U,$ we immediately get the following corollary to Theorem 1.

Corollary 1. Let $E^* \neq \emptyset$. Then, there is an extreme point of $E$, which is an optimal solution to the problem (2.2).

From Theorem $3.40$ in ^[6], because $U$ is a non-empty, compact and convex polyhedron in $\mathbb{R}^n$, and the objective functions $c_i x, \; i = 1, 2, \cdots, p$ are convex, we can conclude that the efficient set $E$ is connected.

Moreover, it is well-known that the efficient set $E$, is comprised of a finite union of faces of $U$ ^[6]. Therefore, we obtain the following corollary:

Corollary 2. The efficient set $E$ is comprised of a finite union of connected faces of the polyhedron $U$.

The Corollary 2 obviously implies that the efficient set $E$ is closed.

Also, the following definition is used in sequel:

Definition 2. ^[22] Let $U \subseteq \mathbb{R}^n$, and $x_1, x_2, \ldots, x_r \in U$. The notation $\gamma(x_1, x_2, \ldots, x_r)$ denotes the set of all convex combinations of $x_1, x_2, \ldots, x_r$.

3.   Theoretical properties

In this section, we will introduce two MOLP problems in such a way that any extreme efficient solution for both problems simultaneously, is an extreme feasible solution (in other words, an extreme point of $IR$) to LBLMFP problem.

Note that $\bar{x} = (\bar{x}^1, \bar{x}^2, \bar{x}^3) \in IR$, i.e., $\bar{x}^2 \in P_1(\bar{x}^1, \bar{x}^3)$ and $\bar{x}^3 \in P_2(\bar{x}^1, \bar{x}^2)$. Therefore, $\bar{x}^2$ is an optimal solution for the following linear program (LP):

and $\bar{x}^3$ is an optimal solution for the following LP:

Now, set $n: = \sum \limits_{\substack{i = 1}}^3n_i$. We construct augmented matrix $\mathscr{A a 1} = \begin{bmatrix} A_1 & A_3 \end{bmatrix}$. Let $rank(\mathscr{A a 1}) = r_1$. Without loss of generality, we assume that augmented matrix $\mathscr{A a 1}$ can be rewritten as $\begin{bmatrix} \bar{A}_1 & \bar{A}_3\\ \hat{A}_1 & \hat{A}_3 \end{bmatrix},$ where $\begin{bmatrix} \bar{A}_1 & \bar{A}_3 \end{bmatrix}$ is $r_1 \times (n_1+n_3)$ matrix and $rank(\begin{bmatrix} \bar{A}_1 & \bar{A}_3 \end{bmatrix}) = rank(\mathscr{A a 1}) = r_1$. [Notice that the augmented matrix $\mathscr{A a 1}$ contains an $(n_1 + n_3)\times(n_1 + n_3)$ identity submatrix corresponding to non-negativity constraints. So, $r_1 = n_1+n_3$]. Similarly, we construct augmented matrix $\mathscr{B a 1} = \begin{bmatrix} B_1 & B_2 \end{bmatrix}$. Let $rank(\mathscr{B a 1}) = r_2$ and augmented matrix $\mathscr{B a 1}$ can be rewritten as $\begin{bmatrix} \bar{B}_1 & \bar{B}_2\\ \hat{B}_1 & \hat{B}_2 \end{bmatrix},$ where $\begin{bmatrix} \bar{B}_1 & \bar{B}_2 \end{bmatrix}$ is $r_{2} \times (n_1+n_2)$ matrix and $rank(\begin{bmatrix} \bar{B}_1 & \bar{B}_2 \end{bmatrix}) = rank(\mathscr{B a 1}) = r_2$. Let $k_i = r_i+2, \; i = 1, 2$ and the $k_i \times n,$ criterion matrices $C_i, \; i = 1, 2$ be defined as follows:

where $O$ and $0$, are zero matrix and zero vectors of conformal dimension, respectively. Also, e is a vector having each entry equal to 1.

Next, consider the following two MOLP problems:

Let $E_i$ be the set of efficient solutions of the MOLPi, $i = 1, 2$. We have the following result:

Proposition 1. Let $IR$ and $E_1$ be defined as above. Then, $IR \subseteq E_1$.

Proof. Assume that $\bar{x} = (\bar{x}^1, \bar{x}^2, \bar{x}^3)\in IR$. It suffices to show that $\bar{x}$ is an efficient solution for the MOLP1. Let us suppose the contrary, i.e., there exists $x = (x^1, x^2, x^3) \in S$ such that $C_1x \leq C_1 \bar{x}$ and $C_1x \neq C_1 \bar{x}$. Because $C_1x \leq C_1 \bar{x}$, using the structure of matrix $C_1$, one obtains:

From inequality (3.6), one obtains:

The last two inequalities imply that:

From equality (3.9) and inequality (3.6), it is easy to see that $\bar{A}_1 x^1+\bar{A}_3 x^3 = \bar{A}_1 \bar{x}^1+\bar{A}_3 \bar{x}^3$. So, we have:

Obviously, $x^2$ is a feasible solution for the problem (3.1)- (3.2). Moreover, due to $C_1x \neq C_1 \bar{x}$ and in view of equalities (3.9) and (3.10), we deduce that $(c^{22})^Tx^2 < (c^{22})^T\bar{x}^2$ which contradicts $\bar{x}^2$ is an optimal solution for the problem (3.1)– (3.2). This completes the proof.

The proof of the following proposition is similar to that of Proposition 1, and we omit it.

Proposition 2. Let $IR$ and $E_2$ be defined as above. Then, $IR \subseteq E_2$.

Now, if we set $E: = E_1 \cap E_2$, from Propositions 1 and 2, we can get:

Remark 1. Let $IR, \; E_1$, and $E_2$ be defined as above. Then, $IR \subseteq E_1 \cap E_2 = E$, and regarding to Assumption $(1)$, $E$ is a non-empty set.

Therefore, this allows us to prove the main result of this section.

Theorem 2. The extreme points of $IR$ and $E$ are identical.

Proof. Let $x = (x^1, x^2, x^3) \in IR_{ex}$ be arbitrary. Then, $x$ is an extreme point of $S$ [^[23], Corollary $4.9$]. Because $IR \subseteq E$, we get $x \in E$. Therefore, $x$ is an extreme point of $E$ (Note that $E \subseteq S$). Since $x \in IR_{ex}$ was chosen arbitrarily, we obtain $IR_{ex} \subseteq E_{ex}$. Now, we will show that $E_{ex} \subseteq IR_{ex}$. Let $x = (x^1, x^2, x^3) \in E_{ex}$ be chosen arbitrarly. There are two cases to be considered here.

Case 1: $x \not \in IR$. In this case, we conclude from the definition of $IR$ that at least one of the following two subcases should occur:

Subcase 1: $x^2 \not \in P_1(x^1, x^3)$. It follows from Assumption $(2)$ that there exists $\hat{x}^2 \in P_1(x^1, x^3)$, so that $f_1(\hat{x}^2, x^3) < f_1(x^2, x^3)$. As a consequence, we get:

Set $\hat{x} = (x^1, \hat{x}^2, x^3)$. By definition of $P_1(x^1, x^3)$, $\hat{x} \in S$. Due to the structure of matrix $C_1$ and inequality (3.11), one has $C_1 \hat{x} \leqslant C_1 x, \; C_1 \hat{x} \not = C_1 x$ that contradicts $x \in E \subseteq E_1$.

Subcase 2: $x^3 \not \in P_2(x^1, x^2)$. By Assumption $(2)$, there exists $\hat{x}^3 \in P_2(x^1, x^2)$ so that $f_2(x^2, \hat{x}^3) < f_2(x^2, x^3)$. As a consequence, we have:

Set $\hat{x} = (x^1, x^2, \hat{x}^3)$. By definition of $P_2(x^1, x^2)$, $\hat{x} \in S$. Due to the structure of matrix $C_2$ and inequality (3.12), one has $C_2 \hat{x} \leqslant C_2 x, \; C_2 \hat{x} \not = C_2 x$, which contradicts $x \in E \subseteq E_2$.

Case 2: $x \in IR$. Since $x \in E_{ex}$ and $IR \subseteq E$ (see Remark 1), we conclude that $x \in IR_{ex}$. This completes the proof.

Now, let us consider the following problem:

Remark 2. Note that Corollary $2$ obviously implies that the efficient set $E$ is closed. Also, since $E$ is a closed subset of the compact polyhedral set of $S$, itself is a compact set. Therefore, problem (3.13) involves the optimization of a linear function over a compact set. Hence, there exists an optimal solution to the problem (3.13), i.e., $E^* \neq \emptyset$. Then, according to the Corollary $1$, there is an extreme point of $E$, which is an optimal solution for the problem (3.13).

The relation between LBLMFP problem and problem (3.13) is stated in the following theorem.

Theorem 3. A point $\bar{x} = (\bar{x}^1, \bar{x}^2, \bar{x}^3) \in IR_{ex}$ is an optimal solution to LBLMFP problem if, and only if, it is an optimal solution to the problem (3.13).

Proof. It is well-known that solving LBLMFP problem is equivalent to solving problem (2.1). Furthermore, there exists an extreme point of $IR$, which is an optimal solution for problem (2.1) ^[23]. Because the optimal solution of problem (3.13) occurs at an extreme point of $E$ and the extreme points of $E$ and $IR$ are the same, we conclude that if $\bar{x}$ is an optimal solution for problem (3.13), it is an optimal solution for LBLMFP problem, and vice versa. This completes the proof.

In the next section, based on Theorem 3, we propose a new algorithm to solve LBLMFP problem.

4.   The Algorithm

Owing to the preceding discussion, we will propose a new algorithm for solving LBLMFP problems. First, one can solve two MOLP$i$, $\; i = 1, 2$ in order to obtain the sets $E_i, \; i = 1, 2$. Let $E$ be the set of efficient points that have been discovered to be efficient solutions to both problems. Then, one can minimize the leader objective function over the set $S$. If the obtained extreme optimal solution lies in the set $E$, it solves the LBLMFP problem. Otherwise, one can solve problem (3.13). Then, by Theorem 3, the obtained extreme optimal solution solves the LBLMFP problem. The algorithm can be described as follows:

The Algorithm:

Step 1. Construct the MOLP$i$, $i = 1, 2$.

Step 2. Find efficient sets $E_i$ with respect to the MOLP$i$, $i = 1, 2$.

$\bullet$ For instance, approaches presented in ^[6,17,20,22] can be used in Step $2$.

Step 3. Set $E = E_1 \cap E_2$.

Step 4. Solve the following LP:

Let $x^*$ be an optimal solution (One can use the common known solution methods for LPs in ^[2]). If $x^* \in E$, stop. Then, $x^*$ is an optimal solution to LBLMFP problem. Otherwise, go to Step 5.

Step 5. Find an optimal solution to problem (3.13) using, for instance, approaches developed in ^[4,11,12,15]. Let $x^*$ be an optimal solution for problem (3.13). Then, it is an optimal solution to LBLMFP problem, too.

$\bullet$ Notice that, by Remark 2, there exists an extreme point of $E$ which is an optimal solution for problem (3.13). Hence, in Step $5$, for a few number of variables and extreme points, we can find an optimal solution by picking the minimum objective function value among all extreme points of $E$.

Note that because the efficient set $E$ is not convex in general, the problem (3.13) is a non-convex optimization problem. Thus, in Step $5$, we face a non-convex optimization problem that is generally difficult to solve. Moreover, the algorithm stops by obtaining an efficient optimal solution. The Step $4$ solves the LP (4.1) and checks whether $x^* \in E$. If $x^* \in E$, the algorithm stops at Step $4$, and does not enter Step $5$. Therefore, Step $4$ is necessary in this algorithm to reduce the computations in some cases.

Prior to applying the proposed algorithm for solving numerical examples, we will state the following lemma:

Lemma 1. Let $E$ be defined as above. Then $E \subseteq conv IR$, where $conv IR$ be the smallest convex set containing $IR$.

Proof. Let $\hat{x} \in E$ be chosen arbitrarly. Suppose the contrary, that is $\hat{x} \not \in conv IR$. Because $IR$ is closed [^[23], Theorem $4.9$], $conv IR$ is a convex and closed set. Therefore, there exists a non-zero vector $P$ [^[3], Theorem $2.4.4$], such that $P^T \hat{x} < P^T y$, for all $y \in conv IR$. Since $S$ is a compact set and $conv IR$ is a closed subset of $S$, $conv IR$ is a compact set as well. Furthermore, because $y \in conv IR$, according to the Representation Theorem ^[3], we have $y = \sum \limits_{\substack{i = 1}}^n \lambda_i x_i, \; \sum \limits_{\substack{i = 1}}^n \lambda_i = 1, \; 0 \leqslant \lambda_i \leqslant1, \; x_i \in (conv IR)_{ex}$. On the other hand, $(conv IR)_{ex} = IR_{ex} = E_{ex}$, thus,

Now, consider the problem $\min \{P^T x : x \in E\}$. By Remark 2, there exists $x_j \in E_{ex}$, which is an optimal solution for this problem. Then, $P^Tx_j \leqslant P^T x$, for all $x \in E$. Because $\hat{x} \in E$, we have:

Since $x_j \in E_{ex}$, it follows from (4.2) that $P^T\hat{x} < P^T x_j$, which contradicts (4.3). Hence, $\hat{x} \in conv IR$.

Note that the efficient set $E$ and the inducible region $IR$ are not convex sets, generally ^[1,5,6,22]. Up to now, we have proved that $IR \subseteq E \subseteq conv IR$. In the following, we show that these inclusions convert to equality in some special cases, as convexity.

Corollary 3. If the efficient set $E$ is a convex set, then $E = conv IR$.

Proof. By the convexity of $E$ and from Remark 1, we obtain $convIR \subseteq E$. Also, according to Lemma 1, we have $E \subseteq conv IR$. Then, $E = conv IR$.

Corollary 4. If the inducible region $IR$ is a convex set, then $E = IR$.

Proof. According to Remark 1, $IR \subseteq E$. Because $IR$ is a convex set, $conv IR = IR$. It follows from Lemma 1 that $E \subseteq IR$. Then, $E = IR$.

5.   Numerical examples

In this section, we apply the proposed algorithm for solving some numerical examples.

Example 1. Consider the following LBLMFP problem:

In this problem, $S = \{ (x^1, x^2, x^3): x^1+ x^2 \leq 8, \; x^1+ 4 x^2 \geq 8, \; x^1+ 2 x^2 \leq 13, \; 7 x^1- 2 x^2 \geq 0, \; x^1 \geq 0, \; x^2 \geq 0, \; 0 \leq x^3 \leq 2\}$, and the extreme points of $S$ are as follows:

By ^[7], one can obtain:

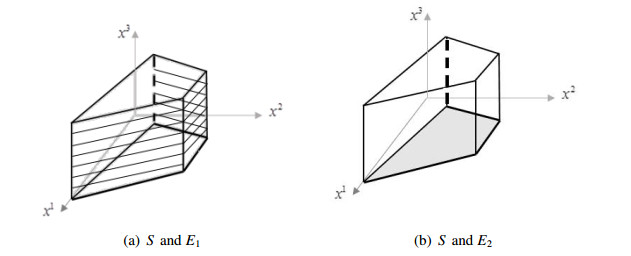
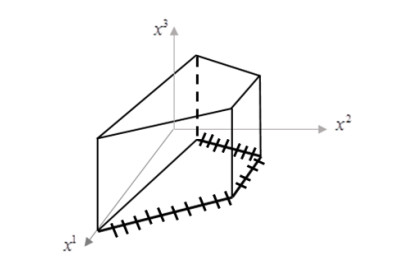
The Figure 1 displays $S$ and $IR$. The inducible region $IR$ is denoted by the hatched lines.

Note that in this example, $S$ and $IR$ are non-empty and $S$ is compact. Also, one can obtain:

Hence, $P_1(x^1, x^3) \neq \emptyset$, $P_2(x^1, x^2) \neq \emptyset$, and $P_1(x^1, x^3)$ and $P_2(x^1, x^2)$ are point-to-point maps with respect to $(x^1, x^3)$ and $(x^1, x^2)$, respectively. Therefore, the Assumptions (1) and (2) hold, and we can solve this problem by the proposed algorithm. Using the proposed algorithm, the process is as follows:

Step 1. The MOLP$i$ problems, for $i = 1, 2$ are constructed as follows, respectively:

Step 2. In order to find the sets $E_i, \; i = 1, 2$, using the approach described in ^[20], one can obtain:

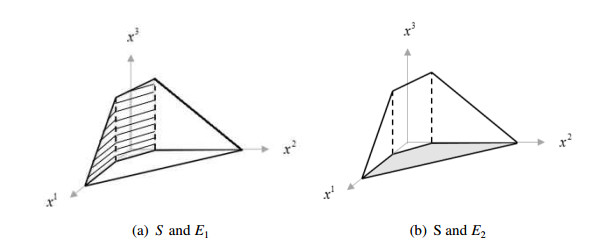
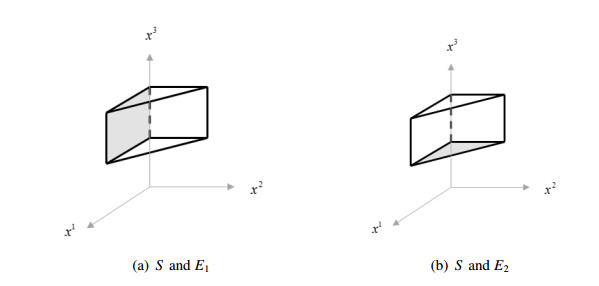
The sets $E_i, \; i = 1, 2$ are shown in Figure 2 (a) and (b), by the hatched regions and gray area, respectively.

Step 3. Set $E = E_1 \cap E_2$. We obtain $E = \gamma{(a_1, a_3)}\cup \gamma{(a_3, a_5)}\cup \gamma{(a_5, a_7)} = IR$ which is shown in Figure 1 by the hatched lines.

Step 4. Solve the following LP:

The optimal solution is $x^* = (\frac{8}{15}, \frac{28}{15}, 0)$. Because $x^* \in E$, stop. We deduce that $x^*$ is an optimal solution for this problem. Also, we solve this example using the multi-parametric approach ^[7]. We obtain $x^* = (\frac{8}{15}, \frac{28}{15}, 0)$ which is equal with the obtained optimal solution using the proposed algorithm.

Example 2. Consider the following LBLMFP problem:

In this problem, $S = \{ (x^1, x^2, x^3):\ 2 x^1+ x^2+ x^3 \leqslant 5, \; x^1 + x^2 \geq 1, \; x^1 \geq 0, \; x^2 \geq 0, \; x^3 \geq 0 \}$, and the extreme points of $S$ are as follows:

By ^[7], one can obtain:

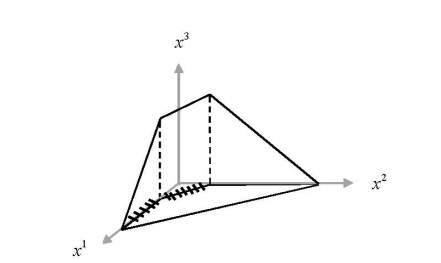
The sets $S$ and $IR$ are drawn in Figure 3. The inducible region $IR$ is denoted by the hatched lines.

Note that in this example, $S$ and $IR$ are non-empty and $S$ is compact. Also, one can obtain:

Hence, $P_1(x^1, x^3) \neq \emptyset$, $P_2(x^1, x^2) \neq \emptyset$, and $P_1(x^1, x^3)$ and $P_2(x^1, x^2)$ are point-to-point maps with respect to $(x^1, x^3)$ and $(x^1, x^2)$, respectively. Therefore, the Assumptions (1) and (2) hold, and we can solve this problem by the proposed algorithm. Applying the proposed algorithm to this example, we have:

Step 1. The MOLP$i$ problems, for $i = 1, 2$ are constructed as follows, respectively:

Step 2. One can obtain the sets $E_i, \; i = 1, 2$, using the approach described in ^[20]:

The sets $E_i, \; i = 1, 2$ are drawn in Figure 4 (a) and (b) by the hatched regions and gray area, respectively.

Step 3. Set $E = E_1 \cap E_2$. So, we obtain $E = \gamma{(a_1, a_2)} \cup \gamma{(a_2, a_3)}$. Here, $E$ coincides with $IR$ which is shown in Figure 3 by the hatched lines.

Step 4. Solve the following LP:

The optimal solution is $x^* = (0, 1, 4)$. Because $x^* \not \in E$, go to step 5.

Step 5. Solve the following problem:

This problem is a non-convex optimization problem. According to Remark 2, we just consider the extreme points of $E$. Then, we conclude that the point $x^* = (0, 1, 0)$ is an optimal solution. Also, one can solve this example using the multi-parametric approach and obtain $x^* = (0, 1, 0)$. The optimal solution is equal with the obtained optimal solution using the proposed algorithm.

Example 3. Consider the following LBLMFP problem:

In this problem, $S = \{ (x^1, x^2, x^3):\ \; x^1+ x^2 \leqslant 2, \; x^1 \geq 0, \; x^2 \geq 0, \; 2 \leqslant x^3\leqslant 4 \}$, and the extreme points of $S$ are as follows:

By ^[7], one can obtain:

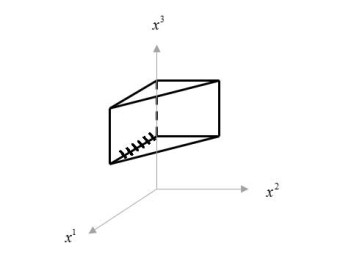
The Figure 5 displays constraint region $S$ and inducible region $IR$. The inducible region is denoted by the hatched line. Note that in this example, $S$ and $IR$ are non-empty and $S$ is compact. Also, one can obtain:

Hence, $P_1(x^1, x^3) \neq \emptyset$, $P_2(x^1, x^2) \neq \emptyset$, and $P_1(x^1, x^3)$ and $P_2(x^1, x^2)$ are point-to-point maps with respect to $(x^1, x^3)$ and $(x^1, x^2)$, respectively. Therefore, the Assumptions (1) and (2) hold, and we can solve this problem by the proposed algorithm. Applying the proposed algorithm to this example, we have:

Step 1. The MOLP$i$ problems, for $i = 1, 2$ are constructed as follows, respectively:

Step 2. One can obtain the sets $E_i, \; i = 1, 2$, using the approach described in ^[20]:

The sets $E_i, \; i = 1, 2$ are drawn in Figure 6 (a) and (b) by the gray areas, respectively.

Step 3. Set $E = E_1 \cap E_2$. So, we obtain $E = \gamma{(a_1, a_2)} = IR$. It is shown in Figure 5 by the hatched line.

Step 4. Solve the following LP:

The extreme optimal solutions are $x^* = (0, 2, 2)$ and $y^* = (0, 2, 4)$. Because $x^*, y^* \not \in E$, go to Step 5.

Step 5. Solve the following problem:

Since $E$ is convex, this problem is the linear programming problem. An optimal solution is $x^* = (2, 0, 2)$. Also, one can solve this example using the multi-parametric approach and obtain $x^* = (2, 0, 2)$. The obtained optimal solution is equal with the obtained optimal solution using the proposed algorithm.

6.   Conclusions

In this paper, we have presented a relation between a class of LBLMFP problems and multi-criteria optimization for the first time. We have shown how to construct two MOLP problems so that the extreme points of the set of efficient solutions for both problems are the same as those of the set of feasible solutions for the LBLMFP problem. It is proved that solving the given LBLMFP problem is equivalent to optimizing the leader objective function over a certain efficient set. Based on this result, we proposed an algorithm for solving the LBLMFP problem, and we also showed that it can be simplified in some special cases. Further studies are being conducted to improve the performance of the proposed algorithm and to extend to other classes of LBLMFP problems.

Conflict of interest

All authors declare no conflicts of interest in this paper.