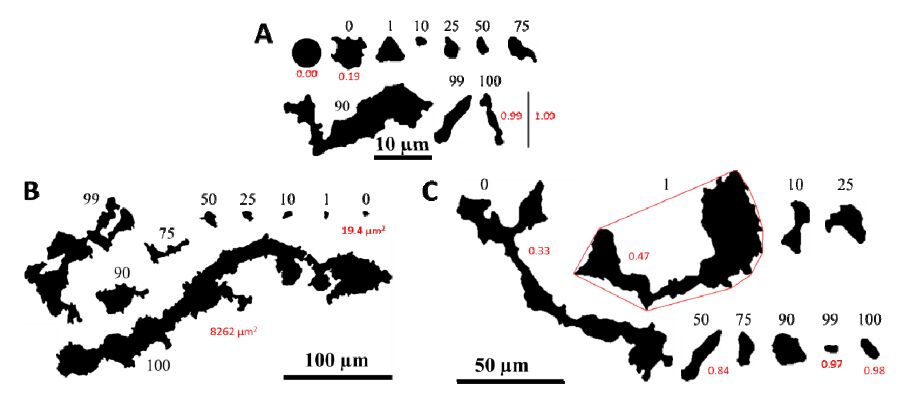
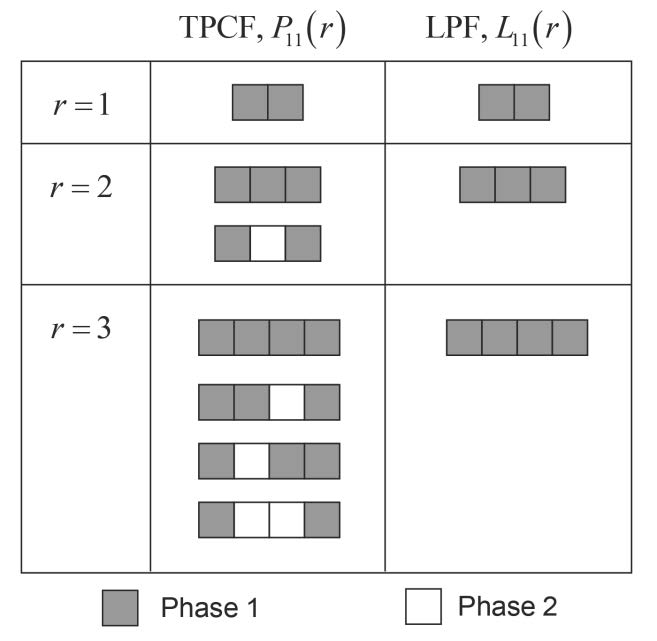
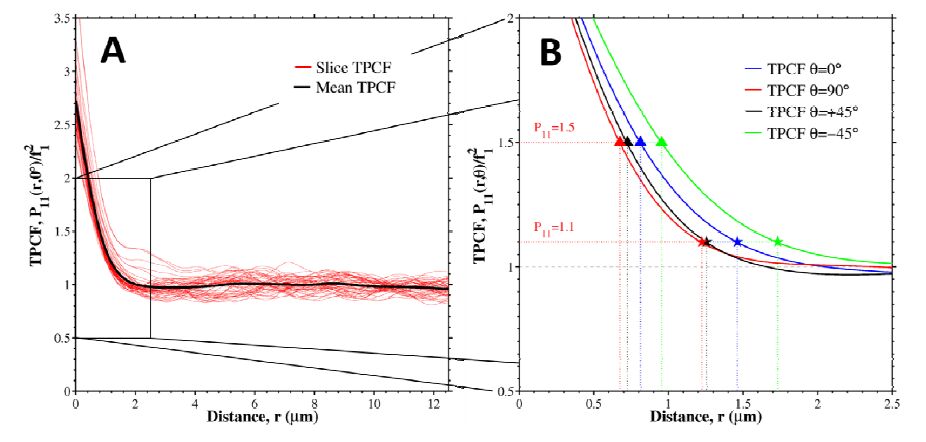
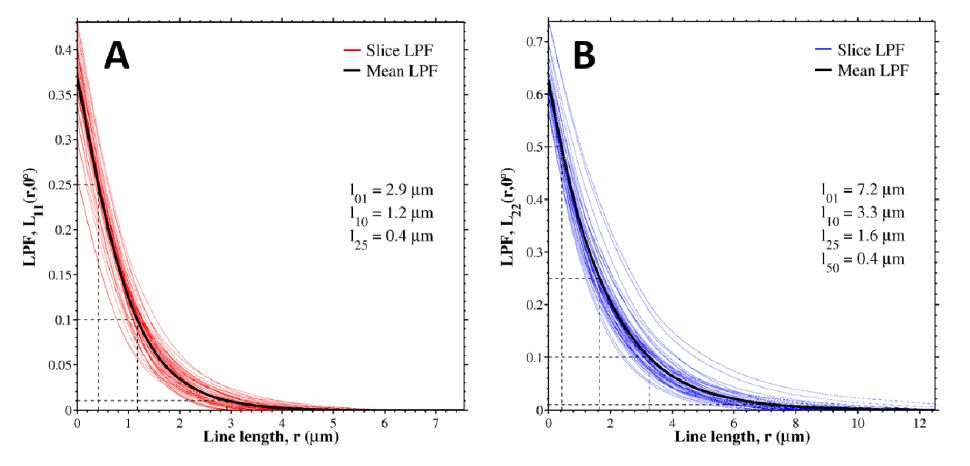
Porous metals can be created through a wide variety of processing techniques, and the pore morphology resulting from these processes is equally diverse. The structural and functional properties of metal foams are directly dependent on the size, shape, interconnectedness and volume fraction of pores, so accurately quantifying the pore characteristics is of great importance. Methods for analyzing porous materials are presented here and applied to a copper-based metallic foam generated through solid state foaming via oxide reduction and expansion. This process results in large voids (10s of microns) between sintered particles and small pores (10 microns to less than 50 nm) within particles. Optical and electron microscopy were used to image the porosity over this wide range, and the pore characteristics were quantified using image segmentation and statistical analysis. Two-dimensional pore analysis was performed using the Chan-Vese method, and two-point correlation and lineal path functions were used to assess three-dimensional reconstructions from FIB tomography. Two-dimensional analysis reveals distinct size and morphological differences in porosity between particles and within them. Three-dimensional analysis adds further information on the high level interconnectedness of the porosity and irregular shape it takes, forming tortuous pathways rather than spherical cells. Mechanical polishing and optical microscopy allow large areas to be created and analyzed quickly, but methods such as focused ion beam (FIB) sectioning can provide additional insight about microstructural features. In particular, after FIB milling is used to create a flat surface, that surface can be analyzed for structural and compositional information.
1.
Introduction
Cooperation can be found in many contexts and at many scales, both in nature and human societies, and can occur even between species [1,2]. Cooperation, defined as the giving up of individual reproductive success (fitness) to provide some fitness benefit to other individual(s), appears on the surface to be incompatible with Darwinian natural selection [3,4]. However, cooperative groups may have a higher average fitness than defective (or selfish) groups. Herein lies the paradox: how can cooperation, which once established is better for everyone, succeed in the face of individual incentive to defect?
The emergence and fixation of cooperation has been explained through a number of mechanisms, including kin selection [5], reciprocity [6], reputation (indirect reciprocity) [7,8], cooperator recognition (green beards) [9], assortative encounter (direct or network-based)[10] and various forms of punishment [11,15,12,14], as well as more complex network effects [18,17,16].These mechanisms, though promoting cooperation, tend to foster higher levels of cooperation between members in the same local community, family group, or language group (in the case of indirect reciprocity). For example, network-based assortment allows clusters of cooperators to avoid contact with the rest of the population [19,20,21]. Indirect reciprocity works by letting players know each other's reputations; players choose whether to cooperate or defect based on whether the prospective player has cooperated or defected in previous interactions; reputation is more easily spread within members of the same language group. Direct reciprocity requires that players have a high probability of encountering one another again, while such repeated interactions are more likely within social groups. Kin selection allows levels of cooperation between individuals according to their relatedness [19]. Clearly, these mechanisms are not as effective at promoting cooperation between individuals which are genetically, spatially, or socially distant. Such mechanisms (or network configurations) are often associated with lower bounds on the benefit/cost ratio [19] for which cooperation can persist [22].
Ever since the first diversification in life forms, the potential for conflict between different groups of individuals has been present. In systems with social structures or groupings, such as ant colonies or human societies, various degrees of cooperation and conflict occur. Consequently, groups are often separated by large distances or unsuitable terrains, so that conflict between groups can be intentionally or unintentionally reduced [23]. Unfortunately, this is not always the case.
Humans are set apart in the sheer number of functional groups we form, such as companies, tribes and nations, and group divisions hold enormous influence in our everyday lives. Conflicts between groups have driven some of the most destructive patterns of human behavior, despite the fact that individuals within groups (who are in effect acting out the conflict) may not even want to support inter-group conflict [24]. Importantly, in most such cases, group membership is viscous but remains exchangeable (e.g. moving into another company or migrating to another country). In reality, the boundaries between groups can range from highly fluid (e.g. company employees) to nearly unbreachable (e.g. ethnic groups). Here we focus on the unbreachable end of this spectrum. While the contexts of inter-group conflicts vary, they share on the individual scale at least one common driver: people are more cooperative with members of their own groups. Studies in social psychology have shown that people are more trusting, more communicative, and less selfish when interacting with a member of a designated 'in-group' even when the group allocation is nothing more than a label given by experimenters [25]; these effects are stronger for pre-existing social identity groupings such as families, ethnic groups, and citizens of a country [26], and functional group identities such as corporate teams, school peer-groups, or neighborhood improvement organizations [27].
A typical paradox of cooperation is the tragedy of the commons [28], in which a shared resource is vulnerable to over-use by unscrupulous individuals. This situation has been encoded mathematically in the form of the public goods game and its philosophically equivalent two-player game, the prisoner's dilemma [6]. While the prisoner's dilemma is a standard tool for explaining the evolution of cooperation, and represents the hardest problem to solve from a game theory perspective, empirical studies have suggested that many scenarios often characterized as prisoner's dilemmas may in fact be better classified as stag hunts, depending on the parameters involved [31,29,30]. The stag hunt represents a scenario where the players must cooperate to achieve a higher goal, such as hunting a stag, but may be assured of some lesser payoff if they choose to act alone, hunting hares instead [32]. A player in a stag hunt is better off 'defecting' (acting alone) if they expect that the other player will defect, but should cooperate if they expect that the other player will cooperate. The lack of consensus regarding which game best represents real social interactions is hardly surprising considering their enormous complexity. Our model lies somewhere between the camps of this dispute.
Evolutionary game theory has looked at the problem of cooperation within and between recognizable groups (often referred to as 'groups with tags') through two broad lenses. One lens looks at the simultaneous evolution of group structure and cooperation [33,34,35], while the other looks at the evolutionary dynamics of identity, conflict and cooperation in the context of pre-existing groups [36,39,38,37]. Studies using spatial models have found that in the context of recognizable group divisions, ethnocentrism - cooperation within the group - dominates, followed by humanitarianism - cooperating regardless of group membership [33,40].
The aim of this work is to develop a simple, tractable model of socio-economic power dynamics and cooperation in a system with two recognizable population groups. The generality of our model places it in an ideal position to be further developed in order to refine restrictive assumptions and address more specific scenarios. The rest of this paper is structured as follows. First, we describe the two social scenarios that we consider, each one a limiting case of certain real-life group dynamics. We then specify the rules governing the dynamics of the system, and analyze the resulting system of differential equations, focusing on conditions for cooperation and group coexistence.
2.
Materials and methods
Our model describes the prevalence of cooperation within two distinct, recognizable groups and the relative socio-economic power of the two groups. People in the model ('players') engage in two-player games, in which each must choose whether to 'cooperate' (C) or 'defect' (D). Players can identify whether they are playing with a member of their own group ('within-group games') or the other group ('cross-group games'). We will focus on two scenarios concerning the difference between within-group and cross-group games.
Payoffs in our model are in terms of socio-economic power, and group size represents the agammaegate socio-economic power of a group. 'Socio-economic power' may take the form of economic, social or cultural influence, and is used interchangeably with 'power'. These are connected in real societies by production and consumption of different sets of practical and artistic products. Our model assumes a ''well-mixed" population, in which encounter rates are determined by group-level socio-economic power and strategy prevalence in each group. In other words, the total socio-economic power of a group determines the rate at which players encounter players of that group.
There is significant evidence to suggest that group membership is an important factor for establishing role-models, and within-group understanding facilitates the copying of successful strategies from fellow group members [41,24]. Following this line of reasoning, players in our model copy successful strategies that they observe being played by other members of their group. Group identities are distinguished by fixed, recognizable characteristics, so that players do not (rather, are unable to) switch groups. Groups shift in relative power due to payoffs, but this does not directly affect the prevalence of cooperators in either group.
2.1. The group cohesion scenario
In the 'group cohesion' scenario, the payoffs for mutual cooperation within a group are enhanced (see Table 1). This reflects the evidence that members of the same group are able to communicate more effectively with one another and trust each other more [25]. Many real-life groups have institutions (formal or social) which support initiatives of the group, punish defectors in the group (thus lowering the effective benefit of defection) or support victims of defection from within the group (thus lowering effective cost of cooperation when the other player defects). We incorporate these into a net enhancement of the payoffs for mutual cooperation within the group, though the magnitude can differ between groups.
Almost every real system has at least some of these properties. This scenario is particularly well-suited to systems in which different groups speak different languages and/or have very different cultural norms, and in which social support is provided primarily by fellow group members. We summarize these effects in a parameter $ \alpha_i > 1 $ we call 'cohesiveness' (see Table 1). Note that cooperators need not act the same way with co-players from a different group and in general cooperate less in cross-group games due to prejudice (see sub-section 2.3).
2.2. The 'inter-dependence' scenario
In the 'inter-dependence' scenario, the payoffs of cross-group cooperation are enhanced (see Table 2). This reflects the fact that in many situations with two groups, each group has something uniquely valuable to offer, though the enhancement to cooperation may not be the same for both groups. This manifests itself in traditional family dynamics (with complementary though unequal roles for men and women), as well as the current trends of inter-disciplinary research teams and multi-cultural offices of leading technology companies. Studies on group identity have shown that people tend to punish defecting members of their own group less, leading to a higher relative payoff of defection [42,24]. These are just a few examples of factors that would contribute to increased payoffs for cross-group cooperation. A group's $ \alpha_i $-value in the inter-dependence scenario is referred to as the group's 'privilege'.
The regions of applicability of the two scenarios are of course not entirely disjoint. We analyze them separately to get a better understanding of the dynamics implied by each. In either case, the enhanced cooperation can shift the within-group or cross-group interactions from a prisoner's dilemma, where defection is always favored, to a stag hunt.
2.3. Strategy dynamics and group power dynamics
Each group consists of 'cooperators' and 'defectors'. Cooperators always cooperate in within-group games and cooperate in cross-group games with probability $ 0 < \beta_i \leq 1 $ (for group i). We refer at times to $ \beta $-values (trust), but also to prejudice levels $ = 1-\beta_{i} $. Defectors always defect. The strategy-update rule is as follows. Players compare their expected payoffs from a single round to the average payoffs of other players in their group. If the average payoff of other players is larger, they update their strategy with a probability proportional to the difference in payoffs between themselves and the average payoff, otherwise they keep playing the same strategy. The rate of change in frequency of strategists* in each group under the strategy update rule is given by the replicator equations[10,43]:
*For the sake of simplicity we describe the within-group dynamics as strategy dynamics, but based on our rule for encounter rates the within-group dynamics could also describe pure power dynamics with no strategy update, or a mixture of strategy update and power dynamics.
where $ n_{iS} $ represents the frequency of players in group $ i $ playing strategy $ S $ in within-group games, while $ P_{iS} $ denotes the expected payoff of those players (e.g. $ P_{2D} $ is the expected payoff of group 2 defectors). Note that the frequencies above are within each group, so that $ n_{1C}+n_{1D} = n_{2C}+n_{2D} = 1 $. The expected payoffs of each group are given by $ \bar{P_1} = n_{1C} P_{1C} + n_{1D} P_{1D} $ and $ \bar{P_2} = n_{2C} P_{2C}+n_{2D}P_{2D} $ [22]. Changes in socio-economic power are governed by the replicator equations:
where $ n_1 $ and $ n_2 $ denote the share (or prevalence) of socio-economic power wielded by group 1 and group 2 respectively; $ n_1+n_2 = 1 $, and we set $ \bar{P} = n_1 \bar{P_1} + n_2 \bar{P_2} $. Notice that the distribution of socio-economic power $ n_i $ (due to its effect on encounter rates) as well as the levels of cooperation in either group determine the expected payoffs at both the strategy ($ P_{iS} $) and actually also at the population ($ \bar{P_i} $) level (see next section).
Note that the definition of the state variables as relative frequencies (and the corresponding form of the replicator equations) allow us to define the system using just three equations and three variables. The state of the system can be specified by a three-tuple $ (n_{1C}, n_{2C}, n_1) $ and the dynamics of the system are defined by Eqs 2.1, 2.3 and 2.5.
3.
Results
The results of a preliminary analysis in which we assume a separation of timescales between strategy-update dynamics (Eqs 2.1, 2.3) and group-power dynamics (Eq 2.5) are displayed in Table 3 (see Appendix for details).
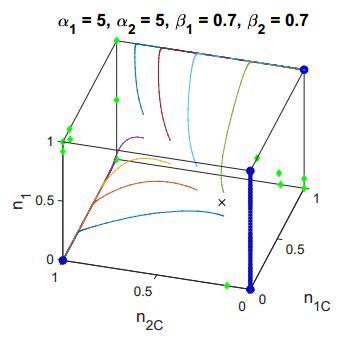
We focus here on the three dimensional 'full system', with no separation of timescales. We solve the system of replicator equations to find fixed points of the system. We analyze the stability of the fixed points analytically where possible. In the non-symmetric case ($ \alpha_1 \neq \alpha_2 $ and/or $ \beta_1 \neq \beta_2 $), this is not possible for all fixed points, so we explore the system numerically. Notice that by model construction if both groups are fully defective the distinction between the two groups becomes irrelevant (i.e. there is a line of trivial attractors, see Figures 1, 2).
3.1. Group cohesion scenario
Based on the payoff structure for the group cohesion scenario, in which the payoffs for within-group cooperation are enhanced (Table 1), we calculate the expected payoffs of group 1 cooperators, group 1 defectors, group 2 cooperators and group 2 defectors†:
†The expected payoffs for defectors are the same in both scenarios so are not repeated in the next section.
Each term in the expected payoffs represents the probability of a certain type of encounter, multiplied by its payoff for the subject player. For example, the $ n_2 n_{2C} \beta_1 \beta_2 (b-c) $ term in $ P_{1C} $ is the probability that a given group 1 cooperator will encounter a group 2 cooperator ($ n_2 n_{2C} $) multiplied by the probability that both players cooperate ($ \beta_1 \beta_2 $), multiplied by the payoff for the group 1 cooperator when both players cooperate $ (b-c) $. The $ \alpha_i $ values appear in the terms corresponding to within-group cooperation.
We then substitute these values into the replicator Eqs 2.1, 2.3 and 2.5. We find the fixed points of the system by setting Eqs 2.1, 2.3, 2.5 to zero and solving for $ n_{1C} $, $ n_{2C} $ and $ n_{1} $. We use the Jacobian eigenvalues and eigenvectors to classify the local stability of each fixed point.
There are 19 analytic solutions to the resulting system of equations. Of these solutions, two correspond to a negative share of power for one group and are discarded. 11 of the 17 realistic solutions do not correspond to the extinction (complete loss of socio-economic power) of one of the groups.
We find that cooperation with group coexistence is not possible. The cooperation and coexistence equilibrium is a saddle point, while the only two non-trivial attractors of the system occur when there is one group dominating and cooperating, and one group extinct and defecting. In symmetric games, while high levels of group cohesion ($ \alpha $) allow one group to become cooperative, it is inevitably at the expense of eliminating the other group. More prejudiced groups (small $ \beta $-values) are more likely to dominate. Initial advantage, however, moves each group's threshold of cooperation according to the ratio of the other group's initial power to its own, while an increase in prejudice (decrease in $ \beta $) corresponds to a linear decrease of the cooperation threshold.
We continue our exploration by examining a few particular cases. In all cases we set $ b = 2 $ and $ c = 0.5 $. We begin with a group-symmetric model, setting $ \alpha_1 = \alpha_2 $, $ \beta_1 = \beta_2 $. The initially more powerful group dominates, after which the losing group moves gradually towards defection (Figure 1). We then break the symmetry of the system to examine the context in which one group has strong within-group cohesiveness and high levels of prejudice, but the results do not differ qualitatively from those of the symmetric case; the basin of attraction for dominance of a group increases as it gets relatively stronger and more prejudiced (high $ \alpha_i $ and low $ \beta_i $). Thus, in the group cohesion scenario, only one group will dominate and cooperate, while the other will lose all of its power and defect.
3.2. Inter-dependence scenario
We now examine the scenario in which cooperation between groups has enhanced payoffs, while within-group game has the payoff structure of the standard prisoner's dilemma (Table 2). Following the same procedure, we calculate the expected payoffs of group 1 cooperators and group 2 cooperators‡:
‡Payoffs for defectors are still given by Eqs 3.2 and 3.4
and substitute these values into the replicator Eqs 2.1, 2.3 and 2.5.
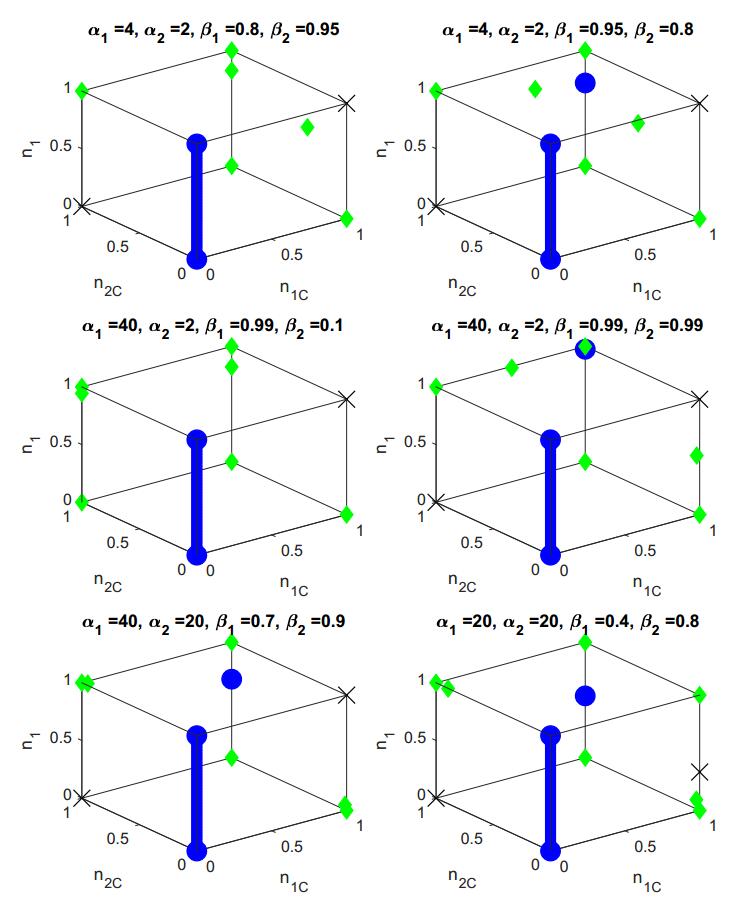
The system has 15 fixed points, two of which correspond to negative group power. Seven fixed points correspond to extinction of one group. Interestingly, none of these are asymptotically stable. There are fixed points where one group cooperates while the other defects and goes extinct, but the inter-dependence means that the cooperation of the dominating group is not stable. The defection of the extinct group is unstable if (for group 2 defecting and extinct) $ \beta_1 (\alpha_2 - 1)(b-c) > c $. This and its group-symmetric equivalent (obtained by swapping group indices) are in fact the conditions for the stability of cooperation (or instability of defection) of the extinct group at all the extinction fixed points. The fact that dominant groups have unstable cooperation while extinct groups may have stable cooperation agrees qualitatively with existing results using density-dependent replicator dynamics [4,22].
Fixed points where one group cooperates while the other defects, but both coexist, enter the system when both $ \beta_i < \frac{b-c}{b} $. These points are however always unstable in at least one direction. Stability would require, for example, that $ \frac{b-c}{\beta_2}-b < -\beta_1 c - \beta_1 \beta_2 (\alpha_1 -1)(b-c) $, which cannot be satisfied with allowed parameter values while the point is in the positive unit cube.
A full-cooperation fixed point occurs at
When the system is symmetrical ($ \alpha_1 = \alpha_2 = \alpha $ and $ \beta_1 = \beta_2 = \beta $) the full-cooperation fixed point is stable if $ -(b-c)(\beta + \alpha \beta^2 - \beta^2 -1) < 0 $ and $ c(1+\beta) - \beta^2(b-c)(\alpha-1) < 0 $. Together these lead to the conditions: $ \alpha > 1+ \frac{1-\beta}{\beta^2} $ for stability in strategy dynamics and $ \alpha > 1+ \frac{c(1+\beta)}{(b-c)\beta^2} $ for stability in group power dynamics. The second condition is usually harder to reach, but for large $ (b-c) $ and high $ \beta $ it may be achieved with lower $ \alpha $. The stability of cooperative coexistence depends approximately hyperbolically on prejudice ($ 1-\beta $).
Unfortunately the analytic forms of the eigenvalues of the full-cooperation fixed point are prohibitively complicated in the non-symmetrical case, but a scan of parameter space assures us that the full-cooperation fixed point can remain stable with non-symmetric parameter values, provided $ \alpha_i $ and $ \beta_i $ values are large enough; stability of full-cooperation is much more sensitive to $ \beta_i $ values, as in the separated-timescales analysis (Figure 2).
4.
Discussion
We modeled the shifts of socio-economic power in a system with two recognizable groups interacting with prejudice. We considered two scenarios: in the group cohesion scenario players received increased payoffs for within-group cooperation, while in the inter-dependence scenario players received increased payoffs for cooperating with members of the other group.
As might be expected, our analysis suggests very different results for the two scenarios. The results for the group cohesion scenario paint a grim picture: while high levels of group cohesion ($ \alpha $) allow one group to become cooperative, it is inevitably at the expense of eliminating the other group. More prejudiced groups (small $ \beta $-values) are more likely to dominate. Initial advantage, however, moves each group's threshold of cooperation according to the ratio of the other group's initial power to its own, while an increase in prejudice (decrease in trust $ \beta $) corresponds to a linear decrease of the cooperation threshold.
The inter-dependence scenario allows stable coexistence of the two groups, but is highly sensitive to prejudice. Even relatively small increases in prejudice (decreases in trust $ \beta $) may necessitate large increases in privilege ($ \alpha $) in order to maintain stable coexistence. Provided prejudice is controlled, stable coexistence can be maintained even with high privilege difference (e.g. $ \alpha_1 > > \alpha_2 $). Hence we observe that in the context of our model, for cooperative coexistence, prejudice plays a stronger role than privilege.
Our work provides a number of suggestions for successful reconciliation and reduction of inequality. Two results stand out: the first is that members of opposite groups should have some incentive to cooperate with one another, and cross-group cooperation must be highly productive, particularly when mutual trust is low (prejudice levels are high). The second is that even moderate levels of prejudice necessitate large incentives, while low levels of prejudice allow cooperation even with modest incentives and inequality.
Organizations working to foster cross-group cooperation should note that that initiatives to increase trust (reduce prejudice) may be needed in order to make a difference; prejudice reduction in high-prejudice contexts is likely to be much more cost effective than direct subsidy of cross-group cooperation. If for example a government were to consider subsidizing multi-group businesses, our model would suggest that this would be effective only when prejudice levels are already reasonably low.
In multi-ethnic societies, affirmative action is sometimes enacted to facilitate economic upliftment of underprivileged groups through integration into sectors of the economy mostly dominated by privileged groups [44]. This in the context of our model can be thought of as incentivizing cross-group cooperation. Despite its significant successes, the practical implementation of affirmative action has come under criticism for its narrow scope of impact and for perpetuating racialist dynamics [44,46,45]. Our model would suggest that affirmative action cannot efficiently drive broad social transformation while prejudice levels remain high, and while different ethnic groups are unable to effectively communicate (necessary for productive cross-group cooperation). In this regard our model agrees qualitatively with other theorists who have suggested that improving mutual language literacy between groups would increase the possibilities for productive cross-group cooperation, and thus move the society toward higher levels of cooperative coexistence [47,48]. These interpretations should not be taken as scientific comments on social issues, but rather as food for thought and inspiration for deeper investigations.
Our model differs from other models of dynamics between recognizable groups in a number of ways. Firstly we assume two discrete recognizable groups, rather than continuous traits [40,49]. The heterogeneity within groups is limited to strategy choice, so we do not address issues of adoption or rejection of group identity within groups (eg self-racialisation and assimilation in [36] or ethnocentric vs humanitarian in [50]). Thirdly, in our model the two groups exist a priori, and players do not change groups (Eqs 2.1–2.4).
Of particular interest to this work is the theory of green beards (so dubbed by Dawkins [51]), which explores the potential for cooperation to emerge amongst bearers of a recognizable set of genes. Bearers of green beard genes (green beards) have a tendency to treat other green beards differently from non-green beards, for example by cooperating only with fellow green beards and thus reducing their chances of cooperating with a defector (see [52,53]).
The model proposed in this paper is intentionally simple, paving the way for a number of natural extensions, many of which could be combined. Assortative encounter could increase the amount of within-group interactions, or could increase the probability that cooperators encounter other cooperators (the usual assumption), with a stronger effect for within-group encounters. The second obvious step would be to include changing prejudice, for example using adaptive dynamics [54], and to relate this to the group-level assortment (more prejudiced people avoid the other group). Real processes are constantly co-evolving, and this type of thinking could be incorporated into many aspects of the model and extensions (see [55] for a recent review).
The effect of population size could be incorporated; while models involving finite populations and stochasticity are more realistic they preclude certain useful analyses and converge to infinite-population models under a range of assumptions [19]. Density-dependent selection, as opposed to frequency dependent selection, may be a more relevant modification to the population structure of our model, where the size of the economy along with opportunities for economic, social and artistic innovation and development take the place of the carrying capacity in traditional ecological models [4,22]. Another layer of realism could be captured by incorporating different payoffs for strategy update than for power transfer, allowing for the inclusion of perception of benefit based on group membership.
These extensions - some of which would implicitly emerge - could then be studied in the context of networks of interacting agents, opening new and interesting avenues for research [56]. Networks naturally support the incorporation of complex and varied strategy-update rules [16], variability in the individual tendencies to separately assimilate and reproduce social norms [57], and form a natural bridge to methods of statistical physics [17]. A significant step towards reality is made with the consideration of complex self-forming social network structures [58]: the list of phenomena which might emerge is near-endless, particularly with complex individual rules for the development of the network [16]. As well as providing extraordinary flexibility, evolutionary game theory on networks has displayed a variety of realistic features including criticality [59], spatial chaos [60], self-organized punishment and rewarding, and territorial competition [17]. Most extensions would however mean sacrificing the analytic tractability of results.
We suggest that those interested in empirical work related to this model look to social media and other online interaction spaces - news site comment sections, forums, etc. - for data. Automated data collection (web crawlers) could be used along with classification techniques to identify sentiments and group membership within such environments - for example the comments, likes, views and endorsements of beauty bloggers on youtube - and observe the progression of these behaviors. Government surveys could also provide valuable data for analysis with a more economic emphasis. A number of experimental methods for the calibration and evaluation of cooperation models have recently been proposed, including accessible and scalable online alternatives to traditional experiments [61,62,63].
5.
Conclusion
We described a socio-economic system of two recognizable groups in two hypothetical scenarios. In the group cohesion scenario, people benefit most from cooperating within their group, while in the inter-dependence scenario cross-group cooperation is more productive. We found that in the group cohesion scenario, one group always dominates the other. In the inter-dependence scenario the groups can both cooperate, even with high inequality, but only if they have low prejudice levels.
The relevance of cooperation between groups is clear in many societies worldwide. Models such as ours may yield insights into the complex dynamics that govern the course of society, and should be developed with the aim of overcoming the barriers inherent to coexistence of multiple groups.
Our findings suggest that, while equitable distribution of the benefits from cooperative behavior plays an important role, organizations working towards improving inter-group relations should focus first on increasing group inter-dependence and reducing prejudice.
Acknowledgments
The authors are grateful to the editorial team for the opportunity to contribute to this special issue, and to the four anonymous reviewers for sharing their time and expertise. P.L. and C.H. acknowledge support from the National Research Foundation (NRF) of South Africa (grant nos. 89967, 109244 and 109683). J.B. acknowledges support from the National Research Foundation (NRF) of South Africa, the African Institute for Mathematical Sciences (AIMS) South Africa and the Southern African Center for Epidemiological Modeling and Analysis (SACEMA).
Conflict of interest
All authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: