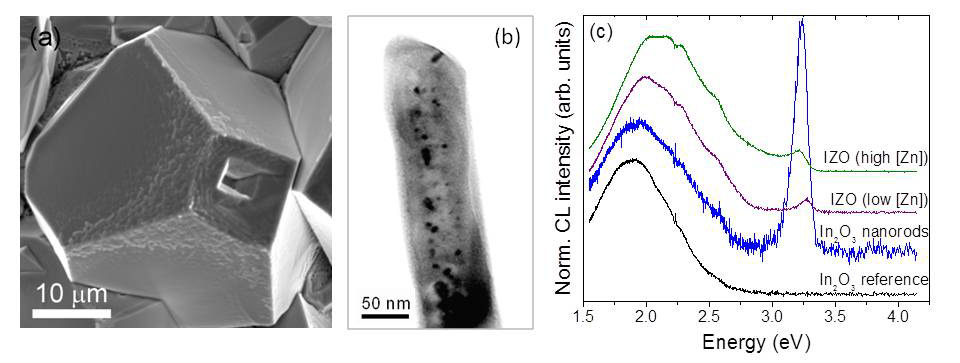
Microtubes and rods with nanopipes of transparent conductive oxides (TCO), such as SnO2, TiO2, ZnO and In2O3, have been fabricated following a vapor-solid method which avoids the use of catalyst or templates. The morphology of the as-grown tubular structures varies as a function of the precursor powder and the parameters employed during the thermal treatments carried out under a controlled argon flow. These materials have been also doped with different elements of technological interest (Cr, Er, Li, Zn, Sn). Energy Dispersive X-ray Spectroscopy (EDS) measurements show that the concentration of the dopants achieved by the vapor-solid method ranges from 0.5 to 3 at.%. Luminescence of the tubes has been analyzed, with special attention paid to the influence of the dopants on their optical properties. In this work, we summarize and discuss some of the processes involved not only in the anisotropic growth of these hollow micro and nanostructures, but also in their doping.
1.
Introduction
Can cats or dogs barter? Trade is one of the essential features of human intelligence. Brosnan et al., (2008) reported that chimpanzees, who are an intelligent species like humans, can trade but are reluctant to trade. This subsequently led to major divergence in the fates of the two species. The market is nothing but an expression of human intelligence. As Malone and Bernstein (2015) mentioned, intelligence does not arise only in individual brains; it also arises in groups of individuals. The securities market, including crypto-assets, is the ultimate expression of human intelligence. Fama (1965) stated that the efficiency of the securities market in the strong or semi-strong sense causes instantaneous changes in traders' subjective equilibrium with the incorporation of securities information, and the speed at which they respond to this information determines the winners and losers. In the weak sense, market equilibrium follows changes in traders' subjective equilibria due to noise. The efficiency of the securities market can be summarized as the correct and rapid incorporation of information into prices, the presence of arbitrage opportunities, countless traders always searching for such opportunities, the gradual loss of arbitrage opportunities, and the market becoming more efficient. However, it should be noted that without noise, transactions would not occur, and the price distortion would persist in the presence of strong bias.
In an efficient market where noise and bias have no effect, and information is perfectly symmetrical, security prices should accurately reflect only information. However, if traders had perfectly and simultaneously symmetrical knowledge and information, including the asset valuation model, the transaction would not function because the traders' valuation of the asset would be the same. They must be doing some rational calculations via intelligence in natural and digital computing. In this sense, a rational representative agent in macroeconomics corresponds to the perfect symmetry of information (Lucas (1976), Kirman (1992), Hartley (1996)).
While Black (1986) treated this "symmetry breaking" as noise, the effect of noise on a security's price is expected to be symmetrical based on its nature. However if there exist so many irrational noise traders synchronizing erroneous stochastic beliefs that both affect prices and earn higher expected returns, the unpredictability of noise traders' beliefs creates a risk in the price of the asset that deters rational arbitrageurs from aggressively betting against them. As a result, prices can diverge significantly from fundamental values even in the absence of fundamental risk. Moreover, bearing a disproportionate amount of risk that they themselves create enables noise traders to earn a higher expected return than rational investors (De Long et al., (1990)).
On the other hand, Tversky and Kahneman (1974) found that the effect of bias is asymmetric. They described three heuristics that are employed in making judgments under uncertainty: 1) representativeness, 2) availability of instances or scenarios, and 3) adjustment from an anchor. These heuristics are highly economical and usually effective, but they lead to systematic and predictable errors. However, the effect of these heuristics has not been detected as a global bias in the securities market. Consequently, identifying the specific effects of noise and bias on security prices is challenging.
If attention is paid to any statistical property in any complex system, the log-normal distribution is the most natural and appropriate among the standard or "normal" statistics to overview the whole system (Kobayashi et al., (2011)). Log-normality emerges as a familiar and typical example of statistical aspects in various complex systems. Since every member of any complex system has its own history, each member is in the process of growth (or retrogression). The log-normal distribution is realized because of Gibrat's law, or the Matthew effect. It is applied to cities' size and growth rate, where the proportionate growth process may cause a distribution of city sizes that is log-normal. When considering the entire size distribution, not just the largest cities, the city size distribution is log-normal (Samuels (1965)). However, it has been argued that it is problematic to define cities through their fairly arbitrary legal boundaries. According to Gabaix (1999), Zipf's law is a very tight constraint on the class of admissible models of local growth. It says that for most countries, the size distribution of cities strikingly fits a power law: the number of cities with populations greater than S is proportional to 1/S. Suppose that, at least in the upper tail, all cities follow some proportional growth process (this appears to be verified empirically). This automatically leads their distribution to converge to Zipf's law.
According to Gibrat's law of proportionate effect, the relative change in a firm's size is not affected by its absolute size, which implies that both small and large firms experience similar average rates of growth. However, Samuels (1965) provides evidence that contradicts this law by showing that larger firms grow significantly faster. Aoki and Nirei (2017) developed a neoclassical growth model that produces Pareto's law of income distribution and Zipf's law of firm size distribution based on firm-level productivity shocks. Executives and entrepreneurs invest in both risk-free assets and their own firms' risky stocks, which affect their income and wealth. They used the model to investigate how changes in tax rates can explain the evolution of top incomes in the US. The model accounts for the recent decline in the Pareto exponent of the income distribution and the trend of the top 1 percent income share. In the same research direction, Nirei and Aoki (2016) developed a neoclassical growth model that incorporates heterogeneous households and explains the Pareto distributions of income and wealth in the upper tail. They introduced households' business productivity risks and borrowing constraints in a standard Bewley (1977) model to generate Pareto distributions. Low-productivity households rely on wages and safe asset returns, whereas high-productivity households do not diversify their business risks. The model can accurately explain the observed income distribution in the United States with reasonable parameter values. The authors conducted comparative statics to investigate how changes in parameters affect Pareto distributions and found that the increase in top income dispersion in recent decades may be attributed to changes in the top tax rates in the 1980s. Their analytical finding offers a consistent explanation for numerical comparative statics.
Few studies are available on global bias in the stock market. The fundamental indicators of stocks include information about the effects of noise and bias on stock prices; however, distinguishing between them is generally hard. In this article, I present the fundamentals hypothesis based on rational expectations (Muth (1961)) and, using a log-normal distribution model, detect global bias components from the price-earnings (P/E), price-to-book (P/B) and price-to-cash flow (P/CF) ratios. The traditional theory of the firm assumes that the firm acts in the stockholders' interests and that stockholders are interested in profits such that the object of the firm is to maximize profit. However, there is a range in the profit concept (Bodenhorn (1964)). The analysis results support our fundamentals hypothesis as the detected biases show similar characteristics. Additionally, the results show that the cash flow indicators contain relatively few bias components and are closer to the fundamentals. I further demonstrate and examine why the positive P/IC ratio among the indicators analyzed is a proxy for the fundamentals that do not include bias components. Globally, this implies that the efficient market hypothesis holds. The shape of the curve, and in particular the strength of the bias, is stable throughout time and independent of whether the economy is good or bad. The answer is simple: Cash is a fact, and profit is an opinion. Namely, opinions of management and accountants are added as noise to fundamentals.
2.
Materials and method
2.1. Hypothesis
When $ X_t $ denotes the true fundamentals of listed companies at time $ t $, and $ R_t $ denotes their growth rates, the following Gibrat process represents the growth of those companies
It is important to note that I assume that the growth rates $ R_t $ are mutually independent random variables that follow the same distribution with finite variance. The initial value of the fundamentals being set as $ X_0 $ yields
at time $ T $. Taking the log of both sides of the equation results in
Therefore,
would hold for a sufficiently large $ T $ based on the central limit theorem. Essentially, the true fundamental $ X_T $ of listed companies follows the log-normal distribution.
Furthermore, by assuming rational expectations through the future point in time $ T $ as of the present point in time 0 on the premise of a going concern, the following equation becomes true:
Therefore, the rational expectations $ X_0 $ for fundamentals follow the log-normal distribution. In other words, the fundamentals $ X_t $ at time $ t $ follow the log-normal distribution.
2.2. Data
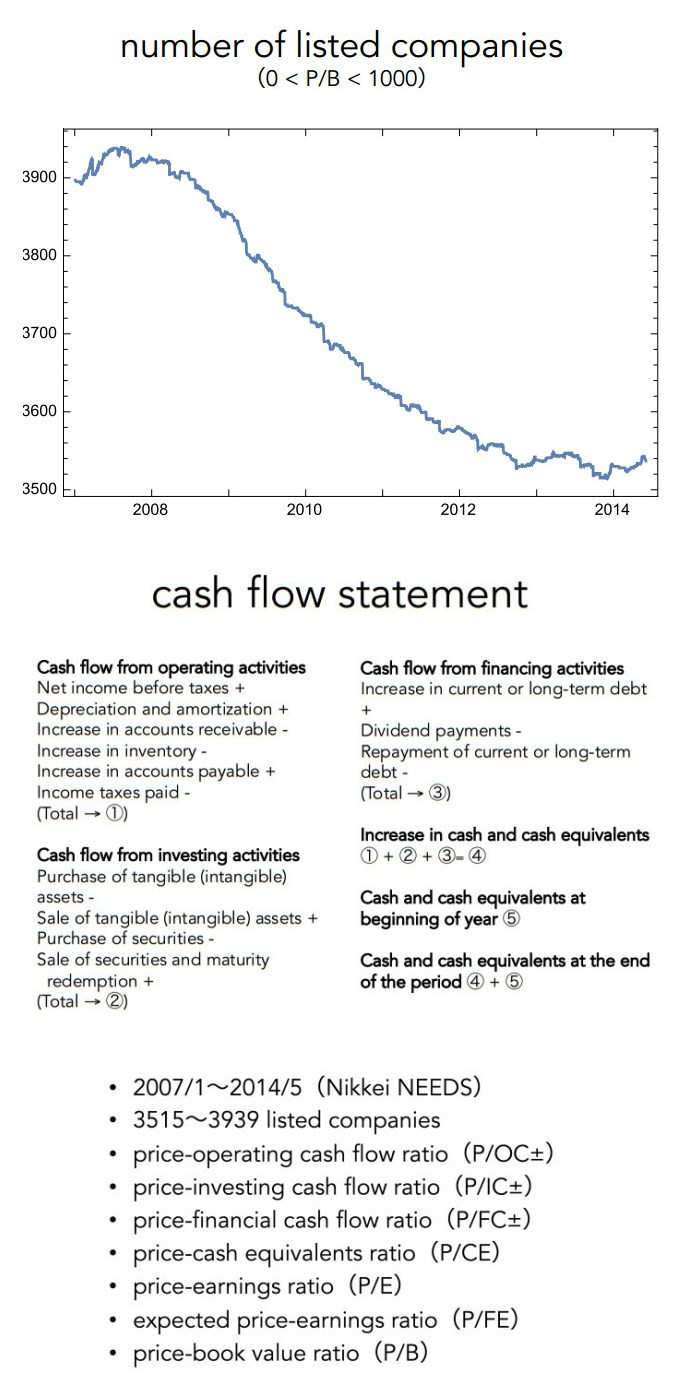
Among the actual fundamental indicators, we analyze the price-earnings (P/E), forward price-earnings (P/FE), price-to-book (P/B), price-to-cash flows from operating activities (P/OC), price-to-cash flows from investing activities (P/IC) price-to-cash flows from financing activities (P/FC), and the price-to-cash equivalents at the year-end (P/CE) ratios. We divide the cash flow ratios into positive and negative data. We use daily data with absolute values less than 1,000 for all companies listed in Japan for the period spanning 1,817 business days from January 2007 to May 2014 (data source: Nikkei NEEDS https://nkbb.nikkei.co.jp/en/service/nikkei-needs/).
2.3. Test
If our fundamentals hypothesis is true, the actual fundamental indicators should follow the log-normal distribution. To test our hypothesis, we calculate the $ p $-values using the Kolmogorov-Smirnov test, Pearson's $ \chi^2 $ test and Anderson-Darling test, to test the goodness of fit to the log-normal distribution.
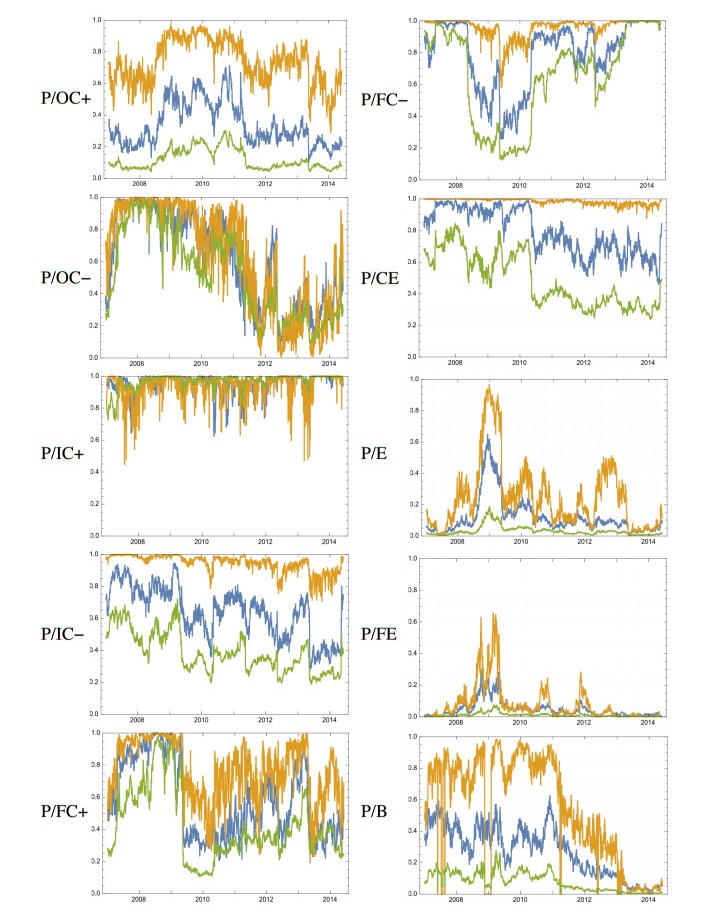
Our tests can be strongly affected by the sample size that differs by indicator, so we extract samples at the 300 quartiles from each data set to calculate the $ p $-value for testing the goodness of fit of the overall average of each indicator to the log-normal distribution with variance. For all cases, the null hypothesis is that "the indicator follows the log-normal distribution, " or the otherwise worded "the indicator is a proxy of true fundamentals." The indicator reflects the fundamentals more when the $ p $-value is closer to 1, and when $ p $-value is closer to 0, the bias is stronger. We show the lowest $ p $-value for each test in Table 1 for the data spanning 1,817 business days.
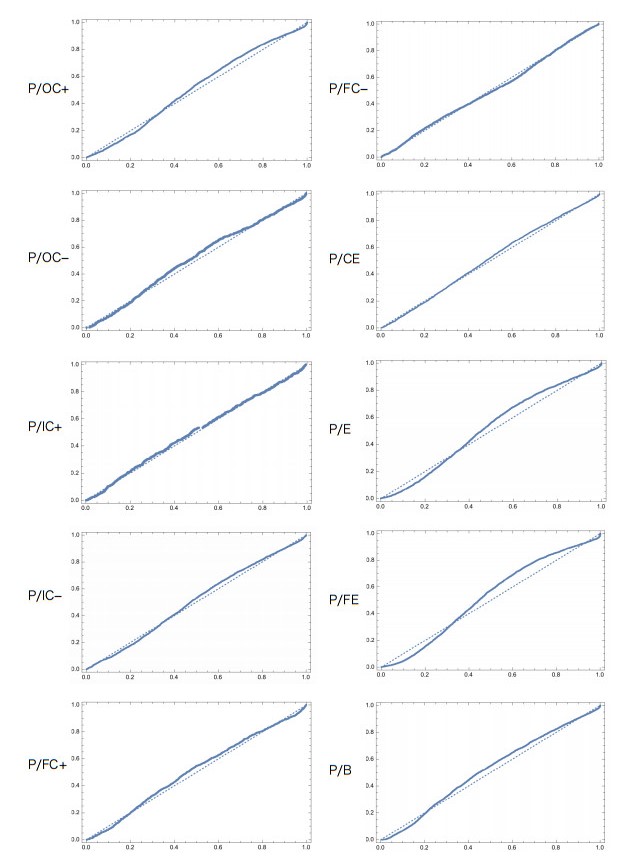
The test results indicate that bias is strong on the P/E, P/FE, and P/B ratios. The forward price-earnings ratio (P/FE) is the most biased. Among all price-to-cash flow ratios, the bias is significant only for the P/OC ratio. It can be easier to manipulate than others. I illustrate the time series of $ p $-values since the $ p $-value is the indicator of the strength of bias. From Table 1, Figure 1, and Figure 2, the positive P/IC ratio is the best proxy for the fundamentals that do not include bias components. Probably, it should be hard to manipulate according to the opinions of management and accounting.
2.4. Shape of Bias
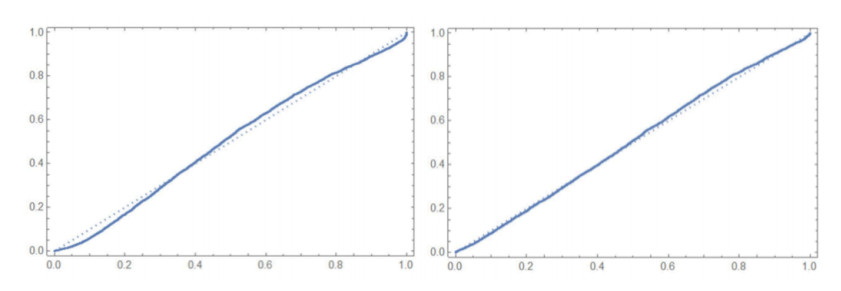
The detected biases exhibit similar characteristics. Each indicator is shown in Figure 2 and compared to the log-normal distribution. While the figures only show the data for the first day of all periods, January 4, 2007, the biases remain unchanged. It is worth noting that the shape and strength of the curve are independent of whether the economy is good or bad. The artificial stock market appears to have natural intelligence.
3.
Discussion
The results indicate that the fundamental indicators, including the P/E, P/FE, and P/B ratios, are strongly affected by bias. Bias also has a significant effect on the positive and negative P/OC ratios. Additionally, there is a weak bias on the negative P/IC, positive and negative P/FC, and P/CE ratios.
When we compare the test results, the positive P/IC ratio is the stable proxy of fundamentals among all these indicators. Positive cash flows from investing activities represent the realized gain or loss from past investments such as marketable securities, tangible fixed assets, the sales of investment securities, and income from the collection on loans declared at the end of the accounting period. In other words, positive cash flow is the indicator that most directly reflects past business decisions. We can interpret the year-end cash equivalent ratio and the other cash flow ratios reflecting the fundamentals because they have less bias of the components.
On the other hand, although the P/E ratio and P/B ratio are definite values, investors might not view them as indicators that reflect the fundamentals because there is a high degree of freedom in accounting. The P/OC ratio might also have a lower credibility than other cash flow indicators.
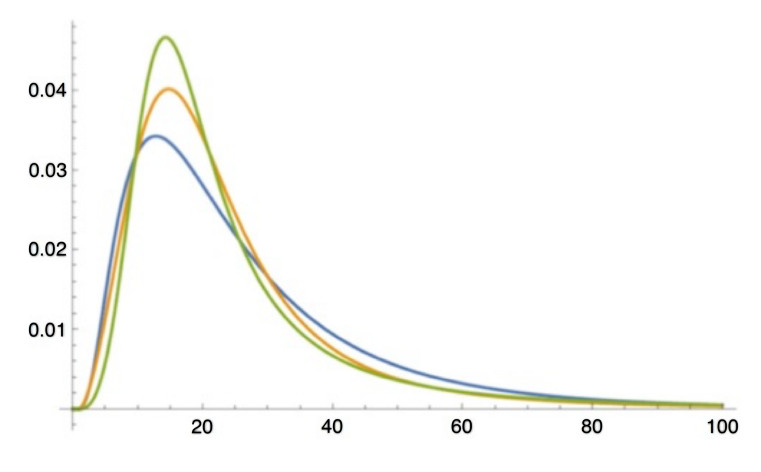
The answer is simple: "Cash is a fact, and profit is an opinion." Namely, opinions of management and accountants are added as noise to true fundamentals. As a result, the Kesten (1973) process
is realized so that the Pareto distribution is obtained. This result means that a positive bias accompanied their opinions.
In fact, these biases fit the Pareto distribution quite well. The following functions represent generalized Pareto distribution (GPD).
4.
Conclusions
What are the implications of the results? Does the existence of bias negate the efficient market hypothesis? From the viewpoint of intelligence in natural and digital computing, how should we deal with this problem? The artificial stock market, where countless traders use digital computers to trade, appears to have natural intelligence. Intelligence does not arise only in individual brains but also arises in groups of individuals. The interest in whether markets are efficient is based on the idea that inefficiencies are the reason active returns are possible. If our fundamentals hypothesis is true, the fundamental indicators, including the P/E, P/FE, and P/B ratios, are strongly affected by bias. This result means that investors might not view them as indicators that reflect the fundamentals since they have a high degree of freedom in accounting. Can we conclude that the market is inefficient because of this? This issue has important economic implications. Globally, our result implies that the efficient market hypothesis holds. The shape of the curve, and in particular the strength of the bias, is stable throughout time and independent of whether the economy is good or bad. It is the path of the ants (Kirman (1993); Sano (2022)) to avoid obstacles, and traders move back and forth along it in response to noise (Black (1986); De Long et al., (1990)). This noise, among other things, plays a role in activating the market system, which knows the fundamentals of firms and represents a stable global bias in the stock market. Nevertheless, when the biases revealed by this study disappear, the stock market will become more efficient. It is the responsibility of firms and financial authorities to disclose fair information.
Use of AI tools declaration
The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The author is grateful to the Department of Economics of Fukui Prefectural University. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflicts of interest
The author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: