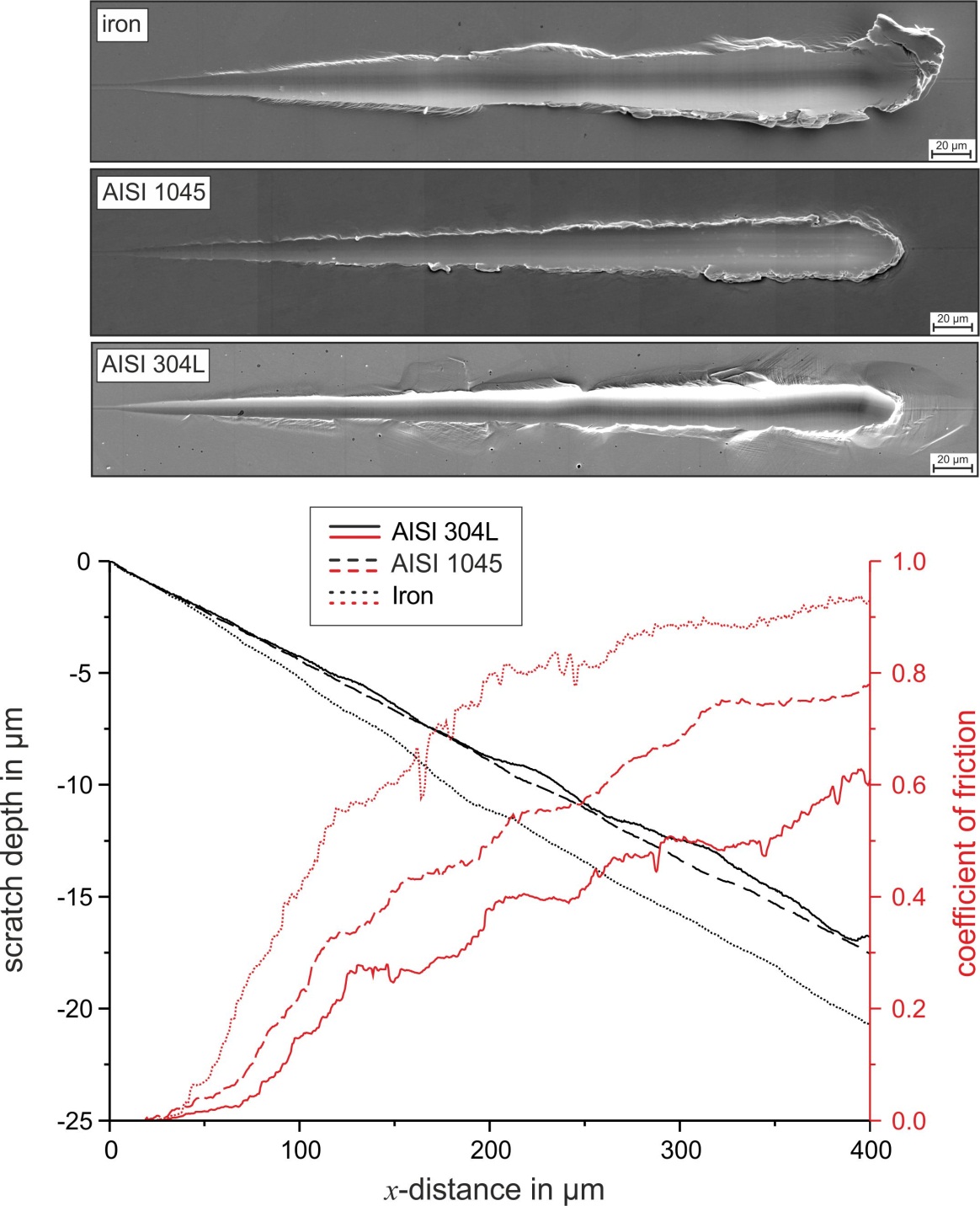
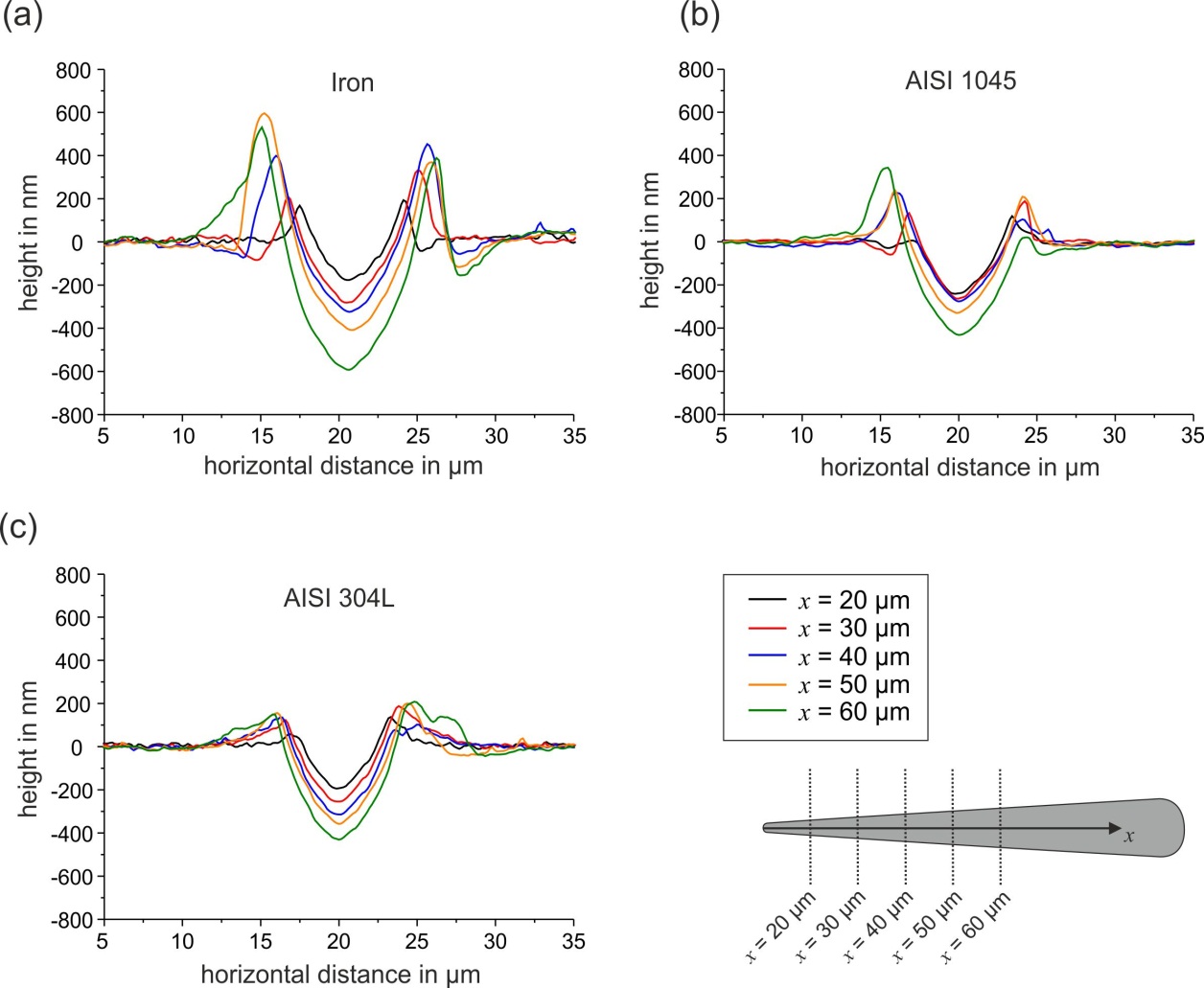
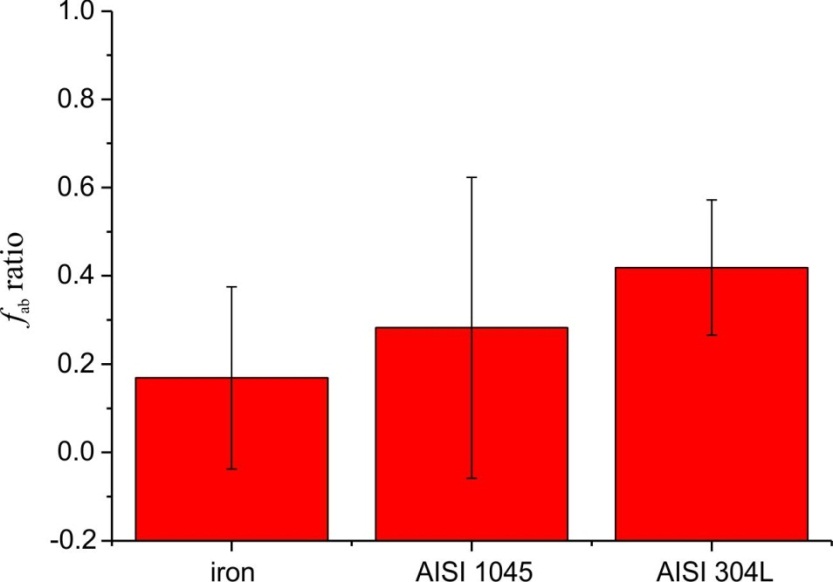
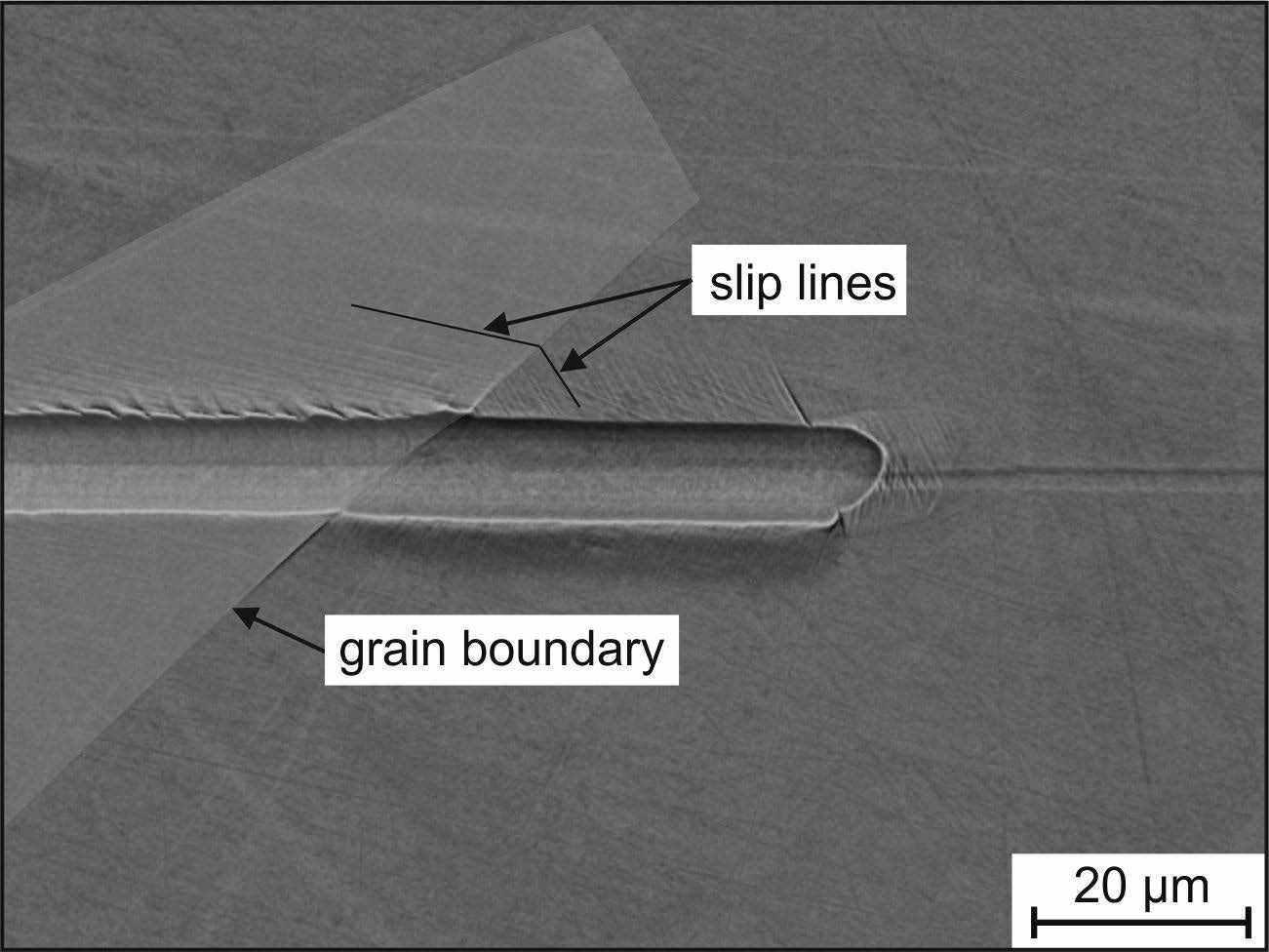
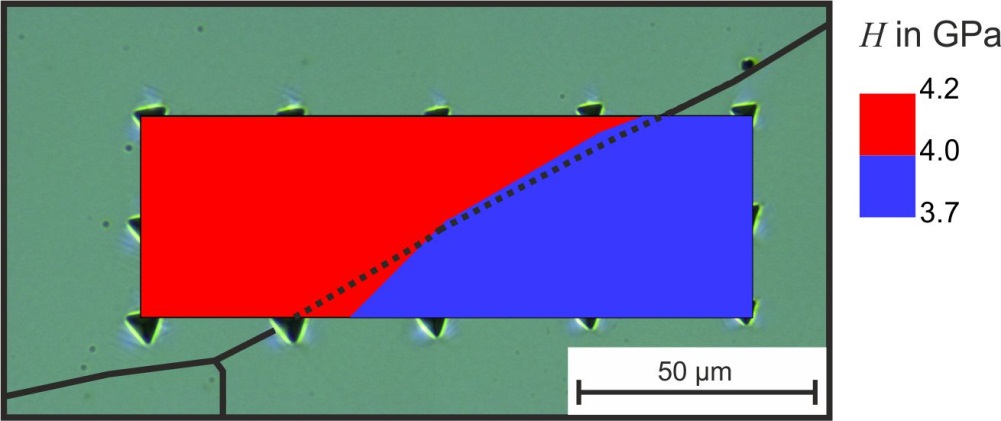
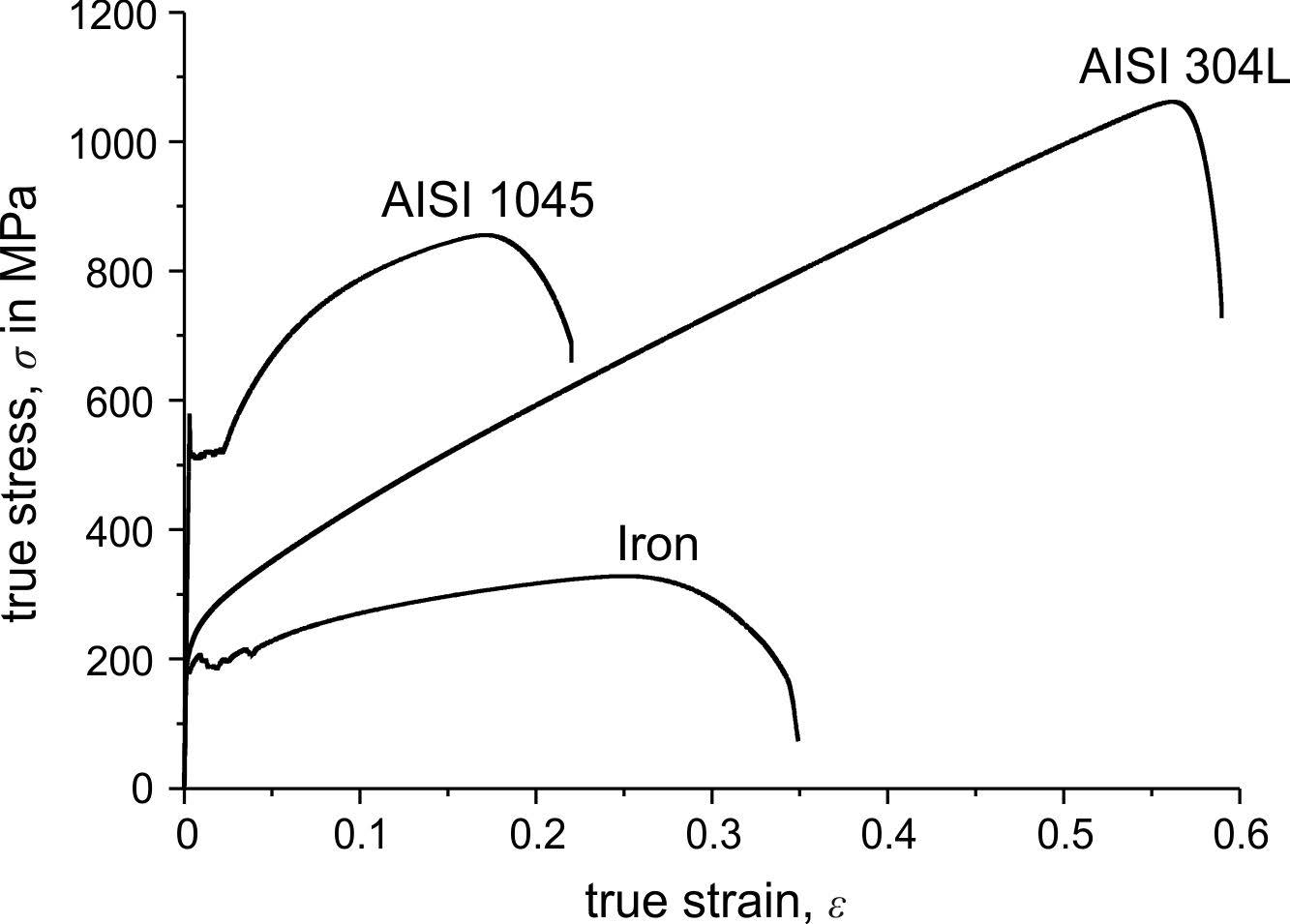
This paper investigates the scratch resistance of metallic materials that include pure iron and the two steels AISI 1045 and AISI 304L. To investigate the deformation behavior under scratch load, tests were performed with a gradually increasing scratch load combined with subsequent analysis by scanning-electron microscopy and by atomic force microscopy. The fab value was determined to quantify the active micro-mechanisms of abrasion. In addition, tensile tests, hardness measurements, and nanoindentation experiments were conducted to correlate the scratch behavior with the mechanical properties. It was shown that there is no general correlation between the individual mechanical properties and the results of the scratch tests. However, the results revealed that work hardening of metallic materials plays a significant role, especially in the development of pile-up, and thus it greatly affects the active micro-mechanisms. The specific work of fracture at least correctly reproduces the order of scratch depth and the tangential force of the investigated materials.
1.
Introduction
Consider the following $ 2\times 2 $ block saddle point problems
where $ A\in R^{n, n} $ is symmetric positive definite, $ B\in R^{m, n}, m\leq n. $ It appears in many different applications of scientific computing, such as constrained optimization [49], the finite element method for solving the Navier-Stokes equation [29,30,31], and constrained least squares problems and generalized least squares problems [1,38,44,45] and so on; see [9,10,11,12,13,14,15,16,17,19,20,35,39,40] and references therein.
In recent years, there has been a surge of interest in the saddle point problem of the form (1), and a large number of stationary iterative methods have been proposed. For example, Santos et al. [38] studied preconditioned iterative methods for solving the singular augmented system with $ A = I $. Yuan et al. [44,45] proposed several variants of SOR method and preconditioned conjugate gradient methods for solving general augmented system (1) arising from generalized least squares problems where $ A $ can be symmetric and positive semidefinite and $ B $ can be rank deficient. The SOR-like method requires less arithmetic work per iteration step than other methods but it requires choosing an optimal iteration parameter in order to achieve a comparable rate of convergence. Golub et al. [32] presented SOR-like algorithms for solving linear systems (1). Darvishi et al. [28] studied SSOR method for solving the augmented systems. Bai et al. [2,3,23,49] presented GSOR method, parameterized Uzawa (PU) and the inexact parameterized Uzawa (PIU) methods for solving linear systems (1). Zhang and Lu [46] showed the generalized symmetric SOR method for augmented systems. Peng and Li [37] studied the unsymmetric block overrelaxation-type methods for saddle point. Bai and Golub [4,5,6,7,8,33,40] presented splitting iteration methods such as Hermitian and skew-Hermitian splitting (HSS) iteration scheme and its preconditioned variants, Krylov subspace methods such as preconditioned conjugate gradient (PCG), preconditioned MINRES (PMINRES) and restrictively preconditioned conjugate gradient (RPCG) iteration schemes, and preconditioning techniques related to Krylov subspace methods such as HSS, block-diagonal, block-triangular and constraint preconditioners and so on. Bai and Wang's 2009 LAA paper [40] and Chen and Jiang's 2008 AMC paper [23] studied some general approaches about the relaxed splitting iteration methods. Wu, Huang and Zhao [42] presented modified SSOR (MSSOR) method for augmented systems. Cao, Du and Niu [19] introduced a shift-splitting preconditioner and a local shift-splitting preconditioner for saddle point problems (1). Moreover, the authors studied some properties of the local shift-splitting preconditioned matrix and numerical experiments of a model stokes problem are presented to show the effectiveness of the proposed preconditioners. Recently, Chen and Ma [22] presented a generalized shift-splitting preconditioner for saddle point problems with symmetric positive definite (1, 1)-block and gave theoretical analysis and numerical experiments.
For large, sparse or structure matrices, iterative methods are an attractive option. In particular, Krylov subspace methods apply techniques that involve orthogonal projections onto subspaces of the form
The conjugate gradient method (CG), minimum residual method (MINRES) and generalized minimal residual method (GMRES) are common Krylov subspace methods. The CG method is used for symmetric, positive definite matrices, MINRES for symmetric and possibly indefinite matrices and GMRES for unsymmetric matrices [39].
In this paper, based on generalized shift-splitting preconditioners presented by Chen and Ma [22], I establish a parameterized shift-splitting preconditioner for saddle point problems with symmetric positive definite (1, 1)-block. Furthermore, the preconditioner is based on a parameterized shift-splitting of the saddle point matrix, resulting in an unconditional convergent fixed-point iteration, which has the intersection with the generalized shift-splitting preconditioner. However, the relaxed parameters of the parameterized shift-splitting methods are not optimal and only lie in the convergence region of the method.
2.
Parameterized shift-splitting (PSS) preconditioner
Recently, for the coefficient matrix of the augmented system (1.1), Chen and Ma [22] made the following splitting
where $ \alpha > 0, \beta > 0 $ are two constant numbers and $ I $ is the identity matrix (with appropriate dimension). Based on the iteration methods studied in [19,22], a parameterized shift-splitting of the saddle point matrix $ \mathcal {A} $ can be constructed as follows:
where $ \alpha > 0, \beta > 0 $ are two constant numbers and $ I $ is the identity matrix (with appropriate dimension). By this special splitting, the following parameterized shift-splitting method can be defined for solving the saddle point problem (1.1):
Parameterized shift-splitting (PSS) method: Given initial vectors $ u^{0}\in R^{m+n} $, and two relaxed parameters $ \alpha > 0 $ and $ \beta > 0 $. For $ k = 0, 1, 2, ... $ until the iteration sequence $ \{u^{k}\} $ converges, compute
where $ \alpha > 0, \beta > 0 $ are two constant numbers. It is easy to see that the iteration matrix of the Parameterized shift-splitting iteration is
If we use a Krylov subspace method such as GMRES (Generalized Minimal Residual) method or its restarted variant to approximate the solution of this system of linear equations, then
can be served as a preconditioner. We call the preconditioner $ \mathcal {P}_{PSS} $ the parameterized shift-splitting preconditioner for the nonsymmetric saddle point matrix $ \mathcal {A} $.
In every iteration of the parameterized shift-splitting iteration (2.5) or the preconditioned Krylov subspace method, we need solve a residual equation
needs to be solved for a given vector $ r $ at each step. Since the matrix $ \mathcal {P}_{PSS} $ has the following matrix factorization
Let $ r = [r_{1}^{T}, r_{2}^{T}]^{T} $ and $ z = [z_{1}^{T}, z_{2}^{T}]^{T}, $ where $ r_{1}, z_{1}\in R^{n} $ and $ r_{2}, z_{2}\in R^{m}. $ Then by (8), it can resuly in
Hence, analogous to Algorithm 2.1 in [19], we can derive the following algorithmic version of the generalized shift-splitting iteration method.
Algorithm 2.1. For a given vector $ r = [r_{1}^{T}, r_{2}^{T}]^{T} $, the vector $ z = [z_{1}^{T}, z_{2}^{T}]^{T} $ can be computed by (9) from the following steps:
Step 1: $ t_{1} = r_{1}-\frac{1-\alpha\beta}{\beta}B^{T}r_{2}; $
Step 2: Solve $ (A+\alpha I+\frac{1-\alpha\beta}{\beta}B^{T}B)z_{1} = t_{1}; $
Step 3: $ z_{2} = \frac{1}{\beta}(Bz_{1}+r_{2}). $
Now, we turn to study the convergence of the parameterized shift-splitting iteration for solving symmetric saddle point problems. It is well known that the iteration method (2.5) is convergent for every initial guess if and only if $ \rho(\Gamma) < 1, $ where $ \rho(\Gamma) $ denotes the spectral radius of $ \Gamma) $. Let $ \lambda $ be an eigenvalue of $ \Gamma) $ and $ [x^{*}, y^{*}]^{*} $ be the corresponding eigenvector. Then we have
or equivalently,
To get the convergence of the parameterized shift-splitting iteration, we first give some lemmas.
Lemma 2.1. Let $ A $ be a symmetric positive definite matrix, and $ B $ has full row rank. Let $ \Gamma $ be defined as in (5) with $ \alpha > 0 $ and $ \beta > 0. $ If $ \lambda $ be an eigenvalue of $ \Gamma, $ then $ \lambda\neq\pm 1. $
Proof. Let $ [x^{*}, y^{*}]^{*} $ be the corresponding eigenvector of $ \lambda. $ if $ \lambda = 1, $ then from (11) we have
It is easy to get that the coefficient matrix of (2.11) is nonsingular. Hence $ x = 0 $ and $ y = 0. $ which contradicts the assumption that $ [x^{*}, y^{*}]^{*} $ is an eigenvector of the iteration matrix $ \Gamma. $ So $ \lambda\neq 1. $
Now, we prove that $ \lambda\neq -1. $ If $ \lambda = -1, $ then from (2.10) we can obtain
Since $ \alpha > 0, \beta > 0, $ from (2.12) we get $ x = 0 $ and $ y = 0, $ which also contradict the assumption that $ [x^{*}, y^{*}]^{*} $ is an eigenvector of the iteration matrix $ \Gamma. $ So $ \lambda\neq -1. $ This completes the proof.
Lemma 2.2. Assume $ A $ be a symmetric positive definite matrix, and $ B $ has full row rank. Let $ \lambda $ be an eigenvalue of $ \Gamma $(with $ \alpha > 0 $ and $ \beta > 0 $) and $ [x^{*}, y^{*}]^{*} $ be the corresponding eigenvector with $ x\in C^{n} $ and $ y\in C^{m}. $ Then $ x\neq 0. $ Moreover, if $ y = 0, $ then $ |\lambda| < 1. $
Proof. If $ x = 0 $, then from (11) we have $ (1+\alpha\beta+\lambda-\lambda\alpha\beta)B^{T}y = 0. $ By Lemma 2.1 we know that $ \lambda\neq -1 $ and $ \alpha > 0, \beta > 0. $ Thus we have $ B^{T}y = 0. $ Because $ B^{T} $ has full column rank, we get $ y = 0, $ which contradicts with the assumption that $ [x^{*}, y^{*}]^{*} $ is an eigenvector. Thus $ x\neq 0. $ From Lemma 2.2 [21], we easy know $ |\lambda|\leq\parallel (\alpha I+A)^{-1}(\alpha I-A)\parallel_{2}. $
Theorem 2.3. Assume $ A\in R^{n\times n} $ be a symmetric positive definite matrix, and $ B\in R^{m\times n} $ has full row rank, and let $ \alpha, \beta $ be two positive constants. Let $ \rho(\Gamma) $ denote the spectral radius of the parameterized shift-splitting iteration matrix. Then it holds that
i.e., the parameterized shift-splitting iteration converges to the unique solution of the saddle point problem (1.1).
Proof. Let $ \lambda $ be an eigenvalue of $ \Gamma $ and $ [x^{*}, y^{*}]^{*} $ be the corresponding eigenvector with $ x\in C^{n} $ and $ y\in C^{m} $. By Lemma 2.1 we obtain $ \lambda\neq 1. $ Then we can obtain from (2.10) that
Substituting (2.14) into the first equation of (2.10), we get
By Lemma 2.2, we obtain that $ x\neq 0. $ Multiplying $ \beta(\lambda-1) $ as well as $ \frac{x^{*}}{x^{*}x} $ on both sides of Eq. (2.15), we have
Let
Because $ A $ is a symmetric positive definite matrix and $ B $ has full row rank, we get $ a > 0 $ and $ b\geq 0. $ Substituting (2.17) into (2.16), we know that $ \lambda $ satisfies the following real quadratic equation
Then from Lemma 2.2, we know that a sufficient and necessary condition for the roots of the real quadratic equation (2.18) to satisfy $ |\lambda| < 1 $ is
and
It is easy to find that (2.19) and (2.20) hold for all $ \alpha > 0 $ and $ \beta > 0 $ when $ a > 0 $ and $ b > 0. $ Also, if $ b = 0 $, there is a $ x\neq 0 $ such that $ Bx = 0. $ Then by Lemma 2.1, from (2.10) we have $ y = 0. $ Hence, by Lemma 2.2 we have $ |\lambda| < 1. $ Thus $ \rho(\Gamma) < 1. $ Then, we get (2.13), e.e., the parameterized shift-splitting iteration converges to the unique solution of the saddle point problem (1.1).
Remark 2.1. When $ \alpha = 0, $ The parameterized shift-splitting preconditioner reduces to the local shift-splitting preconditioner. Moreover, the parameterized shift-splitting preconditioner in this paper and the generalized shift-splitting preconditioner in [21] are two different preconditioning modes. Moreover, they have an intersection.
Remark 2.2 From Theorem 2.3, we know that the parameterized shift-splitting iteration method is uncondit0inally convergent.
3.
Numerical examples
In this section, I present one example to illustrate the effectiveness of the parameter shift-splitting preconditioner for GMRES(m) method and MINRES to solve the linear systems (1) in the sense of iteration step (denoted as "It"), elapsed CPU time in seconds (denoted as "CPU"), and relative residual error (denoted as "RES"). All numerical examples are carried out in Matlab 7.0. In our experiments, all runs with respect to both GSS method and PSS method are started from initial vector $ ((x^{(0)})^{T}, (y^{(0)})^{T})^{T} = 0, $ and terminated if the current iteration satisfy $ {\rm RES} < 10^{-6} $.
Example 3.1. [18] Consider the linear system of equations (1) with
where $ V = \rm{tridiag}(-1, 2, -1)\in \mathcal{R}^{l\times l}, V_{C} = V-e_{1}e_{l}^{T}-e_{l}e_{1}^{T}\in\mathcal{R}^{l\times l} $ and $ e_{1} $ and $ e_{l} $ are the first and last unit vectors in $ \mathcal{R}^{l} $, respectively. Here $ T $ and $ K $ correspond to the five-point centered difference matrices approximating the negative Laplacian operator with homogeneous Dirichlet boundary conditions and periodic boundary conditions, respectively, on a uniform mesh in the unit square $ [0, 1]\times [0, 1] $ with the mesh-size $ h = \frac{1}{l+1} $.
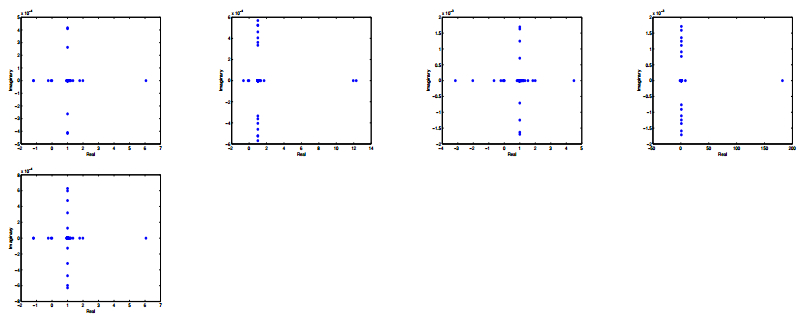
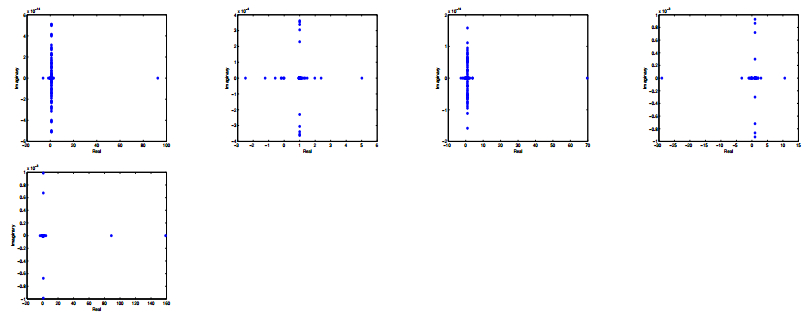
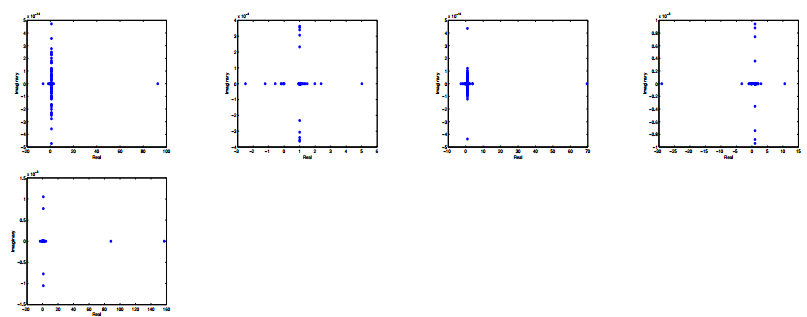
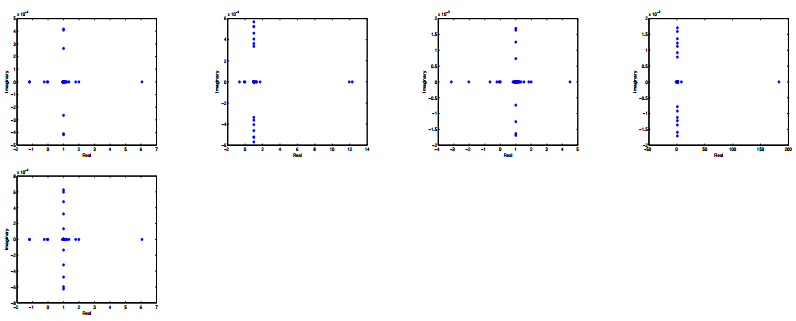
In Figures 1 ~ 4, I report the eigenvalue distribution for the generalized shift-splitting preconditioned matrix $ \mathcal{T}_{GSS}^{-1}\mathcal {A} $ and the parameter shift-splitting preconditioned matrix for different parameter, respectively. In Tables 1 ~ 4, we report iteration counts, relative residual and cpu time about preconditioned matrices $ \mathcal {T}_{GSS}^{-1}\mathcal {A} $ and $ \mathcal {T}_{PSS}^{-1}\mathcal {A} $ with $ l = 16 $ and $ l = 24 $ when choosing different parameters. Figures 1 ~ 4 and Tables 1 ~ 4 show that the GSS preconditioner and PSS preconditioner have the same eigenvalue distribution and the convergence when choosing different parameters.
4.
Discussion and conclusion
In this paper, the author presents a parameterized shift-splitting preconditioner for saddle point problems with symmetric positive definite $ (1, 1)- $block. Theoretical analysis shows that PSS method is an unconditional convergent fixed-point iteration. Furthermore, numerical example indicates that the GSS preconditioner and PSS preconditioner have the same eigenvalue distribution and the convergence when choosing different parameters.
Acknowledgments
This research of this author is supported by the National Natural Science Foundation of China (11226337, 11501525), Excellent Youth Foundation of Science & Technology Innovation of Henan Province (184100510001, 184100510004), Science & Technology Innovation Talents in Universities of Henan Province(16HASTIT040, 17HASTIT012), Aeronautical Science Foundation of China (2016ZG55019, 2017ZD55014), Project of Youth Backbone Teachers of Colleges and Universities of Henan Province (2015GGJS-003, 2015GGJS-179), Advanced Technological Research Project of Henan Province (182102110129), Henan Province Postdoctoral Science Foundation (2013031), Research on Innovation Ability Evaluation Index System and Evaluation Model (142400411268). The work of Chaoqian Li is supported partly by the Applied Basic Research Programs of Science and Technology Department of Yunnan Province [2018FB001], Outstanding Youth Cultivation Project for Yunnan Province [2018YDJQ021] and Program for Excellent Young Talents in Yunnan University. The work of Yaotang Li is supported by National Natural Science Foundation of China (11861077).
Conflict of interest
All authors confirm that there is no conflict of interest in this paper.









 DownLoad:
DownLoad: