1. Introduction
Color center activation refers to the process in which a defect—such as an oxygen vacancy—traps an electron that in turn can exist in different energy levels within the trap, thus giving the trap special absorption and luminescence characteristics [1]. Color centers may be, for example, optically active oxygen vacancies (VO) containing one, two, or three trapped electrons, denoted as F+‑, F‑, and F‑‑centers, respectively. This work presents a detailed investigation of color centers in yttrium aluminum garnet (Y3Al5O12, YAG) activated by UV excitation at room temperature. YAG is one of the most important optical materials. It is widely used in solid state lasers and has potential applications in scintillation and illumination devices. It has the garnet structure of the A3B2C3O12 form, where A, B, and C are cations, typically metals, and B and C can be the same element. The cations are organized with dodecahedral (A site), octahedral (B site), and tetrahedral (B site) coordination of oxygen ions. The unit cell of a garnet is a cubic structure containing of 8 characteristic A3B2C3O12 molecules, or 160 individual atoms, and belongs to the space group Ia3d. In YAG, the yttrium ion occupies the dodecahedral site while the aluminum ion occupies the octahedral and tetrahedral sites. YAG has a lattice constant of 12 Å [2].
Investigation of color centers in YAG is crucial to its applications in high energy optics and detection. In lasers and scintillation detectors, for example, the crystals are exposed to high energy photons or particles that induce color centers. Thus, these crystals usually operate in color center activated states and it is crucial to understand how they behave under such conditions. Despite the large number of studies on color centers in YAG [3,4,5,6,7,8,9,10,11,12,13,14], explanations of color centers are still mostly speculative and occasionally contradictory. In the following we will give a brief review on the previous works, then describe and discuss our new experimental results on YAG color centers which take into account the effect of doping and growth and annealing atmosphere. To better understand the source of color centers we combine the study with impurity measurements in YAG crystals.
UV-induced stable absorption bands in YAG at room temperature were first reported by Bass and Paladino [5], but no explanation regarding their origin was suggested. Then, Mori [12] identified a number of color centers in YAG activated by electron trapping. He resolved new absorption peaks in colored YAG at 353, 495, and 833 nm and attributed them to oxygen vacancies based on electron spin resonance and thermo-luminescence measurements. His work also showed that UV excitation decreased an absorption peak at 255 nm, which was then attributed to Fe2+ ions. All absorption peaks were detected at room temperature. Masumoto and Kuwano [11] discussed Mori’s findings and how they were affected by varying degrees of oxidation. They attributed the series of peaks at 353, 495, and 833 to F+-centers. Mn2+ and Mn4+ impurities on Al3+ sites were also suggested to act as electron traps leading to band maxima at 350 nm, 400 nm, or 460 nm at room temperature [6]. Electron traps are reported in other wide band gap materials (see e.g. [15]).
F centers often play an important role in oxides. Ashurov el al. [3] observed a luminescence peak near 500 nm at room temperature that did not appear to come from recombination of opposite sign charge carriers. The peak disappeared with heating but would quickly reappear with high-energy γ-irradiation, suggesting that the peak arose from trapped electrons at an oxygen vacancy. Comparison of the luminescence decay time of this peak to the known F+-center decay time of Al2O3 suggested that this 500 nm peak arose from F+-centers. F+- and F-centers and their absorption and luminescence spectra were studied in greater details by Zorenko et al. [14]. They identified multiple peaks and shoulders in measurements conducted at 10K. From these measurements, they were able to map out the energy levels of the F+- and F-centers. They found F+-centers to have three excited energy states with absorption energies at 5.54, 6.0, and 6.51 eV relative to the ground state, denoted as 1A→2A, 1A→2B, and 1A→3P. Two F-center absorption peaks were found with energies of 5.19 and 5.62 eV, labeled as 1S→3P and 1S→1P transitions. Effect of neutron irradiation on the formation of color centers in YAG single crystals has been investigated [8] and showed different effects from g-irradiation. This is probably because neutrons not only activate color centers, but they can also induce new defects in the lattice.
To better understand the mechanisms during color center activation, it is important to examine the role of different impurities and how they trap charge carriers. Batygov et al. [16] studied YAG crystals: undoped and doped with Ce, Pr, Nd, Sm, Eu, Tb, Dy, Yb, Lu, Er, or Ho separately. Their findings showed that only Eu3+ and Yb3+ can encounter transition to the divalent state and act as electron traps at room temperature. Sm3+ has the third largest electron affinity of the studied activators, but it was found that Sm2+ is unstable at room temperature. Pr3+ and Tb3+ were found to act as hole traps due to their ease of transition to the tetravalent state. It has been argued that the same effect can be produced by Ce3+, but the strong absorption characteristic of Ce3+ in YAG made this difficult to observe. Kovaleva et al. [10] studied color centers in Nd doped YAG crystals and showed the effects of co-doping with Cr, Fe, and Nd. The presence of Cr leads to a color center with an absorption peak near 500 nm, which has been detected after g-excitation. A band at 260 nm was observed and again attributed to Fe3+ impurities. Co-doping with Ce on the other hand appeared to prevent the formation of color centers typically associated with Nd doped YAG. Since Kovaleva et al. characterized Ce3+ to likely act as hole traps, this finding seemed to suggest that the typical color centers of Nd:YAG resulted from hole trapping. Kaczmarek [9] studied the effects of several dopants on the color centers of YAG including Ce, Fe, Mg, V, Cr, and Pr dopants. They observed a peak just below 300 nm and a broad peak just below 500 nm in the absorption spectrum of Cr doped YAG after excitation. Two other absorption peaks related to Cr were identified at 380 nm and 480 nm by Bagdasarov [4].
As mentioned above, the current study focuses on investigating color centers in undoped and doped YAG single crystals grown in various growth environments. By changing growth environment, different types of defects can be populated. We also apply various annealing procedures to alter and modify defects. Impurities in crystals were also investigated to illustrate their effects on the formation of color centers.
2. Materials and Method
Crystals used in this study were obtained from different manufacturers. They were all grown from the melt by Czochralski (cz) method in molybdenum or iridium crucibles in <111> direction and the raw materials were highly pure oxide powders of Y2O3 and Al2O3. The growth atmospheres varied as follows: 1) argon only, 2) 100 ppm oxygen in nitrogen (oxidizing conditions), and 3) 30% H2 in argon (reducing conditions). All samples were cut perpendicular to <111> direction and optically polished. A number of samples were annealed to modify defects. The various growth and annealing atmospheres are summarized below in Table 1.
Table 1. Samples used in this study, organized by dopant type and concentration, manufacturer, growth atmosphere, and treatment. Color centers in YAG are known to be affected by the impurities; information about impurities can be found from the manufacture. Their name is listed in the table.
| Sample | Manufacturer | Growth Atmosphere | Treatment |
| YAG (undoped) | United Crystals | Ar | 48 hour air anneal at 1200°C |
| YAG (undoped) | United Crystals | Ar | 96 hour air anneal at 1200°C |
| YAG (undoped) | Crytur | 40% H2 in Ar | |
| YAG (undoped) | Crytur | 100 ppm O2 in Ar | |
| Nd:YAG 1% | United Crystals | Ar | 48 hour air anneal at 1200°C |
| Tm:YAG 0.8% | United Crystals | Ar | 48 hour air anneal at 1200°C |
| Yb:YAG 1% | Marketech | 5-30% H2 in Ar | |
| Yb:YAG 3% | Marketech | 5-30% H2 in Ar | |
| Yb:YAG 5% | United Crystals | Ar | 96 hour air anneal at 1200°C |
| Yb:YAG 10% | United Crystals | Ar | 48 hour air anneal at 1200°C |
The as-grown or annealed samples were then exposed to UV light at room temperature and the formation of color centers was examined through optical absorption measurements. UV excitation can activate color centers by promoting electrons to the conduction band, allowing them to roam freely throughout the crystal lattice until they either relax back into their orbit around an atom or become trapped at a defect. Some defects, such as an oxygen vacancy, gain optical properties upon trapping an electron A large enough concentration of these activated color centers can change the color of the crystal. Even if the change in color cannot be observed with the naked eye, absorption measurements usually can distinguish subtle changes in color. UV excitation was performed with an Ocean Optics PX-2 Pulsed Xenon Light Source with a broad emission range from 220-700 nm. The lamp was operated at 200 Hz flash rate with a pulse duration full width at half maximum (FWHM) of 5 μs and 4.5 μJ per pulse maximum. The irradiation time was 30 minutes for most measurements. Absorption measurements were conducted using a Perkin Elmer UV/VIS Spectrometer. This spectrometer uses double-beam operation for measurement stability, a concave grating with 1053 lines per mm, and deuterium and tungsten lamps with an automatic switchover at 326 nm. It can scan over wavelength range from 190 to 1100 nm with a resolution of 1 nm and accuracy of ±0.1 nm. For the current measurements, we used a scan speed of 120 nm/minute and 1 nm slit width. To free the trapped electrons from defects, allowing them to return to the conduction band, thermal energy was applied by heating the samples to 400 °C. Sample heating was performed on an Instec Inc. HCS302-01 hot/cold stage. The temperature was kept low at 400 °C, much lower than the annealing temperature of defects in YAG, to allow the liberation of charge carriers without modifying the type of defects. Glow Discharge Mass Spectrometry (GDMS) analyses were conducted on a few YAG samples to confirm the presence of iron. The analyses took place at Evans Analytical group and at Crytur Inc.
3. Results and Discussion
Absorption spectra are presented for ambient and UV irradiated samples. To display how the absorption changes after the color center activation processes, absorption shift plots are generated by subtracting the ambient absorption spectrum from the absorption spectrum of the crystal after UV excitation or heating. Following the procedure of Mori [12], some of these subtracted spectra were fit to Gaussian curves to attempt to resolve individual peaks and determines which centers are dominant in the crystals.
3.1. Color centers in undoped YAG
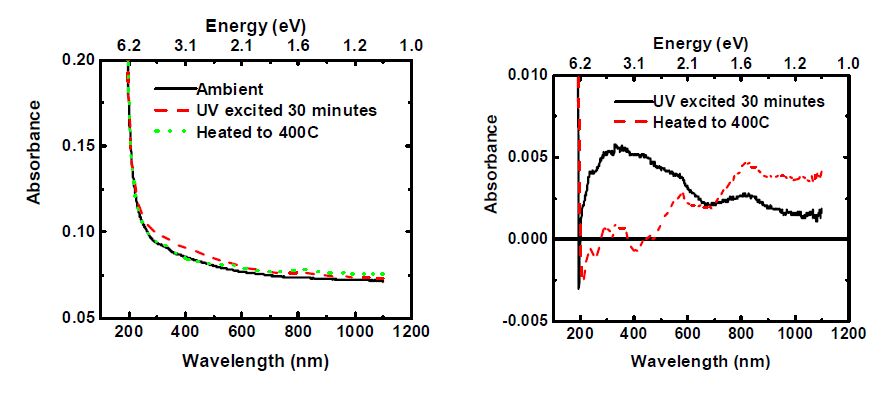
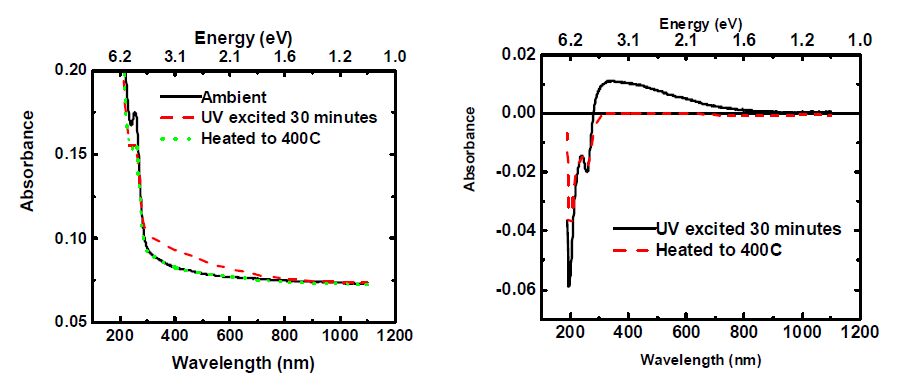
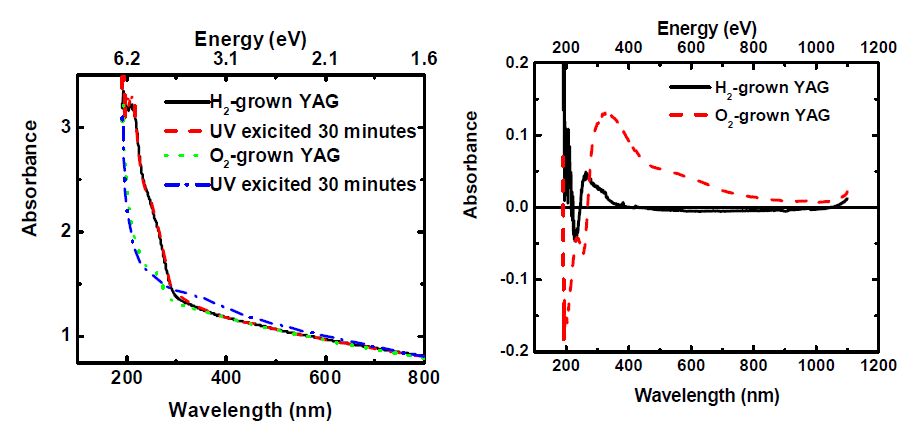
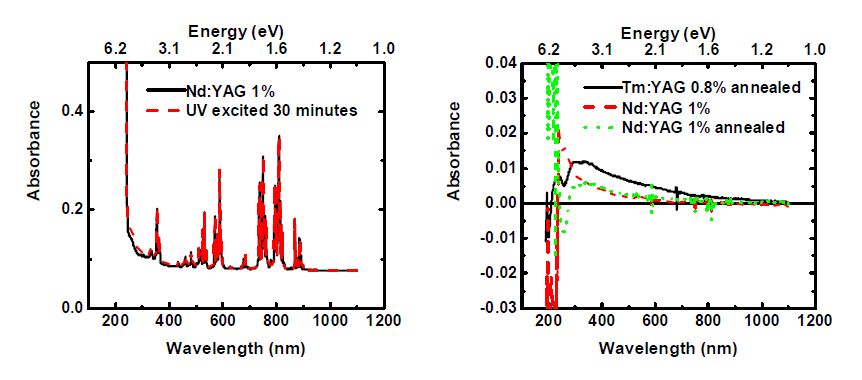
Figure 1 shows the change in absorption spectra immediately after 30 minutes UV excitation and after heating to 400 °C for YAG crystals grown in a pure Ar atmosphere. Figure 2 shows these measurements for air annealed Ar-grown YAG and Figure 3 shows the spectra of UV-excited O2-grown (100 ppm O2 in Ar) and H2-grown (40% H2, 60% Ar) YAG.
It should be mentioned that Ar-grown YAG samples annealed in air turned from colorless to orange after UV excitation while O2-grown YAG samples turned grayish. Figs. 1-3 show that the formation of color centers strongly depends on the growth and annealing atmospheres. A peak at 256 nm is observed to decrease after UV excitation in samples containing a low concentration of oxygen vacancies and increases in other samples. This 256 nm is peak believed to arise from O2−→Fe3+ charge transfer [4,17]. The decrease of this nm peak has been suggested to arise from electron capture by iron [12], though for the decrease to occur, a change in the charge state of either Fe3+ or O2- must occur such that the O2−→Fe3+ charge transfer can no longer take place. Our recent measurements [17] also supported the association of the 256 nm peak with this charge transfer and revealed a luminescence at 800 nm related to Fe3+ [18]. In all samples, we observed a peak around 315 nm, which may be related to Fe2+ [12]. This interpretation seems to correspond well with the decrease of the 256 nm peak in O2-grown and air annealed Ar-grown YAG, though H2-grown YAG does not appear to show these features. However, Fig.4 below seems to contradict this conclusion regarding the peak near 315 nm, and thus this peak at 315 remains of unknown origin as explained below. Following Mori’s procedure, fitting the peaks to Gaussians resolved a weak peak near 500 nm in all samples except the H2-grown YAG. PL measurements confirmed the presence of Cr3+ ions in each of these samples except H2-grown YAG, thus it seems appropriate to attribute this 500 nm additional peak that arises after UV excitation to chromium [4,9,10].
The YAG sample grown in Ar atmosphere likely contains F--centers. Although the shift in absorption for this sample is very weak, it seems to show peaks near 350, 500, and 800 nm, which is consistent with the peaks at 360, 480, and 830 reported to be characteristic of F--centers [13]. These peaks appear to be robust against heating to 400 °C. After heating to 400 °C, the color centers in the O2-grown sample persisted. However, the sample did become clear again after heating to 450 °C suggesting relatively high binding energy for the trapped electrons at defects. Figure 4 compares the response of as-grown and annealed Ar-grown samples to UV excitation. It shows that the increase over the range of visible wavelengths with a maximum near 310 nm increases independent of the increase or decrease of the 256 nm peak. Thus, it appears that this is not actually related to Fe2+ and is instead of some unknown origin.
3.2. Color centers in Nd:YAG, Tm:YAG, and Yb:YAG
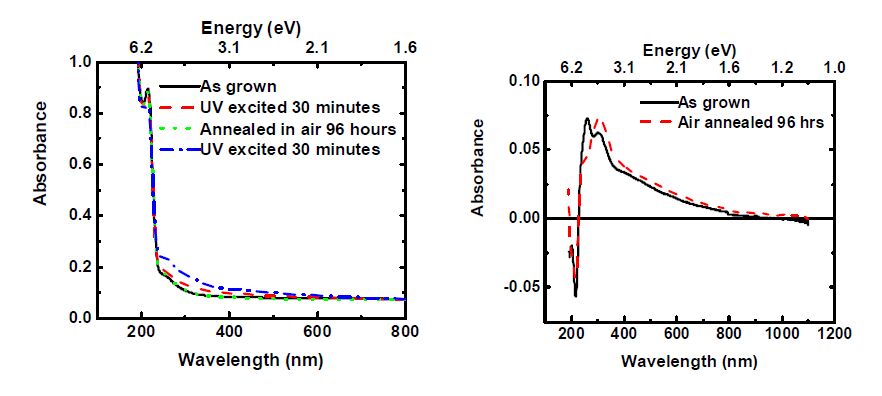
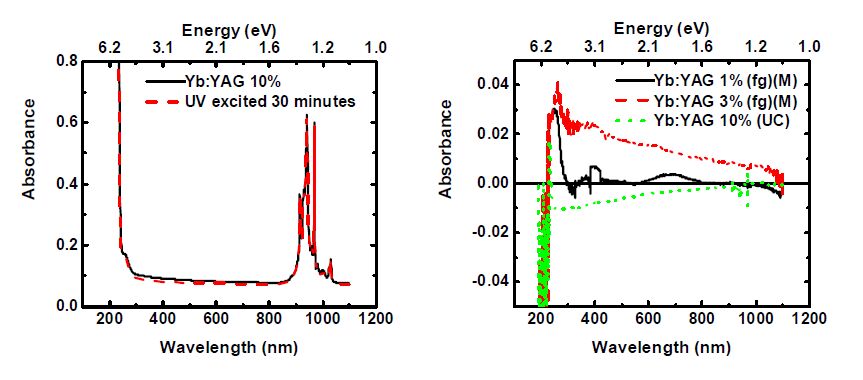
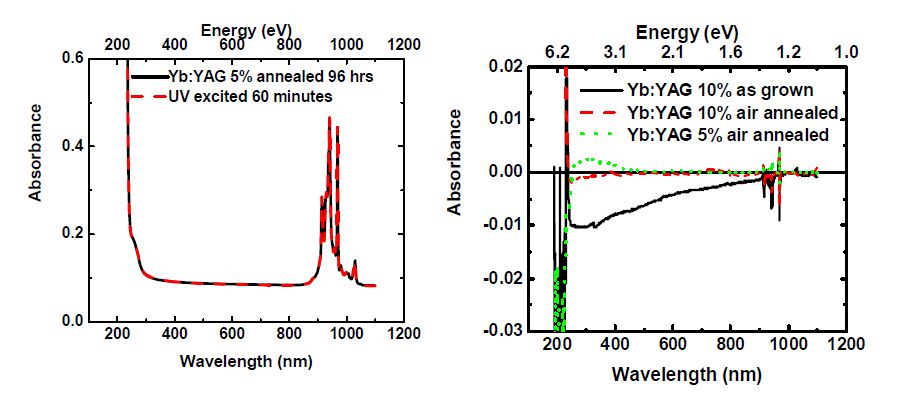
Color centers were examined in a number of RE doped samples. The change in absorption spectra after UV-excitation of as-grown Nd:YAG doped to 1%, air annealed Nd:YAG doped to 1%, and air annealed Tm:YAG doped to 0.8% is shown in Fig5. Figure 6 displays the change in absorption spectra for UV-excited Yb:YAG doped to 1%, 3%, and 10% while Fig.7 illustrates the effect of air annealing on color centers in Yb:YAG doped to 10% and 5%. In all of these samples, heating to 400°C eliminated the color centers.
Figure 5 shows a significant change in the 256 nm peak after UV excitation in all samples. The peak has been enhanced for as-grown YAG doped with 1% Nd but decreased for air annealed samples. It has been shown that annealing in air oxidizes Fe2+ to Fe3+ in YAG [19], so this result is to be expected. The majority of iron in the as grown sample is divalent, while the majority of iron ions in the air annealed samples are trivalent. On top of that, there exist more oxygen vacancies in the as grown sample. As a result, UV excitation of the as grown sample frees electrons from Fe2+ ions that become trapped at oxygen vacancies, leaving behind Fe3+ ions and thus increasing 256 nm absorption. UV excitation of air annealed samples works differently because the Fe3+ ions do not have the extra electron to excite and also there are fewer oxygen vacancies (VOs). With such a low concentration of VO, electrons can trap at other locations, including Fe3+ ions, which forms Fe2+ and decreases the absorbance at 256 nm. Figure 6 also shows a very strong increase at 256 for lower dopant concentrations of Yb. The absence of the absorption band associated with the f-d transitions of Yb2+ indicate that the majority of Yb ions do not exist in +2 charge state. This is probably because the crystals were grown in Ar atmosphere or 5% H in Ar, which is mostly neutral atmosphere. It seems that 5% hydrogen is not enough to produce reducing conditions to keep Yb in the +2 charge state.
Figure 5 shows that the increase over the range of visible wavelengths with a maximum near 310 nm increases independent of the increase or decrease of the 256 nm peak confirming what we observed above for as-grown YAG samples in Fig.4. This clearly indicates that this peak is not actually related to Fe2+ and disagrees with what has been suggested in earlier works [4].
There appears to be a decrease in UV absorption in as grown Nd- and Yb-doped samples but an increase in the UV absorption of the air annealed Nd:YAG and Yb:YAG. This likely arises from a similar mechanism to the one discussed with the 256 nm peak. Yb3+ ions are known to behave as electron traps in YAG, but Nd3+ ions are expected not to act as hole or electron traps [16]. In fact, no significant trapping defects was detected in Nd:YAG crystals [20]. Thus this effect is most likely dependent on oxygen concentration. This is explored in details below with Yb:YAG (10%) in Figs. 6 and 7, which show a decrease over a broad range of wavelengths in the absorption spectra after UV excitation. Yb3+ ions act as electron traps, and their concentration in this sample is very high. The growth atmosphere of argon allows for an appreciable concentration of VOs, and one method of charge compensation is the inclusion of Yb in the divalent state instead of the trivalent state. In the case of the Yb:YAG 10% sample, the Yb3+ ions form after UV excitation and act as the primary electron traps, reforming Yb2+ ions. This is further evidenced by the large decrease in O2-→Yb3+ charge-transfer absorption at short wavelengths (characterized by a strong peak at about 210 nm [21,22,23,24]) as well as the decrease in the Yb3+ absorption band around 1000 nm. The overall decrease in absorption comes from excitation freeing electrons from the electron traps responsible for those particular bands and subsequent trapping at ytterbium. An oxidizing anneal almost entirely removed these coloring effects, as demonstrated in Fig.7, where the only changes seem to be an increase in O2−→Yb3+ charge-transfer absorption at 210 nm and very slight decreases in O2−→Fe3+ charge-transfer absorption at 256 nm and Yb3+ absorption near 1000 nm. The oxidizing anneal filled VOs and oxidized impurities and dopants, changing some divalent ions to trivalent or even tetravalent. It is possible that electrons at oxygen sites that formed O3- were freed to trap at Fe3+ and Yb3+ or Yb4+, thus increasing the availability of O2− ions for charge transfer. Overall, the decrease in concentration of Fe3+ ions led to the decrease in O2−→Fe3+ charge-transfer absorption. It is difficult to tell how much the concentration of Yb3+ changed since some Yb3+ was ionized to Yb2+ while some Yb4+ was ionized to Yb3+, but the increase in O2−→Yb3+ charge-transfer absorption seems to suggest that the increase in O2− concentration was much higher than any potential decrease in Yb3+ concentration.
It is important to interpret these absorption curves and the formation of color centers with conjunction to defects and impurities. GDMS analysis indicated the presence of iron impurities and confirmed the association of the 256 nm absorption peak with iron. Our recent studies on defects in YAG single crystals have shed the light on the dominant defects in single crystals [25,26,27,28]; Al vacancies, O-vacancies and Al-O vacancies were identified as possible defects in YAG single crystals. Based on positron lifetime measurements and defect wavelength dispersive X-ray measurements, we anticipate the presence of antisite defects Yttrium ions on Al sites YAl3+, which is consistent with the low formation energy for YAl3+ predicted from first principle calculations [29,30]. YAl can act as an electron trap, as yttrium can be divalent. Zorenko et al. [31] suggested that YAl3+ could form a shallow electron trap, which is not stable at room temperature.
4. Conclusions
O-vacancies and iron impurities are the main sources for color centers in undoped YAG single crystals. In samples deficient in oxygen with high concentration of oxygen vacancies, iron primarily exists in the divalent state, and UV excitation frees electrons from O2− and Fe2+, as both of them can lose electrons during UV excitation. As a result, excitation greatly increases Fe3+ concentration, increasing O2−→Fe3+ charge transfer and increasing the 256 nm peak. Other dopants that do not easily transition to other valence states see a decrease in charge transfer absorption due to the decreased O2− concentration. For the doped samples, the effect of iron impurities is not observed and therefore the 256 nm absorption peak does not appear in the spectra. After air anneal, the oxygen concentration in the samples is much higher, and thus there are few oxygen vacancies and less electron traps. There is also high concentration of trivalent iron in the annealed sample. Thus, UV excitation does not have the same effect it does on the as-grown samples. To charge compensate some lattice defects such as aluminum vacancies, oxygen can incorporate as O− instead of O2−. Thus, UV excitation allows electrons to trap at O− to form O2−. Fe3+ in these conditions also acts as an electron trap, hence the 256 nm decreases after UV excitation while charge transfer bands with other dopants increases.
Ytterbium presents a special case where the dopant can act as an electron trap in the as-grown sample. Annealing of Yb doped samples in air filled oxygen vacancies and stabilized Yb3+ so that Yb could no longer act as an electron trap. Thus, after annealing UV excitation did not cause electrons to trap at ytterbium ions and there was no change over the majority of the absorption spectrum aside from the charge transfer band.
Finally it is concluded from the current measurements that air or O-anneal can significantly reduce or eliminate color centers in YAG single crystals. This is important for many applications as the formation of color centers and change in absorption with short wavelength irradiation can greatly affect the performance of YAG crystals in laser applications. Similarly, formation of color centers in response to X-ray and g-ray absorption reduces the efficiency of YAG crystals as scintillators [32].
Acknowledgements
This work was supported by the National Science Foundation under Grant No. DMR 10-06772. We wish to thank David Mackay and Autumn Pratt for their contributions to the measurements.
Conflict of Interest
The authors report no conflict of interests in this research.









 DownLoad:
DownLoad: