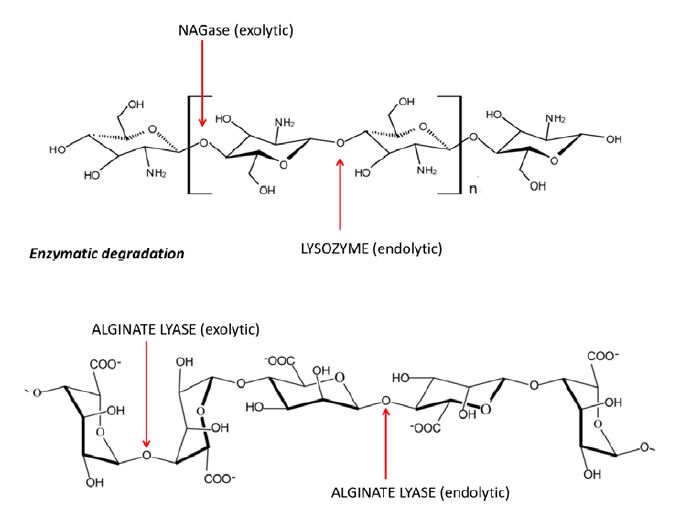
Polysaccharides are long monosaccharide units which are emerging as promising materials for tissue engineering and drug delivery applications due to their biocompatibility, mostly good availability and tailorable properties, by to the wide possibility to modify chemical composition, structure—i.e., linear chain or branching—and polymer source (animals, plants, microorganisms). For their peculiar behaviour as polyelectrolites, polysaccharides have been applied in various forms, such as injectable hydrogels or porous and fibrous scaffolds—alone or in combination with other natural or synthetic polymers—to design bioinspired platforms for the regeneration of different tissues (i.e., blood vessels, myocardium, heart valves, bone, articular and tracheal cartilage, intervertebral discs, menisci, skin, liver, skeletal muscle, neural tissue, urinary bladder) as well as for encapsulation and controlled delivery of drugs for pharmaceutical devices. In this paper, we focus on the pH sensitive response and degradation behaviour of negative (i.e., alginate) and positive (i.e., chitosan) charged polysaccharides in order to discuss the differences in terms of metabolic activity of polyelectrolytes with different ionic strength for their use in drug delivery and tissue engineering area.
1.
Introduction
Accurate knowledge of spine loading is critical for understanding spinal functions and the mechanisms of spinal injuries/diseases as well as for developing surgical techniques for the treatment of spinal pathologies. However, experimental measurements of spinal forces during functional activities remain a challenge [1,2,3,4]. Numerous studies have used computational models to estimate spine loads [5,6,7,8]. Stokes and Gardner-Morse recommended static stiffness models to investigate spine joint and muscle forces [6,7,8]. Shirazi-Adl et al. studied lumbar spine forces and stability during various body postures and loading conditions using finite element modeling and optimization methods [1,5].
Early research assumed the spine joint as a "ball-and-socket" joint that lies at the inter-vertebral disc center [6], and these studies used inverse dynamic optimization methods to calculate the joint reaction forces for various postures of the spine [1,5,9,10]. The concept of follower load—constant loading path method (CLPM) in this study—assumes that physiological directions of the spine loads in motion segments follow the same path of the spine lordosis, and it has been popularized in spine biomechanics research [9,11,12]. Han et al. reported that the combination of spine muscle forces could generate spinal forces that perfectly follow spine lordosis in a neutral standing posture [9]. Dreischarf et al. predicted intervertebral rotations by both non-optimal and optimal follower loading paths using a finite element model and various optimization methods [13]. Kim et al. used a modified concept of the follower load by assuming a shear force as great as 20%–50% of the resultant joint force at each motion segment [11,12].
However, in the application of an inverse dynamic optimization method to calculate spinal loads, the assumption on the location of the loading path may introduce extra-constraints to the joint, resulting in variations in the predicted joint reaction forces. To avoid over-constraining to the joint, the global convergence optimization method (GCOM) has been introduced into the inverse dynamic optimization method [14,15]. In this method, an instantaneous center of rotation (ICR) of the joint where the joint reaction moment is actually zero is defined; it is calculated as a variable in inverse dynamic optimization.
In this study, we used the GCOM and CLPM to simulate the lumbar spine biomechanics of the same human subject during flexion, upright standing, and extension postures of the body, and we compared the data of the joint reaction forces, ICRs, and muscle contraction forces predicted using the two methods.
2.
Materials and method
The human musculoskeletal joint system is an indeterminate mechanical system because the number of variables (joint and muscle forces) exceeds the number of equilibrium equations. Therefore, the inverse dynamic optimization method is widely used to predict joint reaction forces and muscle forces of the joint [7,8,9,14,16]. Thus, an inverse dynamic optimization model is used for estimating the loads in human lumbar spine in this study. Modeling of the spine musculoskeletal system and two different optimization methods, GCOM and CLPM, were introduced. Then, comparison between two methods were explained in this section.
2.1. Inverse dynamic optimization model of the lumbar spine
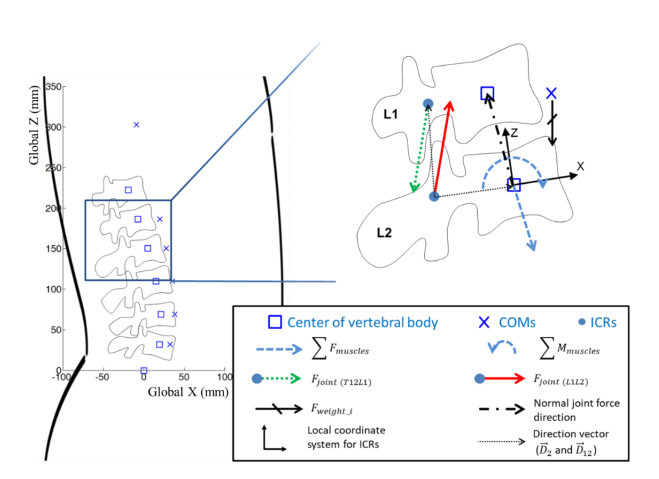
A numerical model of the human lumbar spine, including 7 vertebrae (from T12–S1) and 90 pairs of spinal muscles (5 longissimus pars lumborum, 4 iliocostalis pars lumborum, 12 longissimus pars thoracis, 8 iliocostalis pars thoracis, 11 psoas, 5 quadratus lumborum, 12 thoracic multifidus, 20 lumbar multifidus, 6 external oblique, 6 internal oblique, and 1 rectus abdominis), is generated based on previously published data [6,17,18], as shown in Figure 1a. To analyze the lumbar spine forces, a free body diagram is established in each motion segment from T12-L1 to L5-S1 [9,14,15], as shown in Figure 2. In each motion segment, the disc was modeled as a "ball-and-socket" joint. A joint force was defined as the total force of the intervertebral disc (IVD), ligaments, and facet joints in each motion segment. In this study, 44% of the body weight (BW) was applied at T12 (head and trunk were considered as one rigid body) and 2.7 % BW was applied at each vertebra (L1–L5) based on the previously published studies [19,20]. The centers of segmental BW were calculated based on previously published data [21,22]. The effect of the intra-abdominal pressure was neglected in this study for simple comparison between GCOM and CLPM.
Therefore, the force and moment equilibrium equations at the joint center could be derived using the free body diagram for the L1–L2 motion segment (Figure 2) as
a) ${{\vec{F}}_{weight\_j}}+\mathop{\sum }^{}f_{i}^{M}{{\vec{e}}_{i}}-{{\vec{F}}_{joint~\left( T12L1 \right)}}+{{\vec{F}}_{joint~\left( L1L2 \right)}}=0$
A local coordinate system at each motion segment was defined for the calculations. The center of the inferior vertebral body in the individual motion segment was defined as the origin of the local coordinate system. The anatomical anterior direction of the vertebra was defined as the x-direction. The z-direction of the local coordinate system was defined to be superior and perpendicular to the x-direction. The ICRs of individual motion segment was assumed to be located on the x-axis of the local coordinate system. The unknowns in the equations are the joint forces (${\vec F_{joint{\rm{}}\left({T12L1} \right)}}$ and ${\vec F_{joint{\rm{}}\left({L1L2} \right)}}$) and the magnitude of the ith muscle force (fiM). ${\vec D_2}$ and ${\vec D_{12}}$ represent the vectors from the center of L1–L2 motion segment to L1 vertebral center and to the center of T12–L1, respectively. The given variables are the directional unit vector of the ith muscle force (${\vec e_i}$), the vector pointing from the vertebral center to the insertion centroid of ith muscle (${\vec r_i}$), and the external forces (${\vec F_{weight\_j}}$) and moments (${\vec M_{weight\_j}}$) representing the effects of the jth segmental BW on the vertebral center. Further, ${\vec M_{joint{\rm{}}\left({T12L1} \right)}}$ and ${\vec M_{joint{\rm{}}\left({L1L2} \right)}}$ represent the joint reaction moments of T12–L1 and L1–L2 motion segments at the joint center, respectively.
In the traditional inverse dynamic optimization method, joint reaction moments were assumed to be zero at the joint center to avoid trivial solutions for the muscle forces [6,14,15]. Similar equations could be established for all other segments from L2–S1.
In this lumbar spine model, there are 6 motion segments with 36 equilibrium equations, representing an indeterminate problem in mechanics. An optimization procedure was introduced in literature that minimizes an objective function and used the equilibrium equations as constraints to calculate the muscle and joint reaction forces. We adopted the objective function proposed by Stokes et al. [7,8] as it minimizes the sum of the joint shear forces normalized by the resultant force and the sum of muscle stress normalized by the maximum muscle stress.
where FSj and Fj represent the joint shear force and resultant joint force of the jth motion segment, respectively; σi represented the stress in ith muscle and σMax the maximum muscle stress of 460 kPa; and nj and nm were the numbers of spinal motion segments and muscles, respectively. Weight factor W1 was set to be 10 times of W2 [7,8]. The normal direction of the shear force was defined from the inferior to the superior vertebral centers (Figure 2).
2.2. Constant loading path method (CLPM)
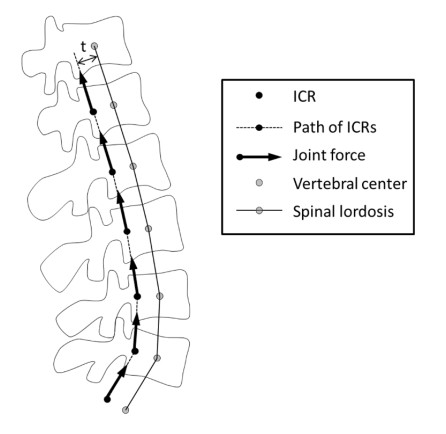
To determine the joint center location for each motion segment, we adopt the CLPM that is similar to the concept of the follower load [9]. The CLPM assumes that the directions of the joint forces and the path of ICRs were constrained along the spinal lordosis direction, which was parallel to the piece-wise straight line connecting the vertebral centers. At each posture of the body, the off-set distance of the ICR from the vertebral center line was defined by the same unknown variable "t" for all motion segments [9,12] (Figure 3). The upper boundary condition for the maximum muscle stress (≤ 460 kPa) was not included in the calculations using the CLPM because of the convergence problem. The cost function of Equation 2 and the constraints of Equation 1 were used in the optimization procedure.
2.3. Global convergence optimization method (GCOM)
In the GCOM, the locations of the joint centers were left unknown and calculated with the joint and muscle forces through an optimization procedure. This treatment makes the joint center as the true ICR of the segment where the resultant moment is zero [14,15]. If ${\overrightarrow {ICR} _j}$ is used to represent the position vector of the ICR of the jth vertebral segment in its local coordinate system, the inverse dynamic optimization procedure is derived to be
where the muscle force (fiM) and the position of ICR (${\overrightarrow {ICR} _j}$) are optimization variables. The tension-only muscle forces are constrained using the maximum muscle stress of 460 kPa [8,11,17].
2.4. Comparison between GCOM and CLPM
To compare the applications of the GCOM and CLPM in a simulation of lumbar spine biomechanics, we calculated the joint reaction forces, muscle forces, and locations of the ICRs for a healthy young female subject (27 years old, 1.63 m height, and 54 kg body weight). This study was approved by our institution review board (Partners #2017D011145). The subject was studied under three different body postures: flexion at 40°, upright standing, and extension at 10°. To do this, coronal and sagittal plane X-ray images were obtained for the three postures of the subject. The subject-specific musculoskeletal model of the lumbar spine from T12–S1 was then created using the X-ray images at the three postures (Figure 1). The joint and muscle forces, and the ICR locations in all motion segments were calculated using the two methods and compared with the data published in the literature. It is noted that for each body posture, the ICR locations were different for all motion segments in the GCOM calculation; however, they were represented by a single offset variable for all segments in the CLPM calculation. The optimization problem was formulated in Excel 2010 (Microsoft, Redmond, USA), and it was solved using the What'sBEST! Software (LINDO system Inc., Chicago, USA).
3.
Results
All locations of the joint centers were used as variables in the GCOM while the only variable, the distance between the paths of the ICRs and vertebra centers, was used in the CLPM. Thus, the GCOM has 6 more variables compared to the CLPM, that results in different numbers of calculations in both methods. About 2,150 million calculations were conducted in the GCOM while about 450 thousand calculations were done in the CLPM. Even though the number of calculations conducted in the GCOM is five thousand times greater than that in the CLPM, these two different methods showed similar computation times. The average computation times for the GCOM and the CLPM were 18 seconds and 14 seconds, respectively.
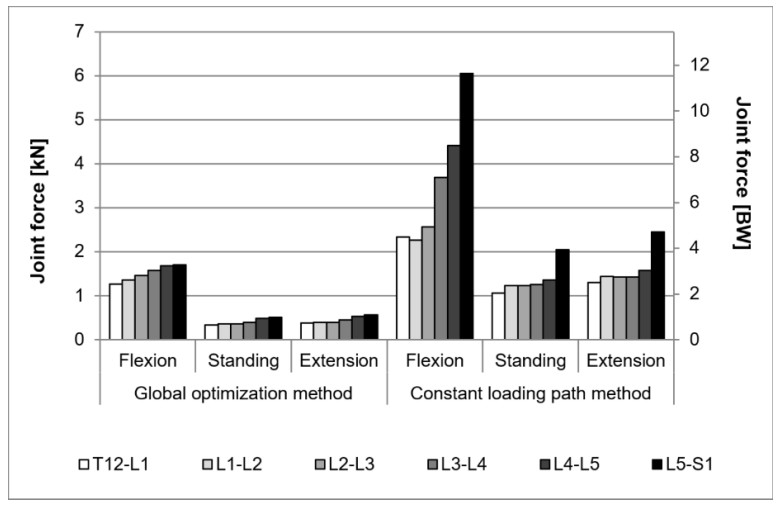
The calculated joint forces in flexion, upright standing, and extension postures using the GCOM and CLPM are shown in Figures 4 and 5. In the flexion posture, the joint forces at the T12–L1 level were 1,267 N via the GCOM and 2,333 N via the CLPM. At the L5–S1 level, the joint forces were 1,697 N and 6,051 N as predicted by the GCOM and CLPM, respectively. In the upright standing posture, the joint forces at the T12–L1 level were 337 N via the GCOM and 1,059 N via the CLPM. At the L5–S1 level, the joint forces were 507 N and 2,051 N predicted by the GCOM and CLPM, respectively. In the extension posture, the joint forces at the T12–L1 level were 376 N via the GCOM and 1,298 N via the CLPM. At the L5–S1 level, the joint forces were 565 N and 2,444 N predicted via the GCOM and CLPM, respectively.
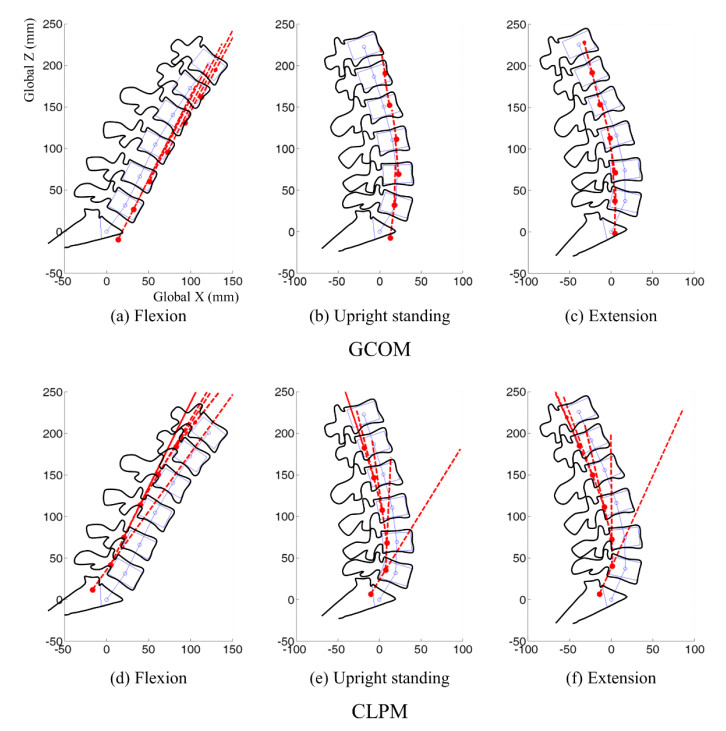
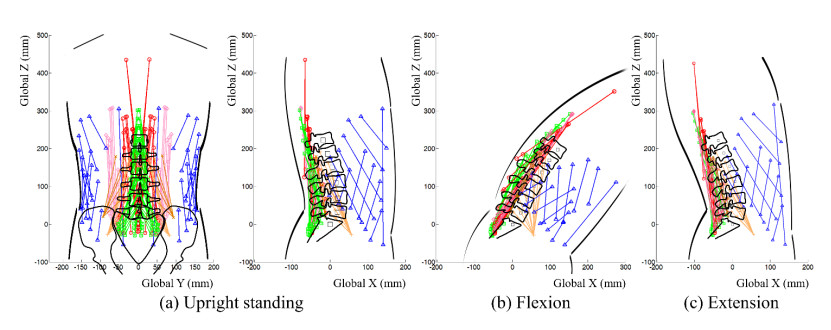
The calculated path of the ICRs and the joint force directions in flexion posture using the GCOM were along the spinal lordosis (Figure 5a). However, both the path of the ICRs and the joint force directions showed smaller curvatures than the lumbar lordosis in the upright standing and extension postures (Figure 5b and 5c). Compared to the upright standing posture, the ICRs calculated from the GCOM moved anteriorly in the flexion by about 9 mm, and posteriorly in the extension by about 12 mm (Table 1). The calculated ICRs by the CLPM were in the posterior portions of the vertebrae in all motions (Table 1 and Figure 5d, 5e, and 5f). The ICRs moved posteriorly in both the flexion and extension postures using the CLPM. The distances between the path of ICRs and the path of vertebral centers were 20.60 mm, 12.20 mm and 15.81 mm in the flexion, upright standing, and extension postures, respectively.
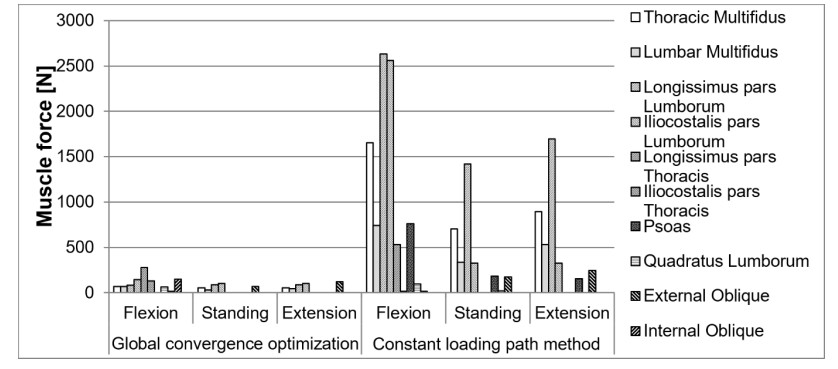
The predicted muscle forces for the three body postures using the GCOM and CLPM are shown in Figure 6. In the flexion posture, the longissimus pars thoracis has the maximum muscle forces of 277 N as predicted by the GCOM, and it has the maximum muscle force of 2,631 N as predicted by the CLPM. In the upright standing and extension postures, the longissimus pars lumborum has the maximum forces of 88 N and 87 N, respectively, as predicted using the GCOM, and 1,418 N and 1,696 N, respectively, as predicted using the CLPM.
4.
Discussion
In this study, we predicted joint and muscle forces, and the ICR locations of the human lumbar spine using the GCOM and CLPM, and we compared the results with each other. The results indicated that the joint and muscle forces predicted using the CLPM were greater than those calculated using the GCOM. The path connecting the ICRs obtained using the GCOM showed a smaller curvature than the lordosis of the lumbar spine in the standing and extension postures of the body. The ICRs moved anteriorly in the flexion and posteriorly in the extension of the body when the GCOM was used. However, the CLPM predicted a more posterior movement of the loading path during flexion than during the extension of the body.
Arjmand and Shirazi-Adl predicted joint forces in the upright standing and flexion postures using a computational simulation [1]. The reported compressive forces from T12–L1 to L5–S1 were 337 N, 405 N, 447 N, 498 N, 535 N, and 570 N in the upright standing, and 933 N, 1,171 N, 1,414 N, 1,669 N, 1,862 N, and 1,912 N in the flexion postures, respectively. The corresponding forces in this study were 333 N, 352 N, 358 N, 396 N, 481 N, and 462 N in the upright standing, and 1,244 N, 1,353 N, 1,453 N, 1,572 N, 1,679 N, and 1,677 N in the flexion postures, respectively when the GCOM was used. When the CLPM was used, the joint forces were 1,059 N, 1,228 N, 1,235 N, 1,255 N, 1,355 N, and 2,051 N in the upright standing, and 2,333 N, 2,269 N, 2,562 N, 3,694 N, 4,407 N, and 6,051 N in the flexion postures, respectively (Figure 4). Wilke et al. measured the intra-discal pressure of the L4–L5 motion segment and reported about 0.5 MPa and 1.1 MPa in the standing and forward flexed standing postures, respectively [2,3]. The physiological cross-sectional area (PCSA) of the IVD was roughly about 1,200 mm2 from the X-ray images. The estimated intra-discal pressures, which were defined as the applied compressive force divided by the PCSA of the IVD and the correction factor 0.77 23, were 0.5 MPa and 1.8 MPa in the upright standing and flexion postures, respectively, when the GCOM was used; and were 1.5 MPa and 4.8 MPa when the CLPM was used. These results indicated that the joint forces predicted by using the GCOM were consistent with those previously published in-vivo experimental and computational studies. The CLPM could result in overestimation of the joint forces when compared with the literature data.
In another study, Han et al. predicted the compressive forces from T12–L1 to L5–S1 based on the concept of follower load in the upright standing posture of the body (543 N, 533 N, 496 N, 501 N, 569 N, and 627 N, respectively for the segments from T12–S1) [9]. The data on joint forces were similar to our data predicted using the GCOM method; however, the values were lower than those predicted using the CLPM method. This could be explained from the differences between the computational models of the lumbar spine used in the two studies. The geometry of the lumbar model used in the previous study [9] is more straight and vertical (with less lordosis) than the model used in this study. A straighter lumbar spine could result in less joint moment produced by the segmental body weight, and it could consequently result in less spinal joint and muscle forces.
Pearcy and Bogduk reported the locations of the ICRs of the lumbar spine when moving from upright to flexion, from upright to extension, and from extension to flexion postures [24]. The ICR in L1–L2 motion segment was located more anteriorly than the other segments by 1–2 mm, 3–6 mm, and 0–2 mm during the upright to flexion, upright to extension, and extension to flexion postures, respectively, when the upper depth of the L2 vertebra was assumed to be 34 mm [25]. The ICRs during upright to flexion postures were located more anteriorly than those during the upright to extension postures. The ICRs were located in the anterior portion of the IVD in the flexion posture and in the posterior portion of the IVD in the extension posture in the experimental and computational studies [26,27]. These data are consistent with our calculations using the GCOM. The predicted ICRs using the GCOM were in the posterior portion of the L4–L5 motion segment and in the anterior portion of the other motion segments in the upright standing posture. They moved anteriorly in the flexion posture and posteriorly in the extension posture.
In the application of the concept of the follower load, Han et al. found that the ICRs were at 11 mm posterior to the vertebral centers [9]; Kim et al. found that the ICRs were at 5 mm or 8 mm posterior to the vertebral centers [12] in the upright standing posture of the body. In this study, the ICRs were calculated to be at 12 mm posterior to the vertebral centers in the upright standing posture using the CLPM method, which is more posterior to the data reported by others [9,12]. The ICRs were also found to move posteriorly in both extension and flexion postures of the body. The data predicted by using the CLPM were inconsistent with the reported data 24 and those predicted by using the GCOM.
In the GCOM, the locations of the ICRs were used as optimization variables in the optimization procedure. The calculated ICRs represent the locations where the joint reaction moments are zero, thus, this represents the real ICRs. However, in the CLPM, the ICRs were constrained along the path parallel to the spinal lordosis, thus introducing an extra constraint condition to the optimization procedure. If an additional constraint was applied, the optimization procedure may not converge to the actual minimum of the objective function as pointed out by Li et al. [14]. The cost function values at the convergence were 27,523.01 in the flexion, 3,599.22 in the upright standing posture, and 5,301.39 in the extension posture by using the CLPM. These are much greater than those calculated by using the GCOM (5.18 in the flexion, 2.82 in the upright standing, and 2.84 in the extension postures). Therefore, the CLPM could not result in a global convergence and resulted in overestimation of the joint and muscle forces.
There are certain limitations in current modeling of the spine musculoskeletal system. Previously published computational simulation studies on spine muscles showed that removing passive stiffness including rotation spring increases both the compressive and shear forces [28,29]. This study only calculated the joint reaction forces without considering the ligament tension, articular contact, and disc deformation forces. Therefore, these data represent the resultant intersegmental forces [30]. Furthermore, the muscles were considered passive force generators with no active contributions. Muscle wrapping was not included in the computer simulation model of the lumbar spine, and the action lines of the muscle forces were assumed to be straight lines between their attachment points. The posture of the upper body including the arm positions was not assumed to affect the location of the body mass center. Moreover, the only numerical model of the human lumbar spine was used to compare the GCOM and CLPM. However, these limitations did not affect the comparison of the GCOM and CLPM in our study because both methods were evaluated under the same geometric and loading conditions of the body. Therefore, the data could serve as a basis to evaluate different computation methods in simulations of human spine biomechanics.
There are certain limitations in current modeling of the spine musculoskeletal system. This study only calculated the joint reaction forces without considering the ligament tension, articular contact, and disc deformation forces. Therefore, these data represent the resultant intersegmental forces [30]. Previously published computational simulation studies on spine muscle forces showed that removing passive stiffness including rotation spring increases both the compressive and shear forces [28,29]. It could be the reason that greater intradiscal pressure was predicted in flexion posture even in the calculation using the GCOM compared to the experimental results [2,3]. The predicted joint forces were compared to the experimental intradiscal pressure because of a lack of experimental joint forces and muscle forces. Furthermore, the muscles were considered passive force generators with no active contributions. Muscle wrapping was not included in the computer simulation model of the lumbar spine, and the action lines of the muscle forces were assumed to be straight lines between their attachment points. The posture of the upper body including the arm positions was not assumed to affect the location of the body mass center.
As different postures showed different joint and muscle forces, spinal alignment can affect the joint and muscle forces. Moreover, anatomical parameters such as pelvic tilt, sacral slope, and Cobb's angle could also affect spinal physiological loads. Because the alternation of physiological loads is one of the critical reasons for spinal injuries and diseases, estimation of the physiological loads in a patient-specific model should be used to provide biomechanical information for evaluation of the injury risks or understanding of the mechanisms of disease development. Therefore, investigation of the relationship between spinal loads and geometry is necessary. However, this study was aimed to compare the GCOM and CLPM for spinal load predictions, we did not include the simulation of the geometry variations of the spinal complex. This limitation did not affect the comparison of the GCOM and CLPM in our study because both methods were evaluated under the same geometric and loading conditions of the body. The data could serve as a basis to evaluate different computation methods in simulations of human spine biomechanics.
5.
Conclusion
In this study, we calculated the joint forces, ICRs, and muscle forces of the human lumbar spine using an inverse optimization calculation of the spine dynamic biomechanics combined with two different computational methods for the ICRs: GCOM and CLPM. The estimated joint forces, ICRs, and muscle forces obtained using the GCOM were consistent with the results from previously published in-vivo experimental and computational studies while the CLPM could result in the overestimation of spine forces. The results of this study suggest that GCOM could be used as a useful method for the accurate investigation of spine biomechanics and other human joints. Moreover, the method could be used for investigating the biomechanical effects of spinal injuries, diseases, as well as in various surgical and athletic treatments.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. NRF-2017R1D1A1B03034668).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: