1. Introduction
Organic electronics allow for large scale, low cost, and low energy device fabrication. Today, organic electronics have found mass market application in digital displays consisting of organic light emitting diodes (OLED). In order to improve the performance of organic electronic devices, a detailed understanding of the device physics is essential. The challenge for highly ordered materials is twofold; on the one hand side, intrinsic properties, such as charge carrier mobility, depend on details of the pi-electron overlap [1] and polymorphism. Polymorphism is common among a variety of organic small molecule semiconductors [2,3,4,5]. Consequently, the domain size and the mutual distribution of the polymorphs are of great concern [6]. On the other hand, processing steps and interface phenomena often induce additional structural changes at the nm to micron scale, which may influence device performance. Close attention should be paid to contact regions because metal top contacts can influence the underlying organic layer by metal clusters diffusing in the organic film [7], while the growth mode of many organic materials on bottom contact metals is strongly disturbed, which changes the energy alignment of these materials [8]. In practice, top contact configuration in pentacene thin film transistors shows preferable device characteristics when not employing bottom contact electrodes which are functionalized [9]. Furthermore, the manufacturing of multilayer devices, such as organic light emitting diodes, organic photovoltaics and ambipolar organic field effect transistors (OFETs), demands the application of various sequential processing steps, including photolithography, imprint, shadow masks, spin casting, and annealing [10]. These subsequent processing steps can also modify the structure of subjacent films [11].
An experimental approach that allows nm-resolved, non-destructive probing of the crystal structure of organic devices, e.g. on top or below metal contacts of an OFET and in the conduction channel, would be very attractive. Recently, we introduced scattering-type scanning near field infrared optical microscopy (s-SNOM) to probe polymorphism in organic films [6]; however, this gentle technique does not work below Au contacts, which reflect back the IR light so that no information from below is accessible. Transmission electron microscopy (TEM) instead allows to image depth profiles of organic devices with close to molecular resolution, revealing interdiffusion of Au, originating from the top contact deposition [7]. However, the demanding cross section preparation requires cutting the device apart and the electron flux alters [12] or even disintegrates the molecular structure at prolonged exposure.
In principle, X-ray techniques combine all needed properties: X-ray reflectometry, for example, is used to depth profile stratified media on sample surfaces as well as buried layers [13], whereas scattering geometries, such as grazing incidence X-ray scattering allow for surface sensitive probing of thin organic single and multilayers [14,15]. Although X-rays are commonly used to probe rather large areas, typically several hundred microns squared, there is so far only a small amount of reports on scanning X-ray diffraction with a sub-micron focused X-ray beam [16,17,18,19]. This microdiffraction imaging was used to study inorganic materials and can for example resolve local strain and lattice orientation of semiconductors like Si and Ge. Studies using microdiffraction techniques on organic semiconductors are mostly limited to transmission measurements which resolve depth profiles of organic devices [20]. Ideally, the energy should be in the vicinity of ~ 20 keV because irradiating organic carbon compounds with high flux per area X-rays at lower energy leads to severe beam damage by incoherent scattering [21]. Here, we employ microdiffraction imaging in reflection geometry to study organic films, using a beam of 300 nm diameter at an energy of 12.5 keV, and cannot observe any beam damage. In this experiment, we map the lateral distribution of artificial and intrinsic structures in organic single- and multilayer thin-film devices. With microdiffraction imaging, it is possible to resolve the local crystalline structure on the surface and in buried layers, by scanning the beam over the sample and recording the intensity at specific angles, matching designated Bragg conditions. Furthermore, we discuss the current limitations of the lateral resolution and possible applications for this method.
2. Materials and Method
2.1. Sample preparation
The organic semiconductor pentacene served as a model system for our microdiffraction experiments. When grown on silicon oxide, pentacene thin films are known to crystallize in two main structural phases, the so-called thin-film phase (TFP) and bulk phase (BP) [4,5,22,23,24].
For measuring buried organic structures in working multilayer devices, an ambipolar organic field-effect transistor (OFET) was fabricated. Here, a 40 nm layer of pentacene was used as p-type semiconductor, followed by 40 nm gold top contacts, and finally 30 nm of fullerene C60 as n-type semiconductor. The channel width and length were 2 mm and 50 µm, respectively. Highly n-doped silicon with 300 nm SiO2 acted as combined gate/dielectric substrate. After consecutively sonicating in acetone, isopropyl alcohol, and de-ionized water for 10 min each, the sample was cleaned with oxygen plasma for 180 s. Prior to pentacene deposition, the dielectric surface was finished with a ~ 5 nm thick layer of cyclic-olefin-copolymere (COC), by spin casting a 0.25% solution of COC in toluene for 30s at 6000 rpm and annealing at 100 °C for 60 s. Pentacene and fullerene C60 layers were produced at room temperature and ~ 90 °C, respectively, by molecular vapor deposition, at a rate of 0.1 Å/s, respectively, and gold contacts were fabricated by electron beam deposition, at a rate of 1 Å/s. All structures were defined by shadow masks under ultra high vacuum conditions. The upper part of the pentacene layer (~ 5 nm) was cross-linked by e-beam irradiation prior to gold evaporation.
To study the polymorphism of TFP and BP pentacene, a 60 nm thick pentacene film was prepared on a silicon wafer with 20 nm thick SiO2. The substrate was cleaned by sonicating, as described above, and the pentacene film was deposited by molecular vapor deposition, at a rate of 0.1 Å/s. With this deposition rate, pentacene crystallizes at room temperature in the TFP with the [001] direction perpendicular to the substrate surface. However for this sample, a substrate temperature between 40 °C and 50 °C was chosen, which is known to induce mixed growth of TFP and BP pentacene [5,22,23,24] and to exhibit ellipsoidal structures on a sub-micron length scale [6]. The coexistence of the two phases on this sample was verified with an in-house reflectometer prior to the reported experiment.
2.2. X-ray diffraction
2.2.1. Reflectometry
The X-ray reflectometry curve shown here was measured at the P08 beamline at PETRA III at DESY in Hamburg, Germany [25]. Here, the X-ray energy E was set to 18 keV, which corresponds to a wavelength λ of 0.6888 Å.
2.2.2. Microdiffraction imaging
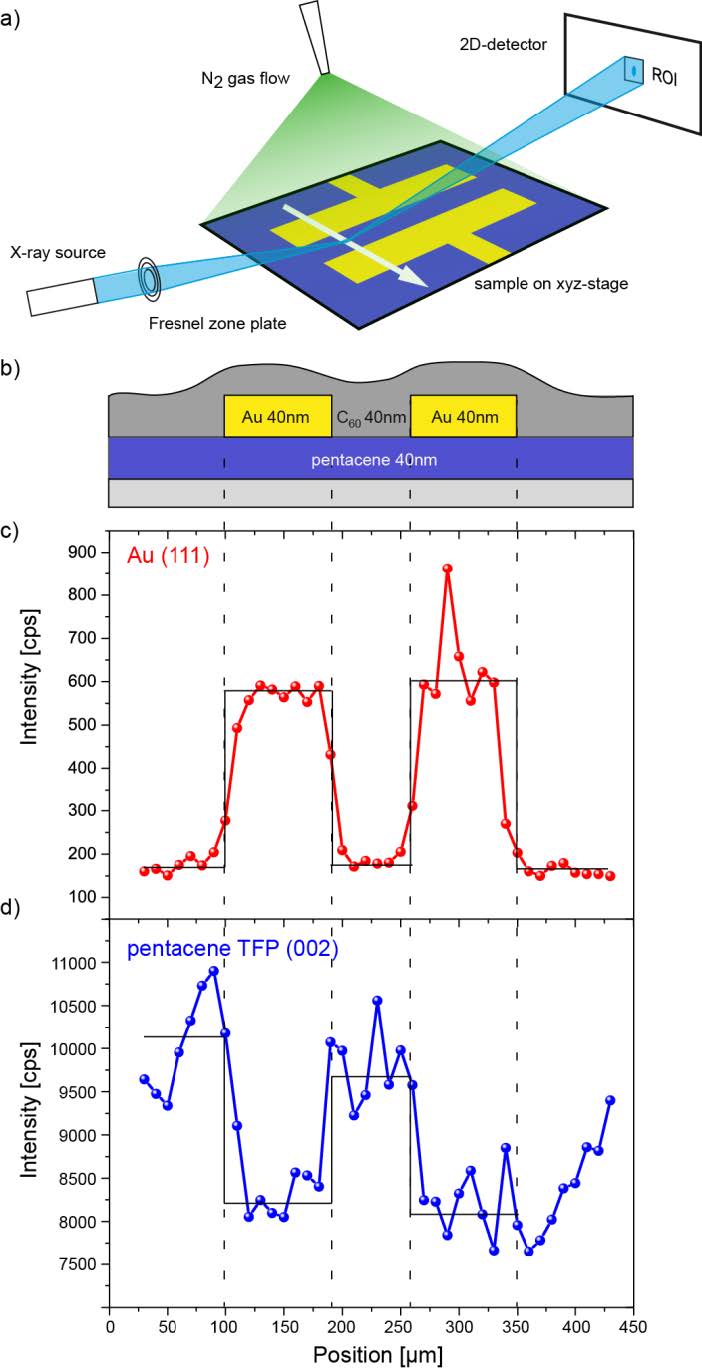
Microdiffraction imaging was performed at the beamline ID01 at the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. Here, the synchrotron X-ray beam with an energy of 12.5 keV, which corresponds to a wavelength λ of 0.9919 Å, was focused by a Fresnel zone plate with a central beam stop, followed by an order sorting aperture (to block unfocused beam parts and higher diffraction orders) to a nominal beam size of 300 nm (for further details, we refer to [17]). A sketch of the measurement geometry is shown in Figure 1a. Here, the angle of the incident beam θ was adjusted to a Bragg condition of the film and the diffracted beam was recorded with a 2D detector (MAXIPIX, 516 × 516 pixels², 55 × 55 µm² pixel size) [26] with adjusted regions of interest (ROI) at about 40 cm distance from the sample holder. Additionally, lead tape between the incident beam and the detector was used as a beam knife-edge to prevent air scattering from disturbing the recorded signal. To avoid radiation damage from reactive oxygen species, the sample was blown with dry nitrogen. First, the sample was positioned with a light microscope, illuminating from the top. Subsequently, the sample was continuously mapped in real space with a piezoelectric stage for short distances (<100 µm) or a hexapod (>100 µm) with step size resolutions of 5 nm and 100 nm, respectively. This so-called K-Map, a quick mapping procedure developed at ID01 has significantly reduced the measurement time needed for these scans, by optimizing positioning, exposure, and data acquisition [17]. The K-Maps in this report had a size of 40 × 40 µm² and a resolution of 80 × 40 pixels² (0.5 × 1 µm²), leading to a total measuring time of only 16 min and 43 min, corresponding to a pixel time of 0.3 s and 0.8 s, respectively.
However, the lateral resolution of the K-Maps is inherently limited by the footprint f of the beam. In the direction perpendicular to the X-ray beam, the footprint f⊥ corresponds to the diameter b of the focused beam, which was set to 300 nm during our experiments. Additionally, in the direction parallel to the incident X-ray beam, the geometrically enlarged footprint f‖ is given by
with the beam diameter b and the incident angle θ. Consequently, the footprint f
‖ is smaller for higher incident angles θ, which improves the lateral resolution of the K-Maps. A good lateral resolution in both directions can be achieved with inorganic crystals like VO
2, Si, or Ge
[16,17,18,19], owing to their high crystallinity. However, it is difficult to record K-Maps at high incident angles θ for organic crystals, because of their overall lower scattered intensity and their larger lattice constants. Therefore, finding a suitable compromise between footprint size and signal to noise ratio is essential, when measuring crystalline organic thin films. Here, the pentacene samples were measured at the (002) and (003) Bragg conditions.
3. Results and Discussion
We characterized an ambipolar pentacene-C60 OFET as a representative sample for multilayer devices, as they are commonly used in organic electronics. A sketch of the experimental geometry is shown in Figure 1 a). Here, the source and drain electrode of the transistor are indicated by the T-structures and the scan profile is indicated by the white arrow. At this position, the gold contacts had a length of 100 µm, each, which adds, together with the channel length of 50 µm, to a total device length of 250 µm. An illustration of the vertical section of the device is shown in Figure 1 b), with the C60 layer depicted on top of the gold and the pentacene layer. The pentacene top contact configuration is needed to optimize charge carrier injection in bi-layer ambipolar transistors [15].
To investigate the pentacene layer beneath the gold contacts, we measured two 400 µm scans over the device. First, we performed a reference measurement, to determine the exact sample position [Figure 1 c)]. The incidence angle θ was set to the Au (111) Bragg condition, i.e. 12.15°, which is very pronounced, since vacuum deposited gold on SiO2 crystallizes in fcc structure in [111] direction [27]. Here, the footprint size parallel to the beam f‖ corresponded to 1.43 µm, according to equation (1). The scan was done using the hexapod because the scan width of 400 µm exceeded the hardware limitation of the high-resolution piezoelectric stage. As seen from Figure 1, the intensity profile of the scan traces the channel geometry quite well. Second, we set the incidence angle to the pentacene TFP (002) Bragg condition, i.e. to 3.69°, which corresponded to a footprint f‖ of 4.65 µm. This led to good signal strength with an acceptable footprint. The intensity profile of the TFP (002) scan indicates a complementary behavior to the Au (111) scan [Figure 1 c)]. The drop in intensity beneath the gold contacts can be explained rather well by absorption of X-rays while passing through the gold layer. The absorption of a planar layer is given by:
|
Ir=I0∗exp(−2d μ *sin(θ))
|
(2) |
where d is the nominal gold layer thickness, θ the incident angle, µ = 3.2 µm the attenuation length of gold and I
0 the scattered intensity without gold. The factor two in the exponent accounts for the way in and out of the gold layer. As a result, the signal intensity should calculate to I
r ~ 0.68 * I
0. However, the acquired signal only drops about 20% and is thus higher than expected from this calculation. One explanation for this observation might be the uncertainty of the actual Au film thickness deposited onto the pentacene layer. The quartz microbalances, which were used to read out the nominal Au thickness, do not address any eventual deviations from growth on e.g. smooth SiO
2 surfaces.
For these reasons, the decrease of the pentacene signal beneath the gold contacts could be ascribed to the absorption of the beam propagating through the gold film. Thus, we have no indication that the top contact strongly reduces the crystallinity of the pentacene film.
Furthermore, the pentacene signal increased only slowly with growing distance to the right gold contact, even though no electrode material was present in the beam pathway. Here, the preparation of the contact geometry could have led to a damaged film. For example, removing the shadow mask could have led to a mechanical damage of the subjacent pentacene film after contact fabrication.
Moreover, it is necessary to address the large variations in the pentacene (002) signal, compared to the Au (111) signal. The grain size of pentacene is usually on the micron scale, far larger than for Au, and its topography shows thickness variations of the order of the nominal film thickness when grown on SiO2. Therefore, the scattered intensity should depend strongly on the beam position on the pentacene surface.
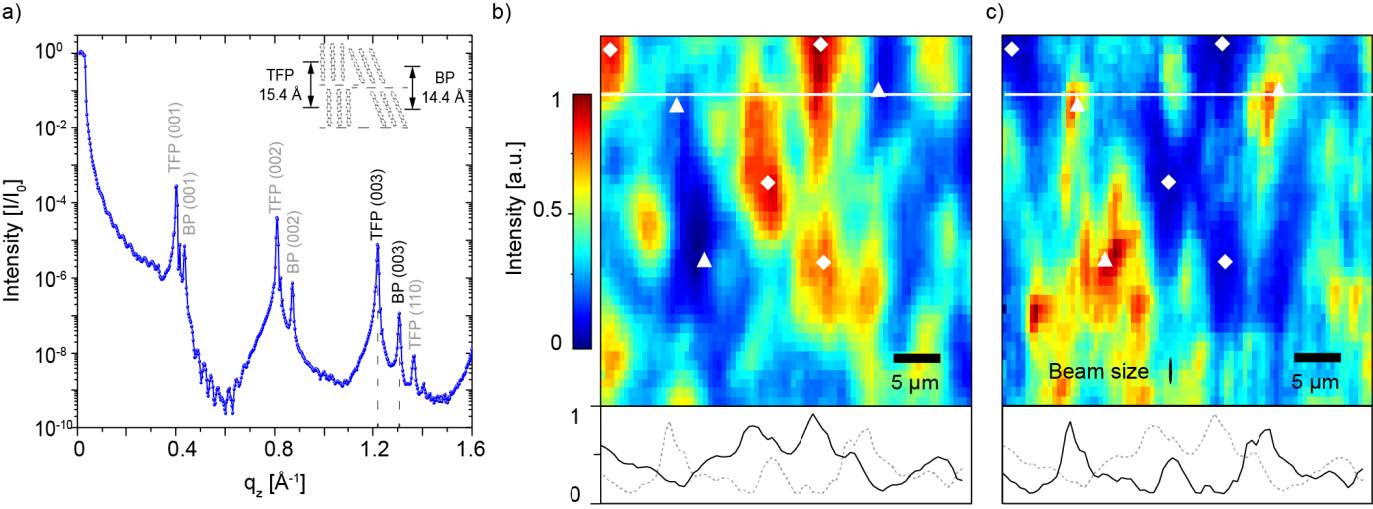
As a representative sample for investigating the local polymorphic structure of organic thin films and to determine the potential of the setup to resolve sub-micron features, we investigated a pentacene thin film, which exhibits three different Bragg signatures from the thin-film phase [TFP (00L)], the bulk phase [BP (00L)] and the lying phase, as verified via X-ray reflectometry (Figure 2 a). The crystalline lying phase nucleates after a critical film thickness, which is strongly dependent on the substrate temperature during the pentacene deposition (>100 nm at room temperature, 30 nm at 87 °C) [24,28]. In contrast, the coexistence of TFP and BP pentacene is induced by temperature dependent stress at the SiO2 interface [5,6,22,23,24]. Here, we focus on this coexistence of TFP and BP pentacene. Using s-SNOM with a lateral resolution as small as 20 nm has shown that, in fact, the lateral distribution of TFP and BP pentacene exhibits ellipsoidal structures on a length scale of 100 nm [6]. However, the s-SNOM probes to a depth of typically 30-50 nm [29], whereas X-ray microdiffraction yields information of the whole depth of the film.
To resolve the intrinsic lateral distribution of TFP and BP pentacene, we recorded two 2D K-Maps of the same sector of the sample surface, one for each polymorph. To gain high lateral resolution, we used the piezoelectric motors to move the sample stage. The incident angle θ was set to 5.54° and 5.93°, which corresponded to a footprint of 3.10 µm and 2.90 µm at the TFP (003) and BP (003) Bragg condition, respectively. Choosing the (003) Bragg conditions therefore reduced the footprint by 33% compared to the (002) Bragg conditions. For this system, choosing higher order Bragg conditions led to an undesirable signal to noise ratio. The K-Maps were recorded with the incident beam along the slow scan direction. To image a lateral inhomogeneity with full resolution, the scan size was set to 40 µm and the motor steps were set to 500 nm in the fast scan direction and 1 µm in the slow scan direction.
We have blown the samples with dry nitrogen during all measurements to minimize radiation damage from reactive oxygen species, activated by hard X-rays in ambient air. During the short exposure times of the maps and scans shown here (typically several seconds per data point), we could not observe any beam damage for repeated measurements, i.e. loss of Bragg signal, and thus conclude that microdiffraction imaging is suited for investigating organic thin films. Recent test measurements indicate that beam damage can be further minimized by using higher beam energies, i.e. at 20 keV exposure times of several minutes are possible.
As result, we obtained a map of the TFP and the BP distribution within the thin film [Figure 2 b) and c)]. The two K-Maps show a complementary intensity profile, revealing micron scaled domains exclusively grown in TFP (diamonds) and BP (triangles), respectively. This behavior can also be seen in the line profiles of TFP and BP pentacene. The elongated beam footprint indicated in Figure 2 c) leads to an overall smearing of the signal parallel to the beam direction.
4. Conclusion
We used microdiffraction imaging with a focused X-ray beam to study the structure of organic thin films. Within these films, we were able to resolve intrinsic structures as well as artificial structures, which are used to build organic electronic devices like multilayer ambipolar OFETs. We demonstrated a lateral resolution for organic thin films of 300 nm in the direction perpendicular to the beam and about 3 µm in the direction parallel to the beam. To acquire K-maps with the lateral resolution of the focus size in both directions, two subsequent K-Maps at the same sample position with a sample rotation of 90° would be needed. By further improving the focusing optics, ID01, for example, offers a beam size of 100 nm diameter after its upgrade in 2014 and it will be interesting to see, if this is confirmed in microdiffraction experiments.
Furthermore, changing the measurement geometry from reflection to transmission, could avoid the problem of large footprints parallel to the beam. This transmission geometry would require thinner substrates, e.g. sapphire [30] or ultra-thin Si3N4 membranes, which are commonly used for scanning transmission X-ray microscopy (STXM) [31,32].
Nevertheless, the current resolution is already well suited to study organic electronic devices, e.g. organic thin-film transistors, because the commonly used channel lengths of these devices are in the range of 20 µm to 50 µm. Furthermore, the local nanostructure of state of the art organic solar cells, fabricated by self-organization or nanoimprint [33], could also be examined, even with metallic contacts on top. X-ray microdiffraction therefore complements to other scanning techniques, like STXM [32], s-SNOM [6,16], scanning photoresponse microscopy [34], or micro-Raman spectroscopy [19], to gain a deeper understanding of fundamental device physics.
Acknowledgments
The authors gratefully acknowledge financial support from Deutsche Forschungsgemeinschaft through the SFB 1032 as well as by the Bavarian Ministry for Science through the initiative "Solar Technologies Go Hybrid” (SolTech). Parts of this research were carried out at the light source PETRA III at DESY, a member of the Helmholtz Association (HGF). We would like to thank Dr. O. H. Seeck for assistance in using beamline P08.
Conflict of Interest
The authors report no conflict of interests in this research.









 DownLoad:
DownLoad: