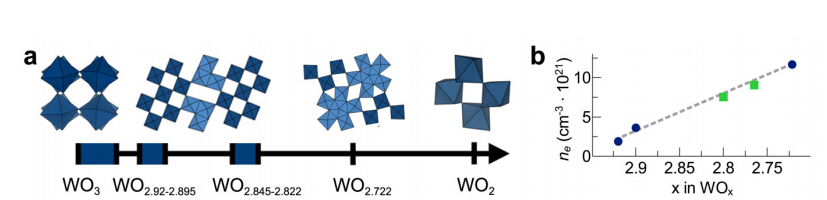
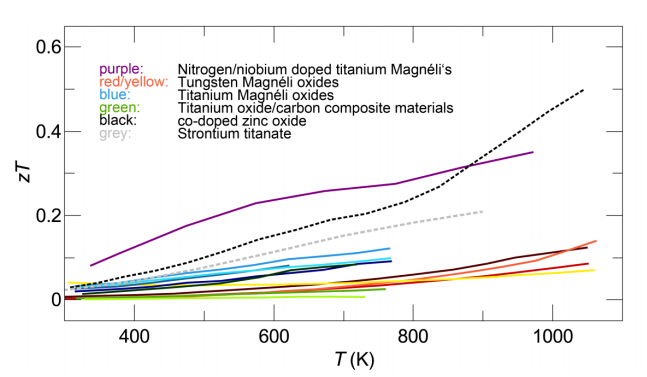
The discovery of a large thermopower in cobalt oxides in 1997 lead to a surge of interest in oxides for thermoelectric application. Whereas conversion efficiencies of p-type oxides can compete with non-oxide materials, n-type oxides show significantly lower thermoelectric performances. In this context so-called Magnéli oxides have recently gained attention as promising n-type thermoelectrics. A combination of crystallographic shear and intrinsic disorder lead to relatively low thermal conductivities and metallic-like electrical conductivities in Magnéli oxides. Current peak-zT values of 0.3 around 1100 K for titanium and tungsten Magnéli oxides are encouraging for future research. Here, we put Magnéli oxides into context of n-type oxide thermoelectrics and give a perspective where future research can bring us.
Introduction
The algebraic classification (up to isomorphism) of algebras of dimension $ n $ from a certain variety defined by a certain family of polynomial identities is a classic problem in the theory of non-associative algebras. There are many results related to the algebraic classification of small-dimensional algebras in many varieties of non-associative algebras [11,12,2,3,4,6,13,9,16]. So, algebraic classifications of $ 2 $-dimensional algebras [16,19], $ 3 $-dimensional evolution algebras [1], $ 3 $-dimensional anticommutative algebras [17], $ 4 $-dimensional division algebras [5,7], $ 4 $-dimensional nilpotent algebras [13] and $ 6 $-dimensional anticommutative nilpotent algebras [12] have been given. In the present paper, we give the algebraic classification of $ 5 $-dimensional nilpotent commutative algebras. The variety of commutative algebras is defined by the following identity: $ xy = yx. $ It contains commutative $ \mathfrak{CD} $-algebras, Jordan algebras, mock-Lie algebras and commutative associative algebras as subvarieties. On the other hand, it is a principal part in the varieties of weakly associative algebras and flexible algebras.
The algebraic study of central extensions of associative and non-associative algebras has been an important topic for years (see, for example, [10,20] and references therein). Our method for classifying nilpotent commutative algebras is based on the calculation of central extensions of nilpotent algebras of smaller dimensions from the same variety (first, this method has been developed by Skjelbred and Sund for Lie algebra case in [20]) and the classifications of all complex $ 5 $-dimensional nilpotent commutative (non-Jordan) $ \frak{CD} $-algebras [11]; nilpotent Jordan (non-associative) algebras [9]; and nilpotent associative commutative algebras [18].
1.
The algebraic classification of nilpotent commutative algebras
1.1. Method of classification of nilpotent algebras
Throughout this paper, we use the notations and methods well written in [10], which we have adapted for the commutative case with some modifications. Further in this section we give some important definitions.
Let $ ({\bf A}, \cdot) $ be a complex commutative algebra and $ \mathbb V $ be a complex vector space. The $ \mathbb C $-linear space $ {\rm Z^{2}}\left( \bf A,\mathbb V \right) $ is defined as the set of all bilinear maps $ \theta \colon {\bf A} \times {\bf A} \longrightarrow {\mathbb V} $ such that $ \theta(x,y) = \theta(y,x) . $ These elements will be called cocycles. For a linear map $ f $ from $ \bf A $ to $ \mathbb V $, if we define $ \delta f\colon {\bf A} \times {\bf A} \longrightarrow {\mathbb V} $ by $ \delta f (x,y ) = f(xy ) $, then $ \delta f\in {\rm Z^{2}}\left( {\bf A},{\mathbb V} \right) $. We define $ {\rm B^{2}}\left({\bf A},{\mathbb V}\right) = \left\{ \theta = \delta f\ : f\in {\rm Hom}\left( {\bf A},{\mathbb V}\right) \right\} $. We define the second cohomology space $ {\rm H^{2}}\left( {\bf A},{\mathbb V}\right) $ as the quotient space $ {\rm Z^{2}} \left( {\bf A},{\mathbb V}\right) \big/{\rm B^{2}}\left( {\bf A},{\mathbb V}\right) $.
Let $ \operatorname{Aut}({\bf A}) $ be the automorphism group of $ {\bf A} $ and let $ \phi \in \operatorname{Aut}({\bf A}) $. For $ \theta \in {\rm Z^{2}}\left( {\bf A},{\mathbb V}\right) $ define the action of the group $ \operatorname{Aut}({\bf A}) $ on $ {\rm Z^{2}}\left( {\bf A},{\mathbb V}\right) $ by
It is easy to verify that $ {\rm B^{2}}\left( {\bf A},{\mathbb V}\right) $ is invariant under the action of $ \operatorname{Aut}({\bf A}). $ So, we have an induced action of $ \operatorname{Aut}({\bf A}) $ on $ {\rm H^{2}}\left( {\bf A},{\mathbb V}\right) $.
Let $ \bf A $ be a commutative algebra of dimension $ m $ over $ \mathbb C $ and $ {\mathbb V} $ be a $ \mathbb C $-vector space of dimension $ k $. For the bilinear map $ \theta $, define on the linear space $ {\bf A}_{\theta } = {\bf A}\oplus {\mathbb V} $ the bilinear product " $ \left[ -,-\right] _{{\bf A}_{\theta }} $" by $ \left[ x+x^{\prime },y+y^{\prime }\right] _{{\bf A}_{\theta }} = xy +\theta(x,y) $ for all $ x,y\in {\bf A},x^{\prime },y^{\prime }\in {\mathbb V} $. The algebra $ {\bf A}_{\theta } $ is called a $ k $-dimensional central extension of $ {\bf A} $ by $ {\mathbb V} $. One can easily check that $ {\bf A_{\theta}} $ is a commutative algebra if and only if $ \theta \in {\rm Z^2}({\bf A}, {\mathbb V}) $.
Call the set $ \operatorname{Ann}(\theta) = \left\{ x\in {\bf A}:\theta \left( x, {\bf A} \right) = 0\right\} $ the annihilator of $ \theta $. We recall that the annihilator of an algebra $ {\bf A} $ is defined as the ideal $ \operatorname{Ann}( {\bf A} ) = \left\{ x\in {\bf A}: x{\bf A} = 0\right\} $. Observe that $ \operatorname{Ann}\left( {\bf A}_{\theta }\right) = (\operatorname{Ann}(\theta) \cap\operatorname{Ann}({\bf A})) \oplus {\mathbb V} $.
The following result shows that every algebra with a non-zero annihilator is a central extension of a smaller-dimensional algebra.
Lemma 1.1. Let $ {\bf A} $ be an $ n $-dimensional commutative algebra such that
Then there exists, up to isomorphism, a unique $ (n-m) $-dimensional commutative algebra $ {\bf A}' $ and a bilinear map $ \theta \in {\rm Z^2}({\bf A'}, {\mathbb V}) $ with $ \operatorname{Ann}({\bf A'})\cap\operatorname{Ann}(\theta) = 0 $, where $ \mathbb V $ is a vector space of dimension m, such that $ {\bf A} \cong {{\bf A}'}_{\theta} $ and $ {\bf A}/\operatorname{Ann}({\bf A})\cong {\bf A}' $.
Proof. Let $ {\bf A}' $ be a linear complement of $ \operatorname{Ann}({\bf A}) $ in $ {\bf A} $. Define a linear map $ P \colon {\bf A} \longrightarrow {\bf A}' $ by $ P(x+v) = x $ for $ x\in {\bf A}' $ and $ v\in\operatorname{Ann}({\bf A}) $, and define a multiplication on $ {\bf A}' $ by $ [x, y]_{{\bf A}'} = P(x y) $ for $ x, y \in {\bf A}' $. For $ x, y \in {\bf A} $, we have
Since $ P $ is a homomorphism, $ P({\bf A}) = {\bf A}' $ and $ {\bf A}' $ is a commutative algebra and also $ {\bf A}/\operatorname{Ann}({\bf A})\cong {\bf A}' $, which gives us the uniqueness. Now, define the map $ \theta \colon {\bf A}' \times {\bf A}' \longrightarrow\operatorname{Ann}({\bf A}) $ by $ \theta(x,y) = xy- [x,y]_{{\bf A}'} $. Thus, $ {\bf A}'_{\theta} $ is $ {\bf A} $ and therefore $ \theta \in {\rm Z^2}({\bf A'}, {\mathbb V}) $ and $ \operatorname{Ann}({\bf A'})\cap\operatorname{Ann}(\theta) = 0 $.
Definition 1.2. Let $ {\bf A} $ be an algebra and $ I $ be a subspace of $ \operatorname{Ann}({\bf A}) $. If $ {\bf A} = {\bf A}_0 \oplus I $ then $ I $ is called an annihilator component of $ {\bf A} $. A central extension of an algebra $ \bf A $ without annihilator component is called a non-split central extension.
Our task is to find all central extensions of an algebra $ \bf A $ by a space $ {\mathbb V} $. In order to solve the isomorphism problem we need to study the action of $ \operatorname{Aut}({\bf A}) $ on $ {\rm H^{2}}\left( {\bf A},{\mathbb V} \right) $. To do that, let us fix a basis $ e_{1},\ldots ,e_{s} $ of $ {\mathbb V} $, and $ \theta \in {\rm Z^{2}}\left( {\bf A},{\mathbb V}\right) $. Then $ \theta $ can be uniquely written as $ \theta \left( x,y\right) = \sum\limits_{i = 1}^{s} \theta _{i}\left( x,y\right) e_{i} $, where $ \theta _{i}\in {\rm Z^{2}}\left( {\bf A},\mathbb C\right) $. Moreover, $ \operatorname{Ann}(\theta) = \operatorname{Ann}(\theta _{1})\cap\operatorname{Ann}(\theta _{2})\cap\ldots \cap\operatorname{Ann}(\theta _{s}) $. Furthermore, $ \theta \in {\rm B^{2}}\left( {\bf A},{\mathbb V}\right) $ if and only if all $ \theta _{i}\in {\rm B^{2}}\left( {\bf A}, \mathbb C\right) $. It is not difficult to prove (see [10,Lemma 13]) that given a commutative algebra $ {\bf A}_{\theta} $, if we write as above $ \theta \left( x,y\right) = \sum\limits_{i = 1}^{s} \theta_{i}\left( x,y\right) e_{i}\in {\rm Z^{2}}\left( {\bf A},{\mathbb V}\right) $ and $ \operatorname{Ann}(\theta)\cap \operatorname{Ann}\left( {\bf A}\right) = 0 $, then $ {\bf A}_{\theta } $ has an annihilator component if and only if $ \left[ \theta _{1}\right] ,\left[ \theta _{2}\right] ,\ldots ,\left[ \theta _{s}\right] $ are linearly dependent in $ {\rm H^{2}}\left( {\bf A},\mathbb C\right) $.
Let $ {\mathbb V} $ be a finite-dimensional vector space over $ \mathbb C $. The Grassmannian $ G_{k}\left( {\mathbb V}\right) $ is the set of all $ k $-dimensional linear subspaces of $ {\mathbb V} $. Let $ G_{s}\left( {\rm H^{2}}\left( {\bf A},\mathbb C\right) \right) $ be the Grassmannian of subspaces of dimension $ s $ in $ {\rm H^{2}}\left( {\bf A},\mathbb C\right) $. There is a natural action of $ \operatorname{Aut}({\bf A}) $ on $ G_{s}\left( {\rm H^{2}}\left( {\bf A},\mathbb C\right) \right) $. Let $ \phi \in \operatorname{Aut}({\bf A}) $. For $ W = \langle \left[ \theta _{1}\right] ,\left[ \theta _{2}\right] ,\dots,\left[ \theta _{s} \right] \rangle \in G_{s}\left( {\rm H^{2}}\left( {\bf A},\mathbb C \right) \right) $ define $ \phi W = \langle \left[ \phi \theta _{1}\right] ,\left[ \phi \theta _{2}\right] ,\dots,\left[ \phi \theta _{s}\right] \rangle $. We denote the orbit of $ W\in G_{s}\left( {\rm H^{2}}\left( {\bf A},\mathbb C\right) \right) $ under the action of $ \operatorname{Aut}({\bf A}) $ by $ \operatorname{Orb}(W) $. Given
we easily have that if $ W_{1} = W_{2} $, then $ \bigcap\limits_{i = 1}^{s}\operatorname{Ann}(\theta _{i})\cap \operatorname{Ann}\left( {\bf A}\right) = \bigcap\limits_{i = 1}^{s} \operatorname{Ann}(\vartheta _{i})\cap\operatorname{Ann}( {\bf A}) $, and therefore we can introduce the set
which is stable under the action of $ \operatorname{Aut}({\bf A}) $.
Now, let $ {\mathbb V} $ be an $ s $-dimensional linear space and let us denote by $ {\bf E}\left( {\bf A},{\mathbb V}\right) $ the set of all non-split $ s $-dimensional central extensions of $ {\bf A} $ by $ {\mathbb V} $. By above, we can write
We also have the following result, which can be proved as in [10,Lemma 17].
Lemma 1.3. Let $ {\bf A}_{\theta },{\bf A}_{\vartheta }\in {\bf E}\left( {\bf A},{\mathbb V}\right) $. Suppose that $ \theta \left( x,y\right) = \sum\limits_{i = 1}^{s}\theta _{i}\left( x,y\right) e_{i} $ and $ \vartheta \left( x,y\right) = \sum\limits_{i = 1}^{s} \vartheta _{i}\left( x,y\right) e_{i} $. Then the commutative algebras $ {\bf A}_{\theta } $ and $ {\bf A}_{\vartheta } $ are isomorphic if and only if
This shows that there exists a one-to-one correspondence between the set of $ \operatorname{Aut}({\bf A}) $-orbits on $ {\bf T}_{s}\left( {\bf A}\right) $ and the set of isomorphism classes of $ {\bf E}\left( {\bf A},{\mathbb V}\right) $. Consequently we have a procedure that allows us, given a commutative algebra $ {\bf A}' $ of dimension $ n-s $, to construct all non-split central extensions of $ {\bf A}' $. This procedure is:
$ 1.\ $For a given commutative algebra $ {\bf A}' $ of dimension $ n-s $, determine $ {\rm H^{2}}( {\bf A}',\mathbb {C}) $, $ \operatorname{Ann}({\bf A}') $ and $ \operatorname{Aut}({\bf A}') $.
$ 2.\ $Determine the set of $ \operatorname{Aut}({\bf A}') $-orbits on $ {\bf T}_{s}({\bf A}') $.
$ 3.\ $For each orbit, construct the commutative algebra associated with a representative of it.
1.2. Reduction to non-$ \frak{CCD} $-algebras
The idea of the definition of a $ \mathfrak{CD} $-algebra comes from the following property of Jordan and Lie algebras: the commutator of any pair of multiplication operators is a derivation. This gives three identities of degree four, which reduce to only one identity of degree four in the commutative or anticommutative case. Namely, a commutative algebra is a commutative $ \frak{CD} $-algebra ($ \frak{CCD} $-algebra) if it satisfies the following identity:
The above described method gives all commutative ($ \mathfrak{CCD} $- and non-$ \mathfrak{CCD} $-) algebras. But we are interested in developing this method in such a way that it only gives non-$ \mathfrak{CCD} $ commutative algebras, because the classification of all $ \mathfrak{CCD} $-algebras is done in [11]. Clearly, any central extension of a commutative non-$ \mathfrak{CCD} $-algebra is a non-$ \mathfrak{CCD} $-algebra. But a $ \mathfrak{CCD} $-algebra may have extensions which are not $ \mathfrak{CCD} $-algebras. More precisely, let $ \mathfrak{D} $ be a $ \mathfrak{CCD} $-algebra and $ \theta \in {\rm Z_\mathfrak{C}^2}(\mathfrak{D}, {\mathbb C}). $ Then $ {\mathfrak{D}}_{\theta } $ is a $ \mathfrak{CCD} $-algebra if and only if
for all $ x,y,a,b\in {\mathfrak{D}}. $ Define the subspace $ {\rm Z_\mathfrak{D}^2}({\mathfrak{D}},{\mathbb C}) $ of $ {\rm Z_\mathfrak{C}^2}({\bf \mathfrak{D}},{\mathbb C}) $ by
Observe that $ {\rm B^2}({ \mathfrak{D}},{\mathbb C})\subseteq{\rm Z_\mathfrak{D}^2}({\mathfrak{D}},{\mathbb C}). $ Let $ {\rm H_\mathfrak{D}^2}({\mathfrak{D}},{\mathbb C}) = {\rm Z_\mathfrak{D}^2}({\mathfrak{D}},{\mathbb C}) \big/{\rm B^2}({\mathfrak{D}},{\mathbb C}). $ Then $ {\rm H_\mathfrak{D}^2}({\mathfrak{D}},{\mathbb C}) $ is a subspace of $ {\rm H_\mathfrak{C}^2}({\mathfrak{D}},{\mathbb C}). $ Define
Then $ {\bf T}_{s}({\mathfrak{D}}) = {\bf R}_{s}( {\mathfrak{D}}) $ ⊍ $ {\bf U}_{s}( {\mathfrak{D}}). $ The sets $ {\bf R}_{s}({\mathfrak{D}}) $ and $ {\bf U}_{s}({\mathfrak{D}}) $ are stable under the action of $ \operatorname{Aut}({\mathfrak{D}}). $ Thus, the commutative algebras corresponding to the representatives of $ \operatorname{Aut}({\mathfrak{D}}) $ -orbits on $ {\bf R}_{s}({\mathfrak{D}}) $ are $ \mathfrak{CCD} $-algebras, while those corresponding to the representatives of $ \operatorname{Aut}({\mathfrak{D}} ) $-orbits on $ {\bf U}_{s}({\mathfrak{D}}) $ are not $ \mathfrak{CCD} $-algebras. Hence, we may construct all non-split commutative non-$ \mathfrak{CCD} $-algebras $ \bf{A} $ of dimension $ n $ with $ s $-dimensional annihilator from a given commutative algebra $ \bf{A} ^{\prime } $ of dimension $ n-s $ in the following way:
$1.\ $If $ \bf{A}^{\prime } $ is non-$ \mathfrak{CCD} $, then apply the procedure.
$2.\ $Otherwise, do the following:
${\rm{(a)}} \ $Determine $ {\bf U}_{s}(\bf{A}^{\prime }) $ and $ \operatorname{Aut}(\bf{A}^{\prime }). $
$ {\rm{(b)}}\ $Determine the set of $ \operatorname{Aut}(\bf{A}^{\prime }) $-orbits on $ {\bf U }_{s}(\bf{A}^{\prime }). $
${\rm{(c)}} \ $For each orbit, construct the commutative algebra corresponding to one of its representatives.
1.3. Notations
Let us introduce the following notations. Let $ {\bf A} $ be a nilpotent algebra with a basis $ e_{1},e_{2}, \ldots, e_{n}. $ Then by $ \Delta_{ij} $ we will denote the bilinear form $ \Delta_{ij}:{\bf A}\times {\bf A}\longrightarrow \mathbb C $ with $ \Delta_{ij}(e_{l},e_{m}) = \delta_{il}\delta_{jm}, $ if $ i\leq j $ and $ l\leq m. $ The set $ \left\{ \Delta_{ij}:1\leq i\leq j\leq n\right\} $ is a basis for the linear space of bilinear forms on $ {\bf A}, $ so every $ \theta \in {\rm Z^2}({\bf A},\bf \mathbb V ) $ can be uniquely written as $ \theta = \sum\limits_{1\leq i\leq j\leq n} c_{ij}\Delta _{{i}{j}} $, where $ c_{ij}\in \mathbb C $. Let us fix complex number $ \eta_k $ ($ \eta_k^k = -1, $ $ \eta_k^l\neq1 $ for $ 0<l<k $). For denote our algebras, we will use the following notations:
Remark 1. All families of algebras from our final list do not have intersections, but inside some families of algebras there are isomorphic algebras. All isomorphisms between algebras from a certain family of algebras constucted from the representative $ \nabla(\Sigma) $ are given in the list of distinct orbit representations. The notation $ \langle \nabla(\Xi) \rangle^{O(\Xi_1) = O(\Xi_2)} $ represents that the elements $ \langle \nabla(\Xi_1) \rangle $ and $ \langle \nabla(\Xi_2) \rangle $ have the same orbit.
1.4. $ 3 $- and $ 4 $-dimensional commutative algebras.
Thanks to [8] we have the complete classification of complex $ 4 $-dimensional nilpotent commutative algebras. It will be re-written by some different way for separating $ \mathfrak{CCD} $- and non-$ \mathfrak{CCD} $-algebras.
2.
Central extensions of $ 3 $-dimensional nilpotent commutative algebras
2.1. $ 2 $-dimensional central extension of $ \mathbf{N}_{02}^{3*} $.
Here we will collect all information about $ \mathbf{N}_{02}^{3*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{4}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{3*}_{02}) . $ Since
we have
We are interested only in $ (\alpha_3,\alpha_4)\neq(0,0) $ and consider the vector space generated by the following two cocycles:
Thus, we have
Consider the following cases.
$ 1.\ $$ \alpha_4\neq0, $ then:
$ {\rm{(a)}} \ $$ \beta_3 = 0, \beta_2\neq 0, \beta_1 = 0 , $ then by choosing $ x = 2 \alpha_4^2, $ $ y = -\alpha_3 \alpha_4, $ $ z = \alpha_3^2-2 \alpha_1 \alpha_4, $ we have the representatives $ \langle \nabla_4, \nabla_2 \rangle; $
${\rm{(b)}}\ $ $ \beta_3 = 0, \beta_2\neq 0, \beta_1\neq 0 , $ then by choosing
we have the representatives $ \langle \nabla_4, \nabla_1 +\alpha \nabla_2 \rangle_{\alpha\neq 0}; $
$ {\rm{(c)}} \ $$ \beta_3 = 0, \beta_2 = 0, \beta_1\neq 0 , $ then by choosing $ y = -\frac{x \alpha_3}{2 \alpha_4}, $ we have two representatives $ \langle \nabla_4, \nabla_1 \rangle $ and $ \langle \nabla_2+\nabla_4, \nabla_1 \rangle, $ depending on $ \alpha_3^2 = \alpha_2 \alpha_4 $ or not. The first representative will be joint with the family from the case (1b);
${\rm{(d)}} \ $$ \beta_3\neq0, 4\alpha_2\beta_3^2 = 4\beta_2\alpha_3\beta_3-\beta_2^2\alpha_4, \beta_2 = 4\beta_1, $ then by choosing
we have the representative $ \langle \nabla_4, \nabla_3 \rangle; $
$ {\rm{(e)}} \ $$ \beta_3\neq0, 4\alpha_2\beta_3^2 = 4\beta_2\alpha_3\beta_3-\beta_2^2\alpha_4, \beta_2\neq4\beta_1, $ then by choosing
we have the representative $ \langle \nabla_4, \nabla_1+\nabla_3 \rangle; $
$ {\rm{(f)}} \ $$ \beta_3\neq0, 4\alpha_2\beta_3^2\neq4\beta_2\alpha_3\beta_3-\beta_2^2\alpha_4, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\nabla_4, \alpha\nabla_1+\nabla_3 \rangle. $
$2.\ \alpha_4 = 0, \alpha_3\neq0, $ then we may suppose that $ \beta_3 = 0 $ and
$ {\rm{(a)}}\ $ if $ \beta_1\neq0, \beta_2 = 4\beta_1, \alpha_2 = 4\alpha_1, $ then by choosing $ x = \alpha_3, y = -\alpha_1, z = 0, $ we have the representative $ \langle \nabla_3, \nabla_1+4\nabla_2 \rangle; $
$ {\rm{(b)}}\ $if $ \beta_1\neq0, \beta_2 = 4\beta_1, \alpha_2\neq4\alpha_1, $ then by choosing $ x = \frac{\alpha_2-4\alpha_1}{\alpha_3}, y = \frac{4\alpha^2_1-\alpha_1\alpha_2}{\alpha_3^2}, z = 0, $ we have the representative $ \langle -24(\nabla_2+\nabla_3), \nabla_1+4\nabla_2 \rangle; $
$ {\rm{(c)}}\ $if $ \beta_1\neq0, \beta_2\neq4\beta_1 , $ then by choosing $ x = \alpha_3(\beta_2-4\beta_1), y = \beta_1\alpha_2-\alpha_1\beta_2, z = 0, $ we have the family of representatives $ \langle \nabla_3, \nabla_1+\alpha\nabla_2 \rangle_{\alpha\neq4}, $ which will be jointed with the case (2a);
$ {\rm{(d)}}\ $if $ \beta_1 = 0, $ then we have the representative $ \langle -3\nabla_3, \nabla_2 \rangle $.
Summarizing, we have the following distinct orbits:
Note that the algebras constructed from the orbits $ \langle \nabla_1+4\nabla_2, -24(\nabla_2+\nabla_3) \rangle, $ $ \langle \nabla_1 + \lambda \nabla_2, \nabla_3 \rangle, $ $ \langle \nabla_1 +\alpha \nabla_2, \nabla_4\rangle, $ $ \langle \nabla_2, -3 \nabla_3 \rangle $ and $ \langle \nabla_2, \nabla_4 \rangle $ are parts of some families of algebras which found below. Hence, we have the following new algebras:
2.2. $ 2 $-dimensional central extension of $ \mathbf{N}_{04}^{3*} $.
Here we will collect all information about $ \mathbf{N}_{04}^{3*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{4}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{3*}_{04}) . $ Since
we have
Consider the following cases:
$ 1.\ $$ \alpha_4\neq0, $ then consider the vector space generated by the following two cocycles:
Thus, we have
Then we consider the following subcases:
$ {\rm{(a)}}\ $$ \beta_3 = 0, \alpha_3 = 0, $ then we have:
${\rm{(i)\ }} $if $ \beta_1 = 0, \alpha_1 = 0, $ then we have the representative $ \langle \nabla_4,\nabla_2 \rangle; $
${\rm{(ii)}}\ $if $ \beta_1 = 0, \alpha_1\neq0, $ then by choosing $ x = \sqrt[5]{ \alpha_1{\alpha_4}^{-1}}, $ we have the representative $ \langle \nabla_1+\nabla_4,\nabla_2 \rangle; $
${\rm{(iii)}}\ $if $ \beta_1\neq0, \beta_2 = 0, $ then by choosing $ x = 1 $ and $ z = - \alpha_2 \alpha_4^{-1}, $ we have the representative $ \langle \nabla_4,\nabla_1 \rangle; $
$ {\rm{(iv)}}\ $ if $ \beta_1\neq0, \beta_2\neq0, $ then by choosing $ x = \sqrt{{\beta_1}{\beta_2}^{-1}} $ and $ z = \frac{\alpha_1\beta_2-\beta_1\alpha_2}{\alpha_4 \sqrt{\beta_1\beta_2}}, $ we have the representative $ \langle \nabla_4,\nabla_1+\nabla_2 \rangle. $
${\rm{(b)}}\ \beta_3 = 0, \alpha_3\neq0, $ then we have:
${\rm{(i)}}\ $if $ \beta_2 = 0, $ then by choosing $ x = \sqrt{{\alpha_3}{\alpha_4}^{-1}} $ and $ z = -{\alpha_2}\sqrt{{\alpha_3} \alpha_4^{-3}}, $ we have the representative $ \langle \nabla_3+\nabla_4,\nabla_1 \rangle; $
${\rm{(ii)}}\ $if $ \beta_2\neq0, \beta_1 = 0, $ then by choosing
we have the representative $ \langle \nabla_3+\nabla_4,\nabla_2 \rangle; $
$ {\rm{(iii)}}\ $if $ \beta_2\neq0, \beta_1\neq0, \beta_2\alpha_3 = \beta_1\alpha_4, $ then by choosing $ x = \sqrt{{\alpha_3}{\alpha_4}^{-1}} $ and $ z = 0, $ we have the family of representatives $ \langle \alpha\nabla_1+\nabla_3+\nabla_4,\nabla_1+\nabla_2 \rangle; $
$ {\rm{(iv)}}\ $if $ \beta_2\neq0, \beta_1\neq0, \beta_2\alpha_3\neq\beta_1\alpha_4, $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_3+\nabla_4,\nabla_1+\nabla_2 \rangle_{\alpha\neq0,1}, $ which will be jointed with the case (1(a)iv).
${\rm{(c)}}\ \beta_3\neq0, \alpha_3 = 0, $ then we have:
$ {\rm{(i)}}\ $if $ \beta_2 = 0, \alpha_1 \neq0, $ then by choosing $ x = \sqrt[5]{ \alpha_1 \alpha_4^{-1}} $ and $ z = -\alpha_2 \sqrt[5]{\alpha_1 \alpha_4^{-6}}, $ we have the family of representatives $ \langle \nabla_1+\nabla_4,\alpha\nabla_1+\nabla_3 \rangle; $
$ {\rm{(ii)}}\ $if $ \beta_2 = 0, \alpha_1 = 0, $ then by choosing $ z = -\frac{\alpha_2x}{\alpha_4}, $ we have two representatives $ \langle \nabla_4,\nabla_3 \rangle $ or $ \langle \nabla_4,\nabla_1+\nabla_3 \rangle $ depending on whether $ \beta_1\alpha_4 = \alpha_2 \beta_3 $ or not;
$ {\rm{(iii)}}\ $if $ \beta_2\neq0, $ then by choosing $ x = {\frac{\beta_2}{\beta_3}} $ and $ z = -\frac{\alpha_2\beta_2}{\beta_3\alpha_4}, $ we have the family of representatives $ \langle \alpha\nabla_1+\nabla_4,\beta\nabla_1+\nabla_2+\nabla_3 \rangle. $
2. $ \alpha_4 = 0, \alpha_3\neq0 $, then we may suppose that $ \beta_3 = 0. $ Thus, we have
and consider the following subcases:
$ {\rm{(a)}}\ $$ \beta_2 = 0, $ then we have two representatives $ \langle \nabla_3,\nabla_1 \rangle $ or $ \langle \nabla_2+\nabla_3,\nabla_1 \rangle, $ depending on whether $ \alpha_2 = 0 $ or not;
$ {\rm{(b)}}\ $$ \beta_2\neq0, \alpha_2 = 0, $ then by choosing $ z = -\frac{\alpha_1x}{\alpha_3}, $ we have two representatives $ \langle \nabla_3,\nabla_2 \rangle $ or $ \langle \nabla_3,\nabla_1+\nabla_2 \rangle, $ depending on whether $ \beta_1 = 0 $ or not.
3. $ \alpha_4 = 0, \alpha_3 = 0, \beta_3 = 0, \beta_2 = 0, \alpha_2\neq0, $ then we have the representative $ \langle \nabla_2,\nabla_1 \rangle. $
Summarizing, we have the following distinct orbits:
Note that, the orbit $ \langle \nabla_1, \nabla_2 \rangle $ after a change of the basis of the constructed algebra gives a part of the family $ {\mathbf{N}}_{79}^{\alpha}, $ which will be found below. Hence, we have the following new algebras:
3.
Central extensions of nilpotent $ \mathfrak{CCD} $-algebras.
3.1. $ 1 $-dimensional central extensions of $ {\mathbf N}_{02}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{02}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{02}) . $ Since
we have
We interested in $ (\alpha_2,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) $ and $ (\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0) . $ Let us consider the following cases:
$ 1.\ $$ \alpha_6 = 0, \alpha_7 = 0, $ then $ \alpha_4\neq0 $ and we have the following subcases:
$ {\rm{(a)}}\ $$ \alpha_8 = 0, \alpha_2\alpha_4-\alpha_1\alpha_5 = 0, $ then we have a split extension;
$ {\rm{(b)}}\ $$ \alpha_8 = 0, \alpha_2\alpha_4-\alpha_1\alpha_5\neq0, \alpha_3 = 4\alpha_1, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_4 \rangle; $
$ {\rm{(c)}}\ $$ \alpha_8 = 0, \alpha_2\alpha_4-\alpha_1\alpha_5\neq0, \alpha_3\neq4\alpha_1, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_3+\nabla_4 \rangle; $
$ {\rm{(d)}}\ $$ \alpha_8\neq0, \alpha_3 = 4\alpha_1, $ then by choosing
we have the representative $ \langle \nabla_4+\nabla_8 \rangle; $
$ {\rm{(e)}}\ $$ \alpha_8\neq0, \alpha_3\neq4\alpha_1, $ then by choosing
we have the representative $ \langle \nabla_3+\nabla_4+\nabla_8 \rangle. $
2. $ \alpha_6 = 0, \alpha_7\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $$ \alpha_4 = 0, \alpha_3 = 0, $ then by choosing
we have the representative $ \langle \nabla_7 \rangle; $
${\rm{(b)}}\ $$ \alpha_4 = 0, \alpha_3\neq0, $ then by choosing
we have the representative $ \langle \nabla_3+\nabla_7 \rangle; $
$ {\rm{(c)}}\ $$ \alpha_4\neq0, \alpha_3\alpha_7^2-2\alpha_4\alpha_5\alpha_7+\alpha_4^2\alpha_8 = 0, $ then by choosing
we have the representative $ \langle \nabla_4+\nabla_7 \rangle; $
${\rm{(d)}}\ $$ \alpha_4\neq0, \alpha_3\alpha_7^2-2\alpha_4\alpha_5\alpha_7+\alpha_4^2\alpha_8\neq0, $ then by choosing
we have the representative $ \langle \nabla_4+ \nabla_5+\nabla_7 \rangle. $
3. $ \alpha_6\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $$ \alpha_6\alpha_8-\alpha_7^2 = 0, \alpha_5\alpha_6-\alpha_4\alpha_7 = 0, \alpha_2\alpha_6-\alpha_1\alpha_7 = 0, $ then we have a split extension;
${\rm{(b)}}\ $$ \alpha_6\alpha_8-\alpha_7^2 = 0, \alpha_5\alpha_6-\alpha_4\alpha_7 = 0, \alpha_2\alpha_6-\alpha_1\alpha_7\neq0, \alpha_3\alpha_6-\alpha^2_4 = 0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_6 \rangle; $
$ {\rm{(c)}}\ $$ \alpha_6\alpha_8-\alpha_7^2 = 0, \alpha_5\alpha_6-\alpha_4\alpha_7 = 0, \alpha_2\alpha_6-\alpha_1\alpha_7\neq0, \alpha_3\alpha_6-\alpha^2_4\neq0, $ then by choosing
and $ w = \frac{(\alpha_4^2-2 \alpha_1 \alpha_6) \sqrt{\alpha_3 \alpha_6-\alpha_4^2}}{2 \alpha_6^3}, $ we have the representative $ \langle \nabla_2+\nabla_3+\nabla_6 \rangle; $
${\rm{(d)}}\ $$ \alpha_6\alpha_8-\alpha_7^2 = 0, \alpha_5\alpha_6-\alpha_4\alpha_7\neq0, 2\alpha_6(\alpha_2\alpha_6-\alpha_1\alpha_7) = \alpha_4(\alpha_5\alpha_6-\alpha_4\alpha_7), $ then by choosing
we have the representatives $ \langle \nabla_5+\nabla_6 \rangle $ and $ \langle \nabla_3+\nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_3\alpha_6 = \alpha_4^2 $ or not;
$ {\rm{(e)}}\ $$ \alpha_6\alpha_8-\alpha_7^2 = 0, \alpha_5\alpha_6-\alpha_4\alpha_7\neq0, 2\alpha_6(\alpha_2\alpha_6-\alpha_1\alpha_7)\neq\alpha_4(\alpha_5\alpha_6-\alpha_4\alpha_7), $ then by choosing $ x = \frac{2\alpha_6(\alpha_2\alpha_6-\alpha_1\alpha_7)-\alpha_4(\alpha_5\alpha_6-\alpha_4\alpha_7)}{2\alpha_6^2(\alpha_5\alpha_6-\alpha_4\alpha_7)}, $ $ t = \frac{\alpha_6^2}{\alpha_5\alpha_6-\alpha_4\alpha_7}x^4, $ $ q = -\frac{\alpha_4}{2\alpha_6}x, $ $ r = \frac{\alpha_6\alpha_7}{\alpha_4\alpha_7-\alpha_5\alpha_6}x^4, $ $ e = 0, $ $ w = \frac{\alpha^2_4-2\alpha_1\alpha_6}{\alpha_6}x, $ we have the representative $ \langle \nabla_2+\alpha\nabla_3+\nabla_5+\nabla_6 \rangle; $
$ {\rm{(f)}}\ $$ \alpha_6\alpha_8-\alpha_7^2\neq0, \alpha_5\alpha_6-\alpha_4\alpha_7 = 0, $ then by choosing
we have the representatives $ \langle \nabla_6+\nabla_8 \rangle $ and $ \langle \nabla_3+\nabla_6+\nabla_8 \rangle $ depending on whether $ \alpha_3\alpha_6 = \alpha_4^2 $ or not.
$ {\rm{(g)}}\ $$ \alpha_6\alpha_8-\alpha_7^2\neq0, \alpha_5\alpha_6-\alpha_4\alpha_7\neq0, $ then by choosing
we have the representative $ \langle \alpha\nabla_3+\nabla_5+\nabla_6+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits
which gives the following new algebras:
3.2. $ 1 $-dimensional central extensions of $ {\mathbf N}_{04}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{04}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{04}) . $ Since
we have
We interested in $ (\alpha_3,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) $ and $ (\alpha_2,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0) . $ Let us consider the following cases:
$1.\ $$ \alpha_6 = 0, \alpha_7 = 0, \alpha_4 = 0, $ then $ \alpha_2\neq0 $ and we have the following cases:
$ {\rm{(a)}}\ $if $ \alpha_8 = 0, \alpha_5 = 0, $ then by choosing $ t = 1 $ and $ r = -\frac{\alpha_3}{\alpha_2}, $ we have a split extension;
$ {\rm{(b)}}\ $if $ \alpha_8 = 0, \alpha_5\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_8\neq0, \alpha_5 = 0, \alpha_1 = 0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_8 \rangle; $
${\rm{(d)}}\ $if $ \alpha_8\neq0, \alpha_5 = 0, \alpha_1\neq0, $ then by choosing
we have the representative $ \langle \nabla_1+\nabla_2+\nabla_8 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_8\neq0, \alpha_5\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5+\nabla_8 \rangle. $
2. $ \alpha_6 = 0, \alpha_7 = 0, \alpha_4\neq0, $ then by choosing $ r = -\frac{\alpha_5}{\alpha_4}t, y = -\frac{\alpha_1x+\alpha_5z}{\alpha_4}, $ we have $ \alpha^*_1 = \alpha^*_5 = 0 . $ Now we can suppose that $ \alpha_1 = 0, \alpha_5 = 0, $ and we have the following subcases:
${\rm{(a)}}\ $if $ \alpha_8 = 0, \alpha_3 = 0, $ then we have a split extension;
$ {\rm{(b)}}\ $if $ \alpha_8 = 0, \alpha_3\neq0, \alpha_2 = 0, $ then by choosing $ x = \alpha_3, $ $ y = 0, $ $ z = 0, $ $ r = 0, $ $ t = \alpha_3^4, $ we have the representative $ \langle \nabla_3+\nabla_4 \rangle; $
${\rm{(c)}}\ $if $ \alpha_8 = 0, \alpha_3\neq0, \alpha_2\neq0, $ then by choosing $ x = \frac{\alpha_2}{\alpha_4}, $ $ y = 0, $ $ z = 0, $ $ r = 0, t = \frac{\alpha_2^5}{\alpha_3\alpha_4^4}, $ we have the representative $ \langle \nabla_2+\nabla_3+\nabla_4 \rangle; $
${\rm{(d)}}\ $if $ \alpha_8\neq0, \alpha_2 = 0, $ then by choosing $ x = 1, y = 0, z = -\frac{\alpha_3}{\alpha_8}, r = 0, t = \sqrt{\frac{\alpha_4}{\alpha_8}}, $ we have the representative $ \langle \nabla_4+\nabla_8 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_8\neq0, \alpha_2\neq0, $ then by choosing $ x = \frac{\alpha_3}{\alpha_4}, y = 0, z = -\frac{\alpha_2\alpha_3}{\alpha_4\alpha_8}, r = 0, t = \frac{\alpha_2^3}{\sqrt{\alpha_4^5\alpha_8}}, $ we have the representative $ \langle \nabla_2+\nabla_4+\nabla_8 \rangle. $
3. $ \alpha_6 = 0, \alpha_7\neq0, $ then by choosing $ r = -\frac{\alpha_8t}{2\alpha_7}, y = -\frac{(\alpha_2\alpha_8-\alpha_3\alpha_7)x}{\alpha_7^2}, z = -\frac{\alpha_2x}{\alpha_7}, $ we have $ \alpha^*_2 = \alpha_3^* = \alpha^*_8 = 0. $ Now we can suppose that $ \alpha_2 = 0, $ $ \alpha_3 = 0, $ $ \alpha_8 = 0, $ and consider the following cases:
${\rm{(a)}}\ $if $ \alpha_4 = 0, \alpha_5 = 0, \alpha_1 = 0, $ then we have the representative $ \langle \nabla_7 \rangle; $
${\rm{(b)}}\ $if $ \alpha_4 = 0, \alpha_5 = 0, \alpha_1\neq0, $ then by choosing $ x = \frac{1}{\alpha_7}, t = \alpha_1, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_1+\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ \alpha_4 = 0, \alpha_5\neq0, \alpha_1 = 0, $ then by choosing $ x = \sqrt{\frac{\alpha_5}{\alpha_7}}, t = 1, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_5+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_4 = 0, \alpha_5\neq0, \alpha_1\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_5}{\alpha_7}}, t = \sqrt{\frac{\alpha_1^2}{\alpha_5\alpha_7}}, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_1+\nabla_5+\nabla_7 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_4\neq0, \alpha_5 = 0, \alpha_1 = 0, $ then by choosing $ x = \sqrt{\alpha_7}, t = \alpha_4, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_4+\nabla_7 \rangle; $
${\rm{(f)}}\ $if $ \alpha_4\neq0, \alpha_5 = 0, \alpha_1\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_1}{\alpha_4}}, t = \sqrt[3]{\frac{\alpha_1\alpha_4^2}{\alpha^3_7}}, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_1+\nabla_4+\nabla_7 \rangle; $
${\rm{(g)}}\ $if $ \alpha_4\neq0, \alpha_5\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_5}{\alpha_7}}, t = \sqrt{\frac{\alpha_4\alpha_5}{\alpha^2_7}}, y = 0, z = 0, r = 0, $ we have the representative $ \langle \alpha\nabla_1+\nabla_4+\nabla_5+\nabla_7 \rangle. $
4. $ \alpha_6\neq0, $ then by choosing $ r = -\frac{\alpha_7t}{\alpha_6}, y = -\frac{\alpha_2x+\alpha_7z}{\alpha_6}, $ we have $ \alpha^*_2 = \alpha_7^* = 0 . $ Now we can suppose that $ \alpha_2 = 0, \alpha_7 = 0, $ and we have:
$ {\rm{(a)}}\ $if $ \alpha_8 = 0, \alpha_5 = 0, $ then $ \alpha_3\neq0 $ and we have the following subcases:
$ {\rm{(i)}}\ $$ \alpha_4 = 0, \alpha_1 = 0, $ then by choosing $ x = \alpha_3, t = \alpha_3^6\alpha_6, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_3+\nabla_6 \rangle; $
${\rm{(ii)}}\ $$ \alpha_4 = 0, \alpha_1\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha_1}{\alpha_6}}, t = \sqrt[5]{\frac{\alpha_1^7}{\alpha_3^5\alpha^2_6}}, y = 0, z = 0, r = 0, $ we have the representative $ \langle \nabla_1+\nabla_3+\nabla_6 \rangle; $
${\rm{(iii)}}\ $$ \alpha_4\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_4}{\alpha_6}}, t = \sqrt[5]{\frac{\alpha_4^7}{\alpha_3^2\alpha^5_6}}, y = 0, z = 0, r = 0, $ we have the representative $ \langle \alpha\nabla_1+\nabla_3+\nabla_4+\nabla_6 \rangle. $
(b) $ \alpha_8 = 0, \alpha_5\neq0, $ then we have the following subcases:
${\rm{(i)}} \ $$ \alpha_4 = 0, \alpha_3 = 0, $ then by choosing $ x = \sqrt[6]{\frac{\alpha_5}{\alpha_6}}, t = 1, z = -\frac{\alpha_1}{\sqrt[6]{\alpha_5^5\alpha_6}},y = 0, r = 0, $ we have the representative $ \langle \nabla_5+\nabla_6 \rangle; $
${\rm{(ii)}}\ $$ \alpha_4 = 0, \alpha_3\neq0, $ then by choosing $ x = \frac{\alpha_3}{\alpha_5}, t = \alpha_3^6\alpha_5^{-7}\alpha_6, z = -\frac{\alpha_1\alpha_3}{\alpha_5^2}, y = 0, r = 0, $ we have the representative $ \langle \nabla_3+\nabla_5+\nabla_6 \rangle; $
${\rm{(iii)}}\ $$ \alpha_4\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_4}{\alpha_6}}, t = \frac{\alpha_4^3}{\alpha_5\alpha^2_6}, z = -\alpha_1\alpha_5^{-1}\sqrt{\alpha_4\alpha_6^{-1}}, y = 0, r = 0, $ we have the representative $ \langle \alpha\nabla_3+\nabla_4+\nabla_5+\nabla_6 \rangle. $
(c) $ \alpha_8\neq0, $ then we have the following subcases:
${\rm{(i)}}\ $$ \alpha_5 = 0, \alpha_4 = 0, \alpha_1 = 0, $ then by choosing $ x = 1, t = \sqrt{\frac{\alpha_6}{\alpha_8}}, z = -\frac{\alpha_3}{\alpha_8},y = 0, r = 0, $ we have the representative $ \langle \nabla_6+\nabla_8 \rangle; $
${\rm{(ii)}}\ $$ \alpha_5 = 0, \alpha_4 = 0, \alpha_1\neq0, $ then by choosing
we have the representative $ \langle \nabla_1+\nabla_6+\nabla_8 \rangle; $
${\rm{(iii)}}\ $$ \alpha_5 = 0, \alpha_4\neq0, $ then by choosing
we have the representative $ \langle \alpha\nabla_1+\nabla_4+\nabla_6+\nabla_8 \rangle; $
$ {\rm{(iv)}}\ $$ \alpha_5\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha^2_5}{\alpha_6\alpha_8}}, $ $ t = \frac{\alpha_5^2}{\sqrt{\alpha_6\alpha_8^3}}, $ $ z = -\frac{\alpha_3\sqrt{\alpha_5}}{\sqrt[4]{\alpha_6\alpha_8^5}}, $ $ y = 0, $ $ r = 0, $ we have the representative $ \langle \alpha\nabla_1+\beta\nabla_4+\nabla_5+\nabla_6+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits:
Hence, we have the following new algebras:
3.3. $ 1 $-dimensional central extensions of $ {\mathbf N}_{08}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{08}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{08}) . $ Since
we have
We are interested in $ (\alpha_3,\alpha_4, \alpha_5, \alpha_6,\alpha_7)\neq(0,0,0,0,0), $ $ (\alpha_2+\alpha_3,\alpha_4, \alpha_6, \alpha_7)\neq(0,0,0,0) $ and $ (\alpha_1,\alpha_2, \alpha_5, \alpha_6)\neq(0,0,0,0). $ Let us consider the following cases:
$ 1.\ $$ \alpha_7 = 0, \alpha_6 = 0, \alpha_5 = 0, \alpha_4 = 0, $ then $ \alpha_3\neq0, $ $ \alpha_2+\alpha_3 \neq 0 $ and $ (\alpha_1,\alpha_2)\neq(0,0). $
${\rm{(a)}}\ $ if $ \alpha_2\neq-\frac{\alpha_3}{4}, $ then by choosing $ x = 4\alpha_2+\alpha_3, y = -\alpha_1, $ we have the representative $ \langle \alpha\nabla_2+\nabla_3 \rangle_{\alpha\neq0,-\frac{1}{4},-1}; $
${\rm{(b)}}\ $if $ \alpha_2 = -\frac{\alpha_3}{4}, $ then we have the representatives
depending on $ \alpha_1 = 0 $ or not.
2. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5 = 0, \alpha_4\neq0, $ then by choosing $ y = -\frac {3\alpha_2}{\alpha_4}x, $ we have $ \alpha_2^* = 0. $ This we can suppose $ \alpha_2 = 0, $ which implies $ \alpha_1\neq 0 $ and choosing $ x = \sqrt {\alpha_1 \alpha_4^{-1}}, $ we have the representative $ \langle \nabla_1+\alpha\nabla_3+\nabla_4 \rangle. $
3. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5\neq0. $
${\rm{(a)}}\ $ if $ \alpha_4 = 0, $ then $ \alpha_2\neq-\alpha_3 $ and choosing
we have the representative $ \langle \nabla_2+\nabla_5 \rangle; $
${\rm{(b)}}\ $if $ \alpha_4\neq0, \alpha_4\neq\alpha_5, 2(\alpha_2\alpha_5-\alpha_2\alpha_4+\alpha_3\alpha_5)+\alpha_3\alpha_4 = 0, $ then by choosing
we have the representative $ \langle \alpha\nabla_4+\nabla_5 \rangle_{\alpha\neq0,1}; $
${\rm{(c)}}\ $ if $ \alpha_4\neq0, \alpha_4\neq\alpha_5, 2(\alpha_2\alpha_5-\alpha_2\alpha_4+\alpha_3\alpha_5)+\alpha_3\alpha_4\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\alpha\nabla_4+\nabla_5 \rangle_{\alpha\neq0,1} $;
${\rm{(d)}}\ $if $ \alpha_4\neq0, \alpha_4 = \alpha_5, $ then by choosing $ y = -\frac{\alpha_2x}{\alpha_5} $ and $ z = \frac{(\alpha_3\alpha_5-\alpha_1\alpha_5+3\alpha_2^2)x}{\alpha_5^2}, $ we have the representatives $ \langle \nabla_4+\nabla_5 \rangle $ and $ \langle \nabla_3+\nabla_4+\nabla_5 \rangle $ depending on whether $ \alpha_3 = 0 $ or not. Note that $ \langle \nabla_4+\nabla_5 \rangle = \langle \nabla_2+\nabla_4+\nabla_5 \rangle $ and it will be jointed with the family from the case (3c).
4. if $ \alpha_7 = 0, \alpha_6\neq0, $ then by choosing $ x = 1, $ $ y = \frac{ \sqrt{( \alpha_4 + 2 \alpha_5)^2 - 36 \alpha_2 \alpha_6}- \alpha_4 - 2 \alpha_5 }{6 \alpha_6}, $
we have $ \alpha_1^* = \alpha_2^* = \alpha_3^* = 0. $ Now we can suppose that $ \alpha_1 = 0, \alpha_2 = 0, \alpha_3 = 0, $ and we have the following cases:
$ {\rm{(a)}}\ $if $ \alpha_4 = 0, \alpha_5 = 0, $ then by choosing $ x = 1, y = 0, z = 0, t = 0, $ we have the representative $ \langle \nabla_6 \rangle; $
${\rm{(b)}}\ $ if $ \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = -\frac{4 \alpha_5}{3 \alpha_6}, y = \frac{8 \alpha_5^2}{9 \alpha_6^2}, z = 0, t = 0, $ we have the representative $ \langle \nabla_4+\frac{1}{4}\nabla_5+\nabla_6 \rangle; $
${\rm{(c)}}\ $if $ \alpha_4\neq0, $ then by choosing $ x = \frac{\alpha_4}{\alpha_6}, y = 0, z = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_6 \rangle, $ which will be jointed with the representative from the case (4b).
5. if $ \alpha_7\neq0, $ then by choosing $ x = 1, $ $ y = -\frac{\alpha_6}{\alpha_7}, $ $ t = \frac{ 2 \alpha_6^3+2 (\alpha_4-\alpha_5) \alpha_6 \alpha_7-3 \alpha_3 \alpha_7^2 }{3\alpha_7^3} $ and $ z = 0, $ we have $ \alpha_3^* = 0, \alpha_6^* = 0. $ Now we can suppose that $ \alpha_3 = 0, \alpha_6 = 0, $ and we have the following cases:
${\rm{(a)}}\ $if $ \alpha_5\neq0, $ then by choosing $ x = \sqrt{\alpha_5\alpha_7^{-1}}, y = 0, z = \sqrt{\alpha_1^2 \alpha_5^{-1}\alpha_7^{-1}}, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_2+\beta\nabla_4+\nabla_5+\nabla_7 \rangle; $
${\rm{(b)}}\ $if $ \alpha_5 = 0, \alpha_2 = 0, $ then $ \alpha_1\neq 0 $ and we have the family of representatives $ \langle \nabla_1+\alpha\nabla_4+\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ \alpha_5 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt[3]{\alpha_2\alpha_7^{-1}}, y = 0, z = 0, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_1+ \nabla_2+\beta\nabla_4+\nabla_7 \rangle. $
Summarizing all cases we have the following distinct orbits
which gives the following new algebras:
3.4. $ 1 $-dimensional central extensions of $ {\mathbf N}_{09}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{09}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{09}) . $ Since
we have
We are interested in $ (\alpha_3,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) $. Let us consider the following cases:
$ 1.\ $$ \alpha_8 = 0, \alpha_7 = 0, \alpha_5 = 0, $ then $ \alpha_3\neq0 $ and we have
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then by choosing $ x = 1, r = \alpha_3, s = -\alpha_2, t = 0, $ we have the representative $ \langle \nabla_3 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \alpha_6, r = \alpha_3\alpha_6^2, s = -\alpha_2\alpha_6^2, t = 0, $ we have the representative $ \langle \nabla_3+\nabla_6 \rangle; $
${\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_6 = 0, $ then by choosing $ x = \alpha_3^2, r = \alpha_3\alpha_4, s = -\alpha_2\alpha_4, t = 0, $ we have the representative $ \langle \nabla_3+\nabla_4 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_6\neq0, $ then by choosing $ x = {\alpha_3}^{-1}\sqrt{\alpha_4\alpha_6}, $ $ r = {\alpha_3}^{-2}{\sqrt{\alpha_4^3\alpha_6}}, $ $ s = -\alpha_2{\alpha_3}^{-3}\sqrt{\alpha_4^3\alpha_6}, $ $ t = 0, $ we have the representative $ \langle \nabla_3+\nabla_4+\nabla_6 \rangle; $
${\rm{(e)}}\ $if $ \alpha_1\neq0, \alpha_4 = 0, \alpha_6 = 0, $ then by choosing $ x = 1, $ $ r = {\alpha_1}{\alpha_3}^{-1}, $ $ s = -{\alpha_1\alpha_2}{\alpha^{-2}_3}, $ $ t = 0, $ we have the representative $ \langle \nabla_1+\nabla_3 \rangle; $
$ {\rm{(f)}}\ $if $ \alpha_1\neq0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \sqrt[3]{\alpha_1\alpha_6 \alpha_3^{-2}}, $ $ r = \alpha_1\alpha_3^{-1}, $ $ s = -\alpha_1\alpha_2\alpha^{-2}_3, $ $ t = 0, $ we have the representative $ \langle \nabla_1+\nabla_3+\nabla_6 \rangle; $
${\rm{(g)}}\ $if $ \alpha_1\neq0, \alpha_4\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\nabla_3+\nabla_4+\alpha\nabla_6 \rangle. $
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_5\neq0 $ and we have
${\rm{(a)}}\ $if $ \alpha_3 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then by choosing $ r = 1, x = \alpha_5, t = -\alpha_1, s = 0, $ we have the representative $ \langle \nabla_5 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_3 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \alpha_5\alpha_6, $ $ r = \alpha_5^5\alpha_6^3, s = 0, t = -\alpha_1\alpha_6, $ we have the representative $ \langle \nabla_5+\nabla_6 \rangle; $
${\rm{(c)}}\ $if $ \alpha_3 = 0, \alpha_2 = 0, \alpha_4\neq0, \alpha_6 = 0, $ then by choosing $ x = 1, r = \alpha_4{\alpha_5}^{-1}, t = -{\alpha_1}{\alpha_5}^{-1}, s = 0, $ we have the representative $ \langle \nabla_4+\nabla_5 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_3 = 0, \alpha_2 = 0, \alpha_4\neq0, \alpha_6\neq0, $ then by choosing
we have the representative $ \langle \nabla_4+\nabla_5+\nabla_6 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_3 = 0, \alpha_2\neq0, \alpha_4 = 0, \alpha_6 = 0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5 \rangle; $
${\rm{(f)}}\ $if $ \alpha_3 = 0, \alpha_2\neq0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5+\nabla_6 \rangle; $
${\rm{(g)}}\ $if $ \alpha_3 = 0, \alpha_2\neq0, \alpha_4\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\nabla_4+\nabla_5+\alpha\nabla_6 \rangle; $
${\rm{(h)}}\ $if $ \alpha_3\neq0, \alpha_4 = 0, \alpha_6 = 0, $ then by choosing $ x = {\alpha_3}{\alpha_5}^{-1}, r = \alpha_3, s = -\alpha_2, t = -{\alpha_1\alpha_3}{\alpha_5^{-2}}, $ we have the representative $ \langle \nabla_3+\nabla_5 \rangle; $
${\rm{(i)}}\ $if $ \alpha_3\neq0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing
we have the representative $ \langle \nabla_3+\nabla_5+\nabla_6 \rangle; $
$ {\rm{(j)}}\ $if $ \alpha_3\neq0, \alpha_4\neq0, $ then by choosing $ x = {\alpha_3}{\alpha_5}^{-1}, r = {\alpha_4}{\alpha_5}^{-1}, s = -{\alpha_2\alpha_4}{\alpha_3^{-1}\alpha_5^{-1}}, t = -{\alpha_1\alpha_3}{\alpha_5^{-2}}, $ we have the family of representatives $ \langle \nabla_3+\nabla_4+\nabla_5+\alpha\nabla_6 \rangle. $
3. $ \alpha_8 = 0, \alpha_7\neq0, $ then by choosing $ x = 2 \alpha_7^2, $ $ t = \alpha_3 \alpha_6-2 \alpha_2 \alpha_7, $ $ s = -\alpha_6, $ $ r = 2 \alpha_7, $ we have $ \alpha_2^* = \alpha_6^* = 0. $ Now we can suppose that $ \alpha_2 = 0 $ and $ \alpha_6 = 0, $ then for $ s = 0 $ and $ t = 0, $ we have:
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then by choosing $ r = 1, x = 1, $ we have the representative $ \langle \nabla_7 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \alpha_7, r = \alpha_5\alpha_7, $ we have the representative $ \langle \nabla_5+\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, \alpha_5 = 0, $ then by choosing $ x = \sqrt{\alpha_7}, r = \sqrt{\alpha_4}, $ we have the representative $ \langle \nabla_4+\nabla_7 \rangle; $
${\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, \alpha_5\neq0, $ then by choosing $ x = \alpha_4\sqrt{\alpha_7 \alpha_5^{-3}}, r = {\alpha_4}{\alpha_5}^{-1}, $ we have the representative $ \langle \nabla_4+\nabla_5+\nabla_7 \rangle; $
${\rm{(e)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, \alpha_5 = 0, $ then by choosing $ r = \alpha_3, x = \alpha_5, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\nabla_7 \rangle; $
$ {\rm{(f)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, \alpha_5\neq0, $ then by choosing $ x = {\alpha_3}{\alpha_5}^{-1}, r = {\alpha_3^2}{\alpha_5^{-1}\alpha_7^{-1}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\nabla_5+\nabla_7 \rangle; $
${\rm{(g)}}\ $if $ \alpha_1\neq0, \alpha_3 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then by choosing $ x = \alpha_1\alpha_7, r = \alpha_1, $ we have the representative $ \langle \nabla_1+\nabla_7 \rangle; $
$ {\rm{(h)}}\ $if $ \alpha_1\neq0, \alpha_3 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_1\alpha_7}{\alpha^{-2}_5}}, r = \sqrt[3]{{\alpha_1^2}{\alpha_5^{-1}\alpha_7^{-1}}}, $ we have the representative $ \langle \nabla_1+\nabla_5+\nabla_7 \rangle; $
$ {\rm{(i)}}\ $if $ \alpha_1\neq0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = {\alpha_1}{\alpha_4}^{-1}, r = {\alpha_1}{\sqrt{\alpha_4^{-1}\alpha_7^{-1}}}, $ we have the family of representatives $ \langle \nabla_1+\nabla_4+\alpha\nabla_5+\nabla_7 \rangle; $
${\rm{(j)}}\ $if $ \alpha_1\neq0, \alpha_3\neq0, $ then by choosing $ x = {\alpha_1\alpha_7}{\alpha_3^{-2}}, r = {\alpha_1}{\alpha_3}^{-1}, $ we have the family of representatives $ \langle \nabla_1+\nabla_3+\alpha\nabla_4+\beta\nabla_5+\nabla_7 \rangle. $
4. $ \alpha_8\neq0, $ then by choosing $ x = \alpha_8, t = - \alpha_3, s = - \alpha_7, r = \alpha_8, $ we have $ \alpha_3^* = \alpha_7^* = 0. $ Now we can suppose that $ \alpha_3 = 0 $ and $ \alpha_7 = 0, $ then for $ s = 0 $ and $ t = 0, $ we have
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then we have the representatives $ \langle \nabla_8 \rangle $ and $ \langle \nabla_5+\nabla_8 \rangle, $ depending on whether $ \alpha_5 = 0 $ or not;
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then we have the representatives $ \langle \nabla_6+\nabla_8 \rangle $ and $ \langle \nabla_5+\nabla_6+\nabla_8 \rangle, $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4\neq0, \alpha_6 = 0, $ then we have the representatives $ \langle \nabla_4+\nabla_8 \rangle $ and $ \langle \nabla_4+\nabla_5+\nabla_8 \rangle, $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4\neq0, \alpha_6\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_6}{\alpha_8}^{-1}}, r = \sqrt{{\alpha_4}{\alpha_8}^{-1}} , $ we have the representative $ \langle \nabla_4+\alpha\nabla_5+\nabla_6+\nabla_8 \rangle; $
${\rm{(e)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, \alpha_4 = 0, \alpha_5 = 0, $ then we have the representatives $ \langle \nabla_2+\nabla_8 \rangle $ and $ \langle \nabla_2+\nabla_6+\nabla_8 \rangle, $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(f)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_2}{\alpha_5}^{-1}}, r = {\alpha_5}{\alpha_8}^{-1}, $ we have the representative $ \langle \nabla_2+\nabla_5+\alpha\nabla_6+\nabla_8 \rangle; $
${\rm{(g)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_2^2 \alpha_4^{-1}\alpha_8^{-1}}}, $ $ r = \sqrt{{\alpha_4}{\alpha_8}^{-1}}, $ we have the representative $ \langle \nabla_2+\nabla_4+\alpha\nabla_5+\beta\nabla_6+\nabla_8 \rangle; $
$ {\rm{(h)}}\ $if $ \alpha_1\neq0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then we have the representatives $ \langle \nabla_1+\nabla_8 \rangle $ and $ \langle \nabla_1+\nabla_6+\nabla_8 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
${\rm{(i)}}\ $if $ \alpha_1\neq0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = {\alpha_1\alpha_8}{\alpha_5^{-2}}, r = {\alpha_5}{\alpha_8}^{-1}, $ we have the representative $ \langle \nabla_1+\nabla_5+\alpha\nabla_6+\nabla_8 \rangle; $
${\rm{(j)}}\ $if $ \alpha_1\neq0, \alpha_2 = 0, \alpha_4\neq0, $ then by choosing $ x = {\alpha_1}{\alpha_4}^{-1}, r = \sqrt{{\alpha_4}{\alpha_8}^{-1}}, $ we have the representative $ \langle \nabla_1+\nabla_4+\alpha\nabla_5+\beta\nabla_6+\nabla_8 \rangle; $
$ {\rm{(k)}}\ $if $ \alpha_1\neq0, \alpha_2\neq0, $ then by choosing $ x = \sqrt[5]{{\alpha_2^2}{\alpha_1^{-1}\alpha_8^{-1}}}, r = \sqrt[5]{{\alpha_1^4}{\alpha_2^{-3}\alpha_8^{-1}}}, $ we have the representative $ \langle \nabla_1+\nabla_2+\alpha\nabla_4+\beta\nabla_5+\gamma\nabla_6+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
3.5. $ 1 $-dimensional central extensions of $ {\mathbf N}_{10}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{10}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{10}) . $ Since
we have
We are interested in $ (\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0) . $ Let us consider the following cases:
$ 1.\ $$ \alpha_8 = 0, \alpha_5 = 0, $ then $ \alpha_7\neq0. $ Now by choosing
we have $ \alpha^*_1 = 0, \alpha^*_2 = 0, \alpha^*_4 = 0, \alpha^*_6 = 0. $ Then we have the representatives $ \langle \nabla_7 \rangle $ or $ \langle \nabla_3+\nabla_7 \rangle $ depending on whether $ \alpha_3 = 0 $ or not.
$ 2.\ $$ \alpha_8 = 0, \alpha_5\neq0, $ then by choosing
we have $ \alpha^*_2 = \alpha^*_4 = \alpha^*_6 = 0 $ and $ \alpha_7^* = 0. $ Therefore, we can suppose that $ \alpha_2 = 0, \alpha_4 = 0, \alpha_6 = 0, \alpha_7 = 0, $ and have the following cases:
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, $ then we have the representative $ \langle \nabla_5 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \frac{\alpha_3}{\alpha_5}, r^2 = x^3, $ we have the representative $ \langle \nabla_3+\nabla_5 \rangle; $
${\rm{(c)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha^2_1}{\alpha^2_5}}, r^2 = x^3, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\nabla_5 \rangle. $
3. $ \alpha_8\neq0, $ then by choosing $ y = -\frac{\alpha_5x^2+\alpha_8z^2}{2\alpha_8x}, s = \frac{\sqrt{x}(\alpha_5z-\alpha_7x)}{\alpha_8}, t = -\frac{\alpha_2x+\alpha_5y+\alpha_7z}{\alpha_8}, $ we have $ \alpha^*_2 = \alpha^*_5 = \alpha^*_7 = 0 . $ Therefore, we can suppose that $ \alpha_2 = 0, \alpha_5 = 0, \alpha_7 = 0, $ and have the following cases:
${\rm{(a)}}\ $if $ \alpha_3 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then we have the representative $ \langle \nabla_8 \rangle $ and $ \langle \nabla_1+\nabla_8 \rangle $ depending on whether $ \alpha_1 = 0 $ or not.
${\rm{(b)}}\ $if $ \alpha_3 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_6}{\alpha_8}}, r^2 = x^3, z = -\frac{\alpha_1}{\sqrt[3]{\alpha^2_6\alpha_8}}, $ we have the representative $ \langle \nabla_6+\nabla_8 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha^2_4}{\alpha^2_8}}, r^2 = x^3, z = \frac{\alpha_6}{3\sqrt[5]{\alpha_4^3\alpha^2_8}}, $ we have the representative $ \langle \alpha\nabla_1+\nabla_4+\nabla_8 \rangle; $
${\rm{(d)}}\ $if $ \alpha_3\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_3}{\alpha_8}}, r^2 = x^3, z = \frac{\alpha_4}{\sqrt{\alpha_3\alpha_8}}, $ we have the representative $ \langle \alpha\nabla_1+\nabla_3+\beta\nabla_6+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
3.6. $ 1 $-dimensional central extensions of $ {\mathbf N}_{11}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{11}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{11}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider the following cases:
$1.\ $$ \alpha_8 = 0, \alpha_7 = 0, \alpha_5 = 0 , $ then $ \alpha_2\neq0 $ and we have
${\rm{(a)}}\ $ if $ \alpha_4 = 0, \alpha_6 = 0, $ then by choosing $ x = 2\alpha_2, z = -\alpha_1, s = 8\alpha_2^2\alpha_3, t = 0, $ we have the representative $ \langle \nabla_2 \rangle; $
$ {\rm{(b)}}\ $ if $ \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \frac{\alpha_2}{\alpha_6}, z = -\frac{\alpha_1}{2\alpha_6}, s = \frac{\alpha_1\alpha_2\alpha_6+2\alpha_2^2\alpha_3}{2\alpha_6^3}, t = 0, $ we have the representative $ \langle \nabla_2+\nabla_6 \rangle; $
${\rm{(c)}}\ $if $ \alpha_4\neq0, \alpha_4 = -2\alpha_2, \alpha_1\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\nabla_2-2\nabla_4+\alpha\nabla_6 \rangle; $
$ {\rm{(d)}}\ $ if $ \alpha_4\neq0, \alpha_4 = -2\alpha_2, \alpha_1 = 0, \alpha_6\neq 0, $ then by choosing $ x = \alpha_2\alpha_6^{-1}, $ $ z = 0, $ $ s = \alpha_2^2\alpha_3\alpha_6^{-3}, $ $ t = 0, $ we have the representative $ \langle \nabla_2-2\nabla_4 +\nabla_6 \rangle; $
$ {\rm{(e)}}\ $ if $ \alpha_4\neq0, \alpha_4 = -2\alpha_2, \alpha_1 = 0,\alpha_6 = 0, $ then by choosing $ x = \alpha_2, $ $ z = 0, $ $ s = \alpha_2^2\alpha_3, $ $ t = 0, $ we have the representative $ \langle \nabla_2-2\nabla_4 \rangle; $
$ {\rm{(f)}}\ $if $ \alpha_4\neq0, \alpha_4\neq-2\alpha_2, \alpha_6 = 0, $ then by choosing
we have the the family of representatives $ \langle \nabla_2+\alpha\nabla_4 \rangle_{\alpha\neq0,-2}, $ which will be jointed with the cases (1a) and (1b);
${\rm{(g)}}\ $if $ \alpha_4\neq0, \alpha_4\neq-2\alpha_2, \alpha_6\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\alpha\nabla_4+\nabla_6 \rangle_{\alpha\neq0,-2}, $ which will be jointed with the cases (1b) and (1d).
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_5\neq0 , $ then we have
$ {\rm{(a)}}\ $ if $ \alpha_6 = 0, \alpha_2 = 0, $ then by choosing
we have the representative $ \langle \nabla_5 \rangle; $
${\rm{(b)}}\ $ if $ \alpha_6 = 0, \alpha_2\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5 \rangle; $
${\rm{(c)}}\ $ if $ \alpha_6\neq0, \alpha_6 = 4\alpha_5, \alpha_3 = 0, \alpha_2 = 0, $ then by choosing $ x = \alpha_5, z = 0, s = -\alpha_4\alpha_5^2, t = -\alpha_1, $ we have the representative $ \langle \nabla_5+4\nabla_6 \rangle; $
$ {\rm{(d)}}\ $ if $ \alpha_6\neq0, \alpha_6 = 4\alpha_5, \alpha_2\alpha_4+\alpha_3\alpha_5 = 0, \alpha_2\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5+4\nabla_6 \rangle; $
${\rm{(e)}}\ $if $ \alpha_6\neq0, \alpha_6 = 4\alpha_5, \alpha_2\alpha_4+\alpha_3\alpha_5\neq0, $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_2+\nabla_3+\nabla_5+4\nabla_6 \rangle; $
${\rm{(f)}}\ $if $ \alpha_6\neq0, \alpha_6\neq4\alpha_5, \alpha_2 = 0, $ then by choosing
we have the family of representatives $ \langle \nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq0,4}, $ which will be jointed with the cases (2a) and (2c);
$ {\rm{(g)}}\ $if $ \alpha_6\neq0, \alpha_6\neq4\alpha_5, \alpha_2\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\nabla_5+\alpha\nabla_6 \rangle_{(\alpha\neq0,4)}, $ which will be jointed with the cases (2a) and (2c).
3. $ \alpha_8 = 0, \alpha_7\neq0 , $ then by choosing $ z = -\frac{\alpha_2}{\alpha_7}x, $ $ s = -\frac{\alpha_6}{2\alpha_7}x^3, $ $ t = \frac{ \alpha_2 (\alpha_6-4 \alpha_5)+\alpha_3 \alpha_7}{\alpha^2_7}x, $ we have $ \alpha_2^* = \alpha_3^* = \alpha_6^* = 0 . $ Now we can suppose that $ \alpha_2 = 0, \alpha_3 = 0, \alpha_6 = 0 $ and have the following subcases:
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then we have the representative $ \langle \nabla_7 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \frac{\alpha_5}{\alpha_7}, z = 0, s = 0, t = 0, $ we have the representative $ \langle \nabla_5+\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_4}{\alpha_7}}, z = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_1}{\alpha_7}}, z = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_4+\beta\nabla_5+\nabla_7 \rangle. $
4. $ \alpha_8\neq0 , $ then by choosing $ z = -\frac{\alpha_5}{2\alpha_8}x, s = -\frac{\alpha_7}{\alpha_8}x^3, t = \frac{\alpha_5\alpha_7-2\alpha_2\alpha_8}{2\alpha^2_8}x, $ we have $ \alpha_2^* = \alpha_5^* = \alpha_7^* = 0 . $ Now we can suppose that $ \alpha_2 = 0, \alpha_5 = 0, \alpha_7 = 0 $ and have the following subcases:
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then we have the representative $ \langle \nabla_8 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_6}{\alpha_8}}, z = 0, s = 0, t = 0, $ we have the representative $ \langle \nabla_6+\nabla_8 \rangle; $
${\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_4}{\alpha_8}}, z = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_6+\nabla_8 \rangle; $
${\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_3}{\alpha_8}}, z = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_6+\nabla_8 \rangle; $
${\rm{(e)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha_1}{\alpha_8}}, z = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_6+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
3.7. $ 1 $-dimensional central extensions of $ {\mathbf N}_{12}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{12}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{12}) . $ Since
we have
We will consider only the action of $ \phi_+ $ for find representatives and after that we will see that the set of our representatives gives distinct orbits under action of $ \phi_+ $ and $ \phi_-. $ We are interested in $ (\alpha_3,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider the following cases:
$ 1.\ $$ \alpha_8 = 0, \alpha_5 = 0, \alpha_7 = 0, $ then $ \alpha_3\neq0 $ and we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then by choosing $ x = \alpha_3, s = -\alpha_2\alpha_3, t = 0, $ we have the representative $ \langle \nabla_3 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = \frac{\alpha_6}{\alpha_3}, s = -\frac{\alpha_2\alpha_6^2}{\alpha_3^3}, t = 0, $ we have the representative $ \langle \nabla_3+\nabla_6 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, $ then by choosing $ x = \frac{\alpha_4}{\alpha_3}, s = -\frac{\alpha_2\alpha^2_4}{\alpha_3^3}, t = 0, $ we have the representative $ \langle \nabla_3+\nabla_4+\alpha\nabla_6 \rangle; $
${\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_1}{\alpha_3}}, s = -\frac{\alpha_1\alpha_2}{\alpha_3^2}, t = 0, $ we have the representative $ \langle \nabla_1+\nabla_3+\alpha\nabla_4+\beta\nabla_6 \rangle. $
2. $ \alpha_8 = 0, \alpha_5 = 0, \alpha_7\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, $ then by choosing $ x = 1, s = -\frac{\alpha_6}{2\alpha_7}, t = \frac{\alpha_3\alpha_6-2\alpha_2\alpha_7}{2\alpha_7^2}, $ we have the representative $ \langle \nabla_7 \rangle; $
${\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_4}{\alpha_7}}, s = -\frac{\alpha_4\alpha_6}{2\alpha^2_7}, t = \frac{\sqrt{\alpha_4}(\alpha_3\alpha_6-2\alpha_2\alpha_4)}{2\alpha_7^2\sqrt{\alpha_7}}, $ we have the representative $ \langle \nabla_4+\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \frac{\alpha_3}{\alpha_7}, s = -\frac{\alpha^2_3\alpha_6}{2\alpha^3_7}, t = \frac{\alpha_3^2\alpha_6-2\alpha_2\alpha_3\alpha_7}{2\alpha_7^3}, $ we have the representative $ \langle \nabla_3+\alpha\nabla_4+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_1}{\alpha_7}}, s = -\sqrt[3]{\frac{\alpha_1^2\alpha^3_6}{8\alpha^5_7}}, t = \frac{\sqrt[3]{\alpha_1}(\alpha_3\alpha_6-2\alpha_2\alpha_7)}{2\alpha_7^2\sqrt[3]{\alpha_7}}, $ we have the representative $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\nabla_7 \rangle. $
3. $ \alpha_8 = 0, \alpha_5\neq0, $ then by choosing $ t = -\frac{\alpha_1}{\alpha_5}x, s = -\frac{\alpha_4}{\alpha_5}x^2, $ we have $ \alpha_1^* = \alpha_4^* = 0. $ Now we can suppose that $ \alpha_1 = 0, \alpha_4 = 0 $ and have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0, \alpha_6 = 0, $ then we have the family of representatives $ \langle \nabla_5+\alpha\nabla_7 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0, \alpha_6\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_6}{\alpha_5}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_5+\nabla_6+\alpha\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ \alpha_2 = 0, \alpha_3\neq0, $ then by choosing $ x = \frac{\alpha_3}{\alpha_5}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_3+\nabla_5+\alpha\nabla_6+\beta\nabla_7 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_2\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_2}{\alpha_5}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\nabla_5+\beta\nabla_6+\gamma\nabla_7 \rangle. $
4. $ \alpha_8\neq0, $ then by choosing $ t = -\frac{\alpha_3}{\alpha_8}x, s = -\frac{\alpha_7}{\alpha_8}x^2, $ we have $ \alpha_3^* = \alpha_7^* = 0. $ Now we can suppose that $ \alpha_3 = 0, \alpha_7 = 0 $ and have the following subcases:
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5 = 0, \alpha_6 = 0, $ then we have the representative $ \langle \nabla_8 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5 = 0, \alpha_6\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_6}{\alpha_8}}, s = 0, t = 0, $ we have the representative $ \langle \nabla_6+\nabla_8 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_5}{\alpha_8}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_5+\alpha\nabla_6+\nabla_8 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_4}{\alpha_8}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\beta\nabla_6+\nabla_8 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha_2}{\alpha_8}}, s = 0, t = 0, $ we have the family of representatives
$ {\rm{(f)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha_1}{\alpha_8}}, s = 0, t = 0, $ we have the family of representatives
Summarizing all cases we have the following distinct orbits:
which gives the following new algebras:
3.8. $ 1 $-dimensional central extensions of $ {\mathbf N}_{13}^{4*}(\lambda) $.
Here we will collect all information about $ {\mathbf N}_{13}^{4*}(\lambda): $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}({\mathbf N}_{13}^{4*}(\lambda)) . $ Since
we have
We are interested in
Let us consider the following cases:
$ 1.\ $$ \alpha_7 = 0, \alpha_6 = 0, \alpha_5 = 0, \alpha_4 = 0, $ then $ \alpha_1\neq0, $ $ \alpha_3\neq0 $ and
$ {\rm{(a)}}\ $ if $ \lambda\notin \{ 1,2,4\}, $ $ (\lambda-4)\alpha_3\neq4(1-\lambda)(\lambda-2)\alpha_1, $ then by choosing $ y = \frac{\alpha_2x}{(\lambda-4)\alpha_3+4(\lambda-1)(\lambda-2)\alpha_1}, $ we have the family of representatives
${\rm{(b)}}\ $if $ \lambda\notin \{ 1,2,4\}, $ $ (\lambda-4)\alpha_3 = 4(1-\lambda)(\lambda-2)\alpha_1, $ $ \alpha_2 = 0, $ then we have the family of representatives $ \langle \frac{\lambda-4}{4(1-\lambda)(\lambda-2)}\nabla_1+\nabla_3 \rangle_{\lambda\neq 1,2,4}, $ which we will be jointed with the family from the case (1a);
$ {\rm{(c)}}\ $if $ \lambda\notin \{ 1,2,4\}, $ $ (\lambda-4)\alpha_3 = 4(1-\lambda)(\lambda-2)\alpha_1, $ $ \alpha_2\neq0, $ then by choosing $ x = \frac{\alpha_2}{\alpha_3}, y = 0, z = 0, t = 0, $ we have the family of representatives $ \langle (\lambda-4)\nabla_1+4(1-\lambda)(\lambda-2) (\nabla_2+\nabla_3) \rangle_{\lambda\neq 1,2,4}; $
${\rm{(d)}}\ $if $ \lambda\in \{ 1,2,4\}, $ then by choosing some suitable $ x $ and $ y $ we have the family of representatives $ \langle \alpha\nabla_1+\nabla_3 \rangle_{\alpha\neq 0, \lambda\in \{1,2,4\}}, $ which will be jointed with the family from the case (1a).
2. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5 = 0, \alpha_4\neq0, $ then we have
${\rm{(a)}}\ $if $ \alpha_3 = 2(2-\lambda)\alpha_1 , $ then by choosing
we have the representative $ \langle \nabla_4 \rangle; $
${\rm{(b)}}\ $if $ \alpha_3\neq2(2-\lambda)\alpha_1 , $ then by choosing
we have the representative $ \langle \nabla_3+\nabla_4 \rangle . $
3. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5\neq0, $ then
${\rm{(a)}}\ $if $ \alpha_4 = 0, $ then $ \alpha_1\neq0 $ and
$ {\rm{(i)}}\ $ if $ \lambda\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\nabla_5 \rangle_{\lambda\neq0}; $
${\rm{(ii)}}\ $if $ \lambda = 0, $ then by choosing $ x = \frac{\alpha_1}{\alpha_5}, y = -\frac{\alpha_1\alpha_3}{2\alpha_5^2}, z = 0, t = 0, $ we have the family representative $ \langle \nabla_1+\alpha\nabla_2+\nabla_5 \rangle_{\alpha\neq0,\lambda = 0} $ and the representative $ \langle \nabla_1+\nabla_5 \rangle_{\lambda = 0}, $ which will be jointed with the family from the case (3(a)i).
(b) if $ \alpha_4\neq0 $ and $ \lambda = 0, $ then we have the followings:
${\rm{(i)}}\ $if $ \alpha_3\alpha_4 = 2\alpha_1(2\alpha_4+\alpha_5), $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_4+\nabla_5 \rangle_{\alpha\neq0,\lambda = 0}; $
${\rm{(ii)}}\ $if $ \alpha_3\alpha_4\neq 2\alpha_1(2\alpha_4+\alpha_5), $ then by choosing
we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\nabla_5 \rangle_{\alpha\neq0, \lambda = 0} ; $
(c) if $ \alpha_4\neq0 $ and $ \lambda\neq 0, $ then we have the followings:
$ {\rm{(i)}}\ $ if $ 4\alpha_4 = \lambda\alpha_5, $ $ 4\lambda(\lambda-4)\alpha_1\alpha_3+\lambda^2\alpha_2\alpha_5+4(3\lambda^3-12\lambda^2+8\lambda+16)\alpha_1^2 = 0, $ $ \lambda\alpha_3+2(\lambda^2-2\lambda-4)\alpha_1 = 0, $ then by choosing $ x = 1, y = -\frac{\alpha_1}{\alpha_4}, z = 0, t = 0, $ we have the family of representatives $ \langle \frac{\lambda}{4}\nabla_4+\nabla_5 \rangle_{\lambda\neq0} ; $
${\rm{(ii)}}\ $ if $ 4\alpha_4 = \lambda\alpha_5, $ $ 4\lambda(\lambda-4)\alpha_1\alpha_3+\lambda^2\alpha_2\alpha_5+4(3\lambda^3-12\lambda^2+8\lambda+16)\alpha_1^2 = 0, $ $ \lambda\alpha_3+2(\lambda^2-2\lambda-4)\alpha_1\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_3+\frac{\lambda}{4}\nabla_4+\nabla_5 \rangle_{\lambda\neq0} ; $
$ {\rm{(iii)}}\ $if $ 4\alpha_4 = \lambda\alpha_5, $ $ 4\lambda(\lambda-4)\alpha_1\alpha_3+\lambda^2\alpha_2\alpha_5+4(3\lambda^3-12\lambda^2+8\lambda+16)\alpha_1^2\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\frac{\lambda}{4}\nabla_4+\nabla_5 \rangle_{\lambda\neq0} ; $
$ {\rm{(iv)}}\ $if $ \lambda\neq0, 4\alpha_4\neq\lambda\alpha_5 , $ then by choosing
we have two families of representatives
depending on $ \alpha_3\alpha_4-2\alpha_1\alpha_5+2(\lambda-2)\alpha_1\alpha_4 = 0 $ or not. These families will be jointed with representatives from cases (3(c)i) and (3(c)ii).
4. $ \alpha_7 = 0, \alpha_6\neq0, $ then by choosing $ y = -\frac{\alpha_4}{2\alpha_6}x, z = -\frac{\alpha_4^2-2\alpha_1\alpha_6}{2\alpha^2_6}x, $ we have $ \alpha_1^* = 0, \alpha_4^* = 0. $ Since we can suppose that $ \alpha_1 = 0, \alpha_4 = 0 $ and
$ {\rm{(a)}}\ $ if $ \lambda\neq0, \alpha_3 = 0, $ then by choosing $ t = {\frac{\alpha_2}{\lambda\alpha_6}}x, $ we have the representatives $ \langle \nabla_6 \rangle _{\lambda\neq0} $ and $ \langle \nabla_5+\nabla_6 \rangle _{\lambda\neq0} $ depending on $ \alpha_5 = 0 $ or not;
${\rm{(b)}}\ $ if $ \lambda\neq0, \alpha_3\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_3}{\alpha_6}}, t = {\frac{\alpha_2\sqrt{\alpha_3}}{\lambda\alpha_6\sqrt{\alpha_6}}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_5+\nabla_6 \rangle _{\lambda\neq0}; $
${\rm{(c)}}\ $if $ \lambda = 0, \alpha_2 = 0, \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_6 \rangle _{\lambda = 0} $ and $ \langle \nabla_5+\nabla_6 \rangle _{\lambda = 0} $ depending on $ \alpha_5 = 0 $ or not, which will be jointed with representatives from the case (4a);
$ {\rm{(d)}}\ $if $ \lambda = 0, \alpha_2 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_3}{\alpha_6}}, t = 0 , $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_5+\nabla_6 \rangle _{(\lambda = 0)}, $ which will be jointed with the family of representatives from the case (4b);
$ {\rm{(e)}}\ $if $ \lambda = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_2}{\alpha_6}}, t = 0, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\beta\nabla_5+\nabla_6 \rangle _{\lambda = 0}. $
5. $ \alpha_7\neq0, \lambda\neq-2, $ then by choosing
we have $ \alpha_1^* = 0, \alpha_4^* = 0, \alpha_6^* = 0. $ Now we can suppose that $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6 = 0 $ then we have
$ {\rm{(a)}}\ $ if $ \alpha_3 = 0, \alpha_5 = 0, \alpha_2 = 0, $ then we have the representative $ \langle \nabla_7 \rangle_{\lambda\neq-2} ; $
$ {\rm{(b)}}\ $ if $ \alpha_3 = 0, \alpha_5 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt[4]{\alpha_2\alpha_7^{-1}}, $ we have the representative $ \langle \nabla_2+\nabla_7 \rangle_{\lambda\neq-2} ; $
$ {\rm{(c)}}\ $ if $ \alpha_5\neq0, $ then by choosing $ x = \sqrt{\alpha_5\alpha_7^{-1}}, $ $ y = -\frac{\alpha_3}{2 \sqrt{\alpha_5 \alpha_7}}, $ $ z = \frac{\alpha_3^2}{ 4 \sqrt{\alpha_5^3\alpha_7}}, $ $ t = 0, $ we have the family of representatives $ \langle \alpha\nabla_2+\nabla_5+\nabla_7 \rangle_{\lambda\neq-2} . $
${\rm{(d)}}\ $ if $ \alpha_3\neq0, \alpha_5 = 0 $ then by choosing $ x = \sqrt[3]{\alpha_3\alpha_7^{-1}}, $ we have the family of representatives $ \langle \alpha\nabla_2+\nabla_3+ \nabla_7 \rangle_{\lambda\neq-2} . $
6. $ \alpha_7\neq0, \lambda = -2, $ then
$ {\rm{(a)}}\ $if $ \alpha_6 = 0, \alpha_5 = 0, $ then by choosing $ z = \frac{y^2}{x}-\frac{\alpha_4x}{2\alpha_7}, t = -\frac{x \alpha_1+y \alpha_4}{\alpha_7}, $ we have $ \alpha_1^* = 0 $ and $ \alpha_4^* = 0. $ Now consider the followings:
$ {\rm{(i)}}\ $if $ \alpha_3 = 8\alpha_1, \alpha_2\alpha_7-\alpha_4^2 = 0, $ then we have the representative $ \langle \nabla_7 \rangle_{\lambda = -2}, $ which will be jointed with the representative from the case (5a);
$ {\rm{(ii)}}\ $if $ \alpha_3 = 8\alpha_1, \alpha_2\alpha_7-\alpha_4^2\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_2\alpha_7-\alpha_4^2}{\alpha_7^2}}, y = 0, $ we have the representative $ \langle \nabla_2+\nabla_7 \rangle_{\lambda = -2}, $ which will be jointed with the representative from the case (5b);
${\rm{(iii)}}\ $if $ \alpha_3\neq8\alpha_1, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_3-8\alpha_1}{\alpha_7}}, y = \frac{\alpha_2\alpha_7-\alpha_4^2}{48\alpha_1\alpha_7-6\alpha_3\alpha_7}x, $ we have the representative $ \langle \nabla_3+\nabla_7 \rangle_{\lambda = -2} . $
(b) if $ \alpha_6 = 0, \alpha_5\neq0, $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_2+\nabla_5+\nabla_7 \rangle_{\lambda = -2}, $ which will be jointed with the representative from the case (5c).
(c) if $ \alpha_6\neq0, $ then we have the following cases:
$ {\rm{(i)}}\ $ if $ \alpha_5\alpha_7 = \alpha_6^2, 8\alpha_1\alpha_7+\alpha_4\alpha_6 = \alpha_3\alpha_7, $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_2+\nabla_5+\nabla_6+\nabla_7 \rangle_{\lambda = -2}; $
$ {\rm{(ii)}}\ $if $ \alpha_5\alpha_7 = \alpha_6^2, 8\alpha_1\alpha_7+\alpha_4\alpha_6\neq \alpha_3\alpha_7, $ then by choosing
we have the family of representatives
${\rm{(iii)}}\ $if $ \alpha_5\alpha_7-\alpha_6^2\neq0, $ then by choosing
we have the family of representatives
which will be jointed with the family from the case (6(c)i).
Summarizing all cases we have the following distinct orbits:
Now we have the following new algebras
3.9. $ 1 $-dimensional central extensions of $ {\mathbf N}_{14}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{14}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{14}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider the following cases:
$1.\ $$ \alpha_8 = 0, \alpha_7 = 0, \alpha_5 = 0, $ then $ \alpha_2\neq0 $ and we have
$ {\rm{(a)}}\ $if $ \alpha_6 = 0, \alpha_4 = 0, \alpha_3 = 0, $ then by choosing $ x = 2\alpha_2, q = 1, r = 0, s = 0, t = -\alpha_1, $ we have the representative $ \langle \nabla_2 \rangle; $
${\rm{(b)}}\ $if $ \alpha_6 = 0, \alpha_4 = 0, \alpha_3\neq0, $ then by choosing $ x = \alpha_3, q = \alpha_2\alpha_3^2, r = 0, s = 0, t = -\frac{\alpha_1\alpha_3}{2\alpha_2}, $ we have the representative $ \langle \nabla_2+\nabla_3 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_6 = 0, \alpha_4\neq0, $ then by choosing $ x = \alpha_4, q = \alpha_2\alpha_4, r = -\frac{\alpha_2\alpha_3}{2}, s = 0, t = -\frac{\alpha_1\alpha_4}{2\alpha_2}, $ we have the representative $ \langle \nabla_2+\nabla_4 \rangle; $
${\rm{(d)}}\ $if $ \alpha_6\neq0, \alpha_3\alpha_6-\alpha_4^2 = 0, $ then by choosing $ x = \alpha_6, q = \alpha_2, r = -\frac{\alpha_2\alpha_4}{\alpha_6}, s = 0, t = -\frac{\alpha_1\alpha_6}{2\alpha_2}, $ we have the representative $ \langle \nabla_2+\nabla_6 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_6\neq0, \alpha_3\alpha_6-\alpha_4^2\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_3+\nabla_6 \rangle. $
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_5\neq0, $ then we have
$ {\rm{(a)}}\ $ if $ \alpha_6 = 0, \alpha_2 = 0, $ then by choosing
we have the representatives $ \langle \nabla_5 \rangle $ and $ \langle \nabla_1+\nabla_5 \rangle $ depending on whether $ \alpha_1 = 0 $ or not;
${\rm{(b)}}\ $ if $ \alpha_6 = 0, \alpha_2\neq0, $ then by choosing
we have the representatives $ \langle \nabla_2+\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_6\neq0, \alpha_5 = -\alpha_6, $ then we have the following subcases:
$ {\rm{(i)}}\ $ if $ \alpha_2 = 0, \alpha_4 = 0, \alpha_1 = 0, $ then we have the representative $ \langle \nabla_5-\nabla_6 \rangle; $
${\rm{(ii)}}\ $ if $ \alpha_2 = 0, \alpha_4 = 0, \alpha_1\neq0, $ then by choosing
we have the representative $ \langle \nabla_1+\nabla_5-\nabla_6 \rangle; $
$ {\rm{(iii)}}\ $if $ \alpha_2 = 0, \alpha_4\neq0, \alpha_1 = 0, $ then by choosing
we have the representative $ \langle \nabla_4+\nabla_5-\nabla_6 \rangle; $
$ {\rm{(iv)}}\ $if $ \alpha_2 = 0, \alpha_4\neq0, \alpha_1\neq0, $ then by choosing
we have the representative $ \langle \nabla_1+\nabla_4+\nabla_5-\nabla_6 \rangle; $
$ {\rm{(v)}}\ $ if $ \alpha_2\neq0, \alpha_4 = 0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_5-\nabla_6 \rangle; $
${\rm{(vi)}}\ $if $ \alpha_2\neq0, \alpha_4\neq0, $ then by choosing
we have the representative $ \langle \nabla_2+\nabla_4+\nabla_5-\nabla_6 \rangle. $
(d) if $ \alpha_6\neq0, \alpha_5\neq-\alpha_6, $ then we have the following subcases:
$ {\rm{(i)}}\ $if $ \alpha_2 = 0, \alpha_1 = 0, $ then by choosing
we have the family of representatives $ \langle \nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq0,-1}, $ which will be jointed with the cases (2a) and (2(c)i);
${\rm{(ii)}}\ $if $ \alpha_2 = 0, \alpha_1\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq0,-1}, $ which will be jointed with the cases (2a) and (2(c)ii);
$ {\rm{(iii)}}\ $if $ \alpha_2\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq0,-1}, $ which will be jointed with the cases (2b) and (2(c)v).
3. $ \alpha_8 = 0, \alpha_7\neq0 $ then by choosing $ r = -\frac{\alpha_5}{\alpha_7}q, s = \frac{\alpha_5\alpha_6-\alpha_4\alpha_7}{\alpha_7^2}q, $ we have $ \alpha_4^* = \alpha_5^* = 0. $ Therefore, we can suppose that $ \alpha_4 = 0, \alpha_5 = 0, $ thus we have
$ {\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_1 = 0, \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_6+\nabla_7\rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_3}{\alpha_7}}, q = 1, r = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_6+\nabla_7\rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2 = 0, \alpha_1\neq0, \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_1+\nabla_7\rangle $ and $ \langle \nabla_1+\nabla_6+\nabla_7\rangle $ depending on whether $ \alpha_6 = 0 $ or not;
${\rm{(d)}}\ $if $ \alpha_2 = 0, \alpha_1\neq0, \alpha_3\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\nabla_3+\alpha\nabla_6+\nabla_7\rangle; $
$ {\rm{(e)}}\ $if $ \alpha_2\neq0, \alpha_3 = 0, $ then by choosing $ q = \frac{\alpha_2}{\alpha_7}, r = 0, s = 0, t = -\frac{\alpha_1}{2\alpha_2}x, $ we have the representatives $ \langle \nabla_2+\nabla_7 \rangle $ and $ \langle \nabla_2+\nabla_6+\nabla_7\rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(f)}}\ $if $ \alpha_2\neq0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_3}{\alpha_7}}, q = \frac{\alpha_2}{\alpha_7}, r = 0, s = 0, t = -\frac{\alpha_1\sqrt[3]{\alpha_3}}{2\alpha_2\sqrt[3]{\alpha_7}} $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha\nabla_6+\nabla_7\rangle. $
4. $ \alpha_8\neq0 $ then by choosing $ r = -\frac{\alpha_7}{\alpha_8}q, s = \frac{\alpha_7^2-\alpha_5\alpha_8}{\alpha_8^2}q, t = -\frac{\alpha_2}{\alpha_8}x, $ we have $ \alpha_2^* = \alpha_5^* = \alpha_7^* = 0. $ Therefore, we can suppose that $ \alpha_2 = 0, \alpha_5 = 0, \alpha_7 = 0, $ then we have
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, $ then we have the representatives $ \langle \nabla_8 \rangle $ and $ \langle \nabla_6+\nabla_8 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_4}{\alpha_8}}, q = 1, r = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_6+\nabla_8 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_3}{\alpha_8}}, q = 1, r = 0, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_6+\nabla_8 \rangle; $
${\rm{(d)}}\ $if $ \alpha_1\neq0, \alpha_3 = 0, \alpha_4 = 0, $ then we have the representatives $ \langle \nabla_1+\nabla_8 \rangle $ and $ \langle \nabla_1+\nabla_6+\nabla_8 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(e)}}\ $if $ \alpha_1\neq0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_4}{\alpha_8}}, q = \sqrt[6]{\frac{\alpha_1^3}{\alpha_4^2\alpha_8}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_1+\nabla_4+\alpha\nabla_6+\nabla_8 \rangle; $
${\rm{(f)}}\ $if $ \alpha_1\neq0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_3}{\alpha_8}}, q = \frac{\sqrt{\alpha_1}}{\sqrt[4]{\alpha_3\alpha_8}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_1+\nabla_3+\alpha\nabla_4+\beta\nabla_6+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
3.10. $ 1 $-dimensional central extensions of $ {\mathbf N}_{15}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{15}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{15}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider the following cases:
$ 1.\ $$ \alpha_8 = 0, \alpha_7 = 0, \alpha_5 = 0, $ then $ \alpha_2\neq0 $ and we have
${\rm{(a)}}\ $ if $ \alpha_6 = 0, \alpha_4 = 0, $ then by choosing $ x = 2\alpha_2, r = 4\alpha_2\alpha_3, s = 0, t = -\alpha_1, $ we have the representative $ \langle \nabla_2 \rangle; $
$ {\rm{(b)}}\ $ if $ \alpha_6 = 0, \alpha_4\neq0, \alpha_2 = 2\alpha_4, $ then we have the representatives $ \langle 2\nabla_2+\nabla_4 \rangle $ and $ \langle 2\nabla_2+\nabla_3+\nabla_4 \rangle $ depending on whether $ \alpha_3 = 0 $ or not;
${\rm{(c)}}\ $if $ \alpha_6 = 0, \alpha_4\neq0, \alpha_2\neq2\alpha_4, $ then by choosing $ x = \alpha_2-2\alpha_4, r = \alpha_3(\alpha_2-2\alpha_4), s = 0, t = \frac{\alpha_1(2\alpha_4-\alpha_2)}{2\alpha_2}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_4 \rangle_{\alpha\neq0,\frac{1}{2}}, $ which will be jointed with representatives from the cases (1a) and (1b);
$ {\rm{(d)}}\ $if $ \alpha_6\neq0, $ then by choosing $ x = \frac{\alpha_2}{\alpha_6}, r = -\frac{\alpha_2^2\alpha_4}{\alpha_6^3}, s = 0, t = -\frac{\alpha_1}{2\alpha_6}, $ we have the representative $ \langle \nabla_2+\alpha\nabla_3+\nabla_6 \rangle. $
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_5\neq0 $ then we have
${\rm{(a)}}\ $if $ \alpha_5\neq-\alpha_6, $ then we have the following subcases:
$ {\rm{(i)}}\ $ if $ \alpha_2 = 0, \alpha_1 = 0, $ then by choosing
we have the family of representatives $ \langle \nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq-1} ; $
${\rm{(ii)}}\ $ if $ \alpha_2 = 0, \alpha_1\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq-1} ; $
$ {\rm{(iii)}}\ $ if $ \alpha_2\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\nabla_5+\alpha\nabla_6 \rangle_{\alpha\neq-1} . $
(b) if $ \alpha_6 = -\alpha_5, $ then we have the following subcases:
$ {\rm{(i)}}\ $if $ \alpha_4 = 0, \alpha_2 = 0, \alpha_1 = 0, $ then we have the representative $ \langle \nabla_5-\nabla_6 \rangle, $ which will be jointed with the family from the case (2(a)i);
$ {\rm{(ii)}}\ $if $ \alpha_4 = 0, \alpha_2 = 0, \alpha_1\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_1}{\alpha_5}}, r = 0, s = -\frac{\alpha_3\sqrt{\alpha_1}}{2\alpha_5\sqrt{\alpha_4}}, t = 0, $ we have the representative $ \langle \nabla_1+\nabla_5-\nabla_6 \rangle, $ which will be jointed with the family from the case (2(a)ii);
$ {\rm{(iii)}}\ $if $ \alpha_4 = 0, \alpha_2\neq0, $ then by choosing $ x = \frac{\alpha_2}{\alpha_5}, r = 0, s = -\frac{\alpha^2_2\alpha_3}{2\alpha^3_5}, t = -\frac{\alpha_1}{2\alpha_5}, $ we have the representative $ \langle \nabla_2+\nabla_5-\nabla_6 \rangle, $ which will be jointed with the family from the case (2(a)iii);
$ {\rm{(iv)}}\ $if $ \alpha_4\neq0, $ then by choosing $ x = \frac{\alpha_4}{\alpha_5}, $ $ s = -\frac{\alpha_3 \alpha_4^2}{ 2 \alpha_5^3}, $ $ r = 0, $ we have the families of representatives
depending on $ \alpha_2 = 0 $ or not.
3. $ \alpha_8 = 0, \alpha_7\neq0, $ then by choosing
we have $ \alpha_3^* = \alpha_4^* = \alpha_5^* = 0. $ Therefore, we can suppose that $ \alpha_3 = 0, \alpha_4 = 0, \alpha_5 = 0, $ and we have
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, $ then we have the representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_6+\nabla_7 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt{\alpha_2\alpha_7^{-1}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_2+\alpha\nabla_6+\nabla_7 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[5]{\frac{\alpha_1}{\alpha_7}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_1+\alpha\nabla_2+\beta\nabla_6+\nabla_7 \rangle. $
4. $ \alpha_8\neq0, $ then by choosing $ r = -\frac{\alpha_7}{\alpha_8}x^2, t = -\frac{\alpha_2}{\alpha_8}x, s = -\frac{\alpha_5x^2+\alpha_7r}{\alpha_8} $ we have $ \alpha_2^* = \alpha_5^* = \alpha_7^* = 0. $ Therefore, we can suppose that $ \alpha_2 = 0, \alpha_5 = 0, \alpha_7 = 0, $ then we have
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, $ then we have the representatives $ \langle \nabla_8 \rangle $ and $ \langle \nabla_6+\nabla_8 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_4}{\alpha_8^{-1}}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_4+\alpha\nabla_6+\nabla_8 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_3}{\alpha_8^{-1}}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_6+\nabla_8 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_1}{\alpha_8^{-1}}}, r = 0, s = 0, t = 0, $ we have the family of representative $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_6+\nabla_8 \rangle. $
Summarizing all cases we have the following distinct orbits:
which gives the following new algebras:
3.11. $ 1 $-dimensional central extensions of $ {\mathbf N}_{16}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{16}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{16}) . $ Since
in the case $ \phi = \phi_1 $, we have
and on the opposite case, for $ \phi = \phi_2, $ we have
We are interested in $ (\alpha_2,\alpha_5,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider the following cases:
$ 1.\ $ $ \alpha_8 = 0, \alpha_7 = 0, \alpha_5 = 0, $ then $ \alpha_2\neq0 $ and
$ {\rm{(a)}}\ $if $ \alpha_4\neq 0, $ then by choosing $ \phi = \phi_1, $ $ x = \alpha_4 \alpha_2^{-1}, $ $ t = -\frac{ \alpha_1 \alpha_4 }{2 \alpha_2^{2}}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\nabla_4 +\beta \nabla_6 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_4 = 0,\alpha_3\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt{ \alpha_3 \alpha_2^{-1}}, $ $ t = -\frac{ \alpha_1 \sqrt{ \alpha_3}}{2 \sqrt{\alpha_2^3}}, $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha \nabla_6 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_4 = 0,\alpha_3 = 0, $ then by choosing $ \phi = \phi_1, $ $ x = 2 \alpha_2, $ $ t = - \alpha_1, $ $ s = 0, $ we have the family of representatives $ \langle \nabla_2+ \alpha \nabla_6 \rangle. $
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_5\neq0 $ and
$ {\rm{(a)}}\ $if $ \alpha_2\neq 0,\alpha_4\neq 0, $ then by choosing
we have the following family of representatives
$ {\rm{(b)}}\ $if $ \alpha_2\neq 0,\alpha_4 = 0, $ then by choosing
we have the following family of representatives $ \langle \alpha \nabla_2+ \nabla_5+ \beta \nabla_6 \rangle_{\alpha\neq0}; $
$ {\rm{(c)}}\ $if $ \alpha_2 = 0, $ then by choosing $ \phi = \phi_2, $ $ y = 1, $ $ t = 0, $ $ s = 0, $ we have the representative with $ \alpha_5^* = 0 $ and $ \alpha_2^*\neq0, $ which was considered above.
3. $ \alpha_8 = 0, \alpha_7\neq0, $ then we have
${\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_5 = 0, \alpha_1 = 0, \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_6+\nabla_7\rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_5 = 0, \alpha_1\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_6+\nabla_7\rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\beta\nabla_5+\gamma\nabla_6+\nabla_7\rangle. $
4. $ \alpha_8\neq0, $ then by choosing $ \phi = \phi_1, $ $ t = -\frac{\alpha_2}{\alpha_8}x, s = -\frac{\alpha_5}{\alpha_8}x, $ we have $ \alpha_2^* = \alpha_5^* = 0. $ Now we can suppose that $ \alpha_2 = 0, \alpha_5 = 0 $ and we have
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then we have the representatives $ \langle \nabla_8\rangle $ and $ \langle \nabla_7+\nabla_8\rangle $ depending on whether $ \alpha_7 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt{{\alpha_6}{\alpha_8^{-1}}}, $ $ s = 0, $ $ t = 0, $ we have the family of representative $ \langle \nabla_6+\alpha\nabla_7+\nabla_8\rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt[3]{{\alpha_4}{\alpha_8^{-1}}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_6+\beta\nabla_7+\nabla_8\rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt[4]{{\alpha_1}{\alpha_8^{-1}}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_6+\mu\nabla_7+\nabla_8\rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
3.12. $ 1 $-dimensional central extensions of $ {\mathbf N}_{17}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{17}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{17}) . $ Since
then in the case $ \phi = \phi_1, $ we have
and in the opposite case $ \phi = \phi_2, $ we have
We are interested in $ (\alpha_3,\alpha_6,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider the following cases:
$ 1.\ $$ \alpha_8 = 0, \alpha_7 = 0, \alpha_6 = 0, $ then $ \alpha_3\neq0 $ and choosing $ \phi = \phi_1, $ $ t = -\frac{\alpha_1}{2\alpha_3}x, $ we get $ \alpha_1^* = 0. $ Now consider the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then we have the representative $ \langle \nabla_3 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt{\frac{\alpha_5}{\alpha_3}}, q = 1, s = 0, t = -\frac{\alpha_1\sqrt{\alpha_5}}{2\alpha_3\sqrt{\alpha_3}}, $ we have the representative $ \langle \nabla_3+\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2 = 0, \alpha_4\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt[3]{\frac{\alpha_4}{\alpha_3}}, q = 1, s = 0, t = -\frac{\alpha_1\sqrt[3]{\alpha_5}}{2\alpha_3\sqrt[3]{\alpha_3}}, $ we have the representative $ \langle \nabla_3+\nabla_4+\alpha\nabla_5 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_2\neq0, \alpha_4 = 0, \alpha_5 = 0, $ then by choosing $ \phi = \phi_1, $ $ x = \alpha_2, q = \frac{1}{\alpha_3}, s = 0, t = -\frac{\alpha_1\alpha_2}{2\alpha_3}, $ we have the representative $ \langle \nabla_2+\nabla_3 \rangle; $
${\rm{(e)}}\ $if $ \alpha_2\neq0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt{\frac{\alpha_5}{\alpha_3}}, q = \sqrt{\frac{\alpha_2^2}{\alpha_3\alpha_5}}, s = 0, t = -\frac{\alpha_1\sqrt{\alpha_5}}{2\alpha_3\sqrt{\alpha_3}}, $ we have the representative $ \langle \nabla_2+\nabla_3+\nabla_5 \rangle; $
$ {\rm{(f)}}\ $if $ \alpha_2\neq0, \alpha_4\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = \sqrt[3]{{\alpha_4}{\alpha_3^{-3}}}, q = \sqrt[3]{{\alpha_2^3}{\alpha^{-2}_3\alpha_4^{-1}}}, $ we have the family of representative $ \langle \nabla_2+\nabla_3+\nabla_4+\alpha\nabla_5 \rangle. $
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_6\neq0, $ and $ \alpha_3 = 0 , $ then by choosing some suitable automorphism $ \phi_2 $ we have $ \alpha_3^*\neq0 $ which is the case considered above. Now we can suppose that $ \alpha_3\neq0, $ and choosing $ t = -\frac{\alpha_1}{2\alpha_3}x, s = -\frac{\alpha_4}{2\alpha_6}x, $ we have $ \alpha_1^* = 0, \alpha_4^* = 0. $ Therefore, we can suppose that $ \alpha_1 = 0, \alpha_4 = 0. $ Consider the following subcases:
$ {\rm{(a)}}\ $$ \alpha_2 = 0, \alpha_5 = 0, $ then by choosing $ \phi = \phi_1, $ $ x = \alpha_6, q = \alpha_3, s = 0, t = 0, $ we have the representative $ \langle \nabla_3+\nabla_6 \rangle; $
$ {\rm{(b)}}\ $$ \alpha_2\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = {\alpha_3^{-1}}{\sqrt{\alpha_2\alpha_6}}, q = \sqrt{\alpha_2\alpha_6^{-1}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha\nabla_5+\nabla_6 \rangle. $
3. $ \alpha_8 = 0, \alpha_7\neq0, $ then by choosing $ \phi = \phi_1, $ $ t = -{\alpha_2}{\alpha_7^{-1}}x, s = -{\alpha_5}{\alpha_7^{-1}}q, $ we have $ \alpha_2^* = 0, \alpha_5^* = 0. $ Therefore, we can suppose that $ \alpha_2 = 0, \alpha_5 = 0. $ Consider the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_3 = 0, \alpha_6 = 0, $ then we have the representative $ \langle \nabla_7 \rangle ; $
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_3 = 0, \alpha_6\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = {\alpha_6}{\alpha_7^{-1}}, q = 1, s = 0, t = 0, $ we have the representative $ \langle \nabla_6+\nabla_7 \rangle ; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_3\neq0, $ and $ \alpha_6 = 0, $ then by choosing some suitable automorphism $ \phi_2, $ we have $ \alpha_6^*\neq0 . $ Thus we can consider the case $ \alpha_6\neq0 $ and choosing $ \phi = \phi_1, $ $ x = {\alpha_6}{\alpha_7^{-1}}, q = {\alpha_3}{\alpha_7^{-1}}, s = 0, t = 0, $ we have the representative $ \langle \nabla_3+\nabla_6+\nabla_7 \rangle ; $
$ {\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_3 = 0, \alpha_6 = 0, $ then by choosing $ \phi = \phi_1, $ $ x = 1, q = {\alpha_4}{\alpha_7^{-1}}, s = 0, t = 0, $ we have the representative $ \langle \nabla_4+\nabla_7 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_3 = 0, \alpha_6\neq0, $ then by choosing $ \phi = \phi_1, $ $ x = {\alpha_6}{\alpha_7}^{-1}, q = {\alpha_4\alpha_7^2}{\alpha_6^{-3}}, $ we have the representative $ \langle \nabla_4+\nabla_6+\nabla_7 \rangle; $
$ {\rm{(f)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_3\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_3+\nabla_4+\alpha\nabla_6+\nabla_7 \rangle ; $
$ {\rm{(g)}}\ $if $ \alpha_1\neq0. $ In case of $ \alpha_4 = 0, $ choosing some suitable automorphism $ \phi_2, $ we have $ \alpha_4^*\neq0. $ Thus, we can suppose $ \alpha_4\neq0 , $ and choosing
we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\nabla_4+\beta\nabla_6+\nabla_7 \rangle . $
4. $ \alpha_8\neq0, $ then by choosing $ \phi = \phi_1, $ $ t = -\frac{\alpha_3}{\alpha_8}x, s = -\frac{\alpha_6}{\alpha_8}q, $ we have $ \alpha_3^* = 0, \alpha_6^* = 0. $ Consider the following cases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_2 = 0, \alpha_5 = 0, $ then we have the representatives $ \langle \nabla_8 \rangle $ and $ \langle \nabla_7+\nabla_8 \rangle $ depending on whether $ \alpha_7 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_2 = 0, \alpha_5\neq0, $ then we have the representatives $ \langle \nabla_5+\nabla_8 \rangle $ and $ \langle \nabla_5+\nabla_7+\nabla_8 \rangle $ depending on whether $ \alpha_7 = 0 $ or not;
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_2\neq0. $ In case of $ \alpha_5 = 0, $ choosing some suitable automorphism $ \phi_2, $ we have $ \alpha_5^*\neq0 . $ Thus, we can suppose $ \alpha_5\neq0 , $ and choosing
we have the family of representatives $ \langle \nabla_2+\nabla_5+\alpha\nabla_7+\nabla_8 \rangle ; $
${\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_2 = 0, \alpha_5 = 0, $ then we have the representatives $ \langle \nabla_4+\nabla_8 \rangle $ and $ \langle \nabla_4+\nabla_7+\nabla_8 \rangle $ depending on whether $ \alpha_7 = 0 $ or not;
$ {\rm{(e)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_2 = 0, \alpha_5\neq0 , $ then by choosing
we have the family of representatives $ \langle \nabla_4+\nabla_5+\alpha\nabla_7+\nabla_8 \rangle ; $
${\rm{(f)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, \alpha_2\neq0 , $ then by choosing
we have the family of representatives $ \langle \nabla_2+\nabla_4+\alpha\nabla_5+\beta\nabla_7+\nabla_8 \rangle ; $
$ {\rm{(g)}}\ $if $ \alpha_1\neq0 $ then by choosing some suitable automorphism $ \phi_2, $ we have $ \alpha_4^*\neq0 $. Thus, we can suppose $ \alpha_4\neq0 , $ and choosing
we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
3.13. $ 1 $-dimensional central extensions of $ {\mathbf N}_{18}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{18}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{18}) . $ Since
we have
We are interested in $ (\alpha_3,\alpha_6,\alpha_7,\alpha_8)\neq(0,0,0,0) . $ Let us consider $ \phi = \phi_+ $ and the following cases:
$ 1.\ $$ \alpha_8 = 0, \alpha_7 = 0, \alpha_6 = 0, $ then $ \alpha_3\neq0 $ and choosing $ t = -\frac{\alpha_1}{2\alpha_3}x, $ we get $ \alpha_1^* = 0. $ Now consider the following subcases:
${\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then we have the representative $ \langle \nabla_3 \rangle ; $
${\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_5}{\alpha_3}}, s = 0, t = -\frac{\alpha_1\sqrt{\alpha_5}}{2\alpha_3\sqrt{\alpha_3}}, $ we have the representative $ \langle \nabla_3+\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_4}{\alpha_3}}, s = 0, t = -\frac{\alpha_1\sqrt[3]{\alpha_4}}{2\alpha_3\sqrt[3]{\alpha_3}}, $ we have the family of representatives $ \langle \nabla_3+\nabla_4+\alpha\nabla_5 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_2\neq0, $ then by choosing $ x = {\alpha_2}{\alpha_3^{-1}}, s = 0, t = -\frac{\alpha_1\alpha_2}{2\alpha^2_3}, $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha\nabla_4+\beta\nabla_5 \rangle. $
2. $ \alpha_8 = 0, \alpha_7 = 0, \alpha_6\neq0, $ then by choosing $ s = -\frac{\alpha_4}{2\alpha_6}x, $ we have $ \alpha_4^* = 0. $ Consider the following cases:
$ {\rm{(a)}}\ $$ \alpha_3 = 0, $ then we have two families of representatives $ \langle \alpha\nabla_1+\beta\nabla_2+\nabla_6 \rangle $ and $ \langle \alpha\nabla_1+\beta\nabla_2+\nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $$ \alpha_3\neq0 $ then by choosing $ x = \frac{\alpha_6}{\alpha_3}, s = -\frac{\alpha_4}{2\alpha_6}, t = -\frac{\alpha_1\alpha_6}{2\alpha_3^2}, $ we have the family of representatives $ \langle \alpha\nabla_2+\nabla_3+\beta\nabla_5+\nabla_6 \rangle. $
3. $ \alpha_8 = 0, \alpha_7\neq0, $ then by choosing $ t = -{\alpha_2}{\alpha_7^{-1}}x, s = -{\alpha_5}{\alpha_7^{-1}}, $ we have $ \alpha_2^* = 0, \alpha_5^* = 0. $ Thus, we can suppose that $ \alpha_2 = 0, \alpha_5 = 0 $ and now consider the following cases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6 = 0, $ then we have the family of representatives $ \langle \alpha\nabla_3+\nabla_7 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_4 = 0, \alpha_6\neq0, $ then by choosing $ x = {\alpha_6}{\alpha_7^{-1}}, s = 0, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_3+\nabla_6+\nabla_7 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_4}{\alpha_7^{-1}}}, s = 0, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_3+\nabla_4+\beta\nabla_6+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = {\alpha_1}{\alpha_7^{-1}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_6+\nabla_7 \rangle. $
4. $ \alpha_8\neq0, $ then by choosing $ t = -\frac{\alpha_3}{\alpha_8}x, s = -\frac{\alpha_6}{\alpha_8}, $ we have $ \alpha_3^* = 0, \alpha_6^* = 0. $ Thus, we can suppose that $ \alpha_3 = 0, \alpha_6 = 0. $ Consider the following cases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then we have the representatives $ \langle \nabla_8 \rangle $ and $ \langle \nabla_7+\nabla_8 \rangle $ depending on whether $ \alpha_7 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_5}{\alpha_8^{-1}}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_5+\alpha\nabla_7+\nabla_8 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_4\neq0 $ then by choosing $ x = \sqrt[4]{{\alpha_4}{\alpha_8^{-1}}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\beta\nabla_7+\nabla_8 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt{{\alpha_2}{\alpha_8^{-1}}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_4+\beta\nabla_5+\gamma\nabla_7+\nabla_8 \rangle; $
$ {\rm{(e)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt{{\alpha_1}{\alpha_8}^{-1}}, s = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_2+\beta\nabla_4+\gamma\nabla_5+\mu\nabla_7+\nabla_8 \rangle . $
Summarizing all cases, we have the following distinct orbits:
which gives the following new algebras:
3.14. $ 1 $-dimensional central extensions of $ {\mathbf N}_{19}^{4*} $.
Here we will collect all information about $ {\mathbf N}_{19}^{4*}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{8}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4*}_{19}) . $ Since
then, in the case $ \phi = \phi_1^{x = 1,q = 1}, $ we have
For define the main families of representatives, we will use $ \phi = \phi_1^{x = 1,q = 1} $ and for find equal orbits we will use other automorphisms. We are interested in
Let us consider the following cases:
$1.\ $if $ \alpha_8 = 0, \alpha_7 = 0, \alpha_6 = 0, $ then $ \alpha_3\neq0 $ and choosing $ t = -\frac{\alpha_1}{2\alpha_3}, $ we have the family of representatives $ \langle \alpha\nabla_2+\nabla_3+\beta\nabla_4+\gamma\nabla_5 \rangle; $
$ 2.\ $if $ \alpha_8 = 0, \alpha_7 = 0, \alpha_6\neq0 $ and $ \alpha_3 = 0, $ then by choosing some suitable automorphism $ \phi_2 $ we have $ \alpha_3^*\neq0 , $ $ \alpha_6^* = 0, $ which is the case considered above;
$ 3.\ $if $ \alpha_8 = 0, \alpha_7 = 0, \alpha_6\neq0, \alpha_3\neq0, $ then by choosing $ t = -\frac{\alpha_1}{2\alpha_3}, s = \frac{\alpha_4}{2\alpha_6}, $ we have the family of representatives $ \langle \alpha\nabla_2+\beta\nabla_3+\gamma\nabla_5+\nabla_6 \rangle_{\beta\neq0} ; $
$ 4.\ $if $ \alpha_8 = 0, \alpha_7\neq0, $ then by choosing $ t = -{\alpha_2}{\alpha_7}^{-1}, s = -{\alpha_5}{\alpha_7}^{-1}, $ we have the family of representatives $ \langle \alpha\nabla_1+\beta\nabla_3+\gamma\nabla_4+\mu\nabla_6+\nabla_7 \rangle; $
$5.\ $if $ \alpha_8\neq0, $ then by choosing $ t = -{\alpha_3}{\alpha_8}^{-1}, s = -{\alpha_6}{\alpha_8}^{-1}, $ we have the family of representatives $ \langle \alpha\nabla_1+\beta\nabla_2+\gamma\nabla_4+\mu\nabla_5+\nu\nabla_7+\nabla_8 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.
Central extensions of nilpotent non-$ \mathfrak{CCD} $-algebras.
4.1. $ 1 $-dimensional central extensions of $ {\mathbf N}_{01}^{4} $.
Here we will collect all information about $ {\mathbf N}_{01}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{01}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and consider following cases:
$ 1.\ $$ \alpha_7 = \alpha_6 = \alpha_4 = 0, $ then $ \alpha_2\neq0, $ and we have the following subcases:
${\rm{(a)}}\ $if $ \alpha_5 = -\alpha_2, $ then we have
$ {\rm{(i)}}\ $ if $ \alpha_1 = 0, \alpha_3 = 0, $ then we have the representative $ \langle \nabla_2-\nabla_5 \rangle; $
$ {\rm{(ii)}}\ $ if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt{{\alpha_3}{\alpha_2}^{-1}}, z = 0, t = 0, $ we have the representative $ \langle \nabla_2+\nabla_3-\nabla_5 \rangle; $
$ {\rm{(iii)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt{{\alpha_1}{\alpha_2}^{-1}}, z = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\nabla_2+\alpha\nabla_3-\nabla_5 \rangle; $
(b) if $ \alpha_5\neq-\alpha_2, $ then by choosing $ z = -\frac{\alpha_1}{\alpha_5+\alpha_2}x, t = 0, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_5 \rangle_{\alpha\neq-1} $ and $ \langle \nabla_2+\nabla_3+\alpha\nabla_5 \rangle_{\alpha\neq-1} $ depending on whether $ \alpha_3 = 0 $ or not, which will be jointed with the cases (1(a)i) and (1(a)ii).
2. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4\neq0, $ then we have the following subcases:
${\rm{(a)}}\ $if $ \alpha_5 = -\alpha_2, \alpha_1 = 0, $
$ {\rm{(i)}}\ $ if $ \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_4 \rangle $ and $ \langle \nabla_2+\nabla_4-\nabla_5 \rangle $ depending on whether $ \alpha_2 = 0 $ or not;
$ {\rm{(ii)}}\ $ if $ \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_3}{\alpha_4}^{-1} }, $ we have the family of representatives $ \langle \alpha\nabla_2+\nabla_3+ \nabla_4-\alpha\nabla_5 \rangle; $
(b) if $ \alpha_5 = -\alpha_2, \alpha_1\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_1}{\alpha_4}^{-1} }, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_2+\beta\nabla_3+ \nabla_4-\alpha\nabla_5 \rangle; $
(c) if $ \alpha_5\neq-\alpha_2, $ then we have
${\rm{(i)}}\ $if $ \alpha_3 = 0, \alpha_2 = 0, $ then by choosing $ x = \frac{\alpha_5}{\alpha_4}, z = -\frac{\alpha_1\alpha_5}{\alpha_4(\alpha_2+\alpha_5)}, t = 0, $ we have the representative $ \langle \nabla_4+\nabla_5 \rangle; $
$ {\rm{(ii)}}\ $if $ \alpha_3 = 0, \alpha_2\neq0, $ then by choosing $ x = \frac{\alpha_2}{\alpha_4}, z = -\frac{\alpha_1\alpha_2}{\alpha_4(\alpha_2+\alpha_5)}, t = 0, $ we have the family of representatives $ \langle \nabla_2+\nabla_4+\alpha\nabla_5 \rangle_{\alpha\neq-1}, $ which will be jointed with a representative from the case (2(a)i);
$ {\rm{(iii)}}\ $if $ \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_3}{\alpha_4}^{-1}}, z = -\frac{\alpha_1\sqrt[3]{\alpha_3}}{(\alpha_2+\alpha_5)\sqrt[3]{\alpha_4}}, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_2+\nabla_3+\nabla_4+\beta\nabla_5 \rangle_{\beta\neq-\alpha}, $ which will be jointed with the family from the case (2(a)i).
3. $ \alpha_7 = 0, \alpha_6\neq0, $ then we consider the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_3 = 0, \alpha_4 = 0, $ then choosing $ z = -\frac{\alpha_2}{\alpha_6}x, t = -\frac{\alpha_1x+\alpha_5z}{\alpha_6}, $ we have representatives $ \langle \nabla_6 \rangle $ and $ \langle \nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_5 = 2\alpha_2 $ or not;
${\rm{(b)}}\ $if $ \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \frac{\alpha_4}{\alpha_6}, z = -\frac{\alpha_2\alpha_4}{\alpha^2_6}, t = \frac{\alpha_4(\alpha_2\alpha_5-\alpha_1\alpha_6)}{\alpha^3_6}, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_6 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_3\neq0, $ then by choosing $ x = \sqrt[4]{\frac{\alpha_3}{\alpha_6}}, z = -\frac{\alpha_2\sqrt[4]{\alpha_3}}{\alpha_6\sqrt[4]{\alpha_6}}, t = \frac{(\alpha_2\alpha_5-\alpha_1\alpha_6)\sqrt[4]{\alpha_3}}{\alpha_6^2\sqrt[4]{\alpha_6}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_5+\nabla_6 \rangle. $
4. $ \alpha_7\neq0, $ then by choosing $ z = -\frac{\alpha_6}{\alpha_7}x, t = \frac{\alpha_6^2+\alpha_2\alpha_7}{\alpha^2_7}x, $ we have $ \alpha_2^* = 0, \alpha_6^* = 0. $ Thus, we can suppose that $ \alpha_2 = 0, \alpha_6 = 0 $ and now consider following subcases:
$ {\rm{(a)}}\ $$ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, $ then we have representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_5+\nabla_7 \rangle $ depending on whether $ \alpha_5\alpha_7-\alpha^2_6 = 0 $ or not;
$ {\rm{(b)}}\ $$ \alpha_1 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_4}{\alpha_7}^{-1}}, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_7 \rangle; $
${\rm{(c)}}\ $$ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_3}{\alpha_7}^{-1}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_5+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $$ \alpha_1\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_1}{\alpha_7^{-3}}}, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_5+\nabla_7 \rangle. $
Summarizing all cases, we have the following distinct orbits:
Hence, we have the following new algebras:
4.2. $ 1 $-dimensional central extensions of $ {\mathbf N}_{02}^{4} $.
Here we will collect all information about $ {\mathbf N}_{02}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{02}) . $ Since
we have
We are interested in $ (\alpha_1,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and consider following cases:
$1.\ $if $ \alpha_7 = \alpha_6 = \alpha_4 = 0, $ then $ \alpha_1\neq0, $ and we have
$ {\rm{(a)}}\ $if $ \alpha_5 = -\alpha_1 , $ then we have the family of representatives
$ {\rm{(b)}}\ $if $ \alpha_5\neq-\alpha_1 , $ then by choosing $ z = -\frac{\alpha_3}{\alpha_1+\alpha_5}, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_2+\beta\nabla_5 \rangle_{\beta\neq-1}; $
2. if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4\neq0, $ then by choosing $ z = -\frac{\alpha_2}{4\alpha_4}, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_1+\beta\nabla_3+\nabla_4+\gamma\nabla_5 \rangle; $
3. if $ \alpha_7 = 0, \alpha_6\neq0, $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_2+\beta\nabla_4+\gamma\nabla_5+\nabla_6 \rangle; $
4. if $ \alpha_7\neq0, $ then by choosing $ z = -{\alpha_6}{\alpha_7}^{-1}, t = ({\alpha^2_6-\alpha_1\alpha_7}){\alpha^{-2}_7}, $ we have the family of representatives $ \langle \alpha\nabla_2+\beta\nabla_3+\gamma\nabla_4+\mu\nabla_5+\nabla_7 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.3. $ 1 $-dimensional central extensions of $ {\mathbf N}_{03}^{4} $.
Here we will collect all information about $ {\mathbf N}_{03}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{03}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_5,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and consider following cases:
$ 1.\ $$ \alpha_7 = \alpha_6 = \alpha_5 = 0, $ then $ \alpha_2\neq0, $ and we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_2 \rangle $ and $ \langle \nabla_2+\nabla_4 \rangle $ depending on whether $ \alpha_4 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_3}{\alpha_2}^{-1}}, t = 0, $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha\nabla_4 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_1}{\alpha_2^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_1+\nabla_2+\alpha\nabla_3+\beta\nabla_4 \rangle. $
2. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_3 = 0, $ then we have the representatives $ \langle \nabla_5 \rangle $ and $ \langle \nabla_4+\nabla_5 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_3}{\alpha_5^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, $ then by choosing $ x = {\alpha_2}{\alpha_5^{-1}}, t = 0, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\beta\nabla_4+\nabla_5 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_1}{\alpha_5^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_2+\beta\nabla_3+\gamma\nabla_4+\nabla_5 \rangle. $
3. $ \alpha_7 = 0, \alpha_6\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0, \alpha_4 = 0, $ then we have representatives $ \langle \nabla_6 \rangle $ and $ \langle \nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_4}{\alpha_6}^{-1}}, t = -\alpha_1 \sqrt[4]{\alpha_4 \alpha_6^{-5}} , $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_6 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[5]{{\alpha_3}{\alpha_6^{-1}}}, t = - \alpha_1\sqrt[5]{\alpha_3 \alpha_6^{-6}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_5+\nabla_6 \rangle; $
${\rm{(d)}}\ $if $ \alpha_2\neq0, $ then by choosing $ x = {{\alpha_2}{\alpha_6^{-1}}}, t = -{\alpha_1\sqrt{\alpha_2 \alpha_6^{-3}}}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_5+\nabla_6 \rangle. $
4. $ \alpha_7\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $$ \alpha_1\alpha_7-\alpha_2\alpha_6 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_5 = 0, $ then we have representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_6+\nabla_7 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $$ \alpha_1\alpha_7-\alpha_2\alpha_6 = 0, \alpha_3 = 0, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_5}{\alpha_7^{-1}}}, $ $ t = -{\alpha_2\sqrt[4]{\alpha_5 \alpha_7^{-5}}}, $ we have the family of representatives $ \langle \nabla_5+\alpha\nabla_6+\nabla_7 \rangle; $
${\rm{(c)}}\ $$ \alpha_1\alpha_7-\alpha_2\alpha_6 = 0, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[7]{{\alpha_4\alpha_7^{-1}}}, $ $ t = -{\alpha_2\sqrt[7]{\alpha_4 \alpha_7^{-8}}}, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\beta\nabla_6+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $$ \alpha_1\alpha_7-\alpha_2\alpha_6 = 0, \alpha_3\neq0, $ then by choosing $ x = \sqrt[8]{{\alpha_3}{\alpha_7^{-1}}}, $ $ t = -{\alpha_2\sqrt[8]{\alpha_3 \alpha_7^{-9}}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_5+\gamma\nabla_6+\nabla_7 \rangle; $
$ {\rm{(e)}}\ $$ \alpha_1\alpha_7-\alpha_2\alpha_6\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_5+\mu\nabla_6+\nabla_7 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.4. $ 1 $-dimensional central extensions of $ {\mathbf N}_{04}^{4} $.
Here we will collect all information about $ {\mathbf N}_{04}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{04}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_5,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and consider following cases:
$ 1.\ $if $ \alpha_7 = \alpha_6 = \alpha_5 = 0, $ then $ \alpha_2\neq0, $ and we have the family of representatives
$ 2.\ $if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5\neq0, $ then we have the family of representatives
$ 3.\ $if $ \alpha_7 = 0, \alpha_6\neq0, $ then by choosing $ \phi = \phi_+, t = -{\alpha_1}{\alpha_6^{-1}}, $ we have the family of representatives
$ 4.\ $if $ \alpha_7\neq0, $ then by choosing $ \phi = \phi_+, t = -{\alpha_2}{\alpha_7^{-1}} $ we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.5. $ 1 $-dimensional central extensions of $ {\mathbf N}_{05}^{4} $.
Here we will collect all information about $ {\mathbf N}_{05}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{05}) . $ Since
we have
We are interested in $ (\alpha_2,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and consider following cases:
$ 1.\ $$ \alpha_7 = \alpha_6 = \alpha_4 = 0, $ then $ \alpha_2\neq0 $ and we have the following subcases:
$ {\rm{(a)}}\ $$ \alpha_3 = -2\alpha_2, $
$ {\rm{(i)}}\ $ if $ \alpha_1 = 0, \alpha_5 = 0, $ then we have the representative $ \langle \nabla_2-2\nabla_3 \rangle; $
$ {\rm{(ii)}}\ $ if $ \alpha_1 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt{{\alpha_2}{\alpha_5^{-1}}}, z = 0, t = 0, $ we have the representative $ \langle \nabla_2-2\nabla_3+\nabla_5 \rangle; $
$ {\rm{(iii)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_1}{\alpha_2^{-1}}}, z = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\nabla_2-2\nabla_3+\alpha\nabla_5 \rangle. $
(b) $ \alpha_3\neq -2\alpha_2, $
$ {\rm{(i)}}\ $if $ \alpha_5 = 0, $ then choosing $ x = 1, z = -\frac{\alpha_1}{\alpha_3+2\alpha_2}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3 \rangle_{\alpha\neq-2}, $ which will be jointed with the case (1(a)i);
$ {\rm{(ii)}}\ $if $ \alpha_5\neq0, $ then by choosing $ x = \sqrt{\frac{\alpha_2}{\alpha_5}}, z = -\frac{\alpha_1\sqrt{\alpha_2}}{(\alpha_3+2\alpha_2)\sqrt{\alpha_5}}, $ we have the family of representatives $ \langle\nabla_2+\alpha\nabla_3+\nabla_5 \rangle_{\alpha\neq-2}, $ which will be jointed with the case (1(a)ii).
2. $ \alpha_7 = \alpha_6 = 0, \alpha_4\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0, $ then we have representatives $ \langle \nabla_4 \rangle $ and $ \langle \nabla_4+\nabla_5 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_3\neq0 , $ then by choosing $ x = {\alpha_3}{\alpha_4^{-1}}, z = 0, t = -{\alpha_1\alpha_3}{\alpha_4^{-2}}, $ we have the family of representatives $ \langle \nabla_3+ \nabla_4+\alpha\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2\neq0 , $ then by choosing $ x = {\alpha_2}{\alpha_4^{-1}}, z = 0, t = -{\alpha_1\alpha_2}{\alpha_4^{-2}}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+ \nabla_4+\beta\nabla_5 \rangle. $
3. $ \alpha_7 = 0, \alpha_6\neq0, $ then by choosing $ z = -{\alpha_2}x{\alpha_6^{-1}} , $ we have $ \alpha_2^* = 0. $ Thus, we can suppose that $ \alpha_2 = 0 $ and consider following subcases:
$ {\rm{(a)}}\ $$ \alpha_4 = 0, $
$ {\rm{(i)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, $ then we have representatives $ \langle \nabla_6 \rangle $ and $ \langle \nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
${\rm{(ii)}}\ $if $ \alpha_1 = 0, \alpha_3\neq0 $ then by choosing $ x = \sqrt[3]{{\alpha_3}{\alpha_6^{-1}}}, z = 0, t = 0, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_5+\nabla_6 \rangle; $
$ {\rm{(iii)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_1}{\alpha_6^{-1}}}, z = 0, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_5+\nabla_6 \rangle. $
(b) $ \alpha_4\neq0 , $ then by choosing $ x = \sqrt{{\alpha_4}{\alpha_6^{-1}}}, t = -{\alpha_1\sqrt{\alpha_4 \alpha_6^{-3}}}, $ we have the family of representatives $ \langle \alpha\nabla_3+\nabla_4+\beta\nabla_5+\nabla_6 \rangle. $
4. $ \alpha_7\neq0, $
$ {\rm{(a)}}\ $if $ \alpha_1\alpha_7-\alpha_2\alpha_4 = 0, \alpha_3 = 0, \alpha_6 = 0, $ then then by choosing $ z = -\frac{\alpha_4}{2\alpha_7}x, t = \frac{\alpha_4\alpha_6-2\alpha_2\alpha_7}{2\alpha^2_7}x, $ we have representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_5+\nabla_7 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1\alpha_7-\alpha_2\alpha_4 = 0, \alpha_3\alpha_7-\alpha_4\alpha_6 = 0, \alpha_6\neq0, $ then by choosing
we have the family of representatives $ \langle \alpha\nabla_5+\nabla_6+\nabla_7 \rangle; $
${\rm{(c)}}\ $if $ 2\alpha_1\alpha_7^2-\alpha_3\alpha_4\alpha_7+\alpha_4^2\alpha_6-2\alpha_2\alpha_4\alpha_7 = 0, \alpha_3\alpha_7-\alpha_4\alpha_6\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_3+\alpha\nabla_5+\beta\nabla_6+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $if $ 2\alpha_1\alpha_7^2-\alpha_3\alpha_4\alpha_7+\alpha_4^2\alpha_6-2\alpha_2\alpha_4\alpha_7\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_5+\gamma\nabla_6+\nabla_7 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.6. $ 1 $-dimensional central extensions of $ {\mathbf N}_{06}^{4} $.
Here we will collect all information about $ {\mathbf N}_{06}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{06}). $ Since
we have
Since $ (\alpha_2,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and for $ \phi = \phi_+, $ we have the following cases:
$ 1.\ $if $ \alpha_7 = \alpha_6 = \alpha_4 = 0, $ then $ \alpha_2\neq0, $ and we have the following subcase:
$ {\rm{(a)}}\ $if $ \alpha_5 = \alpha_3+2\alpha_2, $ then we have the family of representatives
$ {\rm{(b)}}\ $if $ \alpha_5\neq\alpha_3+2\alpha_2, $ then by choosing $ z = 0, t = \frac{\alpha_1}{\alpha_3+2\alpha_2-\alpha_5} , $ we have the family of representative $ \langle \nabla_2+\alpha\nabla_3+\beta\nabla_5 \rangle_{\beta\neq\alpha+2}; $
2. if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4\neq0, $ then by choosing $ z = 0, t = \frac{\alpha_1}{\alpha_4}, $ we have the family of representatives $ \langle \alpha\nabla_2+\beta\nabla_3+\nabla_4+\gamma\nabla_5 \rangle; $
3. if $ \alpha_7 = 0, \alpha_6\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_6 = \alpha_4, $ then by choosing $ z = -{\alpha_2}{\alpha_6^{-1}}, t = 0, $ we have the family of representatives $ \langle \alpha\nabla_1+\beta\nabla_3+\nabla_4+\gamma\nabla_5+\nabla_6 \rangle; $
$ {\rm{(b)}}\ $if $ \alpha_6\neq\alpha_4, $ then by choosing $ z = -\frac{\alpha_2}{\alpha_6}, t = \frac{\alpha_1\alpha_6-\alpha_2\alpha_5+\alpha_2\alpha_3}{\alpha_6(\alpha_4-\alpha_6)}, $ we have the family of representatives $ \langle \alpha\nabla_3+\beta\nabla_4+\gamma\nabla_5+\nabla_6 \rangle_{\beta\neq1}; $
4. if $ \alpha_7\neq0, $ then by choosing $ z = -\frac{\alpha_4}{2\alpha_7}, t = \frac{\alpha_4\alpha_6-2\alpha_2\alpha_7}{2\alpha^2_7}, $ we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.7. $ 1 $-dimensional central extensions of $ {\mathbf N}_{07}^{4} $.
Here we will collect all information about $ {\mathbf N}_{07}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{07}) . $ Since
we have
We are interested in $ (\alpha_3,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0) $ and consider following cases:
$ 1.\ $$ \alpha_7 = \alpha_6 = \alpha_4 = 0, $ then $ \alpha_3\neq0, $ and we have the following subcases:
${\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, $ then we have representatives $ \langle \nabla_3 \rangle $ and $ \langle \nabla_3+\nabla_5 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt{{\alpha_2}{\alpha_3^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_1}{\alpha_3^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_2+\nabla_3+\beta\nabla_5 \rangle. $
2. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0 , $ then we have the familty of representative $ \langle \nabla_4+\alpha\nabla_5 \rangle; $
${\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_3\neq0 , $ then by choosing $ x = {\alpha_3}{\alpha_4^{-1}}, t = -{\alpha_1\alpha_3}{\alpha_4^{-2}}, $ we have the family of representatives $ \langle \nabla_3+ \nabla_4+\alpha\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_2}{\alpha_4^{-1}}}, t = -{\alpha_1\sqrt[3]{\alpha_2 \alpha_4^{-4}}}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+ \nabla_4+\beta\nabla_5 \rangle. $
3. $ \alpha_7 = 0, \alpha_6\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_3 = 0, \alpha_4 = 0, $ then we have representatives $ \langle \nabla_6 \rangle $ and $ \langle \nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1\alpha_6 = \alpha_2\alpha_4, \alpha_3 = 0, \alpha_4\neq0, $ then choosing $ x = \sqrt{{\alpha_4}{\alpha_6^{-1}}}, t = -{\alpha_2\sqrt{\alpha_4} \alpha_6^{-3}}, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_6 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\alpha_6 = \alpha_2\alpha_4, \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{\frac{\alpha_3}{\alpha_6}}, t = -\frac{\alpha_2\sqrt[3]{\alpha_3}}{\alpha_6\sqrt[3]{\alpha_6}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_5+\nabla_6 \rangle; $
${\rm{(d)}}\ $if $ \alpha_1\alpha_6\neq\alpha_2\alpha_4 , $ then choosing $ x = \sqrt[7]{\frac{\alpha_1\alpha_6-\alpha_2\alpha_4}{\alpha^2_6}}, t = -\frac{\alpha_2\sqrt[7]{\alpha_1\alpha_6-\alpha_2\alpha_4}}{\alpha_6\sqrt[7]{\alpha^2_6}}, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_3+\beta\nabla_4+\gamma\nabla_5+\nabla_6 \rangle. $
4. $ \alpha_7\neq0, $ then we have the following subcases:
$ {\rm{(a)}}\ $$ \alpha_1 = 0, \alpha_2\alpha_7 = \alpha_3\alpha_6, \alpha_4 = 0, \alpha_5 = 0, $ then we have representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_6+\nabla_7 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
${\rm{(b)}}\ $$ \alpha_1 = 0, \alpha_2\alpha_7 = \alpha_3\alpha_6, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_5}{\alpha_7^{-1}}}, t = -{\alpha_3\sqrt[4]{\alpha_5 \alpha_7^{-5}}}, $ we have family of representatives $ \langle \nabla_5+\alpha\nabla_6+\nabla_7 \rangle; $
$ {\rm{(c)}}\ $$ \alpha_1\alpha_7 = \alpha_3\alpha_4, \alpha_2\alpha_7 = \alpha_3\alpha_6, \alpha_4\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_4}{\alpha_7^{-1}}}, t = -{\alpha_3\sqrt[4]{\alpha_4 \alpha_7^{-5}}}, $ we have family of representatives $ \langle \nabla_4+\alpha\nabla_5+\beta\nabla_6+\nabla_7 \rangle; $
${\rm{(d)}}\ $$ \alpha_1\alpha_7 = \alpha_3\alpha_4, \alpha_2\alpha_7\neq\alpha_3\alpha_6, $ then by choosing $ x = \sqrt[7]{(\alpha_2\alpha_7-\alpha_3\alpha_6)\alpha^{-2}_7}, $ $ t = -{\alpha_3\sqrt[7]{(\alpha_2\alpha_7-\alpha_3\alpha_6)\alpha_7^{-9}}}, $ we have the family of representatives
$ {\rm{(e)}}\ $$ \alpha_1\alpha_7\neq \alpha_3\alpha_4, $ then by choosing
we have family of representatives $ \langle \nabla_1+\alpha\nabla_2+\beta\nabla_4+\gamma\nabla_5+\mu\nabla_6+\nabla_7 \rangle. $
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.8. $ 1 $-dimensional central extensions of $ {\mathbf N}_{08}^{4} $.
Here we will collect all information about $ {\mathbf N}_{08}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{08}) . $ Since
we have
Since $ (\alpha_2,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0), $ we have the following cases:
$1.\ $if $ \alpha_7 = \alpha_6 = \alpha_4 = 0, $ then $ \alpha_2\neq0, $ and we have the family of representatives
$2.\ $if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4\neq0, $ then by choosing $ t = -{\alpha_1}{\alpha_4^{-1}}, $ we have the family of representatives
$ 3.\ $if $ \alpha_7 = 0, \alpha_6\neq0, $ then by choosing $ t = {\alpha_3}{\alpha_6^{-1}}, $ we have the family of representatives
$ 4.\ $if $ \alpha_7\neq0, $ then by choosing $ t = -{\alpha_2}{\alpha_7^{-1}}, $ we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.9. $ 1 $-dimensional central extensions of $ {\mathbf N}_{09}^{4} $.
Here we will collect all information about $ {\mathbf N}_{09}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{09}) . $ Since
we have
Since $ (\alpha_3,\alpha_5,\alpha_6,\alpha_7)\neq(0,0,0,0), $ we have the following cases:
$ 1.\ $$ \alpha_7 = \alpha_6 = \alpha_5 = 0, $ then $ \alpha_3\neq0, $ and we have the following subcases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2 = 0, $ then we have representatives $ \langle \nabla_3 \rangle $ and $ \langle \nabla_3+\nabla_4 \rangle $ depending on whether $ \alpha_4 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1 = 0, \alpha_2\neq0, $ then by choosing $ x = \sqrt[4]{{\alpha_2}{\alpha_3^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_2+\nabla_3+\alpha\nabla_4 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_1}{\alpha_3^{-1}}}, t = 0, $ we have the family of representatives $ \langle \nabla_1+\alpha\nabla_2+\nabla_3+\beta\nabla_4 \rangle. $
2. $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5\neq0, $ then we have the following cases:
${\rm{(a)}}\ $if $ \alpha_2 = 0, \alpha_3 = 0, $ then we have representatives $ \langle \nabla_5 \rangle $ and $ \langle \nabla_4+\nabla_5 \rangle $ depending on whether $ \alpha_4 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_2 = 0, \alpha_3\neq0, $ then choosing $ x = {\alpha_3}{\alpha_5^{-1}}, t = -{\alpha_1\alpha_3}{\alpha_5^{-2}}, $ we have the family of representatives $ \langle \nabla_3+ \alpha\nabla_4+\nabla_5 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_2\neq0, $ then by choosing $ x = \sqrt[5]{{\alpha_2}{\alpha_5^{-1}}}, t = -{\alpha_1\sqrt[5]{\alpha_2 \alpha_5^{-6} }}, $ we have the family of representatives $ \langle \nabla_2+\alpha\nabla_3+ \beta\nabla_4+\nabla_5 \rangle. $
3. $ \alpha_7 = 0, \alpha_6\neq0, $ then we have the following cases:
$ {\rm{(a)}}\ $if $ \alpha_1\alpha_6 = \alpha_2\alpha_5, \alpha_3 = 0, \alpha_4 = 0, $ then we have representatives $ \langle \nabla_6 \rangle $ and $ \langle \nabla_5+\nabla_6 \rangle $ depending on whether $ \alpha_5 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1\alpha_6 = \alpha_2\alpha_5, \alpha_3 = 0, \alpha_4\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_4}{\alpha_6^{-1}}}, t = -{\alpha_2\sqrt[6]{\alpha_4 \alpha_6^{-7} }}, $ we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\nabla_6 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\alpha_6 = \alpha_2\alpha_5, \alpha_3\neq0, $ then by choosing $ x = \sqrt[3]{{\alpha_3}{\alpha_6^{-1}}}, t = -{\alpha_2\sqrt[3]{\alpha_3 \alpha_6^{-4}}}, $ we have the family of representatives $ \langle \nabla_3+\alpha\nabla_4+\beta\nabla_5+\nabla_6 \rangle; $
$ {\rm{(d)}}\ $if $ \alpha_1\alpha_6\neq \alpha_2\alpha_5 , $ then by choosing
we have the family of representatives
4. $ \alpha_7\neq0, $ then we have the following cases:
$ {\rm{(a)}}\ $if $ \alpha_1 = 0, \alpha_2\alpha_7 = \alpha_3\alpha_6, \alpha_4 = 0, \alpha_5 = 0, $ then choosing $ x = 1, t = -\frac{\alpha_3}{\alpha_7}, $ we have representatives $ \langle \nabla_7 \rangle $ and $ \langle \nabla_6+\nabla_7 \rangle $ depending on whether $ \alpha_6 = 0 $ or not;
$ {\rm{(b)}}\ $if $ \alpha_1\alpha_7 = \alpha_3\alpha_5, \alpha_2\alpha_7 = \alpha_3\alpha_6, \alpha_4 = 0, \alpha_5\neq0, $ then by choosing $ x = \sqrt[6]{{\alpha_5}{\alpha_7^{-1}}}, t = -{\alpha_3\sqrt[6]{\alpha_5 \alpha_7^{-7} }}, $ we have the family of representatives $ \langle \nabla_5+\alpha\nabla_6+\nabla_7 \rangle; $
$ {\rm{(c)}}\ $if $ \alpha_1\alpha_7 = \alpha_3\alpha_5, \alpha_2\alpha_7 = \alpha_3\alpha_6, \alpha_4\neq0, $ then by choosing
we have the family of representatives $ \langle \nabla_4+\alpha\nabla_5+\beta\nabla_6+\nabla_7 \rangle; $
$ {\rm{(d)}}\ $$ \alpha_1\alpha_7 = \alpha_3\alpha_5, \alpha_2\alpha_7\neq\alpha_3\alpha_6, $ then by choosing
we have the family of representatives
$ {\rm{(e)}}\ $$ \alpha_1\alpha_7\neq\alpha_3\alpha_5, $ then by choosing
we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.10. $ 1 $-dimensional central extensions of $ {\mathbf N}_{10}^{4} $.
Here we will collect all information about $ {\mathbf N}_{10}^{4}: $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{10}) . $ Since
we have
Since $ (\alpha_2,\alpha_4,\alpha_6,\alpha_7)\neq(0,0,0,0), $ we have the following cases:
$ 1.\ $if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4 = 0, $ then $ \alpha_2\neq0, $ and we have the family of representatives
$ 2.\ $if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_4\neq0, $ then we have the family of representatives
$ 3.\ $if $ \alpha_7 = 0, \alpha_6\neq0, $ then we have the family of representatives
$ 4.\ $if $ \alpha_7\neq0, $ then we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
4.11. $ 1 $-dimensional central extensions of $ {\mathbf N}_{11}^{4}(\lambda) $.
Here we will collect all information about $ {\mathbf N}_{11}^{4}(\lambda): $
Let us use the following notations:
Take $ \theta = \sum\limits_{i = 1}^{7}\alpha_i\nabla_i\in\mathrm{H}^2_{\mathfrak{C}}(\mathbf{N}^{4}_{11}(\lambda)) . $ Since
we have
Since $ (\alpha_3,\alpha_5,\alpha_6,\alpha_7)\neq(0,0,0,0), $ we have the following cases:
$ 1.\ $if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5 = 0 , $ then $ \alpha_3\neq0 $ and we have the family of representatives
$ 2.\ $if $ \alpha_7 = 0, \alpha_6 = 0, \alpha_5\neq0 $ then by choosing $ t = -{\alpha_1}{\alpha_5^{-1}}, $ we have the family of representatives
$ 3.\ $if $ \alpha_7 = 0, \alpha_6\neq0 $ then by choosing $ t = -{\alpha_2}{\alpha_6^{-1}}, $ we have the family of representatives
$ 4.\ $if $ \alpha_7\neq0 $ then by choosing $ t = -{\alpha_3}{\alpha_7^{-1}}, $ we have the family of representatives
Summarizing, we have the following distinct orbits:
which gives the following new algebras:
Remark 2. Note that the algebras $ \mathbf{N}^{4}_{11}(\lambda) $ and $ \mathbf{N}^{4}_{11}(-\lambda) $ are isomorphic. Hence, there are some additional isomorphism relations for algebras from the present subsection $ \mathbf{N}^{\lambda, \Xi} \cong \mathbf{N}^{-\lambda, \Xi} . $
5.
Classification theorem.
Theorem 5.1. Let $ \mathbf N $ be a complex $ 5 $-dimensional nilpotent commutative algebra. Then we have one of the following situations.
${\mathit{1.}} \ $If $ \mathbf N $ is associative, then $ \mathbf N $ is isomorphic to one algebra listed in [15].
${\mathit{2.}} \ $If $ \mathbf N $ is a non-associative Jordan algebra, then $ \mathbf N $ is isomorphic to one algebra listed in [9].
$ {\mathit{3.}} \ $If $ \mathbf N $ is a non-Jordan $ \mathfrak{CD} $-algebra, then $ \mathbf N $ is isomorphic to one algebra listed in [11].
${\mathit{4.}}\ $If $ \mathbf N $ is a non-$ \mathfrak{CD} $-algebra, then $ \mathbf N $ is isomorphic to one algebra listed in the following list.









 DownLoad:
DownLoad: