Abbreviations: SCEC: Southern California Earthquake Centre; GoF: Goodness-of-Fit; BBP: Broadband Platform; GMPE: Ground Motion Prediction Equations; RS: Response Spectra; GP: Graves & Pitarka; SDSU: San Diego State University; UCSB: University of California, Santa Barbara; EXSIM: Stochastic Extended Simulation; CSM: Composite Source Model; SMSIM: Stochastic point source simulation; FINSIM: Finite fault simulation; K-NET: Kyoshin network; KiK-net: Kiban Kyoshin network; PSA: Pseudo Spectral Acceleration; NGA: Next Generation Attenuation; J-SHIS: Japan Seismic Hazard Information Station
1. Introduction
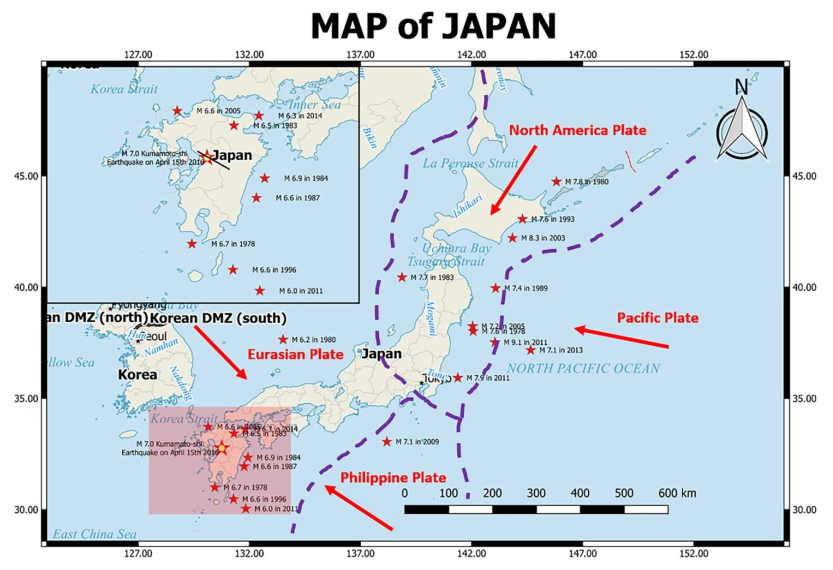
Japan is one of the world's highly seismically active regions on the planet due to its complex crustal structure where four tectonic plates meet around the boundary of Japanese Islands. About 1/10th of the earthquakes on the globe occur nearby Islands of Japan, which are due to collision and subduction of these four plates. Earthquakes in the Eastern part of Japan occur due to subduction of Pacific plate under the North American and Eurasian plate, and South-western part activity is due to the Philippine Sea plate descending beneath the Eurasian [1]. The region is characterized by the several huge earthquakes including the great Tohoku M 9.0 in 2011. The continuous interaction of these four plates makes the region highly seismic and volcano prone [2]. Seismic and volcanic hyperactivities of the region around Japan are characterized by structural divergence in the crust and upper mantle [3,4]. Hence, shallow earthquakes are predominant in Japanese Islands.
On 15 April 2016, an earthquake of magnitude Mw 7.0 occurred north of Kumamoto, in southwest Japan in the midst of foreshocks (M 6.2 and 6.0) and aftershocks in the same region. The peak ground acceleration of 1157 gals (cm/s2) was measured at Mashiki town during this earthquake. Numerous structures collapsed and caught fire and few were severely damaged in the region of Mashiki which is 10 km away from Kumamoto city due to high ground acceleration and shallow depth of epicenter [5]. The earthquake was due to subduction of Philippine Sea plate beneath Japan and Eurasia plate at a velocity of 58 mm/yr, which killed 9 people and injured about 800. The earthquake was a result of strike-slip faulting at shallow depth. Fault mapping of the region revealed an east-west or northeast-southwest trend, which complies with right-lateral strike-slip faulting. The Philippine fault, which is over a length of 1200 km is seismically active and involved in major earthquakes of historic importance including M 7.6 Luzon earthquake of 1990 [6].
The boundary of the Philippine Sea plate which is considered as seismically more active has produced 7 Great (M > 8.0) earthquakes and 250 large (M > 7.0) events. The most catastrophic events in the list are 1923 Kanto, the 1948 Fukui and the 1995 Kobe (Japan) earthquakes with 99000, 5100 and 64000 causalities respectively, the 1935, the 1999 Chi-Chi (Taiwan), the 1976 M 7.6 Moro Gulf and 1990 M 7.6 Luzon (Philippines) earthquake are among the other [7]. Figure 1 shows the map of Japan region demarcated with plate boundaries and its major earthquake locations. As the seismic activity in this region is intense, a proper understanding of the response of structures is a paramount problem. Hence, modelling studies have been taken for this earthquake.
Simulation of strong motion data precisely in the broad frequency range (0.1 to 20 Hz) is vital in predicting PGA levels and generating synthetic accelerograms at locations other than recording stations. Fortunately, state-of-art broadband accelerographs are installed at the seismic sensitive regions of the world which use sophisticated technology for recording strong motion data accurately. Broadband ground motion simulations can generate synthetic accelerograms which can be utilised for dynamic analysis of structures, in the absence of real accelerograms. They also fill in the gap where there are fewer recordings for major magnitudes in the near field [9]. The primary objective of the paper is to simulate ground motions of 15 April 2016 Mw 7.0 Kumamoto-Shi earthquake, making use of the SCEC BBP and validate them. Further, utilizing the validated seismological model of this study, acceleration time series and 5% damped Pseudo acceleration spectra (PSA) are generated in the frequency range of engineering interest, for sites where considerable damages occurred that lacked strong-motion stations, in Kyushu region of Japan.
A building, a bridge and a tunnel site that are devoid of strong-motion stations, are selected to assess the ground motions, that were damaged during the earthquake. A popular tourist destination in Kumamoto, the Kumamoto castle suffered severe damages to the stone walls and roof. Significant damages also occurred to the Great Aso Bridge due to the event and landslide post-earthquake. Shear cracks developed in the Tawarayama tunnel and several concrete lining elements fell causing a massive threat to the stability of tunnel [10].
The present work was run on an Intel i7 processor with 4GB RAM, which took 15 minutes for each simulation. With the advent of high performance computing facilities, enough simulations can be run for developing GMPE. In the past, seismological models which simulate acceleration time histories were used for deriving GMPEs, in the absence of strong motion data [11,12,13,14,15].
2. Simulation methods
Different methods have been proposed by pioneers in this field for simulating ground motions. The first class of methods to simulate the accelerograms is by filtering and windowing Gaussian noise which is based on random-vibration theory [16,17]. A different approach in the same path is to match the simulated response spectra with the target response spectrum [18,19,20].
Another class of methods for strong ground motion simulation involves a physical approach employing source, path, and site effects. Source intricacy was addressed by empirical Green's functions [21,22] and stochastic sub-event summation approach [23,24,25,26]. A more advanced, if not accurate, class of methods are numerical solutions to 3D Wave propagation equation which is based on finite-difference method [27] used by Graves [28], Pitarka [29], Aoi and Fujiwara [30], Moczo et al. [31], Lee et al.
[32], or spectral element methods [33] employed by Komatitsch et al.
[34], Priolo [35], Komatitsch et al. [36], Lee et al. [37] and Stupazzini et al. [38] for ground motion simulation.
Software tools with high computing capabilities are the best option for simulating ground motions accurately. Various ground motion simulation programs were developed by researchers to meet the requirement by employing finite-fault approach, and hybrid deterministic-stochastic methods. These programs use a different set of input files which is a principal drawback leading to an unfair comparison between them. A group of researchers teamed together to develop a single program which serves the purpose and eligible for fair comparison. One of the outcomes of these efforts was the BBP developed by the Southern California Earthquake Centre (SCEC).
Southern California Earthquake Centre developed an open-source program, known as the SCEC BBP for simulating strong motion data from earthquakes. The platform was first introduced in the year 2013 and underwent many software updates over these years such as updating 4 simulation methods (GP, SDSU, UCSB, and CSM), integrating multiple post-processing codes, adding 4 GMPEs of NGA-West 2 and 3 GMPEs of NGA-East [39]. The main advantage of the BBP lies in its varied applicability for different regions like US, Canada, and Japan where earthquakes are more frequent. Presently, version 15.3 is the latest and was used for simulating the strong motion data of 15 April 2016 Mw 7.0 Kumamoto-shi, Japan earthquake.
Several scientific methods were included in the platform namely, Graves & Pitarka (GP) [40], San Diego State University (SDSU) [41], University of California, Santa Barbara (UCSB) [42], Stochastic Extended Simulation (EXSIM) [43] and Composite Source Model (CSM)—under development [44] which the user can select for generating the synthetics. Comparisons with the recorded data are performed using two Goodness-of-Fit (GoF) modules. Available GoF modules on the platform are GP and SDSU. GoF comparisons are performed mainly by comparing the response spectra of calculated seismograms with the observed seismograms. The stations which do not have observed seismograms data will not be included in the automatically generated GoF comparisons.
2.1. Methodology
The present study employs EXSIM methodology of the platform. EXSIM is an extended stochastic finite-fault simulation methodology proposed by Motazedian and Atkinson [43], which is a developed form of SMSIM (Stochastic point source simulation) proposed by Boore [45,46] and FINSIM (Finite fault simulation) proposed by Beresnev and Atkinson [25,47]. In the past, the same methodology was successfully used in simulating ground motions for 1980 Irpinia earthquake [48], 2003 Bam earthquake [49], 2008 Iwate-Miyagi Nairiku earthquake [50], 2011 Tohoku, Japan earthquake [51] and 2015 Nepal (Gorkha) earthquake [52].
Stochastic point source model assumes the source process is concentrated at a single point and the acceleration time series generated at a site carry both deterministic and stochastic faces of ground motion. The deterministic part which is a function of both magnitude and distance is specified by Fourier spectrum and the stochastic aspects are obtained by treating the motion as noise. This methodology worked well only when the hypocentral distance is much larger than the source dimension. The total point source spectrum is calculated by the Eq 1 [53]:
|
Acc(Mo,R,f)=Source(Mo,f)Path(R,f)Site(f)
|
(1)
|
Where Acc (Mo, R, f) represents the total point-source spectrum observed at site; Source (Mo, f) represents the source spectrum at unit distance; Path (R, f) is the path effects which includes both geometric spreading and inelastic attenuation; Site (f) represents the site effects; Mo is the seismic moment [54]; R is the hypocentral distance and f is the frequency.
The key factor that determines the ground motions which are not included in the stochastic point source model is the effect of faulting geometry, distributed rupture, and rupture heterogeneity. To include these in the modelling of ground motions, Hartzell [21] proposed subdividing the fault into several small grids, which are treated as point sources. These sub-source contributions are summed up at the observation site, with proper delays. This methodology was coded into FINSIM by Beresnev and Atkinson [25,47]. Later, Motazedian and Atkinson [43] introduced the concept of dynamic corner frequency to reduce the dependencies to sub source size. This, in turn, eliminated multiple triggering of sub-events. The sub source dependency was terminated by Boore [55] with modification to sub-event normalization. This methodology was named as EXSIM and implemented in the BBP by Southern California Earthquake Centre [56]. The major advantage of EXSIM over FINSIM is its insensitivity to sub-fault size, conservation of energy radiated during the rupture process and only a portion of fault will be active at any given point of time [57].
The algorithm of EXSIM is:
|
Acctot(t)=∑Ni=1HixAcc(t−Δti−Ti)
|
(2)
|
Where Acctot (t) is the total seismic signal; Hi is the normalization factor for the ith sub source; Acc (t) is the signal of ith sub source; N is the total number of sub-sources; Δti is the time delay of sub source; Ti is a fraction of rise time.
|
Hi=(N∑{f/[1+(f╱−f0)2]}2/∑{f/[1+(f╱f0i−)2]}2)1/2
|
(3)
|
Where f0 is corner frequency; f0i is the corner frequency of the ith sub source; and f is counter over frequency.
2.2. Strong motion data
Strong motion data has been acquired from K-NET and KiK-net which is Japan's nation-wide strong-motion seismograph network consisting of more than 1,000 observation stations distributed uniformly every 20 km. Instrumentation used for both the networks are same. The sensor type used is V403 or V404 tri-axial force-balance accelerometer with a natural frequency of 450 Hz and damping factor of 0.707. The sampling rate for stations recorded by K-NET and KiK-net are 100 and 200 samples per second respectively [58].
2.3. Source parameters
To carry out simulations for an earthquake, the main set of inputs are, the source file containing the moment magnitude, hypocentral location in latitude and longitude, and fault geometry, the station file containing longitude, latitude, station code and shear wave velocity VS30 for all the stations. VS30 is the average shear wave velocity in the top 30 m of the subsurface profile. Apart from these, the platform also need the 3-component acceleration time histories of real accelerograms for generating comparison plots between recorded and synthetic data.
The seismic moment, strike, dip, and rake are fixed to be 4.46 × 1026 dyne-cm, 128o, 74o and –14o based on global CMT. The fault dimensions, the location of hypocentre and depth to the top of fault for the Kumamoto-Shi, Japan earthquake are fixed to be 42 km in length and 18 km wide, –12 km and 11 km along strike and dip, and 2 km respectively based on Asano and Iwata [59]. The fault of size 42 × 18 km is discretised into 2 × 2 km size sub-faults (189 in total), and the slip weights are obtained from Asano and Iwata [59] for this earthquake. The stress drop is fixed based on different trial simulations made between values from 75 to 125 bars until a better match for residuals were obtained. The stress drop of 114 bars gave best results which was used for validation with a new set of data [60]. The sub source window is selected as Saragoni-Hart taper window for time-modulating Gaussian white noise. The epsilon and eta values of the tapered window are fixed as 0.35 and 0.15 respectively. The velocity with which the rupture propagated during this event, rupture velocity (Vrup) is obtained from literature as 2.4 km/s [59]. The sub surface structure of entire Japan had been digitalized and available on J-SHIS (Japan Seismic Hazard Information Station) website [61]. The shear wave velocity (Vs), density is obtained from the website for southwest Japan region as 3.41 km/s and 2.75 g/cm3 respectively and the ratio of Vrup/Vs
~0.7. The rise time is taken as the inverse of sub source corner frequency (1/f0). The pulsing percentage is the maximum percentage of the fault that may be active at any time which describes how much the fault plane is slipping at any moment in time. It is assigned a large aleatory variability from 10% to 90%. This parameter does not exert a significant influence on simulated amplitudes at most frequencies [57]. A median value of 50% has been assumed while running simulations.
The total path duration is calculated based on Edwards and Rietbrock [62] as t={9.52+0.8∗R,R≤50km49.52+0.02∗(R−50),R>50km.
2.4. Path parameters
The geometric spreading parameter for southwest Japan region is taken from literature Edwards and Rietbrock [62] as G={1R,R≤30 km1R1.27,30≤R≤110 km1R1.59,R>110 km and quality factor for the region of study is taken from Petukhin et al. [63] as Q = 180 f0.7.
2.5. Site parameters
H/V ratio method even though does not capture the entire site amplification but only predominant frequency, it fairly predicts the amplification of a site, especially for the sites in the proximity of the epicenter. In the absence of a reference rock-site stations or bore hole arrays, the H/V ratio serves as a practical alternative to the standard site amplification estimation A(f) [64,65,66,67]. The overall site effects term, site (f) is obtained by multiplying A(f) with near-surface attenuation term, D(f) = e−πKvf. Where Kv is Kappa factor, which characterizes near-surface attenuation [68].
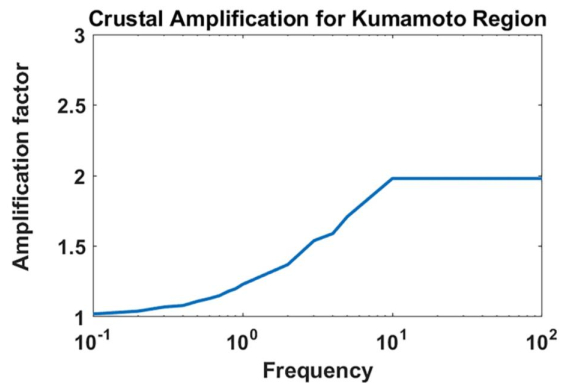
The crustal amplification factors were worked out with the regional velocity model for Kumamoto region from J-SHIS website [61] using quarter wavelength technique, and the variation of crustal amplification factor with frequency is shown in Figure 2.
Kappa value is fixed as 0.035 based on Chen and Atkinson [69]. The response spectra are computed at 5% damping. Time step is fixed as 0.01 as per the observational data. Finally, VS30 values were obtained from site data application (1.3.2) developed by the University of Southern California and OpenSHA.org based on the topographic slope [70]. The input parameters included for running the simulation are given in Table 1.
Table 1. Source, path and site parameters of the 15 April 2016 Kumamoto-Shi Japan earthquake simulation.
| Source |
| Magnitude (Mw) |
7.0 |
| Fault geometry |
42 × 18 Km |
| Slip model |
Slip weights from Asano and Iwata (2016) |
| Slip model seed |
platform-specified |
| Subsource size |
2 × 2 Km |
| Stress Drop |
75–125 bars |
| Subsource window |
Saragoni-Hart (ε = 0.35, η = 0.15) |
| Vrup/Vs |
0.7 |
| Rise time |
1/fo |
| Pulsing % |
50% |
| Subsource duration, t |
= 9.52 + 0.8 × R R up to 50 km = 49.52 + 0.02 (R–50) R > 50 km |
| Path |
| Geometric spreading |
R–1 up to 30 km and R–1.27 between 30 and 100 km and R–1.59 beyond 110 km |
| Anelastic attenuation |
Q(f) = max (150,180 f0.7) |
| Shear wave velocity |
3.41 km/s |
| Density |
2.75 g/cc |
| Site |
| Site amplification crustal amplification |
Average of H/V ratios for all stations |
| Kappa |
0.035 (high-frequency fall off slope) |
The details of the station name, latitude, longitude, epicentral distance and VS30 values are given in Table 2.
Table 2. Station metadata for the simulated stations of 15 April 2016 Kumamoto-Shi Japan earthquake.
| Sl.No. |
Name of the Station |
Station Code |
Longitude |
Latitude |
Epicentral distance (km) |
Vs 30 (m/s) |
| 1 |
CHIKUSHINO |
FKO009 |
130.5163 |
33.4952 |
85.67 |
370.5520 |
| 2 |
AMAGI |
FKO010 |
130.6689 |
33.4235 |
75.08 |
420.5705 |
| 3 |
UKIHA |
FKO012 |
130.7939 |
33.3319 |
64.46 |
444.0663 |
| 4 |
YAME |
FKO013 |
130.5607 |
33.2252 |
55.78 |
258.9047 |
| 5 |
IZUMI |
KGS002 |
130.3519 |
32.0916 |
83.03 |
285.5654 |
| 6 |
YAMAGA |
KMM002 |
130.6846 |
33.0185 |
30.40 |
333.2913 |
| 7 |
HITOYOSHI |
KMM016 |
130.7757 |
32.1966 |
61.90 |
365.9602 |
| 8 |
TARAGI |
KMM017 |
130.9257 |
32.2561 |
57.36 |
283.7520 |
| 9 |
SHINWA |
KMM020 |
130.1807 |
32.3636 |
69.61 |
420.0199 |
| 10 |
AMAKUSA |
KMM021 |
129.9997 |
32.3793 |
82.67 |
389.8910 |
| 11 |
TAKACHIHO |
MYZ001 |
131.3089 |
32.7050 |
51.45 |
394.2328 |
| 12 |
NANGOH |
MYZ004 |
131.3339 |
32.3889 |
67.19 |
520.2060 |
| 13 |
EBINO |
MYZ009 |
130.8110 |
32.0461 |
78.76 |
197.8679 |
| 14 |
KOBAYASHI |
MYZ010 |
130.9721 |
31.9968 |
86.40 |
317.7205 |
| 15 |
SHIIBA |
MYZ020 |
131.1470 |
32.4550 |
48.99 |
613.0866 |
| 16 |
KUCHINOTSU |
NGS014 |
130.1849 |
32.6106 |
56.30 |
323.1902 |
| 17 |
AMAGASE |
OIT008 |
131.0203 |
33.2555 |
60.87 |
447.1545 |
| 18 |
KARATSU |
SAG002 |
129.9195 |
33.4247 |
108.38 |
468.9557 |
| 19 |
FUJI |
SAG003 |
130.2074 |
33.3730 |
86.19 |
524.8462 |
| 20 |
KASHIMA |
SAG008 |
130.0996 |
33.1038 |
73.12 |
340.2311 |
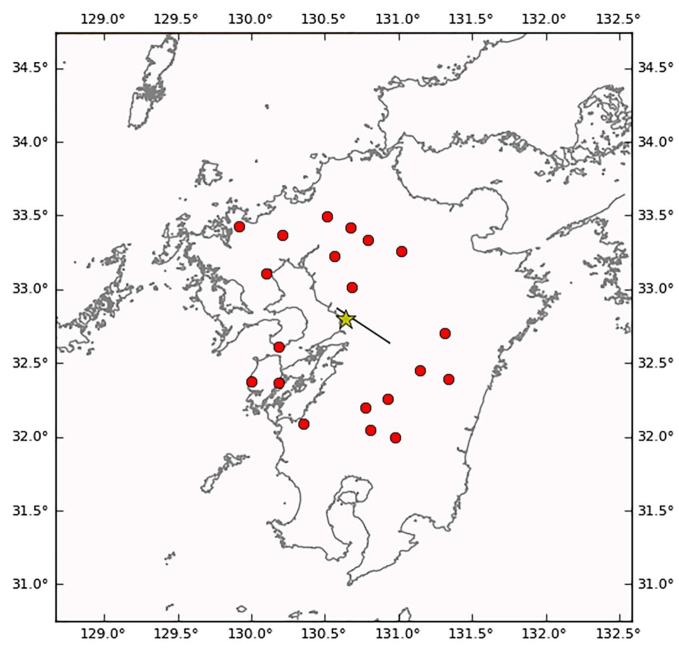
Observational data from 20 stations were used in running simulations. A map view of the simulation region showing the locations of recording stations used in the simulation along with fault plane and epicenter are shown in Figure 3.
3. Results and discussions
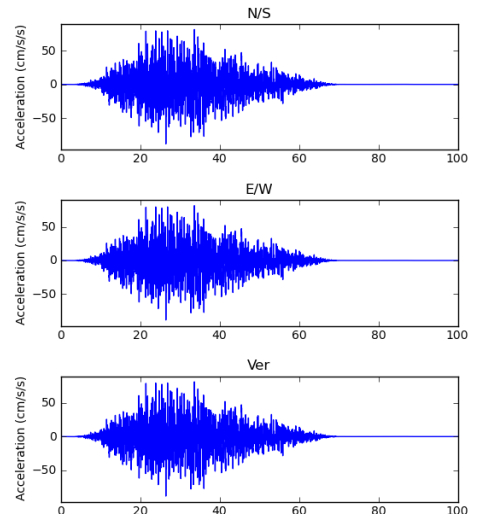
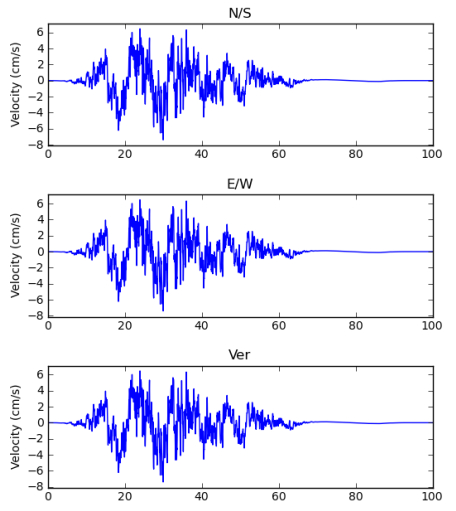
Simulations for 15 April 2016 Kumamoto-Shi Japan earthquake, were run with EXSIM method. Figures 4 and 5 shows the simulated acceleration and velocity time histories respectively along N-S, E-W, and U-D, at sample station Taragi, generated by the platform.
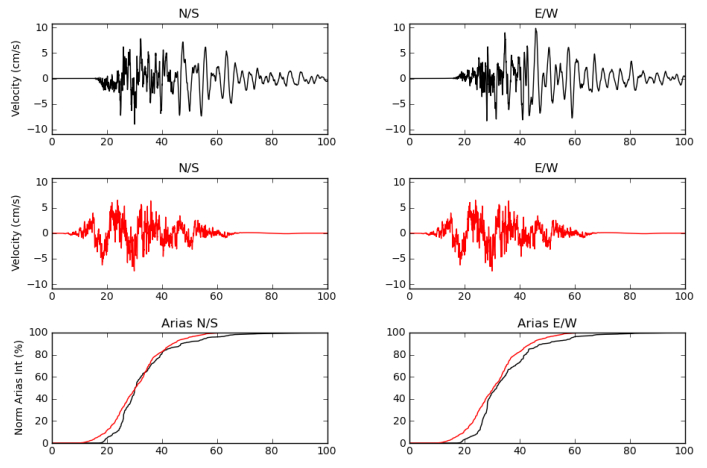
A combined plot showing the actual data and the synthetic velocity time series along with the Husid plot (normalized Arias intensity as a function of time) along the two horizontal directions are generated for each station to make sure the waveforms look reasonably well. The plot for a sample station, Taragi is shown in Figure 6. The plot in Black colour corresponds to actual data, and in red corresponds to synthetic data. The normalized Arias intensity plot shows a good resemblance of synthetics produced by the BBP with the actual data.
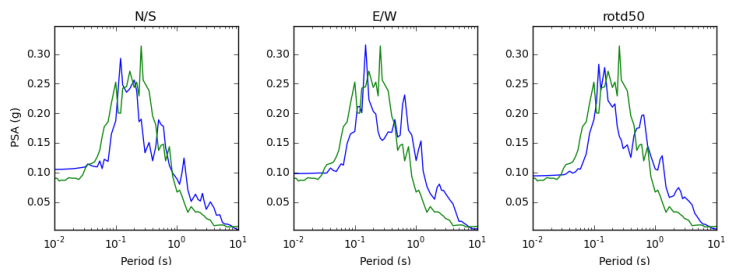
The BBP calculates response spectra for the two horizontal components, and RotD50 [71] (which is an average median horizontal component Pseudo Spectral Acceleration (PSA)) for periods ranging from 0.01 to 20 seconds. Figure 7 shows the comparison of PSA spectra (5% damping) for the simulated time-series against that of the recordings of Kumamoto-Shi earthquake, calculated by RotD50 module for N-S, E-W directions, and the RotD50 component for the Taragi station. The blue line indicates actual data and green line for synthetic data. The response spectra of simulated time histories are in good compliance with those of actual data.
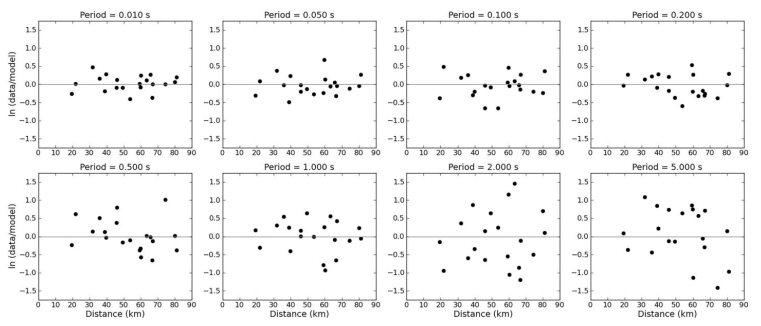
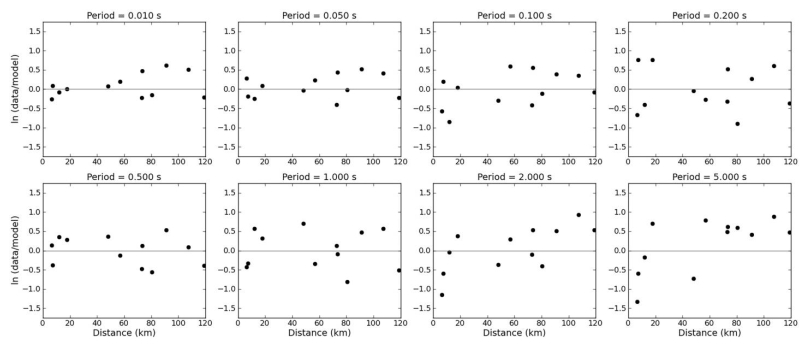
Along with this, the platform also generates several GoF comparisons. The prime comparison is a residual plot also known as distance-based GoF plot. The residual here is defined as the natural logarithm of the ratio of PSA of observed to PSA of synthetic data computed by RotD50 module for a given period. Residuals are computed for 112 time periods (between 20 to 0.01 sec.) and are plotted as a function of hypocentral distance for a subset of eight (0.01, 0.05, 0.1, 0.2, 0.5, 1.0, 2.0 and 5.0 seconds) time periods (Figure 8). The residuals shown in Figure 8 for different periods are distributed around zero. Positive residuals indicate under prediction by the model, and negative residuals indicate over prediction.
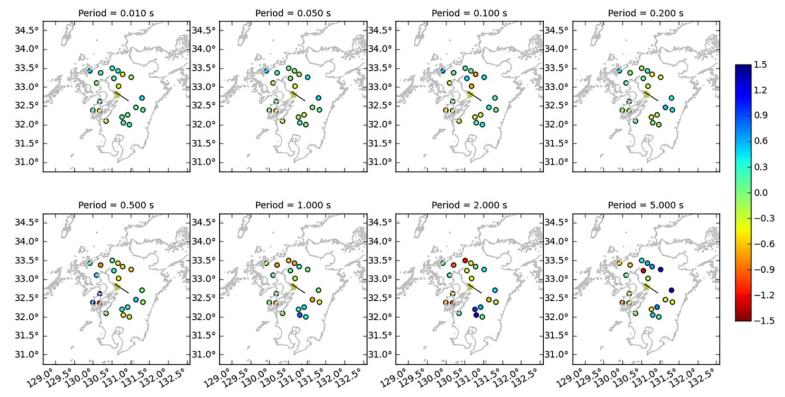
Residuals are also plotted for the same subset of time periods as a map view to identify their spatial distribution (Figure 9). Neither the residuals in Figure 8 nor those in Figure 9 seem to display any pattern.
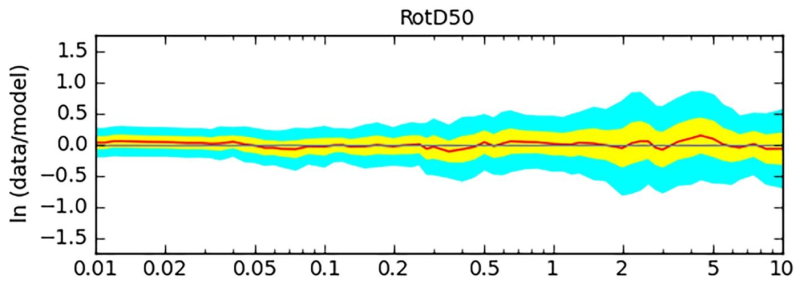
The average GoF metric computed for all stations using the RotD50 module as a function of the time period (from 0.01 to 10 seconds) is shown in Figure 10. The red line corresponds to the mean GoF over all stations of this earthquake. The narrow band in yellow, which is 90% confidence limit, indicates the mean is well constrained by data. The close proximity of the solid red curve in this plot suggests the simulations are effectively predicting the data.
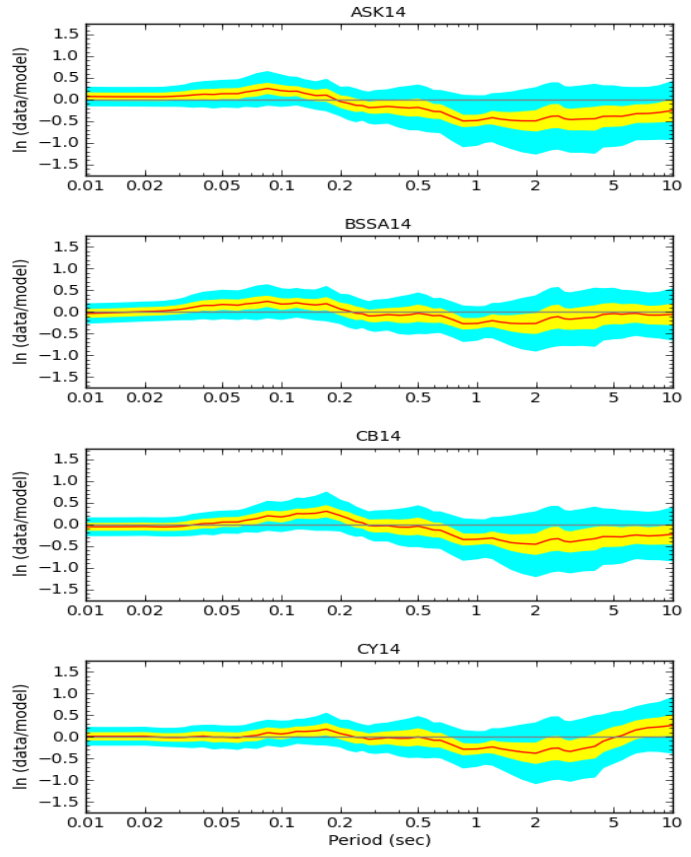
Figure 11 shows the comparison plots of the simulated data against the GMPE models existing in the BBP. The platform has 3 GMPE sets, NGA-West 1, NGA-West 2 and CENA Group 1. Out of the three GMPE sets, NGA-West 2 is predicting close to data which was shown below. 4 built-in GMPE models for NGA-West 2 was developed by Abrahamson et al. 2014 [72] (ASK14), Boore et al. 2014 [73] (BSSA14), Campbell and Bozorgnia 2014 [74] (CB14) and Chiou and Youngs 2014 [75] (CY14). Out of the four GMPE plots, the GMPE developed by Boore et al. 2014, (BSSA, 2014) is in good agreement with the synthetic data generated during simulations.
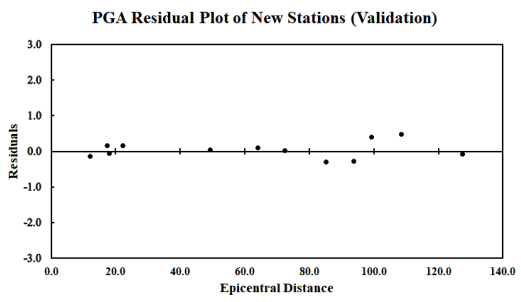
To validate the results, a new set of data from 12 stations were utilised and ran in BBP. The metadata of 12 stations along with the obtained PGA values from validation is given in Table 3 and plotted in Figure 12. The PGA residuals in the plot are close to zero line which indicates very good compliance between recorded and predicted values.
Table 3. Metadata of stations used for validation along with predicted values of PGA and computed residuals.
| Sl.No |
Station Name |
Station Code |
Longitude |
Latitude |
Epi-central distance (km) |
Vs 30 m/s |
Recorded PGA cm/s2 |
Predicted PGA cm/s2 |
Residuals ln(Recorded/Predicted) |
| 1 |
KITAKYUSHU |
FKOH01 |
130.9798 |
33.8849 |
127.5 |
395.1 |
15.5 |
16.8 |
–0.08 |
| 2 |
MIYANOJO |
KGS005 |
130.4513 |
31.9006 |
99.2 |
367.0 |
65.4 |
43.5 |
0.41 |
| 3 |
OHZU |
KMM005 |
130.8774 |
32.8761 |
17.4 |
445.3 |
482.3 |
409.8 |
0.16 |
| 4 |
UTO |
KMM008 |
130.6582 |
32.6878 |
12.1 |
213.1 |
771.1 |
883.6 |
–0.14 |
| 5 |
YABE |
KMM009 |
130.9856 |
32.6858 |
22.2 |
381.2 |
639.5 |
540.9 |
0.17 |
| 6 |
TOMOCHI |
KMM011 |
130.8652 |
32.6167 |
18.0 |
386.8 |
602.4 |
642.1 |
–0.06 |
| 7 |
TANOURA |
KMM013 |
130.5099 |
32.365 |
49.2 |
385.5 |
137.8 |
132.8 |
0.04 |
| 8 |
KAWAMINAMI |
MYZH08 |
131.5309 |
32.2132 |
93.9 |
354.8 |
28.7 |
37.8 |
–0.28 |
| 9 |
KITSUKI |
OIT007 |
131.6142 |
33.4169 |
108.4 |
322.0 |
42.5 |
26.4 |
0.48 |
| 10 |
TAKEDA |
OIT015 |
131.397 |
32.9722 |
64.1 |
289.4 |
76.6 |
69.6 |
0.10 |
| 11 |
NOTSUHARA |
OITH05 |
131.542 |
33.1525 |
85.3 |
760.0 |
31.6 |
42.5 |
–0.29 |
| 12 |
KOKONOE |
OITH11 |
131.2118 |
33.2844 |
72.5 |
462.6 |
66.6 |
65.6 |
0.01 |
Further, the residuals (Goodness-of-Fit Plot) of PSA at eight periods as a function of hypocentral distance for 12 stations is generated within BBP and shown in Figure 13. The residual at different periods shown in the plot are distributed around zero, which illustrate fair prediction of simulations conducted for Kumamoto earthquake within SCEC BBP.
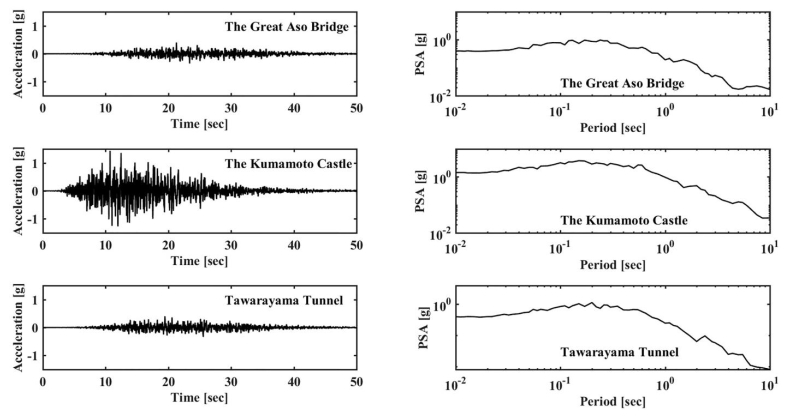
Utilizing the validated seismological model of this study, we generated acceleration time series and 5% damped PSA in the frequency range of engineering interest, at three sites: The Kumamoto castle, the Great Aso bridge and the Tawarayama tunnel, where considerable damages occurred that lacked strong-motion stations, in Kyushu region of Japan. Figure 14 shows the acceleration time series and 5% damped PSA at the selected locations.
The PGA at the Kumamoto castle is more than 1 g due to its proximity to the earthquake source. Even though the PGA of the Great Aso bridge site is considerably less that Kumamoto castle site, the landslide post-earthquake might have contributed to its significant damage. Being an underground structure, the tunnel is susceptible to slope failures, ground subsidence, liquefaction and soil-structure interaction effects during an earthquake. Hence, this signifies the importance of multi-hazard assessment on infrastructure in Japan.
These results can be employed for conducting dynamic and response spectrum analysis of structures in the damaged regions, for earthquake resistant design. Further, these results can also be utilized as inputs for evaluating liquefaction potential of soils, analysis of slope failures and landslide runout estimation, as the earthquake triggered numerous landslides in the nearby mountainous areas of Kyushu region [76].
4. Conclusions
Simulation of ground motions was conducted for the Mw 7.0 Kumamoto main shock utilising recordings at 20 stations using SCEC BBP. Residuals at several time periods are shown to be unbiased. Additionally, the spatial variation of residuals at low to high time periods doesn't exhibit any pattern. Furthermore, the goodness-of-fit at all time-periods for the average horizontal is obtained close to zero. The BSSA 14 appears to have better agreement with the data, more so for shorter periods (periods less than 1 sec) where response spectrum usually exhibits peak values.
Validation exercise is run for a new set of data to check the accuracy of Kumamoto earthquake simulations. Finally, we generated ground motions for three severely damaged locations of Kyushu region in Japan, the Kumamoto castle, the Great Aso Bridge and the Tawarayama tunnel, with the validated seismological model. The ground motions obtained can be considered as input for dynamic, response spectrum analysis of structures, liquefaction potential of soils, stability analysis and landslide runout estimation of slopes.
Acknowledgments
The authors thank the anonymous reviewer of the paper for his constructive comments and suggestions for improving the manuscript. We would like to extend our gratitude to Japan's nation-wide strong-motion seismograph network K-NET and KiK-net for making the data available online. We also thank National Institute for Earth Science and Disaster Resilience (NIED) for sharing digital data of the sub surface structure of entire Japan at J-SHIS website. This study is funded by SERB/F/9146/ 2017-2018.
Conflicts of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: