1. Introduction
MicroRNAs (miRNAs) are small non-coding RNA molecules discovered in the early nineties in nematodes [1] and repeatedly shown to play a crucial role in regulation of gene expression in various animal models [2] and human diseases [3,4,5]. MiRNAs mainly exert their function as negative regulators by binding in a sequence-specific manner to miRNA recognition elements (MREs) particularly in the 3' untranslated region (UTR) of a target mRNA and thus preventing mRNA translation [6]. In animals, the miRNA::mRNA base-pairing is usually limited to the so-called "seed region", i.e., the miRNA sequence (often between the 2nd and the 8th nucleotide) that provides most of the pairing specificity [7]. The mRNA region complementary to the miRNA seed is called "seed match" and its genetic alteration could have important phenotypic consequences in terms of risk of developing cancer [8], myocardial infarction [9] and chemo-resistance [10]. The identification of the miRNA:mRNA pairing has been widely addressed using publically available bioinformatics tools followed by experimental validation [11].
We and other research groups have previously identified several miRNAs targeting CFTR (Cystic Fibrosis Transmembrane conductance Regulator) mRNA that encodes for an ATP-regulated anion channel present on the apical surface of epithelial cells [12,13,14,15,16,17,18]. Mutations in the CFTR gene are the primary cause of cystic fibrosis (CF), a life-threatening disorder characterised by chronic airway inflammation and infection. CF is the most common lethal genetic disease among the Caucasian population, with 1 in 3000 newborns found to be affected by CF worldwide [19]. Although about 2000 CFTR mutations have been identified, only 281 have been confirmed as CF-causing to date, including ΔF508, G542X, G551D and W1282X [20].
MiRNA expression has been reported to be altered in CF patients, thereby affecting several biological processes such as ion conductance, endoplasmic reticulum stress, inflammation and infection [21]. In particular, we and others have shown that several miRNAs targeting CFTR were up-regulated in CF bronchial brushings [15] and CF primary cultures [17]. Although different experimental situations were investigated, such as the use of different cell lines and examining response to cigarette smoke, miR-101, miR-145, miR-223, miR-494 and miR-509-3p have been repeatedly implicated in many studies, strongly highlighting their roles in regulating CFTR expression [12,13,14,15,16,17,18]. In addition to these miRNAs, data from our previously published miRNA profiling indicate miR-143 as a potential regulator of CFTR mRNA. Its levels are increased in CF vs. non-CF bronchial brushings [22], and there are two potential miR-143-5p binding sites in the CFTR 3'UTR. In this article, we confirmed the up-regulation of miR-143-5p in CF cell lines and tested the hypothesis that miR-143-5p regulates CFTR expression via binding sites on CFTR 3'UTR.
2. Materials and methods
2.1. Cell culture and treatments
Non-CF (16HBE14o-) and CF (CFBE41o-, genotype ΔF508/ΔF508) human bronchial epithelial cells were kindly donated by D. Gruenert (California Pacific Medical Centre Research Institute, San Francisco, CA, USA) and maintained in MEM+Glutamax (Gibco) with 10% fetal calf serum (FCS; Gibco) and 1% penicillin–streptomycin (Pen-Strep; Gibco). IB3 cells are ΔF508/W1282X CF bronchial epithelial cells, S9 are their isogenic non-CF counterpart and both were obtained from Pamela Zeitlin (Johns Hopkins Children's Centre, Baltimore, MD, USA) and cultured in LHC-8 medium (Gibco) with 5% FCS and 1% Pen–Strep. Non-CF (Nuli-1) and CF (Cufi-1, genotype ΔF508/ΔF508) human bronchial epithelial cells were received as a gift from Prof Zabner (University of Iowa, USA) and grown in Bronchial Epithelium Basal Medium (BEBM, Lonza) supplemented with BEGM SingleQuots Kit (Lonza, containing epidermal growth factor, hydrocortisone, bovine pituitary extract, transferrin, bovine insulin, triiodothyronine, epinephrine, retinoic acid), gentamicin (Gibco, 10 µg/mL), and amphotericin B (Gibco, 1.25 µg/mL).
For cell treatments, bronchoalveolar lavage (BAL) fluid was recovered from CF patients (n = 6, mean ± SD age 28 ± 12 years, male:female 3:3) as previously reported in [23,24] and pooled for experiments. CF individuals were confirmed by sweat testing and/or genotyping and are listed in online Supplementary Table S1. After 24-h serum starvation, CF cells (CFBE41o-, IB3 and Cufi-1) seeded in 24-well plates (100,000 cells/well) were treated with 1% CF BAL fluid (10 µL/mL) or 1% saline solution (0.9% w/v NaCl) for a further 20 hours in medium containing 1% FCS. RNA was extracted for miRNA expression analysis performed with quantitative real-time PCR (qRT-PCR). Three independent experiments were carried out in duplicate for each cell line.
For luciferase assays, the human embryonic kidney cell line HEK293 was obtained from the European Collection of Cell Cultures (Salisbury, UK) and maintained in DMEM (Lonza) with 10% FCS and 1% Pen-Strep.
All the cell lines were maintained in a humidified incubator at 37 ℃ in 5% CO2.
2.2. miRNA qRT-PCR
RNA from CF and non-CF cell lines (n = 6 for each cell line) was purified by using Tri-Reagent (Sigma Aldrich) according to the manufacturer's instructions and its purity and concentration were measured using a Nanodrop 8000 (ThermoFisher Scientific). Tri-Reagent was also used to extract RNA from CF cells treated for 20 hours with 1% CF BAL fluid/1% saline solution. The TaqMan® MicroRNA Reverse Transcription Kit (ThermoFisher Scientific) was employed for reverse transcription using stem-loop specific miRNA primers starting from 100 ng of total RNA. Expression of miR-143-5p (assay ID: 002146) was measured using a pre-designed TaqMan MicroRNA assay (ThermoFisher Scientific) on the LC480 LightCycler (Roche). In each well, 1.33 μL of cDNA were added to the reaction mixture which consisted of 7.67 μL of deionized H2O, 1 μL of specific TaqMan Assay probe and primer mixture, and 10 μL of TaqMan® Universal Master Mix Ⅱ NO UNG (ThermoFisher Scientific). Each sample was run in triplicate with the following the thermocycling conditions: 10 min at 95 ℃ followed by 40 cycles of 15 s at 95 ℃ and 60 s at 60 ℃. Expression of miR-143-5p relative to U6 snRNA (assay ID: 001973) was determined using the 2(–ΔΔCt) method [25].
2.3. Plasmid construction and dual-luciferase assay
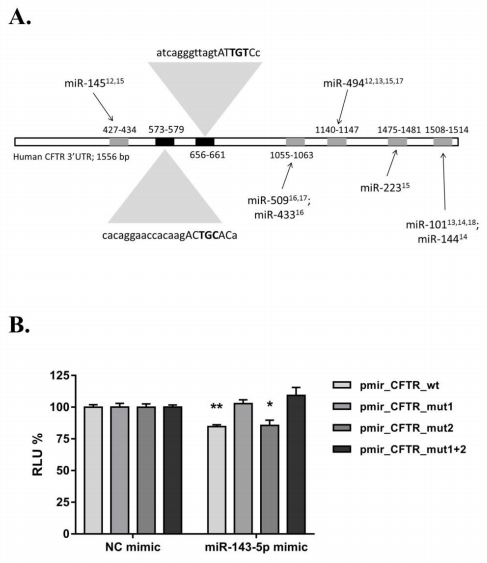
In silico prediction analyses for miR-143-5p binding sites on the CFTR 3'UTR were performed with TargetScan 7.1 (release June 2016, [26]), miRanda (release August 2010, [27]) and RNA22 [28] software.
The full length of the human CFTR 3'UTR (1556 bp) was amplified by Q5 high-fidelity DNA polymerase (NEB) from DNA extracted from a healthy individual without CF. The PCR amplicon was subsequently purified with Wizard® SV Gel and PCR Clean-Up System (Promega) and cloned into the XhoⅠ site of the pmirGLO vector (Promega) using CloneEZ PCR Cloning Kit (GenScript), downstream to the luciferase reporter gene sequence. The plasmid carrying the wild-type (wt) sequence of CFTR 3'UTR is now on referred as "pmir_CFTR_wt". Plasmids were isolated from bacterial cultures with Plasmid Midi Kit (Qiagen). Subsequent mutagenesis reactions aimed to disrupt the miR-143-5p binding sites within the 3'UTR sequence were performed using with QuikChange Ⅱ Site-Directed Mutagenesis Kits (Agilent) and screened with allele-specific oligonucleotide PCR (ASO-PCR). Three mutant plasmids were generated: two single mutants in which the first (starting at residue 558 of CFTR 3'UTR, wt: cacaggaaccacaagACTGCACa, mutant: cacaggaaccacaagACGAAACa) or the second (starting at residue 644 of CFTR 3'UTR, wt: atcagggttagtATTGTCc, mutant: atcagggttagtATCACCc) miR-143-5p site is mutated and one in which both miR-143-5p sites are mutated (a double mutant). The three plasmids are now on referred as "pmir_CFTR_mut1",
"pmir_CFTR_mut2" and "pmir_CFTR_mut1+2". The fidelity of the resulting constructs was confirmed by sequencing, using the pmirGLO external primers. The sequence of cloning, mutagenesis and sequencing primers is reported in Supplementary Table S2.
In luciferase assay experiments, HEK293 cells were seeded in a 96-wells plate at a final density of 10,000 cells/well and incubated for 24 hours. Cells were then co-transfected with 100 ng of pmir_CFTR_wt/mut1/mut2/mut1+2 and 100 nM of miR-143-5p mimic or negative control mimic (ThermoFisher Scientific, assay ID MC12540 and 4464058, respectively). Transfection mixes were prepared in Optimem reduced-serum media (Gibco) using Genejuice and Ribojuice (Novagen) as transfection reagents for plasmid DNA and miRNA mimics, respectively. Luciferase activity was assessed at 24 hours after transfection using Dual-Luciferase Reporter Assay (Promega) according to the manufacturer's instructions. Briefly, cells were washed with PBS and harvested with 20 μL of passive lysis buffer (PLB 1x). Firefly luciferase activity was measured by adding LAR Ⅱ buffer to the cell lysates in a white 96-wells plate. Then, Stop & Glo reagent was added and the Renilla luciferase activity, used as normaliser for cell number and transfection efficiency, was assessed. RLU (relative luciferase units) expressed as mean value of the firefly luciferase/Renilla luciferase ratio of three independent experiments performed in triplicate were used for statistical analyses.
2.4. Statistical analysis
All statistical analyses were performed using GraphPad PRISM 7.0 (San Diego, CA). Results are expressed as the mean ± standard error of the mean (SEM) and were compared by Student's t test or ANOVA, as appropriate. Differences were considered statistically significant when P ≤ 0.05.
3. Results
3.1. miR-143-5p is overexpressed in CF airway epithelial cells and the levels increase in response to treatment with the CF BAL fluid
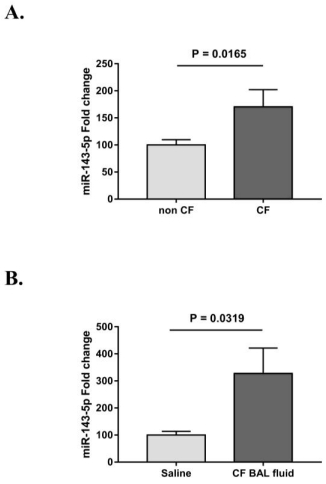
We previously reported that levels of miR-143 are increased 2.3-fold in CF vs. non-CF bronchial brushings (p = 0.049, n = 5 each) [22]. Here, we aim to determine whether matched immortalised CF and non-CF bronchial epithelial cell lines represent useful models to recapitulate our in vivo findings. We first compared the basal expression of miR-143-5p in matched pairs of CF vs non–CF cell lines. MiR-143-5p levels were trending upwards in each of the three CF cell lines versus their non-CF counterparts (Supplementary Figure S1). Overall miR-143-5p expression in CF versus non-CF cells was significantly increased by 1.7-fold (Figure 1A).
Moreover, in order to assess whether the highly inflamed environment of CF lungs affected miR-143-5p expression in vitro, CF cells were treated for 20 hours with CF BAL fluid or saline solution (as control vehicle) prior to RNA extraction in three independent experiments. We observed an increasing trend for miR-143-5p expression in all cell lines following treatment with CF BAL fluid (Supplementary Figure S2), and overall the fold-increase was 3.3 (Figure 1B).
3.2. miR-143-5p mediates repression of the CFTR 3'UTR via one binding site
In order to assess the ability of miR-143-5p to regulate CFTR expression, we employed publically available software to identify putative MREs in the CFTR 3'UTR. TargetScan 7.1 and miRanda identified the same binding site, starting at residue 558 (seed match 573–579) of the CFTR 3'UTR, while RNA22 predicted a second binding site starting at residue 644 (seed match 656-661), as shown in Figure 2A. Site-directed mutagenesis was successfully performed in order to disrupt these MREs and an example of post-mutagenesis screening with ASO-PCR is provided in Supplementary Figure 3.
For luciferase assays, HEK293 cells were transiently transfected with a luciferase reporter plasmid containing the full length of wild type CFTR 3'UTR or with the same plasmid where the MREs were mutated to assess whether CFTR is a true target of miR-143-5p. Transfection efficiency was normalised between wells by measuring the activity of the internal control reporter Renilla and by using RLU values in the statistical analyses. Cotransfection with miR-143-5p mimic resulted in a significant decrease (minus (–)15%) of luciferase activity, expressed as RLU, in the pmir_CFTR_wt plasmid when compared to the negative control (NC) mimic cotransfected wells (Figure 2B). Interestingly, mutations of the first but not the second MRE abolished the inhibitory effect of miR-143-5p on the luciferase activity. When both the sites were mutated, miR-143-5p was not able to decrease luciferase activity, suggesting that the disruption of the first MRE was necessary and sufficient to rescue the miRNA-mediated repression of the reporter activity.
4. Conclusions
In this paper, we observed increased levels of miR-143-5p in CF versus non-CF cell lines and we proved that it directly targets CFTR 3'UTR through a binding site starting at residue 558. In detail, unstimulated CF cell lines expressed significantly higher basal levels of miR-143-5p when compared with their non-CF counterparts, and the increase was even more evident when CF cell were treated with CF BAL fluid, suggesting that the inflamed environment of CF lungs could trigger the upregulation of miR-143-5p (Figure 1). The detailed mechanism is currently unknown and beyond the scope of this study. We have previously shown that proinflammatory mediators such as Pseudomonas conditioned media or IL-1β (potentially present in the CF BAL fluid) could increase expression of CFTR-targeting miRNAs [15]. Similarly, increased levels of miR-509-3p and miR-494 were observed by Ramachandran et al. when treating non-CF airway epithelia with the proinflammatory cytokines TNF-α and IL-1β [17]. Overall, these findings suggest that CF airway epithelial cells, especially when treated with ex vivo CF stimuli, can recapitulate our in vivo findings about the upregulation of miR-143.
Luciferase reporter assay is considered the most reliable technique to identify functional MREs within 3'UTRs [29]. Here we observed a decrease in luciferase activity after transfection of miR-143-5p mimic from the reporter plasmid carrying the wild-type CFTR 3'UTR suggesting that this miRNA directly regulates CFTR. The site-directed mutagenesis is necessary to determine whether the predicted binding sites are functional, and our results showed that the MRE starting at residue 558 was actually active, as its disruption led to a rescue of the reporter activity inhibition by miR-143-5p mimic. According to our data, the second site (starting at residue 644) was not active, showing once again that bioinformatic target prediction can give false positive results, and experimental validation is ultimately required to truly determine miRNA::mRNA binding and biological function.
MiR-143 is located in the 5q32 chromosomal region and it has been previously identified as tumour suppressor in several types of cancer [30]. In particular, miR-143-5p inhibits cell proliferation, migration and invasion in gallbladder cancer targeting HIF-1α, ultimately preventing the epithelial-to-mesenchymal transition [31]. Similar anti-tumorigenic properties were observed in gastric cancer where miR-143-5p induced apoptosis directly targeting COX2 [32].
Beyond the importance of describing the regulators of CFTR expression, identifying cognate miRNAs could have valuable therapeutic effects. Over the past decades, therapies for CF aimed to cure the symptoms of the disease rather than its primary cause. Ivacaftor (VX-770) has been approved for marketing in Europe and the USA for CF patients carrying the G551D mutation (and the other mutations recently added [33]) as the first drug targeting the actual CFTR dysfunction [34]. In order to correct the CFTR misfolding due to ΔF508 mutations, a new molecule called lumacaftor (VX-809) has been developed but its administration in clinical trials did not provide significant benefits for ΔF508/ΔF508 CF patients [35]. Even the combination of VX-770 and VX-809 led only to modest improvement of the respiratory function in phase Ⅱ [36] and Ⅲ [37] clinical trials in ΔF508/ΔF508 CF patients, suggesting an urgent need of boosting the activity of CFTR modulators. As miRNAs act upstream of correctors and potentiators, blocking miRNA-mediated CFTR repression may increase the efficacy of CFTR modulators in ΔF508/ΔF508 patients. Viart and collaborators treated nasal epithelial cells from CF patients with miRNA-binding blocker oligonucleotides (MBBOs) specifically designed to bind the MREs of several CFTR-targeting miRNAs (including miR-101 and miR-145) and found a significant increase in CFTR expression and function [18]. Very recently, Zarrilli and co-authors developed peptide nuleic acids (PNAs) in order to prevent miR-509-3p binding from its MREs on CFTR mRNA and showed that a PNA was able to rescue the miRNA-mediated inhibition in luciferase assay [38]. Altogether, these studies suggest that interfering with CFTR-targeting miRNAs represents a promising therapeutic strategy, although the combination with existing correctors or potentiators has not been explored yet.
Although further studies are necessary to establish whether miR-143-5p represents a valuable miRNA for future therapeutic studies in CF, here we suggest another functional MRE in the CFTR 3'UTR worthy to be investigated. The mapping of MREs on the CFTR 3'UTR could help to design combination therapies where more than one miRNA is blocked and thus a greater effect on CFTR expression could be achieved. This knowledge would not be limited to CF, but it could also potentially be applied to any disease that shows an acquired CFTR dysfunction and where modulation of CFTR could be beneficial [39,40].
Acknowledgments
The authors thank Dr Gruenert, Dr Zeitlin and Prof Zabner for the donation of CF and non-CF cell lines. The authors also thank Dr Kevin Molloy for the collection of the CF BAL fluid employed in this article. This work was supported by Cystic Fibrosis Foundation Therapeutics.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: