1. Introduction
Brucellosis, also called Malta fever, is a highly contagious zoonosis caused by bacteria of the genus Brucella and is one of the most wide-spread infectious diseases in the world. Brucellosis is rarely fatal and the mortality of livestock due to the disease is practically zero. But brucellosis has important impacts on the livestock industry and the loss due to the fact that abortions can be very high if no control is applied. Human brucellosis is commonly caused by exposure to infected livestock or livestock products[32]. There is no recorded transmission of the infection among humans and they can very rarely infect animals. Human brucellosis remains the commonest zoonotic disease worldwide with more than half a million new cases annually.
The global epidemiology of the disease has drastically evolved over the past decade. Pappas et al[29] depict the global distribution of the disease before 2006 and draw a new global map of human brucellosis. The papers[4,32] describe the history and development of brucellosis in China till the early 2000s and briefly present the variation of epidemic situation, epidemiological characteristics, application of vaccines, and disease controls. After implementing comprehensive measures, great progress had been actually achieved in the prevention and control of brucellosis in China[32]. Brucellosis, however, still remains a serious public health issue. Since 1992, new foci of human brucellosis have emerged in China and the situation in certain regions is rapidly worsening, particularly in Inner Mongolia, one of the most important animal husbandry provinces of China. The brucellosis spreads all over Inner Mongolia and most of the confirmed cases are peasants and herdsmen[6]. The incidence of human brucellosis in Inner Mongolia increased from 3.42 per 100 000 in 2002 to 33.32 per 100 000 in 2006[15]. In recent years, Inner Mongolia has the largest number (40%) of new annually confirmed cases of human brucellosis in China. Most of the cases in Inner Mongolia are attributed to Brucella melitensis (sheep brucella) (92%) and then to Brucella abortus (5%) due to the rapid development of sheep farming[30]. In Inner Mongolia, some of human brucellosis cases recover to susceptible under good treatment while the others become chronic cases[41]. In particular, in rural areas, due to the lower awareness of the disease and the limited medical resources, many infected cases miss the best time to treat and become chronic cases[30,32]. The prevention and control of brucellosis require substantial financial support. So, it is necessary to find a balance between the control effectiveness and the control resources and then to formulate an optimal control strategy with the very limited support from the government.
The use of mathematical formulations and models has emerged as a means to better describe, understand and predict the dynamical properties of brucellosis evolution and provide insight into the mechanisms that lead to those dynamics[1,2,3,5,10,16,14,26,44]. Most study is based on statistical models (static study) [2,3,10,26,34]. There are also several dynamical models proposed to explore the transmission of brucellosis[1,5,14,16,44].
Most existing models of brucellosis only consider transmission within a single livestock population and the transmission to humans is rarely considered[1,5,14]. According to the domestic situation of Mongolia, Zinsstag et al[44] present a livestock-to-human brucellosis transmission model, which considers brucellosis transmission within sheep and cattle populations and spreading to humans as additive components. Based on the model, the authors[44] estimate demographic (birth rate, mortality) and transmission (contact rates) parameters between livestock and livestock to humans for cost-effectiveness analysis of a nation-wide mass-vaccination programme. Recently, Hou et al[16] propose a brucellosis transmission model, which involves sheep population, human population and brucella in the environment. The results[16] show that vaccinating and disinfecting both young and adult sheep are appropriate and effective strategy to control brucellosis in Inner Mongolia of China.
As far as we know, available dynamic models of brucellosis transmission are developed without considering the limitedness of control resources. In this study, we develop and analyze a dynamic model, which considers brucellosis transmission within sheep population and the transmission to humans as additive components, and explore the optimal control of brucellosis in resources-limited setting. The paper is organized as follows. In Section 2, a new sheep-to-human brucellosis transmission model is formulated. The global dynamics of the model is explored in Section 3 with the help of asymptotic autonomous system theory and Lyapunov direct method. Section 4 formulates a multi-objective optimization problem in resources-limited setting and then, by the weighted sum method, transforms it into a scalar optimization problem with minimizing the cost for vaccination and health education and also the incidences of brucellosis both in sheep and in human. Section 5 characterizes the effects of sheep recruitment, vaccination of sheep, culling of infected sheep, and health education on the dynamics of brucellosis and on its optimal control. The paper ends with some conclusions and enlightening discussions.
2. Model formulation
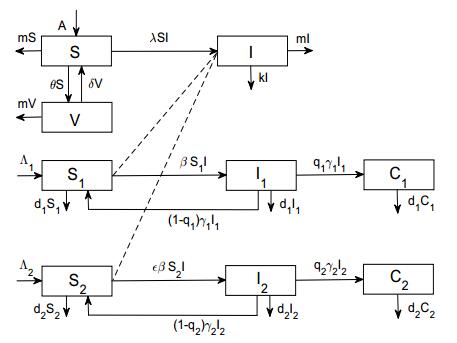
Based on the transmission characteristics of brucellosis in Inner Mongolia of P. R. China, we consider both the sheep population and the human population. The sheep population is divided into three epidemiological classes, the susceptible (S), infectious (I), and vaccinated (V). The human population consists of a high risk subpopulation (G1) and a low risk subpopulation (G2) according to the infection risk. Each human subpopulation is partitioned into three classes, the susceptible, acute human brucellosis, and chronic human brucellosis, with population size denoted by Si, Ii, Ci, i=1,2, respectively. The dynamic transfer of hosts is depicted in Fig. 1.
In sheep population, the susceptible admits effective vaccination at a constant rate θ. The influx of susceptible comes from two sources, a constant recruitment A and hosts that lost immunity δV. The natural elimination rate is assumed to be the same constant m for all the hosts and the infectious hosts suffer an extra culling with constant rate k. The incidence term is of the bilinear mass-action form λSI.
In human population, each subpopulation admits a constant recruitment Λi and natural death at a constant rate di. 1/γi denotes the acute onset period of human brucellosis. qi is the fraction of acute human brucellosis turned into chronic cases. Both incidence terms of G1 and G2 are also of the bilinear type. The per capita transmission rate of G1 is set to be β and that of G2 reads εβ with ε (0<ε≪1) being the infection risk attenuation coefficient of G2 compared to G1.
The description, unit, default value and reference resource for each parameter are given in Table 1. The default value for each of the parameters are derived from the references[8,9,27,33,41,42] on brucellosis of P. R. China.
Table 1. Parameters of model (1) with default values used for numerical studies.
| Parameter |
Value/Range |
Unit |
Definition |
Reference |
| A | 3300 | 104/year | Constant recruitment of sheep | [8] |
| m | 0.6 | year−1 | Natural elimination or death rate of sheep | [8] |
| 1/δ | [1, 3] | year | Mean effective period of vaccination | [9,33,42] |
| k | 0−50% | year−1 | Culling rate of infectious sheep | [17,35,40,41] |
| θ | [0, 0.85] | year−1 | Effective vaccination rate of susceptible sheep | [9,42,33] |
| Λ1 | 12 | 104/year | Recruitment of G1 (high risk) | [27] |
| Λ2 | 11 | 104/year | Recruitment of G2 (low risk) | [27] |
| di | 0.006 | year−1 | Natural death rate of human | [27] |
| 1/γi | 0.25 | year | Acute onset period of human | [41] |
| qi | [0.32, 0.74] | year−1 | Fraction of acute human cases turned into chronic cases | [41] |
| λ | 2.55×10−4 | year−1 | Transmission rate of sheep | Fitting |
| β | 4.895×10−6 | year−1 | Transmission rate between sheep and G1 | Fitting |
| ε | 0.17 | year−1 | Infection risk attenuation coefficient of G2 compared to G1 | Fitting |
| Note: i=1,2 |
The transfer diagram in Fig. 1 leads to the following system of differential equations
|
{dSdt=A+δV−λSI−mS−θS,dIdt=λSI−mI−kI,dVdt=θS−δV−mV,dS1dt=Λ1+(1−q1)γ1I1−βS1I−d1S1,dI1dt=βS1I−γ1I1−d1I1,dC1dt=q1γ1I1−d1C1,dS2dt=Λ2+(1−q2)γ2I2−εβS2I−d2S2,dI2dt=εβS2I−γ2I2−d2I2,dC2dt=q2γ2I2−d2C2.
|
(1)
|
3. Global dynamics of (1)
In this section, the global dynamics of (1) will be explored. By the standard next generation method [37], the basic reproduction number of (1) reads
|
R0=λ(m+δ)Am(m+k)(m+δ+θ).
|
(2)
|
It is trivial to show that the following compact feasible region
|
Γ={(S,I,V,S1,I1,C1,S2,I2,C2)∈R9+|0≤S+I+V≤Am,0≤S1+I1+C1≤Λ1d1,0≤S2+I2+C2≤Λ2d2}
|
is positively invariant with respect to (1), and (1) always has the disease-free equilibrium
|
E0=(S0,0,V0,S01,0,0,S02,0,0),
|
where
|
S0=(m+δ)Am(m+δ+θ), V0=θAm(m+δ+θ), S0i=Λidi, (i=1,2).
|
(3)
|
Follow Theorem 2 of [37], it is not difficult to reach the following claim on the stability of E0.
Theorem 3.1. The disease-free equilibrium E0 is locally asymptotically stable if R0<1, and is unstable if R0>1.
Moreover, (1) has a unique endemic equilibrium
|
E∗=(S∗,I∗,V∗,S∗1,I∗1,C∗1,S∗2,I∗2,C∗2)
|
if and only if R0>1, where
|
S∗=m+kλ, V∗=θm+δS∗,I∗=m(m+δ+θ)λ(m+δ)[Aλ(m+δ)m(m+δ+θ)(m+k)−1]=m(m+δ+θ)λ(m+δ)(R0−1),S∗1=γ1I∗1+d1I∗1βI∗, C∗1=q1γ1I∗1d1, I∗1=βΛd1I∗βq1γ1I∗+βd1I∗+d1(γ1+d1),S∗2=γ2I∗2+d2I∗2εβI∗, C∗2=q2γ2I∗2d2, I∗2=εβΛd2I∗εβq2γ2I∗+εβd2I∗+d2(γ2+d2).
|
(4)
|
Next, we explore the globally asymptotic stability of (1). The main approach involves the theory of asymptotic autonomous systems [23,36]. For the reader's convenience, we shall first summarize below a few concepts and results of asymptotic autonomous system from [23] that will be basic for the following discussion.
Consider the following differential equations
(5) is called asymptotically autonomous with limit equation (6) if
|
f(t,x)→g(x),t→∞, locally
uniformly in x∈Rn,
|
i.e., for x in any compact subset of Rn. Assume that f(t,x),g(x) are continuous functions and locally Lipschitz in x.
Lemma 3.2 ([23]). The ω-limit set Ω of a forward bounded solution x to (5) is non-empty, compact, and connected. Moreover, Ω attracts x, i.e.,
Finally Ω is invariant under (6). In particular any point in Ω lies on a full orbit of (6) that is contained in Ω.
Lemma 3.3 ([23]). Let e be a locally asymptotically stable equilibrium of (6) and Ω the ω-limit set of a forward bounded solution x of (5). If Ω contains a point y0 such that the solution y of (6), with y(0)=y0, converges to e for t→∞, then Ω={e}, i.e., x(t)→e,t→∞.
Now, consider the following sub-model of (1)
|
{dSdt=A+δV−λSI−mS−θS,dIdt=λSI−mI−kI,dVdt=θS−δV−mV.
|
(7)
|
Lemma 3.4. For system (7), we have the following claims:
(1) If R0≤1, then the disease-free equilibrium (S0,0,V0) of (7) is globally asymptotically stable;
(2) If R0>1, then the unique endemic equilibrium (S∗,I∗,V∗) of (7) is globally asymptotically stable.
Proof. (1) Consider a Lyapunov function defined by
|
L(S,I,V)=(S−S0−S0lnSS0)+(V−V0−V0lnVV0)+I.
|
Differentiating L(S,I,V) along the solutions of (7) and using the equilibrium equations A=mS0+θS0−δV0 and mV0=θS0−δV0, we obtain
|
dLdt=(1−S0S)dSdt+(1−V0V)dVdt+dIdt=(m+k)(R0−1)I+A(2−SS0−S0S)+δV0(1+VV0−SS0−S0VSV0)+θS0(1+SS0−VV0−SV0S0V)=(m+k)(R0−1)I+mS0(2−SS0−S0S)+θS0(2−SS0−S0S)−δV0(2−SS0−S0S)+θS0(1+SS0−VV0−SV0S0V)−δV0(1+SS0−VV0−SV0S0V)+δV0(1+SS0−VV0−SV0S0V)+δV0(1+VV0−SS0−S0VSV0)=(m+k)(R0−1)I+mS0(2−SS0−S0S)+mV0(3−S0S−VV0−SV0S0V)+δV0(2−SV0S0V−S0VSV0).
|
If R0≤1, then dL/dt≤0 and dL/dt=0 if and only if (S,I,V)=(S0,0,V0). Therefore, the largest compact invariant set in {(S,I,V)|dL/dt=0} is the singleton {(S0,0,V0)}. The LaSalle's invariant principle [20] implies that (S0,0,V0) is globally asymptotically stable when R0≤1.
(2) Consider the Lyapunov function
|
L(S,I,V)=S−S∗−S∗lnSS∗+I−I∗−I∗lnII∗+V−V∗−V∗lnVV∗.
|
Differentiating L(S,I,V) along solutions of (7) produces
|
dLdt=(1−S∗S)(A+δV−λSI−mS−θS)+(1−I∗I)(λSI−mI−kI)+(1−V∗V)(θS−δV−mV)=A(2−S∗S−SS∗)+δV∗(SS∗−1)(S∗VSV∗−1)+θS∗(VV∗−1)(SV∗S∗V−1)=2A+δV∗+θS∗−SS∗(mS∗+λS∗I∗)−mV−AS∗S−δVS∗S−θSV∗V=(λS∗I∗+mS∗)(2−S∗S−SS∗)+δV∗(2−S∗VSV∗−SV∗S∗V)+3mV∗(3−S∗S−VV∗−SV∗S∗V)≤0.
|
Obviously, dL/dt=0 if and only if (S,I,V)=(S∗,I∗,V∗). It implies that, when R0>1, the largest compact invariant set of the sub-model (7) in {(S,I,V)|dL/dt=0} is the singleton {(S∗,I∗,V∗)}. Therefore, the equilibrium (S∗,I∗,V∗) of (7) is globally asymptotically stable.
Theorem 3.5. For system (1), we have the following conclusions:
(1) If R0≤1, then the disease-free equilibrium E0 of (1) is globally asymptotically stable;
(2) If R0>1, then the unique endemic equilibrium E∗ of (1) is globally asymptomatically stable.
Proof. (1) Note that, the first three equations of (1) are independent of Si, Ci and Ii, i=1,2. Moreover, Lemma 3.4 asserts the globally asymptotic stability of the disease-free equilibrium for the first three equations of (1) when R0≤1.
Now, consider the rest equations of (1) except (7), that is,
|
{dS1dt=Λ1+(1−q1)γ1I1−βS1I(t)−d1S1,dI1dt=βS1I(t)−γ1I1−d1I1,dC1dt=q1γ1I1−d1C1dS2dt=Λ2+(1−q2)γ2I2−εβS2I(t)−d2S2,dI2dt=εβS2I(t)−γ2I2−d2I2,dC2dt=q2γ2I2−d2C2.
|
(8)
|
When R0≤1, one has limt→∞I(t)=0. Then, the limiting system of (8) is
|
{dS1dt=Λ1+(1−q1)γ1I1−d1S1,dI1dt=−γ1I1−d1I1,dC1dt=q1γ1I1−d1C1,dS2dt=Λ2+(1−q2)γ2I2−d2S2,dI2dt=−γ2I2−d2I2,dC2dt=q2γ2I2−d2C2.
|
(9)
|
Obviously, the linear system (9) admits a unique equilibrium (Λ1/d1,0,0,Λ2/d2,0,0) being globally asymptotically stable.}} From the theory of asymptotic autonomous systems, it follows that the disease-free equilibrium of (8) (Λ1/d1,0,0,Λ2/d2,0,0) is globally asymptotically stable.
(2) When R0>1, the limiting system of (8) is
|
{dS1dt=Λ1+(1−q1)γ1I1−βS1I∗−d1S1,dI1dt=βS1I∗−γ1I1−d1I1,dC1dt=q1γ1I1−d1C1dS2dt=Λ2+(1−q2)γ2I2−εβS2I∗−d2S2,dI2dt=εβS2I∗−γ2I2−d2I2,dC2dt=q2γ2I2−d2C2.
|
(10)
|
It is not difficult to show that the linear system (10) has an equilibrium (S∗1,I∗1,C∗1,S∗2,I∗2,C∗2) being globally asymptotically stable. By the theory of asymptotic autonomous systems, the equilibrium (S∗1,I∗1,C∗1,S∗2,I∗2,C∗2) of (8) is globally asymptotically stable.
4. Optimal control strategy
The brucellosis asserts heavy burden to human health and local economy. The government consequently has to adopt a series of measures to control the brucellosis. In theory, by the global threshold dynamics of (1), from the explicit expressions of R0 in (2) and I∗,I∗1,I∗2 in (4), it follows that R0,I∗,I∗1,I∗2 decrease with the decreasing of λ,δ,A and with the increasing of k,θ,m. That is to say, in order to control the brucellosis, it is reasonable to reduce the transmission between sheep (e.g., improve the living conditions of sheep), effectively inoculate more sheep with vaccine having long immunization period, reduce the size of sheep population, remove (cull or naturally eliminate) more infectious sheep. In the long run, all those measures benefit the control of brucellosis and should be policy suggestions. It may be so in theory, but how will it work in practice?
In reality, the financial support from the government is very limited and can not meet the real requirement of the brucellosis control. The testing of sheep brucella and the culling of infected sheep can not be sustainedly and effectively implemented in large scale[41]. Some moderate measures have been carried out to control the brucellosis such as vaccination program in sheep stock and health education in human population aiming to raise the consciousness among publics to protect against brucellosis by influencing self examination behavior.
Taking into account the serious situation of the brucellosis in Inner Mongolia and the limited financial support from the government, one has to find a balance between the loss induced by brucellosis and the cost of control effort. It is very important and reasonable to achieve the best control effect with given limited financial budget.
Optimization has been playing a key role in the design, planning and operation of infectious disease control and related processes. It is reasonable and challenging to develop optimal strategy for more effective control or treatment options of infectious diseases in resource-limited settings. Brucellosis infections and their control are a world-wide challenge due to limited available resources.
In the following, we explore the optimal control strategy for brucellosis by considering both the control effectiveness and resource limitation. According to the reality of brucellosis control in Inner Mongolia, we still take vaccination in sheep stock and health education in human population as control measures in our optimal control model. Then the vaccination rate θ, in (1), is set to be time-dependent θ(t) describing the time-varying vaccination strategy. The functions φi(t) measure the effort of health education in subpopulation Gi(i=1,2), respectively. It means that φi(t)Si(t)(i=1,2) are of susceptible who have acquired effective brucellosis prevention measures (i.e., only β(1−φ1(t))S1(t)I(t) and εβ(1−φ2(t))S2(t)I(t) susceptible are infected brucellosis in high and low risk subpopulation per unit time, respectively). Since it seems impossible to vaccinate all the susceptible sheep and to educate the entire human population due to the limited resources, it is realistic to assume that there exist ˉθ,¯φi∈(0,1) such that 0≤θ(t)≤ˉθ<1 and 0≤φi(t)≤¯φi<1,i=1,2. In the fixed time interval [0,T] with T>0, the feasible decision space or constraint set reads
|
U={(θ(t),φ1(t),φ2(t))|0≤θ(t)≤ˉθ, 0≤φi(t)≤¯φi, 0≤t≤T, θ(t)and φi(t)are Lebesgue measurable,i=1,2}.
|
(11)
|
In most real-life optimization scenarios and designs of the control of brucellosis, multiple objectives under consideration arise naturally and often conflict with each other. Anyone actually prefers to achieve best control by using less effort or cost, i.e., minimize cost, maximize performance, maximize reliability, etc. It seems very difficult but realistic.
Here our key objectives are to minimize the cost for vaccination and health education and to minimize the economic loss caused by culling of infected sheep and treatment of infected human cases. These costs during [0,T] read
|
∫T0B0S(t)θ(t)dt,∫T02∑i=1BiSi(t)φi(t)dt,∫T0D0kI(t)dt,∫T0(D1(I1(t)+I2(t))+D2(C1(t)+C2(t)))dt,
|
(12)
|
respectively, where B0 is the cost of brucellosis vaccine for each sheep, Bi is the cost of health education per unit time for subpopulation Gi(i=1,2), D0 denotes the economic loss of culling each infected sheep, D1 and D2 denote the cost of medical resources for each acute and chronic human brucellosis case respectively.
Now, we are facing with a multi-objective optimization problem
|
min∫T0D0kI(t)dt,min∫T0(D1(I1(t)+I2(t))+D2(C1(t)+C2(t)))dt,min∫T0B0S(t)θ(t)dt,min∫T02∑i=1BiSi(t)φi(t)dt,
|
(13)
|
subject to
|
dSdt=A+δV−λSI−mS−θ(t)S,dIdt=λSI−mI−kI,dVdt=θ(t)S−δV−mV,dS1dt=Λ1+(1−q1)γ1I1−β(1−φ1(t))S1I−d1S1,dI1dt=β(1−φ1(t))S1I−γ1I1−d1I1,dC1dt=q1γ1I1−d1C1,dS2dt=Λ2+(1−q2)γ2I2−εβ(1−φ2(t))S2I−d2S2,dI2dt=εβ(1−φ2(t))S2I−γ2I2−d2I2,dC2dt=q2γ2I2−d2C2,(θ(t),φ1(t),φ2(t))∈U,
|
(14)
|
with initial conditions
|
0≤S(0)≤M,0≤I(0)≤M,0≤V(0)≤M,0≤Si(0)≤M,0≤Ii(0)≤M,0≤Ci(0)≤M, i=1,2,
|
(15)
|
where M is a positive constant.
In term of methodology, there are several different approaches to solve general continuous multi-objective optimization problems[24]. One of the most common approaches is in general known as the weighted sum or scalarization method, which minimizes a positively weighted convex sum of the objectives by combining its multiple objectives into one single-objective scalar composite function with equal or weighted treatment.
By the weighted sum method, we transformed the vector-valued optimization problem (13)-(15) into a scalar quadratic optimization problem with a unique objective function of the following form
|
J(θ(t),φ1(t),φ2(t))=∫T0[ω1(D0kI(t))2+ω2((D1(I1(t)+I2(t)))2+(D2(C1(t)+C2(t)))2)+ω3(B0S(t)θ(t))2+ω4∑2i=1(BiSi(t)φi(t))2]dt,
|
(16)
|
subjected to (14), (15), and 4∑i=1ωi=1, ωi∈[0,1]. Here, the objective function J(θ(t),φ1(t),φ2(t)) measures the total economic loss caused by the brucellosis.
To facilitate the discussions below, let X=(S,I,V,S1,I1,C1,S2,I2,C2)′, u=(θ(t),φ1(t),φ2(t))′, F(t,X,u)=(f1,f2,...,f9)′, where the prime represents the transpose of a row vector and fi is the i-th right-hand side function of (14). Then the above single objective optimization problem rewrites
|
min(θ(t),φ1(t),φ2(t))∈UJ(θ(t),φ1(t),φ2(t)),
|
(17)
|
subject to
|
dXdt=F(t,X,u), X(0)≥0,
|
(18)
|
where ‖X(0)‖≤3M and ωi∈[0,1] such that 4∑i=1ωi=1.
In the optimal control theory, after formulating the model and the corresponding objective functionals appropriate to the scenarios, one has to explore several basic problems such as proving the existence of an optimal control and characterizing the optimal control. In order to prove the existence of an optimal control, we introduce the following conclusion ([12], Theorem 4.1 and Corollary 4.1).
Lemma 4.1. Consider the optimal control problem
|
minu∈DJ(u)=minu∈D∫t1t0L(t,x,u)dt+ϕ(e)
|
subject to dxdt=f(t,x,u) with e=(t0,t1,x(t0),x(t1))∈S⊂R2n+2, where L(t,x,u):R1×Rn×Rm→R1, ϕ(e):R1×R1×Rn×Rn→R1, and f(t,x,u):R1×Rn×Rm→Rn are continuous and f(t,x,u) satisfies Lipschitz property with respect to x, D={u(t)=(u1(t),u2(t),...,um(t)):ui(t)is Lebesgue measurable on [t0,t1],i=1,2,...,m}. Assume that, (i) f(t,x,u) is C1, the partial derivatives of f(t,x,u) and f(t,0,0) are bounded, (ii) The set of control u and corresponding state variable x is non-empty, (iii) D is closed, (iv) S is compact and ϕ is continuous on S, (v) There exist constants C1>0, C2, and γ>1 such that L(t,x,u)≥C1|u|γ−C2, (vi) D+={(n,m)|∃v∈D,m=f(t,x,v), n≥L(t,x,v)} is convex for (t,x). Then there exists an optimal control u∗∈D.
Theorem 4.2. There exists an optimal pair (u∗,X∗) such that
|
J(θ∗(t),φ∗1(t),φ∗2(t))=min(θ,φ1,φ2)∈UJ(θ(t),φ1(t),φ2(t))
|
subject to (18), where u∗=(θ∗(t),φ∗1(t),φ∗2(t)) is the optimal control, X∗=(S∗(t), I∗(t), V∗(t), S∗1(t), I∗1(t), C∗1(t), S∗2(t), I∗2(t), C∗2(t)) is the state solution corresponding to the optimal control.
Proof. It suffices to show that the conditions of Lemma 4.1 are satisfied with ϕ(0,T,X(0),X(T))=0 since (17)-(18) is a special case of the optimal control problem in Lemma 4.1 with ϕ(e)≡0.
The claim (i) of Lemma 4.1 follows from the properties of F(t,X,u) and the state variables of (18). The existence of solutions of (18) with u∈U is guaranteed by Theorem 9.2.1 in [19], which implies (ii) of Lemma 4.1. The constraint set U is closed and convex since u∈U is bounded and Lebesgue measurable (i.e., L∞ bound hold). (iv) of Lemma 4.1 holds due to ϕ(0,T,X(0),X(T))=0 and the set of X(0) is bounded and closed.
Let Φ(t,X,v)=ω1(D0kI(t))2+ω2((D1(I1(t)+I2(t)))2+(D2(C1(t)+C2(t)))2)+ω3(B0S(t)θ(t))2+ω4∑2i=1(BiSi(t)φi(t))2. It is not difficult to verify that there exist C1>0, C2, and γ>1 such that
|
Φ(t,X,v)≥C1(|θ|2+|φ1|2+|φ2|2)γ2−C2
|
since θ(t), φ1(t), and φ2(t) are bounded.
In order to verify (vi) of Lemma 4.1, set
|
U+={(n,m)|∃v∈U,m=F(t,X,v), n≥Φ(t,X,v)}.
|
For any (ni,mi)∈U+, i=1,2, i.e., there exist v1∈U and v2∈U such that
|
m1=F(t,X,v1), n1≥Φ(t,X,v1),m2=F(t,X,v2), n2≥Φ(t,X,v2).
|
Since F(t,X,u) is linear in u, for any s∈[0,1],
|
sm1+(1−s)m2=sF(t,X,v1)+(1−s)F(t,X,v2)=F(t,X,sv1+(1−s)v2).
|
Note that the control set U is convex. Then, there exists a u∈U such that u=sv1+(1−s)v2 and
|
sm1+(1−s)m2=F(t,X,sv1+(1−s)v2)=F(t,X,u)
|
for s∈[0,1]. On the other hand, since Φ(t,X,u) is convex in u, one has
|
sn1+(1−s)n2≥sΦ(t,X,v1)+(1−s)Φ(t,X,v2)≥Φ(t,X,sv1+(1−s)v2)=Φ(t,X,u).
|
Then, for s∈[0,1], s(n1,m1)+(1−s)(n2,m2)=(sn1+(1−s)n2,sm1+(1−s)m2)∈U+. That is, U+ is convex. The proof is complete.
Next, we characterize the optimal control by deriving necessary conditions for the optimal control with the help of Pontryagin's Maximum Principle.
Theorem 4.3. The optimal control of (17) is characterized by
|
θ∗(t)=min{ˉθ,max{λ1−λ32ω3B20S∗(t),0}},φ∗1(t)=min{¯φ1,max{(λ5−λ4)βI∗(t)2ω4B21S∗1(t),0}},φ∗2(t)=min{¯φ2,max{(λ8−λ7)εβI∗(t)2ω4B22S∗2(t),0}},
|
(19)
|
where λi,i=1,2,...,9 are the adjoint variables satisfying the adjoint equations (20) and the transversality conditions (21).
Proof. In order to facilitate the discussion below, we kill the stars in the optimal state X∗(t)=(S∗(t),I∗(t),V∗(t),S∗1(t),I∗1(t),C∗1(t),S∗2(t),I∗2(t),C∗2(t))′ corresponding to the optimal control u∗=(θ∗(t),φ∗1(t),φ∗2(t)) and simply denote it by (S(t),I(t),V(t),S1(t),I1(t),C1(t),S2(t),I2(t),C2(t))′.
By Pontryagin's Maximum Principle, as in [7,28,31], to find the optimal control of (17)-(18) is equivalent to minimize the following Hamiltonian
|
H=ω1(D0kI(t))2+ω2((D1(I1(t)+I2(t)))2+(D2(C1(t)+C2(t)))2)+ω3(B0S(t)θ(t))2+ω42∑i=1(BiSi(t)φi(t))2+9∑i=1λifi,
|
where λi,i=1,2,...,9, are the adjoint variables satisfying the following adjoint equations
|
λ′1=−∂H∂S=−2ω3B20θ2(t)S(t)+λ1λI+λ1m+λ1θ(t)−λ2λI−λ3θ(t),λ′2=−∂H∂I=−2ω1D20k2I(t)+λ1λS−λ2(λS−m−k)+λ4β(1−φ1(t))S1−λ5β(1−φ1(t))S1+λ7εβ(1−φ2(t))S2−λ8εβ(1−φ2(t))S2,λ′3=−∂H∂V=−λ1δ+λ3(δ+m),λ′4=−∂H∂S1=−2ω4B21φ21(t)S1(t)+λ4(β(1−φ1(t))I+d1)−λ5β(1−φ1(t))I,λ′5=−∂H∂I1=−2ω2D21(I1(t)+I2(t))−λ4(1−q1)γ1+λ5(γ1+d1)−λ6q1γ1,λ′6=−∂H∂C1=−2ω2D22(C1(t)+C2(t))+λ6d1,λ′7=−∂H∂S2=−2ω4B22φ22(t)S2(t)+λ7(εβ(1−φ2(t))I+d2)−λ8εβ(1−φ2(t))I,λ′8=−∂H∂I2=−2ω2D21(I1(t)+I2(t))−λ7(1−q2)γ2+λ8(γ2+d2)−λ9q2γ2,λ′9=−∂H∂C2=−2ω2D22(C1(t)+C2(t))+λ9d2
|
(20)
|
and the transversality conditions
|
λi(T)=0, i=1,2,...,9.
|
(21)
|
The optimality conditions
|
∂H∂θ(t)|(θ∗,φ∗1(t),φ∗2(t))=0, ∂H∂φi(t)|(θ∗,φ∗1(t),φ∗2(t))=0
|
lead to
|
θ∗(t)=λ1−λ32ω3B20S∗(t), φ∗1(t)=(λ5−λ4)βI∗(t)2ω4B21S∗1(t), φ∗2(t)=(λ8−λ7)εβI∗(t)2ω4B22S∗2(t).
|
Moreover, taking into account the fact that (θ∗,φ∗1(t),φ∗2(t))∈U, i.e., using the lower and upper bounds of u∗, we find that the optimal control u∗=(θ∗(t),φ∗1(t),φ∗2(t)) is well characterized by (19).
5. Sensitivity analyses and numerical simulations
In this section, we first use (1) to simulate the reported sheep brucellosis and human brucellosis data of Inner Mongolia from 2001 to 2010 and to predict the trends of the brucellosis. Then, we perform sensitivity analysis of some key parameters, numerically simulate the optimal control, and seek for some effective control and prevention measures.
The data of sheep population is extracted from China Animal Husbandry Yearbook [8] (see Table 2). The data, concerning human brucellosis from 2001 to 2014, are adopted from China Health Statistics Yearbook[25] (see Table 3). The data of sheep brucellosis can not be acquired easily since there are few published studies on the population dynamics of sheep, and we calculate the number of brucellosis sheep in Inner Mongolia (see Table 2) from data of sheep population in Table 2 and the annual seroprevalence of sheep brucella in key monitoring regions of Inner Mongolia[11,13,22,30,38,39,43].
Table 2. Sheep population in Inner Mongolia (unit: 104).
| Year | 2001 | 2002 | 2003 | 2004 | 2005 |
| Sheep Breeding[8] | 3551.6 | 3515.9 | 3951.7 | 4450.6 | 5318.48 |
| Sale and Slaughter[8] | 2081.2 | 2146.5 | 2156 | 2867.74 | 3782.99 |
| Brucellosis sheep1 | 33.74 | 35.15 | 59.27 | 89.1 | 132.95 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 |
| Sheep Breeding[8] | 5419.99 | 5594.44 | 5063.29 | 5125.3 | 5197.2 |
| Sale and Slaughter[8] | 4539.6 | 5011.05 | 4874.94 | 5183.7 | 5339.2 |
| Brucellosis sheep1 | 162.57 | 195.79 | 202.52 | 230.63 | 259.85 |
| 1 Calculated from data of sheep breeding and the annual seroprevalence of sheep brucella in key monitoring regions of Inner Mongolia[11,13,22,30,38,39,43]. |
Table 3. Annual new confirmed cases of human brucellosis in Inner Mongolia[25,41].
| Year | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
| Reported Human Cases | 420 | 610 | 1280 | 4140 | 8740 | 8050 | 8117 |
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| Reported Human Cases | 11105 | 16551 | 16935 | 20845 | 12817 | 9310 | 10538 |
In Inner Mongolia, the total population was about 24 million in the past decade with the birth rate less than 1%, and the rural population accounted for nearly half of the total population[25]. Since the vast majority of human brucellosis cases in Inner Mongolia are herdsmen, farmers, veterinarians, slaughters, and milkers, who live in rural region. So, we view the rural population in Inner Mongolia as the high risk subpopulation G1 while the urban population in Inner Mongolia is considered as the low risk subpopulation G2. Recent studies (e.g., [30]) revealed that, before 1980s, 94% of human brucellosis cases in Inner Mongolia were from high risk subpopulation G1, and, after 1990s, this percentage decreased to 85%. Therefore, for the current brucellosis outbreak in Inner Mongolia, it is reasonable to assume that 85% of new confirmed human brucellosis are from the high risk subpopulation G1 and the rest 15% are from the low risk subpopulation G2.
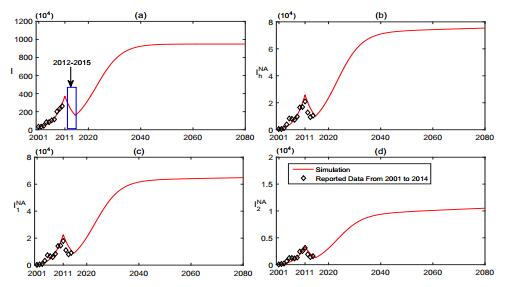
In order to carry out numerical simulations, most parameters of (1) are obtained from literature or assumed on the basis of common sense(see Table 1). The transmission rates of brucellosis (i.e., λ, β and ε, see Table 1) are estimated by the nonlinear least-square method that produced the best fit between the model outputs and the data (see Fig. 2).
With the help of (1), we fit it with the data from 2001 to 2011 and predict the dynamics of both sheep brucellosis infection and human brucellosis infection in Inner Mongolia (Fig. 2). The numerical simulations show that the model (1) with reasonable parameter values provides a good match to the reported data. From 2001 to 2011, the brucellosis sheep and human brucellosis cases kept increasing. From 2012 to 2015, due to the government's strong intervention on the transmission of brucellosis (e.g., a special fund was set to cull the infected sheep) [17,35,40], the size of brucellosis sheep and human brucellosis cases had a significant decline. However, the epidemic situation will become more serious in the coming decades and reach a peak at about 2040 if the government of Inner Mongolia can not sustainedly provide enough support to cull the infected sheep (see Fig. 2).
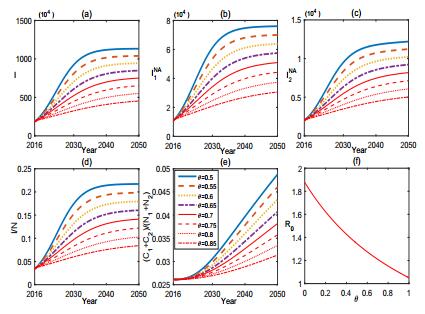
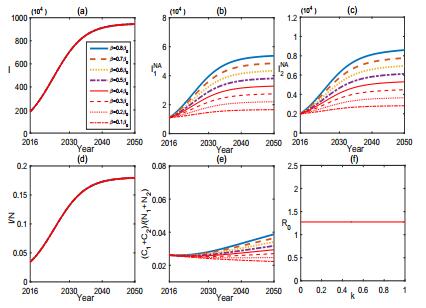
In order to better understand the mechanism and the control of brucellosis, we characterize the influence of some key parameters or factors in (1) by sensitivity analysis. Fig. 3-6 provide sensitivity analysis for (1) in terms of θ, A, k, and β, respectively.
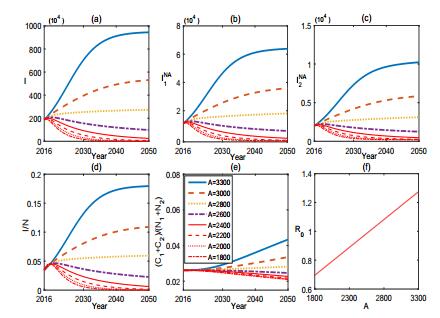
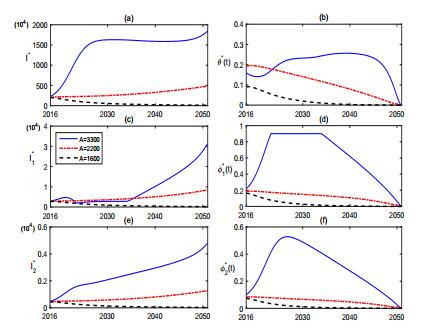
From Fig. 3, we find that the vaccination of sheep can effectively control the brucellosis in some extent but can not eradicate it from either the sheep or human. Fig. 4 shows the sensitivity of (1) to A. It reveals that the population size of sheep has potential effect on the control of brucellosis. In fact, the number of sheep in Inner Mongolia has increased about 2.042×107 from 2001 to 2007. Reducing the breading scale of sheep and keeping the population size of sheep in a reasonable range or dividing the sheep into small sub-populations will facilitate the control of brucellosis.
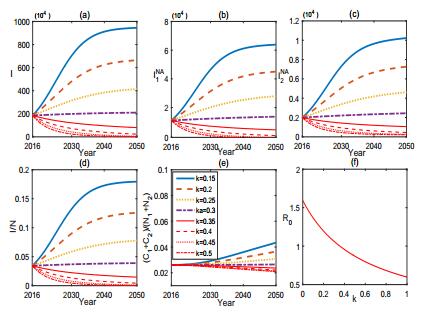
Culling the infected sheep is another effective measure to control the brucellosis. Fig. 5 depicts that increasing the culling rate k of infected sheep could effectively reduce the incidence of brucellosis in both sheep and human and can even eradicate the brucellosis if the culling rate exceeds some certain threshold level. Fig. 6 shows that reducing the transmission rate β between the sheep and the high risk subpopulation G1 facilitates the control of brucellosis but can not eliminate it. One typical way commonly used to effectively reduce β is to carry out health and prevention education, which can enhance people' awareness and knowledge about brucellosis and the emergency measure and treatment to decrease the rate of clinical outbreak. From Fig. 6, we can see that the epidemic of brucellosis can be relieved, but cannot be eradicated with the current prevention and control measures.
According to the above sensitivity analysis and numerical experiments, by comparing those figures, the recruitment of susceptible sheep and the culling of infected sheep are more sensitive than vaccination and health education in the current brucellosis outbreak in Inner Mongolia. In conclusion, controlling the population of sheep, reducing the birth rate of sheep, increasing the vaccination rate of sheep, improving the culling management of infected sheep, enhancing the people's awareness of brucellosis, and any combination of these measures are effective to control brucellosis. In practice, some policy involving comprehensive measures must be brought into operation.
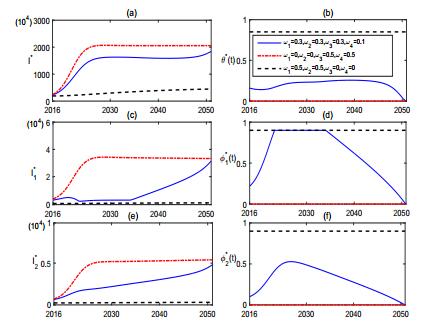
By Forward-Backward sweep method [21], we further expound the optimal control by numerical experiments. According to the current economic status in Inner Mongolia, the cost of culling each infected sheep is about 1000 CNY (D0=1), the treatment cost of each acute and chronic human case is about 5000 CNY (D1=5) and 3000 CNY (D2=3) per year respectively, the vaccination of each susceptible sheep needs about 200 CNY (B0=0.2), and the cost of health education for each person of high and low risk subpopulation are 300 CNY (B1=0.3) and 200 CNY (B2=0.2), respectively. Fig. 7 simulates the optimal control functions θ∗(t), φ∗1(t), φ∗2(t), and the corresponding states variables I(t)∗, I∗1(t), I∗2(t). The numeral simulations indicate that, with the current prevention and control strategy such as keeping sheep population in large size (A=3300) and culling rate of infected sheep at low level (k=0.1), putting majority of control resources into vaccination program and education plan, etc., the epidemic of brucellosis can be relieved in the short run, but can not be better controlled and eradicated in the long run. Even though 85% of sheep population are effectively vaccinated and 90% of human population admit a good prevention and health education (i.e., maximal supply of control resources), the number of brucellosis sheep still has a significant increase, the human brucellosis infection cases would continue decreasing in the next couple years but can not be eliminated(see Fig. 7).
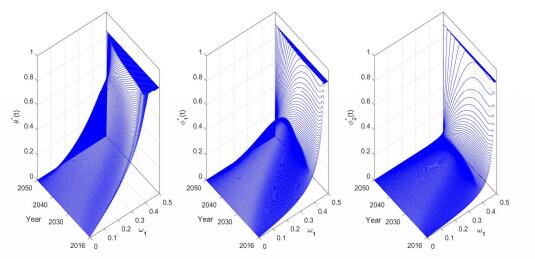
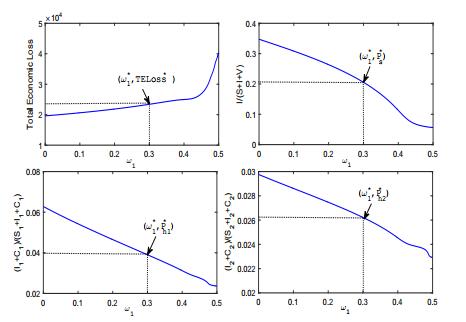
The optimal control strategy explored in Section 4 sensitively depends on the selection of weighted coefficients. Since the principal aim is to reduce the number of brucellosis human and sheep cases, it is reasonable to assume that both ω1 and ω2 are greater than ω3 and ω4. For simplicity, we also could assume that the vaccination programme and the health education plan are equally important, i.e., ω3=ω4 when searching for an optimal control strategy. Fig. 8 illustrates the optimal control strategy with varying weighted coefficients. From the numerical simulation, we observe that the weighted coefficients have significant effect on the optimal control strategy. When ω1 increases from 0 to 0.5, the key minimizing targets transfer from vaccination and health education to culling of brucellosis sheep and treatment of human cases, and then the optimal control gradually increases from θ∗(t)=φ∗1(t)=φ∗2(t)=0 to θ∗(t)=¯θ, φ∗1(t)=¯φ1 and φ∗2(t)=¯φ2. Fig. 9 illustrates the varying of the total economic loss (i.e., the sum of the four integrals in (12)) and prevalence rates with respect to the weighted coefficients. In real application, the policy-maker should confirm some reasonable weighted coefficients according to the financial budget for brucellosis (e.g., TELoss∗ in Fig. 9) and the prevalence rates in both sheep and human population (e.g., P∗s,P∗h1,P∗h2 in Fig. 9)).
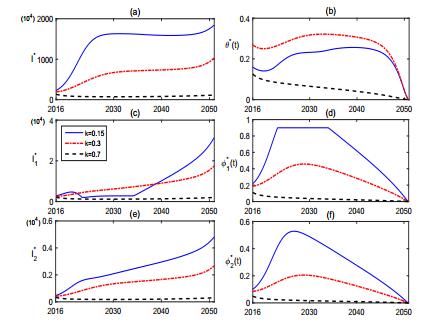
Simulations in Fig. 10-11 reveal that the culling of infected sheep and the recruitment of sheep play important roles on the optimal control of brucellosis. Fig. 10 shows that, when the culling rate k increases from k=0.15 to k=0.7, the brucellosis in both sheep and human is effectively controlled. Fig. 11 illustrates the role of the recruitment of sheep. When the constant influx rate of sheep decreases from A=3300 to A=1600, the brucellosis in both sheep and human can be better controlled.
6. Discussion and conclusions
The transmission of brucellosis has been a growing public concern in China, particularly in Inner Mongolia. In this study, we formulate a multigroup epidemiological model to study the transmission dynamics and explore control strategies for the brucellosis in Inner Mongolia. Our theoretical and numerical findings indicate that the brucellosis gradually increases in the next decades and reaches a peak at about 2030. Vaccination and health-prevention education, which are the main currently working control measures, positively affect and facilitate the disease control (see Fig. 3 and Fig. 6), but can not eliminate the brucellosis in Inner Mongolia (see Fig. 7). Sensitivity analyses in Fig. 4 and Fig. 5 show that the population size of sheep and the culling rate of brucellosis sheep are two important factors triggering the serious epidemic situation. The brucellosis in both sheep and human can be well controlled when the breeding size of sheep is reduced or the culling rate of infectious sheep is enhanced. Fig. 10 and Fig. 11 provide a series of effective and time-variable control strategies when the culling rate of brucellosis sheep is increased and when the population size of sheep is decreased, respectively. The numerical solutions of the optimal controls illustrated in Fig. 10 and Fig. 11 provides practical guidance for policymakers to make effective control policy and to implement it in resources-limited setting.
The study reveals that the brucellosis in Inner Mongolia of China is hardly eliminated if the policymakers still pay most attentions to the vaccination in sheep stock and the health-prevention education in human population. Our studies suggest that the government and the policymakers must take a new look at the current working control strategies. A reasonable and effective control strategy must involve comprehensive control measures based on the optimal control study.
Finally, we would like to point out that, even if a costly policy can prevent the disease spread, the prevention policy might not be well executed in resource-limited setting. A fundamental challenge in many control problems in epidemics is to find the right balance amongst several objectives. Although the weighted sum method is a typical method or technique to solve the multi-objective optimization, the problem lies in the correct selection of the weights to characterize the decision-makers preferences. In practice, it can be very difficult to precisely and accurately select these weights, even for someone very familiar with the problem domain. In addition, perturbations in the weights can lead to different solutions (see (19)). For this reason and others, decision-makers often prefer a set of promising solutions given the multiple objectives. In addition, recently, some evolutionary approaches have been proposed to deal with multi-objective optimization problems. Genetic algorithms, being a population based approach, is a well suited heuristic approach, see[18] for an overview and tutorial of multiple-objective optimization methods using genetic algorithms (GA). It is interesting but challenging to investigate the optimal control problem in this study by GA and compare it with the weighted sum method. It is left for our future work.
Acknowledgments
This work is partially supported by the National Natural Science Foundation of P. R. China (No. 11671072,11271065,11426045), the Research Fund for the Doctoral Program of Higher Education of P. R. China (No.20130043110001), and the Research Fund for Chair Professors of Changbai Mountain Scholars Program.









 DownLoad:
DownLoad: