Abbreviations
MES: Microbial electrochemical system; MFC: Microbial fuel cell;
MDC: Microbial desalination cell; MEC: Microbial electrolysis cell;
BES: Bioelectrochemical system; EAB: Electroactive biofilm;
EET: Extracellular electron transfer; DEET: Direct extracellular transfer;
PEET: Pilin-mediated extracellular electron transfer;
SEET: Shuttle mediated extracellular electron transfer;
QUIET: Quinone-mediated interspecies electron transfer;
DIET: Direct interspecies electron transfer; EPS: Extracellular polymeric substance;
NMR: Nuclear magnetic resonance; SHE: Standard hydrogen electrode;
ARB: Anode respiring bacteria; AHQDS: Anthrahydroquinone-2,6-disulfonate;
PCE: tetrachloroethene
1. Introduction
Like all living organisms, bacteria need to interact with their surrounding biotic and abiotic environment for survival. A major end goal of these interactions is for the microorganism to acquire energy through its metabolic and respiratory pathways. To provide some environmental control, most microbes are found in biofilms at interphases in the environment. The formation of a biofilm basically develops a microcosmic city with nutrient transportation, communication and waste management networks contained within it. Additionally, the formation of biofilms protects microbes from environmental stresses such as antibiotics, predation and desiccation [1]. Electroactive biofilms (EABs) form on electrode surfaces in microbial electrochemical systems (MESs), also referred to as bioelectrochemical systems (BESs). MESs encompass a wide range of technologies such as microbial fuel cells (MFCs), microbial desalination cells (MDCs), photo microbial fuel cells (photoMFCs) and microbial electrolysis cells (MECs) [2,3]. A major difference in these technologies is whether they are designed to produce power, such as MFCs generate power, or if energy is required, such as MECs to provide a product or other output. In all these systems, microbes within the EAB are acting as semi-catalysts to facilitate the electrode interactions to occur.
An EAB comprises of electricigens, microorganisms capable of donating to or receiving electrons from electrodes, via EET within a MES. These EAB communities can be enriched from nearly any natural environment including rice-paddy soils [4], compost [5], ocean sediments [6,7] and various wastewaters [8,9,10]. The EAB contains many similarities with traditional biofilms being composed of a matrix comprising water, microorganisms and extracellular polymeric substance (EPS), of which the latter is made up of nucleic acids, lipids, proteins and polysaccharides [11].
EAB structure and function are determined by a multitude of different factors including biological, electrode material, system design and operating parameters which have recently been reviewed extensively [12]. This review will focus specifically on what differentiates anode from cathode biofilms in terms of mechanisms of electron transfer, biofilm architecture and function, and microorganisms that are selected for in each of these specialized environments. We will first discuss the intricacies of microbe-electrode interactions within anode biofilms, where microorganisms are transferring electrons toward the anode surface through a variety of EET mechanisms including direct EET (DEET), electron shuttle mediated EET (SEET) or pilin-mediated EET (PEET). DEET involves inner and outer membrane redox proteins, SEET utilizes endogenously produced redox mediators and PEET requires pilin structures or periplasmic extensions. This will be followed by a discussion of what is currently known about cathode biofilms and their formation. Lastly, we will conclude with what is known about mixed-community biofilms and how the microorganisms contained therein interact with one another via direct interspecies electron transfer (DIET), ultimately affecting the efficiency of microbe-electrode interactions.
2. Anode Biofilm Dynamics: Microbe to Anode Electron Transfer
Biofilms on anodes, electrodes acting as electron acceptors, have been demonstrated to decrease the amount of charge transfer resistance in MFCs, leading to an increase in their power output [13]. Electrode associated biofilms are essential for MFCs and therefore, an understanding of their function is essential for optimization of MFC performance. Although anode biofilms are similar in many ways to non-electroactive biofilms, several key features distinguish these biofilms from their counterparts and will be discussed in the following section. First, the presence of an external electron acceptor, the anode, selects for exoelectrogens over microorganisms that can only utilise soluble electron acceptors. Secondly, microorganisms in EABs adhere to an electrode surface that not only acts as a scaffold for attachment, but also works as a breathing apparatus, providing an endless sink for electrons and influences structural and functional gradients within the biofilm matrix. Furthermore, the EET components of exoelectrogens, such as their pili, c-type cytochromes or endogenous electron mediators, play a major role in the structure and conductivity of anode biofilms. Within the biofilm, c-type cytochrome heme-containing proteins are reduced during substrate oxidation by exoelectrogens and become oxidized as they pass electrons to an electron acceptor (either pili, electron shuttles or an external electron acceptor, such as metals) [14,15]. Alternatively, pili of some species may act as a direct redox interface between substrate and electrode in long-distance EET [16]. Lastly, the ability to adjust the potential applied to the electrode or choose the electrode material, enables its modification as an additional operating parameter that influences biofilm composition and behaviour.
2.1. Electrodes promote growth of exoelectrogens
Most biofilms are reported as being insulating whereas biofilms formed on anode surfaces and utilizing the electrode as a final electron acceptor may be conductive [17,18]. This key difference is due to the predominance of electricigenic microbes found in EABs, which are capable of utilizing non-soluble electron acceptors at distance via conductive pili networks or endogenous electron shuttles [18,19]. This predominance occurs due to the selective action of electrodes where anode potentials theoretically increases the Gibbs free energy gained for the microbes over other available electron acceptors [20]. MFCs placed in situ, such as in anaerobic digesters or aquatic sediments, are exposed to a variety of different electron acceptors and complex organic substrates. A mixed species population, whose metabolic pathways can interact syntrophically, utilizes a range of mixed substrates by fermentation and anaerobic respiration with the electrode acting as a final electron acceptor [21]. Hence, it is not surprising that most studies indicate mixed species biofilms result in higher power production than pure culture biofilms [22]. However, Geobacter sulfurreducens pure cultures are an exception to this rule, as they can produce equivalent power to mixed-species biofilms [22]. Pure culture anode biofilms of G. sulfurreducens, G. metallireducens, Shewanella oneidensis [23,24,25,26], Pseudomonas aeruginosa [27], Escherichia coli, Desulfovibrio desulfuricans [28,29], Thermincola potens [30] and T. ferriacetica have been examined thus far. From all pure cultures aforementioned, G. sulfurreducens has been found to produce the highest current densities [22]. In general, Gram-negative bacteria are reported to produce more electrical output than Gram-positive microbes, which may change as more Gram-positive electricigens are discovered [31]. Due to the absence of an outer membrane in Gram-positives that is present in Gram-negatives, it will be valuable to understand whether the differences in membrane structure, and intermembrane electron transfer mechanisms, lead to a Gram-negative microorganisms increased capacity to interact with electrode surfaces.
Although the anode electron acceptor plays a major role in selection of microorganisms with EABs, electron donor substrate concentration and type also play a significant role in determining the community structure and electrical output of mixed-species anode biofilms [32,33]. Acetate fed-MFCs inoculated with anaerobic sludge promote different microbial communities from glucose, butyrate or propionate fed-MFCs and are also capable of producing higher coulombic efficiencies [32]. The natural microbial communities that arise within mixed-species MFC anodes have also been elucidated for many different niches including various wastewater streams and aquatic sediments and different microbial community structure does not always equate to differences in coulombic efficiency or power outputs [21,34]. Measurement of power production from marine, freshwater and salt-marsh sediment MFCs, which all contain their own distinct substrate profiles, yielded similar results for all three of these environments, despite the differences found in microbial community composition [34]. Moreover, examination of community members via sequencing of 16S rRNA clone libraries revealed similar but distinct microbial profiles; where all environments enriched for microorganisms capable of Fe(III) reduction, however the sediment type influenced which clades of Fe(III) reducers prevailed. Geobacteraceae made up over half of bacterial sequences isolated from marine and salt-marsh sediments of which most were traced to Desulfuromonas species. Conversely most sequences of Geobacteraceae from freshwater sediment comprised of Geobacter or Pelobacter species [34]. Therefore, although electrical output has been positively correlated with the presence of Geobacter in anaerobic brewery wastewater aggregates [35], it is not necessarily a requirement for high power output as other electricigens are also capable of significant power output. However, Geobacter may be important for stable power densities. Comparison of different wastewater anode biofilm communities revealed structural as well as initial power output differences. Examination of electrical output from three wastewater anode biofilms, two from different wastewater treatment plants and one from anaerobic bog sediment, indicated an initial difference in power production where the bog anode biofilm community produced higher power densities followed by a convergence to similar electrical outputs after 20 MFC cycles [36]. The predominance of Geobacter in all samples emerged after 16 cycles, which corresponded to the convergence of power outputs from the different anode communities. Similarly, it has been previously shown that microbial communities in brewery wastewater reactors are fairly stable and resilient to fluctuation within each environmental niche over time [37].
2.2. The anode surface promotes structural and functional gradients
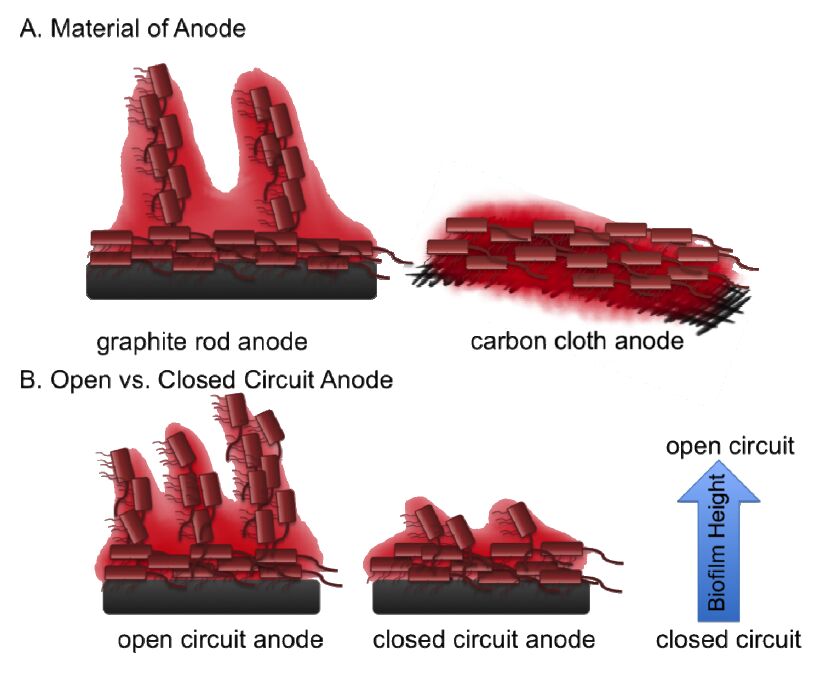
In addition to cells, the biofilm matrix contains pockets and channels that do not contain any bacterial cells but are filled with nutrients and waste products from metabolism. Due to the heterogeneous nature of these systems, biofilms consist of several microniches with varying proton gradients, metabolic activities and cell viabilities. Unlike biofilms on non-conductive solid surfaces that serve primarily as an attachment scaffold, EABs also utilize the electrode surface as a respiratory device. Given this dual functionality of the electrode surface, it has been determined that the metabolic activity of biofilm cells near the surface of the anode does not significantly differ to those located in the outer edges of the biofilm [38]. By encasing anode biofilms of G. sulfurreducens in resin and then sectioning them via microtoming, it was possible to study the transcriptional activity through microarrays of cells within 0-20 μm from the anode surface and compare that to those in the 30-60 μm outer layers of the biofilm [38]. Despite the increasing proton gradient that exists within the inner layers of EABs [39], genes involved in the tricarboxylic acid cycle were expressed uniformly in both layers indicating that cells are viable and metabolically active throughout the thickness of the biofilm. Not surprisingly however, there is increased expression of stress response genes within the inner layers of the biofilm to handle the lower pH environment [38]. Given the existing pH variations in the biofilm matrix, the viability of cells within the biofilm differs throughout in closed circuit versus open circuit MFCs. Comparing the Live/Dead staining of closed circuit and open circuit biofilms of Gram-negative (P. aeruginosa, G. sulfurreducens and S. oneidensis) and Gram-positive (C. acetobutylicum and E. faecium) pure cultures reported that viability for all is higher closer to the anode in closed circuit MFCs and higher at the top of the biofilm (further away from the anode) in open circuit MFCs where nitrate and fumarate act as the final electron acceptors (Figure 1) [40]. It should be recognized that the Live/Dead stain might be more a measure of cell permeability then viability with environmental isolates.
In addition to the functional gradients created by the presence of anodes, these unique electron-accepting surfaces also dictate the overall physical structure of EABs. G. sulfurreducens form biofilms on anodes that can be greater than 50 μm thick [22,41,42]. Current production in MFCs has been shown to be linear with increasing biofilm thickness and biomass on the anode, suggesting that cells not in direct contact with the anode are still contributing to its reduction by long-distance electron transport [42]. This indeed has proven to be the case with G. sulfurreducens, which uses conductive pili, referred to as nanowires that exhibit metallic-like conductivity to transfer electrons over large distances to the anode surface [18]. However, biofilms thicker than 50-70 μm have been found to no longer contribute to current production [43,44]. The reasons for this upper limit are still not clearly defined, however it is known that varying anode material and size can greatly influence anode biofilm thickness and conductivity. Pure cultures of G. sulfurreducens showed that varying the anode size and material affected the thickness of biofilm developed [22]. Carbon cloth full-sized anodes compared to 1/8-sized anodes resulted in biofilms of 2.2-8.5 μm and 3-18 μm thick biofilms respectively. The smaller anode produced thicker biofilms because cathode limitation was minimized, highlighting the effect that different MES architecture can have on power output and biofilm structure.
It is important to note that the architecture of anode biofilms is also not always a uniform distribution of cells layered on top of one another. Biofilms can have various different forms such as ones that form pillars and ones that form thick homogenous layers [22,42]. When carbon cloth is used as an anode material, G. sulfurreducens forms a thick homogenous layer of cells with minimal pillar structures and an even distribution of cells throughout the biofilm (Figure 1) [22]. However, when a solid graphite rod is used as the anode instead, heterogeneous pillar structures form in the biofilm with more viable cells observed near the surface of the anode than further away from it [22]. The height of biofilm pillars also varies between Gram-negative and Gram-positive bacteria and depends on whether the MFC is a closed circuit or open circuit system. Pillar height is higher for Gram-negatives and declines in closed circuit MFCs for both Gram-negatives and Gram-positives [40]. One reason for pillar formation may be to optimize the biofilm cells exposure to both soluble substrates found in the medium and to the anode surface. A similar but more exaggerated example of pillar formation has recently been discovered in marine sediments, where Desulfobulbaceae form long electric cables that couple sulphide oxidation in the anaerobic sediment layers to oxygen reduction at the sediment surface [45]. However, this phenomenon of pillar formation in anode biofilms requires further investigation to determine its exact significance.
The viability studies of anodic biofilms may not necessarily separate live from dead cells but be a measure of membrane permeability and integrity. Further studies accessing viability are warranted and post-genomic techniques such as metatranscriptomics, metaproteomics and metabolomics on different sections of biofilm could provide unequivocal insight into the functional and metabolic activities within different EAB sections. These “omics” technologies could be combined to provide understanding at the RNA, protein and chemical levels of activities within the cells of the biofilm.
2.3. Extracellular electron transfer components drive biofilm formation and conductivity
Anode biofilms are electrically energized entities due to the constant extracellular relay of electrons from the outer layers of the biofilm, through the EPS space and eventually to the electrode surface. Electricigens found on anode biofilms are distinct from non-electroactive microbes in that they rely on expression of their EET components, such as c-type cytochromes, pili or endogenous electron mediators, for the reduction of an insoluble electron acceptor. These EET components play a major role in the structure and conductivity of anode biofilms. The three currently described mechanisms of EET in anode biofilms include PEET, DEET and SEET [46,47]. Anode biofilm structure and conduction is reliant on the different EET mechanisms employed in either pure or mixed culture EABs. The substrate available for oxidation also plays a major role in what type of mechanism of EET the biofilm cells will use and has been summarized previously [47]. For instance, G. sulfurreducens employs its pili and OmcS for the oxidation of Fe(III) oxides whereas it does not produce pili when grown in soluble electron acceptors like Fe(III) citrate [48,49]. Anode biofilms of G. sulfurreducens utilize both PEET and DEET, while DEET and SEET have been demonstrated thus far for anode biofilms containing pure cultures of S. oneidensis; with SEET depending on DEET and accounting for the majority of EET to insoluble electron acceptors [15,50,51,52].
2.3.1. Long-distance extracellular electron transfer via pili or periplasmic extensions
There are two characterized mechanisms in which microbes transfer electrons from the outer layers of the biofilm through to the electrode surface; 1) via electron shuttles or 2) via PEET. Pili are extracellular amino acid based structures that are found in many Gram-negative
bacteria [53,54]. They aid in biofilm formation via adhesion and, in specialized cases, can form dense networks of electrically conductive microbial nanowires within the biofilm matrix [18,53,54]. These appendages are normally 50 to over 150 nm in diameter and can be up to tens of micrometers in length [49,53,55]. Their increased presence has been positively correlated to enhanced electrical current production in Geobacter [42]. Although various debates exist around biofilm conductivity and its effect on current density, it has been demonstrated that biofilm conductivity within anode biofilms does dictate the activation energy of electron transfer and current density produced [56].
Pili in the model exoelectrogens, G. sulfurreducens and S. oneidensis, have commonly been referred to as having metallic-like conductivity and thus the term ‘nanowires’ has been coined to describe the pili structures in both these microbes. There has been significant debate however regarding this claim for both microorganisms. Recently, an electron hopping model has been proposed for electrical conduction in S. oneidensis [57,58,59] nanowires, or loosely termed ‘nanopods’, as their nanowires have recently been found to be periplasmic protrusions rather than conductive pilin structures [60]; however further support for this model is still needed [52]. Doubts have also arisen over whether G. sulfurreducens pili are in fact capable of metallic-like conductivity. It has been argued that redox hopping between cytochrome proteins like OmcS, localized on pili structures, may be a more likely method for electron flow rather than actual electrical conductance via pili aromatic amino acids. In an attempt to resolve this debate for G. sulfurreducens, a mutant strain in which a Type IV PilA gene from P. aeruginosa replaced the indigenous PilA gene in G. sulfurreducens was constructed. The G. sulfurreducens mutant strain no longer exhibited metallic-like conductivity nor was capable of reducing Fe(III) oxide despite still localizing OmcS on the P. aeruginosa derived pili [61]. Additionally, deletion mutants of OmcS in G. sulfurreducens produced more PilA and generated more electrical current than wild-type strains [62,63]. Furthermore, a G. sulfurreducens mutant was constructed in which the genetic sequence coding for five aromatic amino acids in PilA were substituted with sequence encoding for five alanine amino acids instead [64]. This mutant was defective in long-range electron transport to electrodes and Fe(III) oxides and did not display any electrical conductivity. Lastly, Synchrotron X-ray microdiffraction has indicated that a spacing of 3.2-? exists between the aromatic amino acid groups within the pili of G. sulfurreducens which would enable π-orbital overlap and thus further supports electron transport via the aromatic amino acid groups within pili [65]. Conflicting reports provide evidence that the spacing required for metallic conduction is insufficient due to packing of aromatic amino acids. Models, using either homology considerations or nuclear magnetic resonance (NMR) spectroscopy characterization from available literature, reported that aromatic amino acids are not packed sufficiently tight for π-π interactions [66]. While the current model for PEET in G. sulfurreducens along the pili still faces some debate, S. oneidensis PEET occurs via periplasmic protrusions [67]. Further testing by a wide variety of groups is expected to provide more consensus in the future.
2.3.2. Direct extracellular electron transfer through cytochromes
Another mechanism of EET, is the shorter distance transfer of electrons from the microbes nearest the electrode to the electrode surface itself and is known as DEET. A few c-type cytochromes have been implicated as being necessary for this direct transfer to anodes including OmcZ from G. sulfurreducens and MtrC from S. oneidensis [47,68]. OmcZ, is located within the EPS matrix, loosely bound to the outer membrane in G. sulfurreducens [73,74]. It has been suggested that this protein behaves as an “electrochemical gate” that enables electron transfer from G. sulfurreducens directly to the anode [73]. OmcS is another c-type cytochrome that is found in G. sulfurreducens and as described above, is localized on the surface of pili. Although on pili, OmcS is critical for the reduction of Fe(III) oxides and has been implicated in DIET between G. metallireducens and G. sulfurreducens. Atomic force microscopy indicate OmcS cytochromes are spaced ~30 nm apart [70] making electron hopping not possible as the hopping model requires spacing of less than 1 nm [60]. OmcS may be involved in capacitor functions instead of EET under certain conditions, storing electrons within the pili during times of electron donor/acceptor depletion [71]. This observation is supported by transcriptomic work done on anode biofilms, which has shown that OmcZ and PilA are the only essential extracellular components in electron transfer to electrodes, whereas OmcS is actually down regulated in current-harvesting biofilms [72]. It has been proposed that cytochrome hemes may not contribute to electrical conductivity so much as electron storage since their abundance is negatively correlated with conductivity but positively correlated with biofilm capacitance [70].
Although the exact processes involved in DEET are still being determined, a step-wise model for DEET has been proposed. This model comprises of a four step process: 1) Oxidation of substrate electron donor and uptake of electrons via periplasmic cytochromes; 2) Electron transfer from periplasmic to exocytoplasmic (matrix) cytochromes; 3) Electron transport from the EPS matrix cytochromes to interfacial cytochromes at the electrode surface; 4) Electron transfer from interfacial cytochromes to the electrode surface [14,69]. The electron transfer rate for each step differs and it was determined that step 1 is the rate-limiting step [69]. Improving electron transfer efficiencies from substrate to anode is thus pivotal to improving MFC current production and gaining further knowledge into these mechanisms is of great value. One of the ways to improve MFC current and increase biofilm biomass is by treating the electrode prior to construction in MFCs, most commonly by heating or acid-washing [29]. Treatment of the anode with acid leads to formation of alcohol and carboxyl groups, which consequently form hydrogen or peptide bonds with the amide groups within cytochromes as in D. desulfuricans anode biofilms [29]. Thus it is clear that outer membrane cytochromes play an important role in the initial attachment of EABs to anode surfaces.
2.3.3. Electron shuttles move electrons within the biofilm matrix
Electron shuttles have also been shown to be critical for proper biofilm formation. Phenazines are redox mediators endogenously produced by P. aeruginosa biofilms and allow for the normally aerobic microorganism to survive under anoxic conditions [75]. Their production is increased within the oxygen-deprived zones of biofilms where they can be used as alternate electron acceptors. Recently it has been shown that P. aeruginosa phenazine mutant strains, with deletions in the phenazine operon, possessed greater wrinkling in their colony morphology than the wild-type strain, most likely as an attempt to increase biofilm surface area exposure to oxygen. This phenotype can be reverted back to wild-type morphology of less wrinkled biofilms when oxygen is added to these mutants [76]. Therefore in the absence of oxygen, which is often the case in EABs, electron shuttles such as phenazine play a critical role in proper biofilm development. In the context of MFCs, an increased presence of phenazine has been reported to enhance current production [27,77,78].
S. oneidensisis another electricigen that has been well characterized for its production of electron shuttles that recycle between reduced and oxidized forms from the cell to the electrode and back, respectively. Supernatants of S. oneidensis anode biofilms contain riboflavin and riboflavin-5’-phosphate which act as electron shuttles [79]. Evidence for their role as soluble electron shuttles was provided when a >70% reduction of electron transfer was observed upon removal of these molecules from the medium. This is in contrast to supernatant replacement in G. sulfurreducens anode biofilms, where very little reduction of current is observed [80]. Their additional ability to bind to and reduce anodes was demonstrated by cyclic and differential pulse voltammetry which for the first time showed that these molecules are not only soluble in the medium but also coat the surfaces of anode biofilms [79]. A recently devised “bound-flavin cofactor model” suggests the EET mechanisms of S. oneidensis and G. sulfurreducens anode biofilms are similar, with different dissociation constants (Kd) of the outer membrane c-type cytochromes and flavin-bound c-type cytochromes. This model accounts for the difference in effect on current production due to supernatant replacement [81].
2.4. Anode potential changes can influence biofilm structure
Various operating parameters including pH, temperature, flow rate, external resistance, substrate loading and applied redox potential strongly influence the performance of MESs. It has been previously reported that a higher applied anode potential to a MES containing a pure culture of G. sulfurreducens resulted in greater biofilm biomass, higher electrical current production and a faster start-up time [82]. However, this only occurred when the potential was increased from -160mV to 0mV versus a standard hydrogen electrode (SHE), whereas no change was observed when increasing the potential from 0mV to 400mV. Other reports using mixed community MESs have shown that increased anode potentials do the opposite and actually decrease the electrical output and biofilm biomass [83,84]. Recently, these seemingly contradictory results have been addressed [85]. Electrical output, biomass production and community structure were recorded in response to potentials of -0.25, -0.009, 0.21, 0.51 and 0.81V versus SHE in mixed culture single chamber MESs. The EAB biomass and current production increased from -0.25 to 0.21V, but declined at higher applied potentials of 0.51 and 0.81V. There are two main hypotheses to explain why this may occur: 1) there is either a change in microbial community composition at the different applied potentials henceforth referred to as the “community restructuring response” or 2) the microbes in the community change their EET pathways in response to the different potentials, henceforth referred to as “EET pathway selection”. Since the communities did not vary significantly between the different potentials applied, the latter explanation was deemed most likely by the authors [85]. However, another recent study has also supported the community restructuring response to anode potential [86]. It was found that microbes in the G. metallireducens clade predominated on lower electrode potentials while Geobacter microbes in subsurface clade 1 and clade 2 preferred growth on higher electrode potentials.
Conversely, EET pathway selection in response to anode potential was further supported by a recent discovery that G. sulfurreducens consists of multiple respiratory pathways, containing redox proteins that can specifically reduce electron acceptors of varying reduction potentials [87]. A G. sulfurreducens deletion mutant of the inner membrane c-type cytochrome redox protein ImcH could only reduce electron acceptors with a potential of ≤-0.1 V versus SHE. Thus an ImcH dependent respiratory pathway is responsible for reduction of electron acceptors with a redox potential above 0.1 V and a separate pathway is involved with reduction of acceptors ≤-0.1 V versus SHE. Similarly it was found that different EET components are expressed in G. sulfurreducens biofilms acclimated at different anode potentials [88]. Therefore, a combination of both EET pathway selection and community restructuring response have thus far described the effect of anode potential on anode biofilms. Further studies observing whether a combinatorial effect of these two hypotheses occurs are still warranted.
In addition to applied potentials playing a major role, the MES cell configuration should also be taken into account when considering the effects of varying applied potential. For instance, a membrane-less bioelectrochemical cell (single-chamber) increased biofilm production and electrical output with increasing applied potentials. However, the opposite was true for membrane separated bioelectrochemical cells (dual-chamber) [89]. The pH of electrogenic biofilms is also an important operating parameter to monitor as there is a narrow window of acceptable proton gradients for the cells within anode biofilms [90].
Further studies need to be conducted in order to draw the full picture of these EET respiratory pathways in Geobacter as well as other electricigens. Such insight will be valuable for numerous applications in bioremediation, power production and biosensor design; from enabling for the molecular engineering of tunable heavy metal biosensors to enhancing electron transfer processes leading to higher electrical output of EABs.
3. Cathode Biofilm Dynamics: Cathode to Microbe Electron Transfer
The utilization of biocathodes, comprising of electrotrophic microorganisms that consume electrons from an electrode, is becoming an attractive potential technology for biofuel and commodity production and for bioremediation of wastewater contaminants. When extra potential voltage is applied to a MES, hydrogen can be produced by electrolysis at the cathode, which is an attractive biofuel. This particular type of MES is referred to as a MEC and its performance and hydrogen yield can be catalyzed by electrotrophic biofilms on the cathode surface; thereby replacing the need for precious metal catalysts [91,92]. EABs are able to reduce the required input of energy into these systems. However, it is important to note that certain microorganisms are hydrogen-consumers and decrease the hydrogen yield of these systems; thus control of their growth is pertinent to successful biogas yield [93,94]. Biocathodes are also useful in sediment MFCs to drive oxygen reduction reactions [95] and in MESs to produce synthetic commercial compounds from carbon dioxide such as ethanol, methane and other organic carbon based commodities [96,97,98]. Furthermore, cathode biofilm communities are capable of reducing various environmental contaminants like nitrates [99,100], radioactive waste [101], chlorinated and aromatic pollutants [102,103,104,105] and toxic heavy metals [106,107] into innocuous forms.
Cathode biofilms are becoming increasingly acknowledged for their useful properties, which prevail when the community structure can be well regulated. However, the proliferation of various microorganisms at the cathode cannot be easily controlled in commercial scale applications of MFCs. There are two major types of biocathodes; aerobic in which microbes reduce oxygen as the final electron acceptor, and anaerobic where sulfates, nitrates and other inorganic compounds are reduced. This section will highlight the specific attributes of cathode biofilms including the types of microorganisms and communities found in these biofilms, the currently known architecture of these biofilm structures and their extracellular electron transport mechanisms.
3.1. Selection for electrotrophs in biocathode biofilms
3.1.1. Known electrotrophs in defined culture cathode biofilms
Cathode biofilm electrotrophs can be grouped into aerobic and anaerobic based on the final electron acceptors they utilize. Anaerobic biocathodes that have been studied include those that use nitrate, fumarate, hydrogen, carbon dioxide or sulfate as electron acceptors [108]. The first identified electrotrophic microorganisms that were found to directly accept electrons from cathodes were the model electricigens, G. sulfurreducens and G.metallireducens [109]. Nitrate or fumarate were used as electron acceptors for G. metallireducens and G. sulfurreducens, respectively, with the cathode poised at -500 mV (versus Ag/AgCl) acting as the sole electron donor. G. sulfurreducens also plays a role in uranium removal from contaminated groundwater by reduction of soluble U(VI) to less soluble U(IV) using a poised cathode as electron donor [110]. Furthermore, another Geobacter species, G. lovleyi, utilizes cathodes as electron donors for the reduction of tetrachloroethene (PCE) to the less toxic form, cis-dichloroethene without the need for added electron shuttles [104]. Evidently, Geobacter electrotrophs are capable of direct consumption of electrons from cathodes and have beneficial applications for various bioremediation efforts.
In addition to G. metallireducens, another identified nitrate reducer, Pseudomonas alcaliphila, has also been determined thus far [111] and methanogenic microorganisms, such as Methanobacterium palustre [112] have also been identified. Other commonly identified anaerobic electrotrophs also include hydrogenase-containing microorganisms that are adept at hydrogen metabolism, such as Desulfovibrio vulgaris and other Desulfovibrio species [113]. Cathodic reduction of oxygen to water has also been reported in many different electrotrophs including P. aeruginosa, Pseudomonas fluorescens, Winogradskyella poriferorum, Shewanella putrefaciens, Shigella flexneri, Escherichia coli, Kingella denitrificans, Enterobacter cloacae, Micrococcus luteus, Moraxella catarrhalis, Bacillus subtilis, Burkholderia cepacia, Brevundimonas diminuta and various species of Acinetobacter and Sphingobacterium [114]. Many more electrotrophs with different metabolic and respiratory capacities remain to be discovered from the diverse array of predominant clades found in mixed species cathode biofilms.
3.1.2. Communities prevalent in mixed-species cathode biofilms
The first demonstration of direct electron transfer from electrodes to microbes was just over a decade ago; when an environmental inoculum from freshwater sediment was observed to reduce nitrate to nitrite using the cathode as a sole electron donor [99]. This inoculum was found to have a predominant population of Geobacteraceae. Nitrate reduction does not occur at a high rate in soils since they are limited in their supply of electron donors [115]. By planting cathode electrodes into the soil, it is possible to promote the growth of a predominantly nitrate reducing biofilm community which can reduce nitrate into the innocuous nitrogen gas or ammonia [116]. Nitrate reducing cathode biofilm communities investigated through metagenomic analyses have been reported to comprise of Thiobacillus sp. in one study and Proteobacteria, Firmicutes and Chloroflexi in another study [117,118]. Of these denitrifiers, Thiobacillus has previously been implicated as a potential electrotroph due to its ability to reduce nitrate by using Fe(II) as an electron donor and its capacity for interspecies electron transfer with G. sulfurreducens through conductive magnetite nanoparticles [119].
Another commonly used electron acceptor in cathode biofilms is CO2. Recently, a purely autotrophic biocathode community has been established, utilizing carbon dioxide as the sole carbon source and the cathode as the electron donor [120]. A small inoculum size of mixed communities from storm water pond sediments and anaerobic wastewater digester was used in fed-batch MES reactors. Metagenomic analysis of the 16S rRNA genes from the electrode biofilms indicated that the biocathode community developed over time. The initial inoculum contained approximately 30% Archaea, however after enrichment in bicarbonate, the population shifted to contain less than 0.1% Archaea and contained 57.3% Proteobacteria, 12.4% Firmicutes, 11.6% Bacteroidetes and 1.1% Actinobacteria. The cathode biofilm sustained long-term growth and hydrogen production, solely utilizing CO2 for carbon and the cathode as an electron source. This illustrates the ability to select against the presence of unwanted microorganisms, such as acetogens and methanogens that consume hydrogen and compete for CO2 by enriching the cathode with bicarbonate as a carbon source rather than acetate. This difference in enrichment substrate helped in minimizing the proliferation of Archaea and specifically select for hydrogen-producing bacteria, thereby increasing the hydrogen yield. This result agrees well with other research which has shown that carbon source can select for the set of microorganisms that predominate in cathode biofilms [121].
3.2. Cathode biofilm structures differ from anode biofilm structures
Cathode biofilms under anaerobic conditions are more difficult to grow than anode biofilms and require a large input of energy to poise the electrode at a negative reduction potential [122]. Unlike the thick biofilms that have been seen to form on anodes in pure culture dual chamber MFCs, cathode biofilms are considerably thinner. However, the thickness of cathode biofilms from environmental samples is much higher; even up to 100 times thicker than anode biofilms [123,124,125]. The anode provides EAB with an inexhaustible electron sink, providing cells with high potential energy gains. However, although the cathode can provide electrotrophic bacteria with an endless supply of electrons, given that they are poised at adequately low potentials, it has some limitations that decrease its attractiveness as an electron donor. First, the cathode does not simultaneously provide microbes with a carbon source. Carbon sources, such as acetate or bicarbonate, can be utilized, however acetate can also potentially provide the microbes with high-energy electrons, bypassing their need for ones provided by the cathode. Thus, several stages of startup are needed to setup cathode biofilms, including the substitution of bicarbonate in place of acetate as a carbon source [126]. However, autotrophic electrotrophs can utilize the electron acceptor as their carbon source, as is the case with carbon dioxide [127]. Many environmentally situated cathodes are exposed to various substrates that could act as electron donors instead and may provide a higher potential energy gain to the microorganisms over that of the cathode [114]. More research into the energy gains from cathodes versus other substrates in situ needs to be done in order to further optimize cathode biofilm function.
The thickness of G. lovleyi cathode biofilms, as visualized by confocal laser scanning microscopy, was found to be thinly distributed on the electrode surface, however in close contact with it [104]. Despite the cathode serving as the sole electron source, biofilm formation was much thinner than that observed with G. lovleyi using an anode as the sole electron acceptor. The transfer of electrons from cathode to microbe was attributed to a direct route rather than through hydrogen since the potential at which the cathode was poised was too high for any production of hydrogen to occur. This thin cathode biofilm architecture, with most cells evenly distributed on the surface and in direct contact with the cathode, was similarly observed in a river sediment MFC [99]. The cause of this difference in biofilm thickness on anodes versus cathodes leads to the question of would thicker cathode biofilms be more efficient at electron consumption? One of the main components implicated in anode conductivity is the expression of pili [18], allowing for long-distance electron transfer from the outer biofilm cells to the anode surface. However, increased pili expression does not necessarily equate to thicker biofilms; G. sulfurreducens KN400 strain produces more pili than DL-1 strain but forms thinner biofilms [128]. Whether cathode biofilms are able to utilize pili for long distance electron transfer from the cathode remains to be answered. Many questions remain to be answered with respect to cathode biofilm formation and their mechanisms of electron consumption, which will gain further insight into cathode biofilm formation and efficiency.
3.3. Mechanisms of extracellular electron transfer from cathode to microbe
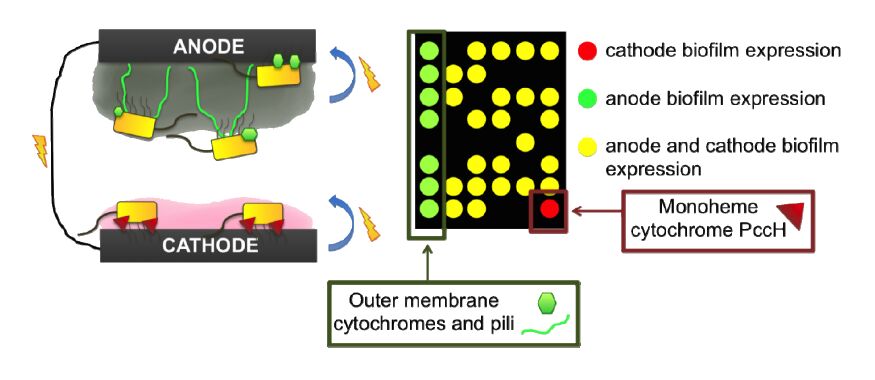
The three major mechanisms of electron transfer to anodes; SEET, PEET and DEET, have not been as clearly defined in cathode biofilms yet. However, the potential mechanisms of EET from biocathodes have been reviewed previously [114,129] and include direct contact via cytochromes and hydrogenases. Thus, the EET machinery used for donating electrons to anodes has similarities to that used for accepting electrons from the cathode, however functioning at different redox potentials [130]. A microarray transcriptional analysis of G. sulfurreducens electricigenic biofilms on anodes and electrotrophic biofilms on cathodes was performed in order to further identify existing differences in anode biofilm versus cathode biofilm EET mechanisms [130]. Interestingly, the genes for outer membrane cytochromes and pili that were highly expressed in anode biofilms were not highly expressed in cathode biofilms. Furthermore, the electron consuming biofilms expressed a distinct gene, GSU3274 that encodes a monoheme c-type cytochrome, PccH, which was not highly expressed in the anode biofilm cells (Figure 2) [130,131].
Recent work on aerobic mixed-species cathode biofilms has suggested that the biofilm community switches from SEET mechanisms to DEET when the applied electrode potential is -100 mV and +200 mV, respectively [132]. Since the electrode at -100 mV provides the biofilm microbes with more energy, microbes that are capable of long distance shuttle mediated electron transfer are able to compete in this environment and gain energy from the cathode poised at the more negative reduction potential. Characterization of the electron shuttles used for this long distance transfer in biocathodes is still needed to better understand this mechanism of cathode SEET.
The ability of cathode biofilms to generate hydrogen by obtaining electrons directly from cathodes depends on the expression of cytochromes and hydrogenases as previously reviewed [114]. The hydrogenase harboring Desulfovibrio paquesii, catalyses the production of hydrogen via direct transfer of electrons from the cathode [113]. However, the exact mechanism for direct electron exchange is not clear and further studies are needed to identify the component required for direct electron consumption.
During methanogenesis in biocathodes, electrotrophs accept cathode electrons and use them for the reduction of carbon dioxide or acetate to methane. In previous studies, the demonstration of hydrogenase-independent electron transfer has been implied through the absence of soluble molecular hydrogen or through kinetic models based on cyclic voltammetry measurements [98,133]. However, a recent study of Methanococcus maripaludis has given genetic evidence for a hydrogenase-independent mechanism of direct (without diffusible electron mediator) electron transport from cathodes to microbes [134]. Methanogenesis by the model hydrogenotrophic methanogen M. maripaludis occurred 10 times faster in wild-type strains compared to hydrogenase mutant MM1284 strain, devoid of all catabolic hydrogenases.
4. Internal Electric Biofilm Community Dynamics: Microbe to Microbe Electron Transfer
To this point, we have reviewed the dynamics of anode and cathode biofilms with respect to microbe-electrode interactions specifically. Now we will discuss the dynamics that exist between microorganisms that make up these biofilm structures. It has been well established that mixed culture biofilms tend to produce more power output than pure culture biofilms, with the exception of G. sulfurreducens biofilms [22]. It is thus beneficial to understand the inner workings of mixed-species interactions occurring within these matrices. The ultimate goal of understanding community dynamics in EABs is to gain necessary information on how to engineer them to be as powerful and efficient as possible in field-scale applications, such as wastewater management, bioremediation, corrosion control and biosensing. However, studying interspecies interactions in field-scale MESs, where a diverse set of microorganisms, nutrients, electron donors and acceptors are present, is more technically challenging than dissecting interactions between a known set of microorganisms in a controlled laboratory environment. Hence, most current research is focused on the latter form, however, some field-scale research has also elucidated recurring patterns in EAB communities. This section will discuss advances in both mixed and pure culture biofilms within lab and field-scale MESs and what we currently know about the mechanisms of interaction between microbes within EABs.
4.1. Pure and defined co-culture electroactive biofilms
Mechanisms of electron transfer between microorganisms within anode or cathode biofilms can be either intraspecies or interspecies interactions, which have been characterized in pure or defined co-culture experiments respectively. One key lesson that has been learned from studying pure-culture biofilms that can be applied to optimizing mixed-species biofilm interactions is that biofilm conductivity increases electrical output. For instance, it has been shown that biofilm conductivity directly correlates to current density [56]. Comparison of the KN400 strain with the DL-1 strain of G. sulfurreducens showed that KN400 generated a more conductive biofilm and consequently also produced higher current densities [128]. The reason for the increased conductivity was attributed to a higher production of pili in KN400. Interestingly, in a mixed-species conductive anode biofilm from anaerobic sludge, the presence of Geobacteraceae was 50% in the inner biofilm layer [19]. This suggested that Geobacter contribute to conductivity in mixed-species biofilms, however the contribution of other organisms to conductivity still needs further study.
A second important lesson learned from defined EAB cultures is that although the presence of more types of species increases the metabolic capacity of the biofilm, it does not necessarily mean that more diverse biofilms generate greater electrical output and enhance electron transfer efficiency. A defined co-culture of E. coli and G. sulfurreducens produces less power output than a pure culture of G. sulfurreducens [135]. An inhibitory intermediate metabolite, succinate, which was generated in the co-culture, was reported to have an inhibitory effect on power output [135]. However, defined co-cultures have also been demonstrated to enhance electrical output. Co-cultures of Gram-negative anode respiring bacteria (ARB) P. aeruginosa, G. sulfurreducens and S. oneidensis biofilms produced more power output when grown in co-culture with Gram-positive Enterococcus faecium, than the pure culture biofilms of these ARBs. However, when these three ARBs were grown in paired co-cultures with Clostridium acetobutylicum, the resulting power produced was less than that of each ARB pure culture [40]. Complex metabolic interplay between fermentative and non-fermentative ARB occurs within MES reactors between species. A pure culture of S. oneidensis fed with lactate performed nearly identically in terms of coulombic efficiency and current production as a co-culture MES of S. oneidensis and Lactococcus lactis fed with glucose. Since S. oneidensis cannot utilize glucose on its own but is able to utilize lactose, it was shown in the latter MES that S. oneidensis was consuming the lactate formed by L. lactis fermentation of glucose [26].
Through such defined co-culture experiments it has become clear that some co-cultures enhance current production compared to pure cultures due to mutualistic syntrophic interactions while others can even have a negative impact due to competition or inhibitory effects. Due to the unique characteristics brought upon by each defined co-culture interaction, an immense array of defined co-culture experiments is still needed to better predict unidentified interspecies interactions. More studies like these will eventually allow for a database of predicted interspecies interactions based on recurring patterns to be developed.
4.2. Components of direct interspecies electron transfer
Many of the currently discovered components required for direct interspecies electron transfer (DIET) are similar to those for DEET, SEET and PEET. So far there are several known non-biological molecules: hydrogen, formate, hematite, magnetite, carbon cloth, granular activated carbon, graphite, biochar; and biological components: pili, flagella, phenazines; known to be involved in DIET. Also anthrahydroquinone-2, 6-disulfonate (AHQDS) was recently demonstrated to aid in quinone-mediated interspecies electron transfer (QUIET), in which the mechanism of this interaction was shown not to depend on outer membrane cytochromes and thus requires additional research [136]. Due to the diverse multitude of interspecies electron transfer interactions possible, many more unique EET components involved in DIET are likely to be revealed in the coming years.
The first observed instance of DIET was observed between G. metallireducens and G. sulfurreducens [137]. Their interaction was promoted by growing them in a selective medium in which ethanol and fumarate were added as electron donor and acceptor, respectively. Only G. metallireducens can oxidize ethanol, whereas fumarate is specifically reduced by G. sulfurreducens. Their interaction was shown to not depend on hydrogen and formate as external electron carriers and instead be driven by pili and pili associated cytochrome, OmcS, EET components.
Recently it has been shown that a defined co-culture of G. metallireducens and Methanosaeta harundinacea syntrophically metabolize ethanol to produce methane, most likely via pili [138]. G. metallireducens oxidizes ethanol and donates the electrons to M. harundinacea which uses them, as well as the acetate produced by ethanol oxidation, to reduce carbon dioxide to methane. It was suggested that this electron transfer most likely occurs via pili from G. metallireducens. This conclusion was drawn due to the inability of M. harundinacea to utilize hydrogen or formate and the fact that ethanol oxidation by G. metallireducens does not produce hydrogen, ruling out the possibility of transfer via electron carriers. Furthermore, G. metallireducens conductive pili were necessary for M. harundinacea methane production and were overexpressed in the co-cultures.
4.3. Mixed-species electroactive biofilms
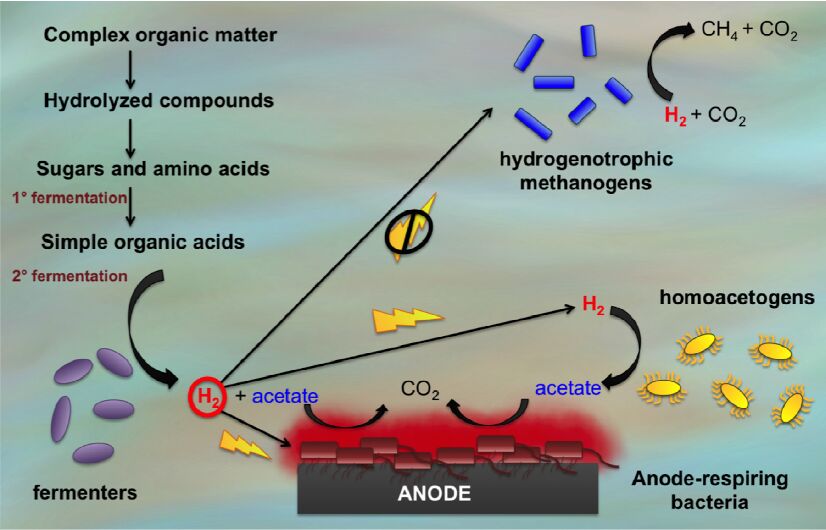
Thus far, insight gathered from mixed-species EABs has been mainly regarding community structure since it is difficult to study the functional interspecies interactions and electron transfer events in such complex systems. However, it is clear that having higher community diversity expands the metabolic capacity of the consortium as a whole. The utilization of ethanol in a mixed culture inoculum from anaerobic digested sludge and return activated sludge was examined to determine whether ARB were oxidizing the ethanol directly for transfer of electrons to the electrode or if some was being converted into acetate and hydrogen by fermenters in the community, of which methanogens would use the latter for hydrogenotrophic methanogenesis [139]. Fermenters were found to be metabolizing some of the ethanol into acetate and hydrogen. A syntrophic interaction was also discovered to exist between the ARB and methanogens in the community once the ethanol was fermented into acetate and hydrogen. Due to this dynamic, the coulombic efficiency was lower than it would be if the ethanol were directly utilized by the ARB to generate current in the MEC (Figure 3). When the activity of the methanogenic population was inhibited with BES (2-bromoethane sulfonic acid), current production increased by 24% since the hydrogen produced by ethanol fermentation was being directly utilized by the ARB instead of by the methanogens. This highlights the fact that syntrophy and greater metabolic diversity do not necessarily lead to higher current production and on the contrary, it shows that inhibiting methanogenesis increases the coulombic efficiency. Recently, the Shannon diversity index has been implemented to predict the power output of MFCs based on community diversity [140]. Increasing Shannon diversity indices within anodic biofilm communities were correlated to enhanced power production of the MES. Syntrophic interactions between fermenters and methanogens influence coulombic efficiency [139]. This may seem contradictory to the results mentioned above, however it is important to note that the positive association of diversity with power output was only observed in anodic biofilm cells and not in the planktonic community of the MFC, which may contribute to competing electron transfer reactions.
Various in situ MFCs have shown a predominance of Geobacter species within the mixed species community. This may be due to their ability for direct electron transfer to electron acceptors via their cytochromes and conductive pili networks [141]. In addition to the presence of an anode selecting for Geobacter, it has also been shown that the addition of specific substrate, in particular acetate, selects for the presence of Gammaproteobacteria of which Geobacter belongs to [32]. Despite its highly efficient and preferred use of acetate, Geobacter spp. have also been found to be present in many brewery wastewaters where ethanol is a major electron source, although community stability in ethanol-selected biofilms as compared to acetate-selected biofilms is lower [142]. Recently, a syntrophic interaction involving DIET between G. metallireducens and M. harundinacea has been discovered [138]. This interaction was favorable for current production. Although it has been observed that hydrogenotrophic methanogens decrease overall MES performance, it may actually be better to instead selectively promote DIET of acetoclastic methanogens like M. harundinacea with ARBs. Other microorganisms that have been demonstrated to dampen MFC performance include sulfate-reducing bacteria, nitrate-reducers, iron-reducers, fermentative microbes, aerobes and hydrogen-utilizing autotrophs [12].
A 16S rRNA metagenomic community profile of brewery wastewater has revealed Geobacter and Methanosaeta species, specifically M. concilii, to be the most predominant microorganisms present [122]. The mixed species aggregates obtained from the upflow anaerobic sludge blanket reactor were found to be electrically conductive in a temperature dependent manner, implying metallic-like conductance [18]. The methanogenic aggregates were also able to convert formate to methane, however at rates much lower than the observed metabolism of ethanol would explain. From these results, it was suggested that some form of syntrophy involving DIET between these clades of microbes might occur to result in such conductive aggregates with high rates of ethanol metabolism. Further defined co-culture experiments in vitro are still required to solidify this claim.
5. Conclusion
Initial research on MES biofilms has mainly focused on anode-associated electricigens, their mechanisms of EET to the anode surface and their electrochemical, biochemical and physical dynamics. These pioneering studies have paved the way for cathode biofilm research within MESs and the complex interplay of microbial metabolisms within mixed-species electrode biofilm networks. Key differences exist between anode and cathode biofilms including the microbial populations enriched for, the components involved in EET to and from the electrodes and their structural and chemical propensities. Further identification of electricigens and electrotrophs through pure culture or metagenomic approaches along with elucidation of more EET components and characterization of their roles in electrode respiration or consumption are still required to gain a better understanding of these systems. Additionally, metabolomics studies of the different sections of anode and cathode biofilms would enhance our understanding of microbial viability and activity within these biofilms. Furthermore, there is a great need to assess the syntrophic and competitive interactions that occur within mixed-species EABs in order to devise the correct approaches for optimization of in situ MESs. Since a complex metabolic food web exists in mixed-species biofilms, a good strategy to gaining insight into syntrophy and competition in EABs is through defined co-culture studies. Furthering our understanding of EABs will continue growing the field of electromicrobiology and enhancing our ability to use these systems in a vast array of biotechnological applications including their currently identified uses in bioremediation, power production, biosensing, biofuel production, chemical synthesis and wastewater treatment to as yet untapped applications in biomedicine, agriculture, corrosion prevention, mining and beyond.
Acknowledgments
The Franks Laboratory receives support from the Defence Science Institute, Defence Science and Technology Organisation, Office of Naval Research Global (Award no. N626909-13-1-N259) and the Australian Research Council (Award no. LP140100459).
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: