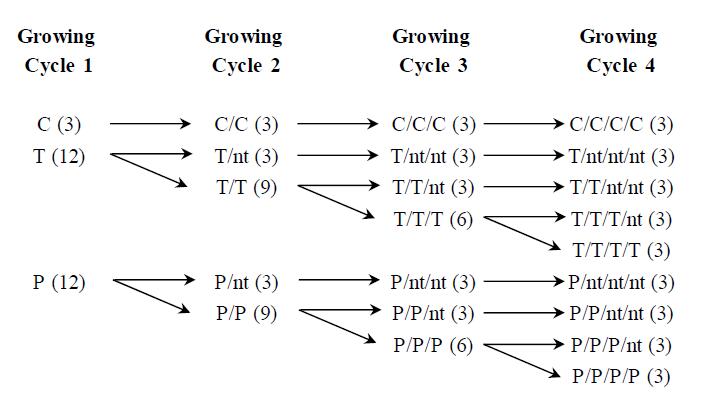
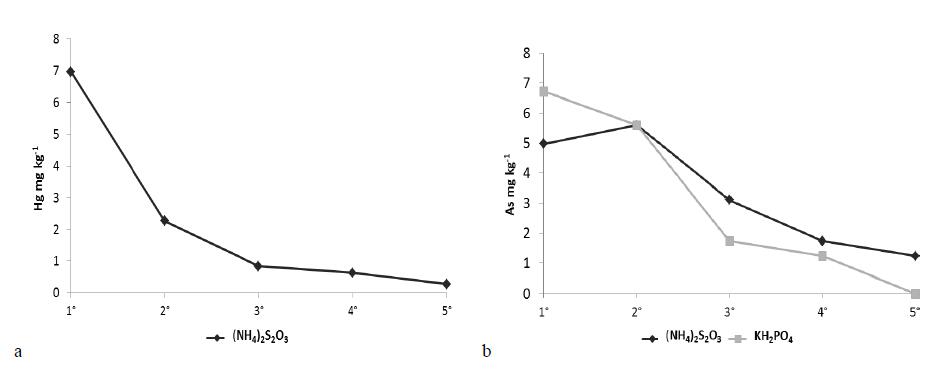
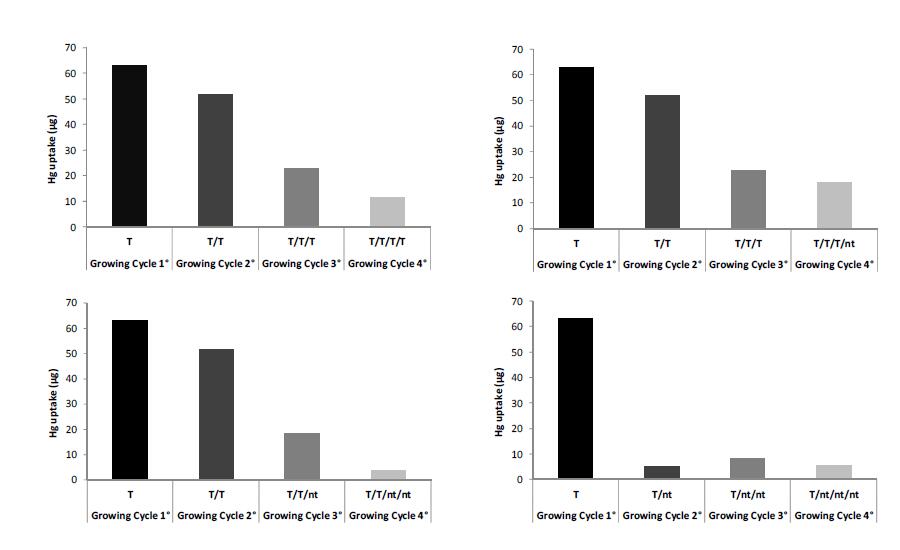
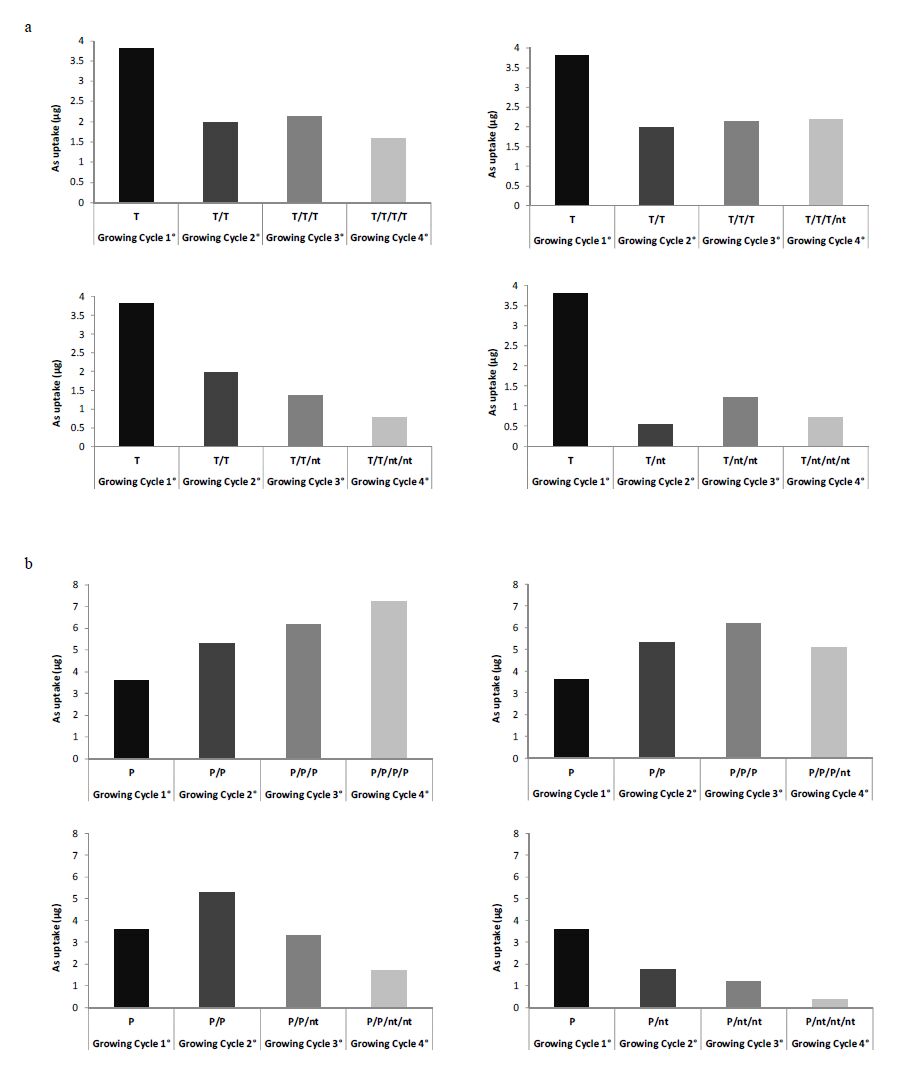
Mercury is widely distributed throughout the environment. In many contaminated soils other contaminants are present along with mercury; of these, arsenic is one of the most frequently found metals. In the presence of mixed contamination of this kind, remediation technologies must overcome many difficulties due to the different chemical characteristics of the various contaminants. In this study, repeated assisted phytoextraction cycles with Brassica juncea, were conducted on a laboratory scale to evaluate the removal efficiency of mercury and arsenic from a multi-contaminated industrial soil. The possibility of using only one additive, ammonium thiosulphate, to remove mercury and arsenic from co-contaminated soil simultaneously was also investigated. The thiosulfate addition greatly promoted the plant uptake of both contaminants, with an efficiency comparable to that of phosphate specifically used to mobilize specifically arsenic. Repeated additions of mobilizing agents increased metal availability in soil, promoted plant uptake and consequently increased the removal of contaminants in the studied soil.
Repeated treatments with thiosulfate increased the concentration of mercury and arsenic in the Brassica juncea aerial part, but due to toxic effects of mercury that reduce biomass production, the total accumulation of both metals in plants tended to decrease at each subsequent re-growth.
The use of a single additive to remove both contaminants simultaneously offers several new advantages to phytoextraction technology in terms of reducing cost and time.
1.
Introduction
In recent years, Leslie-Gower type predator-prey models appear in various fields of the Mathematical Ecology, which have been proposed and studied extensively due to their increasing importance [1,2]. Among the most widely used mathematical predation models of this type, the Holling-Tanner model [3] (or May-Holling-Tanner [4,5]) plays a special role in view of the interesting dynamics it possesses [5]. It was proposed by James T. Tanner in 1975 [6] and based on the Leslie-Gower scheme [7], which was raised by the ecologist Patrick H. Leslie in 1948 [8].
These models are described by an autonomous bidimensional differential equation system characterized by the following aspects:
ⅰ) The prey-dependent functional response or predator consumption rate (depending only on the prey population) is hyperbolic, a particular form of Holling type Ⅱ [9,10]. It is described by the function h(x)=qxx+a, where x=x(t) is the prey population size. This function is known as the Michaelis-Menten function in Biochemical Kinetic.
ⅱ) The equation for predators is a logistic-type growth function [12,11,10]. So, the conventional environmental carrying capacity for predators Ky is expressed by a function of the available prey quantity [10]; in the seminal paper of P. H. Leslie [8], Ky is assumed proportional to prey abundance, i.e., Ky=K(x)=nx. Implicitly, this formulation presupposes that the predator is a specialist.
In the logistic predator model, the quotient ynx, called the Leslie-Gower term, measures the loss in the predator population due to rarity (per capita yx) of its favorite food [13], where y=y(t) the predator population size. The importance of the Holling-Tanner model is highlighted by J. B. Collings in 1997 [14], who assured that it provides a way to avoid the biological control paradox wherein classical prey-dependent exploitation models generally do not allow for a pest (the prey) equilibrium density that is both low and stable [14].
The May-Holling-Tanner model [15,5,10] is studied partially in [3] and in the Murray's book [16]; it has been used in [17] to investigate numerically the dynamics of a predator-prey system for a pest in fruit-bearing trees, under the hypothesis that the parameters depend on the temperature; it has also shown its efficacy for describing the real ecological systems like mite/spider mite, canadian lynx/ snowshoe hare, sparrow/sparrow hawk and more [15].
In the paper by Saez and González-Olivares (1999) [5], its bifurcation diagram is described, establishing the existence of two limit cycles, surrounding the unique positive equilibrium point. Moreover, it is demonstrated that locally asymptotic stability of that equilibrium point does not imply global stability in this predator-prey model. This result implies the coexistence of a stable equilibrium and persistent oscillations [5]. Nevertheless, some authors have achieved conditions under which local stability of a positive equilibrium point implies its global stability [18].
The interesting phenomenon that local and global stability are not equivalent has also been shown in Leslie-Gower type models considering other mathematical form to describe the consumption function, as is shown in [12,19,4,20], where a non-monotonic functional response is assumed.
But the Leslie-Gower type models may present anomalies in its predictions, because it predicts that even in very low prey population density, when the consumption rate per predator is almost zero, predator population might increase, yet if the predator/prey ratio is very small [10]. Even so, it has been used to describe the interaction of certain populations [14,21].
Nonetheless, in the case of severe scarcity, some predator species can switch over to other available food, although its populational growth could be limited by the fact that its most favorite food is not available in abundance. This ability can be modelled by adding a positive constant c to the environmental carrying capacity for predators [22,13]. Thus, the c>0 indicates the quantity of alternative aliment available for the predators.
Then, we have that environmental carrying capacity for predators K(x)=nx+c; in that case, it is said that the model is represented by a Leslie-Gower scheme and it is also known as modified Leslie-Gower model [23,24]; if x=0, then K(0)=c, concluding that the predator is generalist since it choices an alternative food to avoid its extinction.
At the approach of the Leslie-Gower type predator-prey model [25] (with c=0, considering implicitly a specialist predator), is assumed that a reduction in a predator population has a reciprocal relationship with per capita availability of its favorite food [13].
When c>0, the modified May-Holling-Tanner model here analyzed has not these abnormalities and it enhances the predictions about the interactions. This model was proposed in [13], but focused on demonstrating the global stability of a unique positive equilibrium point.
On the other hand, one of the main elements of the predator-prey relationship is the predator functional response or consumption function, which refers to the change in attacked prey density per unit of time per predator when the prey population size changes [9]. In many predator-prey models is assumed that the functional response grows monotonic, being the inherent assumption the more prey in the environment, the better for the predators [10].
We will consider that the predator consumption function is prey-dependent and expressed by the hyperbolic function h(x)= q xx + a [26,27] a particular case of a Holling type Ⅱ functional response [9]. The parameter a is a abruptness measure of the functional response [28]. If a→0, the curve grows quickly, while if a→K, the curve grows slowly, that is, a bigger amount of prey is needed to obtain q2.
The behavior of the system will be described according to the obtained constraints on the parameter values and classifying the different and rich dynamics resulting that have not been exposed on earlier works.
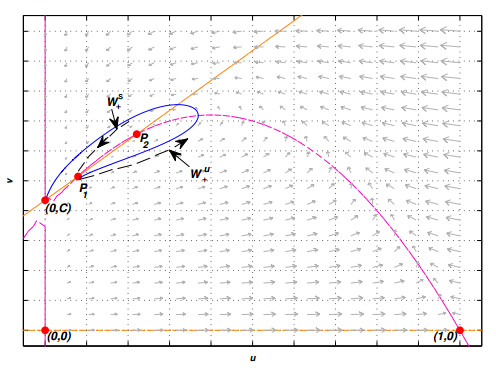
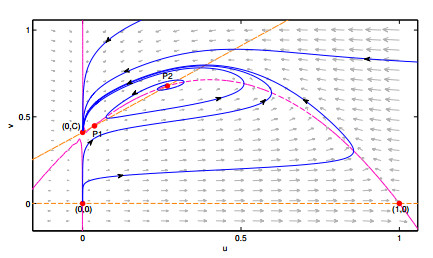
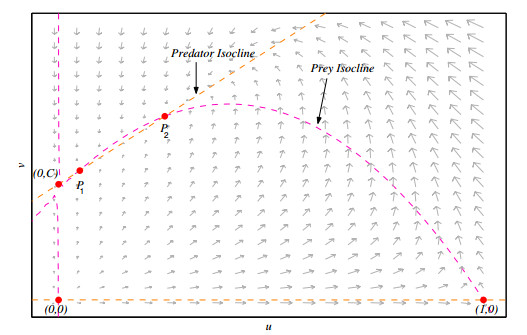
Although there are various works in which the model here proposed has been partially analyzed [23,24,1,29,30,2], new and novel properties of the model are here established such as: the existence of different class of bifurcations (Bogdanov-Takens, generalized Hopf, homoclinic and heteroclinic bifurcations); the existence up to two positive equilibrium points (see Figure 1), depending on the relative positions of isoclines, being one of them always a saddle point; the existence of at least one limit cycle encircling a stable positive equilibrium point; a separatrix curve in the phase plane which divides the behavior of the trajectories, that implies the existence of solutions nearest to that separatrix having different ω−limit, i.e., they are highly sensitives to the initial conditions [4,31].
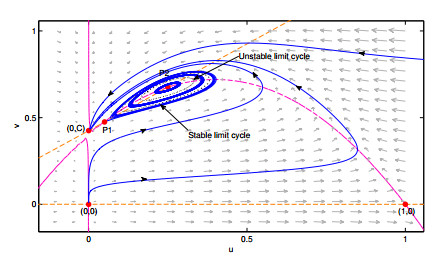
Furthermore, using the computation of Lyapunov numbers (or quantities) [32,33], we were able to demonstrate the existence of two limit cycles, when a weak (or fine) focus occurs, being the innermost unstable and the outermost stable, showing examples to illustrate this property for different obtained cases.
Hence, our analysis allows to extend the properties of the model proposed in a highly cited article [13] and we complement the outcomes of the Holling-Tanner model established in [5], showing the existence of the phenomenon of multistability, when it exists: a local attractor positive equilibrium, a stable limit cycle and a stable equilibrium point over the y−axis.
The rest of the paper is organized as follows: In the next Section, the modified May-Holling-Tanner model is presented; in Section 3, the main properties of the model are proved; in Section 4 we discuss the obtained results, giving the ecological meanings of them. To reinforce these results, some numerical simulations are shown in the last section.
2.
The model
The modified May-Holling-Tanner model [4,5] to be analyzed, considering a generalist predator, is described by the following autonomous bidimensional differential equation system of Kolmogorov type [34]
:
where x=x(t) and y=y(t) indicate the prey and predator population sizes respectively, for t≥0, measured as the number of individuals, biomass, density by unit of area or volume. The parameters are all positives, i. e., μ=(r,K,q,a,s,n,c)∈R7+ and for ecological reasons a<K; the parameters have their meanings are given in the following table:
The parameter n indicates also how the predators turn eaten prey into new predator births, and c is expresses that the predator is generalist, i.e., if it does not exist available prey, it switch to an alternative food. We note if c=0 the May-Holling-Tanner model is obtained which is not defined in x=0 and whose dynamics was described in [5].
In system (2.1), the growth population rate of predators, expressed by dydt, becomes larger when c increases. This is in accordance with the ecological fact that if the predator is more capable of changing from its favorite prey to other food options, it can survive more easily when the prey is lacking severely [13].
As system (2.1) is of Kolmogorov type, the coordinates axis are invariable sets and the model is defined at
The equilibrium points of system (2.1) or vector field Xμ are (K,0), (0,0), (0,c) and (xe,ye), where xe and ye satisfy the equation of the isoclines y=nx+c and y=rq(1−xK)(x+a). Clearly, (xe,ye) can be a positive equilibrium point (equilibrium at the interior of the first quadrant) or cannot exists there, depending on the sign of factor 1−xK.
System (2.1) has been used to study non-autonomous versions by incorporating delay [29] or impulses [35,2] as well as autonomous model considering partial derivatives [36]. In spite of these recent studies, the dynamics of the system (2.1) have not fully analyzed and some obtained results are not true or well established.
In this paper, we show that local and global stabilities are not equivalent to this class of predator-prey models. The existence of subsets on the parameter space is proved for which there exist a bifurcation manifold of semistable limit cycles and an open manifold, where a positive equilibrium point is locally stable and surrounded by at least two limit cycles.
In order to simplify the calculations, it is convenient to reduce system (2.1) to a normal form; so, we follow the methodology used in [37,20,11,5], making a change of variable and a time rescaling, by means of a diffeomorphism [32]. So we have the following:
Proposition 1. (Topological equivalent system)
System (2.1) is topologically equivalent to the polynomial system given by
where η=(A,S,C,Q)∈ ]0,1[×R3+ with A=aK<1, S=sr, C=cKn and Q=nqr.
Moreover, system (2.2) is defined on the set ˉΩ={(u,v)∈R2:0≤u, 0≤v}.
Proof. Let x=Ku and y= nKv; substituting into the system (2.1), simplifying and factoring, we obtain
Now, using the time rescaling given by τ=r(u+aK)(u+cnK)t;
then,
Rearranging and simplifying
Making the above indicated substitution, system (2.2) is obtained.
Remark 2. 1. We have constructed the diffeomorphism φ:ˉΩ×R⟶Ω×R, so that
The Jacobian matrix of φ is
and we have that detDφ(u,v,τ)=nK2r(u+cnK)(u + aK)>0.
Then, the diffeomorphism φ is a smooth change of variables with a rescaling of the time preserving the time orientation; thus, the vector field Xμ(x,y), is topologically equivalent to the vector field Yη=φ∘Xμ with Yη(u,v)=M(u,v)∂∂u+N(u,v)∂∂v and the associated differential equation system is given by the polynomial system of fourth degree of Kolmogorov type [34].
2. With this parameterization and time rescaling we have obtained a representative system with the least quantity of parameters possible; system (2.2) describes the dynamical behaviors of all those systems topologically equivalent to the system (2.1). Therefore, more important than knowing the influence of a specific parameter in the dynamical behavior of the system (2.1), it may be best to know the relationships between some of them, which also permits a simple description of the system properties.
The equilibrium points of system (2.2) or singularities of vector field Yη are (1,0), (0,0), (0,C) and the points (ue,ve) which lie over the curves:
Then, the abscissa u of the positive equilibrium points is a solution of the second-degree equation:
Considering the Descartes' Rule of Signs and according to the sign of the factors B1=1−A−Q and B0=CQ−A and Δ(η)=(1−A−Q)2−4(CQ−A), the equation (2.3) has two, one or none positive roots. In the following, we describe the diverse cases existing for the equation (2.3).
1) Assuming B1=1−A−Q>0, B0= CQ−A>0 and
1.1 Δ(η)>0, the solutions are:
1.2 Δ(η)=0, the solution is u∗=12(1−A−Q),
1.3 Δ(η)<0, there is no positive solution.
2) The solutions are u1<0<u2, if and only if,
2.1)1−A−Q>0 and CQ−A<0, or else,
2.2)1−A−Q<0 and CQ−A<0.
3) If 1−A−Q>0 and CQ−A=0, there are two solutions
u1=0 and u2= G=1−A−Q=1−A−AC>0.
4) If 1−A−Q=0 and CQ−A<0, we have two solutions, u1<0<u2.
5) Moreover, equation (2.3) does not have real roots, if and only if,
5.1 1−A−Q=0 and CQ−A>0, or
5.2 1−A−Q<0 and CQ−A>0.
According to the above analysis of equation (2.3) we have:
1. Assuming B1=1−A−Q>0 and B0=CQ−A>0, then, there exists three possibilities for system (2.2):
1.1. There are two equilibrium points at interior of the first quadrant, if and only if, C<14Q(4A+(1−A−Q)2), which are P1=(u1,u1+C) and P2=(u2,u2+C) with 0<u1<u2<1.
We note that the coordinates of the points P1 and P2 do not depend on the parameter S.
1.2. There is a unique equilibrium point at interior of the first quadrant, if and only if, Δ(η)=0. In this case, the points P1 and P2 coincide, i.e.,
with E=1−A−Q2 and C=14Q(4A+(1−A−Q)2).
1.3. For 1−A−Q>0 and CQ−A=0, there are not equilibrium points at interior of the first quadrant, if and only if, C>14Q(4A+(1−A−Q)2).
The case 1.1 is shown in the Figure 1.
2. In this case, the unique equilibrium point at interior of the first quadrant is, P2=(u2,u2+C)=(L,L+C)
with L=12(1−A−Q+√Δ(η)). According to the relation between C and L, the point P1 lies in the second or the third quadrant.
3. Clearly, the point P1 coincides with (0,C). Then, (C−A−ACC,(C−A)(C+1)C) is the unique equilibrium point at interior of the first quadrant.
4. For 1−A=Q, the unique equilibrium point at interior of the first quadrant is P2=(F,F+C) with F=√A−C(1−A), and A−C(1−A)>0. So, C<A1−A. Moreover, the point P1=(−F,−F+C) lies in the second or the third quadrant.
5. There are not equilibrium points at interior of the first quadrant, if and only if,
5.1. 1−A−Q=0 and CQ−A≥0, or
5.2. 1−A−Q<0 and CQ−A≥0.
The above classification 1-5 implies the study of different cases in this family of systems, according to the quantity of the equilibrium points and the relations between the parameters A, C and Q. We note that A is the intercept of the prey isocline with the v−axis; then, the relative position among C and A over this axis, influences the quantity of positive equilibrium points and the nature of these equilibriums.
In short, we summarize the different cases to study in the following table (Table 2).
We note system (2.1) has a significant difference with May-Holling-Tanner model (when C=0), respect to the quantity of equilibrium points [5], since system (2.1) can have up to two positive equilibrium points, apart from of the new equilibrium (0,C) (see Figure 1). Meanwhile, in the May-Holling-Tanner model [3,5] there exists a unique positive equilibrium point (the point P1 lies in the third quadrant); nevertheless, other dynamical differences between both models will be established.
To determine the local nature of the equilibrium points we will use the Jacobian matrix of system (2.2) which is:
with
3.
Main results
For system (2.2) we have the following general properties:
Lemma 3. (Existence of positevely invariant region)
The set ˜Γ={(u,v)∈ˉΩ/ 0≤u≤1,v≥0} is a region positevely invariant.
Proof. Clearly the u−axis and the v−axis are invariant sets because the system is a Kolmogorov type. If u=1, we have
and whatever it is the sign of
the trajectories enter and remain in the region ˜Γ.
Lemma 4. (Boundedness of solutions)
The solutions are bounded
Proof. See [13] or else, applying the Poincaré compactification and the directional blowing-up method [32,33], using the change of variables X=rw and Y=w and the time rescaling given by ζ=w2T; after doing a large algebraic work ([38,39]) a new system is obtained, in which the point (0,∞) is a non-hyperbolic saddle point.
3.1. Nature of equilibrium points over the axis
Lemma 5. For all η=(A,S,C,Q)∈]0,1[×R3+
1. The equilibrium (1,0) is a saddle point.
2. The equilibrium (0,0) is a repeller point.
Proof. Evaluating the Jacobian matrix in each point is immediate that
1) detDYη(1,0)=−S(A+1)2(1+C)2<0.
Therefore, the equilibrium (1,0) is saddle point.
2) detDYη(0,0)=A2C2S>0 and trDYη(0,0)=AC(1+S)>0.
Then, the equilibrium (0,0) is a repeller point.
Lemma 6. The equilibrium (0,C) is
i) a saddle point, if and only if, CQ−A<0.
ii) an attractor point, if and only if, CQ−A>0.
iii) a non hyperbolic attractor point, if and only if, CQ−A=0.
Proof. It is immediate, since evaluating the Jacobian matrix in the point (0,C) we obtain
Therefore, the point (0,C) is
ⅰ) a saddle point, if and only if, CQ−A<0, because detDYη(0,C)<0.
ⅱ) an attractor point, if and only if, CQ−A>0, since detDYη(0,C)>0 and trDYη(0,C)<0.
ⅲ) If CQ−A=0, then, we obtain that detDYη(0,C)=0, trDYη(0,C)<0 and the Jacobian matrix has an eigenvalue zero.
Remark 7. 1. These above results confirm the fact that the predator population is generalist; then, its extinction is avoided.
When the favorite prey is scarse(u=0), the predators attain their environmental carrying capacity C.
2. Let us Wu(1,0), the unstable manifold of the hyperbolic saddle point (1,0), and ˉΣ=Ws(0,C), the stable manifold of the saddle point (0,C) (hypebolic or not).
Then, the relative position of both manifold determines a heteroclinic curve, when Wu(1,0)∩ˉΣ≠ϕ.
3. We note that the positive equilibria lie in the region
3.2. Nature of the positive equilibria
In the following, we consider only the case 1, in which there exists two positive equilibrium point at interior of the first quadrant, they collapse or they do not exist there. In this case, the point (0,C) is a local attractor.
The positive singularities must fulfill the equation of the predator isocline v=u+C and the prey isocline (1−u)(u + A)−Qv=0; so. we obtain
Thus,
Remark 8. Remembering B1=1−A−Q>0, the sign of detDYη(u,u+C) depends on the factor 2u−(1−A−Q).
At once, the sign of trDYη(u,u+C) depends on the sign of
T(u,A,S)=u(1−2u−A)−S(A+u).
We have,
a) If u>1−A−Q2 implies that detDYλ(u,u+C)>0 and the nature of singularity depends on the sign of the trDYλ(u,u+C).
b) If u<1−A−Q2, then detDYλ(u,u+C)<0 and (u,u+C) is a saddle point.
c) If u=1−A−Q2, then the two equilibrium points coincide.
Theorem 9. Nature of the first positive equilibrium
The equilibrium point P1=(u1,u1+C) is a saddle point.
Proof. As detDYη(u1,u1+C)=Su1(C+u1)2(A+u)(2u1−(1−A−Q)), then
Therefore, the equilibrium (u1,u1+C) is a saddle point.
We note that the point (u1,u1+C) is not in the interior of the first quadrant, if and only if, CQ−A<0, and it coincides with (0,C), if and only if, CQ−A=0.
Remark 10. Existence of a separatrix curve
Let Ws+(P1) be the superior stable manifold of P1=(u1,u1+C); it originates a separatrix curve ˉΣ, in the phase plane, whose α−limit can stay out or inside ˉΓ. Any solutions having initial conditions above this separatrix has the point (0,C) as its ω−limit.
Theorem 11. (Existence of a heteroclinic curve)
A subset of parameter exists for which a heteroclinic curve joining the equilibrium points (1,0) and (u1,u1+C).
Proof. Let Wu(1,0) the unstable manifold of the saddle point (1,0) and Ws+(P1) the superior stable manifold of P1=(u1,u1+C). It is clear that the curve determined by the unstable manifold Wu(1,0) remains at ˉΓ by Lemma 3 and its ω−limit can be the point P2=(u2,u2+C) or a stable limit cycle surrounding that point.
Assuming that the α−limit of Ws+(P1) is out of ˉΓ, then the curve ˉΣ, is above the curve determined by Wu(1,0). If the α−limit of Ws+(P1) is inside of ˉΓ, then the curve ˉΣ is below the curve determined by Wu(1,0).
Then, by the Existence and Uniqueness Theorem of solutions [32], there exists a subset on the parameter space for which the two manifolds coincide, forming a heteroclinic curve.
Remark 12. The nature of the equilibrium P2=(u2,u2+C) depends of the relation between vu and vs, the ordinate of the points (u∗,vu)∈Wu(1,0) and (u∗,vs)∈ˉΣ, respectively.
Theorem 13. (Nature of the second positive equilibrium)
Let us u=u∗, any value of u such that u1<u∗<1.
Considering (u∗,vs)∈Ws(u1,v1)=ˉΣ and (u∗,vu)∈Ws(1,0), and
a) Assuming vu<vs, we have:
The equilibrium point P2=(u2,u2+C) is
a1) an attractor point, if and only if, S>u2(1−2u2−A)u2+A,
a2) a repeller, if and only if, S<u2(1−2u2−A)u2+A; furthermore, there exists, at least a limit cycle surrounding this equilibrium point.
a3) a weak focus, if and only if, S=u2(1−2u2−A)u2+A and a Hopf bifurcation occurs.
b) Assuming vu>vs, it has that: The equilibrium P2=(u2,u2+C) is
b1) an attractor surrounded by a unstable limit cycle, if and only if, S>u2(1−2u2−A)u2+A,
b2) a repeller (node or focus) and the trajectories have the point (0,u2+C) as their ω−limit, being this point an almost globally stable equilibrium [45,43].
Proof. a) As the Jacobian matrix is
then,
detDYη(u2,u2+C)=S(u2+C)2(u2+A)(2u2−M)u2>0.
Since 2u2−(1−A−Q)=1−A−Q+√Δ(η)−(1−A−Q)=√Δ(η)>0
the nature of (u2,u2+C) depends on the sign of
i.e., the sign depends on the factor
We have,
a1) trDYη(u2,u2+C)<0, if and only if, S>u2(1−2u2−A)u2+A; therefore, the point (u2,u2+C) is an attractor.
a2) trDYη(u2,u2+C)>0, if and only if, S<u2(1−2u2−A)u2+A; then, the point (u2,u2+C) is a repeller.
As the trace changes sign, a Hopf bifurcation occurs [32] at the equilibrium point (u2,u2+C); then, the point (u2,u2+C) is surrounded by a stable limit cycle.
Furthermore, the transversality condition [32] is verified, since we have that
a3) trDYη(u2,u2+C)=0, if and only if, S=u2(1−2u2−A)u2+A; thus, the point (u2,u2+C) is a weak focus, whose weakness must be determined.
b) When vu>vs, the α−limit of the Ws(u1,v1) can be the repeller equilibrium P2=(u2,u2+C) or an unstable limit cycle surrounding the point P2, when this is an attractor equilibrium.
In the first situation, the Wu+(P1) must coincide with the Wu+(1,0), since the Existence and Uniqueness Theorem applies in the region ˉΛ, or its ω−limit is the equilibrium (0,C).
Assuming the existence of the an unstable limit cycle surrrounding the point P2, therefore this point must be an attractor equilibrium. Then, when the parameters change, that limit cycle coincides with the Ws+(P1), and after is broken. Thus, all the trajectories, except the point P2, tends to the equilibrium (0,C), which is an almost global attractor [45,43].
Remark 14. The equilibrium P2=(u2,u2+C) can be node or focus depending of the quantity
After a few algebraic manipulations it has that the sign of H depends on the factor
H1=(A+u2)2S2+2u2(A+u2)(A+2(1−A−Q)−2u2−1)S+u22(A+2u2−1)2
As it is well-known, the point (u2,u2+C) is a focus, if and only if, H1<0; it is a node, if and only if, H1>0.
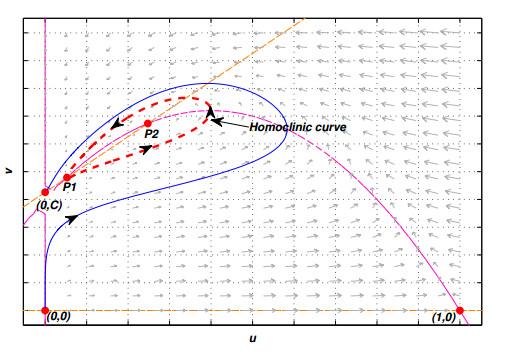
Theorem 15. (Existence of homoclinic curve)
There are conditions on the parameter values for which:
a) It exists a homoclinic curve determined by the stable and unstable manifold of point P1=(u1,u1+C).
b) It exists a non-infinitesimal limit cycle that bifurcates from the homoclinic [41,44] surrounding the point P2=(u2,u2+C).
Proof. We note that if the point (u,v)∈¯P1P2, then dudt>0; clearly, the direction of the vector field at the point lying in the straight line v=u+C is to the right, since
Considering Ws+(P1) and Wu+(P1), the superior stable manifolds and the right unstable manifolds of P1, we have:
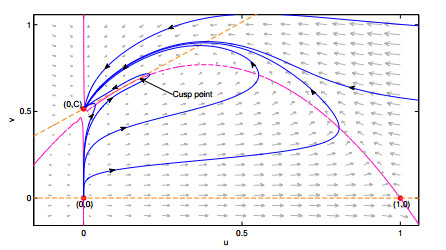
a) As ˉΓ is an invariant region, the orbits cannot cross the straight line u=1 towards the right. The trajectory determined by the right unstable manifold Wu+(P1) cannot cut or cross the trajectory determined by the superior stable manifold Ws+(P1), by Theorem of existence and uniqueness (see Figure 2).
Moreover, the α−limit of the Ws+(P1) can lie at the point (1,0) by lemma 3 or at infinity in the direction of u−axis.
On the other hand, the ω−limit of the right unstable manifold Wu+(P1) must be:
ⅰ) the point P2, when this is an attractor;
ⅱ) a stable limit cycle, if P2 is a repeller.
ⅲ) the point (0,C).
Then, there is a subset on the parameter space for which Wu+(P1) intersects with Ws+(P1) and a homoclinic curve is obtained. In this case, the same point P1 is the ω−limit of the right unstable manifold Wu+(P1).
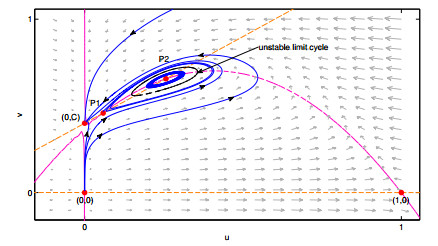
b) When the point P2=(u2,u2+C) is an attractor and the ω−limit of the right unstable manifold Wu+(P1) is the point (0,C), there exists an unstable limit cycle dividing the behavior of trajectories in the neighborhood of P2=(u2,u2+C), which is the frontier of the basin of attraction of that point.
In Figure 2 we show the relative position of the upper stable manifold Ws+(P1) and the right unstable manifold Wu+(P1), meanwhile in Figure 3 the homoclinic curve is shown.
Remark 16. An interesting aspect happens when the homoclinic curve is broken, since a non-infinitesimal limit cycle is generated [41]. To determine the nature (stability) of this non-infinitesimal limit cycle, we will consider R, the absolute value of the ratio between the negative and positive eigenvalues of the Jacobian matrix evaluated in the saddle point P1=(u1,u1+C), denoted by λ− and λ+, respectively, i.e., R=|λ−λ+|.
Considering a little modification of the criterion described in [26] it has that if R>1, the non-infinitersimal limit cycle generated by homoclinic bifurcation is stable (orbitally); if R<1, this limit cycle is unstable and if R=1 the limit cycle is neutrally stable [26]. So, R depends on the sign of the difference ∇=|λ−|−λ+.
We know that
Then, the eigenvalues of the Jacobian matrix evaluated on P1 are:
with λ−<0<λ+ and
We have the following:
Theorem 17. (Stability of the non-infinitesimal limit cycle)
The non-infinitesimal limit cycle is:
a) stable, if and only if, T(u1,A.S)>0, i.e., S<u1(1−2u1−A)A+u1.
b) unstable, if and only if, T(u1,A.S)<0, i.e., S>u1(1−2u1−A)A+u1.
c) neutrally stable, if and only if, T(u1,A.S)=0, i.e., S=u1(1−2u1−A)A+u1.
Proof. Clearly, ∇= |λ−|−λ+= (C+u1)trDYη(u1,u1+C)=0.
By remark the sign of trDYη(u1,u1+C) depends on the sign of the factor
Considering R=1, we have S=u1(1−2u1−A)A+u1 and the non-infinitesimal limit cycle is neutrally stable.
Then, the other possibles cases a) and b) are obtained with R>1 and R<1, respectively.
Remark 18. 1. The breaking of the homoclinic curve determined by the intersection of the upper stable manifold and the unstable right manifold of the saddle point P1=(u1,u1+C), i.e., Ws+(P1)∩Wu+(P1), generates a non-infinitesimal limit cycle (originating a homoclinic bifurcation), which could coincide with other limit cycle obtained via Hopf bifurcation (infinitesimal limit cycle), when P2=(u2,u2+C) is a center-focus.
2. The non-infinitesimal limit cycle increases until concide with Ws+(P1); then is broken, and the point P2 becomes to a repeller focus or node; so, the point (0,C) an almost global attractor [45,43].
3.2.1. Multiple Hopf bifurcation
In the next Theorem we determine the weakness of the focus P2=(u2,u2+C), i. e., the number of the limit cycles bifurcating of a weak (fine) focus [32,33]; for this we will use the calculations of the Lyapunov numbers (or quantities) [32,44].
Theorem 19. (Order of the weak focus)
The singularity P2=(u2,u2+C) of vector field Yη is at least a two order weak focus, if and only if, S=L(1−2L−A)A+L, with u2=L=12(1−A−Q+√Δ(η)) and η2 can change of sign.
Proof. As S=L(1−2L−A)A+L and Q=1L+C(1−L)(L+A), system (2.2) can be expressed by
where ν=(A,L,C)∈(]0,1[)2×R+.
Setting u=U+L and v=V+C+L, then the new system translated to origin of coordinates system is
The Jacobian matrix of the vector field Zν at the point (0,0) is
DZν(0,0)=(L(1−2L−A)(C+L)−(1−L)(A+L)LL(1−2L−A)(C+L)−L(1−2L−A)(C+L)),
the same that DYη(L,L+C). Denoting
it has
the first Lyapunov quantity [32] is
The Jordan matrix associated [3] to vector field Zν is
Then, the matrix change of basis [3] is given by
Now consider the change of variables given by
that is,
or
Then the new system is
After a large algebraic calculations and by means of a time rescaling given by γ=Wτ, we obtain the normal form ˜Zν [32] to vector field Zν given by
with
Using the Mathematica package [46] for the symbolic calculus, we obtain that the second Lyapunov quantity [32] is given by
with f1(A,C,L)=f10(A,L)+Cf11(A,L)+C2f12(A,L)+C3f13(A,L)
where
Because to the difficulty in deciding whether a change of sign occurs in the factor f1(A,C,L), a numerical evaluation will be made for the factor f10(A,L), considering it is most influential when C tends to 0.
Choosing A=0.1 we have
with
and choosing L=0.175 it has,
then,
Analogously, choosing A=0.1 and L=0.2, we have
So, η2 change the sign depending of the above relations, existing at least, two limit cycles when η2=0.
Then, the sign of η3 must be obtained to prove the existence of exactly two limit cycles.
Remark 20. 1. As we have seen, the computation of weakness of the focus P2=(L,L+C) requires the fulfilment of two strict relationships between the parameters of the model; a little deviation in one of them causes the condition for the existence of one or more limit cycles. So, these relations determine a subset of measure non-zero for the existence of two limit cycles.
2. This is ecologically important, inasmuch as in reality none of the equalities given in the above Theorem will be possible to maintain for a long time; thus, any tiny change in some of the involved parameters will imply inequality rather than equality; hence, we have a structurally unstable system.
3. We note that the proof of the above theorem does not depend on the sign of a0=CQ−A.
Case 1.2 By considering Δ(η)=(1−A−Q)2−4(CQ−A)=0, the points P1=(u1,u1+C) and P2=(u2,u2+C) are coincident.
So, u1=u2=E=1−A−Q2, if and only if, C=(1−A−Q)2+4A4Q. The point (u2,u2+C) lies in the first quadrant, if and only if, 1>A+Q.
Theorem 21. (Collapse of the positive equilibria)
The equilibrium point (E,E+C) with E=1−A−Q2, is:
i) a saddle-node attractor, if and only if, S>Q(1−A−Q)A−Q+1,
ii) a saddle-node repeller, if and only if, S<Q(1−A−Q)A−Q+1,
iii) a cusp point, if and only if, S=Q(1−A−Q)A−Q+1.
Proof. The Jacobian matrix is
Then, detDYη(E,E+C)= 0, and
which depends on the sign of factor
Then, the point (E,E+C) is
ⅰ) a saddle-node attractor, if and only if, S>Q(1−A−Q)A−Q+1,
ⅱ) a saddle-node repeller, if and only if, S<Q(1−A−Q)A−Q+1,
c) If S=Q(1−A−Q)A−Q+1, the Jacobian matrix is
whose Jordan form matrix is J=(0100) [3], and we have the Bogdanov-Takens bifurcation or bifurcation of codimension 2 [47], and the point (E,E+C) is a cusp point.
In this case, the point (0,C) is an attractor almost globally asymptotically stable [45,43], since an unique trajectory exists in the phase plane having the point (E,E+C) as its ω−limit.
Case 1.3 If B1=1−A−Q>0 and B2=CQ−A>0 and Δ(η)<0, there were not exist positive equilibrium points.
Theorem 22. (Non-existence of positive equilibria)
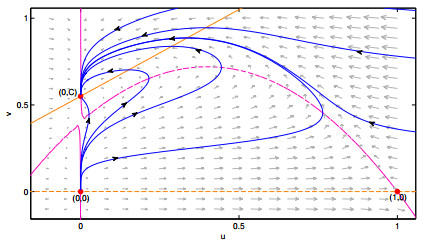
When there exists no positive equilibria, the point (0,C) is globally asymptotically stable.
Proof. By lemma 5, we know the solutions are bounded; by lemma 3, ˉΓ is invariant region. As it was stated before, the equilibrium (1,0) is a saddle point, then the Poincaré-Bendixon Theorem applies and the unique ω−limit of the trajectories is the point (0,C).
4.
Some simulations
In order to reinforce the obtained results, we show some numerical simulations (Figures 4–9), considering only the case 1, i.e., B1=1+A−Q>0, B0=CQ−A>0 and Δ>0, being in this case the point (0,C) always attractor (local or global).
4.1. Bifurcation diagram
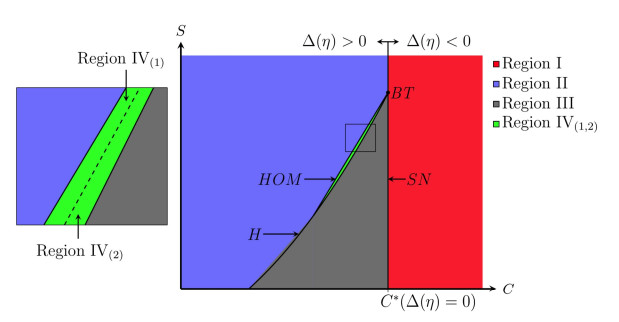
In the following picture (Figure 10) the bifurcation diagram of system (2.2) is shown.
Considering A and Q fixed it was created with the numerical bifurcation package MaTCont [40] showing that the bifurcation curves divide the (C,S)-parameter space into five parts. Modifying the parameter C impacts the number of positive equilibrium points of system (2.2).
The modification of the parameter S changes the stability of the positive equilibrium point P2 of system (2.2), while the other equilibrium points do not change their behaviour.
There are no positive equilibrium points in system (2.2) when the parameters C and S are located in the red area where Δ<0. In this case, the origin is a global attractor.
For C=C∗, which is the saddle-node curve SN, the equilibrium points P1 and P2 collapse since Δ=0. So that, system (2.2) experiences a Bogdanov-Takens bifurcation. When the parameters C and S are located in the green, grey or blue area, system (2.2) has two equilibrium points P1 and P2.
The equilibrium point P1 is always a saddle point, while P2 can be unstable (grey area) or stable (blue area). For C and S in the green area the stable equilibrium point P2 can be surrounded by an unstable limit cycle (green Region IV(1)) or surrounded by two limit cycle (green Region IV(2)).
5.
Conclusions
In this work, a modified May-Holling-Tanner predator-prey model was studied, particularly a modified Leslie-Gower model [13,25,5], considering that predators can eat other prey in the case of severe scarcity of its most favorite food. This situation was taken into account by adding a positive constant c in the function Ky representing the environmental carrying capacity for predators. This implies the existence of a new equilibrium point (0,c) in the y−axis.
By means of a diffeomorphism, we analyzed a topologically equivalent system depending only on four parameters. It was shown that the model has a rich dynamic since this model can exhibit various kinds of bifurcations (e.g. saddle-node, Hopf-Andronov, Bogdanov-Takens, homoclinic, Hopf multiple bifurcations) as likewise infinitesimal and non-infinitesimal limit cycles, generated by Hopf and homoclinic bifurcation, respectively.
Conditions for the existence of equilibrium points and their nature were established. We proved that the equilibrium point (0,0) is always a repeller for all parameter values, which means that there is no extinction of both populations simultaneously; moreover, (1,0) is a saddle point, implying that the predator population can go to depletion, meanwhile the prey attains its maximum population size in the common environmental.
Also, a wide subset of the parameter values was determined, for which there exist two positive equilibrium points P1=(u1,u1+C) and P2=(u2,u2+C), being the first of them always a saddle point. The other equilibrium can be an attractor, a repeller or a weak focus, depending on the sign of the trace of its Jacobian matrix. Furthermore, both equilibrium points can collapse, obtaining a cusp point, i.e., Bogdanov-Takens bifurcation or codimension 2 bifurcation [47].
When two equilibrium points exist at the interior of the first quadrant in the system (2.2), the singularity (0,C) is an attractor and the stable manifold Ws(P1) of P1 determines a separatrix curve which divides the phase plane into two regions. The trajectories having initial conditions above this curve have the point (0,C) as their ω−limit, meanwhile, those that lie below the separatrix can have a positive equilibrium point or a stable limit cycle as their ω−limit. This implies that there exists a great possibility for the prey population to go to extinction, although the ratio prey-predator is high (many prey and little predators).
We also prove the existence of a homoclinic curve determined by the stable and unstable manifolds of the positive saddle point P1, encircling the second positive equilibrium point P2; when it breaks up it originates a non-infinitesimal limit cycle.
The dynamics of the studied model, in which the predators have an alternative food to low densities of prey, differs from the May-Holling-Tanner model [3,5], since:
ⅰ) System (2.1) can have one, two or none positive equilibrium points at the interior of the first quadrant with a more varied dynamic; whereas, the May-Holling-Tanner model has a unique positive equilibrium point, which can never be a cusp point, then there no exists Bogdanov-Takens bifurcation for this model.
ⅱ) In system (2.1) there is a parameter constraint for which a homoclinic curve exists, something that does not appear in the May-Holling-Tanner model.
ⅲ) Each model has a separatrix curve dividing the behavior of the trajectories, which are originated by, the non-hyperbolic saddle point (0,0), in the May-Holling-Tanner model, and in the modified model is created by the hyperbolic attractor point (0,C).
ⅳ) Both models have in common the existence of triple or bi-stability since two limit cycles can bifurcate of a weak focus, surrounding an attractor positive equilibrium point, being the innermost unstable (frontier of the attraction basin) and the outermost stable.
But, in the model here analyzed, this situation also can appear when exist two positive equilibria (see Figure 7) or when exists a unique equilibrium at the interior of the first quadrant (For instance, when A=0.2, C=0.4, Q=0.5 and S=0.12005, i.e., CQ−A=0, when A=0.2000001, C=0.39999925, Q=0.5 and S=0.12005, i.e., CQ−A<0). In the Holling-Tanner model, the two limit cycles appear when there is one positive equilibrium point.
The triple-stability phenomenon exists in the system (2.2) when simultaneously are stable: (1) the point (0,C); (2) the positive equilibrium P2; and (3) a limit cycle, for a determined set of parameters; then, for these parameter values, both populations can coexist, oscillate around specific population sizes or prey population can be depleted and the predators survive as an alternative food.
It can conclude that for certain parameters values in the system (2.2), there exists self-regulation since the species can coexist experimenting oscillations of their population sizes surrounded a fix point, or else, the population sizes can tend to that fix point. But, depending on the ratio prey/predator the prey population can go to extinction for the same parameters values.
Moreover, system (2.2) is sensitive to disturbances of the parameter values, since there exist changes of the basin of attraction of P2 as it is shown in Figures 4–8.
The self-regulation depends mainly on the parameter S= sr. This implies that increasing the intrinsic predator growth rate s or decreasing the intrinsic prey growth rate r, the possibility of oscillations of the population sizes increase. Similar statements can be derived for other parameters values of the system (2.2).
The complex dynamic of the analyzed model is a prominent issue to be considered by the ecologists and agencies responsible for conservation and management of renewable resources, as the open access fisheries.
This concern must be especially with those populations more sensitive to disturbances of the environment, considering that for given initial condition the dynamic of the model predicts the long term persistence of the populations, or else, the extinction of one of them.
On the other hand, the system (2.1) could have a behavior nearest to the model studied in [22], where c=0, or with the model analyzed in [37], since the Allee effect implies a closer dynamic, due to the existence of two positive equilibria.
In short, in this article, we extend the dynamical properties of the model proposed in [13] and the partial results obtained in previous papers [23,24,1,29,2]; we also complement the outcomes obtained in [5] for the May-Holling-Tanner model, showing that the modified model has interesting and rich mathematical dynamics, describing different possible ecological behaviors.
Acknowledgments
This work was partially financed by DIEA PUCV 124.720/2012.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: