1. Introduction
Working forest landscapes in the northern United States are characterized by a mosaic of ownership and management strategies that reflect a variety of conservation and resource utilization goals [1]. The Wild Rivers Legacy Forest area in northeastern Wisconsin is an example of such a landscape, with federal, state, and county forest, as well as areas managed by timber investment management organizations (TIMOs) and private industrial and non-industrial owners. Though each owner operates to achieve individual goals, impacts on land cover composition and configuration are realized at the landscape scale and over the long term. Management actions interact with natural disturbances to impact ecosystem functions and provisioning of ecosystem services, especially timber and other forest products. The magnitude and frequency of management can have unforeseen consequences at large spatial (103-106 ha) and temporal (decades to centuries) scales [2,3,4]. Therefore, land managers and conservation practitioners can benefit from insights into the possible cumulative outcomes of management activities which can be key in landscape-scale management planning and achieving conservation goals.
Modeling spatially defined scenarios can assist in assessing the impacts of different management strategies on land cover and inform management planning and decision-making [5,6,7,8]. Scenario development is often used as a tool to conceptualize how management and other factors such as climate change and socioeconomic conditions may impact landscapes at broad spatial scales [9]. Furthermore, landscape scenario analysis can be used to develop adaptive management strategies that better respond to broader spatio-temporal challenges [10], with some limitations attributable to inherent simplification [11].
State-and-transition simulation modeling (STSM) has been used to project ecosystem responses to different disturbances, such as land use change, management practices, and climate change. Provencher and colleagues used STSM to simulate alternative scenarios of livestock grazing, vegetation management, and fire disturbance on western public lands [12]. In another example, Frid and colleagues used STSM to capture the effects of different management strategies on the invasion of bufflegrass in Arizona’s Sonoran Desert [13]. In STSMs, ecological systems are represented by a set of states that represent defined assemblages of plant species, often capturing different seral stages. Transitions define the direction and probability of a state change based on stand succession (aging), natural disturbances, or management activities. While some STSMs are aspatial, the VDDT/TELSA platform used here simulates the spatial dynamics of land cover and disturbances on the landscape [14,15].
At the forefront of STSM and other ecological modeling efforts is the need to incorporate climate change and its impacts. Land managers and conservation practitioners must consider the potential impacts of climate change on ecosystem dynamics and potential interactions with management strategies when planning for the future of their landscapes. A variety of approaches to capturing climate change in STSM are emerging [16,17,18,19]. Two specific examples of these efforts include Nowacki and Abrams, who incorporated temperature patterns and species tolerance into STSM to project potential vegetation changes and predict future tree species habitats [20], and Costanza and colleagues, who used historical emissions data to inform and develop scenarios of alternative wildfire probabilities to capture climate change using STSM and determine the impacts that varied anthropogenic disturbances may have on the resilience of a Pinus palustris ecosystem [21].
We have developed an approach that uses collaborative scenario development and STSMs to provide land managers and conservation practitioners with a comparison of potential landscape outcomes of alternative management scenarios and climate-related disturbances, and we have applied this approach in the Wild Rivers Legacy Forest (WRLF) area. Three scenarios were developed with input from local land managers, scientists, and conservation practitioners to represent a range of conservation strategies: 1) continuation of current management, 2) expanded working forest conservation easements (WFCE), and 3) cooperative ecological forestry [22]. Scenarios were modeled under current climate with contemporary natural disturbance regimes and under increased probability of windthrow and wildfire. Potential changes in these natural disturbances were of particular concern to local and regional land managers [22], and they are projected to be important potential drivers of landscape change over the next century in northern forests [23,24].
Here, we describe how we incorporated two potential impacts of climate change on natural disturbances and alternative management scenarios into a STSM to inform management decisions in the WRLF area. We compare landscape and class metrics of composition and configuration that together indicate landscape scale heterogeneity in the WRLF. Landscape heterogeneity can act as an indicator of resilience, where areas that contain more diverse forest and wetland patches in terms of cover class, age, patch size and spatial arrangement may better maintain ecosystem function under stressors such as climate change [6,25]. We also discuss how these results can inform management decisions in this area, as well as implications for applying STSMs to explore potential interactions between changes in natural disturbances and management in working forest landscapes.
2. Materials and Methods
2.1. Study area: Wild Rivers Legacy Forest, Wisconsin
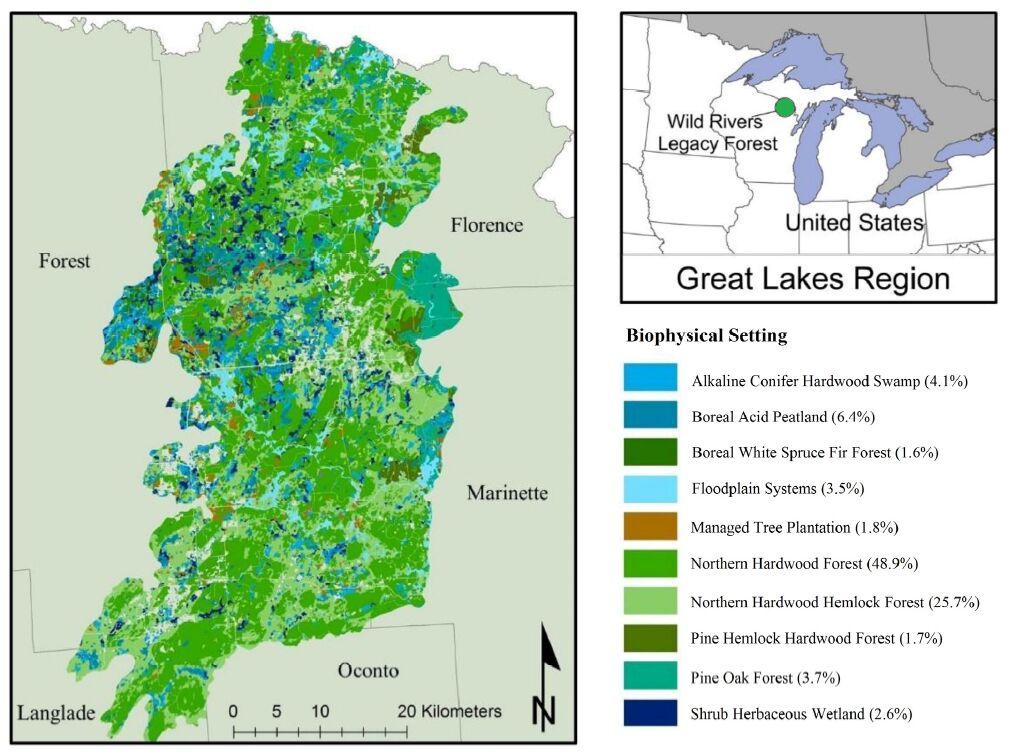
The Wild Rivers Legacy Forest (WRLF) study area encompasses 218,792 ha of forests and wetlands in northeastern Wisconsin (Figure 1). The conservation and land management organizations in this area initially collaborated to conserve a smaller area directly adjacent to the Pine and Popple Wild Rivers to create the WRLF, which makes up approximately 1% of this study area. Taking its name from this reserve, the larger study area boundary encompasses five land type associations (LTAs), which were chosen to represent landscape scale processes and incorporate multiple ownerships and land cover classes.
Land cover was represented by LANDFIRE Biophysical Settings (BpS) and successional-class data [26,27,28]. Local experts—scientists and land management practitioners working in this landscape—reviewed both data sets for accuracy. The BpS data represents vegetation that would dominant each 30 m pixel based on abiotic features (e.g., soils, surficial geology and the natural disturbance regime). The current land cover was represented by combining BpS data with the successional class data which represents the developmental stage of each BpS during the mapping period (ca 2000) as classified and described in the BpS models [26,29]. Land cover in the WRLF falls into ten classes: Northern Hardwood Forest (48.9%), Northern Hardwood Hemlock Forest (25.7%), Boreal Acid Peatland (6.4%), Alkaline Conifer Hardwood Swamp (4.1%), Pine Oak Forest (3.7%), Floodplain Systems (3.5%), Shrub Herbaceous Wetland (2.6%), Managed Tree Plantation (1.8%), Pine Hemlock Hardwood Forest (1.7%), and Boreal White Spruce Fir Forest (1.6%) (Figure 1). All of these land cover types are described in detail in Appendix A.
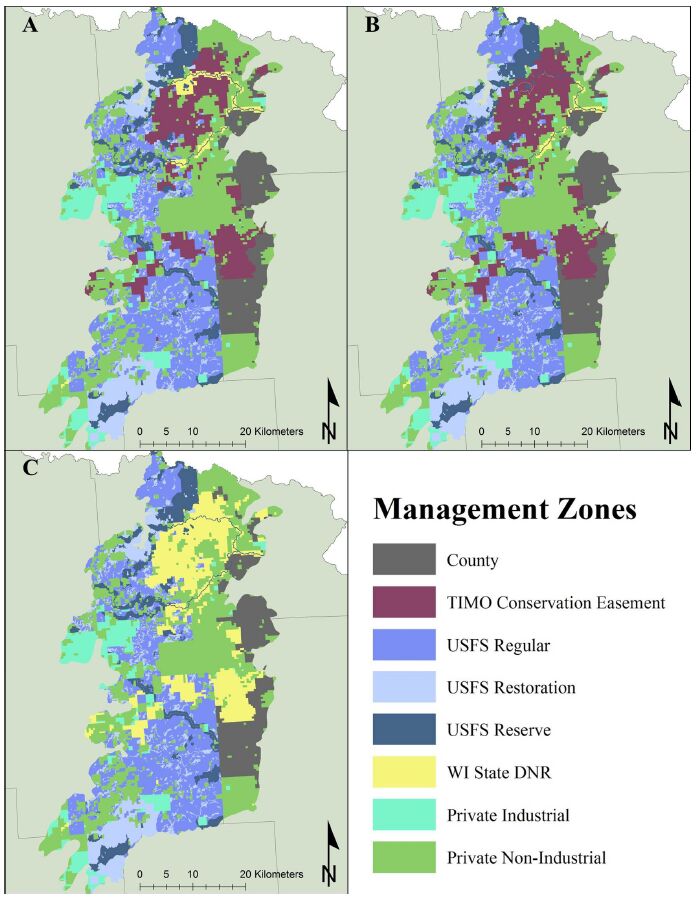
Lands within the study area are owned and managed by the United States Forest Service (USFS), Wisconsin Department of Natural Resources (WIDNR), county governments, private non-industrial land owners, private industrial land owners, and timber investment management organizations (TIMOs) (Figure 2A). USFS lands are divided into three different management zones —regular, restoration, and reserve. Management objectives for the USFS regular management zone are to provide habitat for wildlife, enable a variety of recreational activities, and support sustainable timber harvest. Primary management goals within the USFS restoration management zone are to maintain or restore unique vegetative communities to their desired conditions while providing habitat for wildlife and opportunities for a variety of recreational activities. The USFS reserve management zone is managed for wilderness qualities, and no timber harvesting or restoration activities occur on these lands unless under exceptional circumstances. Low-impact recreation and limited research activities are allowed. The WIDNR’s management goals in the study area are to maintain or restore the hardwood ecosystem and water quality of the Pine River, a headwater tributary to Green Bay and the Great Lakes. Some timber harvesting compatible with these goals takes place on WIDNR land. County forests are managed for multiple uses, with the goals of providing timber, recreational opportunities, wildlife habitat, watershed protection, and stabilization of stream flow. While the individual goals of private non-industrial forest land owners vary, we assume that these individuals are enrolled in either Wisconsin’s Managed Forest Law or Forest Crop Law programs, which are forest tax programs that encourage sustainable forest management on private lands by providing property tax incentive to landowners [30]. Management objectives for private industrial forest owners typically maximize economic returns on timber harvest with no ecological or recreational use goals. The management goals of TIMOs in this study area are primarily to conduct sustainable timber harvesting while maintaining the ecological integrity of the lands they control in agreement with WFCEs. While several easements are encompassed within the study area, each with a unique set of restrictions, all include restrictions on timber harvesting, development, and subdivision.
To meet these goals, land managers in each management zone employed a variety of silvicultural systems, principally even-aged management, uneven-aged management, and restoration forestry. Even-aged management is simulated here by sequential treatments of thinning and clearcutting. Thinning is the removal of trees within a stand, often malformed stems or undesirable species, to reduce the density of trees in the stand and facilitate the growth of the remaining trees. Here, thinning is an intermediate stand treatment and does not change the seral stage or “state” of a stand in these models. Once a stand has matured, clearcutting is used as the final timber harvest method, where all trees in a stand are removed at the same time. In these models, clearcutting changes the seral stage or “state” of the stand changes to the youngest class in the cover type. Stands managed in an even-aged silvicultural system have trees in a single age class. It is these even-aged, stand-replacing disturbance activities that create patches on the landscape. Uneven-aged management is simulated here through selection cutting, where single trees or groups of trees are removed from a stand while the majority of the trees in the stand remain. Similar to thinning, selection cutting does not change the seral stage or “state” of a stand in these models. Selection cutting may also be employed to occasionally harvest individual trees or groups of trees in a cover type managed under even-aged silviculture. Restoration forestry captures a range of management activities aimed at maintaining or improving the ecological conditions of a stand, such as gap creation, removal of undesirable species, and planting. Depending on the cover type, restoration forestry may change the state of a stand or a stand may remain in the same state.
The management activities employed in each cover type as well as their entry size, spatial arrangement, and annual area goal varied by management zone and by management scenario. Information about these activities is aggregated to the landscape level to respect the privacy of stakeholders and encourage trust and collaboration. Generally, entry sizes for thinning and clearcutting activities were 8-121 hectares (ha), 4-121 ha for selection cutting, and 8-20 ha for restoration forestry. Annual area totals for each management activity varied by scenario and are described in further detail in the next section.
2.2. Scenario development
Plausible alternative management scenarios for this study area were developed by a team of local experts that consisted of scientists and land management practitioners who work on this landscape. Local experts included foresters, forest ecologists, and wildlife biologists from the WIDNR; forest ecologists, conservation specialists, and wildlife ecologists from The Nature Conservancy (TNC); biologists and forest ecologists from the USFS; foresters from the TIMOs that fall within the boundaries of the study area; and landscape ecologists from the University of Wisconsin-Madison. Information was elicited from these participants through a series of in-person workshops, web-based workshops, and one-on-one interviews. The process was fully described by Price et al. [22]. Scenarios were captured by varying spatial arrangement of ownership on the landscape to redefine the spatial extent and location of the different management zones (Figure 2).
2.2.1 Current management scenario
This scenario captured the current spatial arrangement of management on the landscape and a continuation of current management practices over time (Figure 2A). Management zones in this scenario in order of percent of the landscape were private non-industrial forestry (30%), USFS under regular management (22%), TIMO under a conservation easement (13%), county (10%), USFS under restoration management (10%), USFS under reserve management (7%), private industrial (6%), and WIDNR (2%). Under this scenario, annual harvest goals for selection cutting were the lowest of all three scenarios and thinning levels were greater than both other scenarios (Table 1).
Table 1. Average annual management goal for each scenario by activity type (ha/year).
| Scenario |
Selection cutting |
Clearcutting |
Thinning |
Restoration |
| Current management |
6382 |
548 |
717 |
11 |
| Expanded conservation easement |
6532 |
547 |
689 |
3 |
| Ecological forestry |
6391 |
547 |
667 |
100 |
2.2.2. Expanded easement scenario
This scenario simulated an alternative landscape in which there was an increase in the area of land managed under WFCE restrictions. Management zones were the same as those defined under the current management scenario except for an increase in land managed by a TIMO under WFCE from 13 to 14% of the landscape and a decrease in the land managed by the WIDNR from 2 to 1% (Figure 2B). Compared to the current management scenario, WFCE restrictions were placed on land adjacent to the federally designated Pine and Popple Wild Rivers, which are a conservation priority. Under this scenario, the annual harvest goal for selection cutting was greater than under the other two scenarios and goals for thinning were less than the current management scenario but greater than the ecological forestry scenario (Table 1).
2.2.3. Ecological forestry scenario
This scenario simulated an alternative landscape in which ecological conservation goals were emphasized through collaborative management among organizations. In this scenario, the portion of land managed by a TIMO under WFCE restrictions in the current management scenario was instead combined with WIDNR lands to form a single cooperative ecological management zone (14% of the landscape), where a conservation organization and the WIDNR collaboratively applied ecological forestry practices. These ecological forestry practices were defined as an increase in restoration forestry to achieve old growth characteristics and smaller average entry size as compared to the other scenarios (Figure 2C). Under this scenario, annual harvest goals for selection cutting were larger under this scenario than under the current management scenario but less than under the expanded easement scenario; thinning goals were the lowest in this scenario; and restoration forestry was the highest of all scenarios (Table 1).
2.3. Climate-related disturbances
All three scenarios were modeled under the current natural disturbance regime and under increased climate-related disturbances. Current climate conditions reflect contemporary return intervals for all natural disturbances, including windthrow and wildfire [26,27,31]. Increased climate-related disturbances were defined in the collaborative stages of this project. We consulted the team of local experts and managers, modeling software developers, and other scientists to define feasible and meaningful ways to model potential increases in stand-replacing disturbances due to climate change. Here, we do not attempt to model climate change, but instead focus on modeling disturbances that are of direct concern to the collaborators and are relevant to this region.
Climate change is projected to result in increased temperature in the study area throughout the year, especially during the winter months. Precipitation is projected to increase in winter and spring and decrease in summer, with an increase in the frequency of heavy precipitation events [23,24]. These changes in climate are expected to have wide-ranging impacts in the study area, from changes in phenology to shifts in species ranges to alterations in the natural disturbance regime. Janowiak and colleagues in their simulations of climate change as well as the Wisconsin Initiative on Climate Change Impacts (WICCI) in their examination of potential climate change impacts, provide in-depth analyses of the full range of potential climate change impacts and vulnerabilities of forests and wetlands in Wisconsin [23,24].
Experts in the WRLF identified increased windthrow and wildfire as the climate change impacts of greatest concern in this landscape. Historically, fire and windthrow were the major disturbances shaping forests of northern Wisconsin [31,32]. Projected increased temperature in fall and spring combined with drier summer months are expected to increase the length of the fire season as well as the susceptibility of landscapes to ignition from natural sources [33,34,35,36,37]. Though, the precise response of fire return intervals and size distribution to climate change and the interactions with fire suppression efforts are difficult to discern, it has been projected that fire could increase 60-100% by 2100 in this area [38].
The response of windthrow events to climate is also difficult to predict. Available data do not indicate a change in the central tendency or 90th percentile of the wind speed distribution in the Midwest from 1979 to 2000 [39] though climate in the region has changed over this period. The frequency of intense wind conditions and blow downs remains less understood. Windthrow events are extremely localized and are the result of conditions that change on a relatively short timescale, including soil saturation and wind gusts [40]. Though efforts are underway to relate severe wind events to climate variables, researchers assert that understanding of tornado and derecho formation remains inadequate for predicting how climate will affect the frequency or severity of windstorms in the future [40,41,42]. In an investigation of the possible influence of climate change on wind damage in northern forests, Peterson concludes that greater understanding of the formation of tornadoes and downbursts as well as improved resolution in global climate models will be needed to enable reliable predictions of changes in windthrow events [40]. However, some positive correlations between mean monthly temperature and tornadoes have been reported [42]. Further, heavy precipitation events in the Midwest are expected to continue to increase in frequency [23,24]. Heavy rains result in saturated soils and are often accompanied by high winds, both of which increase the likelihood of windthrow events. Increased windthrow was modeled as a climate-related disturbance expected to increase because of local experts’ interest in its possible impacts on the study landscape.
Under the increased climate disturbance conditions, the probability of wildfire and windthrow were gradually and linearly increased over the duration of the simulation from current probability to a maximum probability 50% greater than current conditions at year 100. The 50% increase was used here as an easily understood heuristic to enable conservation practitioners and land managers to explore and visualize the potential impacts of climate disturbances in the WRLF. While changes in windthrow and wildfire are uncertain, we have modeled an increase in their probability rather than a decrease or no change, because an increase in these stand-replacing disturbances could compound land management and timber harvest planning in the study area. These scenarios are meant to be illustrations of possible future conditions rather than predictions. This approach of incorporating the increase of two possible stand replacing disturbances allows for the testing of a range of conditions when uncertainty is high.
2.4. Modeling
All scenarios were modeled using the VDDT/TELSA modeling suite developed by ESSA Technologies Ltd. [14,15]. Modeling methodology was fully described in Price et al. [22] and is described briefly here. Aspatial STSMs of succession and natural disturbance in each land cover type were developed in VDDT (Vegetation Dynamics Development Tool) by modifying Vegetation Dynamics Models previously created and validated by LANDFIRE [26]. Natural disturbances included in the STSMs used here are windthrow, wildfire, insect pests and diseases, and flooding. The LANDFIRE base models used in this project are fully described in the LANDFIRE Biophysical Setting Model description for Map Zone 50, and can be downloaded from LANDFIRE [26,43] (Appendix A). In each BpS model, forest communities are static—species composition and structure are defined a priori for each seral stage or “state” within a land cover type. An ecological model for managed tree plantations on this landscape was also designed specifically for this landscape to represent white pine plantations. These plantations are exclusively white pine (Pinus strobus) and managed under an even-aged silvicultural system. States in this ecological model represent early and mid-succession seral stages, and the probabilities of natural disturbances are the same as in the Pine Oak BpS model (Appendix A). For all land cover models used here, probabilities of windthrow and wildfire were modified and transitions representing management activities were added based on input from local experts. These VDDT models along with maps of land cover and management zones were used as inputs for TELSA (Tool for Exploratory Landscape Scenario Analyses).
TELSA is a spatially interactive forest landscape model designed to project the spatial interactions of succession, natural disturbances, and management at the broad spatial scales (up to 250,000 ha) over decades to centuries. For each simulation year, TELSA first simulates natural succession for every polygon based on the rate and direction of succession and the resulting polygon characteristics defined in the VDDT STSMs. Next, TELSA simulates natural disturbances in a random order. For each natural disturbance type, the model calculates the expected area affected annually by the disturbance as the sum of the products of the area of all polygons with a non-zero probability of that disturbance and the probability of the disturbance multiplied by the annual variation and long-term trend for the disturbance. The size distribution for the disturbance is used to distribute the total area affected annually into multiple, discrete disturbance events. Then, disturbance events are applied to the landscape—a target disturbance size is drawn from the size distribution; initiated in a random, eligible polygon; and spreads to neighboring eligible polygons until the target size has been met or no adjacent polygons are eligible. Simulation of a disturbance type is complete when the expected area affected annually has been met or no eligible polygons remain. Lastly, TESLA simulates management by generating a list of management units (groups of neighboring polygons under the same management system) based on their current vegetation state and orders them according to management priority, which can be random or based on user defined criteria (e.g. stand age or volume). Management is applied until the area limit for each activity has been reached or all eligible units have been managed [14].
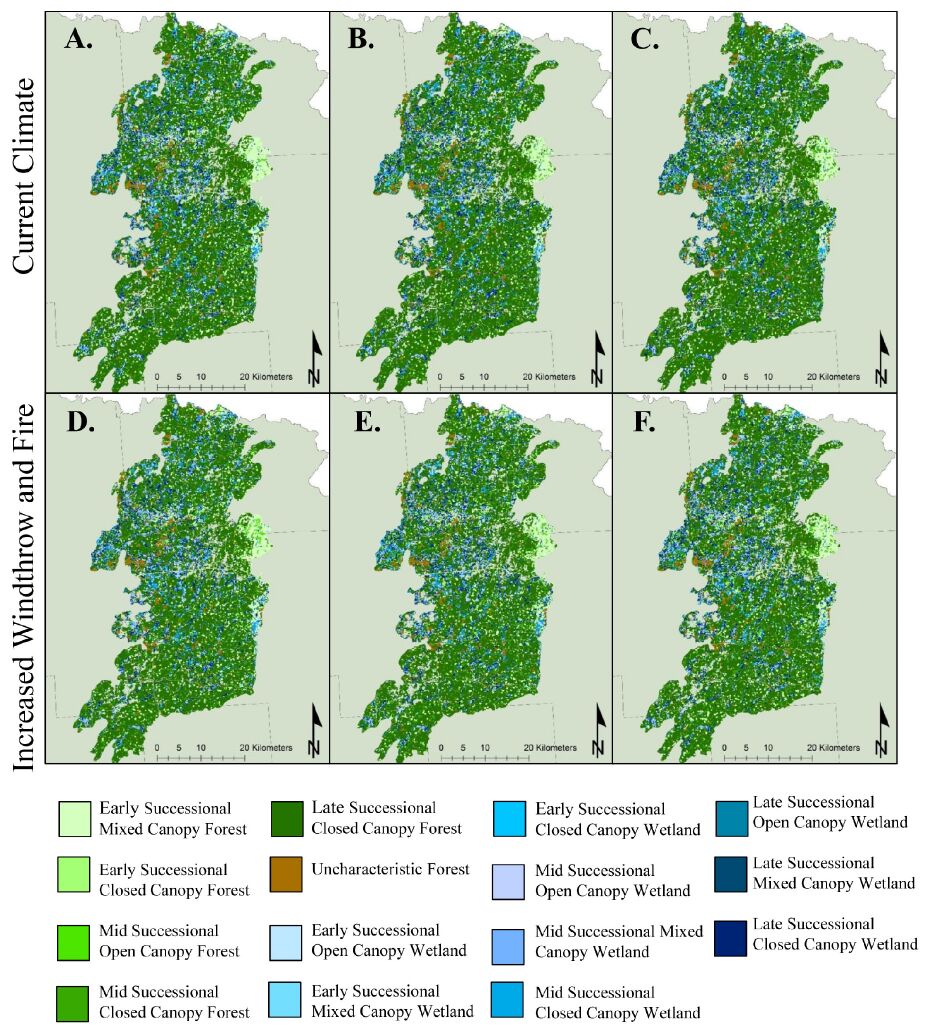
Maps of current management and alternative management boundaries were created in ArcMap 9.3 [44] based on TNC data, USGS Gap Protected Areas data, and scenario descriptions. TELSA® was used to simulate the spatial land cover change with a yearly time step. The scenarios were modeled for 100 years, from 2010 to 2110, under two natural disturbance regimes—the current natural disturbance regime and increased probability of windthrow and wildfire—to produce maps of potential future land cover. Each scenario was modeled for 10 Monte Carlo iterations under both climate conditions. Appendix B shows the accumulated disturbances for each scenario to illustrate the relative influence of each disturbance on the outcomes of the simulations.
2.5. Analysis
Land cover maps resulting from each scenario at year 100 were reclassified as forest and wetland classes of a specific age and canopy closure (Appendix C) using ArcGIS 9.3 [44]. Spatial analysis was performed to quantify the impact of different management scenarios and climate disturbance conditions. Metrics measuring land cover composition and configuration under initial conditions and at year 100 were calculated using the 4-neighbor rule in FRAGSTATS [45]. In this context, metrics of composition capture what land cover classes are present and in what amount. Metrics of configuration measure how land cover classes are arranged on the landscape. We chose metrics that quantify each of these characteristics at the landscape level and within each class as recommended in landscape ecological literature [25,46] to assess how land cover composition and configuration differed between scenarios. We took care to choose metrics that were not closely correlated [47].
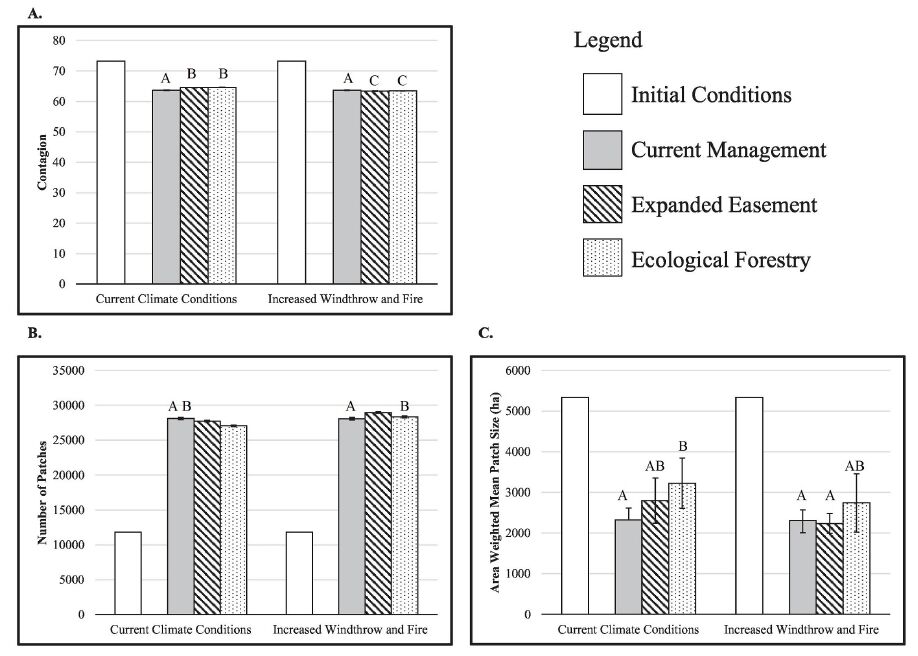
At the landscape level, metrics of composition were number of patches within the landscape as a whole and area-weighted mean patch size, a calculation of the average patch size within the landscape using a weighted mean based on total number of patches and the area they cover. Configuration was calculated using contagion, which ranges between 0 and 100, where 0 indicates that patches of all land cover types are maximally disaggregated on the landscape and 100 indicates that patches of all land cover types are maximally aggregated on the landscape.
At the class level, composition was calculated as the percentage of the landscape occupied by each land cover class and the number of patches of each land cover class. Configuration was measured by calculating the contagion of each land cover class (using CLUMPY, a class level measure of contagion), ranging from -1 to 1, where -1 indicates maximum disaggregation and 1 indicates maximum aggregation of the cover class.
Landscape and class level metrics were compared between scenarios at year 100. Using “R” statistical software [48], the mean and standard deviation of each metric were calculated from the 10 Monte Carlo iterations for each scenario under each disturbance regime. Tukey’s HSD test was calculated to determine if landscape and class metrics were significantly different between scenarios. Significance for all statistical tests was determined at the 95% confidence level (p < 0.05).
3. Results
3.1. Scenario analysis
Composition and configuration of the landscape were similar across all three scenarios (Figure 3), with narrow ranges in landscape and class metric values (Figure 4). These results indicate a similar level of spatial variation, or spatial heterogeneity, in the size and spatial arrangement of forest and wetland patches. All treatments increased patchiness across the landscape (Figure 4), but differences between treatments were small. Given the narrow range in metric values, the landscapes resulting from each scenario are likely to be functionally and ecologically similar even though some metrics are statistically significantly different between scenarios.
The current management scenario was the only scenario in which landscape level metrics were not significantly different between the two climate conditions. However, the land cover was more spatially heterogeneous under the expanded easement and ecological forestry scenarios under increased windthrow and wildfire disturbances than under the current natural disturbance regime, with significantly more patches and lower contagion values. Landscape contagion and average area weighted mean patch size were statistically similar under the expanded easement and ecological forestry scenarios were under both climate conditions (Figure 4).
Under both the current natural disturbance regime and increased windthrow and wildfire conditions at year 100, mature, or late successional, forest cover classes were the primary contributors to landscape composition and configuration for the current management scenario and the expanded easement scenario (Table 3). Under the ecological forestry scenario, mid-successional closed canopy forests occupied the majority of the forested landscape under both climate conditions. This dominant class was composed of significantly fewer patches than the same cover class in the other two scenarios, negatively contributing to landscape heterogeneity (Table 3). Under all projections, the dominant wetland class was mature, late successional closed canopy wetland. This class had the largest number of patches of the wetland classes and a lower average contagion value, positively contributing to landscape heterogeneity in all scenarios.
Table 3. Average A) percentage of the landscape, B) number of patches, and C) contagion at the class level for each scenario under both natural disturbance regimes +/- the standard deviation (n = 10). Significant difference among scenarios is illustrated by * at p > 0.05 and by Ŧ when significantly different from each other at p > 0.05 but not different from the third scenario under the same natural disturbance regime.
| A. Percentage of the Landscape |
Current Climate Conditions |
Increased Windthrow and Fire Disturbances |
| Current Management |
Expanded Easement |
Ecological Forestry |
Current Management |
Expanded Easement |
Ecological Forestry |
| Forest Cover Types |
| Early, Mixed |
9.1* +/- 0.1 |
7.0 +/- 1.3 |
6.8 +/- 1.2 |
10.1Ŧ+/- 0.0 |
8.7 +/- 0.1 |
7.5Ŧ+/- 2.1 |
| Early, Closed |
0.7 +/- 0.1 |
1.6 +/- 1.7 |
6.6* +/- 0.1 |
0.8* +/- 0.0 |
1.2* +/- 0.0 |
7.1* +/- 0.1 |
| Mid Open |
0.4 +/- 0.1 |
0.3 +/- 0.0 |
0.3 +/- 0.1 |
0.3* +/- 0.0 |
0.4 +/- 0.0 |
0.4 +/- 0.0 |
| Mid, Closed |
7.3 +/- 0.1 |
6.1 +/- 1.7 |
48.1* +/- 23.0 |
8.6 +/- 0.1 |
7.3 +/- 0.1 |
40.9* +/- 25.9 |
| Late, Closed |
57.8 +/- 0.1 |
59.7 +/- 0.1 |
12.9* +/- 24.0 |
55.1 +/- 0.1 |
57.6 +/- 0.1 |
18.1* +/- 25.8 |
| Uncharacteristic |
3.0 +/- 0.0 |
3.7 +/- 1.3 |
3.6 +/- 1.2 |
3.5 +/- 0.0 |
3.2 +/- 0.0 |
4.3 +/- 2.2 |
| Wetland Cover Types |
| Early, Open |
0.3 +/- 0.0 |
0.3 +/- 0.3 |
0.3 +/- 0.0 |
0.3 +/- 0.0 |
0.3 +/- 0.0 |
0.3 +/- 0.0 |
| Early, Mixed |
1.8 +/- 0.1 |
1.7 +/- 0.9 |
2.3 +/- 2.2 |
1.9 +/- 0.1 |
1.7 +/- 0.0 |
2.1 +/- 1.2 |
| Early, Closed |
0.7 +/- 0.0 |
1.5 +/- 0.8 |
1.2 +/- 0.9 |
0.7 +/- 0.0 |
0.8 +/- 0.0 |
1.6* +/- 1.0 |
| Mid, Open |
3.5 +/-0.1 |
3.8 +/- 3.2 |
1.8 +/- 0.8 |
3.5 +/- 0.1 |
3.5 +/- 0.1 |
3.5 +/- 3.2 |
| Mid, Mixed |
2.7 +/-0.0 |
2.8 +/- 2.1 |
2.2 +/- 1.0 |
2.1 +/- 0.1 |
2.0 +/- 0.1 |
2.8 +/- 1.8 |
| Mid, Closed |
2.6 +/- 0.1 |
1.9 +/- 0.9 |
2.0 +/- 0.9 |
2.6 +/- 0.0 |
2.5 +/- 0.0 |
1.8* +/- 0.9 |
| Late, Open |
2.0 +/-0.0 |
2.0 +/- 0.1 |
1.9 +/- 0.4 |
2.0 +/- 0.0 |
2.0 +/- 0.0 |
2.0 +/- 0.09 |
| Late, Mixed |
0.6* +/- 0.0 |
1.6 +/- 1.1 |
2.0 +/- 1.0 |
0.5 +/- 0.0 |
0.6 +/- 0.0 |
1.9* +/- 1.2 |
| Late, Closed |
8.0 +/- 0.1 |
6.1 +/- 3.0 |
7.9 +/- 1.5 |
8.0 +/- 0.1 |
8.2 +/- 0.1 |
5.7* +/- 2.9 |
| B. Number of Patches |
Current Climate Conditions |
Increased Windthrow and Fire Disturbances |
| Current Management |
Expanded Easement |
Ecological Forestry |
Current Management |
Expanded Easement |
Ecological Forestry |
| Forest Cover Types |
| Early, Mixed |
2199* +/- 24 |
1661 +/- 246 |
1555 +/- 217 |
2428* +/- 39 |
2075* +/- 42 |
1749* +/- 429 |
| Early, Closed |
317 +/- 25 |
1071 +/- 1446 |
4756* +/- 49 |
342* +/- 22 |
625* +/- 15 |
4933* +/- 43 |
| Mid Open |
239 +/- 17 |
256 +/- 17 |
247 +/- 15 |
231* +/- 18 |
310* +/- 19 |
274* +/- 24 |
| Mid, Closed |
5269 +/- 50 |
4855 +/- 1414 |
2691* +/- 1190 |
4365* +/- 35 |
5516* +/- 31 |
2909* +/- 1514 |
| Late, Closed |
3401 +/- 23 |
3655 +/- 35 |
1177* +/- 1199 |
4328 +/- 56 |
3938 +/- 44 |
1602* +/- 1498 |
| Uncharacteristic |
848 +/- 22 |
1028 +/- 247 |
990 +/- 207 |
1018 +/- 15 |
946 +/- 16 |
1123 +/- 417 |
| Wetland Cover Types |
| Early, Open |
248 +/- 10 |
238 +/- 14 |
251 +/- 11 |
242 +/- 13 |
229* +/- 15 |
253* +/- 7 |
| Early, Mixed |
998 +/- 26 |
1023 +/- 289 |
1687 +/- 1853 |
962 +/- 31 |
927 +/- 38 |
1258* +/- 399 |
| Early, Closed |
369 +/- 14 |
734 +/- 365 |
597 +/- 402 |
395* +/- 21 |
457 +/- 17 |
714* +/- 433 |
| Mid, Open |
1660 +/- 31 |
2875 +/- 2792 |
142 +/- 293 |
1677 +/- 35 |
1593 +/- 25 |
2958 +/- 2831 |
| Mid, Mixed |
1411 +/- 32 |
1855 +/- 1745 |
1311 +/- 329 |
1386 +/- 25 |
1387 +/- 21 |
1922 +/- 1827 |
| Mid, Closed |
1239Ŧ+/- 34 |
862Ŧ+/- 366 |
955 +/- 406 |
1232Ŧ+/- 25 |
1168 +/- 17 |
883Ŧ+/- 443 |
| Late, Open |
1727 +/- 32 |
1710 +/- 26 |
1638 +/- 281 |
1731 +/- 21 |
1731 +/- 16 |
1657 +/- 244 |
| Late, Mixed |
813 +/- 13 |
1089 +/- 322 |
1186 +/- 346 |
820 +/- 12 |
822 +/- 9 |
1213 +/- 387 |
| Late, Closed |
7303Ŧ+/- 76 |
4836Ŧ+/- 2790 |
6601 +/- 1669 |
7316 +/- 71 |
7258 +/- 51 |
4891* +/- 2982 |
| C. Contagion |
Current Climate Conditions |
Increased Windthrow and Fire Disturbances |
| Current Management |
Expanded Easement |
Ecological Forestry |
Current Management |
Expanded Easement |
Ecological Forestry |
| Forest Cover Types |
| Early, Mixed |
0.91 +/- 0.00 |
0.91 +/- 0.00 |
0.91 +/- 0.00 |
0.91 +/- 0.00 |
0.91 +/- 0.00 |
0.91 +/- 0.00 |
| Early, Closed |
0.88* +/- 0.00 |
0.87* +/- 0.00 |
0.87* +/- 0.00 |
0.88* +/- 0.00 |
0.88* +/- 0.00 |
0.87 *+/- 0.00 |
| Mid Open |
0.88Ŧ+/- 0.01 |
0.87Ŧ+/- 0.00 |
0.87 +/- 0.01 |
0.86 +/- 0.01 |
0.86 +/- 0.00 |
0.87 +/- 0.01 |
| Mid, Closed |
0.87 +/- 0.000 |
0.86 +/- 0.00 |
0.89* +/- 0.00 |
0.88* +/- 0.00 |
0.86* +/- 0.00 |
0.88* +/- 0.00 |
| Late, Closed |
0.89 +/- 0.00 |
0.89 +/- 0.00 |
0.88* +/- 0.01 |
0.88 +/- 0.00 |
0.89Ŧ+/- 0.00 |
0.88Ŧ+/- 0.01 |
| Uncharacteristic |
0.90 +/- 0.00 |
0.90 +/- 0.00 |
0.90 +/- 0.00 |
0.90 +/- 0.00 |
0.90 +/- 0.00 |
0.90* +/- 0.00 |
| Wetland Cover Types |
| Early, Open |
0.85 +/- 0.00 |
0.85 +/- 0.01 |
0.85 +/- 0.00 |
0.85 +/- 0.00 |
0.86* +/- 0.00 |
0.85 +/- 0.00 |
| Early, Mixed |
0.87 +/- 0.00 |
0.86 +/- 0.02 |
0.85 +/- 0.03 |
0.87 +/- 0.00 |
0.87 +/- 0.00 |
0.85* +/- 0.03 |
| Early, Closed |
0.87 +/- 0.00 |
0.87 +/- 0.00 |
0.87 +/- 0.00 |
0.87 +/- 0.00 |
0.87 +/- 0.00 |
0.87 +/- 0.004 |
| Mid, Open |
0.87Ŧ+/-0.00 |
0.85Ŧ+/- 0.03 |
0.86 +/- 0.02 |
0.88 +/- 0.00 |
0.88 +/- 0.00 |
0.84* +/- 0.02 |
| Mid, Mixed |
0.86 +/-0.00 |
0.86 +/- 0.02 |
0.86 +/- 0.02 |
0.86 +/- 0.00 |
0.86 +/- 0.00 |
0.86 +/- 0.01 |
| Mid, Closed |
0.88 +/- 0.00 |
0.88 +/- 0.00 |
0.88 +/- 0.00 |
0.88 +/- 0.00 |
0.88Ŧ+/- 0.00 |
0.88Ŧ+/- 0.00 |
| Late, Open |
0.84 +/- 0.00 |
0.84 +/- 0.00 |
0.84 +/- 0.01 |
0.84 +/- 0.00 |
0.84 +/- 0.00 |
0.84 +/- 0.01 |
| Late, Mixed |
0.81* +/- 0.00 |
0.84 +/- 0.03 |
0.86 +/- 0.02 |
0.80 +/- 0.01 |
0.81 +/- 0.00 |
0.85* +/- 0.03 |
| Late, Closed |
0.83* +/- 0.00 |
0.85 +/- 0.01 |
0.84 +/- 0.01 |
0.83 +/- 0.00 |
0.83 +/- 0.00 |
0.85* +/- 0.02 |
4. Discussion
Comparing the outcomes of these alternative scenarios provides insight into how different amounts and arrangements of management and their interaction with natural disturbances can shape the future of forests and wetlands in the WRLF study area. In all, we found that landscape composition and configuration of projected land cover was functionally similar between scenarios under both natural disturbance regimes. These findings serve as a starting point for collaborative management and future analysis of future management and natural disturbance dynamics on this landscape. These results highlight the importance of evaluating the effectiveness of conservation strategies, the role of active management on a forested Northern Wisconsin landscape, and the relative impact of climate-related disturbances versus management in this region.
Modeling outcomes indicate that small differences in management between scenarios result in statistically different outcomes for landscape composition and configuration. However, these differences, which were small in magnitude, may or may not be ecologically relevant. In the current management scenario, land neighboring the Pine and Popple Rivers was purchased in fee with the goal of preserving areas adjacent to these federally designated Wild Rivers. Under the expanded easement scenario, this land was placed under a conservation easement instead, a less costly conservation mechanism. Although it changed management of only 1% of the land in the study area, this change represents a realistic conservation alternative for this landscape. Slight differences in land cover composition and configuration between these scenarios may imply a minimum return on investment for the large conservation investments made under the current management scenario. In other words, our results indicate that the difference between the selected conservation strategies have a minor impact on the outcome of this landscape at this scale of analysis, and given the management context. However, the benefits of this additional protection may not be realized at the landscape scale or within the landscape and class metrics used for this analysis. The slight differences between scenarios may also indicate a strong effect of the surrounding landscape relative to the protected and eased area.
The WRLF landscape is predominantly composed of Northern Hardwood forest where the primary management strategy is uneven-aged management. The results of this analysis indicate that this modeling approach may not be ideal to understand these types of questions in landscapes that are predominately managed using an uneven-aged silviculture system. Though uneven-age management impacts stand density and age diversity, it does not alter the successional stage of a stand. Therefore, the consequences of this management activity were not captured as a change in land cover class in our STSM model. In forest systems where the predominant management strategy does not alter the seral stage of the stand, an STSM approach may be insufficient to determine the long-term implications of management. In addition, it may be more telling to evaluate the ecological benefits and success of WFCEs and collaborative ecological management strategies on finer-scales. As WFCEs are increasingly used as a conservation tool, the assessment of their success, both socially and environmentally, is important for future conservation work [49].
The analysis of the ecological forestry scenario showed, unlike the other two scenarios, that mid-successional closed canopy forest would be the largest cover class at year 2110. Because STSMs use age-range as a part of the successional definition of forest classes, the actual difference in age between the mid-successional and late successional forest is most likely small for all scenarios as they are both closed canopy forests. This can be viewed as an artifact of this modeling process, wherein the magnitude of difference between the scenarios in terms of these age classes appears to be larger than it likely is. While using a greater number of states in an STSM may be able to better capture the gradation between successional conditions, the use of discrete states to represent continuous ecological variation will invariably yield results with modeling artifacts such as these. However, benefits of using a small number of states in an STSM include the ability to link with available spatial datasets, ease of review and deconstruction by stakeholders and collaborators, and reduction in the potential for creating a false impression of the modeling capacity.
Similar to findings by Nowacki et al. and Costanza et al., we found that management is an important determinant of the landscape outcomes in the face of climate change [20,21]. Here, management as defined by each of the three scenarios, influences the landscape more than an increase in the probability of wildfire and windthrow. This can be seen in the limited differences in the outcomes of the same scenario under the different natural disturbance conditions. This may be due to the reduction of forest stands eligible to be disturbed by wildfire and windthrow in the model after management disturbances, where even-aged management sets land cover back to an early successional stage, which is less susceptible to wildfire and windthrow. Therefore, in a landscape with a lot of even-aged management, an increase in the probability of wildfire and windthrow may have less of an impact, so that management activities seem to overwhelm the effects of the natural disturbances.
Potential impacts related to climate change were incorporated into this model through a manipulation of two specific disturbances—windthrow and wildfire. However, these two impacts do not capture the full range of possible biotic and abiotic factors expected to be influenced by a changing climate. Climate change in northern Wisconsin is predicted to impact forests in terms of changes in drought, snowpack, moisture, and shifts in native and non-native species ranges, which will affect forest structure and composition [23,24]. These additional variables were not integrated into this model, as they will occur more gradually or unpredictably, and the VDDT/TELSA modeling platform does not dynamically model ecosystem processes [14,50]. Potential changes and interactions in insect pests and diseases and other disturbances, such as deer browsing, were not captured in this model. Therefore, the results of this modeling process must be interpreted with these limitations in mind. The changing climate may or may not impact the landscape in more dramatic ways that further differentiate the management scenarios.
Through this approach, we were able to explore differences among potential alternative conservation scenarios. The ability to incorporate these differences as spatial landscape harvesting goals in the VDDT/TELSA modeling platform and simulate these scenarios under different natural disturbance regimes allowed practical comparisons of conservation outcomes on this landscape. This approach was effective for this study area as coarse management and climate concerns could be defined through probabilistic disturbances. However, on a landscape where disturbances of concern are anticipated to interact in more complex ways, a more process-based approach may be required. For example, in this landscape, the selection cutting was not captured as a stand-replacing disturbance. If this management style was expected to have greater influence on the ecosystem and conservation goals, a different strategy for capturing the impact of this disturbance would be required, in the form of a more complex STSM or other modeling methodology. Limitations of this approach, including coarse scale vegetation units, spatially static BpS land cover types, and the small differences between scenario definitions contributed to very similar outcomes among scenarios.
5. Conclusions
The WRLF study area is a landscape characterized by multiple management and conservation goals. As land managers must consider long-term influences of management and possible interactions with climate change, the use of comparable scenario projections can inform planning and decision-making [51,52]. These results show that management and potential climate-related impacts on natural disturbance regimes may play a role in determining the landscape composition and configuration of this study area, and this landscape is likely to become more heterogeneous in the future under a variety of management and climate conditions. Here, we demonstrated how STSMs can be used to provide a preview of specific conservation mechanisms, management strategies, and stand-replacing climate-related disturbances. This approach does not rely on complex mechanistic modeling of uncertain dynamics, and therefore, can serve as both a heuristic to understand the threats climate-related disturbances may pose within this landscape and a starting point for planning and further analysis.
This project used scenario development in a collaborative effort among land managers, scientists, and conservation practitioners. The scenarios modeled here were tailored to this location and this group of collaborators. Due to this local application, these results cannot be extrapolated to other areas of conservation and management concern [53,54,55]. However, the approach and methodology of building and modeling scenarios to inform future management decisions can be applicable to other locations. Eliciting local knowledge through these workshops allowed the use of management and land use information that was not otherwise available in published literature [56]. Involving these experts allowed this project to be more aligned with local concerns and management strategies and to better support decision-making.
Applying landscape modeling to evaluate alternative scenarios of conservation and management strategies is a growing application of STSMs and can be effective in considering the potential implications of different management activities on ecosystems over the long term and at a landscape scale [9]. Scenario development and evaluation in particular can be a useful conceptual tool in informing landscape-scale conservation planning [10], in adapting management strategies and achieving longer-term conservation goals. This is highlighted through our approach, where local experts were collaborative members of the research team throughout the project, allowing them to tailor the scenarios to their specific concerns and use the results as their own informative tool in future decision-making.
Acknowledgments
This research was funded with support from The Nature Conservancy’s Rodney Johnson/Katherine Ordway Stewardship Endowment grant, USDA Forest Service State and Private Forestry Redesign, the Doris Duke Conservation Fellowship Program sponsored by the Doris Duke Charitable Foundation, the NSF IGERT Fellowship Program (DGE- 0549407), and the University of Wisconsin at Madison. Special thanks to all of the experts that contributed to this project.
Conflict of Interest
The authors declare that they have no conflict of interest.
Supplementary
Appendix A.
Descriptions of the ten land cover classes found in the Wild Rivers Legacy Forest study area along with the associated LANDFIRE BpS model number. These summaries of site conditions and vegetation are based on detailed descriptions of each cover type’s corresponding LANDFIRE Biophysical Settings Models for Map Zone 50, which served as starting points in this project [26].
Table .Appendix A.
| Cover Class and Area |
Description |
Northern Hardwood Forest
BpS 5013021
48.9% of the landscape |
Site Conditions. This forest type occurs on moist to dry-mesic sites occurring principally on moraines, fine-textured glacial lake beds, and flat to rolling uplands grading into steep slopes. Soils are typically well- to moderately-well-drained loams and silt loams, with rich loam soils over glacial till. These “rich soils” have circumneutral pH. |
|
Vegetation. Shade tolerant trees dominate or co-dominate the canopy, including sugar maple, eastern hemlock, American beech, and yellow birch. Other important canopy trees include American basswood, white pine, red oak, and others, while the sub-canopy can include ironwood, American elm, and balsam fir. The northern hardwood forest of this region have a rich and diverse understory with relatively few shrubs and many spring ephemerals and perennial herbs, ferns, and club mosses. |
Northern Hardwood Hemlock Forest
BpS 5013022
25.6% of the landscape |
Site Condition. This forest type occurs on coarse-textured ground and end moraines, on glacial till over bedrock and medium-textured moraines, and on kettle-kame topography. |
|
Vegetation. These uneven-aged forests are characterized by large volumes of coarse, woody debris under multi-storied canopies of different-aged cohorts, with super canopies of century old trees. The dominant tree species, including sugar maple, hemlock, yellow birch, balsam fir, cedar, spruce, and beech, are among the most moisture and nutrient demanding species in the eastern US, and their distribution is confined to glacial landforms underlain by fertile soils. Composition of the ground flora and understory varies along a moisture-nutrient gradient and typically consists of shade-tolerant tree species and mesophilic herbaceous species (blue cohosh, yellow violet, sweet cicely, various ferns and ginseng). In hemlock-dominated stands, ground layer diversity is low due to the nutrient-poor and acidic mor humus and low understory light intensity.
Conifer-dominated mesic northern forests usually have hemlock and yellow birch as primary canopy components. |
Boreal Acid Peatland
BpS 5014770
6.4% of the landscape |
Site Conditions. Peatlands form in small ice-block basins and poorly drained, level terrain, ranging in size from a few thousand square meters to several thousand hectares. The overall topography of peatlands is flat to gently undulating with micro-topography characterized by hummocks and hollows, which can lead to extreme and fine-scaled gradients in soil moisture and pH. The accumulation of peat within these systems alters drainage patterns and raises water tables. |
|
Vegetation. The canopy is composed of a few, stunted and flood tolerant conifer species, including tamarack and black spruce, or low ericaceous shrubs and a poor herbaceous layer. Sphagnum moss increases in extent as this landscape matures, reaching peak density in open bogs. |
Alkaline Conifer Hardwood Swamp
BpS 5014810
4.1% of the landscape |
Site Conditions. This system is characterized by dense to open, low to medium tall forest of needle-leaf evergreen and deciduous trees on shallow organic and deep peatland soils, occurring as discontinuous pockets within upland vegetation communities or in large contiguous patches in the eastern U.P. Soils are poorly drained and saturated throughout the growing season in most years. |
|
Vegetation. Northern white cedar is the characteristic dominant canopy species, and balsam fir, black spruce, and tamarack are common. Occasional canopy species include white spruce, hemlock, white pine, black ash, red maple, yellow birch, paper birch, American elm, quaking aspen, and bigtooth aspen.
Characteristic shrubs include tag alder, winterberry, mountain holly, red-osier dogwood, elderberrry, huckleberry, autumn willow, and Canada yew. Mosses and a diverse array of sedges, ferns and orchids dominate the surface layer. |
Pine Oak Forest
BpS 5013621
3.7% of the landscape |
Site Conditions. This forest type occurs principally on sandy glacial outwash, sandy glacial plains, and less frequently on glacial drift over bedrock, dune ridges, and moraines. Soils typically coarse to medium textured sand or loamy sand and moderately to extremely acidic. |
|
Vegetation. Here, a super-canopy of white and/or red pine is found over a canopy of red maple, paper birch, bigtooth aspen, trembling aspen, white oak, red oak, northern pin oak, and hemlock. Sugar maple, beech, or yellow birch can be found in the understory. |
Floodplain Systems
BpS 5014750
3.5% of the landscape |
Site Condition. This system is defined by a river and its floodplain or by glacial melt and outwash. Active hydrologic processes of the adjacent river maintain this system and terraces are created through sand and sediment deposits. |
|
Vegetation. Species that dominate this system include black ash, balsam, and poplar. Alders, dogwood, mountain maple, bluejoint, and sedges can be found in the understory or non-forested areas. |
Shrub Herbaceous Wetland
BpS 5014940
2.6% of the landscape |
Site Condition. This wetland type occurs along streams or rivers that are defined by seasonal or beaver-induced flooding. Soils within this wetland type are typically organic sediments and saturated mineral soils. Soils are typically high in minerals such as calcium and magnesium and range from neutral to alkaline in pH. |
|
Vegetation. A large array of vegetation types are found within these wetlands, including many species of sedges, grasses, forbes, and low shrubs. |
Managed Tree Plantation
1.8% of the landscape |
Site Condition. Soil and site characteristics vary between plantations, but soils are generally sandy, well-drained, and moderately acidic. |
|
Vegetation. This cover type is composed exclusively of white pine plantations, which are managed intensively to eliminate understory vegetation. Vegetation in this cover type existed in early successional, mixed canopy forest; mid successional, closed canopy forest; and mid successional, open canopy forest successional stages. |
Pine Hemlock Hardwood Forest
BpS 5013660
1.7% of the landscape |
Site Conditions. This forest type occupies moist, moderately drained silty/clayey lake plains and moderate to poorly-drained till plains and outwash plains, especially in the western U. P., predominately around lake and bog margins and in complex mosaics with sugar maple-hemlock forest on the surrounding better-drained soils. Elevations are low to moderate, generally less than 2000 ft. Soil pH is circumneutral. |
|
Vegetation. Tolerant species, including eastern hemlock, white pine, and yellow birch, can dominate or co-dominate the canopy with balsam fir and white cedar components. Commonly sub-canopy species include ironwood or hop-hornbeam, american elm, hemlock, and yellow birch.
Ground layer diversity is low due to the nutrient-poor and acidic mor humus as well as the low understory light intensity. |
Boreal White Spruce Fir Forest
BpS 5013651
1.6% of the landscape |
Site Condition. This forest is found on flat to sloping areas of lakeplain outwash. The soil here is characterized by sand, loamy sand, and sandy loam soils. |
|
Vegetation. Dominant tree species are balsam fir, white spruce, northern white cedar, and quaking aspen, with pines, poplars, and spruce in the canopy. The forest floor includes many low shrubs, forbes, sphagum mosses, and lichens. |
Appendix B.
Averages and standard deviations were calculated from the 10 Monte Carlo iterations over the 100 year simulations to illustrate the differences in (A) management disturbances and (B) natural disturbances between scenarios of management and climate. These graphs indicate the amount of disturbance in an average year, showing the annual average harvest occurring in each scenario, as well as the increase in climate-related disturbances of windthrow and fire in the scenarios modeled under that climate regime.
Appendix C.
Categorical definitions for reclassifying seral stage classes into forest or wetland classes based on age and canopy structure for landscape analysis.
Table .Appendix C
| Forest and Wetland Classes |
LANDFIRE Cover and Seral Stage |
| Forest, Early Mixed Canopy |
Pine Oak Forest Mid2 - Closed
Pine Oak Forest Early3 - All
Pine Oak Forest Early1 - All
Pine Oak Early3 - All
Pine Oak Early1 - All
Pine Hemlock Hardwood Forest Early1 - All
Pine Hemlock Hardwood Early1 - All
Northern Hardwood HemlockForest Early2 - All
Northern Hardwood Hemlock Forest Early1 - All
Northern Hardwood Hemlock Early2 - All
Northern Hardwood Hemlock Early1 - All
Northern Hardwood Forest Early2 - All
Northern Hardwood Forest Early1 - All
Northern Hardwood Early2 - All
Northern Hardwood Early1 - All |
| Forest, Early Closed Canopy |
Pine Oak Early2 - Closed
Pine Hemlock Hardwood Forest Early2 - Closed
Pine Hemlock Hardwood Early2 - Closed
Boreal White Spruce Fir Forest Early2 - Closed
Boreal White Spruce Fir Forest Early1 - Closed
Boreal White Spruce Fir Early2 - Closed
Boreal White Spruce Fir Early1 - Closed |
| Forest, Mid Open Canopy |
Pine Oak Mid1 - Open Pine Oak Forest Mid1 - Open |
| Forest, Mid Closed Canopy |
Pine Oak Mid2 - Closed
Pine Hemlock Hardwood Mid1 - Closed
Pine Hemlock Hardwood Forest Mid1 - Closed
Northern Hardwood Mid2 - Closed
Northern Hardwood Mid1 - Closed
Northern Hardwood Hemlock Mid2 - Closed
Northern Hardwood Hemlock Mid1 - Closed
Northern Hardwood Hemlock Forest Mid2 - Closed
Northern Hardwood Hemlock Forest Mid2 - Closed
Northern Hardwood Hemlock Forest Mid1 - Closed
Northern Hardwood Hemlock Forest Mid1 - Closed
Northern Hardwood Forest Mid2 - Closed
Northern Hardwood Forest Mid1 - Closed
Boreal White Spruce Fir Mid1 - Closed
Boreal White Spruce Fir Forest Mid1 – Closed |
| Forest, Late Closed Canopy |
Pine Oak Late1 - Closed
Pine Oak Forest Late1 - Closed
Pine Hemlock Hardwood Late1 - Closed
Pine Hemlock Hardwood Forest Late1 - Closed
Northern Hardwood Late1 - Closed
Northern Hardwood Hemlock Late1 - Closed
Northern Hardwood Hemlock Forest Late1 - Closed
Northern Hardwood Forest Late1 - Closed
Boreal White Spruce Fir Late1 - Closed
Boreal White Spruce Fir Forest Late1 - Closed |
| Uncharacteristic Forest |
Pine Oak Mid3 - Closed
Northern Hardwood Un-N - Closed
Northern Hardwood Hemlock Un-N - Closed
Managed Tree Plantation Mid2 - Open
Managed Tree Plantation Mid1 - Closed
Managed Tree Plantation Early1 - All |
| Wetland, Early Open Canopy |
Shrub Herbaceous Wetland Early1 - Open |
| Wetland, Early Mixed Canopy |
Floodplain Systems Early1 - All
Boreal Acid Peatland Early1 - All
Alkaline Conifer Hardwood Swamp Early1 - All |
| Wetland, Early Closed Canopy |
Alkaline Conifer Hardwood Swamp Early2 - Closed |
| Wetland, Mid Open Canopy |
Floodplain Systems Mid1 - Open
Boreal Acid Peatland Mid3 - Open
Boreal Acid Peatland Mid1 - Open |
| Wetland, Mid Mixed Canopy |
Boreal Acid Peatland Mid2 - All |
| Wetland, Mid Closed Canopy |
Alkaline Conifer Hardwood Swamp Mid1 - Closed
Floodplain Systems Mid1 - Closed |
| Wetland, Late Open Canopy |
Shrub Herbaceous Wetland Late1 - Open
Boreal Acid Peatland Late3 - Open |
| Wetland, Late Mixed Canopy |
Boreal Acid Peatland Late2 - All |
| Wetland, Late Closed Canopy |
Shrub Herbaceous Wetland Late3 - Closed
Shrub Herbaceous Wetland Late2 - Closed
Floodplain Systems Late1 - Closed
Boreal Acid Peatland Late1 - Closed
Alkaline Conifer Hardwood Swamp Late1 - Closed |









 DownLoad:
DownLoad: