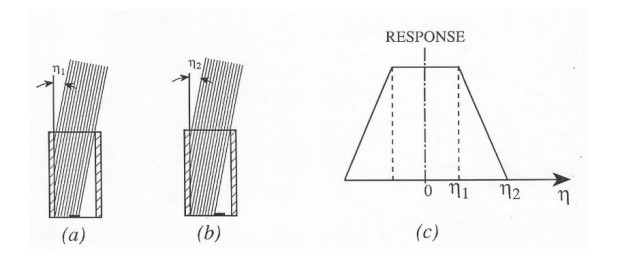
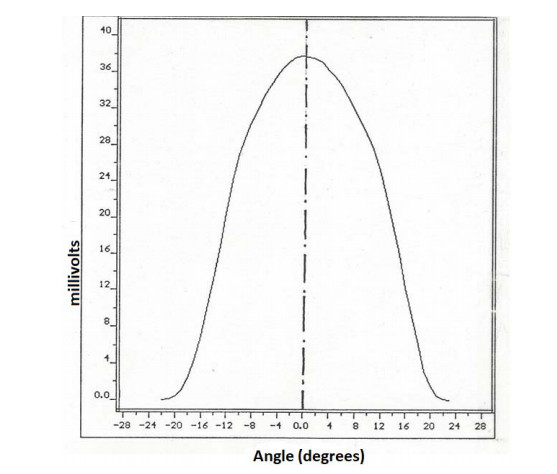
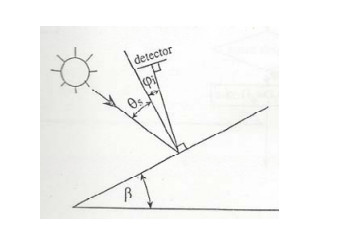
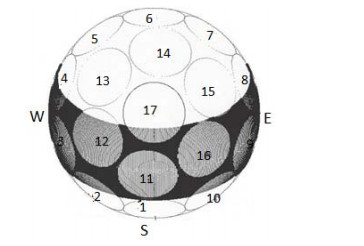
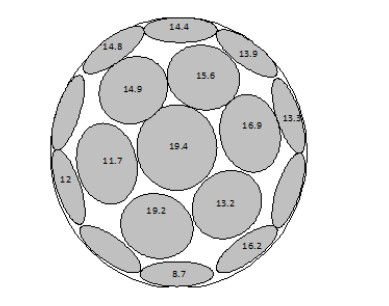
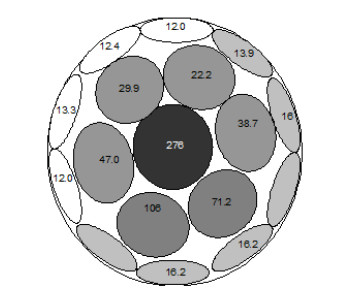
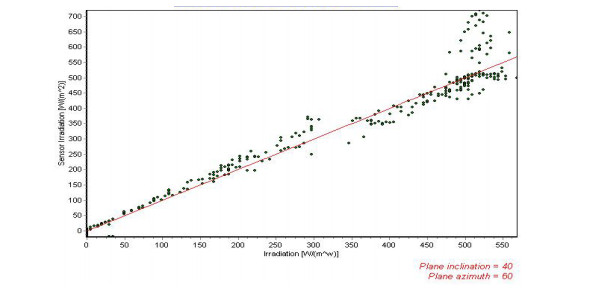
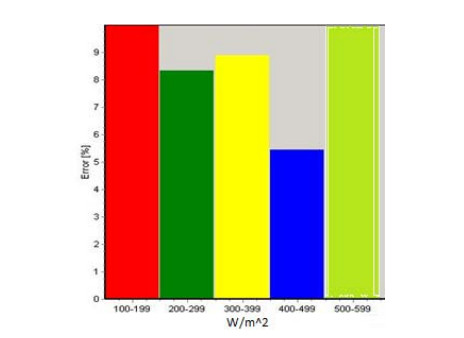
A small static solar radiation sensor comprising of 17 photodiode detectors deployed evenly on a hemispherical-member is proposed. The sensor is capable of measuring the intensity and time dependent of the solar radiation components on any desired inclined and oriented plane, including the distribution of the diffuse radiation in the sky. The sensor may also be used in solar tracking systems for pointing to the highest radiation intensity at any time. An inverted sensor may also measure reflected radiation from different objects. As a first design, the accuracy obtained is about 10 to 15 percent, depending of the solar radiation intensity, and the aiming is to improve the accuracy to about 5 percent. The objective was to construct a static sensor with small dimensions and of light-weight, detectors and hemispherical-dome hermetically sealed and machined close to a prototype product.
1.
Introduction
Epidemic refers to the disease that can spread in a certain scale within a relatively short period of time. It caused a major hazard to human health. For example, the H1N1 influenza virus, which erupted in Mexico in 2009 and soon spread around the globe, is a dangerous virus and can develop to pneumonia. Some infectives may even appear respiratory failure, multiple organ damage, and finally be kicked to death. The H1N1 has killed about 16 thousand people throughout the world then and over 1.3 million people had been infected. Studying the transmission mechanism of epidemics can help reduce the spread of the diseases. Many researchers use the mathematical models to describe the transmission of epidemics [1], and various methods are derived to investigate the dynamics of the diseases [2,3].
Researchers have proposed mathematical models of infectious diseases and studied their dynamical behaviours extensively [4,5]. The dynamical behaviours of ordinary differential equations have been widely studied, and abundant dynamical behaviours have been found, such as periodic oscillations, bifurcations, stable limit cycles and time-delay effects [6,7,8,9,10]. To investigate the dynamics of cholera which spread in the European Mediterranean regions, Capasso and Paveri-fontana proposed an epidemic model in 1979 as follows [6]:
where u and v represent the concentration of the infectious agent and the infected population, respectively. 1α1 denotes the average lifetime of the infectious agent, 1α2 denotes the average infectious period of infected people, thus α1, α2>0. a denotes the multiplicative factor of the virus caused by the increasing number of infected people. The function g(u) represents the infectivity of the virus to people, and can be affected by the concentration of the virus. They speculated that the infection process follow the nonlinear saturation pattern. They draw the conclusion of epidemic evolution by analyzing the equations in phase space, which provided a reference for public health policies. The validity of the model is verified by comparing it with available data from Bari town in Italy.
In fact, system (1.1) can be modified to simulate other epidemics with oral-faecal transmission [6], such as typhoid fever, infectious hepatitis, poliomyelitis, etc. Moreover, system (1.1) can also be used to investigate the spreading of man-environment epidemics [6,11,12]. The man-environment epidemics refer that, the infected people may increase the concentration of the virus in the environment, thus people maybe infected by eating the contaminated food [11].
Scientific researches show that the virus is highly sensitive to its environment. The concentration of the virus is not evenly distributed in space thus the effect of diffusion cannot be ignored. In 1997, Capasso and Wilson [11] studied the following diffusive epidemic model:
where u(x,t),v(x,t) represent the spatial concentration of the bacteria and the infected people, respectively. α1, α2 are the same as they are in (1.1). For system (1.2), they performed a detailed analysis of the steady-state bifurcation at the endpoints of a one-dimensional interval based on the monotone techniques. They speculated that the system (1.2) has saddle point structure in the natural function space, similar to the ODE case in which the diffusivity of bacteria is also set to zero.
In the transmission of the epidemics, an important factor that can not be ignored is the delay [13,14,15]. For example, there is time delay between the release of the virus from the infected person and its successful entry into the susceptible people. For those infected people, it also takes time from being infected to being able to release the virus. All of these can lead to time-delay feedback in the epidemics [16,17,18,19]. Time delay usually destroys the stability of the solutions, devotes to the complex dynamics of the system. Recently, systems with two delays have been used in characterizing the phenomena in various fields, such as power systems and predator-prey systems [20,21,22,23,24], etc.. Among them, Wu and Hsu [24] proposed a monostable epidemic model with double delays as follows:
They studied the existence of entire solutions in the system (1.3) with and without the quasi-monotone condition. Some special cases of system (1.3) have been extensively investigated. For example, when τ1=d2=0, τ2, d1>0, Zhao and Wang [25] studied the properties of the existence and non-existence of the traveling wave fronts; when τ1=τ2=d2=0, d1>0, Xu and Zhao [26] proved the existence, uniqueness and global exponential stability of the bistable traveling wave fronts; Hsu et al. [27] studied the existence and exponential stability of traveling wave solutions in an extended form of system (1.3).
Motivated by the previous works, we study an epidemic model with two delays subjecting to the Neumann boundary conditions in the following form:
where u(x,t) and v(x,t) denote the concentration of the virus and the number of the infected people, respectively. 1α1 denotes the average lifetime of the infectious agent, 1α2 denotes the average infectious period of infected people, S(v) represents the contribution of infected people to the growth of the virus, T(u) represents the infection rate of the virus to people. d1,d2>0 are the diffusion coefficients, τ1 represents the average time taken by the infected people from being infected to being able to release the virus, τ2 represents the average time taken by the virus from being released to entrying the susceptible people and ¯τ=max{τ1,τ2}.
In the spread of an epidemic, the concentration of the virus would increase with the number of the infected people, and the susceptible people would more likely to be infected. Therefore, S(v) and T(u) are increasing functions of v and u respectively in general. However, the increasing number of the virus poses a threat to public health, people will take effective measures to avoid them from being infected by the virus, including isolating the infected people, regular disinfection, reminding people to pay attention to hygiene through media reports and so on [28,29]. Scientific studies have shown that these measures are effective in reducing infection rates [30]. Once the virus exceeds a certain concentration u0, even if the concentration continues to increase, people begin to take certain measures to reduce the infectivity of the virus. So in this paper, we assume that once if u>u0, T(u) is a decreasing function with respect to u.
In this paper, we study the existence of the positive constant steady state. By analyzing the zeros of characteristic equations of (1.4), we investigate the local stability of constant steady state. We found that when the sum of two delays reaches a critical value, the system undergoes Hopf bifurcation. By taking one of two delays as a bifurcation parameter, we calculate the normal form on the center manifold near the Hopf singularity.
This paper is organized as follows. In section 2, the stability of the positive constant steady state of the system (1.4) and the existence of Hopf bifurcation are established by analyzing the distribution of the eigenvalues. In section 3, the normal form on the center manifold near the Hopf bifurcation point is derived. In section 4, we carry out some numerical simulations to illustrate the theoretic results.
2.
Stability of the positive constant steady state and existence of Hopf bifurcation
In this section, we will study the local stability of the positive constant steady state and the existence of Hopf bifurcation by analyzing the distribution of the eigenvalues.
For S(v) and T(u) in (1.4), we make the following assumption:
Normally speaking, the contribution function S(v) is sufficiently smooth with respect to the infected people v, the infection rate T(u) is sufficiently smooth with respect to u. For the research purposes, we assume S,T∈C3(R,R). Particularly, if no one is infected (v=0), then no infected people contribute to the growth of the virus, i.e., S(0)=0. Similarly, if the concentration of the virus is zero(u=0), then no one can be infected by the virus, i.e., T(0)=0. In the early stage of a transmission, the virus concentration is low but the number of the susceptible people is large, thus the epidemic would spread at a certain speed; as the epidemic continues to spread, although the virus concentration is high, a reduction in the number of the susceptible people will limit the spread of the epidemic. Thus the virus and the population may reach a coexistence state. In (H1), we denote the number of infected people in this coexistence state as v∗.
Define u∗=S(v∗)/α1, under the assumption (H1) system (4) has two constant steady states E0(0,0) and E∗(u∗,v∗). Obviously, E∗ is a positive constant steady state. To investigate the dynamics of the epidemics, we focus on the properties of E∗.
the linearized equation of system (1.4) at E∗ is
where
and u(x,t), v(x,t) still satisfy the homogeneous Neumann boundary conditions.
The characteristic equations of the system (2.1) are given by
where I2 is a 2 × 2 identity matrix, Mn=−n2l2D. Since
denote m=Sv∗×Tu∗, Eq (2.2) becomes
Denote τ=τ1+τ2, then Eq (2.3) becomes
For convenience, denote k1=d1n2l2+α1,k2=d2n2l2+α2, then we have k1,k2>0. Now the characteristic Eq (2.4) with τ=0 is in the following form:
To ensure all the roots of Eq (2.5) have negative real parts, we further make the following assumption
Then we can conclude the following lemma.
Lemma 2.1. When τ=0, all the roots of Eq (2.4) have negative real parts under the assumption (H2).
Since the proof of Lemma 2.1 is intuitive, here we omit it.
Now we will study the stability of E∗ and investigate the existence of Hopf bifurcation of system (1.4). Assume that λ=iω(ω>0) is a root of (2.4). Substituting iω into (2.4) and separating the real and imaginary parts leads to
This yields
Denote z=ω2, then the above equation becomes
the roots of (2.7) can be given by
Clearly, z2<0. To maintain the existence of a positive ω that satisfies (2.6), z1>0 should hold. Obviously, z1>0 provided that m2>k21k22.
If m2≤α21α22, then for all n∈N0, we have m2≤(d1n2l2+α1)2(d2n2l2+α2)2, and thus z1≤0, all roots of (2.4) have negative real parts. Moreover, if m<α1α2 and m2≤α21α22 are satisfied, i.e., −α1α2≤m<α1α2, then E∗ is locally asymptotically stable. We can draw the following proposition.
Proposition 1. If −α1α2≤m<α1α2, all roots of (2.4) have negative real parts, then E∗ is locally asymptotically stable.
Now we further make the following assumption:
Then we study the existence of purely imaginary roots of (2.4) in the following lemma.
Lemma 2.2. If (H3) is satisfied, then Eq (2.4) with n∈{0,1,⋯,N−1} has a pair of purely imaginary roots ±iωn when τ=τj,n, where
Proof. From (H3) we know that Eq (2.7) with n∈{0,1,⋯,N−1} has a positive root denoted by zn. Hence, ωn=√zn>0 makes sense. Define
From the second equation of (2.6) one obtains that τ0,nωn∈(0,π]. Then (ωn,τj.n) solves (2.6), which implies that ±iωn is a pair of purely imaginary roots of Eq (2.4) with τ=τj,n.
Lemma 2.3. If assumptions (H2) and (H3) are satisfied, then ωn is monotone decreasing with respect to n.
Proof. By Lemma 2.2, we know that ωn exists for n=0,1,⋅⋅⋅N−1. Assumptions (H2) and (H3) imply that m<0. We know that
Hence, zn is monotone decreasing with respect to n. For i=0,1,⋯,N−1 we have zi>zi+1. Thus ωn is monotone decreasing with respect to n.
Lemma 2.4. If assumption (H2) and (H3) are satisfied, then τ0,nωn is monotone increasing with respect to n. Moreover, τ0,0=min{τ0,n}0≤n≤N−1.
Proof. From Lemma 2.3, for n=0,1,⋯,N−2, we have ωn>ωn+1 and
By −ωn2<−ω2n+1 and m<0, we have −ωn2+(d1n2l2+α1)(d2n2l2+α2)m is monotone decreasing with respect to n. Since the anti-trigonometric function y=arccosx is monotone decreasing with respect to x, from the properties of composite functions, we can obtain that τ0,nωn is monotone increasing with respect to n. The last conclusion follows from ωn>ωn+1.
Under the assumption (H2) and (H3), let λ(τ)=α(τ)+iβ(τ) be the root of Eq (2.4) with n∈{0,1,⋯,N−1} satisfying α(τj,n)=0 and β(τj,n)=ωn.
Lemma 2.5. Suppose that (H2) and (H3) are satisfied. Then
Proof. Since Eq (2.4) can be rewritten in the following form:
Substituting λ(τ) into (2.9) and taking the derivative of both sides of Eq (2.9) with respect to τ gives
Then we have
Hence,
This completes the proof. By Lemmas 2.1, 2.4, 2.5 and applying Corollary 2.4 in [31], we have the following conclusions on the distribution of the roots of the characteristic Eq (2.4).
Lemma 2.6. Suppose that (H2) and (H3) are satisfied. Then there exists a sequence values of {τj,n}(j=0,1,2,⋯;n=0,1,⋯,N−1), such that all the roots of Eq (2.4) have negative real parts when τ1+τ2∈[0,τ0,0); When τ1+τ2=τ0,0, all the other roots of Eq (2.4) have negative real parts, except for a pair of pure imaginary roots ±iω0; When τ1+τ2>τ0,0, Eq (2.4) has at least a couple of roots with positive real parts.
From Lemma 2.6, we have the following the conclusions on the stability of the positive equilibrium of the system (1.4) and the existence of Hopf bifurcations directly.
Theorem 2.7. Suppose that (H1),(H2) and (H3) are satisfied. Then the positive constant steady state E∗ of system (1.4) is asymptotically stable when τ1+τ2∈[0,τ0,0), unstable when τ1+τ2>τ0,0, and system (1.4) undergoes a Hopf bifurcation at E∗ when τ1+τ2=τj,n, j=0,1,2,⋯;n=0,1,⋯,N−1.
3.
Normal form of the Hopf bifurcation on the center manifold
In this section, we will calculate the normal form of Hopf bifurcation on the center manifold. To investigate the dynamical behaviours of system (1.4) near the Hopf bifurcation point, we will study the normal form of Hopf bifurcation by making use of the normal form method of partial functional differential equations [32,33].
Without loss of generality, we assume that τ1>τ2, let ¯u(x,t)=u(x,τ1t)−u∗, ¯v(x,t)=v(x,τ1t)−v∗ and take out of the bars, the system (1.4) becomes
with the boundary and initial conditions:
where
We define the real-valued Hilbert space
and the complexification of Y
with the general complex-value L2 inner product
for U=(u1,u2)T,V=(v1,v2)T∈YC.
Let C:=C([−1,0],YC) represents the phase space with the sup norm. We write ut∈C for ut(θ)=u(t+θ), −1≤θ≤0.
In the previous section, we have obtained that when τ=τ0,0, all the roots of Eq (2.4) have negative real parts except ±iω0. We denote the Hopf bifurcation point by (τ∗1,τ∗2) with τ∗1+τ∗2=τ0,0, and introduce parameter μ by setting τ1=τ∗1+μ with fixing τ2=τ∗2 and |μ| sufficiently small. Then we have τ=τ1+τ2=τ∗1+τ∗2+μ=τ0,0+μ, and μ=0 is the Hopf bifurcation value of system (3.1).
Denote U(t)=(u(x,t),v(x,t))T and substitute τ1=τ∗1+μ,τ2=τ∗2 into (3.1). We have
where
and
Consider the linearized system of (3.3)
In Y, the eigenvalues of DΔ are −d1n2l2 and −d2n2l2, n∈N0, with the corresponding normalized eigenvectors: β(1)n(x)=γn(x)e1, β(2)n(x)=γn(x)e2, where
and e1=(1,0)T,e2=(0,1)T are the unit coordinate vectors of R2.
Define the subspace of C as Bn, by
we write (v(⋅),βn)=((v(⋅),β(1)n),(v(⋅),β(2)n))T for simplification. Then on Bn, the linear Eq (3.4) is equivalent to retarded functional differential equation on R2:
By Riese representation theorem, there exists a 2×2 matrix function ηn(μ,θ), θ∈[−1,0], whose entries are of bounded variation such that
In fact, we can choose
For simplicity, we write ηn(θ) for ηn(0,θ), define A as the infinitesimal generator of the semigroup generated by Eq (3.5) with μ=0 and n=0. Define the adjoint operator A∗ of A on C∗:=C([0,1],(R2)∗) as
with the bilinear form
Let
be the eigenvectors of A and A∗ corresponding to iω0τ∗1 and −iω0τ∗1 respectively. Thus
where
We choose M as
which assures that ⟨q∗(s),q(θ)⟩=1.
Let
and define Aμ as the infinitesimal generator of the C0 semi-group of solution maps of the linear equation of (3.3):
with
where
On BC, Eq (3.3) can be rewritten as an abstract ordinary differential equation
Using the same notations in Wu [34], we compute the coordinates to describe the center manifold C0 at μ=0. Let Ut be the solutions of Eq (3.3) with μ=0. Define
On the center manifold C0, we have
where
z and ˉz are local coordinates for center manifold C0 in the direction of q∗ and ¯q∗ respectively. Notice that W is real if Ut is real, we consider real solutions.
For the solution Ut∈C0 of the system (3.3) with μ=0,
It can be denoted as
where
Base on (3.7) and (3.8), similar to the method used in Zhao and Wei [35], we obtain
where
By expanding the above series and comparing the coefficients, we have
Notice that
where
and
We have
Comparing the coefficients with (3.9), we obtain that
We need to compute W20(θ) and W11(θ) for θ∈[−1,0), since
Comparing the coefficients with (3.9), we obtain
From (3.10), it can be given that
Solving for W20(θ), we have
and similarly
where E1 and E2 can be determined by setting θ=0 in H. Since
we have
From (3.10) and the definition of A0, we have
Noting that
substituting (3.12) into (3.16), we obtain
Substituting (3.14) into this, we have
Solving Eq (3.17) for (E(1)1,E(2)2)T=E1, we get
Similarly, we can get
and hence,
Then g21 can be confirmed. Therefore, we can calculate the following quantities
By the general theory in Hassard [36], we obtain that μ2 determines the direction of the Hopf bifurcation: When μ2>0(<0), the direction of the Hopf bifurcation is forward (backward), in other words, for τ1>τ∗1(τ1<τ∗1), there exist the bifurcating periodic solutions; β2 determines that whether the bifurcating periodic solutions are stable: When β2<0(>0), the bifurcating periodic solutions are orbitally asymptotically stable (unstable); T2 determines the period of the bifurcating periodic solutions: When T2>0(<0), the period of the bifurcating periodic solutions increases (decreases).
4.
Numerical simulations
In this section, we choose
and take the following data:
Then system (1.4) with (4.1) and (A) has a unique positive constant steady state E∗=(16.8,0.336). By direct calculation, we have Sv∗=40, Tu∗=−0.068 and m=−2.72. Thus the assumptions (H1) and (H2) are satisfied, and E∗ is asymptotically stable when τ1=τ2=0.
By calculation, we get that when N=3,m2>(d1n2l2+α1)2(d2n2l2+α2)2 for 0≤n<Nandm2≤(d1N2l2+α1)2(d2N2l2+α2)2, thus assumption (H3) is satisfied. From Eq (2.8), we get that
And Eq (2.7) has no positive roots for n≥3. Clearly, τ0,0≈0.7023.
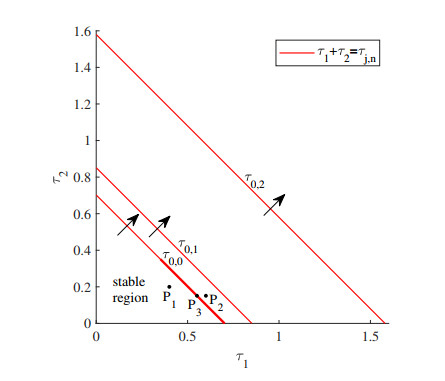
From Theorem 2.7, we know that the positive constant steady state E∗ is asymptotically stable when τ1+τ2∈[0,τ0,0), and unstable when τ1+τ2>τ0,0. Meanwhile, (1.4) undergoes a Hopf bifurcation at E∗ when τ1+τ2=τj,n, n=0,1,2;j∈N0. The bifurcation set on (τ1,τ2) plane is shown by Figure 1.
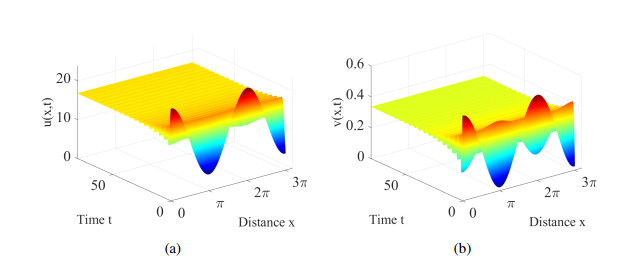
When (τ1,τ2) are chosen as P1(0.4,0.2), we have τ1+τ2<0.7023, thus E∗ is asymptotically stable, this is illustrated in Figure 2.
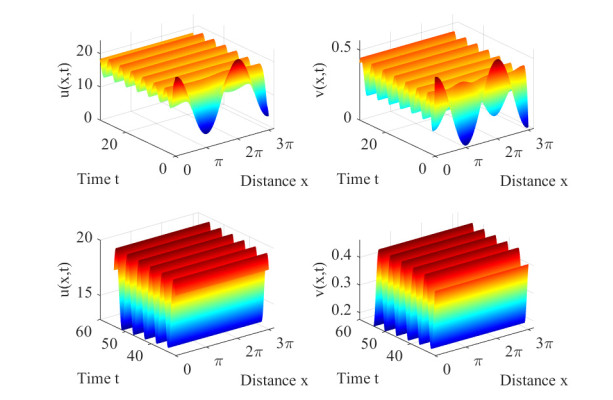
We choose the point P3(0.55115,0.15115) on the curve τ=τ0,0, that is τ∗1=0.55115 and τ∗2=0.15115. According to the algorithm given in the previous section, we can obtain that c1(0)=−0.00155−0.00290i, λ′(τ∗1)=0.92063−0.94716i, μ2=0.00168>0, β2=−0.0031<0 and T2=0.00565>0. This implies that the direction of the Hopf bifurcation is forward, the bifurcating periodic solutions are stable and the period of the bifurcating periodic solutions increases, which are illustrated by Figure 3.
In fact, with the help of the norm form calculated in section 2, we get that when τ∗1 and τ∗2 satisfying τ∗1+τ∗2=τ0,0 and τ∗1>τ∗2, the corresponding Rec1(0) would be negative, we list some values of c1(0) in Table 1.
5.
Conclusions
In this paper, we study the dynamics of epidemics by using a diffusive model with two delays. First we perform the stability analysis at the constant steady state in the system. Then we present the conditions for the existence of the purely imaginary roots of the characteristic equations. Moreover, we investigate the existence of Hopf bifurcation by taking two delays as parameters. Theoretical result shows that the sum of two delays affect the stability of the steady state and the existence of Hopf bifurcation. Considering the sum of two delays as one parameter, we verify that τ∗1+τ∗2=τ0,0 is the critical Hopf bifurcation curve and the stability switching curve of this system. To calculate the normal form on the center manifold near the Hopf singularity, we fix τ2 as a constant and take τ1 as a parameter. Finally, numerical simulations are carried out to verify the theoretical results. The simulations show that when τ1+τ2<τ0,0, E∗ is locally asymptotically stable; when τ1+τ2>τ0,0, the bifurcating periodic solutions are stable. Both theoretical verifications and numerical simulations reveal that when τ1+τ2<τ0,0, the system is locally stable at E∗; when τ1+τ2>τ0,0 and close enough to τ0,0, E∗ is unstable, the periodic solutions generated by the Hopf bifurcation is stable. All the analysis shows that the sum of two delays plays an important role in the dynamics of the system.
Acknowledgments
The authors are grateful to the anonymous referees for their helpful comments and valuable suggestions which have improved the presentation of the paper. This research is supported by National Natural Science Foundation of China (No.11771109).
Conflict of interest
The authors declared that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.









 DownLoad:
DownLoad: