Search Advanced

AIMS Energy

2019, Volume 7, Issue 6: 944-956. doi: 10.3934/energy.2019.6.944
Previous Article Next Article
Research article

Multilayer perceptron artificial neural network for the prediction of heating value of municipal solid waste

  • 1.
    Department of Mechanical Engineering Science, University of Johannesburg, South Africa
  • 2.
    Department of Mechanical Engineering, Walter Sisulu University, South Africa
  • 3.
    Department of Mechanical Engineering, Covenant University, Sango Ota, Nigeria
  • Received: 18 July 2019 Accepted: 22 October 2019 Published: 16 December 2019

  • Energy from municipal solid waste is steadily being integrated into the global energy feedstock, given the huge amount of waste being generated from various sources. This study develops a Multilayer Perceptron Artificial Neural Network for the prediction of High Heating Value of municipal solid waste as a function of moisture content, carbon, hydrogen, oxygen, nitrogen, sulphur, and ash. A total of 123 experimental data were extracted from reliable database for training, testing, and validation of the model. This model was trained, validated and tested with 70%, 20%, and 10% of the municipal solid waste biomass datasets respectively. The predicted High Heating Value was compared with the experimental data for two different training functions: Levenberg Marquardt backpropagation and Resilience backpropagation, and with some correlation from the literature. The accuracy of the model was reported based on some known performance criteria. The values of Root Mean Squared Error (RMSE), Mean Absolute Deviation (MAD), Mean Absolute Percentage Error (MAPE), and Coefficient of Correlation (CC) were 3.587, 2.409, 21.680, 0.970 respectively for RP and 3.095, 0.328, 22.483, 0.986 for LM respectively. Regression analysis was also carried out to determine the level of correlation between the experimental and predicted High Heating Values (HHV). The authors concluded that these models can be a useful tool in the prediction of heating value of MSW in order to facilitate clean energy production from waste.

    Citation: Obafemi O. Olatunji, Stephen Akinlabi, Nkosinathi Madushele, Paul A. Adedeji, Ishola Felix. Multilayer perceptron artificial neural network for the prediction of heating value of municipal solid waste[J]. AIMS Energy, 2019, 7(6): 944-956. doi: 10.3934/energy.2019.6.944

    Related Papers:

    [1] Anbazhagan Geetha, S. Usha, J. Santhakumar, Surender Reddy Salkuti . Forecasting of energy consumption rate and battery stress under real-world traffic conditions using ANN model with different learning algorithms. AIMS Energy, 2025, 13(1): 125-146. doi: 10.3934/energy.2025005
    [2] Constantinos S. Psomopoulos . Residue Derived Fuels as an Alternative Fuel for the Hellenic Power Generation Sector and their Potential for Emissions ReductionConstantinos S. Psomopoulos. AIMS Energy, 2014, 2(3): 321-341. doi: 10.3934/energy.2014.3.321
    [3] Tsepo Sechoala, Olawale Popoola, Temitope Ayodele . Economic and environmental assessment of electricity generation using biogas and heat energy from municipal solid waste: A case study of Lesotho. AIMS Energy, 2023, 11(2): 337-357. doi: 10.3934/energy.2023018
    [4] Romain Akpahou, Marshet M. Admas, Muyiwa S Adaramola . Evaluation of a bioenergy resource of agricultural residues and municipal solid wastes in Benin. AIMS Energy, 2024, 12(1): 167-189. doi: 10.3934/energy.2024008
    [5] Robinson J. Tanyi, Muyiwa S Adaramola . Bioenergy potential of agricultural crop residues and municipal solid waste in Cameroon. AIMS Energy, 2023, 11(1): 31-46. doi: 10.3934/energy.2023002
    [6] Jialin Song, Haoyi Zhang, Yanming Zhang, Zhongjiao Ma, Mingfei He . Research progress on industrial waste heat recycling and seasonal energy storage. AIMS Energy, 2025, 13(1): 147-187. doi: 10.3934/energy.2025006
    [7] NY Abd Halim, NIS Muhammad . Investigation of moisture content and higher heating value in refuse-derived fuel from agricultural residues using statistical modelling. AIMS Energy, 2025, 13(1): 1-12. doi: 10.3934/energy.2025001
    [8] Aklilu T. Habtewold, Demiss A. Ambie, Wondwossen B. Eremed . Solar assisted pyrolysis system for High-Density polyethylene plastic waste to fuel conversion. AIMS Energy, 2020, 8(3): 455-473. doi: 10.3934/energy.2020.3.455
    [9] Boua Sidoine KADJO, Mohamed Koïta SAKO, Kouadio Alphonse DIANGO, Amélie DANLOS, Christelle PERILHON . Characterization and optimization of the heat treatment of cashew nutshells to produce a biofuel with a high-energy value. AIMS Energy, 2024, 12(2): 387-407. doi: 10.3934/energy.2024018
    [10] Abdelrahman Kandil, Samir Khaled, Taher Elfakharany . Prediction of the equivalent circulation density using machine learning algorithms based on real-time data. AIMS Energy, 2023, 11(3): 425-453. doi: 10.3934/energy.2023023
  • Energy from municipal solid waste is steadily being integrated into the global energy feedstock, given the huge amount of waste being generated from various sources. This study develops a Multilayer Perceptron Artificial Neural Network for the prediction of High Heating Value of municipal solid waste as a function of moisture content, carbon, hydrogen, oxygen, nitrogen, sulphur, and ash. A total of 123 experimental data were extracted from reliable database for training, testing, and validation of the model. This model was trained, validated and tested with 70%, 20%, and 10% of the municipal solid waste biomass datasets respectively. The predicted High Heating Value was compared with the experimental data for two different training functions: Levenberg Marquardt backpropagation and Resilience backpropagation, and with some correlation from the literature. The accuracy of the model was reported based on some known performance criteria. The values of Root Mean Squared Error (RMSE), Mean Absolute Deviation (MAD), Mean Absolute Percentage Error (MAPE), and Coefficient of Correlation (CC) were 3.587, 2.409, 21.680, 0.970 respectively for RP and 3.095, 0.328, 22.483, 0.986 for LM respectively. Regression analysis was also carried out to determine the level of correlation between the experimental and predicted High Heating Values (HHV). The authors concluded that these models can be a useful tool in the prediction of heating value of MSW in order to facilitate clean energy production from waste.


    1.   Introduction

    Waste utilization and management is a major challenge in sustainable development, given the mammoth amount of waste being generated from various sources across the globe. Presently, the main trend in waste management is the production of value-added products from Municipal Solid Waste (MSW) [1,2,3], since it leads to the reduction in the amount of MSW deposited at the landfill and also decreases the consumption of traditional fossil fuel [3]. MSW is gaining momentum as a viable source of biofuel [4,5,6], this place a relative advantage on it and biomass as other renewable sources cannot be readily converted to liquid fuel. Also, there exists a high prospect of MSW utilization in electricity generation [7]. The United Nation (UN) projected that the world population will increase by 2.2 billion between 2017 and 2050 [8]. This seemingly exponential increase in the world population and the quest for urban life will subsequently lead to increase in both the MSW generation and energy demand. The main driver of the increase in MSW in urban areas is the change in consumption pattern and living standard of the urban population. In 2016 only, 2.01 billion tonnes of solid waste was generated at the rate of 0.74 kg/person in a day across the global cities with 33% not managed in an environmentally safe manner [9]. From the statistics, the waste generated in cities across the globe may increase to 3.40 billion tonnes from 2016 level by year 2050 [9]. In low-income countries, around 90% of the waste generated are not properly disposed [10]. The MSW generated from developing countries are made of 55–80 % household, followed by market and commercial areas, which are made of industrial, institutional, and other related sources with 10–30% contribution [11,12]. Residents of developing countries are at risk due to unsustainable and indiscriminate disposal of waste [13]. In view of the severe risk associated with this practice, managing waste is very germane to environmental protection and climate change mitigation. Several countries have moved to quantify and utilize the MSW which they generate [14,15,16,17]. Given the cost implication of waste management, waste to energy (WTE) can be considered as a sustainable pathway to waste management. This has a high prospect of serving as an alternative source of energy [18] and in the production of other value-added products [3], which are economically viable and environmentally sustainable [18,19]. MSW is made up of various heterogeneous substances, from which energy can be produced through various conversion processes such as biological, thermochemical, anaerobic digestion, pyrolysis incineration and so on [20,21,22,23,24,25]. Also, methane capturing was proposed as a way to sustainably manage the MSW [16].

    However, the design of new systems that can extract fuels from MSW requires knowledge of the fundamental properties of the MSW, especially its High heating value (HHV) and elemental composition as this gives the scientists and engineers a clue to the utility of the MSW in fuel production [26,27]. Heating value is used to determine the quantity of energy, which can be recovered from an amount of waste when subjected to conversion processes [20]. Although the heating value can be experimentally determined using bomb calorimeter, the current trend in global economy requires an urgent need to minimize the cost of production of energy, which include the determination of the heating value of MSW. The information from routine data such as moisture content, carbon, hydrogen, oxygen, nitrogen and sulphur, ash content enables rapid decisions about utilization of MSW. This will further provide a first-hand information regarding the gaseous emission and global warming potential of the MSW.

    Several models have been developed based on the experimental data from gravimetric composition, ultimate and proximate analysis and moisture content of waste [20]. However, most of these models do not account for the nonlinear dependencies of MSW [26,27,28]. This has therefore created a knowledge gap regarding the prediction of HHV of MSW [29,30]. A nonlinear dependency exists in MSW when a change in a property does not correspond to a change in other properties. For instance, a change in the moisture content or carbon content of MSW may not linearly correspond to a change in oxygen, hydrogen, nitrogen, or sulphur content. Previous correlations and models based on ultimate analysis were developed by Kathiravale, et al. [31], Wilson [32], Meraz et al [33], Boumanchar, et al. [34], Niessen [35], Chang [36] and Shi, et al. [37] to estimate the heating value of waste.

    Presented in Table 1 is an overview of correlations for the prediction of HHV of MSW feedstock. Also, Boumanchar, et al. [34] investigated Multiple Regression Analysis (MLR) and Genetic Programming (GP) formulation for the prediction of the HHV of MSW. Most of the correlations reported (Table 1) were based on the MSW [31,33,34,37], while others were based on organic waste [32,35,36].

    Table 1.  Correlations for the prediction of HHV.
    References Sample size Feedstock class Equation HHV (MJ/kg)
    Kathiravale et al [31] 60 MSW 0.416638C−0.570017H+0.259031O−0.598955N−5.829078
    Boumanchar et al [34]-MLR 187 MSW 0.3805C+0.7700H−4.0219
    Boumanchar et al [34]-GP 187 MSW 2.775+0.004027C−0.004027C2+H+0.05706H−12.97+0.02323H−6.661+0.009398H−5.961+12.97−HH3−5.922C
    Shi et al [37] 193 MSW 0.350C+1.01H−0.0826O
    Meraz et al [33] 100 MSW (1−0.01H2O)((−0.3708C)−1.1123H+0.1391O−0.3178N−0.1391S)
    Wilson [32] 100 Organic waste (1−0.01H2O)((−0.3279C)−1.5330H+0.1668O−0.0242N−0.0928S)
    Chang [36] 150 Organic waste 35.8368+0.7523H−0.2674S−0.4654)−0.3814Cl−0.2802N
    Niessen [35] 80 Waste water sludge 0.2322C+0.7655H−0.0698S−0.072O−0.0262Cl−0.1814P
    Note: C=Carbon; H=Hydrogen; O=Oxygen; S=Sulphur; N=Nitrogen; Cl=Chlorine; P=Phosphorous (on dry basis in % weight); H2O=Moisture content (as discarded, in % weight).
     | Show Table
    DownLoad: CSV

    Apart from the above-mentioned issues which are related to the prediction of the HHV of MSW, to the best of our knowledge, the literature survey revealed that there is no model which have compared the HHV of biomass using LM and RP. Therefore, the present study constructs a Multilayer Perceptron Artificial Neural Network (MLP-ANN) model for the prediction of High Heating Value (HHV) of MSW using Levenberg Marquardt (LM) and Resilient backpropagation (RP) as the training algorithms with moisture content, carbon, hydrogen, oxygen, nitrogen and sulphur, ash as the input variables.

    2.   Materials and methods

    2.1.   Data collection and processing

    The data of experimental measurements from previous studies comprising 123 MSW samples were extracted from literature credited to Meraz, et al. [33] and Phyllis2 [38] since they are the most comprehensive database for MSW. Most of the MSW fall within the classes of domestic waste, plastic, paper, municipal residue, textile and so on. The input variables are the percentage elemental constituents (C, O, H, N, S, ash on dry basis, and moisture content) and the output variable is the HHV (MJ/kg). The dataset for the model was divided into training, testing, and validation in the ratio 70%, 10%, and 20% respectively. The descriptive statistical distribution of the MSW data applied in this study is as shown in Table 2.

    Table 2.  Descriptive statistical analysis of MSW experimental dataset.
    Composition H20 (%) C (%) H (%) O (%) N (%) S (%) Ash (%) HHV(MJ/kg)
    Minimum 0.2 0.5 0.08 0.23 0.04 0.01 0.26 0.14
    Maximum 78.7 87.1 14.2 47.8 10 1.5 98.9 45.9
    Average 20.4 42.8 5.7 27.1 1.2 0.3 23.2 16.2
    Std 22.5 18.3 2.7 13.8 1.7 0.3 28.9 9.6
     | Show Table
    DownLoad: CSV

    2.2.   Principles of MLP-ANN

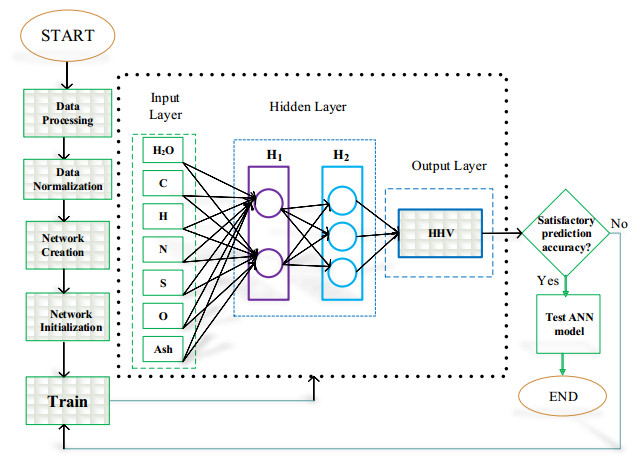
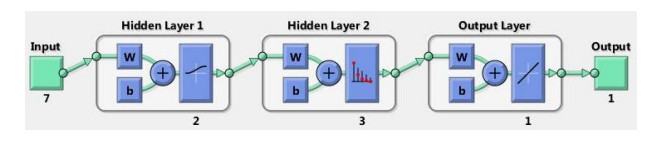
    The Multilayer Perceptron (MLP) is a popular supervised learning technique in ANN whose architecture has been used for several forecasting problems in the literature [39,40,41]. It is a distributed mathematical model inspired by the behaviour of human brain and nervous system. The MLP basically consists of three layers; the input layer, hidden layer, and the output layer. The hidden layer may have one or more activation function(s) [42,43,44,45]. The input for this study is the elemental composition including the ash content of the MSW while the output is the HHV. In order to determine the optimal prediction model for the HHV, two training algorithms which are Levenberg Marquardt (LM), and Resilient Backpropagation (RP) algorithms were applied. The network is made of two hidden layers H1 and H2 with 2 and 3 neurons in the first and second layer respectively. After initial trials, the activation function used at the first layer was logarithmic sigmoid [46,47] while the second layer was SoftMax [42] and linear function was chosen for the output layers. Figure 1 and 2 show the schematic diagram of MLP-ANN and neural network architecture respectively. The training and testing steps involved in the MLP-ANN for the prediction of the heating value were presented in Figure 1 while the transfer functions used in the model formulation were represented in Figure 2.

    Figure 1.  The schematic diagram for MLP-ANN.
    DownLoad: Full-Size Img PowerPoint
    Figure 2.  Neural network architecture for the prediction of HHV.
    DownLoad: Full-Size Img PowerPoint
    2.2.1.   Levenberg-Marquardt backpropagation (LM)

    The Levenberg Marquardt algorithm is well-known algorithm which exhibits adaptive behaviour according to the solution distance [48]. It has shown better performance in variety of application when compared to gradient descent and other conjugate gradient methods [49,50]. This method was developed to approach the second-order training speed such that the need for the computation of Hessian matrix is ruled out [51,52]. Considering the effectiveness and efficiency of Newton's method, LM aims at shifting to Newton's method for a quick convergence. The Hessian matrix is approximated when the scalar α is zero, but for a large size of α, a gradient descent with small step size is adopted. This is such that the scalar α is reduced after each successful step and an increase is observed only when an increase in performance function is envisaged by a preliminary step. Thus, a reduction in the performance function, which is typically a sum of the squares for feedforward backpropagation networks is observed at every iteration during the network training process [53]. The Jacobian matrix, which contains the first derivatives of the network errors as a vector with respect to the weights and biases can be computed using a standard backpropagation technique. This computation is observed to be less complex than the Hessian matrix. The weight update is achieved as follows:

    wjk(t+1)=wjk(t)+Δwjk(t) (1)

    such that

    Δwjk(t)=1[JT(w)J(w)+αI]JT(w)E(w) (2)

    where J is the Jacobian matrix, α is a scalar constant and I is an identity matrix.

    2.2.2.   Resilient backpropagation (RP)

    RP algorithm was developed to overcome the local minima error related to backpropagation. Resilient algorithm provides quick local adaptation during the training process. As one of the faster training algorithms, RP eliminates the effects caused by partial derivatives often associated with multi-layered networks trained with sigmoid functions. Slope of sigmoid functions used in multi-layer perceptron approach zeros as input size gets larger. This becomes a problem when steepest descent with sigmoid functions are used for network training. A slight change in the gradient value causes a slight change in the values of the weights and biases, even when the weights and biases are not close to their optimal values [53]. Rather than using the magnitude of the partial derivatives, RP algorithm applies the weight step based local gradient sign to update the weight. When the updated value of each weight is adapted, the delta weights, Δwjk are transformed as follows [52]:

    Δwjk(i)={−Ajk(i)if∂E∂wjk(i−1)∂E∂wjk(i)>0Ajk(i)if∂E∂wjk(i−1)∂E∂wjk(i)<00else (3)

    where individual value change is Ajk(i) and the error function is E. RP algorithm gives a faster convergence during neural network training compared to most other algorithms. Table 3 presents the user-defined parameters for the training of the MLP model.

    Table 3.  User defined parameters for MLP-ANN.
    User-defined Parameters Value
    Data division ratio 7:1:2
    Number of iterations 600
    Transfer functions logsig and softmax
    Activation function LM and RP
    Number of hidden layers 2
    Number of input variables 7
    Number of output variable 1
    Normalization method Min-max
    Stopping criteria Minimum training error
     | Show Table
    DownLoad: CSV

    2.3.   Performance analysis

    The performance of the MLP-ANN model was based on some statistical measures which are; mean absolute deviation (MAD), root mean square error (RMSE), mean absolute percentage error (MAPE), and coefficient of correlation (CC). The choice of these metrics is based on their application in numerous related studies as an effective means of determining the eligibility of the model for prediction. The MAPE gives an information about the average error as a percentage of the predicted value whether the error is positive or negative. It is a dimensionless index. The lower the value of MAPE, the better the performance of the model [37]. According to Chang et al [54], if MAPE is < 10%, the performance of the model is said to be excellent, for values between 10% to less than 20%, the model is considered good; MAPE value from 20% to less than 50% is classified as acceptable, however, a MAPE value > 50 is classified as unacceptable [54]. Although this classification is not absolute since the acceptable MAPE baseline also depend on the characteristics of the dataset. CC measure the strength of the association between two variables. If the value stands at 0, it means there is no correlation between the variables, but if ranges between ﹣1 to 1 then it means there is a strong negative or positive correlation between the variables. As the RMSE is becoming lower, the model is expected to become better.

    Correlation Coefficient (CC)

    CC=1−∑ni=1(yk−^yk)2∑ni=1(yk−¯yk)2 (4)

    Root Mean square Error (RMSE):

    MSE=√∑Nk=1[yk−^yk]2N (5)

    Mean Absolute Deviation (MAD):

    MAD=1NN∑k=1|yk−ˉyk| (6)

    Mean absolute percentage error (MAPE)

    MAD=1NN∑k=1|yk−ˉyk| (7)

    3.   Results and discussion

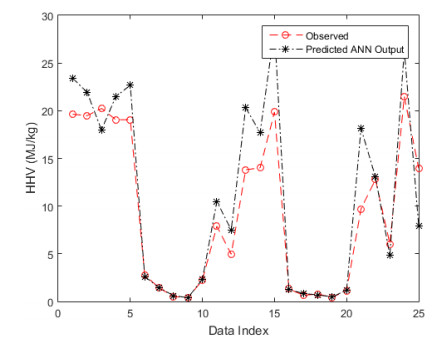
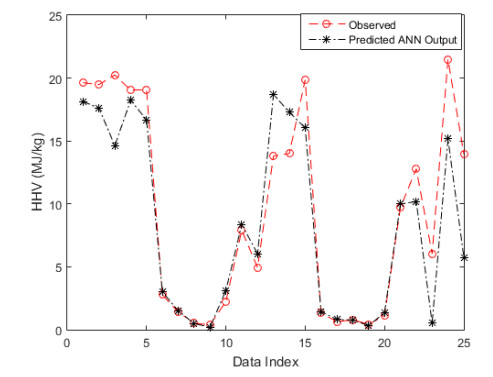
    The observed and predicted HHV at the testing phase using RP and LM are shown in Figure 3 and 4 respectively in order to compare the prediction performance of both models. It was observed that the predicted HHV and the actual HHV showed similar trend with the minimum and maximum absolute discrepancies being 0.0148 and 8.2034 MJ/kg respectively for LM and 0.0048 and 8.6719 MJ/kg respectively for RP. Both models follow a similar pattern across 90% of the dataset, this further shows the similarity between the predicted and the actual HHV and underlines the advantage of nonlinear regression model in the prediction of variation between the input and output variables. The results obtained in Figure 3 and 4 could improve if the moisture content were ignored in the development of the model [27], but the significance of this parameter in practical application of MSW means that it should be accounted for.

    Figure 3.  Predicted HHV for resilient back propagation (RP).
    DownLoad: Full-Size Img PowerPoint
    Figure 4.  Prediction of HHV based on Levenberg Marquardt (LM).
    DownLoad: Full-Size Img PowerPoint

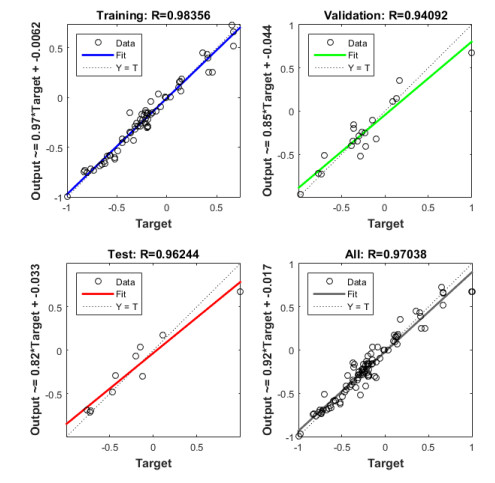
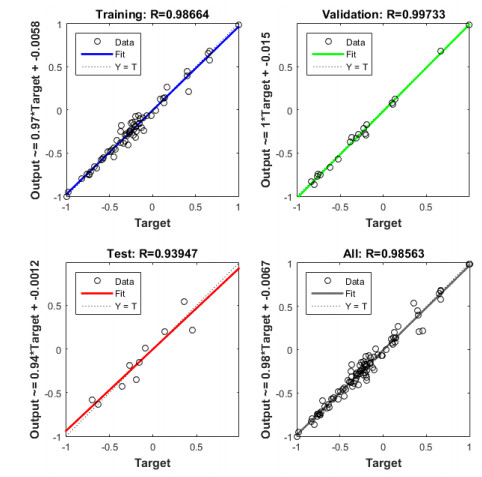
    Figure 5 and 6 shows the regression analysis of the network output and the input for training, validation, testing, and overall dataset. The regression between the network input and the target function for RP and LM are 0.9704 and 0.9857 respectively. This shows that LM have better coefficient of regression which translates to better explaining power than RP; the explanatory power of LM is 2% greater than RP. Both learning algorithms showed that the ANN output are in close agreement with the actual HHV.

    Figure 5.  Regression analysis for RP.
    DownLoad: Full-Size Img PowerPoint
    Figure 6.  Regression analysis for LM.
    DownLoad: Full-Size Img PowerPoint

    Table 4 presents the evaluation of the accuracy of the model based on RMSE, MAD, MAPE and CC. Both algorithms showed better performance with good coverage when tested and validated. However, the comparative analysis of their performance metrics showed that LM has lower RMSE (3.095), MAD (0.328) and higher CC (0.986), though at the expense of lower MAPE which is obtained in the case of RP algorithm. The improved MAPE value obtained based on RP may have benefitted from improved speed of convergence, less sensitivity to the training parameters [55] and minimum learning steps attributed to RP.

    Table 4.  Evaluation indices for the models.
    Metrics RP LM GP [34] MLR [34]
    RMSE 3.587 3.095 2.865 4.3559
    MAD 2.409 0.328 - -
    MAPE (%) 21.680 22.483 - -
    CC 0.970 0.986 0.970 0.9459
     | Show Table
    DownLoad: CSV

    To ensure the validity of the developed model, the statistical measures were compared for GP and MLR developed by Boumanchar et al [34]. A comparison with the GP with LM and RP shows that the CC is the same for RP but lesser than LM. Also, the RMSE observed in GP is lesser than RP and LM, though at the expense of CC. The MLR shows the highest RMSE and lowest CC of all the models reported. It is safe to conclude that both LM and RP algorithms can be used for the prediction of the HHV of MSW since the variation in their performance is low.

    Also, the model developed in this study was further juxtaposed with the existing linear correlation from the literature. The comparison was only drawn with the correlations that used MSW as their dataset and based on this, Shi et al [37], Meraz et al [33], and Kathiravale et al [31] were selected. All the correlations were developed based on the data that was applied in this study to ensure the uniform condition. The deviation of the correlations from the actual experimental data and MLP-ANN model is shown in Table 5. The LM-based model shows the least deviation from the experimental results compared to the RP-based model. This may have been due to the inherent ability of the ANN model to learn the hidden patterns and adapt to non-linear distribution of the data, which is not the strength of linear regression.

    Table 5.  Experimental and predicted HHV based on different models.
    Experiment Deviation
    LM RP Shi etal [37] Meraz et al [33] Kathiravale et al [31]
    17.960 0.346 3.991 2.710 2.841 4.204
    17.400 0.126 0.305 1.770 1.607 3.177
    16.850 0.169 5.828 1.907 1.806 4.290
    16.050 0.008 12.480 3.134 3.107 3.391
    15.337 0.165 11.035 1.670 0.199 2.866
    14.663 0.028 3.326 2.272 2.091 2.092
    9.960 0.227 3.096 9.898 5.374 9.213
    9.780 0.208 8.362 10.026 8.142 10.106
    8.221 0.137 2.260 3.367 0.004 3.791
    6.030 0.013 1.477 5.025 0.672 6.105
    5.691 0.056 2.254 16.786 0.152 0.012
    3.970 0.862 1.640 15.111 0.008 17.572
    2.772 0.228 0.171 0.196 0.032 0.210
    1.416 0.086 0.025 1.292 1.395 0.960
    1.314 0.044 0.109 0.044 0.158 1.432
    0.779 0.015 0.083 0.107 0.016 0.005
    0.523 0.009 4.301 0.016 0.084 3.523
    0.437 0.052 0.172 0.084 0.017 2.698
     | Show Table
    DownLoad: CSV

    Conclusions

    The MSW ultimate analysis data with different sort of waste were applied to develop MLP-ANN model given the simplicity of this approach as only little calculation is required. This model was applied to predict the HHV of MSW as an avenue for waste to energy production. It was concluded that both LM and RP algorithms can be used for the prediction of the HHV of MSW, however, the LM-based model performs better than the RP-based model. This tool will be very useful in decision-making process for the designing of thermal conversion system and accelerate the MSW to energy conversion process. Further study will include the larger dataset with an ANN optimization, in order to further improve the robustness of the model.

    Conflict of interest

    The authors declare no conflict of interests.



    [1] Negi H, Agrawal R, Verma A, et al. (2019) Municipal solid waste to bioenergy: current status, opportunities, and challenges in Indian context. New Future Developments Microb Biotechnol Bioeng 191-203.
    [2] Doña-Grimaldi VM, Palma A, Ruiz-Montoya M, et al. (2019) Energetic valorization of MSW compost valorization by selecting the maturity conditions. J Environ Manage 238: 153-158. doi: 10.1016/j.jenvman.2019.02.125
    [3] Dutta S, Priya DN, Chakradhar B, et al. (2019) Value added by-products recovery from municipal solid waste, Waste Valorisation and Recycling, Singapore: Springer, 71-80.
    [4] Perlack RD (2005) Biomass as Feedstock for a Bioenergy and Bioproducts Industry: the Technical Feasibility of a Billion-ton Annual Supply, Oak Ridge National Laboratory.
    [5] Guo M, Song W, Buhain J (2015) Bioenergy and biofuels: History, status, and perspective. Renew Sust Energ Rev 42: 712-725. doi: 10.1016/j.rser.2014.10.013
    [6] Olatunji OO, Akinlabi S, Madushele N, et al. (2019) Property-based biomass feedstock grading using k-nearest neighbour technique. Energy 2019: 116346.
    [7] Istrate IR, García-Gusano D, Iribarren D, et al. (2019) Long-term opportunities for electricity production through municipal solid waste incineration when internalising external costs. J Clean Prod 215: 870-877. doi: 10.1016/j.jclepro.2019.01.137
    [8] United nations department of economic and social affairs/population division, World population prospects: The 2008 Revision. United nations department of economic and social affairs/population division, 2010. Available from: http://esa.un.org/unpp.
    [9] World Bank, Solid Waste Management. World Bank, 2018. Available from: http://www.worldbank.org/en/topic/urbandevelopment/brief/solid-waste-management.
    [10] Toumi H, Abidli S, Bejaoui M (2019) Microplastics in freshwater environment: the first evaluation in sediments from seven water streams surrounding the lagoon of Bizerte (Northern Tunisia). Environ Sci Pollut Res 26: 14673-14682. doi: 10.1007/s11356-019-04695-0
    [11] Abdel-Shafy HI, Mansour MSM (2018) Solid waste issue: sources, composition, disposal, recycling, and valorization. Egyptia J Petrol 27: 1275-1290. doi: 10.1016/j.ejpe.2018.07.003
    [12] Nabegu AB (2010) An analysis of municipal solid waste in Kano metropolis, Nigeria. J Hum Ecol 31: 111-119. doi: 10.1080/09709274.2010.11906301
    [13] Ikhlayel M (2018) Development of management systems for sustainable municipal solid waste in developing countries: a systematic life cycle thinking approach. J Clean Prod 180: 571-586. doi: 10.1016/j.jclepro.2018.01.057
    [14] Lokahita B, Samudro G, Huboyo HS, et al. (2019) Energy recovery potential from excavating municipal solid waste dumpsite in Indonesia. Energ Procedia 158: 243-248. doi: 10.1016/j.egypro.2019.01.083
    [15] Dalmo FC, Simão NM, de Lima HQ, et al. (2019) Energy recovery overview of municipal solid waste in São Paulo State, Brazil. J Clean Prod 212: 461-474. doi: 10.1016/j.jclepro.2018.12.016
    [16] Ghosh P, Shah G, Chandra R, et al. (2019) Assessment of methane emissions and energy recovery potential from the municipal solid waste landfills of Delhi, India. Bioresource Technol 272: 611-615. doi: 10.1016/j.biortech.2018.10.069
    [17] Dlamini S, Simatele MD, Serge Kubanza N (2019) Municipal solid waste management in South Africa: from waste to energy recovery through waste-to-energy technologies in Johannesburg. Local Environ 24: 249-257. doi: 10.1080/13549839.2018.1561656
    [18] Suresh H, Chanakya HN, Malayil S (2019) Creating value addition for MSW biogas plants: increasing mushroom yields with biogas plant digester liquid. Waste Valorisation and Recycling, Singapore: Springer, 447-451.
    [19] Kumar A, Samadder SR (2017) A review on technological options of waste to energy for effective management of municipal solid waste. Waste Manage 69: 407-422. doi: 10.1016/j.wasman.2017.08.046
    [20] Drudi KC, Drudi R, Martins G, et al. (2019) Statistical model for heating value of municipal solid waste in brazil based on gravimetric composition. Waste Management 87: 782-790. doi: 10.1016/j.wasman.2019.03.012
    [21] Al-Salem SM (2019) Energy production from plastic solid waste (PSW). Plast Energ 2019: 45-64.
    [22] Fox JT, Zook AN, Freiss J, et al. (2019) Thermal conversion of blended food production waste and municipal sewage sludge to recoverable products. J Clean Prod 220: 57-64. doi: 10.1016/j.jclepro.2019.02.055
    [23] Mboowa D, Quereshi S, Bhattacharjee C, et al. (2017) Qualitative determination of energy potential and methane generation from municipal solid waste (MSW) in Dhanbad (India). Energy 123: 386-391. doi: 10.1016/j.energy.2017.02.009
    [24] Lee U, Han J, Wang M (2017) Evaluation of landfill gas emissions from municipal solid waste landfills for the life-cycle analysis of waste-to-energy pathways. J Clean Prod 166: 335-342. doi: 10.1016/j.jclepro.2017.08.016
    [25] Li W, Loh KC, Zhang J, et al. (2018) Two-stage anaerobic digestion of food waste and horticultural waste in high-solid system. Appl Energ 209: 400-408. doi: 10.1016/j.apenergy.2017.05.042
    [26] Olatunji OO, Akinlabi S, Madushele N, et al. (2019) Estimation of the elemental composition of biomass using hybrid adaptive neuro-fuzzy inference system. BioEnerg Res 12: 642-652. doi: 10.1007/s12155-019-10009-6
    [27] Olatunji O, Akinlabi S, Madushele N, et al. (2019) Estimation of municipal solid waste (MSW) combustion enthalpy for energy recovery. EAI Endorsed T Energ Web 6: 1-9.
    [28] Obafemi O, Stephen A, Ajayi O, et al. (2019) A survey of artificial neural network-based prediction models for thermal properties of biomass. Procedia Manuf 33: 184-191. doi: 10.1016/j.promfg.2019.04.103
    [29] Baghban A, Ebadi T (2019) GA-ANFIS modeling of higher heating value of wastes: application to fuel upgrading. Energ Source Part A 41: 7-13. doi: 10.1080/15567036.2017.1344746
    [30] Akkaya E, Demir A (2010) Predicting the heating value of municipal solid waste-based materials: An artificial neural network model. Energ Source Part A 32: 1777-1783. doi: 10.1080/15567030902882950
    [31] Kathiravale S, Yunus MNM, Sopian K, et al. (2003) Modeling the heating value of Municipal Solid Waste. Fuel 82: 1119-1125. doi: 10.1016/S0016-2361(03)00009-7
    [32] Wilson DL (1972) Prediction of heat of combustion of solid wastes from ultimate analysis. Environ Sci Technol 6: 1119-1121. doi: 10.1021/es60072a011
    [33] Meraz L, Domı́nguez A, Kornhauser I, et al. (2003) A thermochemical concept-based equation to estimate waste combustion enthalpy from elemental composition. Fuel 82: 1499-1507. doi: 10.1016/S0016-2361(03)00075-9
    [34] Boumanchar I, Chhiti Y, M'hamdi Alaoui FE, et al. (2019) Municipal solid waste higher heating value prediction from ultimate analysis using multiple regression and genetic programming techniques. Waste Manage Res 37: 578-589. doi: 10.1177/0734242X18816797
    [35] Niessen WR (2010) Combustion and Incineration Processes: Applications in Environmental Engineering, 2 Eds., Massachusetts: CRC Press.
    [36] Chang YC (1982) Estimating heat of combustion for waste materials. Pollut Eng 14.
    [37] Shi H, Mahinpey N, Aqsha A, et al. (2016) Characterization, thermochemical conversion studies, and heating value modeling of municipal solid waste. Waste Manage 48: 34-47. doi: 10.1016/j.wasman.2015.09.036
    [38] ECN Phyllis2, Database for biomass and waste. ECN Phyllis2, 2018. Available from: https://phyllis.nl/Browse/Standard/ECN-Phyllis.
    [39] Zarei F, Rahimi MR, Razavi R, et al. (2019) Insight into the experimental and modeling study of process intensification for post-combustion CO2 capture by rotating packed bed. J Clean Prod 211: 953-961. doi: 10.1016/j.jclepro.2018.11.239
    [40] Darvishan A, Bakhshi H, Madadkhani M, et al. (2018) Application of MLP-ANN as a novel predictive method for prediction of the higher heating value of biomass in terms of ultimate analysis. Energ Source Part A 40: 2960-2966. doi: 10.1080/15567036.2018.1514437
    [41] Sedighizadeh M, Mohammadpour AH, Alavi SM (2019) A two-stage optimal energy management by using ADP and HBB-BC algorithms for microgrids with renewable energy sources and storages. J Energ Storage 21: 460-480. doi: 10.1016/j.est.2018.12.010
    [42] Sibi P, Jones SA, Siddarth P (2013) Analysis of different activation functions using back propagation neural networks. J TheorAppl Inf Technol 47: 1264-1268.
    [43] Karlik B, Olgac AV (2011) Performance analysis of various activation functions in generalized MLP architectures of neural networks. Int J Artif Intell Expert Syst 1: 111-122.
    [44] Cao W, Wang X, Ming Z, et al. (2018) A review on neural networks with random weights. Neurocomputing 275: 278-287. doi: 10.1016/j.neucom.2017.08.040
    [45] Ertuğrul ÖF (2018) A novel type of activation function in artificial neural networks: Trained activation function. NeurNet 99: 148-157.
    [46] Uzun H, Yıldız Z, Goldfarb JL, et al. (2017) Improved prediction of higher heating value of biomass using an artificial neural network model based on proximate analysis. Bioresource Technol 234:122-130. doi: 10.1016/j.biortech.2017.03.015
    [47] Meesaraganda LP, Saha P, Tarafder N (2019) Artificial neural network for strength prediction of fibers' self-compacting concret, Soft Computing for Problem Solving, Singapore: Springer, 15-24.
    [48] Marquardt DW (1963) An algorithm for least-squares estimation of nonlinear parameters. J Soc for Ind Appl Math 11: 431-441. doi: 10.1137/0111030
    [49] Chu Y, Xu K, Zhong Y, Ye X, et al. (2018) Fast microwave through wall imaging method with inhomogeneous background based on Levenberg-Marquardt algorithm. IEEE T Microw Theory 67: 1138-1147.
    [50] Costa MA, de Pádua Braga A, de Menezes BR (2007) Improving generalization of MLPs with sliding mode control and the Levenberg-Marquardt algorithm. Neurocomputing 70: 1342-1347. doi: 10.1016/j.neucom.2006.09.003
    [51] Bahremand S, Ko HS, Balouchzadeh R, et al. (2019) Neural network-based model predictive control for type 1 diabetic rats on artificial pancreas system. Med Biol Eng Comput 57: 177-191. doi: 10.1007/s11517-018-1872-6
    [52] İçer S, Kara S, Güven A (2006) Comparison of multilayer perceptron training algorithms for portal venous doppler signals in the cirrhosis disease. Expert Syst Appl 31: 406-413. doi: 10.1016/j.eswa.2005.09.037
    [53] Demuth H, Beale M, Hagan M (2004) Neural Network Toolbox 2 Eds.,User's Guide, version 4, The Mathworks. Natick, The MathWorks, Inc.
    [54] Chang YF, Lin CJ, Chyan JM, et al. (2007) Multiple regression models for the lower heating value of municipal solid waste in Taiwan. J Environ Manage 85: 891-899. doi: 10.1016/j.jenvman.2006.10.025
    [55] Arora I, Saha A (2016) Comparison of back propagation training algorithms for software defect prediction. 2016 2nd International Conference on Contemporary Computing and Informatics (IC3I), Noida, India.

  • This article has been cited by:

    1. Felix Ishola, Damola Adelekan, Angela Mamudu, Temitope Abodunrin, Abraham Aworinde, Obafemi Olatunji, Stephen Akinlabi, Biodiesel production from palm olein: A sustainable bioresource for Nigeria, 2020, 6, 24058440, e03725, 10.1016/j.heliyon.2020.e03725
    2. Ankun Xu, Huimin Chang, Yingjie Xu, Rong Li, Xiang Li, Yan Zhao, Applying artificial neural networks (ANNs) to solve solid waste-related issues: A critical review, 2021, 124, 0956053X, 385, 10.1016/j.wasman.2021.02.029
    3. T.O. Babarinde, S.A. Akinlabi, D.M. Madyira, F.M. Ekundayo, P.A. Adedeji, Dataset and ANN model prediction of performance of graphene nanolubricant with R600a in domestic refrigerator system, 2020, 32, 23523409, 106098, 10.1016/j.dib.2020.106098
    4. Fatima Ezzahra Yatim, Imane Boumanchar, Bousalham Srhir, Younes Chhiti, Charafeddine Jama, Fatima Ezzahrae M'hamdi Alaoui, Waste-to-energy as a tool of circular economy: Prediction of higher heating value of biomass by artificial neural network (ANN) and multivariate linear regression (MLR), 2022, 153, 0956053X, 293, 10.1016/j.wasman.2022.09.013
    5. Paul A. Adedeji, Obafemi O. Olatunji, Nkosinathi Madushele, Abiola O. Ajayeoba, 2021, 9780128245552, 79, 10.1016/B978-0-12-824555-2.00026-5
    6. Hoang Lan Vu, Kelvin Tsun Wai Ng, Amy Richter, Jianbing Li, Seyed Ashkan Hosseinipooya, Impacts of nested forward validation techniques on machine learning and regression waste disposal time series models, 2022, 72, 15749541, 101897, 10.1016/j.ecoinf.2022.101897
    7. Usman Alhaji Dodo, Evans Chinemezu Ashigwuike, Jonas Nwachukwu Emechebe, Sani Isah Abba, Prediction of energy content of biomass based on hybrid machine learning ensemble algorithm, 2022, 8, 27724271, 100157, 10.1016/j.nexus.2022.100157
    8. Wanjun Xia, Yanping Jiang, Xiaohong Chen, Rui Zhao, Application of machine learning algorithms in municipal solid waste management: A mini review, 2022, 40, 0734-242X, 609, 10.1177/0734242X211033716
    9. Usman Alhaji Dodo, Evans Chinemezu Ashigwuike, Sani Isah Abba, Machine learning models for biomass energy content prediction: A correlation-based optimal feature selection approach, 2022, 19, 2589014X, 101167, 10.1016/j.biteb.2022.101167
    10. Oluwatobi Adeleke, Stephen Akinlabi, Tien-Chien Jen, Paul A. Adedeji, Israel Dunmade, Evolutionary-based neuro-fuzzy modelling of combustion enthalpy of municipal solid waste, 2022, 34, 0941-0643, 7419, 10.1007/s00521-021-06870-2
    11. Jithina Jose, T. Sasipraba, Estimation of Higher Heating Value for MSW Using DSVM and BSOA, 2023, 36, 1079-8587, 573, 10.32604/iasc.2023.030479
    12. Anna Matveeva, Aleksey Bychkov, How to Train an Artificial Neural Network to Predict Higher Heating Values of Biofuel, 2022, 15, 1996-1073, 7083, 10.3390/en15197083
    13. Olusegun Abayomi Olalere, Chee‐Yuen Gan, Paul Adeola Adedeji, Modupeola Elizabeth Olalere, Nawzat Aljbour, Multi‐objective Deng's grey incidence analysis, orthogonal optimization, and artificial neural network modelling in hot‐maceration‐assisted extraction of African cucumber leaves ( Momordica balsamina ) , 2022, 100, 0008-4034, 588, 10.1002/cjce.24138
    14. Ivan Brandić, Lato Pezo, Nikola Bilandžija, Anamarija Peter, Jona Šurić, Neven Voća, Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis, 2022, 10, 2227-7390, 3732, 10.3390/math10203732
    15. Shiv Kumar Verma, Dharamveer Singh Sagar, 2022, Segregation of Municipal Solid Waste With Use of Residual Network, 978-1-6654-5635-7, 1, 10.1109/ICERECT56837.2022.10060151
    16. Fuquan Song, Heying Ding, Yongzheng Wang, Shiming Zhang, Jinbiao Yu, A Well Production Prediction Method of Tight Reservoirs Based on a Hybrid Neural Network, 2023, 16, 1996-1073, 2904, 10.3390/en16062904
    17. Fatima Ezzahra Yatim, Rachid Ait Belale, Ilham Abala, Younes Chhiti, Natalia Munoz Rujas, Fernando Aguilar, Fatima Ezzahrae M'hamdi Alaoui, Blending biomass-based liquid biofuels for a circular economy: Measuring and predicting density for biodiesel and hydrocarbon mixtures at high pressures and temperatures by machine learning approach, 2024, 234, 09601481, 121146, 10.1016/j.renene.2024.121146
    18. Tirthankar Basu, Arijit Das, Ketan Das, Paulo Pereira, Urban expansion induced loss of natural vegetation cover and ecosystem service values: A scenario-based study in the siliguri municipal corporation (Gateway of North-East India), 2023, 132, 02648377, 106838, 10.1016/j.landusepol.2023.106838
    19. Seyyed Amirreza Abdollahi, Seyyed Faramarz Ranjbar, Dorsa Razeghi Jahromi, Applying feature selection and machine learning techniques to estimate the biomass higher heating value, 2023, 13, 2045-2322, 10.1038/s41598-023-43496-x
    20. Adnane Mounadel, Hamid Ech-Cheikh, Saâd Lissane Elhaq, Ahmed Rachid, Mohamed Sadik, Bilal Abdellaoui, Application of artificial intelligence techniques in municipal solid waste management: a systematic literature review, 2023, 12, 2162-2515, 316, 10.1080/21622515.2023.2205027
    21. Usman Alhaji Dodo, Mustapha Alhaji Dodo, Asia'u Talatu Belgore, Munir Aminu Husein, Evans Chinemezu Ashigwuike, Ahmed Saba Mohammed, Sani Isah Abba, Comparative study of different training algorithms in backpropagation neural networks for generalized biomass higher heating value prediction, 2024, 2, 29497205, 100060, 10.1016/j.gerr.2024.100060
    22. C. U. Ezeh, K. A. Adjei, S. Schönbrodt-Stitt, O. Igwe, M. Y. Asare, K. Preko, Scale-Related Variations in Soil Loss and Validation of the RUSLE Model in Anambra State, Nigeria, 2024, 1064-2293, 10.1134/S1064229324600015
    23. Amin Shahsavar, Mojtaba Sepehrnia, Ali Fateh Moghaddam, Somayeh Davoodabadi Farahani, Effects of sonication time on thermophysical properties of ternary hybrid nanofluid and modeling thermophysical properties utilizing two GMDH and SVR models based on machine learning, 2024, 163, 18761070, 105650, 10.1016/j.jtice.2024.105650
    24. Iffadhiya Fathin Adiba, Sudathip Sae‐tan, Wattinee Katekhong, Pitiporn Ritthiruangdej, Ravipim Chaveesuk, Savitree Ratanasumawong, Effect of ingredients on cooking quality, textural properties, and microstructure of fresh mung bean by‐product gluten‐free pasta, 2024, 59, 0950-5423, 2581, 10.1111/ijfs.16997
    25. Evita Intan Cahyaningtyas, Youllia Indrawaty Nurhasanah, Hary Nugroho, 2024, Performance Analysis of Integrated GeoAI Using Multi-Layer Perceptron Based on Hyperparameter to Identify Landslide Prone Areas: A Case Study from West Bandung, 979-8-3503-6880-2, 1, 10.1109/CENIM64038.2024.10882700
    26. Saptarshi Mondal, Islam M. Rafizul, Predicting calorific value through proximate analysis of municipal solid waste using soft computing system, 2025, 7, 3004-9261, 10.1007/s42452-025-06643-9
    27. Oluwatobi Adeleke, Obafemi O. Olatunji, Tien-Chien Jen, 2024, An Assessment of Clustering Performance in Neuro-fuzzy system for prediction of Energy Content of Waste-derived Biomass, 979-8-3315-4255-9, 1, 10.1109/NIGERCON62786.2024.10927205
    28. Nasreen Banu Mohamed Ishaque, S. Metilda Florence, Development of a Deep Learning Predictive Model for Estimating Higher Heating Value in Municipal Solid Waste Management, 2025, 26667908, 100966, 10.1016/j.clet.2025.100966
  • Reader Comments
  • © 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
AIMS Energy
1.8 3.8

Metrics

Article views(5082) PDF downloads(593) Cited by(28)

Preview PDF
Download XML
Export Citation
Article outline
Abstract
   Introduction
   Materials and methods
   Results and discussion
Conclusions
Conflict of interest
References

Figures and Tables

Figures(6)  /  Tables(5)

Other Articles By Authors

Related pages

Tools

Copyright © AIMS Press

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog