The problem of global warming has led to increased research on solar energy and other renewable energy. Solar cells are a building block of solar energy. Different materials for solar cells fabrication exist with silicon-based being commercially viable and common. The bulk of the alternate materials aimed at providing cheap, efficient and sustainable solar cells. Nanostructured Metal oxides solar cells goes a step further to providing a clean, affordable, sustainable solar cells although the efficiency is still low. This study examined the numerical modelling of the annealing effect on the efficiency of nanostructured CuO/TiO2 pn heterojunction using SCAPS. The motivation for the study is to provide a basis for experimental design of affordable, non-toxic and efficient alternate material for silicon solar cells. The modelling was performed using Solar cells capacitance simulator (SCAPS). The input parameters, obtained from literature, include a working point of 300 K for the as-deposited CuO/TiO2 which was compared with air and nitrogen annealed (423.15 K) nanostructured CuO/TiO2 pn heterojunction. Other working condition included simulated sunlight using illumination of AM 1.5G with a 500 W Xenon lamp, silver was used as the electrode/contact. Film thickness of 2000 nm and 200 nm for absorber and buffer respectively. The results gave an optimum efficiency of 0.47 obtained from Nitrogen annealed CuO/TiO2 pn heterojunction. Also, the optimum Fill Factor was obtained to be 64.01% from Nitrogen annealed. The annealed samples performed better than the as-deposited CuO/TiO2 pn heterojunction. This result will help in the experimental fabrication of improved efficiency metal oxide-based solar cells.
Abbreviations: CuO: Cupric Oxide; FF: Filled Factor; Ⅰ-Ⅴ: Current-voltage; J-V: Current density–voltage; Jsc: Short-circuit current; NMO: Nanostructured Metal Oxide; PN: p-type (excess hole), n-type (excess electron) heterojunction; SCAPS: Solar cells capacitance simulator; TiO2: Titanium dioxide; Voc: Open circuit voltage; ZnO: Zinc Oxide; η: Efficiency
1.
Introduction
Numerical modeling has been employed to offer a theoretical road map for speedy experimental optimization of processes. Simulation have been used for optimization of parameters in energy [1], transportation [2,3], production planning [4], water and food production [5]. Numerical simulation has also been employed in improving the properties of solar cells [6,7]. Nanostructured metal oxide is among the emerging solar cells. Modeling of nanostructured metal oxide interest has increased significantly for decades due to the simplicity and ease of manipulation of the tool [8,9].
Photovoltaic continue to gain prominence in Europe and other part of the world [10]. However, affordability and other factor continue to hinder the usage in Africa and other developing countries [11,12,13]. Although, nanostructured metal oxides solar cells show promise of low cost, clean and efficient photovoltaic usage in Africa [14,15]. Nanostructured metal oxides (NMO) continue to attract interest due to the versatility in energy applications [16,17,18,19]. However, most of them still exhibit weak conversion efficiencies resulting in several experiments in the laboratory in an attempt to obtain the optimum power conversion efficiency. Although, metal oxide efficiency is still low compared to other solar cells, similar efficiency of 20% recorded by CIGS-based solar cells [20]. Though the progress of numerous physical and chemical fabrication techniques for PV [21,22,23]. While, different explanations could describe this condition, such as several loss mechanisms owed to absorber structures.
Cupric oxide also known as copper (Ⅱ) oxide is a black solid stable oxide of copper. CuO has a band gap of 1.2 eV [24]. The metal oxide has a p-type semiconductor property, monoclinic structure with adsorption coefficient 105 cm-1, electrical resistivity of about 10 to 105 Ω.cm and high thermal conductivity [25,26,27].
Solar cells produce about 0.1 volts to 0.6 volts of open circuit voltage and 1 to 8 amps DC current depending on a range of factors but mainly related to the semiconductor used [28]. About 36 to 72 solar cells are stacked together in series to form a module which can produce meaningful output. A solar panel is an arrangement of solar modules either in series or parallel. When the solar modules are connected in parallel the currents are added and voltage is the same, while for series the voltages are added and current produced remains the same [29].
The first solar cells simulation work was reported by Lee using ADEPT 1dimension program developed at Purdue [30]. Lee and Gray [31] investigated the effect of grain boundaries, non-ideal back contact, and specified the various necessary parameters for measuring cell performance. Gloeckler, et al. [32] defined the initial simulating parameters by setting CdTe baseline. The study defined the influence of thin layer of CdS amid the regions of TCO and CdTe. J-V curves was defined in the simulation. The study used AMPS Simulation software developed at Pennsylvania university by S. Fonash and coworkers. Various parameters in this simulation software are temperature independent. The simulation of graded junction is conceivable. J-V in spectral response measurement, dark and light can be simulated when the device definition is completed. Nonetheless, AMPS compared to supplementary simulating tools is slow in solving problem [33].
This study was able to model the annealing effect on efficiency of nanostructured CuO/TiO2 pn heterojunction using SCAPS. The annealing temperatures were varied between 300 K and 423.15 K. The sunlight beam was simulated using AM 1.5G with a 500 W Xenon lamp. The highest fill factor and efficiency of 64.01 and 0.47 was obtained for nitrogen annealed nanostructured CuO/TiO2 heterojunction.
2.
Numerical modeling overview
Numerous simulating tools are currently accessible. The earliest simulating program was developed as a PhD thesis by Mark S. lundstrom. Additional programs include; TFSSP (Thin-Film Semiconductor Simulation Program), Solar Cell Analysis Program in 1dimension (SCAPS 1D), Solar Cell Analysis Program in 2Dimension, PUPHS and PUPHS 2D. A number of solar cell models has been used in thin-film Si: H, Si, Ge, CdS/CIS, CdS/CdTe and GaAs cells in one spatial dimension and high efficiency Si and GaAs solar cells in 2Dimension [34].
For this current work, SCAPS is adopted for the simulation of nanostructured CuO/TiO2 thin film solar cells. The nanostructured CuO/TiO2 pn heterojunction solar cells was simulated at different working point and subjected to different annealing samples for thermal investigation using SCAPS.
2.1. Solar cells capacitance simulator (SCAPS)
It is a solar cells simulation package for solar cells structures used initially at Gent University for solar cells of CdTe and CuInSe2 family [35]. It has since been used for other family of solar cells [36]. It describes mathematically the performance of a solar cell using finite difference methods and solves differential equations which, along with several relations from physics of semiconductors. SCAPS performs a complete simultaneous numerical solution of the two continuity equations and Poisson's equation conditional on the boundary conditions appropriate to one and two-dimensional cells [37]. The equations are expressed as shown in Eqs 1–3.
The general terms of Eqs 2 and 3 can be represented as:
The hole and electron current densities which appear in Eqs 2 and 3 are given by
where vp and vn represent the effective potentials expressed in Eqs 7 and 8. ∆G and γ account for variations in the band structure, such as the density of band gap and states, and account for Fermi-Dirac statistics. Expression Jn and Jp represent the current density of the electron and holes respectively. Similarly, μn and μp represent the mobility of electron and hole respectively.
2.2. Absorber (CuO) and Buffer (TiO2) layer properties
The absorber layer is made of a p-type semiconductor copper(Ⅱ) oxide known as cupric oxide (CuO). The CuO has electron affinity of 4.07 eV and a large hole mobility [38,39]. However, the buffer layer is made of a widely studied material TiO2, a transition metal oxide [40]. TiO2 has unique optoelectronic properties, durable with great refractive index making it ideal material for several applications including solar cells [41].
3.
Simulation model and results
3.1. SCAPS simulation of the CuO/TiO2 pn heterojunction
The input parameters used for the SCAPs simulation were adapted from literature using properties and values of TiO2 and CuO and are presented in Table 1 [39,42,43].
The input parameters for the back and front contact were optimized values using the SCAPS software and is shown in Table 2.
3.2. Effect of Annealing on the nanostructured CuO/TiO2 heterojunction solar cells
Sunlight passes through a conducting substrate onto the absorber layer and buffer layer in a typical p-n heterojunction. Incident photons from the sun light is absorbed by the absorber layer which is a p-type semiconductor. The unabsorbed photons are dissipated in the form of heat. However, the buffer layer completes the p-n heterojunction with the absorber layer.
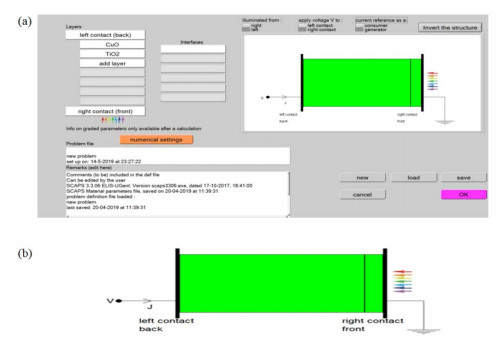
In this study, CuO is used as the absorber layer, TiO2 as the buffer layer and the effect of annealing on the efficiency, and Ⅰ-Ⅴ characteristics is observed. The simulation mimicked as-deposited CuO at room temperature and compared it with air and nitrogen annealed at 423.15 K. Researches have shown that titanium dioxide is a top n-type for CuO pn heterojunction solar cells with a great efficiency [44]. In this study, 2000 nm and 200 nm was used for the absorber and buffer layer thickness respectively. These values are within the optimize thickness range and also thickness of the buffer layer should be made thin to minimize resistance series in solar cell device [45]. A schematic representation of the nanostructured solar cells layer simulated using SCAPS is shown in Figure 1. The main panel showing layer definition and numerical setting is shown in Figure 1a. Schematic of the nanostructured CuO/TiO2 pn Heterojunction Solar Cells is shown in Figure 1b.
3.2.1. The Simulated J-V result
The efficiency is obtained using Eq 9 as shown.
The parameters of solar cells analysed from J-V curve are presented in Table 3. The nitrogen annealed nanostructured CuO/TiO2 had the highest fill factor of 64.01% with an efficiency of 0.47%. The as-deposited/modeled nanostructured CuO/TiO2 had the lowest with a FF of 41% and efficiency of 0.21. The increase in the annealed samples validate the fact that annealing has consequence on relieving strain caused by lattice mismatch and adjust the surface morphology, improve formation of CuO/TiO2 films [46].
3.3. Solar cell efficiency
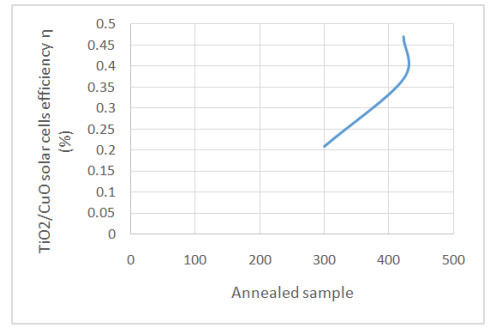
Figure 2, shows the different annealing variables plotted against the solar cell efficiency. This shows the effect of annealed sample and how it influences the rate of change in efficiency. The result shows the effect of annealing sample on solar cells efficiency as it increased from 0.21% efficiency at 300 K of annealed sample to 0.47% at an annealed sample of 423.15 K. This is an increase compared to the as-deposited CuO/TiO2 pn heterojunction efficiency of 0.21% annealed at 300 K and 0.36% reported by Saehana M., et al., [47].
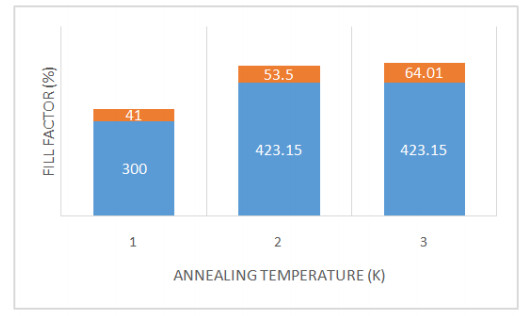
Figure 3 below shows the distribution of annealed temperature at different fill factor of the nanostructured CuO/TiO2 solar cells. From the figure 3, it was observed that the fill factor was 41% at 300 K annealing temperature, and at 423.15 K it was seen to be 53.5%. However, when the temperature was maintained at 423.15 in Nitrogen environment after a period of time, the fill factor increased to 64.01%. This increment in the fill factor when the sample was annealed validates the fact that annealing has impact on the structural, electrical and optical properties of solar cells [48]. This shows that the solar cell FF increases as annealing temperature increased from 300 K and continued to increase when an annealing temperature of 423.15 K was maintained.
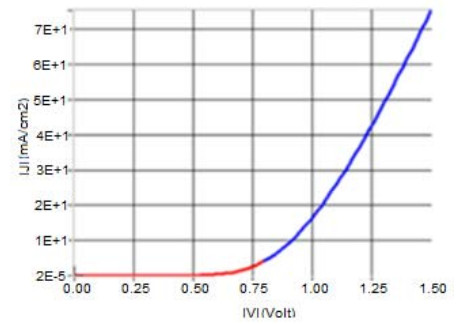
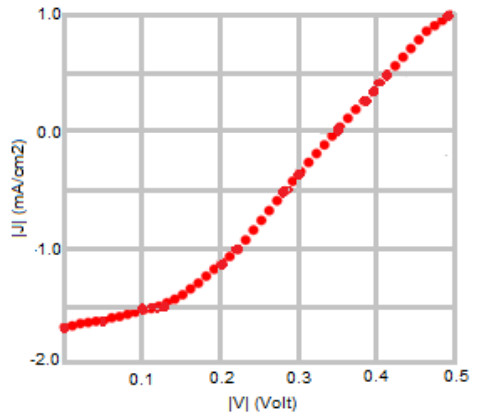
Figure 4 gives the J-V curve of as deposited CuO/TiO2 heterojunction solar cells. It shows a short-circuit current (Jsc) of 0.81A, open-circuit voltage (Voc) of 323 mV, fill factor of 41% and an efficiency of 0.21%. The resultant J-V curve is in alignment with the standard J-V curve of solar cell under illumination.
Figure 5 gives the J-V curve for the air annealed CuO/TiO2 pn heterojunction solar cells. This plot reports that a short circuit current (Jsc) of 0.98A was exhibited, open-circuit voltage (Voc) of 350 mV, fill factor (FF) of 53.50% and an efficiency of 0.37%.
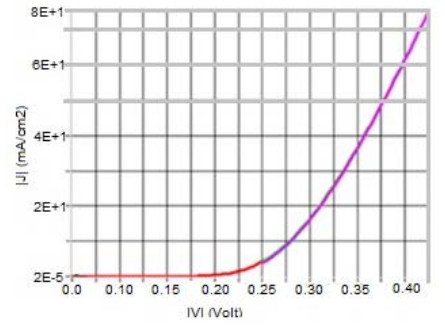
Figure 6 displays the result of the J-V curve for the nitrogen annealed CuO/TiO2 pn heterojuction solar cells. The curve shows a short-circuit current (Jsc) of 1.04A, open-circuit voltage (Voc) of 354 mV, fill factor (FF) of 64.01% and an efficiency of 0.47%. The fill factor (FF) obtained was 0.21%, at a working point of 300 K. This curve is in accordance with standard J-V curve of a solar cell experiencing illumination [49].
3.3.1. Effect of defect density
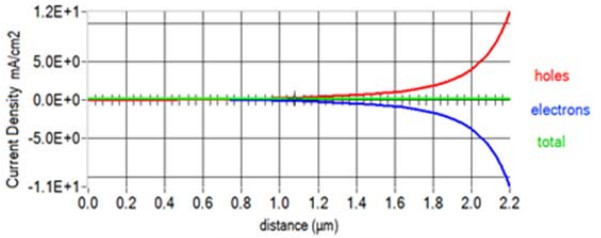
Defect in density of the absorber layer (CuO) influence the solar cells performance. Decrease in densities effect yield limited recombination and trap cores and extend the performance of solar cells [50]. Figure 7 shows that the total charge remains steady at 0.0E + 0 mA/cm2 at an absorber thickness of 2000 nm and buffer of 200 nm, with annealed sample at 423.15 K. The red-line signifies the hole, the blue signifies the electron and green is total (charge).
4.
Conclusions
This simulation result shows the effect of annealing of nanostructured CuO/TiO2 heterojunction solar cells by means of SCAPS.
➢ The different annealed samples were observed to have influenced the solar cells efficiency. This interprets that, with an annealed sample within the range of 300 K to 423.15 K the change in the solar cells efficiency is quite significant and this agrees with [51].
➢ The performance of CuO/TiO2 cells is influenced by defect density. A lesser defect density mainly at absorber layer (CuO) increases the photovoltaic effect.
➢ The annealed result shows the cell efficiency of 0.47% at an annealed sample of 423.15 K, which is an increase compared to the as-deposited CuO/TiO2 pn heterojunction efficiency of 0.21% at working point of 300K, and 0.36% efficiency reported by Masudy S, et al., [52].
➢ The values of this simulation model will offer a guide in experimental, fabrication and optimization of CuO/TiO2 solar cells.
Acknowledgments
The authors acknowledge the SCAPS software team for the computational resources. Professor Jen and Dr. Ukoba acknowledges financial support of NRF and URC University of Johannesburg.
Conflict of Interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: