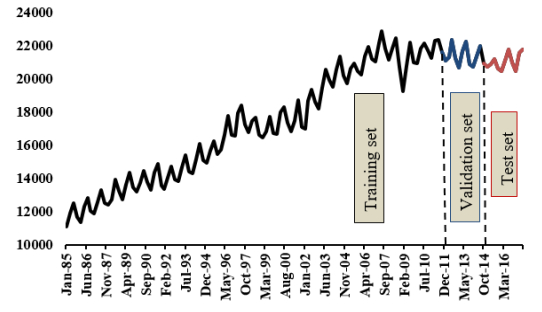
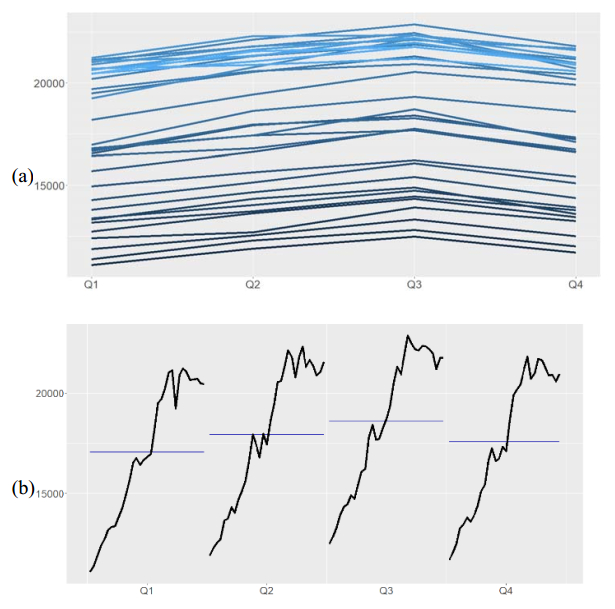
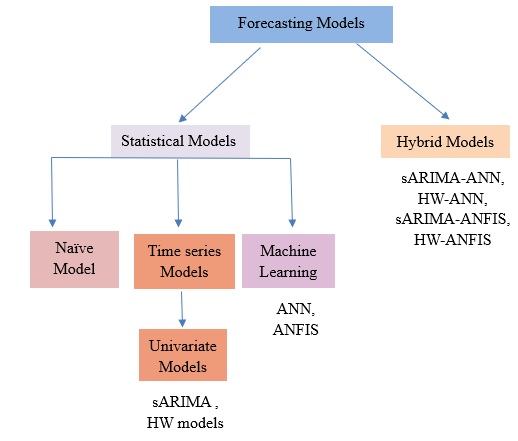
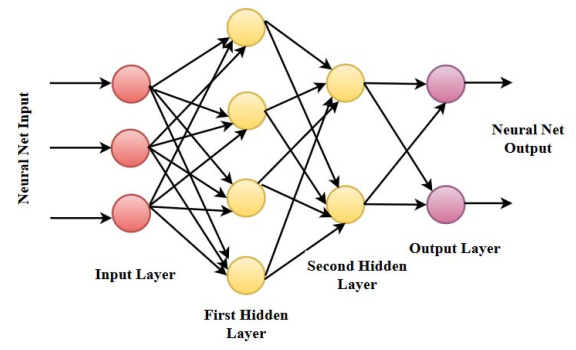
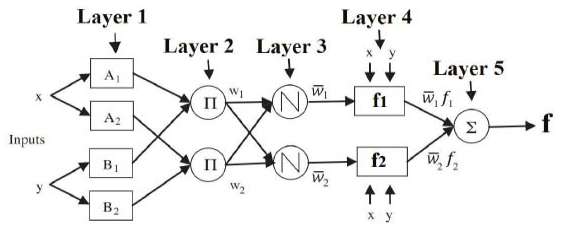
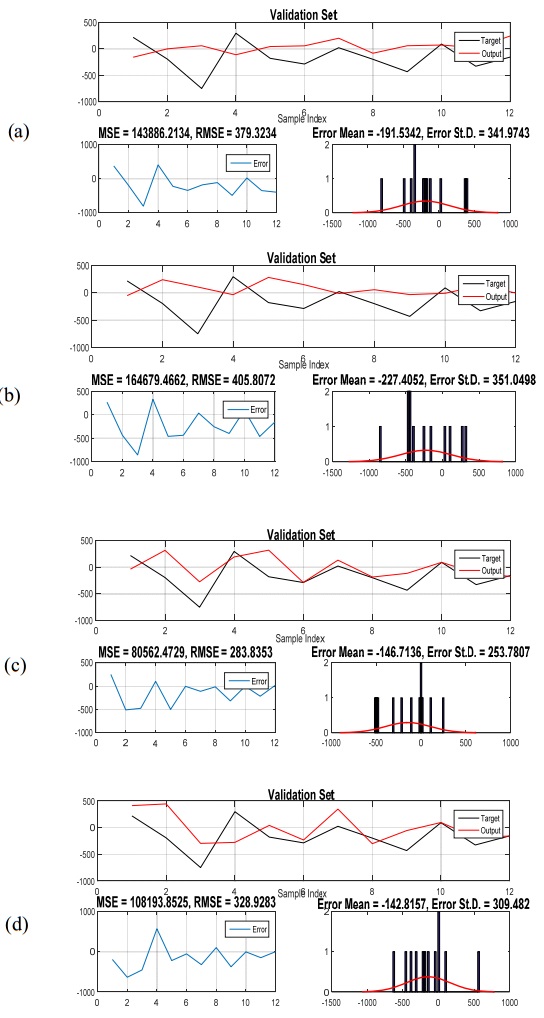
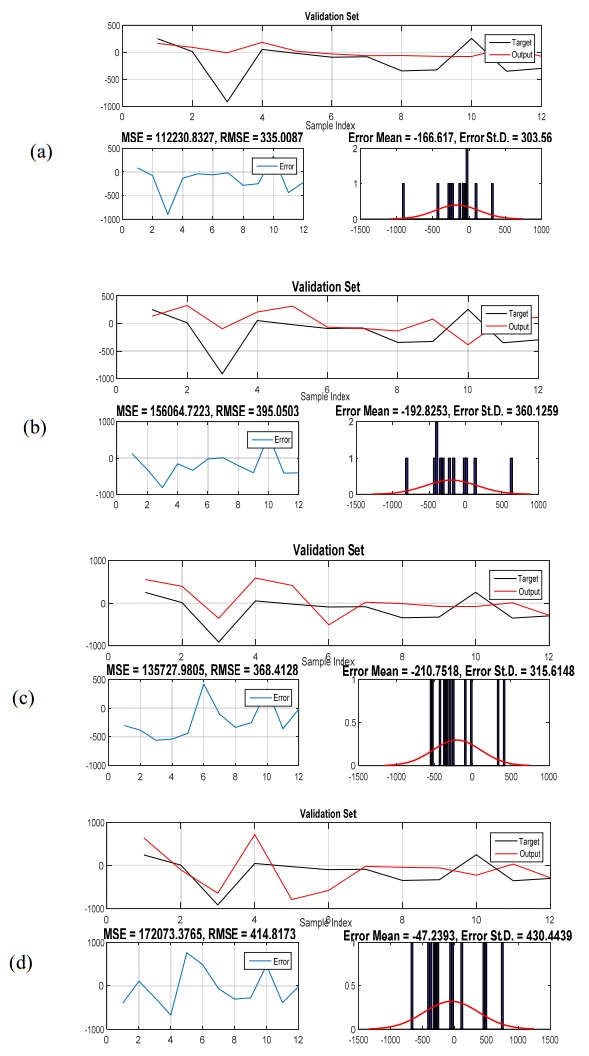
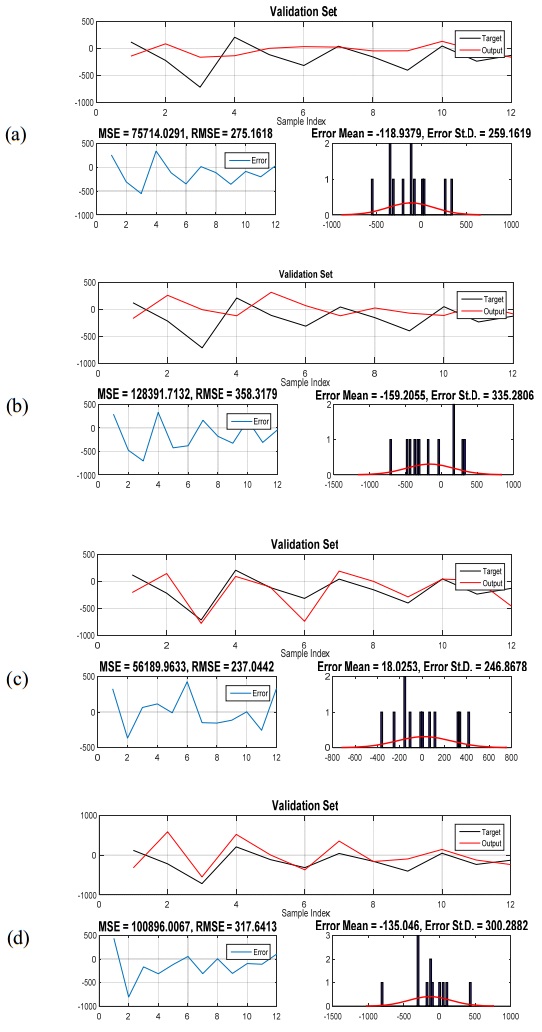
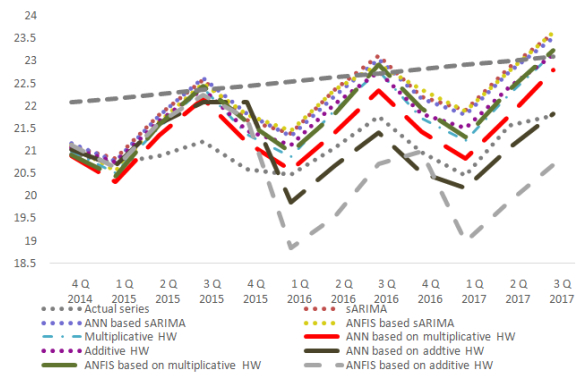
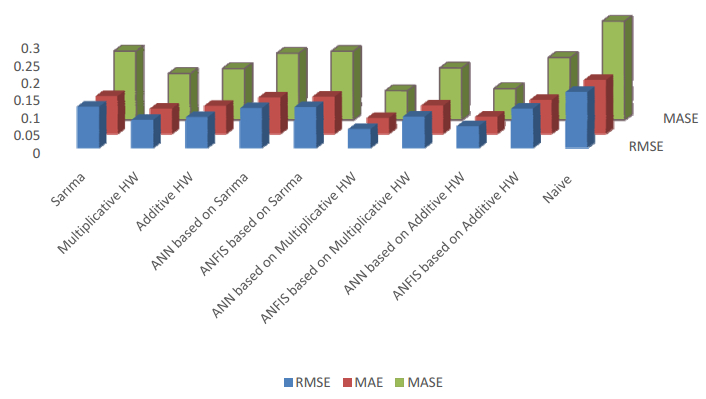
Electricity plays an important role in the South African economy with the industrial sector consuming the highest proportion followed by the residential and mining sector. Besides the fact that electricity is considered as an important energy sources, an adequate supply of electricity remains an important factor that affects the development and economic growth of a country. Therefore, it becomes even more important to forecast the total electricity production in South Africa. It turns out that the comparison of the predictive performance of different forecasting methods is inevitable. Hybrid forecasting approaches, such as artificial neural network (ANN) based seasonal Autoregressive Integrated Moving Average (sARIMA) model, ANN based multiplicative Holt-Winters (HW) model, ANN based additive HW model, an adaptive neuro-fuzzy inference system (ANFIS) based sARIMA model, ANFIS based multiplicative HW model and ANFIS based additive HW model, are employed as some valuable alternatives compared with the conventional univariate time series models, such as sARIMA model and both multiplicative and additive HW models. The aim of this study is not only to provide evidence on the weakness of the univariate time series models, but also to show that hybrid forecasting method has the superior ability over the univariate time series models, with achieving a higher forecasting accuracy. In addition, random walk model is used as benchmark model, allowing for the fair competition. The results show that the hybrid model, ANN based on multiplicative HW model, is the most fitted for the total electricity production in South Africa. This study presents an empirical framework to guide the field of prediction research by providing a more comprehensive empirical investigation of the total electricity production forecasting by using various hybrid models.
1.
Introduction
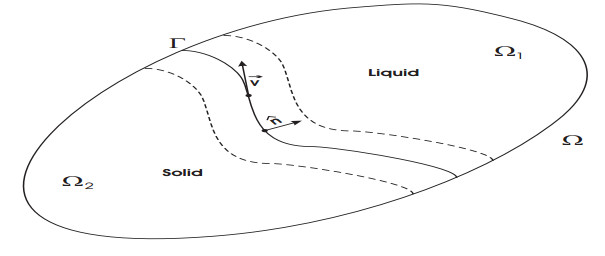
We consider a material in a region Ω⊂Rn, n≤3, which may be in either of two phases, e.g., solid and liquid (see Figure 1). Let us denote by
the reduced temperature distribution, where θ(t,x) represent the temperature of the material and θM is the melting temperature (the temperature at which solid and liquid may coexist in equilibrium, separated by an interface).
In the following we will describe the framework of our problem. So, let us consider the interface as a continuous region, more vast (in which the liquid can coexist with the solid) and of finite thickness, in which the change of phase occurring continuously.
The following nonlinear parabolic system
with the non-homogeneous Cauchy-Neumann boundary conditions
and with the initial conditions
represents the mathematical model called the phase field transition system, introduced by G. Caginalp (see [3] and references therein) to model the transition between the solid and liquid phase in melting/solidification process to a matter occupying a region Ω, while:
● u(t,x) - represents the reduced temperature distribution in Q;
● φ(t,x) - is the phase function (the order parameter) used to distinguish between the states (phases) of material which occupies the region Ω at every time t∈[0,T];
● Cρ=ρV; ρ - the density, V - the casting speed;
● ℓ,k,α,ξ,h are physical parameters representing, respectively: the latent heat, the thermal conductivity, the relaxation time, the measure of the interface thickness, the heat transfer coefficient;
● sξ=m[S]E2σTE, a bounded and positive quantity, expressed by positive and bounded physical parameters: m=1∫−1(2F(s))12ds, F(s)=14(s2−1)2, [S]E - the entropy difference between phases per volume, σ - the interfacial tension, TE - the equilibrium melting temperature (see Caginalp & Chen [4]);
● w1(t,x)∈W1−12p,2−1pp(Σ), p≥2, - is a given function: the temperature of the surrounding at ∂Ω for each time t∈[0,T] (can also be interpreted as boundary control);
● w2(t,x)∈W1−12p,2−1pp(Σ) - is a given function;
● u0,φ0∈W2−2pp(Ω), with k∂∂νu0+hu0=w1(0,x) and ξ∂∂νφ0=w2(0,x);
The model (1.1)–(1.3) represents a refinement of the classical Stefan problem (see [21,23,24]) in two phases by adding a new nonlinear parabolic equation, derived from the Euler-Lagrange equations for the free energy in Landau-Ginzburg field theory. This new mathematical model reflects more accurately the physical phenomenon of solidification, like: superheating, supercooling, etc.
Different other nonlinearities capable to come out the complexity of the physical phenomena (the effect of surface tension, separating zone of solid and liquid states, etc) have been proposed by several authors (see Cârjă, Miranville & Moroşanu [5], Kenmochi & Niezgódka [8], Miranville & Moroşanu [9], Moroşanu [16], Moroşanu & Motreanu [20], Penrose & Fife [22] and Temam [24]). The general nonlinear term in Moroşanu & Motreanu [20], is (possibly) non-convex and non-monotone and cover a large class of nonlinearities, including the known cases as well as other new relevant situations. Moreover, different types of boundary conditions on Σ can be associated to (1.1) (see Moroşanu [16] for more details).
2.
Well-posedness of solutions to the nonlinear system (1.1)–(1.3)
In the present section we will investigate the solvability of the first boundary value problems of the form (1.1)–(1.3) in the class W1,2p(Q), p≥2.
The main result of this section establishes the dependence of the solution u(t,x), φ(t,x) in the nonlinear parabolic system (1.1)–(1.3) on the terms w1(t,x), w2(t,x) in the right-hand side of (1.2).
Theorem 2.1 Problem (1.1)–(1.3) has a unique solution (u,φ) with u∈W1,2p(Q) and φ∈W1,2ν(Q), where ν=min{q,μ}, q≥p≥2. In addition (u,φ) satisfies
where the constant C depends on |Ω| (the measure of Ω), T, n, p, q and physical parameters, but is independent of u, φ, w1 and w2.
Moreover, given any number Md>0, if (u1,φ1) and (u2,φ2) are solutions to (1.1)–(1.3) for the same initial conditions, corresponding to the data w11,w21, w12,w22∈ W1−12p,2−1pp(Σ), respectively, such that ‖φ1‖Lν(Q), ‖φ2‖Lν(Q)≤Md, then the estimate below holds
where the constant C depends on |Ω|, T, Md, n, p, q and physical parameters, but is independent of u1,u2, φ1,φ2, w11, w21, w12 and w22.
Proof. The basic tools in the analysis of the problem (1.1) (see [16] and references there in) are the Leray-Schauder degree theory, the Lp-theory of linear and quasi-linear parabolic equations, as well as the Lions and Peetre embedding Theorem, which ensures the existence of a continuous embedding W1,2p(Q)⊂Lμ(Q), where the number μ is defined as follows
The proof of Theorem 2.1 was given in Moroşanu [16] noting that there formulation differs from this by certain physical parameters, which implies different values for the constant C in (2.1) and (2.2). Moreover, corresponding to different boundary conditions (including nonlinear and nonhomogeneous boundary conditions), similar results were proved in Cârjă, Miranville & Moroşanu [5] and Miranville & Moroşanu [9].
Corollary 2.2 Under hypotheses H0 and H2 in [20] the problem (1.1) possesses a unique solution (u,φ)∈W1,2p(Q)×W1,2p(Q).
Proof. Let w11=w21=w12=w22=w in the Theorem 2.1. Then (2.2) shows that the conclusion of the corollary is true.
3.
Approximating scheme
The aim of this section is to use the fractional steps method in order to approximate the solution of the system (1.1)–(1.3), whose uniqueness is guaranteed by Corollary 2.2. To do that, let us associate to the time-interval [0,T] the equidistant grid of length ε=TM, for any integer M≥1. Then, the following approximating scheme can be written in order to approximate the solution of the nonlinear boundary value problem (1.1)–(1.3):
where Qεi=[iε,(i+1)ε]×Ω, Σεi=[iε,(i+1)ε]×∂Ω, i=0,⋯,M−1, and z(t,φε−(iε)) is the solution of the Cauchy problem
computed at s=ε, for i=0,⋯,M−1. Here φε+(iε)=limt↓iεφε(t) and φε−(iε)=limt↑iεφε(t).
For later use, we set: W=L2(0,T;H1(Ω))∩W1,2([0,T];(H1(Ω))′).
Definition 3.1. By weak solution to the problem (1.1)–(1.2) we mean a pair of functions (u,φ)∈W×W which satisfy (1.1)–(1.2) in the following sense
for all (ψ,ζ)∈L2(0,T;H1(Ω))×L2(0,T;H1(Ω)), together with the initial conditions (1.3). In (3.4) and (3.5) we have denoted by the symbol ∫Q the duality between L2(0,T;H1(Ω)) and L2(0,T;(H1(Ω))′).
The main result of this section is the following
Theorem 3.2. Assume that u0,φ0∈W2−2pp(Ω) with k∂∂νu0+hu0=w1(0,x) and ξ∂∂νφ0=w2(0,x). Let (uε,φε) be the solution of the approximating scheme (3.1)–(3.3). Then, for ε→0, we have
for any t∈[0,T], where u∗,φ∗∈W1,2([0,T];L2(Ω))∩L(0,T;H2(Ω)) is the weak solution to the problem (1.1)–(1.3).
Proof.(see [2]) The proof is based on compactness methods. As a matter of fact it turns out from Theorem 3.2 that if u0,φ0∈L2(Ω), then the weak solution (u∗(t),φ∗(t)) of the system (1.1)–(1.3) is a strong solution, i.e., it is absolutely continuous in t on [0,T] and satisfies a.e. the system (1.1)–(1.3). So Theorem 3.2 can be also viewed as a constructive way to prove the existence in (1.1)–(1.3).
The result in Theorem 3.2 remains true by replacing the boundary condition (1.2) with k∂∂νu+hu=w(t)g(x) and ξ∂∂νφ=0 (see [6,7,10,11,12,13,14,15,16,17,18,19]).
The Cauchy problem (3.3) has the solution
and then the general algorithm to compute the approximate solution by means of fractional steps method consist in the following sequence (i denotes the time level)
Begin algfrac
i:=0 →uε,0=u0, φε,0=φ0 from the initial conditions (1.3);
For i:=0 to M−1 do
Compute z(ε,φε−(iε,x)) from (3.7);
φε+:=z(ε,φε−(iε,x));
Compute φε,i+1,uε,i+1 solving the linear system (3.1)-(3.2);
End−for;
End.
A comparison between the fractional steps method and the standard iterative Newton method can be found in Moroşanu [16].
4.
Numerical model. The 2D case
The finite element method (fem in short) is a general method for approximating the solution of boundary value problems for partial differential equations. This method derives from the Ritz (or Gelerkin) method (see Axelson & Barker [1]), characteristic for the finite element method being the chose of the finite dimensional space, namely, the span of a set of finite element basis functions.
The steps in solving a boundary value problem using fem are:
P0. (D) The direct formulation of the problem;
P1. (V) A variational (weak) formulation for problem (D);
P2. The construction of a finite element mesh (triangulation);
P3. The construction of the finite dimensional space of test
function (called finite element basis functions);
P4. (Vnn) A discrete analogous of (V);
P5. Assembly of the system of linear equations;
P6. Solve the system in P5.
The finite element method is used in the sequel in order to deduce the discrete state equations. A conceptual numerical algorithm of fractional step type is then formulated to approximate the weak solution corresponding to (3.1)–(3.2), that is:
together with the initial conditions
By (⋅,⋅) we have denoted the scalar product in L2(Ω).
Let ε=T/M be the time step size. We assume that Ω⊂R2 is a polygonal domain. Let Tr be the triangulation (mesh) over Ω and ˉΩ=∪K∈TrK, and let Nj=(xk,yl),j=¯1,nn, be the nodes associated to Tr. Denoting by Vnn the corresponding finite element space to Tr, then the basic functions {bj}nnj=1 of Vnn are defined by
and so
For i=¯1,M, we denote by ui and φi the Vnn interpolant of uε and φε, respectively. Then ui,φi∈Vnn and
where uil=uε(ti,Nl), φil=φε(ti,Nl), i=¯1,M, l=¯1,nn are the unknowns to be computed.
Using in addition an implicit (backward) finite difference scheme in time, we introduce now the discrete equations corresponding to (4.1)–(4.2) as follows (see [7,12,13,14,15,16]) for more explanations)
where uil and φil, l=¯1,nn, are the vectors of unknowns for time level i.
From the initial conditions (1.3) we have
and then from (4.6) we get (see (4.3)–(4.4))
The numerical algorithm to compute the approximate solution by fractional steps method can be obtained from the following sequence (again, i denotes the time level)
Begin algfrac_fem
i:=0 → Compute u0l,φ0l, l=¯1,nn from (4.7);
Choose wi,l1=w1(ti,Nl), wi,l2=w2(ti,Nl), Nl∈∂Ω, i=¯0,M−1,l=¯1,nn;
For i:=1 to M do
Compute zl=z(⋅,Nl), l=¯1,nn from (3.7);
φi−1:=zl, l=¯1,nn;
Compute uil, φil, l=¯1,nn, solving the linear system (4.5);
End−for;
End.
The convergence result established by Theorem 2.1 guaranty that the approximate solution computed by the conceptual algorithm algfrac_fem is in fact the approximate solution of the nonlinear parabolic system (1.1)–(1.3).
5.
Industrial implementation
The aim of this section is to present an industrial implementation of conceptual algorithm algfrac_fem established in the preview section (in fact an implementation of the numerical model stated by the linear system (4.5) (see P5)).
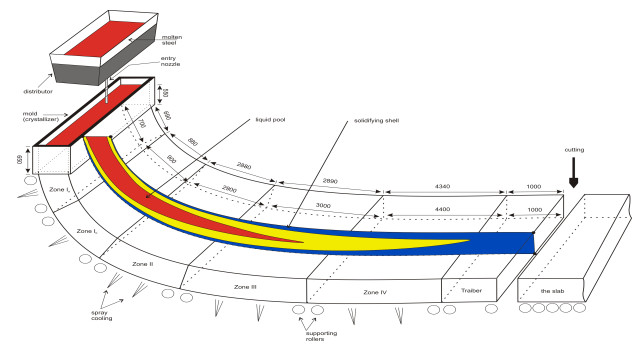
From the thermo-kinetics point of view, the solidification and cooling, as well as the simultaneous heating in a continuous casting process of steel, represents a very complex problem of non-stationary heat and mass transfer (see [25]). To solve at present such a problem it is impossible without numerical models of the temperature field and computer technology. In the sequel we will present in short a continuous casting machine, including the key phenomena of interest and a new numerical model that we have used in the settlement of the problem mentioned above.
The continuous casting process in the metallurgy. In a modern steel casting machine (its essential features are illustrated in Figure 2), the molten metal is tapped from a ladle into a copper mold (crystallizer). Here, the water-cooled walls of the mold (the primary cooling zone) extract heat what leads to solidify a shell that contains the liquid pool. Below the mold (the secondary cooling zone), the product is supported by rollers and is cooled down by water sprays that extract heat from the surface, and, eventually, the core becomes fully solid when the metallurgical length increase at 12÷13m. After the end of secondary cooling zone the product is cooled only by radiation (traiber). Finally, the continuous-casting product must be cut into the optimum lengths (cutting) to achive a maximum yield of metal.
The application of the numerical model (4.5) to the continuous casting process, requires experimental research and measurements of operational parameters at MTC2 from Mittal Steel S.A. Galaţi, as well as laboratory research. So, the most important input data in order to do this are (in round bracket we have written the value used by our Matlab program to do the numerical simulations):
● the casting speed (V=12.5 mm/s);
● physical parameters:
∘ the density (ρ=7850 kg/m3),
∘ the latent heat (ℓ=65.28kcal/kg),
∘ the relaxation time (α=1.0e+2),
∘ the length of separating zone (ξ=.5),
∘ the coefficients of heat transfer (h=32.012),
∘ T=44s;
● the boundary conditions: (w1(ti,Nl), Nl∈∂Ω, i=¯0,M−1,l=¯1,nn, in the primary cooling zone (see Figure 4)), (w1(ti,Nl), Nl∈∂Ω, i=¯0,M−1,l=¯1,nn, in the secondary cooling zone (see Figure 8)) and w2(ti,Nl)=0, Nl∈∂Ω, i=¯0,M−1,l=¯1,nn;
● dimensions of cristallizer (650 x 1900 x 220), in mm;
● the casting temperature (u0=15300C);
● the termal conductivity k(u):
k(u) = [20 100 200 300 400 500 600 700 800 850 900 1000 1100 1200 1600;
1.43e-5 1.42e-5 1.42e-5 1.42e-5 1.42e-5 9.5e-6 9.5e-6 9.5e-6 8.3e-6...
8.3e-6 8.3e-6 7.8e-6 7.8e-6 7.4e-6 7.4e-6].
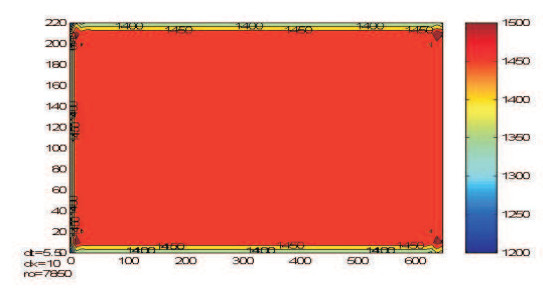
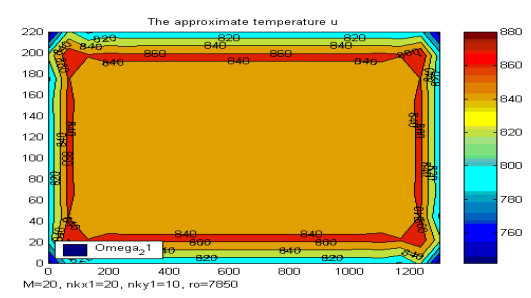
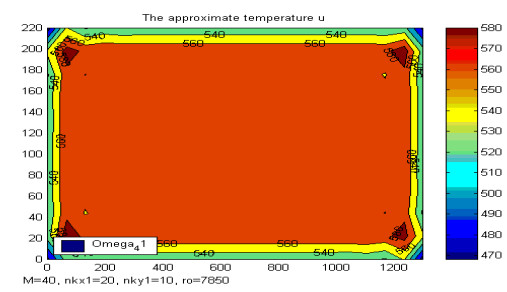
Numerical experiments. In Figure 3 it can be seen the number of nodes associated to the mesh Tr in the x1 and x2 – axis directions of one half of a rectangular profile. Considering the symmetrical heat removal from the continuous casting (CC) according to the vertical symmetry axis of the rectangular profile, only a half of the cross-section is used in the computation program.
The numerical model (4.5) uses the temperatures w(t,x,y),t∈[0,T], (x,y)∈∂Ω measured by the thermocouples; the values are illustrated in the Figure 4.
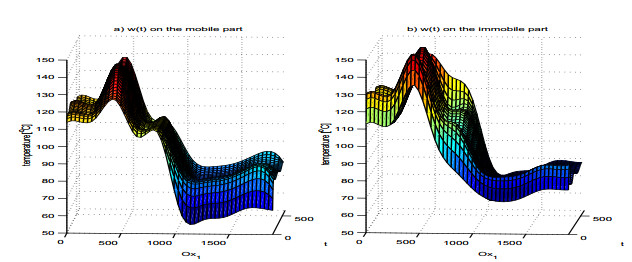
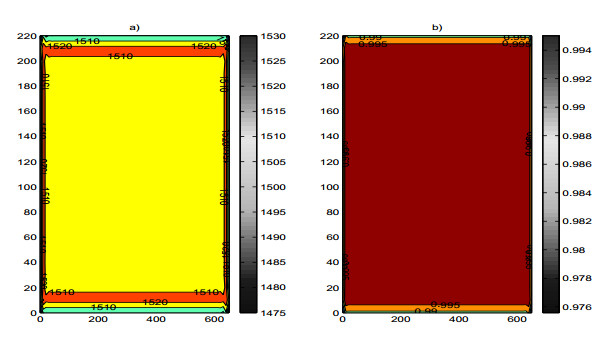
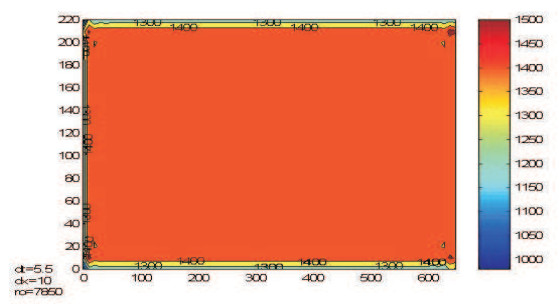
Figures 5–7 represents the approximate solution ui, φi (see (4.3), (4.4)), corresponding to different moments of time (i=1, i=5 and i=M).
A close examination of the Figures 5–7 tell us the dimension of the solid and liquid zone resulting by runing the Matlab computation program developed on the basis of the conceptual algorithm algfrac_fem.
Moreover (see [17]), the shape of the graphs shows the stability and accuracy of the numerical results obtained by implementing the fractional steps method.
The most interesting aspect that we can observe analysing the Figures 6–7 are the supercooling and superheating phenomenon.
6.
Conclusions
● The solidification model that we have considered in this work consist in a nonlinear system of two parabolic differential equations [4]. This new mathematical description of the real phenomenon reflects more accurately the physical aspects, like: superheating, supercooling (see Figures 7 and 11, for example), the effects of surface tension, separating zone of solid and liquid states, etc.
● From numerical point of view, the main difficulty in treating the phase field transition system (1.1) is due to the presence of the nonlinear equation corresponding to phase function φ. Thus it is intensely motivated the work in finding more efficient algorithms in order to compute numerically the solution of such system. A scheme of fractional steps type is considered in this sense. This numerical method avoids the iterative process required by the classical methods (e.g., Newton's type approaches) in passing from a time level to another. Numerical tests show that the fractional steps method is faster (CPU-time spent is very small) and the stability and accuracy are higher (see [16,17]) than the Newton's methods.
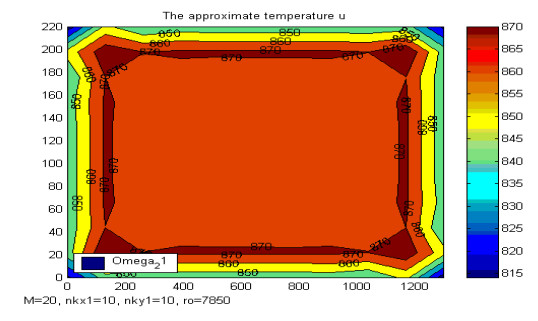
● The distribution of the temperature and the thickness of the solidifying shell, calculated with the numerical model (4.5) obtained following this technique, show that it really is (see Figures 5–7). New fundamental material properties can also be extracted by analysing the implementation of the numerical model 4.5 (see Figure 7).
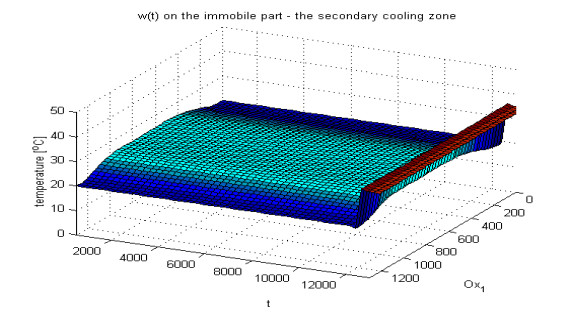
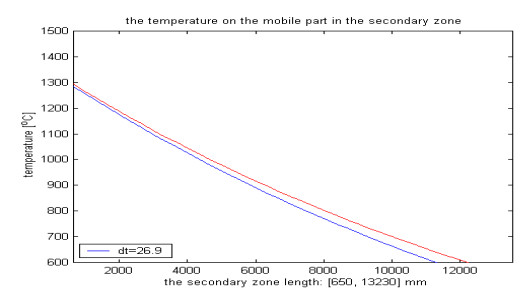
This model is able to simulate the temperature field of a CCM (Continuous Casting Machine) as a whole or any of its parts. In addition, the program elaborated may be used for different slab profiles. The industrial implementation of the numerical model enable us the analysis of the temperature field of the slab when it passes through primary, secondary and traiber zone. The Figures 9–11 display the calculated isotherms in the secondary cooling zone, while the Figure 12 display the temperature curves on the mobile part, corresponding to the final time level tM.
● In order to refer the continuous casting process, the following boundary conditions was considered: ∂∂νu+hu=w1(t,x,y), where h is the heat transfer coefficient and the given function w1(t,x,y) represents the temperature of the surrounding at t∈[0,T] and (x,y)∈∂Ω, Ω⊂R2.
Generally, the numerical method considered here can be used to approximate the solution of a nonlinear parabolic equation (system) containing a general nonlinear part.
● The numerical solution of the phase field transition system of solidification, approximated by this numerical scheme, can be considered as an admissible one for the corresponding boundary optimal control problem (see [16]), formulated in order to study the optimization of the continuous casting process. The numerical results presented in Figures 9-11 illustrate the accuracy of the numerical model (the influence of the density of the net: M = 20, nkx1 = 10, nky1 = 10; M = 20, nkx1 = 20, nky1 = 10; M = 40, nkx1 = 20, nky1 = 10). So, it is strongly motivated to investigate in further the numerical stability of this new numerical model taking into account all parameters (steel casting parameters, physical parameters, net parameters, etc.)
A detailed discussions on the errors produced by the fractional steps method, illustrate the influence of time and space parameters as well as of all physical parameters (see [17]).
Conflict of interest
The author declares that there is no conflicts of interest in this paper.









 DownLoad:
DownLoad: