1. Introduction
Load monitoring techniques determine the turned on appliances and their individual energy consumption within a given period of time [1]. They play a critical role in a variety of smart grid applications in the both customer and supplier sides. Load monitoring allows to customers and utilities to determine the appliances that consume more energy, the appliances that are the faulty and time to retrofit old appliances; to forecast demand more accurately; to control the supply and demand side power; to perform smart billing; and for intelligent appliance monitoring and controlling [1,2,3].
Load monitoring can be performed both intrusively as well as non-intrusively. Non-Intrusive Load Monitoring (NILM) attempts to identify the turned-on appliances from the power supply entry point without attaching any sensors to each individual appliance. The necessity for effective and efficient NILM methods for residential appliance identification has recently escalated due to its application potential for smart grids [4,5].
Numerous NILM techniques such as: steady state based analysis [1,5], transient state based analysis [6,7], current harmonics based analysis [8] and voltage-current (V-I) trajectory based analysis [9] have been proposed in the literature. Steady state based NILM methods cannot accurately identify non resistive appliances [10]. Moreover, NILM methods on transient state based analysis, current harmonics based analysis and V-I trajectory based analysis require very high sampling rates to capture the unique features from the measurement signals [11]. Further, some of the above mentioned NILM methods [1,5,6,7,9] require more than one electrical measurement (such as voltage, current, active power, etc.). Therefore, such NILM methods demand a large communication bandwidth and high processing power [12]. Further, such methods need multi functional smart meters that are also costly.
Recent work reported in [5,10,13] on NILM methods are based on very few smart meter measurement parameters with a low sampling rate. They focus on constructing signatures of residential appliances based solely on time domain information. The work proposed in [5], uses the steady state time domain signals of active and reactive power to detect events using an edge detection algorithm. Therefore, when multiple appliances with similar events are connected, this technique is prone to provide erroneous results. Moreover, time domain active and reactive power profiles are used in [10]. The fast switching events in active power signal are recorded as ‘triangle’ signal parts and steady events are recorded as ‘rectangle’ signal parts. Matching such shapes is a tedious and error prone process and such shape based features can easily be distorted when aggregating. Further, the conversion of signals to events such as rectangles and triangles may cause loss of significant signature information. In [13] a state of the art Hidden Markov Model (HMM) is used for disaggregation of turned on appliances based on low sampled active power measurements. Although this is an unsupervised method that uses expert knowledge to set initial models for states of known appliances, the models’ reliable operation depends on correctly setting the priori-values for each state of each appliance and using a training set where appliance operation does not overlap. None of these papers take into account the small signal level fluctuations of the time domain signal, which may contain significant and unique spectral information. However, so far, there are no widely available efficient solutions for NILM, with high accuracy, at low sampling rates [14].
Recently, the authors of this paper proposed a NILM method relying only on active power signals which could perform satisfactorily with very low sampling rates, i.e. 1 Hz, without suffering any essential information loss [15]. Here, a Karhunen Loéve (KL) expansion based subspace separation method was used for the extraction of uncorrelated spectral information and to construct appliance signatures. It was shown that the KL expansion based method renders a more accurate signature for NILM compared to typical Fourier Series expansion based methods.
This paper presents a piece of work based on the NILM method proposed in [15]. However, the performance of the NILM method was enhanced to reduce the computational burden and improve the convergence speed of the identification process while improving the accuracy. Some of the novel methods suggested in this paper are: performing a clustering method to group similar time windows in individual and aggregated active power signals, simultaneously carrying out appliance identification and energy disaggregation, and integrating the appliance usage patterns as the priori probability with the proposed NILM approach.
2. Used residential appliance and measurement data set
Two publicly available data sets, tracebase [16] and the Reference Energy Disaggregation Data Set (REDD) [17], that contain data from real measurements were used for proposing and performance validation of the proposed NILM method.
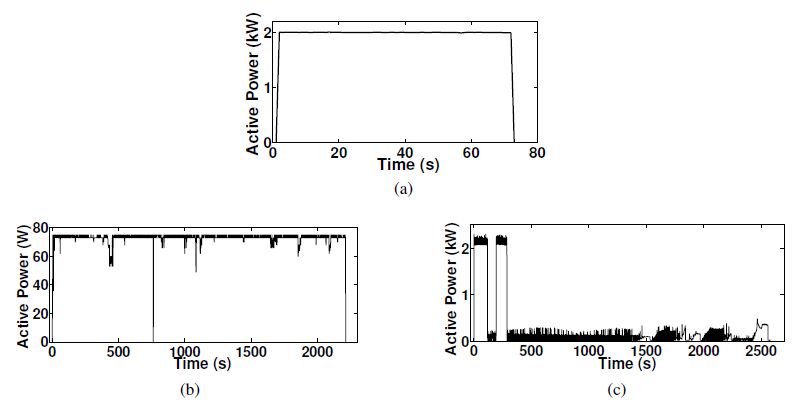
The tracebase repository is a continually growing collection of diurnal active power consumption traces at 1 Hz sampling rate collected from individual residential appliances in German households and office spaces. Out of 122 appliances in the data set, 20 appliances were selected for this research. Based on the operation styles of residential appliances, they are categorized as ‘single state’ (SS), ‘continuous varying’ (CV) and ‘multi state’ (MS) appliances [6]. Appliances selected from these categories are given in Table 1. The active power consumption of a water kettle (WK1), a LCD television (TV_LCD) and a washing machine (WM) from tracebase is presented in Figure 1(a),Figure 1(b) and Figure 1(c) respectively.
Table 1. Appliance categories and their selected appliances.
| Appliance Categories | Selected Appliances |
| SS | 60 W and 100 W lamps (LM1 and LM2), 1800 W and 2000 W water kettle (WK1 and WK2), microwave oven (MW), toaster (TT), iron (IR), video projector (VP) |
| CV | LCD television (TV_LCD), CRT television (TV_CRT), CRT monitor (M_CRT), TFT monitor (M_TFT), remote desktop (RD), personal computer desktop (PCD), cooking stove (CS) |
| MS | refrigerator (RF), washing machine (WM), dish washer (DW), laundry dryer (LD), washer dryer combo (WDC) |
REDD consists of whole-home and circuit/device specific electricity consumption for a number of US houses over several months. Whole-home active power consumption signal was down-sampled to a 3 s sampling interval to match the circuit/device specific active power consumption data which was sampled at 3 s intervals (i.e. 0.33 Hz). Active power measurements obtained from six US households were selected from the REDD database. Appliances used in these houses are listed in Table 2.
Table 2. Appliances used in selected six houses in REDD database.
| House Number | Appliances |
| House 1 | MW, RF, DW, WDC, CS, Water Kettle (WK), kitchen outlets (KO), lamp (LM) |
| House 2 | MW, RF, DW, WDC, CS, KO, LM, disposal (DI) |
| House 3 | MW, RF, DW, WDC, KO, LM, DI, furance (FU), smake alarms (SA), bathroom GIF(B GIF) |
| House 4 | DW, WDC, CS, KO, LM, SA, B GIF, air conditioning (AC) |
| House 5 | MW, RF, DW, WDC, KO, LM, DI, FU, WK, B GIF |
| House 6 | RF, DW, WDC, KO, LM, CS, WK, AC |
3. The overview of the proposed NILM method
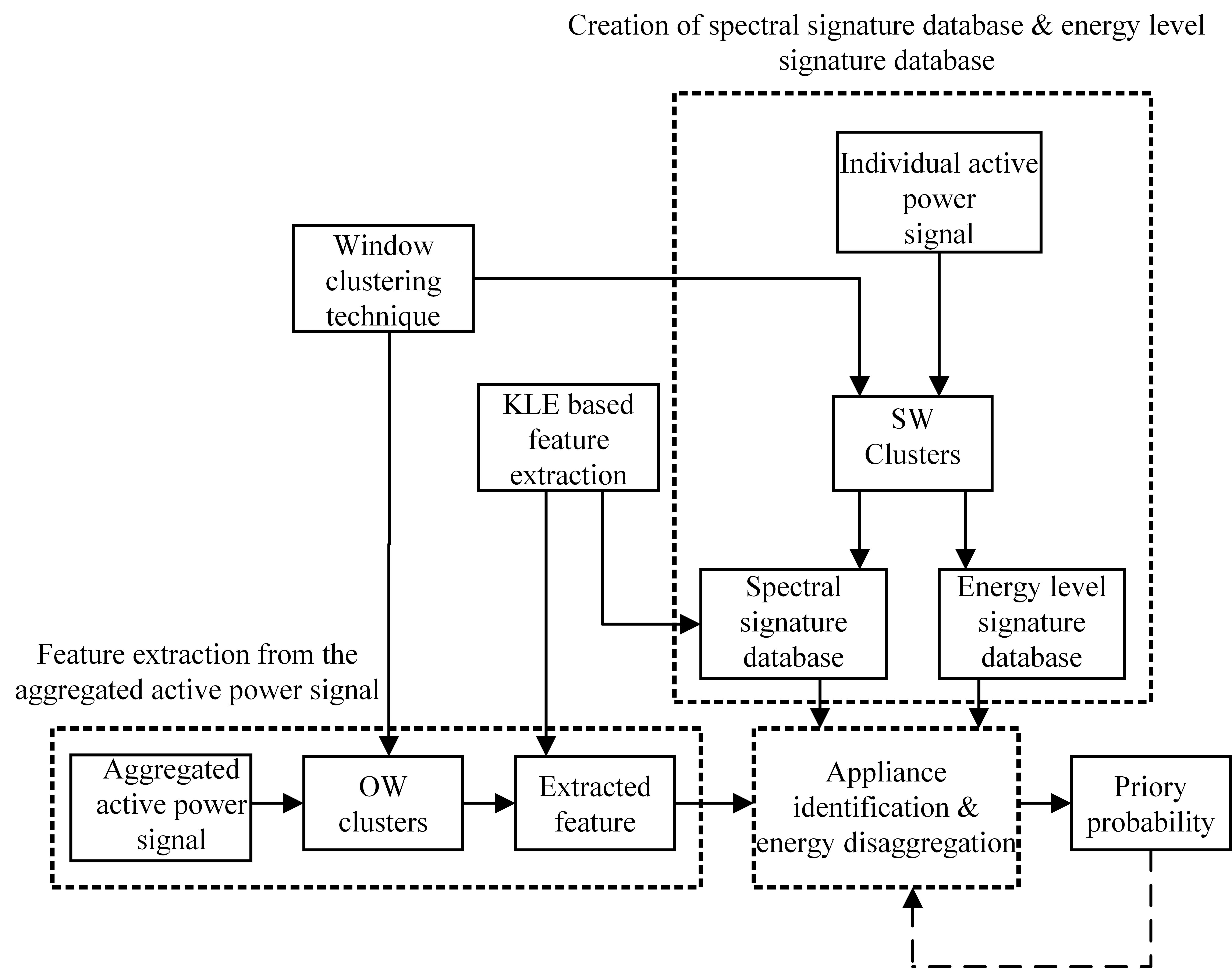
Block diagram for the proposed NILM method used in this paper is shown in Figure 2. The main steps in the proposed method are as follows:
· step 1: creation of the spectral signature database and energy level signature database.
· step 2: feature extraction from the aggregated active power signal.
· step 3: appliance identification and energy disaggregation.
A KLE based feature extraction method and a clustering technique were integrated with the first two steps. Learning of priori probabilities for appliance usage patterns and its utilization were integrated with step 3. Prior to discussing the main three steps involved in the proposed NILM method, the KLE based feature extraction and the clustering technique are presented.
3.1. The KLE based feature extraction method
3.1.1. Theoretical background
Let Ñ be the order of the auto-correlation matrix (ACM) used for subspace separation for a given N length (Ñ < N) signal X = [X(0) X(1) ...X(i)... X(N)]; where X(i) is the ith sample of the signal X. The ACM, ΦXX, of a signal X is denoted as,
|
@\Phi_{XX} = [RXX(0)⋯RXX(˜N−1)⋮⋱⋮RXX(˜N−1)⋯RXX(0)]
@
|
(1) |
Here,
RXX(
τ) (where 0 <
τ <
Ñ - 1)) is the auto-correlation function of the signal
X which is defined as,
|
@R_{XX}(\tau)= E[X(i)X(i+\tau)], @
|
(2) |
where E[:] denotes the statistical expectation operator and i and are positive integers indicating the time samples. Since, the size of ACM, Φ
XX, is
Ñ ×
Ñ, by applying the eigen decomposition to Φ
XX, an
Ñ number of mutually orthonormal (i.e. unit length and mutually uncorrelated) eigenvectors
q0,
q1 ...
qÑ-1 were determined. Then the KL transform
[18] was applied to signal
X as,
where @\tilde{x}@ is the KL transformed signal.
Since the matrix Q is unitary (i.e. QTQ = QQT = I, where I is the Ñ × Ñ identity matrix), the inverse KL transform can fully recover the original X signal. This process of reconstructing the original signal X was represented as an KL expansion (KLE) using,
|
@X=Q\tilde{x}=\sum_{i=0}^{\tilde{N}-1}q_{i}^{T}Xq_{i}.@
|
(4) |
According to (4), it is clear that signal
X can be decomposed or broken down into
Ñ mutually uncorrelated spectral components named as
x0,
x1, ...,
xÑ-1 (
xi =
qiT Xqi). These uncorrelated spectral components are called the subspace components of the signal X.
Moreover, considering (4), each qi can be realized as coefficients of a Finite Impulse Response (FIR) digital filter. Therefore, each xi corresponds to the output of the eigen filter (or digital filter) realized by the ith eigenvector qi. The frequency domain bandwidth of a subspace component can be obtained from the frequency response of the FIR filter given by the eigenvector associated with that subspace component. Moreover, according to (4) it can be clearly seen that, the KLE is another expansive method of representing a signal similar to the Fourier Series expansion (FSE). Further the KLE is a method of representing the signal in a more effective way to highlight its unique frequency domain characteristics which is useful in the NILM context than the FSE [15]. Therefore the same KLE method was used for the feature extraction of individual active power signal and aggregated active power signals.
3.1.2. Feature extraction of individual active power signals
Prior to the identification of residential appliances from the NILM method, an appliance signature should be constructed from the individual active power signals of all given residential appliances. The signature generated for each appliance should be unique and be able to characterize their individual behavior. Since the method presented here is based only on low frequency active power measurements, such unique signature information might not be apparent in time domain due to the low sampling rate. Hence, in the proposed NILM method, hidden features of the time domain active power signals were extracted by utilizing their uncorrelated spectral information.
As shown in Figure 1, it can be clearly seen that the active power signals of CV and MS appliances have little or/and large sudden power fluctuation in the time domain. Hence, the spectral information of these signals may vary with respect to time. Therefore, the active power signal was split into sliding windows of length N and uncorrelated spectral components of each such sliding window were extracted separately. The KLE in (4) was used to extract such uncorrelated spectral components which are referred to as subspace components (SCs) hereafter. The sliding was done with a sliding interval of one sample to capture the time varying nature of the signal as information to enrich the signature. If windowing is not performed, essential spectral information would be lost since only the average spectrum of the entire wave is taken. The sliding window used in this paper is referred to as a signature window (SW).
A very small length compared to the length of the active power signal was selected for length N of the SW in order to capture all non stationary variations of that signal. The length of some active power signals of the water kettle, microwave oven and lamps are limited to 60–80 s. Considering this fact, N or the SW length was selected as ten samples. Since Ñ < N, Ñ or the ACM order was selected as five samples. By selecting small SWs, stationarity is established within the SW. Hence, the SCs can be assumed to be stationary as well.
3.1.3. Feature extraction of aggregated active power signals
The smart meter measurement which comprises of an aggregated active power signal was partitioned into non overlapping windows of length N (ten samples). Such a window is referred to as an observation window (OW). Then for each OW, Ñ number of uncorrelated SCs were extracted using the KLE in (4).
3.2. The window clustering technique for the active power signals
The operation of an appliance within a SW or a OW may be repeated many times within an operation cycle of that appliance. Hence there are a number of similar SWs or OWs in a given active power signal. If there is a less complex clustering method to find the similar SW or OW groups, spectral features could be extracted only for a number of similar SW or OWgroups (one group contains similar windows) instead of extracting the features for all SWs or OWs. Furthermore, appliance identification and energy disaggregation cauld be performed only for similar OW groups instead of taking all OWs in a given aggregated signal. Hence clustering helps to reduce the data storage space and the number of mathematical calculations. Therefore, a window clustering algorithm with less computational complexity has been introduced in this paper.
The main challenge of the clustering component of this research is that the number of clusters are not known as a prior information. For such applications, the Mean-shift clustering algorithm [19] has been used in the field of computer vision and pattern recognition for various signal clustering applications. As presented in [20], the computational complexity of the mean-shift algorithm is @O(\bar{n}^{2}\bar{N})@; where @\bar{N}@ is the number of iterations while @\bar{n}@ is number of vectors or data points to be clustered. Further O(.) denotes the standard big O notation [20] for determining the computational complexity of algorithms. For large a number of data points, the computational complexity of the mean shift algorithm is very high. As there are a large number of data points in this window clustering application, the original mean-shift algorithm is too complex. Hence, the original mean shift algorithm was modified as discussed in Section 3.2.1 to suit this clustering application by reducing the computational complexity.
3.2.1. The modified mean-shift clustering algorithm
All windows were considered as a set of vectors in 10 dimensional euclidean vector space as the length of a vector was 10 samples. For simplicity in explanation, SWs are named as signature vectors (SVs) while OWs are named as observation vectors (OVs). Moreover, a given set of SVs of a appliance is called as a signature space of that appliance. Furthermore, a given set of OVs of a given aggregated power signal is called an observation space of that aggregated signal.
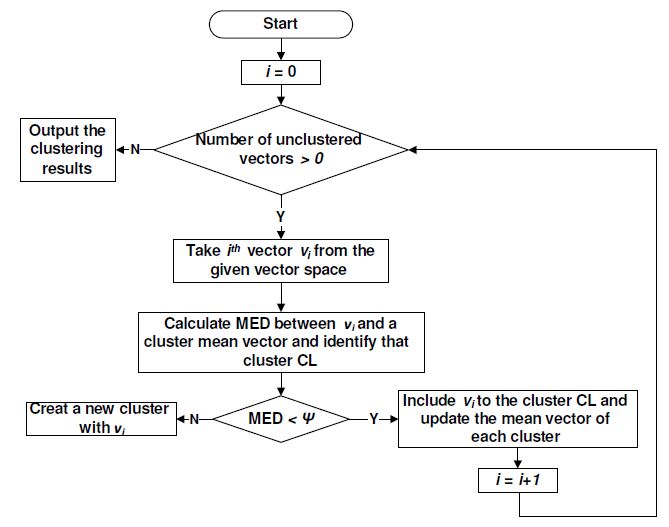
The window clustering procedure for a signature space or observation space is shown in Figure 3. As presented in the flow chart, the clustering algorithm is an iterative approach. In the ith iteration, vector vi from a given vector space is taken. Then, the euclidean distance between vi and cluster mean vectors for each of the clusters are calculated. The cluster with the Minimum Euclidean Distance (MED) is selected (this vector is denoted as CL) and the corresponding MED is stored. At the first iteration (i.e. i = 1), both the cluster mean vector and CL are equal to vi. Next, according to the maximum distance that can occurred between the cluster mean and the vectors in a cluster, which is denoted as ψ, and MED, it is decided whether vi belongs to a new cluster or else vi is included to CL. Finally, the mean vector of each cluster is updated. This process iterates until all vectors of the given vector space are clustered. The mean vector of the cluster j, i.e. MV j, is updated at each iteration as,
|
@MV_{j}=\frac{\sum_{k=1}^{w}v_{j}\_{k}}{w}, @
|
(5) |
where vj_k is the kth vector of cluster j and w represents the number of vectors of the cluster j after a given iteration.
The value of ψ was selected to become smaller than the minimum length of SV used in this paper. The minimum length of SV was nearly 224. Therefore, 0.5 was chosen as the value of ψ.
For the given kth vector, the computational complexity is calculated as follows:
· In the worst case, the number of Euclidean distance calculations from the given kth vector to all mean vectors is k - 1. Hence the complexity of this calculation is O(k - 1).
· The worst case computational complexity of calculating minimum value of n numbers is O(ˉn). Therefore, the complexity of calculating MED from the given kth vector to all mean vectors is O(k - 1)
· Total complexity for a given kth vector is O(k - 1) + O(k - 1) = O(2(k - 1))
The computational complexity for all @\bar{n}@ number of vectors is @O(2(\sum_{k=2}^{\bar{n}}(k-1)))=O(\bar{n}(\bar{n}-1))@. Therefore the complexity of the modified algorithm is less than @\frac{1}{\bar{N}}@ times compared to the complexity of the original algorithm.
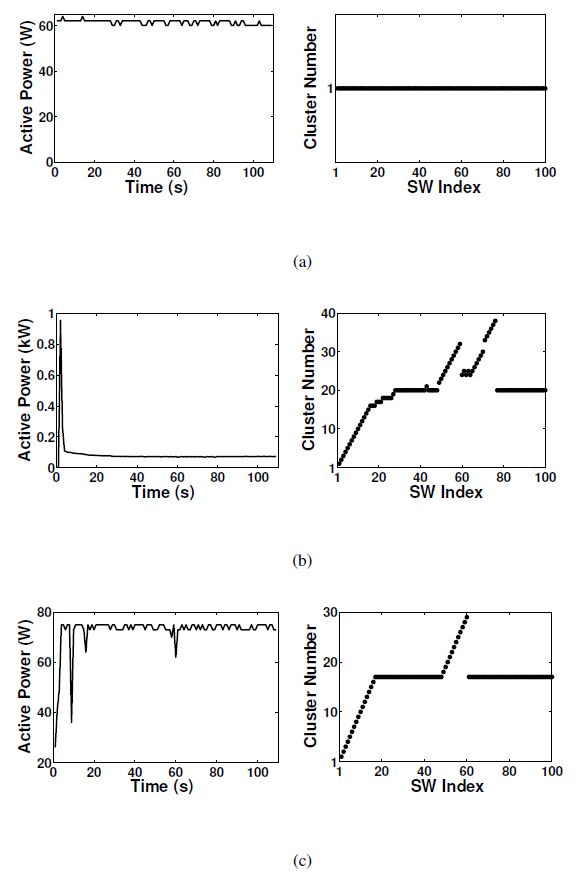
To demonstrate clustering in the signature space, the proposed clustering algorithm was applied to three individual active power signals. The first 100 SWs (signal length is 109 s) of one active power signal for LM1, RF and TV are shown in the left column of Figure 4(a),Figure 4(b) and Figure 4(c) respectively (here first SW is a active power signal from 0 s to 10 s, second SW is the active power signal from 1 s to 11 s etc.). The proposed clustering algorithm was applied to these three signals and the corresponding clustering results are shown in the right column of each figure. For an example, 1st to 17th SWs (17 SWs) of the given TV signal shown in Figure 4(c) were clustered into 17 clusters labelled as 1 to 17. Further, 50th to 60th SWs (11 SWs) were clustered into 11 clusters labelled as 19 to 29. Then, 18th to 49th SWs and 61st to 100th SWs (72 SWs) were clustered into one cluster labeled as 18.
A similar kind of clustering was applied to the observation space.
4. The main steps in the proposed NILM method
4.1. Creation of the spectral signature database and energy level signature database
Prior to the identification of residential appliances from the NILM method, two appliance signature databases that contain unique information of each individual appliance were constructed [15]. In order to obtain accurate NILM results, it is required to incorporate all possible active power fluctuations of each appliance that could occur in practice. Hence, several active power signals (referred to as traces [16] or realizations) of the same appliance were used to construct appliance signatures.
Before creating signatures of appliances, the simplified mean-shift algorithm discussed in section 3.2.1 was applied to all SWs of a given appliance in order to automatically group together similar SVs (i.e. SVs with their euclidean distance less than 2ψ) in signature space for a given appliance.
4.1.1. Spectral signature database
After clustering, the mean vector of a SW cluster (i.e. the number of similar windows that were compressed into one cluster) was used for extracting uncorrelated spectral information of active power signals of a given appliance. Therefore, the KLE given in (4) was used to extract uncorrelated spectral components, i.e. SCs, of each mean vector of SW clusters.
The spectral bandwidth of each SCs is very small compared to its maximum possible frequency (i.e. 0.5 Hz or 0.167 Hz). Therefore, it is reasonable to assume that each SC has an approximately sinusoidal shape in which the center frequency is referred to as the frequency of SC. Therefore, the average absolute amplitude and the phase angle of a SC for the mean vector of a given SW cluster were determined and this SC was transformed to the rectangular form in the complex domain (i.e. Re + jIm; Re = Am cos θ and Im = Am sin θ, where Am and θ are the average absolute amplitude and the phase angle of the SC).
The KLE breaks down the mean vector of a given SW cluster into five uncorrelated SCs. Then, each of the SCs of the mean vector of a given SW clusters were transformed to the complex domain. This implies that the mean vector of a given SW cluster is decorrelated and placed in a five dimensional complex value feature space where each SC corresponds to an uncorrelated spectral location. This means ten uncorrelated feature dimensions could be utilized for classification.
For a given appliance, the KLE coefficient (i.e. Re + jIm) of a given SC was labelled as its frequency and the energy level of corresponding mean vector of SW cluster of that SC. Energy consumption of a given SW cluster was calculated through area integration as illustrated in [6]. Then, the KLE coefficients with these labels of each SW cluster and the number of SWs in each cluster for all selected realizations of a given appliance was determined and stored in a database. This database is referred to as the spectral signature database.
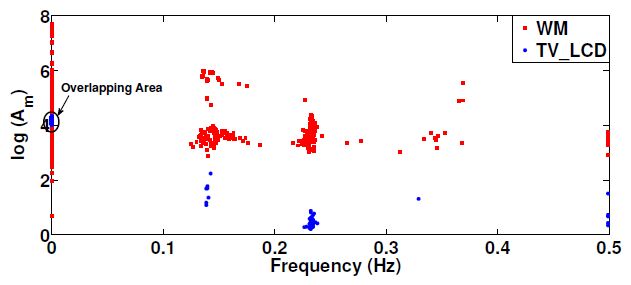
A scattergram of the log(Am) with its frequency for all SCs of all SWs for ten realizations of WM and TV LCD selected from tracebase is presented in Figure 5.
The number of SWs/clusters and the number of data points to be stored with and without clustering for TV_LCD and RF in the active power signature database is shown in Table 3. It can be clearly seen from Table 3 that the SW clustering approach helps to reduce the number of mathematical calculations and storage space in the spectral signature database by a significant amount.
Table 3. Performance improvement and comparison achieved through SW clustering.
| Without Clustering | With Clustering |
| TV LCD: | |
| Number of SWs | 7639 | 103 |
| Number of data points to be stored | 7639 × 5 × 3 = 114585 | 103 × 5 × 3 + 103 = 1648 |
| RF: | |
| Number of SWs | 170151 | 387 |
| Number of data points to be stored | 170151 × 5 × 3 = 2552265 | 387 × 5 × 3 + 387 = 6192 |
4.1.2. Energy level signature database
Distinct energy levels out of mean vectors of all SW clusters and the number of SWs in such an energy level for each appliance was calculated and stored in a database. This is referred to as the energy level signature database. Calculated energy levels for selected appliances in tracebase database are presented in Table 4.
Table 4. Calculated energy levels for selected appliances in tracebase database.
| Appliance | Energy Level (kJ) |
| LM1 | 0.6 |
| LM2 | 1 |
| WK1 | 20 |
| WK2 | 22 |
| TT | 7 |
| IR | 15 |
| VP | 2.3 |
| MW | 14.5 |
| TV_LCD | 0.6, 0.7 |
| TV_CRT | 1.1, 1.3 |
| M_CRT | 1, 1.2 |
| M_TFT | 0.45 |
| RD | 1.5 |
| PCD | 0.95 |
| CS | 9 |
| RF | 0.75, 1, 5 |
| WM | 1.1, 1.7, 2, 2.4, 20, 23 |
| DW | 1, 27 |
| LD | 2.2, 2.5, 3.1, 3.9, 28.5, 30, 35 |
| WDC | 1, 1.3, 1.8, 2.9, 4.5, 20 |
4.2. Feature extraction from aggregated active power signals
The simplified mean-shift algorithm was used to automatically cluster similar OVs (i.e. OVs of their euclidean distance less than 2ψ) in a observation space of a given aggregated active power signal.
Therefore, Ñ number of uncorrelated SCs for mean vectors of OW clusters were extracted using the KLE given in (4). Then the proposed matching algorithm was applied to the mean vector of each cluster. The identified turned-on appliance combination for the mean vector of a given cluster was considered as the identified appliance combination of each OW in that cluster.
SCs of the mean vector of a given OW cluster was sorted in dominant order (i.e. descending order of their absolute amplitude). It should be noted that the most dominant (i.e. the 1st dominant) SC of any OW or SW is the zero frequency.
4.3. Appliances identification and energy disaggregation
If nt appliances are turned-on at time t, the total active power drawn, P(t), is given by,
|
@P(t)=\sum_{k=1}^{n_{t}}p_{k}(t), @
|
(6) |
where pk(t) represents the active power consumption of the kth turned-on appliance at time t. The aggregated active power signal measured from main power supply at a given time is a linear addition of active power signals of the turned-on appliances at the same time. Hence two relationships were obtained as follows:
· Summation of one of the energy level combinations (obtained from the energy level signature database) of the turned on appliance combination in a given OW should be equal to the energy in that OW.
· A SC with frequency f in a given OWextracted from the aggregated active power signal can only be generated from a linear addition of the individual SCs with the same frequency f in SWs of power signals out of the turned-on appliances in that OW.
These relationships are given in (7) and (8) respectively as follows:
|
@e_{ow} = \sum_{k=1}^{n}e_{a_{k\_j}}, @
|
(7) |
| Algorithm 1 Main Work Flow of the Proposed Matching Algorithm for Turned on Appliances Identification and Energy Disaggrgation |
| 1: | Set i = 1 |
| 2: | Set execution = 1 |
| 3: | Take 1st dominant SC; |
| 4: | Apply the PES and obtain S 0; |
| 5: | while execution do |
| 6: | Apply the FES to S 0 or S 2 and obtain S 1; |
| 7: | Apply the SES to S 1 and obtain S 2; |
| 8: | Apply the MAP criteria to S 2; |
| 9: | if γ1 > 99% or i == 5 then |
| 10: | Output the NILM results; |
| 11: | Set execution = 0; |
| 12: | else |
| 13: | i = i + 1 |
| 14: | Take ith dominant SC; |
| 15: | end if |
| 16: | end while |
|
@Re_{f_{i}}+jIm_{f_{i}}=\sum_{k=1}^{n}(Re_{f_{i}}\_{e_{a_{k\_j}}}+jIm_{f_{i}}\_{e_{a_{k\_j}}}), @
|
(8) |
where the quantity eak_j denotes the jth energy level of the appliance ak. Moreover, Refi + jImfi denotes the rectangular form of the ith dominant SC of a given OW and fi is its frequency. The quantity Refi_eak_j + jImfi_eak_j represents the individual SC of frequency fi for the jth energy level of the appliance ak of the turned-on appliance combination in the OW; n is the number of appliances which are turned-on in the given OW.
The fundamental logic behind the appliance identification and energy level disaggrgation is the relationship described in (7) and (8). Further, (8) is valid for all Ñ number of SCs in a given OW. This SC matching is valid as these SCs formed by breaking down the active power signal using the KLE are uncorrelated. Hence, the matching of each SC of a given OW with the linear addition of individual appliance SCs obtained from the spectral signature database enables the identification of actual turned-on appliances and their energy level in that OW.
Algorithm 1 presents the main work flow of the matching process for turned on appliance identification and their energy disaggregation. The algorithm was applied for each OW separately in order to identify the turned-on appliance combination within each OW and to disaggregate their energy contribution. As shown in Algorithm 1, the proposed matching algorithm is an iterative approach whose maximum iteration number equals the number of SCs of a given OW, i.e. five. For any given OW, the ith dominant SC was taken for calculations for the ith iteration of the algorithm.
The matching algorithm consists of four main steps. Namely, the pre elimination step (PES), the first elimination step (FES), the second elimination step (SES) and the Maximum a Posteriori (MAP) estimation.
4.3.1. Pre Elimination Step (PES)
Prior to entering the iterative loop, an elimination was conducted in three stages based on energy levels of individual appliances to reduce the number of possible appliance combinations and energy level combinations. These three stages are as follows:
| Algorithm 2 Main Work Flow of the Energy Level Matching |
| 1: | Set Y = 0, X = Ea1 |
| 2: | for k = 1, ..., n - 1 do |
| 3: | for j = 1, ..., Nak+1 do |
| 4: | X = X(f ind(X < eow)) |
| 5: | Y = [Y X + Eak+1 (j)] |
| 6: | Update energy level of individual appliance for each energy level in Y |
| 7: | end for |
| 8: | X = Y, Y = 0 |
| 9: | end for |
| 10: | Take energy level of all n individual appliance at the index of f ind(X == eow) |
1. First the energy consumed within the given OW (denoted as eow) was determined through area integration illustrated in [6]. Then the operating energy levels of each possible appliance combination were obtained from the energy level signature database. If the eow of the given OW is less than the minimum energy level of a given appliance, clearly that appliance cannot be in the appliance combination for that OW. This is because if that appliance is turned-on, it will alone generate a larger energy than the energy of the given OW, i.e. eow and hence, violates (6). Such appliances were eliminated at the first stage of the PES.
2. If a combination remaining in the reduced set of possible appliance combinations obtained after stage 1 violates the same condition mentioned above (now applied for combinations, instead of single appliances, as in stage 1), it was eliminated in stage 2. This is the second stage of the PES. The rule associated with the stage 2 is given by,
|
@e_{ow} \geq \sum_{k=1}^{n}\min(e_{a_{k}}), @
|
(9) |
where
n is the number of appliances in a combination and
eak denotes the energy levels of appliance
ak.
3. The main work flow of the stage 3 is presented in Algorithm 2. Initially, all possible energy level combinations of a given possible appliance combination were computed and any energy level combination that does not match the energy consumption of the active power signal at the selected OW was removed. Further, for a given appliance combination if all energy level combinations do not match the energy consumption of the selected OW, that combination was eliminated. For example, lets assume RF+TV_LCD was a possible appliance combination obtained at PES. According to the energy level signature database, RF has er f1, er f2 and er f3 energy levels and TV_LCD has etv1 and etv2 energy levels. Algorithm 2 removes any energy level combination that does not satisfy er fi + etv j = eow; where i = 1, 2, 3 and j = 1, 2. Further if all energy level combination satisfy er fi + etv j ≠ eow; where i = 1, 2, 3 and j = 1, 2, RF+TV_LCD appliance combination is eliminated.
In Algorithm 2, term n denotes the number of turned on appliances for the given OW, term Nak denotes the number of SW energy levels of appliance ak, and term Eak contains all operating energy levels of appliance ak.
4.3.2. First Elimination Step (FES)
While inside the iterative loop, this is the first stage of reducing the number of possible appliance combinations and their energy level combinations in a given OW. This exploits the triangular law for complex numbers to eliminate combinations. At the first iteration, the FES was carried out for the reduced set of possible combinations obtained from the PES ( denoted as set S 0). At any other iterations, the FES was applied to the reduced set of possible combinations obtained from the SES (denoted as set S 2). The underlying logic is that for a given SC of frequency fi (i.e. ith iteration) of a given OW, if the addition of maximum power contribution of the same frequency fi (i.e. ith iteration) for a given energy level combination of each appliance in a given appliance combination, is less than the power at that SC of a given OW(denoted as U), that energy level combination was eliminated from consideration. This condition can be summarized as,
|
@U~\geq~\sum_{k=1}^{n}\max(V_{k})\:, @
|
(10) |
where @V_{k}~=~\sqrt{((Re_{f_{i}}\_{e_{a_{k\_j}}}^{2}+Im_{f_{i}}\_{e_{a_{k\_j}}}^{2}))}@ and @U~=~\sqrt{(Re_{f_{i}}^{2}+Im_{f_{i}}^{2})}@.
4.3.3. Second Elimination Step (SES)
While inside the iterative loop, this is the second stage of reducing number of possible appliance combinations and energy level combinations in a given OW. At each iteration, the SES was applied to the set of possible appliances and energy level combinations obtained from FES (denoted as the set S 1). A likelihood estimation was carried out to determine the likelihood value (denoted as LHV)of getting the real and imaginary value of the observed SC (i.e. @z_{f_{i}}=Re_{f_{i}}+jIm_{f_{i}}@ with frequency fi) from a given appliance combination cj and a given energy level combination lk. This LHV is referred to as @P(\frac{z_{f_{i}}}{c_{j}\cap l_{k}})@. As the first step of obtaining @P(\frac{z_{f_{i}}}{c_{j}\cap l_{k}})@, a joint likelihood function (JLF) which gives likelihood values of having @z_{f_{i}}@ SCs of frequency fi was generated for a given energy level of a individual appliance of the appliance combination cj. Then the LHV of @P(\frac{z_{f_{i}}}{c_{j}\cap l_{k}})@ was calculated using the 2-dimensional (2D) convolution operation of the JLF of individual appliances a1 with energy level e1 and a2 with energy level e2 of combination cj given by,
|
@P(\frac{z_{f_{i}}}{c_{j}\cap l_{k}})=\sum_{r_{1}=\min(Re_{f_{i}\_{a_{1}}})}^{\max(Re_{f_{i}\_a_{1}})}\sum_{r_{2}=\min(Im_{f_{i}\_a_{1}})}^{\max(Im_{f_{i}\_a_{1}})} P(\frac{r_{1}+jr_{2}}{a_{1}\cap e_{1}})P(\frac{(Re_{f_{i}}-r_{1})+j(Im_{f_{i}}-r_{2})}{a_{2}\cap e_{2}}), @
|
(11) |
where @P(\frac{r_{1}+jr_{2}}{a_{1}\cap e_{1}})@ is a JLF which gives likelihood values of having r1 + jr2 SCs of frequency fi at SWs corresponding to energy level e1 of appliance a1 out of each SCs of all SWs for appliance a1. For simplicity, (10) is presented only for n = 2 condition (n is number of appliance in combination cj). This 2D convolution operation was extended to determine the combinational JLF for combinations with more than two appliances in a recursive manner.
If the LHV of @P(\frac{z_{f_{i}}}{c_{j}\cap l_{k}})@ was close to zero or below a certain threshold, such cj and lk combinations were eliminated.
4.3.4. MAP Estimation
At the ith iteration, there may be multiple appliance and energy level combinations that would produce first i dominant SCs of a given OW. We want to find the most likely appliance combination cj and its energy level combination lk for the given Zi (Zi represents first i dominant SCs of the given OW). By Bayes's rule we have,
|
@P(\frac{c_{j}\cap l_{k}}{Z_{i}})=\frac{P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(c_{j}\cap l_{k})}{P(Z_{i})}, @
|
(12) |
where @P(\frac{Z_{i}}{c_{j}\cap l_{k}})@ denotes the LHV of producing first
i dominant SCs of a given OW using SCs of an energy level combination lk of a given appliance combination
cj. Further, the term @P(\frac{c_{j}\cap l_{k}}{Z_{i}})@ represents the LHV of
cj and its
lk as being the turned-on appliance combination and energy level combination of the given OW, when its first
i dominant SCs are considered. The LHV of appliance combination
cj and energy level combination
lk occurring in the given OW, is denoted by @P(c_{j}\cap l_{k})@. Since the occurring of
cj and
lk are independent,
|
@P(c_{j}\cap l_{k})=P(c_{j})P(l_{k}).@
|
(13) |
The LHV of appliance combination
cj occurring in the given OW (denoted by
P(
cj)) depends on the usage behavior pattern of the combination
cj with respect to time of a day. In this section, such usage behavior patterns were not taken into account and assumed that the LHV of all
P(
cj) were equally likely. Moreover, the LHV of occurring energy level combination
lk of appliance combination
cj (denoted as
P(
lk)) was calculated based on information in energy level signature database. Since
P(
Zi) is common to all combinations and all
P(
cj) are equally likely, they do not make any difference to the rank when ordering ‘likely combinations’ in terms of likelihood. Hence, the LHV of @P(\frac{c_{j}\cap l_{k}}{Z_{i}})@ is linearly proportional to the LHV of @P(\frac{Z_{i}}{c_{j}\cap l_{k}})@. Since the LHV of producing any SC of the OW from SCs of SWs of a given energy level combination for a combination
cj are independent, we have,
|
@P(\frac{Z_{i}}{c_{j}\cap l_{k}}) = \prod_{m=1}^{i}P(\frac{z_{f_{m}}}{c_{j}\cap l_{k}}).@
|
(14) |
The LHV of @P(\frac{z_{f_{m}}}{c_{j}\cap l_{k}})@ was determined at the SES.
At iteration i, if the percentage LHV of the most likely appliance combination cj and energy level combination lk, which has the highest LHV out of the remaining combinations, was greater than a predefined threshold or confidence level, then the appliance combination cj and energy level combination lk was selected as the identified turned-on appliance combination and its operating energy levels. Once this condition was satisfied, the execution of the algorithm was terminated. The percentage LHV for most likely combination (denoted as γ1) at iteration i is given as,
|
@\gamma_{1}=\frac{\max(P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(l_{k}))}{\sum_{j=1}^{N_{c_{j}}}\sum_{k=1}^{N_{l_{c_{j}}}}P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(l_{k})}\times 100\%, @
|
(15) |
where Nc j is the number of appliance combinations and Nlc j is the number of energy level combinations in appliance combination cj of the set S 2 at iteration i. Similarly, γ2, γ3, ..., γl etc., are the percentages of the LHV for 2nd, 3rd, ..., lth most likely combination. According to (13), summation of the percentage LHVs of all l combinations equal to 100%.
If the termination condition was not satisfied by any appliance and energy level combination after all 5 iterations (i.e. i = 5), then the combination appliance combination cj and energy level combination lk with the maximum LHV (i.e. arg max(c j, lk) @P(\frac{Z_{5}}{c_{j}\cap l_{k}})@, was selected as the identified result.
Typically in statistics 95% or 99% confidence level is used [21]. Therefore, 99% confidence level was selected as the pre-defined threshold.
5. Case study
Three case studies were conducted to emphasize the robustness of the proposed NILM method. The case study 1 and 2 were conducted using tracebase real household data set while case study 3 was conducted using REDD real house hold data set.
5.1. Evaluation metric
Three evaluation metrics were used to evaluate the robustness of the proposed NILM method as follows:
5.1.1. F-measure
A metric called F-measure (Fm) [22] was used as an evaluation metric to identify any given turned on appliance combination. It is given by,
|
@F_{m}=\frac{2TP}{2TP+FN+FP}\times100\%.@
|
(16) |
where
TP,
FN and
FP, for each identified turned on appliance combination are defined as:
· If the appliance in a given OW is identified as cj, and cj was on, then the identification is true positive (TP).
· If the combination in a given OW is not identified as cj, and cj was on, then the identification is false negative (FN)
· If the combination in a given OW is identified as cj, and cj was off, then the identification is false positive (FP)
The metric Fm for any given appliance combination is denoted as CFm and average Fm over all appliance combinations in a given aggregated active power signal is denoted as AFm.
5.1.2. Total energy correctly assigned
To evaluate the performance of the energy disaggregation, we used the ”total energy correctly assigned (Acc)” metric described in [1,17]. Metric Acc is formally defined as follows [17]:
|
@A_{cc}=1-\frac{\sum_{t=1}^{T}{\sum_{i=1}^{n}{|\hat{y_{t}}^{(i)}-y_{t}^{i}|}}}{2\sum_{t=1}^{T}\bar{y_{t}}} \times 100\%, @
|
(17) |
where @\hat{y_{t}}^{(i)}@ denotes the estimated energy level of the proposed method for ith appliance at the tth OW while @y_{t}^{i}@ denotes the measured energy level for ith appliance at the tth OW in a given aggregated signal. Moreover, @\bar{y}=\sum_{i=1}^{n}{y_{t}^{i}}@.
The metric Acc for OWs of a given turned on appliance combination is denoted as CAcc and Acc for all OWs in a given aggregated active power signal is denoted as AAcc .
5.1.3. Average execution time
All algorithms in this paper were executed on a workstation with Intel(R) Core(TM) i5 processor and 8.00 GB RAM running at 2.53 GHz, with the Windows 7 Professional operating system. In order to demonstrate the execution time to identify turned on appliance combinations and estimate their individual energy consumption in OWs, the average execution time of a OW (denoted as AET) was used. The AET is given by,
|
@AET=\frac{T_{ET}}{N_{tow}}, @
|
(18) |
where TET denotes the total execution time of the algorithms to identify turned on appliance combinations and estimate their individual energy consumption for all OWs in a given aggregated active power signal.
5.2. Case study 1
In case study 1, in order to demonstrate the ability of the proposed NILM method to accurately identify turned-on appliance combinations and estimate their individual energy consumption when a large number of appliances are operating simultaneously, 20 appliances from the tracebase data set mentioned in Section II were assumed to be operating. For each appliance, 25 different traces that have different fluctuations and different power signatures were used. For example, 3 different such traces for TV_LCD and WM are shown in Figure 6(a) and Figure 6(b) respectively. Ten different traces from these 25 were used for training (i.e. to create active power signature database and energy level signature database) while the other 15 were used for testing and validation.
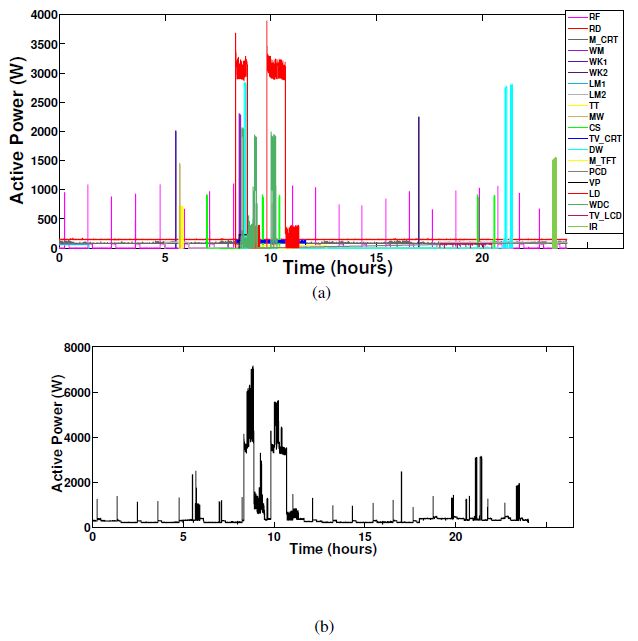
In order to generate turned on appliance combinations, 15 aggregated active power signals (referred to as test signals) were generated manually from all 20 appliances, for a period of over 24 hours. Each aggregated active power signal contained different active power signals of the 20 appliances. A typical test signal out of the 15 aggregated active power signals is presented in Figure 7. The active power consumption of individual appliances and the aggregated active power consumption are shown in Figure 7(a) and Figure 7(b) respectively. Further, Table 5 presents the appliance combinations which are turned on over more than 25 OWs in the signal in Figure 7(b) and the notations for these combinations (The notation will be used in the results and discussion section).
Table 5. Notations for Turned on Appliance Combinations in Aggregated Signal in Figure 7(b).
| Actual Turned on Appliances | Notation |
| RD+M_CRT | c1 |
| RD+M_CRT+TT | c2 |
| RD+M_CRT+LM1 | c3 |
| RD+M_CRT+LM2 | c4 |
| RD+M_CRT+LM1+RF | c5 |
| RD+M_CRT+LM2+WK1 | c6 |
| RD+M_CRT+LM2+MW | c7 |
| RD+M_CRT+LM2+TT | c8 |
| RD+M_CRT+LM2+DW | c9 |
| RD+M_CRT+RF+IR | c10 |
| RD+M_CRT+LM2+WK2 | c11 |
| RD+M_CRT+TV LCD+CS | c12 |
| RD+M_CRT+M_TFT+TV_LCD+LD | c13 |
| RD+M_CRT+M_TFT+TV_LCD+LD+PCD+RF | c14 |
| RD+M_CRT+M_TFT+TV_LCD+PCD+VP+LD+RF | c15 |
| RD+M_CRT+M_TFT+TV_LCD+LD+PCD+WM+VP | c16 |
| RD+M_CRT+M_TFT+TV_LCD+LD+PCD+WM+VP+RF+DW | c17 |
The algorithm 01 was applied to all the OWs of all 15 aggregated active power signals. Hence, the turned-on appliance combination for each OW and its energy level combination were identified.
5.2.1. Results and Discussion
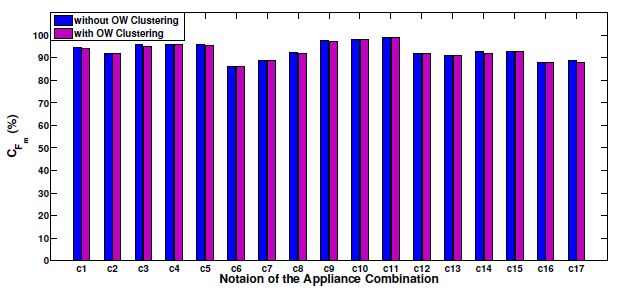
The appliance identification accuracy, i.e. CFm of the proposed method with and without the clustering technique for the appliance combinations in the aggregated power signal shown in Figure 7(b) is presented in Figure 8. According to Figure 8, they show approximately the same appliance identification accuracy with and without the clustering technique. Most of the appliance combinations in Figure 7(b) were identified with more than 90% accuracy.
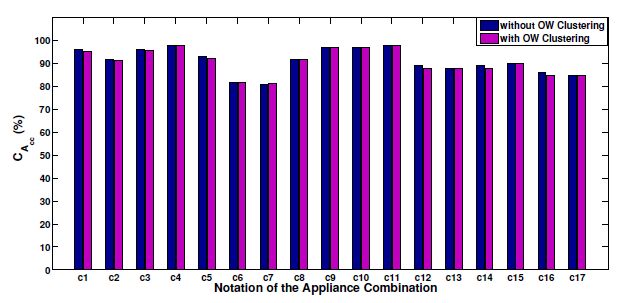
The energy disaggregation accuracy (with and without the clustering technique), i.e. CAcc for the appliance combinations in the aggregation signal in Figure 7(b) is presented in Figure 9. According to Figure 9, approximately the same energy disaggregation with and without the clustering technique can be seen.
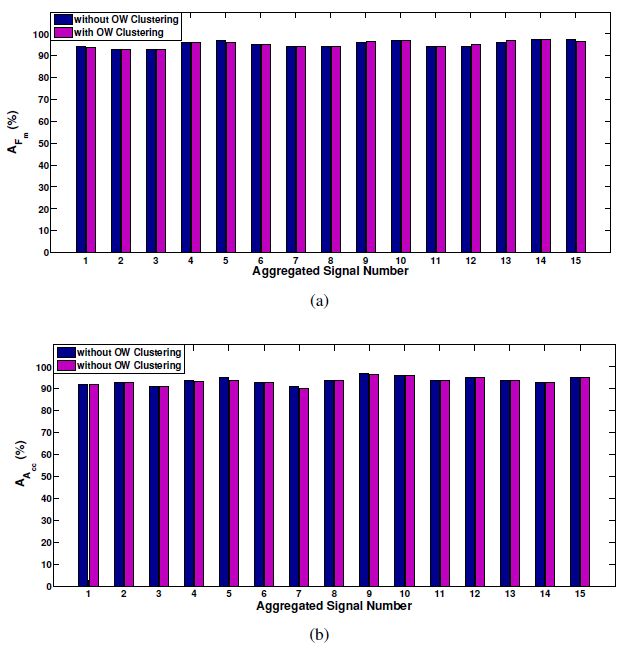
Furthermore, AFm and AAcc (with and without the clustering technique) for all 15 test aggregated active power signals used in this case study are presented in Figure 10(a) and Figure 10(b) respectively.
According to the results in Figure 8,Figure 9 and Figure 10, it is clear that the proposed NILM method identifies turned on appliances and disaggregates their individual energy with high accuracy under fluctuations in active power signals of individual appliances and different traces of appliances and appliance combinations with a relatively large number of appliances (even 10) turned on simultaneously.
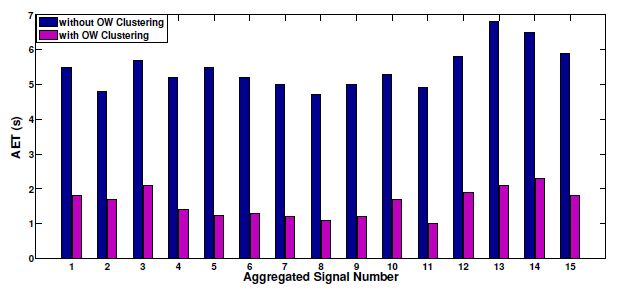
The AET (with and without the clustering technique) for all 15 test aggregated active power signals is presented in Figure 11. With the OW clustering, the AET reduced by more than 55% of the AET without OW clustering.
Therefore, it can be clearly seen that the clustering method, while being more computationally efficient and fast, provides similar identification results compared to the situation where clustering is not used. Hence, the clustering method was employed for case studies 2, 3 and 4.
5.3. Case study 2
Most households in reality have a number of identical or similar appliances with same active power signal which might be turned-on once in a given time. For instance a household may turn on many lamps of the same power level at once. Therefore, case study 2 was developed to demonstrate the applicability of the proposed NILM method for such a scenario.
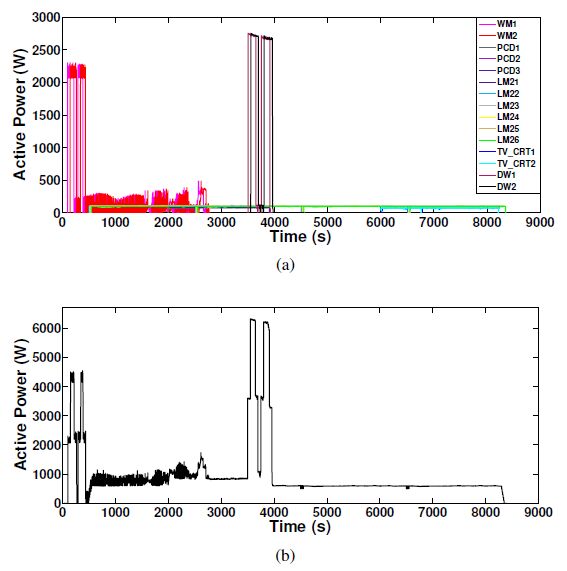
In this case study, two numbers of the same WM (WM1 and WM2), three numbers of the same PCD (PCD1, PCD2 and PCD3), two numbers of the same TV_CRT (TV_CRT1 and TV_CRT2), two numbers of the same DW (DW1 and DW2) and six numbers of the same LM2 (LM21, LM22, LM23, LM24, LM25 and LM26) were assumed to be operating. As in case study 1, 15 aggregated active power signals were generated manually and Figure 12 shows one typical aggregated active power signal out of 15. The active power consumption of individual appliances and aggregated active power consumption is shown in Figure 12(a) and Figure 12(b) respectively.
The proposed NILM method was applied to all 15 aggregated active power signals by considering each number of similar appliance as another separate appliance in addition to the previously used 20 appliances.
5.3.1. Results and Discussion
The appliance identification and their energy disaggregation accuracy of the proposed method for the turned on appliance combination in the aggregated active power signal in Figure 12(b) is presented in Table 6. According to the results in Table 6, most of the similar appliance combinations in the aggregated active power signal, were identified with more than 89% accuracy of CFm using the proposed method. Further, the energy disaggregation of most of the appliance combination in Figure 12(b) was done with more than 84% accuracy of CAcc.
Table 6. Appliance identification accuracy and energy disaggregation accuracy for appliance combination in aggregated signal in Figure 12(b).
| Actual Turned on Appliances | CFm (%) | CAcc (%) |
| 2WM | 92.0 | 91.6 |
| 2WM+6LM2 | 92.9 | 94.2 |
| 2WM+6LM2+3PCD | 91.0 | 89.0 |
| 6LM2+3PCD | 94.1 | 93.1 |
| 6LM2+3PCD+2DW | 85.7 | 85.9 |
| 6LM2 | 100 | 95.7 |
| 6LM2+2TV_CRT | 94.1 | 92.9 |
Furthermore, Table 7 presents AFm, AAcc and AET for all 15 test aggregated active power signals in this case study.
Table 7. Appliance identification accuracy, energy disaggregation accuracy and average execution time for OW of all aggregated test signal used in case study 2
| Aggregated test signal number: |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| AFm (%) | 93.2 | 92.5 | 94.9 | 91.4 | 95.2 | 93.1 | 91.9 | 92.3 | 90.1 | 93.3 | 91.8 | 93.3 | 93.4 | 92.6 | 94.1 |
| AAcc (%) | 90.2 | 91.4 | 90.0 | 91.4 | 93.3 | 91.7 | 89.6 | 88.5 | 90.6 | 92.1 | 91.4 | 93.1 | 92.8 | 87.9 | 94.2 |
| AET (s) | 1.91 | 2.10 | 1.72 | 1.67 | 1.84 | 2.35 | 2.18 | 1.71 | 1.64 | 1.32 | 1.37 | 1.95 | 2.07 | 1.84 | 1.89 |
5.4. Case study 3
All six houses in the REDD database were used in case study 3 to demonstrate the ability of algorithms to accurately identify turned on appliances and estimate their individual energy consumption for real measured active power signals from actual households. In addition to that, the results obtained from the proposed method were compared with the state of the art HMM based method given in [13] that is designed for low sampling rate. The proposed algorithm and HMM based algorithm utilized the same amount of data from the REDD database for training and testing. Four weeks of active power data for each house in the REDD database was used in this case study. The first 10 days of circuit/device specific data was used for the training phase in both algorithms. For the next 18 days, the proposed NILM method and HMM based method were applied to the aggregated active power signals measured from these households (denoted as testing signals).
5.4.1. Results and Discussion
The appliance identification and the energy disaggregation accuracy of the proposed NILM method and HMM based method in [13] for test signals in each house in the REDD database is presented in Table 8. Results in Table 8 shows that when aggregated active power signals measured from each of the six households were used, the turned on appliance combinations were identified with more than 85% accuracy of AFm and their energy disaggregation was done with more than 82% accuracy of AAcc by the proposed NILM method in this paper. Furthermore, it can be clearly seen that the proposed NILM method in each house outperformHMMbased method. HMMhas good performance in disaggregating RF events, thus it performs well in House 6, where RF events are very frequent compared to the event of other appliances. Note that RF is always turned on, hence there are more samples to train than for other appliances, leading to improve the performance of HMM based method. On the other hand, HMM based method performs poorly for DW and similar appliances that run only occasionally, and required large training dataset to generate a good Markov model.
Table 8. Appliance identification accuracy and energy disaggregation accuracy of aggregated test signals used in Case study 3
| Proposed Method | HMM based Method |
| House | AFm (%) | AAcc (%) | AFm (%) | AAcc (%) |
| House 1 | 93.2 | 90.7 | 71.1 | 70.4 |
| House 2 | 93.9 | 89.2 | 59.3 | 57.2 |
| House 3 | 88.1 | 86.4 | 54.3 | 56.3 |
| House 4 | 87.3 | 83.3 | 63.1 | 67.1 |
| House 5 | 85.4 | 82.9 | 60.7 | 58.9 |
| House 6 | 86.3 | 83.7 | 85.3 | 84.5 |
According to results given in Table 8, the appliance identification and energy disaggregation accuracy of houses 3, 4, 5 and 6 were slightly lower than house 1 and house 2. The main reason for this was that there was a considerable number of unknown appliances in houses 3, 4, 5 and 6. When these unknown appliances were turned on collectively with the other known appliances, the NILM accuracy suffered slightly. However, any known appliance combination was identified and its energy was disaggrgated with extremely high accuracy (over 94% AFm and 88% AAcc ) from the aggregated active power signals measured from real households by the proposed method.
6. Integrating residential usage patterns
Mathematical representation of usage behavior pattern, i.e. P(cj), which was not taken into account in (12) was utilized in this section.
User behaviour pattern or statistical models on turned-on time period of residential appliances within a day are presented in [4,14,15]. However, the models from [4,14,15] represent the general usage behavior of the residential appliances. Appliance usage behavior of the occupants may change from house to house or region to region. Moreover, the usage behavior may change with respect to time in a house. Hence, using general statistical models of turned-on time period of residential appliance within a day is not reasonable or practical for the process of identifying turned on appliances. Therefore, an adaptive model according to appliance usage behavior of individual house was constructed. The adaptively learned probability models on turned-on time period (hours) of the residential appliances and/or appliance combinations within a day were integrated with the proposed NILM approach in order to significantly improve its quality.
Since the proposed method gives very accurate results for appliance identification, these results were used to automatically learn the usage behavior pattern in real time for all hours of the day. A priori probability function (PPF) which represents the likelihood of a given appliance combination that is turned-on within an hours of a day was chosen as P(cj) in (12). The probability P(cj) for a given hour of a day, (i.e. LHV that appliance combination cj is turned-on within a given hour of a day), was estimated from,
|
@P(c_{j})= \frac{n_{c_{j}}}{n_{ow}\times d}, @
|
(19) |
where
now is number of OW within a given hour and
d is the number of days which were used to learn the PPF. Further
nc j is number of OW which the appliance combination
cj is turned-on out of all number of OW
now ×
d.
After learning PPF for each hour in a day, Algorithm 1 was used to identify turned on appliance combination in a given OW. Since P(cj) is not equally likely as in (12), @P(\frac{c_{j}\cap l_{k}}{Z_{i}})@ in the MAP criteria is now linearly proportional to LHV of @P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(c_{j})P(l_{k})@ instead of LHV of @P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(c_{j})@. Therefore γ1 in (15) was changed as,
|
@\gamma_{1}=\frac{\max(P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(c_{j})P(l_{k}))}{\sum_{j=1}^{N_{c_{j}}}\sum_{k=1}^{N_{l_{c_{j}}}}P(\frac{Z_{i}}{c_{j}\cap l_{k}})P(c_{j})P(l_{k})}\times 100\%, @
|
(20) |
The procedure of applying the proposed NILM approach integrated with the clustering method and the PPF to a given aggregated active power signal of a day is briefly presented as follows:
· Group each OW into clusters using the proposed clustering algorithm.
· Group OWs of a cluster into subgroups of hours. For example, OW sub groups of 6.00 to 7.00,
7.00 to 8.00, etc. for a given OW cluster.
· Apply the matching algorithm integrated with (19) and (20) to each subgroup of a given OW
cluster.
6.1. Case study 4
All six houses in the REDD database were used in this case study to validate the importance of integrating the PPF to Algorithm 1. Four weeks of usage data is in this database for each house. The first 10 days of circuit/device specific data was used for the training phase (for generation of active power signature database and energy level signature database). The algorithm 1 (without (PPFs)) was applied to next 10 days of aggregated active power signal measured from real households in order to learn the PPFs of each hours in a given house. Afterwords, the algorithm 1 (with PPF) was applied to last 8 days of aggregated active power signal (denoted as testing signals).
6.1.1. Results and Discussion
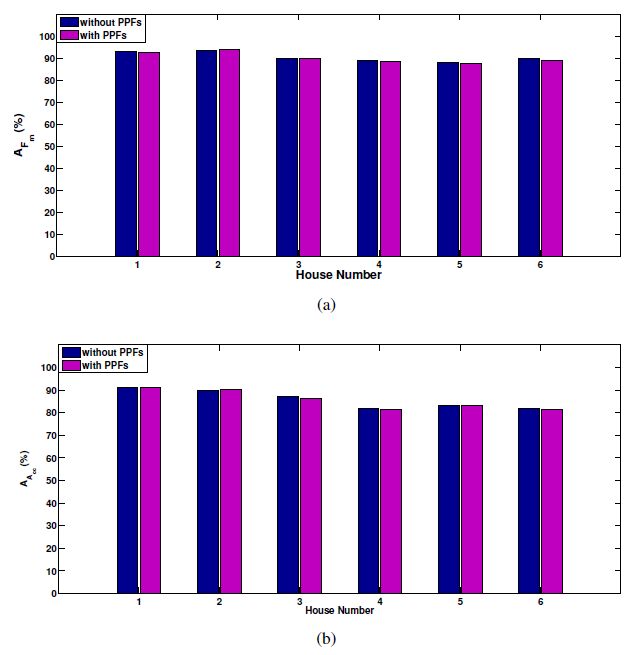
The AFm and AAcc for last 8 days of aggregated signals in each house in the REDD database with and without learned PPFs are presented in Figure 13(a) and Figure 13(b) respectively. According to Figure 13, NILM accuracy with and without PPF are approximately the same.
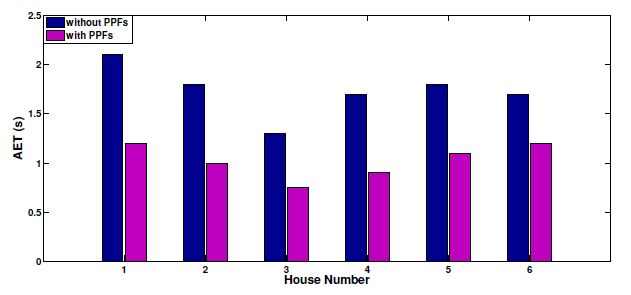
The AET for last 8 days of aggregated signals in each house in the REDD database with and without learned PPFs are presented in Figure 14. According to the results in Figure 14, AET of each house had reduced from more than 30% after integrating PPF. Hence, it can be clearly seen that the convergence speed of the matching algorithm in proposed NILM method is increased after incorporating the usage behaviour patterns while maintaining the high NILM accuracy.
In order to demonstrate the performance of increasing the convergence speed after integrating PPF, a term called effective number of iteration (ENI) for a OW cluster was introduced. For a given cluster, the maximum number of iterations out of number of iterations of all subgroups of the given cluster was defined as the ENI of that cluster.
For the aggregated active power signal in house 1, the number of OW clusters whose identification results were given in each iteration without the PPF is presented in Table 9. In addition to that, the distribution of a given number of OW clusters with their ENIs after integrating PPFs is also presented in Table 9.
Table 9. Performance Improvement and Comparison Achieved Through Integrating PPFs.
| Without PPF | With PPF |
| Distribution of no. of clusters with their ENIs: |
| ENIs | No. of clusters (%) | 1 | 2 | 3 | 4 | 5 |
| 1 | 18 | 18 | 0 | 0 | 0 | 0 |
| 2 | 20 | 4 | 15 | 1 | 0 | 0 |
| 3 | 19 | 3 | 8 | 7 | 0 | 1 |
| 4 | 34 | 0 | 19 | 12 | 3 | 0 |
| 5 | 9 | 0 | 0 | 6 | 2 | 1 |
For example, as shown in the fourth row in Table 9, 34% OW clusters out of all clusters in the aggregated signal in house 1 identified their turned-on appliance combinations after executing 4 ENI without PPF. After integrating PPF, 19 clusters out of this 34% identified their turned-on appliance combinations from 2 ENIs and 12 clusters identified from 3 ENIs while only 3 clusters identified from 4 ENIs.
According to the results in Table 9, nearly 43% of OW clusters of the aggregated power signal in house 1 were identified after 4 or 5 ENIs without PPFs. Further 57% of OW clusters were identified after 1, 2 or 3 ENIs. However, after integrating the PPFs, only 7% of OW clusters were identified after 4 or 5 ENIs and 93% of OW clusters were identified 1, 2 or 3 ENIs.
Hence, it can be clearly seen that the convergence speed of the matching algorithm is increased after incorporating the usage behaviour patterns while maintaining the high identification accuracy.
7. Conclusions
A Non-Intrusive Load Monitoring (NILM) method that utilizes the Karhunen Loéve (KL) expansion to construct a unique set of features from individual and aggregated active power signals was developed. In the proposed method, similar signal windows were clustered in to one group using a modified mean shift algorithm prior to feature extraction. After the feature extraction, energy levels of signal windows and power levels of subspace components were utilized to reduce the number of possible appliance combinations and their energy level combinations. Then, the turned on appliance combination and the energy contribution from individual appliances were determined through the Maximum a Posteriori estimation. Finally, the proposed method was modified to adaptively accommodate the usage patterns of appliances in each residence.
From the case studies carried out, it was found that the clustering method is more computationally efficient and fast and provides similar identification results compared to the situation where clustering is not used. It was also found that the proposed method can accurately identify the appliance combinations operating within an observation window and disaggregate its individual energy contribution with high accuracy. This was true even when multiple similar or identical appliances are turned-on. Finally, it was found that incorporating the prior probabilities of usage behaviour further reduced the average execution time without any compromize to the accuracy of identification.
All conducted case studies utilize a large number of practical appliances with variations among the test signals of the same appliance to demonstrate the high performance accuracy of the proposed NILM algorithm. The requirement of a single measurement i.e., the total active power signal, the capability of identifying turned-on appliances and determining individual energy contributions while operating within a ten sample window with a few iterations and high mean accuracy offered by this technique makes it an ideal NILM method to identify turned-on appliance combinations within a time window for smart grid applications.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: