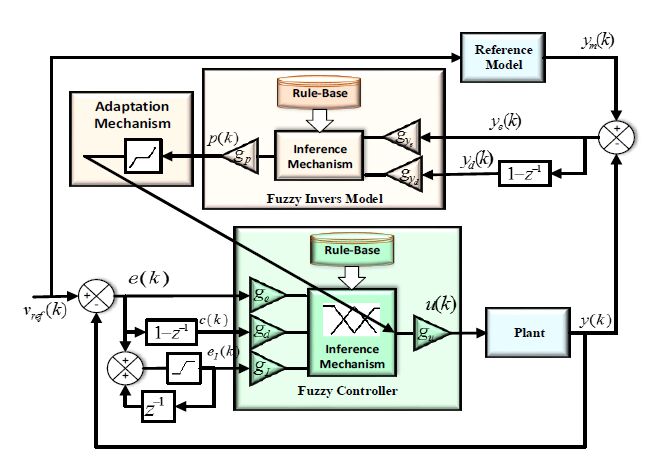
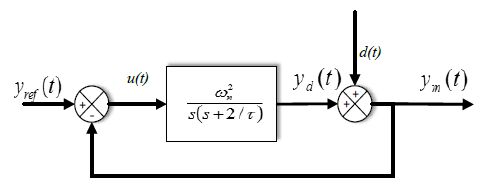
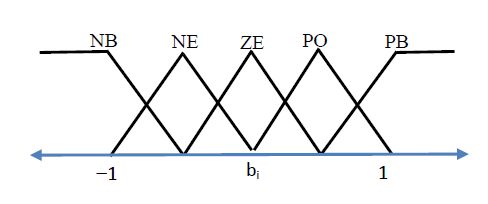
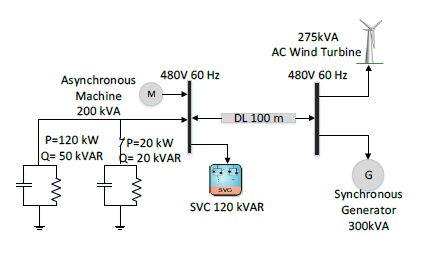
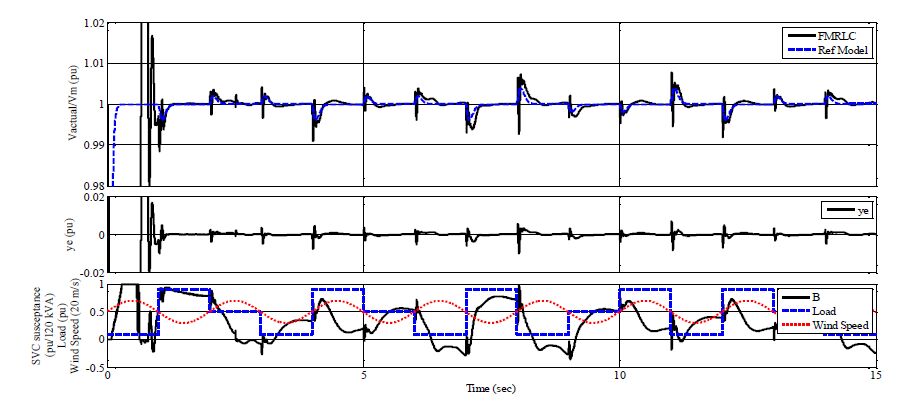
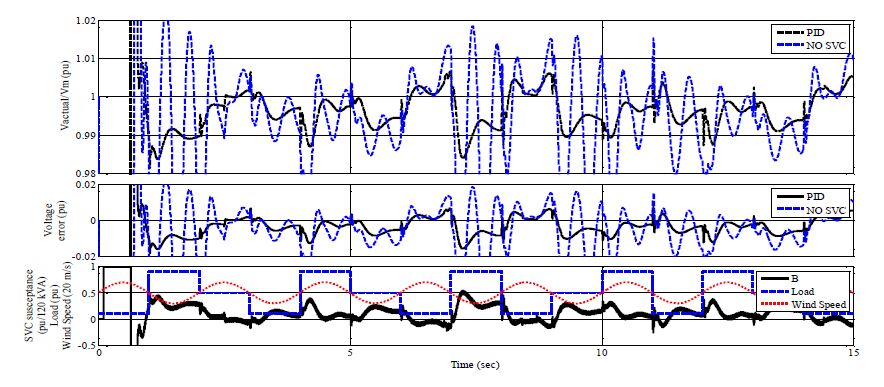
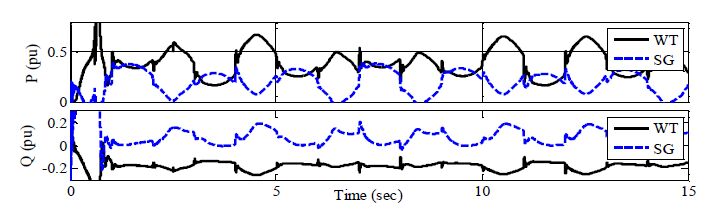
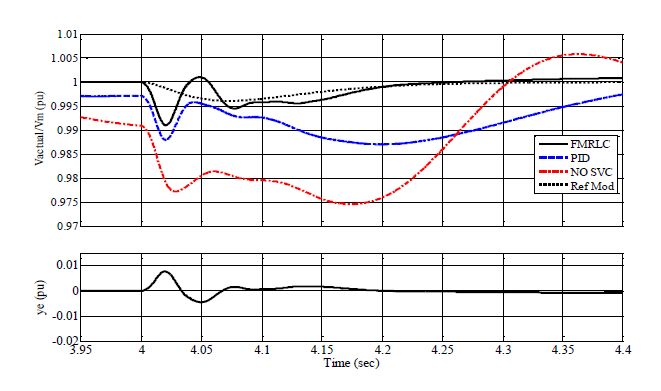
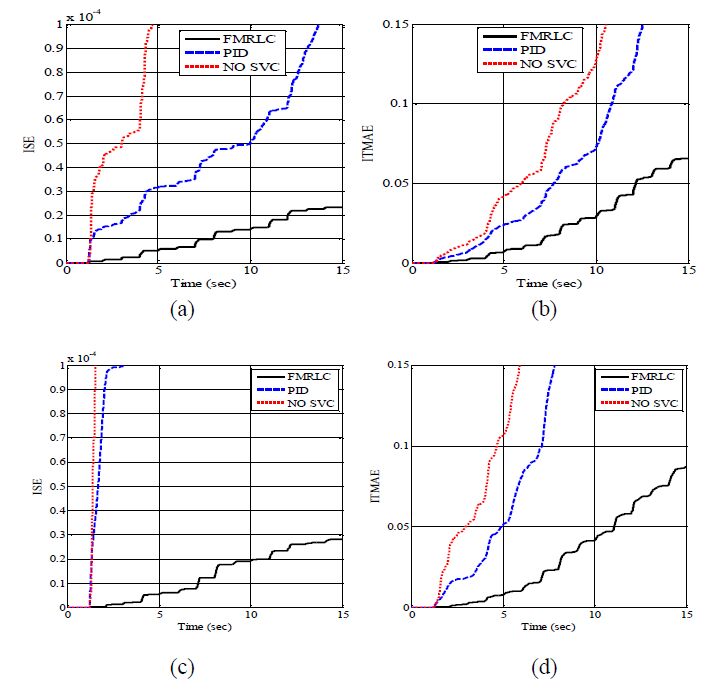
Maintaining voltage stability, within acceptable levels, for islanded Microgrids (MGs) is a challenge due to limited exchange power between generation and loads. This paper proposes an algorithm to enhance the dynamic performance of islanded MGs in presence of load disturbance using Static VAR Compensator (SVC) with Fuzzy Model Reference Learning Controller (FMRLC). The proposed algorithm compensates MG nonlinearity via fuzzy membership functions and inference mechanism imbedded in both controller and inverse model. Hence, MG keeps the desired performance as required at any operating condition. Furthermore, the self-learning capability of the proposed control algorithm compensates for grid parameter’s variation even with inadequate information about load dynamics. A reference model was designed to reject bus voltage disturbance with achievable performance by the proposed fuzzy controller. Three simulations scenarios have been presented to investigate effectiveness of proposed control algorithm in improving steady-state and transient performance of islanded MGs. The first scenario conducted without SVC, second conducted with SVC using PID controller and third conducted using FMRLC algorithm. A comparison for results shows ability of proposed control algorithm to enhance disturbance rejection due to learning process.
1.
Introduction
First, I take this opportunity to express my great admiration toward Professor Goong Chen by dedicating this paper to him on the occasion of his 70th birthday.
In this paper, we mainly consider the problem of vibrations governed by 1D wave equation $ w_{tt}-c^2w_{xx} = 0 $, where $ c $ denotes wave propagation speed, associated with a generalized boundary condition. Recall the definition of chaos for this kind of system, which is firstly introduced in [1], as below:
Definition 1.1. Consider an initial-boundary problem $ (S) $ governed by 1D wave equation $ w_{tt}-c^2w_{xx} = 0 $ defined on a segment $ I $, where $ c > 0 $ denotes the propagation speed of the wave. The system is said to be chaotic if there exists a large class of initial data $ (w_0, w_1) $ such that
(i) $ |w_x|+|w_t| $ is uniformly bounded,
(ii) $ V(t)\overset{def}{ = }V_I(w_x(\cdot, t))+V_I(w_t(\cdot, t)) < +\infty $ for all $ t\geq0 $,
(iii) $ \liminf\limits_{t\to+\infty}\frac{\ln V(t)}{t} > 0 $.
Remark 1.1. When chaos occurs, the function $ x\mapsto \left(|w_x|+|w_t|\right)(x, t) $ is uniformly bounded, whereas the length of the curve $ \{(x, \; \left(|w_x|+|w_t|\right)(x, t)), \; x\in[0, 1]\} $ grows exponentially w.r.t. time $ t $. Therefore, the system $ (S) $ must undergo extremely complex oscillations as time $ t $ increasing.
Remark 1.2. There are lots of work about chaos studies, see e.g., [2,3,4] and references therein. As we know, there is no a common mathematical definition for chaos, which is actually a challenge to give. However, Li-Yorke chaos is probably one of the most popular and acceptable notions of chaos. We will study the relationship between Li-Yorke chaos and chaos in the sense of Definition 1.1 in our future work. Particularly, if chaos happens and the solution $ (w_x, w_t) $ can be represented by two interval maps, denoted by $ K_1 $ and $ K_2 $, respectively, then $ K_1 $ and $ K_2 $ have positive entropy, which implies $ K_1 $ and $ K_2 $ are chaotic in the sense of Li-Yorke.
Let us take a classical model to introduce the research background and our motivation, as below:
where $ \alpha, \beta $, and $ \eta $ are given constants. If $ \eta = 1 $, the system (1.1) is not well-posed. Thus throughout this paper we assume $ \eta\not = 1 $. The wave equation itself is linear and represents the infinite-dimensional harmonic oscillator. Let
be the energy function of this system. And assume that (1.1) admits a $ C^2 $ solution, then the boundary conditions show
The right-handed side boundary condition (at $ x = 1 $) is nonlinear when $ \beta\ne 0 $, which is usually called a van der Pol type boundary condition (see, e.g., [1,5,6,7,8,9]). The left-handed side boundary condition (at $ x = 0 $) is linear, where $ \eta > 0 $ indicates that energy is being injected into the system at $ x = 0 $. Thus if $ \eta > 0 $, the system (1.1) has a self-excited mechanism that supplies energy to the system itself, which induces irregular vibrations [1,6]. In particular, when $ \eta = 0 $, the free end at $ x = 0 $ has no effect to the energy, which is also called an energy-conserving boundary condition.
The existence and uniqueness of the classical solution of (1.1) can be found in [5,6]. Furthermore, the system (1.1) has a smooth solution $ w\in \mathcal{C}^2 $ if the initial data satisfy
where
see Theorem 6.1 in [6]. The weak solution as well as its numerical approximation are discussed in [9].
The PDE system (1.1) has received considerable attention since it exhibits many interesting and complicated dynamical phenomena, such as limit cycles and chaotic behavior of $ (w_t, w_x) $ when the parameters $ \alpha, \beta $ and $ \eta $ assume certain values [1,6]. Different from dynamics of a system of ODEs, this is a simple and useful infinite-dimensional model for the study of spatiotemporal behaviors as time evolutes. For instance, the propagation of acoustic waves in a pipe satisfies the linear wave equation: $ {w}_{tt}-{w}_{xx} = 0. $ As we know, the solution of 1D wave equation describes a superposition of two traveling wave with arbitrary profiles, one propagating with unit speed to the left, the other with unit speed to the right. The boundary conditions appeared in (1.1) can create irregularly acoustical vibrations ([1,6,7]). This type of vibrations, for example, can be generated by noise signals radiated from underwater vehicles, and there are intensive research for the properties of acoustical vibrations in current literature (see e.g., [10] and references therein). Hence the study of this type of vibration is not only important but also may lead to a better understanding of the dynamics of acoustic systems.
In this paper, we mainly consider the oscillation problems described by the following models:
where the function $ h\in\mathcal{C}^0(\mathbb{R}) $ satisfies
(A1) $ \phi: t\mapsto \frac{1}{2}\left(h(t)-\frac{1}{c}t\right) $ strictly monotonically decreases on $ \mathbb{R} $,
(A2) $ \phi(\mathbb{R}) = \mathbb{R} $.
It is clear that $ \phi^{-1}:\mathbb{R}\to \mathbb{R} $ is well-defined and strictly decreases on $ \mathbb{R} $. In fact, the model (1.4) is a generalized case of the van del Pol type boundary condition, $ h(x) = \alpha x-\beta x^3 $, say. Denote the total energy of system (1.4) as
then the boundary conditions show
Hence $ \eta > 0 $ can cause the energy of system to increase. Moreover, the system (1.1) has a generalized self-excited mechanism if we assume that, roughly speaking, $ \frac{h(y)}{y} > 0 $ if $ |y| $ is small and $ \frac{h(y)}{y} < 0 $ if $ |y| $ is large. Thus if $ \eta > 0 $, the system (1.4) has a self-excited mechanism that supplies energy to the system itself, which could induce irregular oscillations. The interesting part is that the system (1.5) may have chaos even though there is no energy supplier at the boundary.
We can treat the initial-boundary problems (1.4) and (1.5) by using wave propagation method. Let's take (1.4) as a start. It is well-known that $ w $, a solution of 1D wave equation, has the following form:
where $ L $ and $ R $ are two $ C^1 $ functions. Then the gradient of $ w $ can be represented as follows:
for $ x\in[0, 1], t\geq0 $. Introduce two new variables
which are called the Riemann invariants. It is evident that $ u $ and $ v $ keeps constants along the lines $ x+ct = const. $ and $ x-ct = const. $, respectively, which are referred to as characteristics.
When $ t > 0 $ and $ x = 0 $, from the boundary condition at the left end $ x = 0 $,
that is
Without confusion, we also take $ \gamma(\eta) $ as a linear map.
When $ t > 0 $ and $ x = 1 $, from the boundary condition at the right end $ x = 1 $, it follows:
that is
which determines a reflection relationship between $ u(1, t) $ and $ v(1, t) $ as follow
where
When $ t = 0 $, from the initial conditions,
which are referred to as the initial date of $ (u, v) $.
For $ x\in[0, 1] $ and $ \tau\geq0 $, it follows from the boundary reflections (1.9) and (1.10) that
and
inductively,
where the superscript $ n\in\mathbb{N} $ denotes the $ n $th iteration of a function. Analogously, for $ x\in[0, 1] $ and $ \tau\in[0, \frac{2}{c}) $,
and
Equations (1.13)–(1.15) show that the system (1.4) is solvable and the dynamics of the solution $ (w, w_x, w_t) $ to the equation (1.4) can be uniquely determined by the initial data and the following two functions:
Note that $ g = \gamma^{-1}(\eta)\circ \psi_\eta\circ\gamma(\eta) $, that is to say there is topological conjugacy between $ \psi_\eta $ and $ g $. Therefore one only needs to consider one of them, say $ \psi_\eta $.
The paper will be organized as follows. In the next two sections, we will present the necessary and sufficient conditions to cause the onset of chaos, respectively. Section 4 shows, as a special case, in which the wave equation has a fixed end, that chaos can occur with the effects of self-regulations and energy-conservation. In Section 5, there are some applications of the theoretical outcomes. In the last section, it is the numerical simulations.
2.
Necessary conditions for the onset of chaos
In this section, we firstly give a necessary condition for the onset of chaos in the following system:
where $ h $ satisfies hypotheses $ (A1) $ and $ (A2) $. In addition, assume the function $ t\mapsto \left(h(t)+\frac{1}{c}t\right) $ is piecewise monotone.
Theorem 2.1. Suppose the system $(2.1)$ is chaotic in the sense of Definition 1.1. Then $ h $ is not even and $ \eta\ne0 $.
Proof. It is equivalent to prove that there is no chaos in the system (2.1) if $ \eta = 0 $ or $ h $ is an even function.
Firstly, assume $ h $ is an even function. Let $ \eta\in\mathbb{R} $ and $ \eta\ne c^{-1} $. Recall the function $ \psi_\eta $ given by (1.16):
Introduce a new map $ Q $ from $ \mathbb{R} $ to $ \mathbb{R} $ as follow:
For $ x\in\mathbb{R} $, let $ y = \phi^{-1}(x) $, then
Since $ \phi^{-1} $ is strictly decreasing and $ \gamma(\eta)\in\mathbb{R}^* $, $ \psi $ is monotonic if and only if $ Q $ is monotonic. Let $ y_1, \; y_2\in \mathbb{R} $ with $ y_1 < y_2 $. From the hypothesis $ h $ being an even function, it follows
which implies $ Q $ strictly monotonically increases. Therefore $ \psi $ strictly monotonically increases (decreases) if $ \gamma(\eta) < 0 (\gamma(\eta) > 0) $. It is easily seen that
Hence the dynamics of $ (w_x, w_t) $ is simple, and the chaos doesn't occur in the system.
Next, assume $ \eta = 0 $, in other words, the system is free at the left end. In this case,
We will show that there is no period point of $ \psi_0 $ with period 2. Let $ x_0\in\mathbb{R} $ satisfy $ x_0 < \psi_0(x_0) $. Define two functions as follows:
Since $ \phi^{-1}(\cdot) $ strictly monotonically decreases and
$ k $ strictly monotonically increases in $ [x_0, \; \psi_0(x_0)] $. Hence
That implies there are no period points of $ \psi_0 $ with period 2. By Sharkovsky's Theorem, there are no periods of $ \psi_0 $ with period lager than 2. By virtue of the Main Theorem 6 in [12], there is still no chaos in the system when $ \eta = 0 $.
Next, we consider the following system governed by 1D wave equation with a fixed end:
where $ h $ satisfies hypotheses $ (A1) $ and $ (A2) $.
Theorem 2.2. Suppose the system $(2.3)$ is chaotic in the sense of Definition 1.1. Then$ h $ is neither an even function nor an odd function.
Proof. Put
By the analysis in Section 1, it is clear that $ (z_x, z_t) $ can be represented by iterations of $ \psi_{\infty} $ and initial data. Hence, the dynamics of $ (z_x, z_t) $ is completely determined by $ \psi_{\infty} $.
If $ h $ is even, $ \psi_{\infty} $ is monotonically monotone. If $ h $ is odd, $ -\psi_{\infty} $ has no periodic points of period larger than 2. Therefore, chaos never occurs in the system 2.3 if $ h $ is either an even function or an odd function.
Remark 2.1. Chaos can definitely happen in the system 2.3 for a special kind of $ h $. One can find more details about that in the later section.
3.
Chaotic oscillations of 1D wave equation with a general boundary feedback control law
In this section, we mainly try to determine some sufficient conditions to ensure the onset of chaotic oscillations in the following system:
where $ h\in\mathcal{C}^0(\mathbb{R}) $ satisfies $ h(0) = 0 $, hypotheses $ (A1) $ and $ (A2) $. When $ w_t(1, t)\equiv0 $, there should be no signals feedback to $ w_x(1, t) $, that's to say the right end should be free. Therefore it is reasonable to let $ h(0) = 0 $.
According to the analysis in the first section, we have known that the function $ \psi_\eta $ given by (1.16) plays a vital role in studying the dynamics of system (3.1). We firstly give two lemmas that are useful in analyzing dynamics of $ \psi_\eta $, as follow:
Lemma 3.1. Let $ I $ be a non-degenerate closed interval, $ J\subseteq\mathbb{R} $ and $ F:I\to J $, $ G:J\to \mathbb{R} $. Assume that $ V_JG < +\infty $ and $ F $ is piecewise monotone. Then
Proof. Let $ I_1 = [a, b] $ be a monotone interval of $ F $. Without loss of generality, let $ F $ monotonically increase in $ I_1 $. Let
be a partition of $ I_1 $. Then
where
is a partition of $ F(I_1) $. Consequently, $ V_{I_1}G\circ F\leq V_{F(I_1)}G $. Conversely, if
is a partition of of $ F(I_1) $, then
where $ \tilde{F}^{-1}(q) = \min\{x\in I_1, F(x) = q\} $, is a partition of $ I_1 $. That implies
Therefore, $ V_{I_1}G\circ F = V_{F(I_1)}G $.
Let $ (I_j)_{1\leq j\leq n} $ be a finite sequence consisting of monotone intervals of $ F $. Assume $ \sqcup_{1\leq j\leq n} I_j = I $ and $ \#(I_i\cap I_j)\leq 1 $ provided $ i\ne j $. Then,
Lemma 3.2. Let $ I $ be a closed interval and $ F\in \mathcal{C}^0(I, I) $ be piecewise monotone. If there exist non-degenerate subintervals $ I_1, I_2\subseteq A $ with $ Card(I_1\cap I_2)\leq 1 $ such that $ I_2\subseteq F(I_1) $ and $ I_1\cup I_2\subseteq F(I_2) $, then
Proof. Let two subintervals $ I_1, I_2\subseteq A $ satisfy the hypothesis. Let $ n\in\mathbb{N} $. Put
where $ F^0 = Id_{\mathbb{R}} $ if $ n = 0 $. Note that $ F(\cdot) $ is continuous and piecewise monotone, it follows from Lemma 3.1 that
and
Let $ (z_n)_{n\in\mathbb{N}} $ be Fibonacci sequence, i.e., $ z_{n+2} = z_{n+1}+z_n $, with the initial data $ z_0 = 0, z_1 = 1 $. It is well known that
It is clear that $ y_1 > 0 $ and $ \forall n\in\mathbb{N}, y_n\geq y_1z_n $. Therefore,
This competes the proof.
Proposition 3.1. Let $ h\in\mathcal{C}^0(\mathbb{R}) $ satisfy the hypothesises $ (A1)-(A2) $ and $ \psi_\eta $ be given by $(1.16)$. In addition, assume $ h(0) = 0 $ and
(i) non-constant function $ Q:t\mapsto\frac12\left(h(t)+\frac{1}{c}t\right) $ is piecewise monotone,
(ii) there is at least one solution to the equation $ h(y)+c^{-1}y = 0 $ in $ \mathbb{R}^* $.
Then there exist $ A > 0 $ and a non-degenerate interval $ I\subseteq(0, +\infty)\setminus\{c^{-1}\} $ such that for any $ \eta\in I $, $ [0, A] $ is an invariant set of $ \psi_\eta $ and
Proof. We need to finish the following two steps:
$ (1) $ Determine an invariant interval $ [0, A] $ of $ \psi_\eta $.
$ (2) $ To make sure the hypothesises of Lemma 3.2 holds.
It has been known that
Put
and
By the hypothesises $ (i)-(ii) $, $ S^-\ne\emptyset $ or $ S^+\ne\emptyset $. Without loss of generality, assume $ S^-\ne\emptyset $. We take
then
Moreover, let
By the definition of $ S^- $, it is evident that $ M = 0 $ or $ m = 0 $.
Case 1: Assume $ M = 0 $. That implies $ m < 0 $. Put
For any $ \eta\in[0, c^{-1}) $, it is easily seen that
and $ \psi_\eta(x) < \psi_\eta(x_0) $ provided that $ x\in[0, x_0) $. We need to prove that $ m\cdot\gamma(0) < A $. Proceed the proof by contradiction. Assume $ m\cdot\gamma(0)\geq A $, which implies
Thus $ \psi_0 $ is turbulent. According to Lemma 3 in [11], $ \psi_0 $ has periodic points of all periods. But from the proof of Theorem 2.1, $ \psi_0 $ has no periodic points whose period is larger than 2. We have thus reached a contradiction. Since that $ m\cdot\gamma(\cdot) $ is strictly increasing in $ [0, c^{-1}) $ and $ m\cdot\gamma(\eta)\to+\infty $ as $ \eta\to(c^{-1})^- $, it is reasonable to put
Then for $ \eta\in[0, \bar{\eta}] $, we have
that is to say $ [0, A] $ is an invariant set of $ \psi_\eta $ provided $ \eta\in[0, \bar{\eta}] $. Put
then $ \underline{\eta} < \bar{\eta} $ and $ \psi(x_0) > x_0 $ if $ \eta > \underline{\eta} $. For $ \eta\in[\underline{\eta}, c^{-1}) $, consider the following set:
It is clear that $ S(\eta, x_0) $ is closed. Since $ x_0 $ is uniquely determined by $ h $ and $ h $ is independent of $ \eta $, the following function is well-defined:
We first prove that $ \alpha(\cdot) $ is strictly monotonically decreasing in $ [\underline{\eta}, c^{-1}) $. Let $ t_1, t_2\in(\underline{\eta}, c^{-1}) $ with $ t_1 < t_2 $. From the definition of $ \alpha(\cdot) $, it follows
Since that
by applying the continuity of $ \gamma(t_1)\cdot\varphi(\cdot) $ there exists $ x\in(\alpha(t_2), x_0) $ such that $ \gamma(t_1)\cdot\varphi(x) = x_0 $. According to the definition of $ \alpha(t_1) $, we have
Therefore, $ \alpha(\cdot) $ strictly monotonically decreases in $ [\underline{\eta}, c^{-1}) $.
Next, prove that $ \alpha(\cdot) $ is continuous from the left. Let $ t_0\in(\underline{\eta}, x_0) $ be fixed. Since $ \alpha $ is monotone, we have
By the continuity of $ \eta\mapsto\gamma(\eta) $ and $ x\mapsto\varphi(x) $, we obtain
which gives $ \gamma(t_0)\cdot\varphi(L) = \gamma(t_0)\cdot\varphi(\alpha(t_0)) = x_0 $. From the definition of $ \alpha(\cdot) $ and (3.10), it follows
Therefore $ \alpha(\cdot) $ is continuous from the left.
In particular, $ \psi_{\bar{\eta}}(\alpha(\underline{\eta})) = \gamma(\underline{\eta})\cdot\varphi\left(\alpha(\bar{\eta})\right) = x_0 $ and $ \psi_{\bar{\eta}}(x_0) = \gamma(\underline{\eta})\cdot\varphi(x_0) = A $. Define a function as follow:
It is easily seen that $ K(\cdot) $ is continuous from right at $ s = 0 $. Note that
hence there exists $ \rho_0\in(0, \bar{\eta}-\underline{\eta}) $ such that
Put
and
Let $ \eta\in I $ be fixed. By (3.13),
which is to say hypotheses of Lemma 3.2 holds. Therefore for any $ \eta\in I $, by applying Lemma 3.2 we have
For the case $ m = 0 $, one just needs to consider $ \eta > c^{-1} $. The proof is similar, we omit it.
Theorem 3.1. Consider the system $(3.1)$ with the hypotheses $ (A1)-(A2) $. Suppose $ h(0) = 0 $ and
(i) non-constant function $ Q:t\mapsto\frac12\left(h(t)+\frac{1}{c}t\right) $ is piecewise monotone,
(ii) there is at least one solution to the equation $ h(y)+c^{-1}y = 0 $ in $ \mathbb{R}^* $.
Then there exists a non-degenerate interval $ I $ such that for all $ \eta\in I $ the system $(3.1)$ is chaotic in the sense of Definition 1.1.
Proof. Without loss of generality, assume the equation $ h(y)+c^{-1}y = 0 $ has at least one solution in $ (-\infty, 0) $. We still use the symbols given in the proof of Proposition 3.1, such as $ A $, $ x_0 $, $ \alpha(\eta) $ and so on. Let $ I $ and $ J_1, J_2 $ be given by (3.14) and (3.15), respectively. Take $ \eta\in I $.
Let $ (w_0, w_1) $ be the initial data of system (3.1) and $ (w, w_x, w_t) $ be a solution of system (3.1). Recall the Riemann invariants as follow
and $ u_0(\cdot) = u(\cdot, 0) $ and $ v_0(\cdot) = v(\cdot, 0) $ are the initial data. Let $ t > 2c^{-1} $, $ n = [\frac{ct}{2}] $ and $ \tau = t-2nc^{-1} $ be fixed. It is clear that $ 0\leq c\tau < 2 $. By using (1.13), (1.14) and (1.15), we obtain
and
Since $ [0, A] $ is an invariant set of $ \psi_\eta $, $ |u|+|v| $ is uniformly bounded if
In addition, assume that $ u_0 $ and $ v_0 $ are piecewise monotone and
Consider the total variations of $ u(\cdot, t) $ and $ v(\cdot, t) $ on $ [0, 1] $. When $ 0\leq c\tau < 1 $, from (1.13)-(1.15) and Lemma 3.1, it follows
Note that $ 0 < \left|\gamma^{-1}(\eta)\right| < 1 $, by Lemma 3.1 and (3.20) we obtain
Then Proposition 3.1 and (3.16) show that
When $ 1\leq c\tau < 2 $, in the same way we can obtain
It is evident that
Hence
Therefore, the system (3.1) is chaotic in the sense of Definition 1.1.
4.
Chaotic oscillations of 1D wave equation with a fixed end
In this section, we mainly consider the oscillation problem governed by 1D wave equation with a fixed end. We will show that only the effect of self-regulation effect at one of the two ends can cause the onset of chaos. But if the fixed end is replaced by a free end, the system never has chaos. As we know, both a fixed end and a free end are called the energy-conserving boundary condition. Even though either a fixed end or a free end has the same effect to the energy of the system, the systems may show completely different dynamics: one with chaos, the other without chaos. Thus the relationship between chaos and energy of the system is much more complicated.
Theorem 4.1. Consider an initial-boundary problem governed by 1D wave equation with a fixed end as follows:
There exists a piecewise linear function $ h $ so that the system is chaotic in the sense of Definition 1.1.
Proof. Without loss of generality, we take $ c = 1 $. Put
where $ \theta\in(0, 1) $ is a fixed parameter. It is clear that $ h_\theta\in\mathcal{C}^0(\mathbb{R}) $ and
is strictly monotonically decreasing and $ \phi_{\theta}(\mathbb{R}) = \mathbb{R} $. Then $ \phi_{\theta}^{-1} $ exists. Let
then
Let $ u = \frac{z_x+z_t}{2} $ and $ u = \frac{z_x-z_t}{2} $ be the Riemann invariants of system 4.1. For some initial date $ (u_0, v_0) $, suppose $ (u, v) $ is solved for $ t\leq2 $. Then for $ t = 2n+\tau $ with $ \tau\in[0, 2) $ and $ n\in\mathbb{N} $, we have
Put
They are monotone intervals of $ \psi_\theta $, respectively. A simple calculation shows that
Let $ \theta\in(0, 1) $ be sufficiently small such that $ \frac12\theta\geq\theta^2 $ and $ \theta^2-2\leq-\theta-1 $, which implies
Let $ n\in\mathbb{N} $. Put
Lemma 3.2 shows that
which implies
Inductively, we obtain
Therefore,
A simple calculation shows that
By (4.3), $ |u|+|v| $ is always uniformly bounded for any initial date. Analogous to the proof of Theorem 3.1, there exists a large class of initial data such that
Therefore, the proof completes.
5.
Applications
We first consider a problem about perturbations at boundaries, described by the following model:
If $ \varepsilon = 0 $, for any initial data $ (w_0, w_1) $ and $ \eta\ne c^{-1} $, by using wave propagation method we can obtain
That shows system (5.1) is of global asymptotical stability.
Assume $ \varepsilon\ne0 $ and $ |\varepsilon| $ is sufficiently small. Put
It is evident that $ i) \; y\mapsto h_\varepsilon(y)+c^{-1}y $ is piecewise monotone, $ ii) \; y\mapsto h_\varepsilon(y)-c^{-1}y $ strictly monotonically decreasing, $ iii) $ there are infinite solutions to the equation $ h_\varepsilon(y)+c^{-1}y = 0 $ in $ \mathbb{R}^* $. That shows the hypotheses of Theorem 3.1 hold. Therefore, system (5.1) is chaotic in the sense of Definition 1.1.
The above analysis shows that this kind of system is no longer stable under small perturbations at one of the boundaries. That is to say this kind of system is not of structural stability.
As we have stated in the previous sections, if the feedback control law is even chaos never happen. In particular, consider the system described by the following model:
The feedback control law at the right end is periodic and even. Therefore there is no chaos in the system (5.2). Moreover, there should exists a compact attractor in the system 5.2.
6.
Numerical simulations
In this section, we will give some numerical simulations to validate the theoretical results of this paper. We first consider the system as follow:
where
Choose
as the initial data of system (6.1). Put
As we show in Section 4, the solution $ (z, z_x, z_t) $ can be represented by the iterations of this $ \psi_{\infty} $ and initial data $ (z_0, z_1) $. Note that $ h $ and $ \psi_\infty $ are piecewise linear, thus the feedback control at the boundaries is easy to implement and the solutions of system are much simpler to be solved and represented.
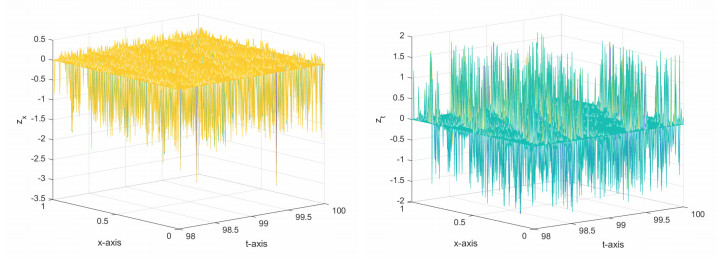
We present the graphics in some detail, for $ z_x, \; z_t $ for $ 98\leq t\leq 100 $. Figure 1 shows that $ z_x, z_t $ are extremely oscillatory in every direction of space and time.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant 11671410 and the Natural Science Foundation of Guangdong Province, China (No.2022A1515012153).
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad: