1. Introduction
Demand forecasting is one of the important inputs for a successful restaurant management system. More often than not, businesses require accurate demand forecasts to optimize their strategies. When such forecasts are available, restaurant managers are able to control costs and inventories, and improve customer service with better efficiency. It also allows managers to prepare an appropriate staff schedule in order to optimize the working time of employees and avoid over-staffing or under-staffing situations, leading to significant savings for the company. Furthermore, restaurant operators often require accurate forecasts of time-related demand so that effective pricing and table-allocation decisions can be made. Thus, it is important to develop mathematical models that assist in the prediction the time-related demand. In the restaurant industry, customer demand varies by the time of year, month, week, day and by the day part and this demand is highly periodic. It contains a year periodicity, and also monthly, weekly and even hourly patterns can occur. However the periodicity of each restaurant is unique, thus the data should be analyzed individually.
In this paper, we study transaction data collected from a franchise restaurant which has more than 60 stores across North America. This data is collected over a period of 5 years, from February 2010 to February 2015. For each store, for each transaction, there exists information such as the transaction date, the number of guests for the transaction, the area of restaurant where the transaction occured (for example, dining, lounge, patio or bar), the meals ordered, the price of the meals and so on. We are interested to study this transaction data, develop models to predict guest count for each store, compare and validate the models.
The rest of this paper is organized as follows. Section 2 contains a literature review of existing forecasting techniques. A more detailed overview of the popular restaurant prediction methods can be found in [6]. A description of the data used in this project is presented in Section 3. Section 4 provides an explanation of the model and algorithm. The results of the experiments are presented in Section 5. Finally, Section 6 includes a summary of our research with remarks.
2. Literature review
One essential element in strategic planning for the restaurant industry is prediction of future demand. Having a good estimation of the future number of guests and restaurant operators can better control inventories, staff schedule or even make effective pricing and table-allocation decisions [5]. Customer demand varies by the time of year, month, week, day and by time of day. Restaurant demand may be higher on weekends (especially on Fridays and Saturdays), during holidays, summer months, or at particular periods as lunch or dinner time. Many different factors influence on number of guests or amount of sales each day. For instance, some important factor are historical sales data, promotions, economic variables, location type of the store or demographics of its location.
Below we describe multiple regression which has been used extensively for similar problems. Also, we review Poisson regression used for prediction of a dependent variable with integer values. Finally, we describe lasso feature selection used in our proposed method.
2.1. Multiple regression
Multiple regression is a simple and commonly used technique used for predicting the unknown value of a dependent variable $Y_t$ from the known explanatory variables (predictors) $X_1, ..., X_k$ . The dependent variable in multiple regression is:
|
$Y_t = \beta_0 + \beta_1 X_{1t} + ... + \beta_k X_{kt} + \varepsilon_t, $
|
where $\varepsilon_t$ is the error, often assumed to be standard normally distributed. Coefficients $\beta_1, ..., \beta_k$ can be estimated using least squares to minimize sum of errors [4].
Multiple regression can be used to model a relationship between the dependent variable (e.g., restaurant sales) and external variables such as disposable income, the consumer price index (CPI), unemployment rate, etc. An advantage of using Multiple Regression for predicting restaurant demand is that a simple relationship between the explanatory variables and future demand can be found. However, a drawback of using this kind of model is that the relationship found between the dependent and independent variables may be superfluous or the regression coefficients can change over time, causing the need for constant update, or a complete redesign of the model. Further, problems may arise when the number of predictors becomes larger than the number of available data. In such cases, efficient methods such as least angle regression (LAR) [2] can be used to estimate optimal regression coefficients corresponding to the predictors that are most correlated with the dependent variable.
An example of using multiple regression is presented in [9]. The purpose of this study was to identify the most appropriate method of forecasting meal counts for an institutional food service facility. The result of the paper showed that multiple regression was the most accurate forecasting method comparing to naive models, moving averages, exponential smoothing methods, Holt's and Winter's methods, and linear regression.
Also in [8] a multiple regression model was used for predicting future sales in the restaurant industry. The authors considered macroeconomic factors such as percentile change in the CPI, in food away from home, in population, and in unemployment. They collected data from 1970 to 2011 from a variety of sources, including the National Restaurant Association (NRA), the United States Department of Agriculture (USDA), the Bureau of Labor Statistics, and the US Census Bureau. The model, trained and tested on aggregated data from the past 41 years, appears to have reasonable utility in terms of forecasting accuracy.
Some regression models used to forecast weekly sales at a small campus restaurant were described in [3]. The results of experiments showed that a multiple regression model with two predictors, a dummy variable and sales lagged one week, was the best forecasting model considered.
Regression model was also used in a specific situation described in [7], where the restaurant was open and close during different times of the week or year.
2.2. Poisson regression
When the dependent variable takes on integer values (for example restaurant guest count) Poisson regression can be used. This technique is one from a family of methods known as the generalized linear model (GLM). The foundation for Poisson regression is the Poisson distributed likelihood and the natural logarithm link function:
|
$ln(Y) =\beta_0 + \beta_1 X_{1} + ... + \beta_k X_{k}, $
|
where $X$ is the predicted guest count, $X_{1}, ..., X_{k}$ are the specific values on the predictors, $ln$ refers to the natural logarithm, $\beta_0$ is the intercept, and $\beta_i$ is the regression coefficient for the predictor $X_i$ .
The method is used e.g., in [1], [11] and [10], where authors noticed that Poisson Regression can be used to predict the number of customers being served at a restaurant during a certain time period.
2.3. Lasso
In multiple regression, the coefficients are estimated by the least squares estimator
|
$\hat{\beta} = {\arg_{\beta} \min} \sum\limits_i^N (y_i - \hat{y_i}(\beta))^2.$
|
The lasso introduces a constraint in the above optimization problem $\sum_{j=1}^k|\beta_j| < \tau$ for some $\tau$ and $k$ independent variables. The consequence is that some of the coefficient will be exactly zero if $\tau$ is chosen to be small enough. The above constraint can be formalized as an $L_1$ regularizer
|
$\hat{\beta}^{lasso} = {\arg_{\beta} \min} \sum\limits_i^N (y_i - \hat{y_i}(\beta))^2 + \lambda \sum\limits_{j=1}^k|\beta_j|, $
|
where $\lambda$ is a Lagrange multiplier, or the regularization strength. If each independent variable is orthonormal to each other, it can be shown that
|
$\hat{\beta_j}^{lasso} = \textrm{sign}(\hat{\beta}_j)(|\hat{\beta}_j|-\lambda)^+, $
|
where the function $(a)^+ = a$ if $a>0$ and 0 otherwise. It is clear that the regularization strength $\lambda$ controls the number of non-zero coefficients. For $\lambda = 0$ , the lasso coefficients are the same as the multiple regression ones.
3. Data description
We study transaction data collected from a chain restaurant. The database contains hundreds of tables describing more than 60 individual stores mounted to 350 GB. The data is collected from February 1, 2010 to February 23, 2015. Among the restaurants in the database, some stores have closed and some stores either do not have any transaction data collected in the database, or have incomplete transaction data. Also, certain stores had been open only recently, and the data provided for such stores are insufficient for analysis, therefore we do not consider such stores for training or testing purposes. In total, we study 52 stores under this chain restaurant for our predictive modeling purposes.
In the restaurant database, we consider the following information of interest: business date for each transaction for each store, number of guests for each transaction for each store, areas of the restaurant (dining, lounge, patio or bar), related guest count for each area, and related guest count for each business hour.
For each existing business date related to a particular store, the feature count indicates the number of guests within a certain period of time. Daily guest count is obtained from the sum of all these count on a given day. We ignore negative count, and count whose values are zero but with positive paid cheque amount. There are no missing data for the guest count data for each store. Note that some stores may not have guest count data for every business date. This might be due to reasons such as renovations. Also note that most of the stores do not operate on Christmas day, but a few stores do open on Christmas day.
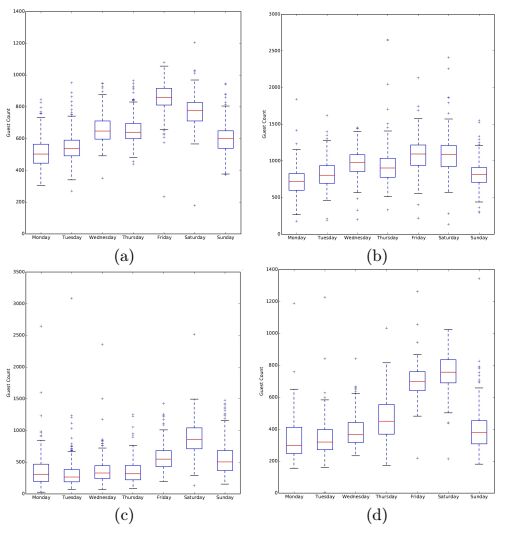
Finally, the distribution of guest counts over the week can be different for each store. This is shown in Figure 1 with boxplots showing the average guest count in each day of the week in four of the restaurants.
3.1. Data preprocessing
In order to predict guest count per day per store, we first exported all daily guest counts for every store. We do not consider stores that have already closed, or stores without guest count data in the database. For training the model, we use all guest count data between the year 2010 to 2013. For testing the model, we consider all guest count data in the year 2014.
3.2. Feature construction
The number of guest count may depend not only on the store's historical data, but also on external factors, such as daily weather, holidays, sports events, locations, customer reviews and so on. In order to model the prediction problem precisely, we consider a combination of both internal features from within the database and external features.
3.2.1. Internal Features
Internal features include business date, store ID, and daily guest count. These features can be obtained from the database directly. In addition to the above 3 internal features, we created 19 boolean features indicating the 7 days of the week, and the 12 months of the year according to the business date. For example, given a business date of 2013-11-18, which is a Monday in the month of November, the value for feature Monday is set to be 1, and the value for feature November is set to be 1 as well. The rest of the 17 boolean features such as Tuesday, Wednesday, ..., Sunday, January, February, ..., December are set to be 0.
● Trend Indicators
The guest count number could be affected by the recent trend or promotions of the store. Although we do not have promotion information in the database, the effect of a recent promotion or event could likely last for a week or two. We consider the historical guest count from 7 days ago, and guest count from 14 days ago as trend indicators. The values for the two trend features are obtained directly from the database.1
1 We have performed experiments to study also using the guest count from 21 days ago as a feature, and the results indicate that the most influential trend features are the guest count from 7 days ago and 14 days ago. Note that we also run experiments using the guest count from 1, 2, 3, 4 days ago. But using data from 1, 2 or 3 day ago is not always practical for restaurant's manager since they might not know the most recent guest count immediately; and data from 4 days ago did not improve accuracy of the model.
3.2.2. External Features
We found that external features affect the volume of guest counts. For example, in a sunny summer day, there are more guests observed. On Mother's day or Father's day, more guests are also recorded. The external features used for the analysis are discussed below.
● Holiday Data
We considered official holidays such as Canada Day and Easter, and unofficial holidays such as Mother's day, Father's day, St.Patrick's day, as boolean features indicating holidays. Since holidays such as Christmas would have a large impact on the restaurant revenue, we constructed two additional features covering the holiday period as Christmas before which indicates whether the business date falls on one week before Christmas, and Christmas time which indicates whether the business date is inbetween Christmas and New Year. There are total of 23 boolean features created for Canadian holidays, and 10 boolean features for American holidays. Canadian holidays were obtained from http://www.statutoryholidays.com. American holidays were obtained from http://www.officeholidays.com/countries/usa/.
● Weather Data
Local weather plays an important role for guests to decide whether one would like to go for a restaurant. Sunny days and rainy days affect the guest count in different ways. For Canadian cities, the historical weather data is obtained from http://climate.weather.gc.ca. For American cities, the historical weather data is from http://www.usclimatedata.com. Note that the historical weather data for American cities have missing values. We have used the values from the previous day to assign the missing values. We considered the amount of rainfall and the amount of snow fall in our model. For cities that have data for the total amount of precipitations instead of rainfall or snowfall separately, we used the temperature as an indication to assign the values for rainfall or snowfall. If the temperature is below or equal to zero, then the precipitation value is considered as snowfall value; if the temperature is above zero, then the precipitation value is assigned to rainfall value.
Since temperature is a strong indicator for weather, we would like to magnify the effects of the local weather. We constructed two additional weather features, diff_high_3 and diff_low_3. diff_high_3 is the cube of the difference between the daily highest temperature and the historical highest temperature of the month. diff_low_3 is the cube of the difference between the daily lowest temperature and the historical lowest temperature of the month. The historical highest and lowest temperatures of a given month for any city were obtained from https://www.wikipedia.org.
● Sports event Local sports events could affect the guest count as well. For these features, we constructed two sets of boolean features for Canadian restaurants and American restaurants. For Canadian restaurants, we considered hockey, NBA, CFL, soccer and Super Bowl events, and created 7 sports related features. For hockey events, we constructed 2 boolean feature to indicate whether the city in which the store is located is a home-playing city or a visiting city. For other sports events, we used the boolean values to indicate whether the event happened on a given business date. For American restaurants, we constructed 7 features including hockey, MLB, NBA, NFL and Super Bowl.
In total, 58 features were constructed for Canadian stores and 47 features were constructed for American stores.
4. Model
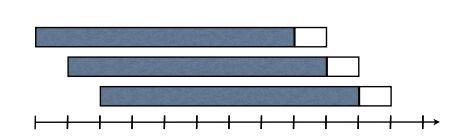
The data can exhibit seasonal variations. We treat the data as a time series and implement a sliding window approach to alleviate the effects of temporal variations in the data. The sliding window consists of training data taken from the previous eight weeks, for instance, giving a set of coefficients for the linear model which are used to give prediction of the guest count in the following week. Then, the sliding window moves one week forward and the procedure is repeated until the whole data set is processed. Mathematically, suppose that at time $t$ , where $t$ is an integer, the training data from the previous weeks is $(X_{train}(t), Y_{train}(t))$ , with $X$ being the features and $Y$ being the response, i.e. the guest count. The one week testing data is denoted as $(X_{test}(t+1), Y_{test}(t+1))$ . The estimated guest count $\hat{Y}(t+1)$ is obtained from the regression coefficients $\beta_t$ such that $\hat{Y}(t+1) = \beta_t X_{test}(t+1)$ . Figure 2 shows this scheme. The assumption made here is that the regression coefficients for the next week is similar to the ones estimated over the past eight weeks.
A common caveat of using a sliding window is data sparsity. When the window size is small, the sample size in the training set can be smaller than the number of features and feature selection is required to reduce the number of features. To this end, we employ the least angle regression (LAR) method with lasso feature selection on each sliding window. The number of features selected by lasso is related to the lasso regularization strength, which is tuned to be $\lambda = 0.3$ for a window size of eight weeks. The LAR training procedure is outline as follows. First, starting with $\beta_i = 0$ for all feature $i$ and let $x_k$ be the feature most correlated with the residual, $r = Y_{train}(t)- \hat{Y}_{train}(t)$ . The corresponding $\beta_k$ is moved towards its least squares value, given by $\langle r, x_k \rangle$ for normalized features, where the brackets denote the dot product. This continues until the correlation of some other features $\langle r, x_m \rangle$ , $m \neq k$ becomes equal to $\langle r, x_k \rangle$ . When this happens, both $\beta_k$ and $\beta_m$ are moved towards their joint least squares value. This is repeated until all variables are included in the model. We denote the implementation of least angle regression with sliding windows and lasso feature selection as SW-LAR-LASSO. The algorithmic scheme is as follows.
SW-LAR-LASSO
At time $t$ , suppose $S$ is the window size in units of weeks, $X(t)$ be the features at week $t$ and $Y(t)$ be the guest count.
1. Obtain training data $D_{train}(t) \leftarrow (X(\alpha), Y(\alpha))$ , where $\alpha \in [t-S+1, t] $
2. Obtain regression coefficients with LAR (LASSO), $\beta_t \leftarrow LAR(D_{train}(t))$
3. Estimate guest counts of next week, $\hat{Y}(t+1) \leftarrow \beta_t X(t+1)$
4. Calculate error for week $t+1$ , $r(t+1) \leftarrow |\hat{Y}(t+1) - Y(t+1)|$
5. Increment $t \leftarrow t+1$ and go to step one until all data have been processed.
5. Experiments
We employ regression models with Python 2.7.9 to estimate daily guest counts. For each restaurant, a regression model for its daily guest count is built.
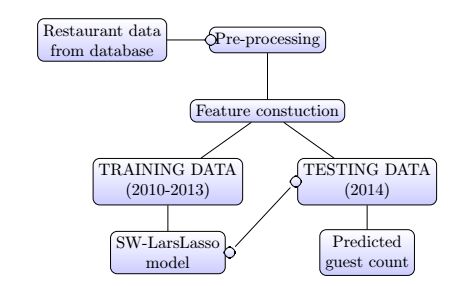
The dataset is first exported from the restaurant database. After pre-processing and feature construction, the dataset is separated into a training set and a testing set. Regression algorithms are then applied to the training data, and the models buit are evaluated on the testing data. Figure 3 shows the experimental process.
The following metrics were used for evaluation the prediction results:
|
${\rm{Mean}}\;{\rm{absolute}}\;{\rm{error}}\;({\rm{MAE}}) = \frac{{\sum\limits_{i = 1}^n | {p_i} - {a_i}|}}{n},$
|
|
${\rm{Average}}\;{\rm{daily}}\;{\rm{guest}}\;{\rm{count}}\;({\rm{AGC}}) = \frac{{\sum\limits_{i = 1}^n {{a_i}} }}{n},$
|
|
${\rm{Prediction}}\;{\rm{Error}}\;{\rm{Rate}} = {\rm{MAE/AGC}},$
|
where $n$ is the number of days in 2014 that are being predicted, $p_i$ ( $1 \le i \le n$ ) is the predicted guest count, $a_i$ is the actual guest count.
As a first evaluation, we tested the predictive accuracy of commonly used algorithms for this problem: multiple regression, decision trees, neural networks, association rules, and poisson regression. We found that multiple regression and poisson regression outperforms the other methods investigated. We found that multiple regression was the most efficient and we chose this method to build our algorithm upon. The resulting algorithm, SW-LAR-LASSO, is described in the last section.
We found that SW-LAR-LASSO outperforms multiple regression by a significant margin, especially in those stores located in the United States, where the improvement in predictive error can be as much as 3 percentage points. This is shown in Table 1. For instance, for store_6 and store_7, multiple regression gives 18.62 % and 16.02 % in predictive error. Whereas for SW-LAR-LASSO the errors are 15.60 % and 12.89 %, respectively. The comparison validates that temporal variations exist in the data. Most importantly, SW-LAR-LASSO is able to predict guest counts accurately in new store locations, where historical data is limited. For example, the data for store_9 and store_10 % Miami, FL are not sufficient for multiple and Poisson regression. Whereas for SW-LAR-LASSO, using an eight week sliding window, we obtained results with a predictive error of 22.57 % and 14.68 %, respectively. Overall, a predictive error of 12.01 % was obtained by SW-LAR-LASSO for daily guest counts over 52 locations. Using multiple regression for the same data we obtained 12.09 %. Some of results for the individual stores in Canada and United States2 are presented in table 1.
Table 1. Table of results from chosen stores. The bolded results denote the lowest predictive error among the three algorithms tested.
| Benchmark Stores | Multiple regression | Poisson regression | SW-LAR-LASSO | localization |
| Store_1 | 7.88 | 8.28 | 8.40 | Canada stores |
| Store_2 | 15.56 | 16.71 | 15.00 |
| Store_3 | 10.20 | 10.86 | 10.25 |
| Store_4 | 13.15 | 14.51 | 12.86 |
| Store_5 | 10.50 | 11.44 | 10.25 |
| Store_6 | 16.04 | 17.66 | 14.19 | US Stores |
| Store_7 | 18.62 | 24.37 | 15.60 |
| Store_8 | 16.02 | 15.69 | 12.89 |
| Store_9 | -- | -- | 22.57 |
| Store_10 | -- | -- | 14.68 | |
2 Note that for confidentiality reasons, we do not list the names and the locations of the stores.
In summary, we have the following observations. First, the trend indicators (guest count from 7-days ago and 14-days-ago) are very effective in improving prediction precisions. Second, SW-LAR-LASSO proves to be the best predictive model for our task, in terms of both precision and efficiency. The majority of the stores perform better with SW-LAR-LASSO algorithm comparing with multiple regression and Poisson regression.
6. Conluding remarks
Demand forecasting plays an essential role in planning operations for restaurant's management. Having reliable predictions for guest counts is the basis for other analysis. Among many different forecasting techniques, our method which captures temporal changes in the data performs better. Moreover SW-LAR-LASSO algorithm is applicable to new stores where the historical data set is small. Thus, this algorithm can be applied not only to restaurant data, but also to other areas where temporal variations exist in the data.









 DownLoad:
DownLoad: