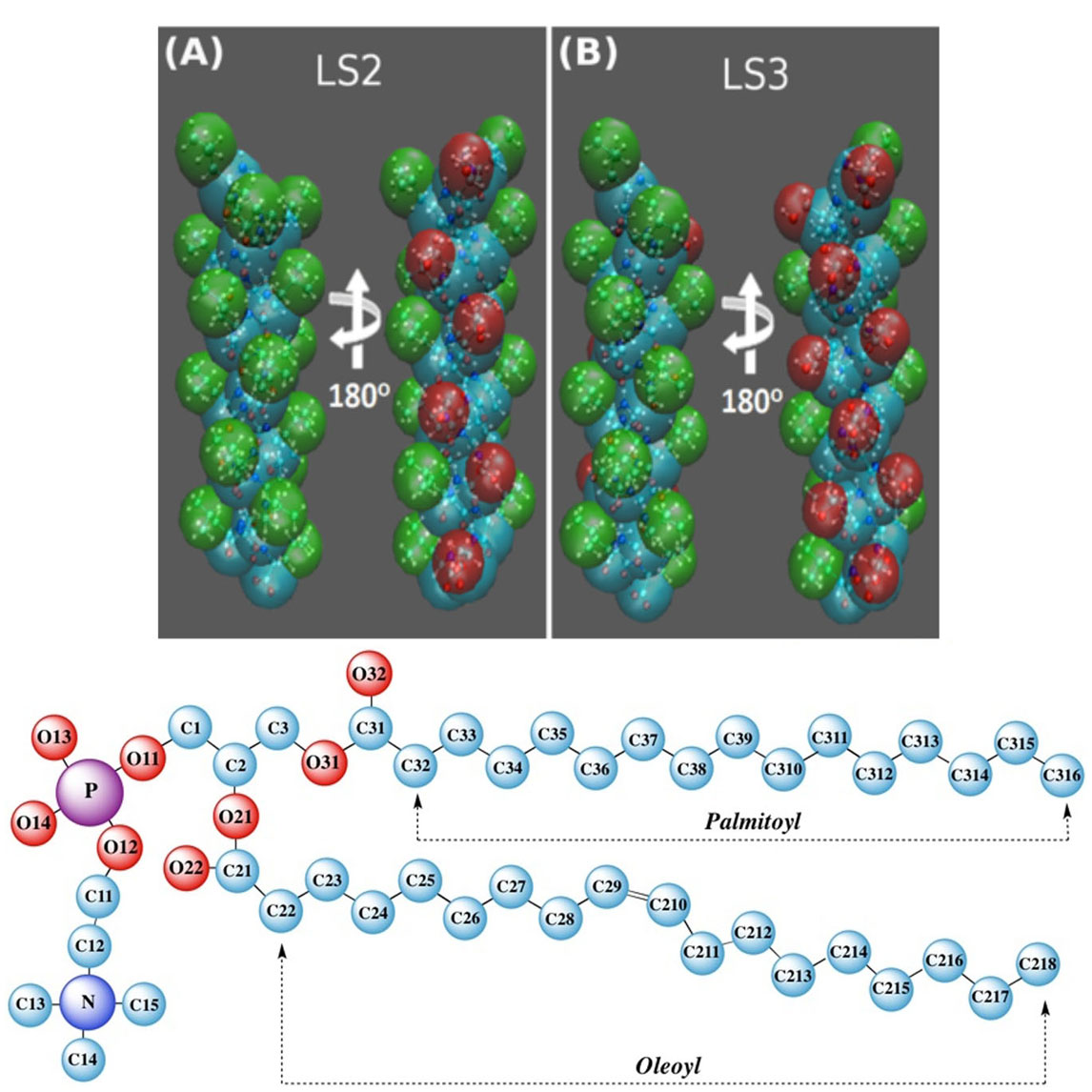
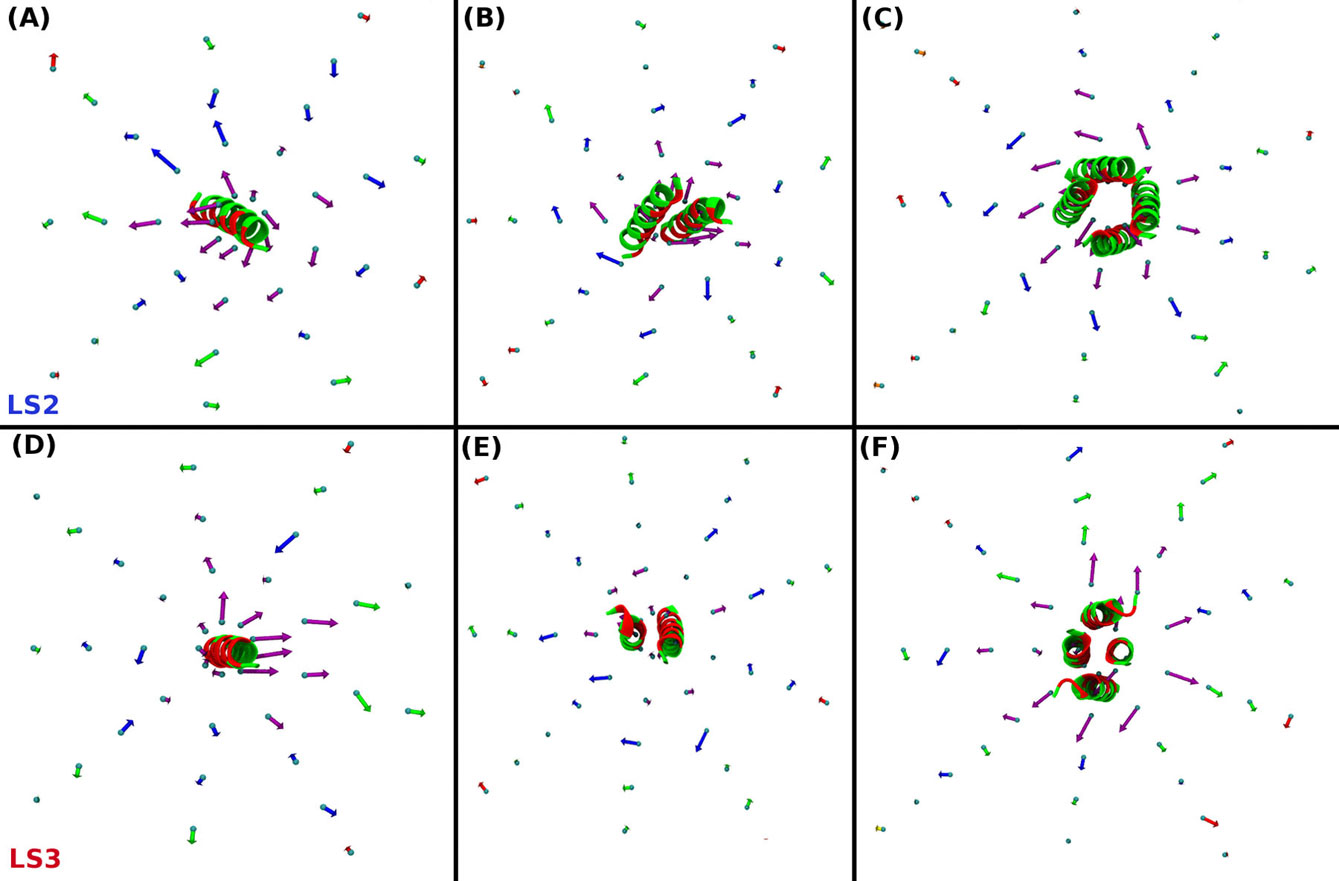
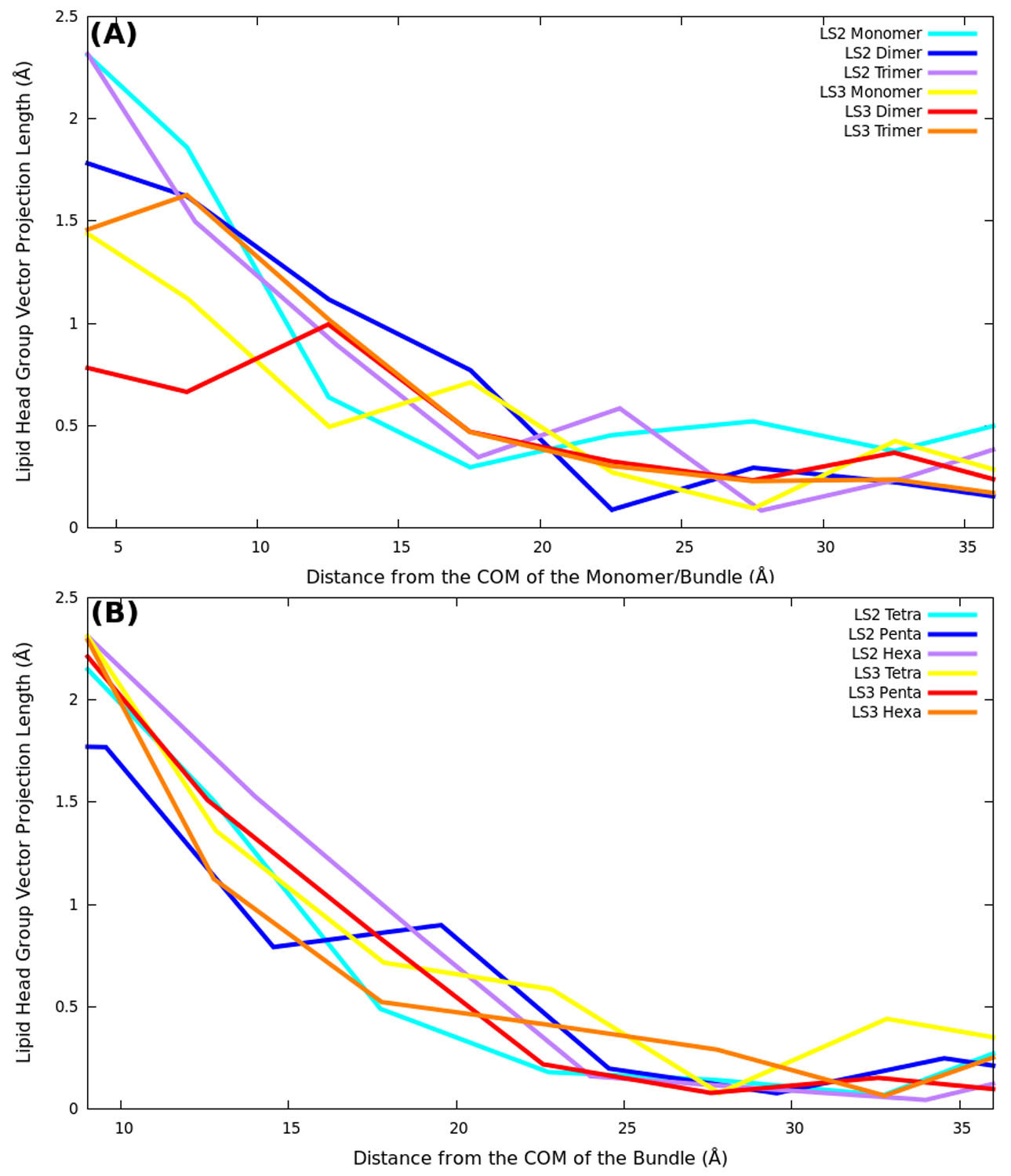
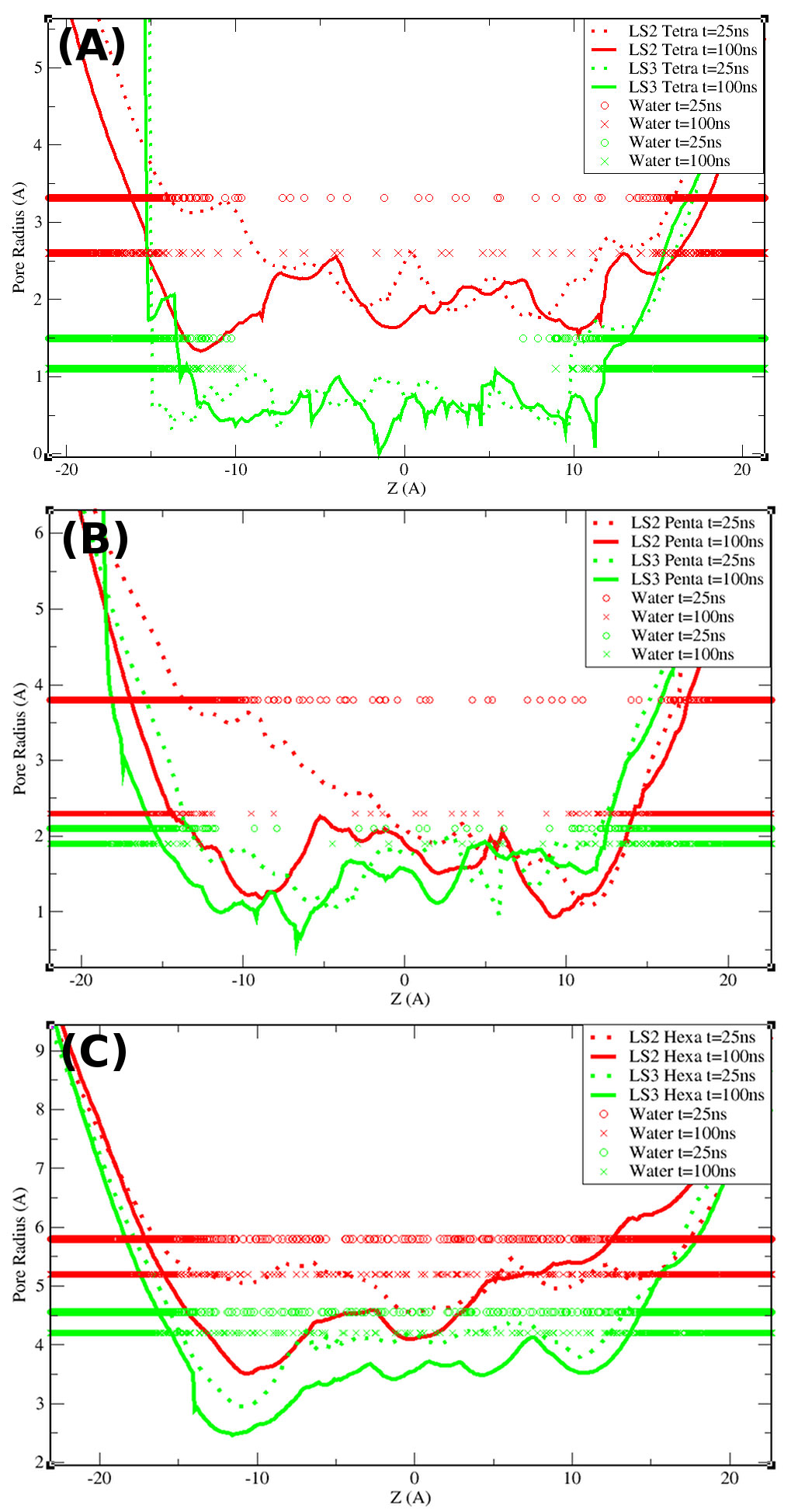
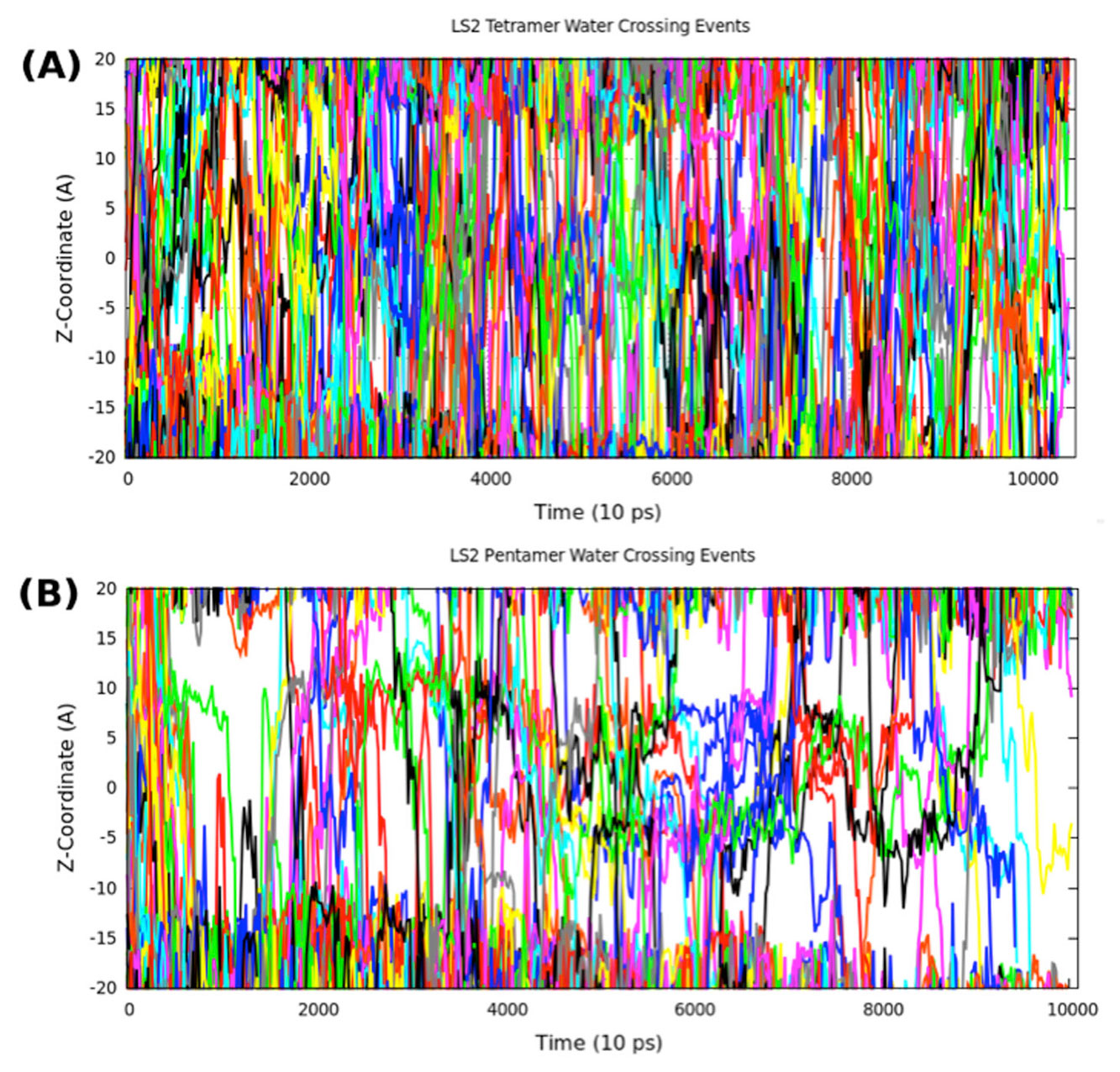
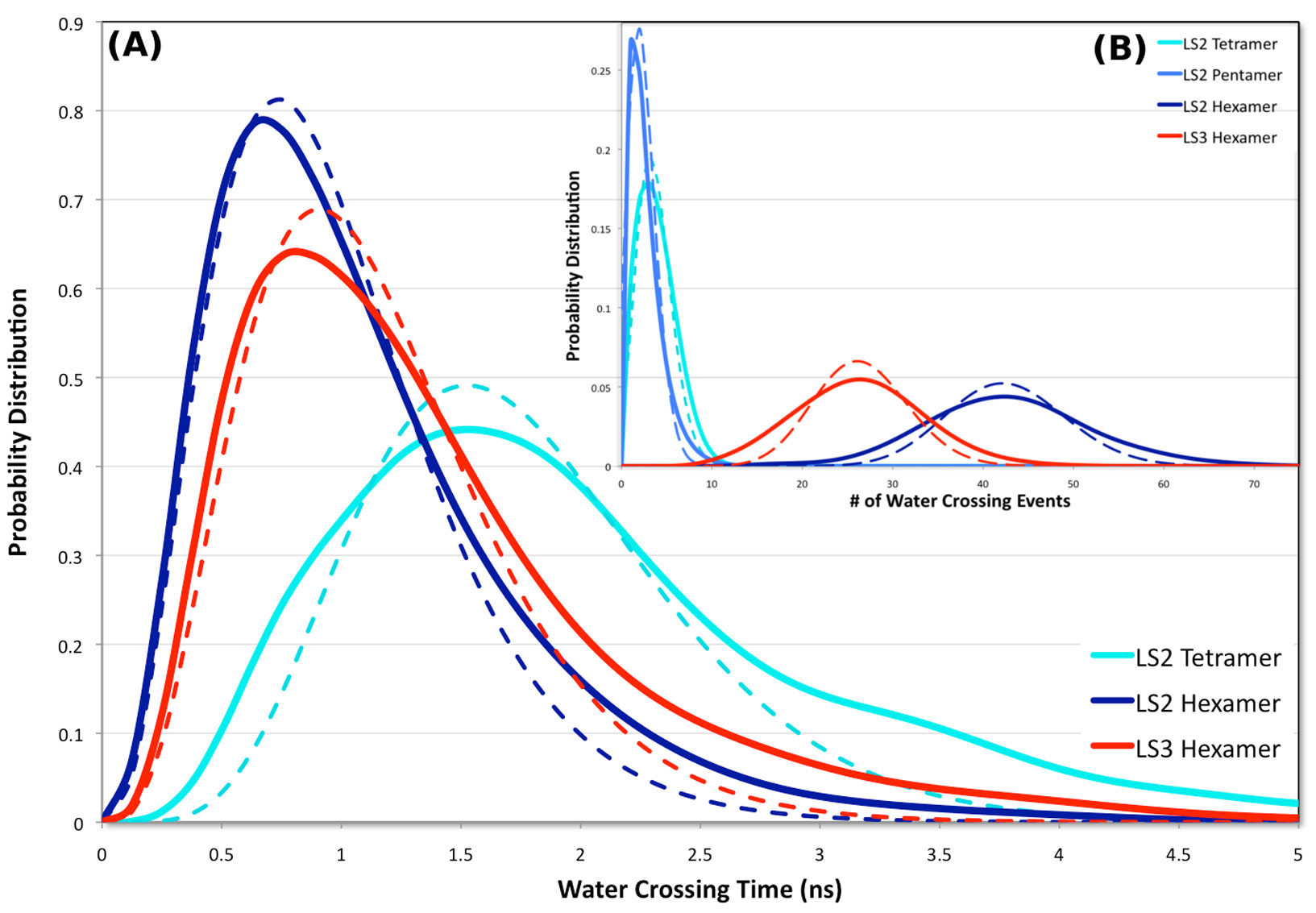
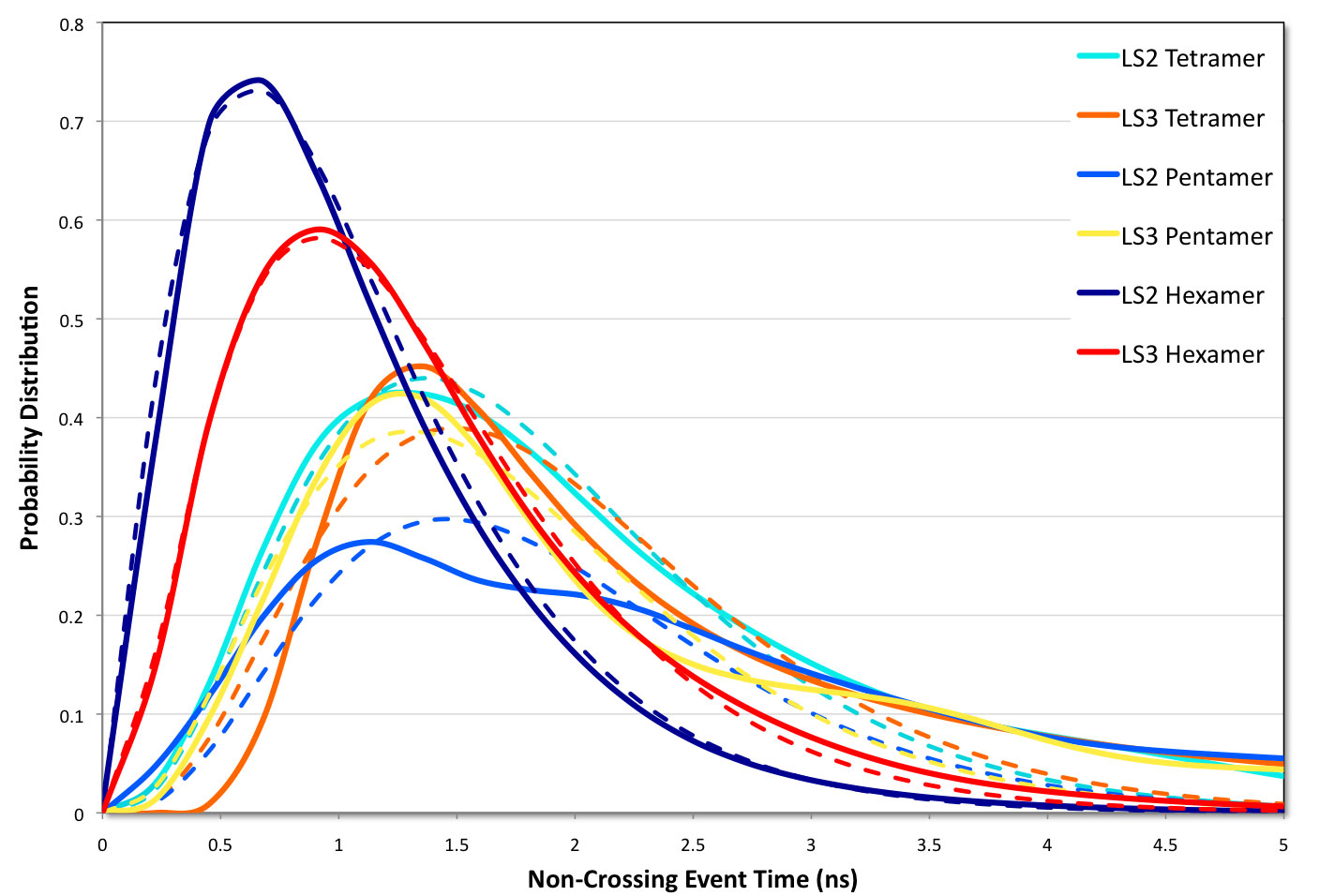
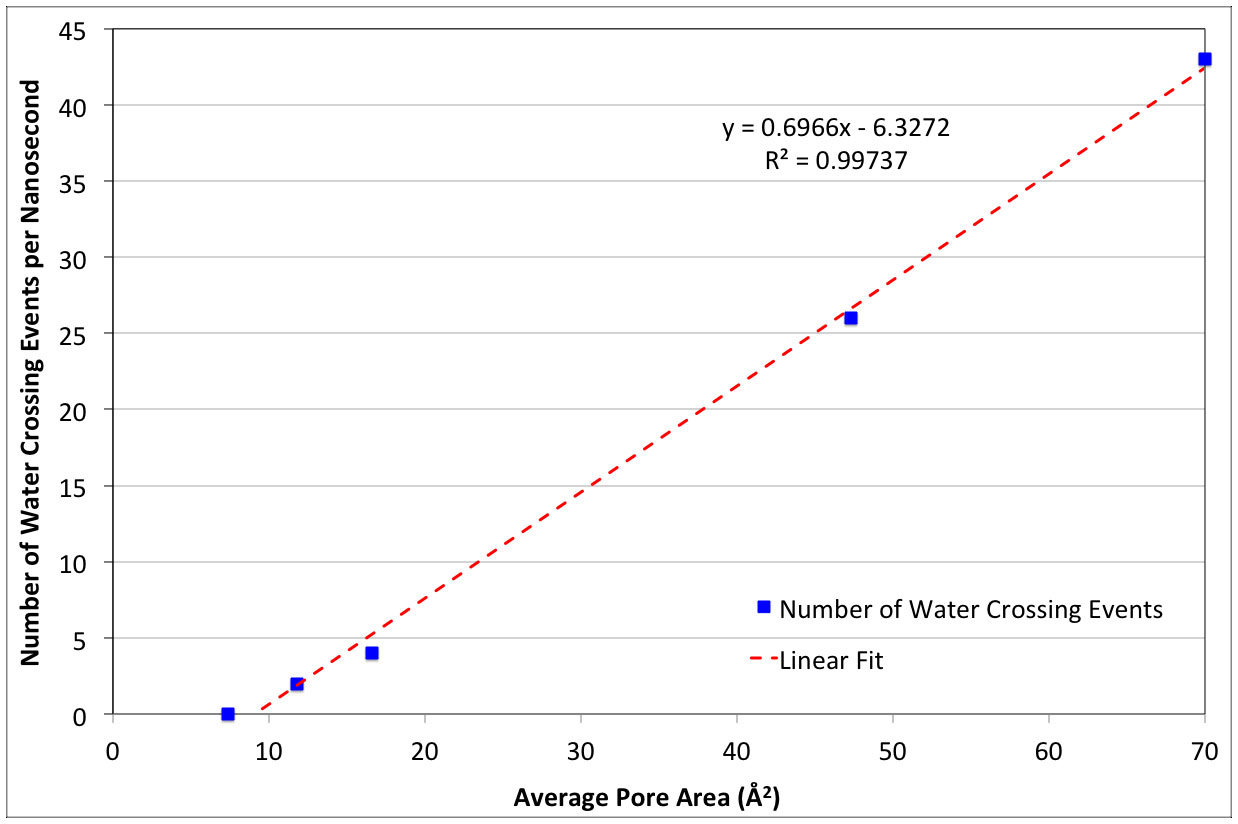
Molecular dynamics study of homo-oligomeric ion channels: Structures of the surrounding lipids and dynamics of water movement

1.   Introduction

The dynamic relationship between prey and predator has been one of the most interesting topics in the qualitative theory of population dynamics ^[1,2]. For example, Bazykin ^[2] considered a prey-predator system with the bounded functional response:

where $ u $ and $ v $ represent the densities of the prey and predator, respectively. Here, $ a $, $ b $, $ k $ and $ m $ are positive constants. The predator consumes the prey based on the prey-dependent functional response $ u/(1+mu) $, and the term $ -bv^2 $ represents the self-limitation for the predator. The above model takes account of not only the interspecies interactions between the prey species and predators, but also the density dependence of predator species.

Recently, there is much evidence from biology and physiology to show that in many situations, especially when predators have to search, share or compete for food, the modeling and analysis of predator-prey systems for each specific case should be further developed according to the ratio-dependent theory ^[3,4,5], which can be roughly stated as that the per capita predator growth rate should depend on the ratio of prey to predators, but not just prey numbers, so it should be the ratio-dependent function response ^[6,7,8,9], i.e., a function of $ u/v $. On the basis of this consideration, substituting $ \frac{u/v}{1+mu/v} $ for $ \frac u{1+mu} $ in the above-mentioned model (1.1), we arrive at the following system:

If $ ma < 1 $, system (1.2) has a unique positive equilibrium $ \widetilde{\textbf{w}} = (\tilde{u}, \tilde{v})^\mathit{T} $, where

Taking into account the inhomogeneous distribution of predator and prey populations in different spatial locations, in this study we will incorporate diffusion and cross-diffusion to system (1.2) and consider a more general system:

where $ \Omega $ is a fixed bounded domain with the sufficient smooth boundary $ \partial\Omega $ in $ \mathbb{R}^N $, $ \nu $ is the outward unit normal vector of the boundary $ \partial\Omega $, and $ \Delta $ is the Laplace operator. The positive constants $ d_{1} $ and $ d_{2} $ are the random diffusion coefficients of prey and predator, respectively, which describe the natural dispersive forces of random movement of individuals. Here, $ d_{12} $ and $ d_{21} $ are the cross-diffusion coefficients that express population fluxes of preys and predators due to the presence of other species ^[10,11,12]. The non-flux boundary condition indicates that the system is self-contained with no external energy exchange. For more related studies on dynamics of population models with diffusion and cross-diffusion, we refer the reader to ^{[12,13,14,15,16,17]} and references therein.

One of our motivations of this study lies in a fact that, in the past few decades there have been continuous interests in the existence of positive steady states of diffusive predator-prey systems, and the majority of works have devoted to discovering the effect of diffusion on positive steady states ^{[18,19,20,21,22,23,24]}. However, little attention has been paid to the case that both diffusion and cross-diffusion are present in population systems ^{[25,26,27,28]}. Therefore, the main purpose of this paper is to make an attempt on the existence and non-existence of non-constant positive steady states of system (1.4). The corresponding steady-state equations of system (1.4) are:

This paper is organized as follows. In Section 2, we discuss a priori estimate of the positive steady state for system (1.4), that is, a priori upper and lower bounds for positive solutions of the elliptic system (1.5). In Section 3, we investigate the existence and non-existence of non-constant positive solutions of system (1.5). In particular, the impact of diffusion and cross-diffusion on the existence of non-constant positive steady states is explored.

2.   A priori estimates

In this section, to establish a priori estimates of upper and lower bounds of positive solutions for system (1.5) in a straightforward manner, we need the following two lemmas.

Lemma 2.1. [22,Maximun Principle] Assume that $ g\in C(\overline{\Omega} \times \mathbb{R}^1). $

$ \rm{(i)} $ If $ \omega \in C^2(\Omega)\cap C^1(\overline{\Omega}) $ satisfies $ \Delta \omega(x)+g(x, \omega(x))\geq 0, \ x\in \Omega; \frac{\partial \omega}{\partial \nu}\leq 0, \ x\in \partial\Omega $; and $ \omega(x_{0}) = \max \limits_{\overline{\Omega}} \omega $, then $ g(x_{0}, \omega(x_{0}))\geq 0 $.

$ \rm{(ii)} $ If $ \omega \in C^2(\Omega)\cap C^1(\overline{\Omega}) $ satisfies $ \Delta \omega(x)+g(x, \omega(x))\leq 0, \ x\in \Omega; \frac{\partial \omega}{\partial \nu}\geq 0, \ x\in \partial\Omega $; and $ \omega(x_{0}) = \min \limits_{\overline{\Omega}} \omega $, then $ g(x_{0}, \omega(x_{0}))\leq 0 $.

Lemma 2.2. [27,Harnack's Inequality] Suppose that $ c(x)\in C(\overline{\Omega}) $. Let $ \omega(x)\in C^2(\Omega) \cap C^1(\overline{\Omega}) $ be a positive solution to

Then there exists a positive constant $ C_{\ast} = C_{\ast}(\|c(x)\|_{\infty}, \, \Omega) $ such that

In the following, the positive constants $ C_{1} $, $ C_{2} $, $ C_1^* $, $ C_2^* $, $ c_1 $ and $ c_2 $ will rely upon the domain $ \Omega $. However, while $ \Omega $ is fixed, we will not mention this dependence explicitly. Also, for convenience, we shall write $ \Lambda $ instead of the set of constants $ (a, b, m, k) $ in the sequel.

Theorem 2.1. [Upper Bounds] Suppose that $ \frac{d_{12}}{d_{1}}\leq D $ and $ \frac{d_{21}}{d_{2}}\leq D $ for an arbitrary fixed number $ D $. Then there exist positive constants $ C_{i} = C_{i}(D, \Lambda) $, $ i = 1, 2 $, such that the positive solution $ (u, v) $ of system (1.5) satisfies

Proof. Set $ \phi = d_{1}u+d_{12}v $ and $ \psi = d_{21}u+d_{2}v $. Then the problem (1.5) becomes

Let $ x_{1}\in \overline{\Omega} $ be a point satisfying $ \phi(x_{1}) = \max \limits_{\overline{\Omega}} \phi $. Applying Lemma 2.1 to the first equation of (2.2), we can obtain $ u(x_{1})\leq \frac 1 k $ and $ v(x_{1})\leq \frac{m}{k}(1-ku(x_1))\leq \frac{m}{k} $. Hence, we obtain

Analogously, let $ x_{2}\in \overline{\Omega} $ be a point satisfying $ \psi(x_{2}) = \max \limits_{\overline{\Omega}} \psi $. Using Lemma 2.1 to the second equation of (2.2), we have $ v(x_{2})\leq \frac{1-ma}{bm} $. Then we have

Before presenting the lower bound, we present the following lemma.

Lemma 2.3. Let $ ma < 1 $, $ d_{1, n}, \, d_{2, n}, \, d_{12, n}, \, d_{21, n} $ be positive constants, $ n = 1, 2, ..., $ and $ (u_{n}, v_{n}) $ be the positive solution of system (1.5) with $ d_{1} = d_{1, n}, \, d_{12} = d_{12, n}, \, d_{21} = d_{21, n} $ and $ d_{2} = d_{2, n} $. Suppose that $ (d_{1, n}, d_{2, n}, d_{12, n}, d_{21, n})\rightarrow (d_{1}, d_{2}, d_{12}, d_{21}) $, and $ (u_{n}, v_{n})\rightarrow (u^{\ast}, v^{\ast}) $ uniformly on $ \overline{\Omega} $. If $ u^{\ast} $ and $ v^{\ast} $ are positive constants, then $ (u^{\ast}, v^{\ast}) $ satisfies

That is, $ (u^{\ast}, v^{\ast}) = (\tilde{u}, \tilde{v}) $, is the unique positive constant solution of system (1.5).

Proof. It is clear that $ \int_{\Omega} u_{n}\left(1-ku_{n}-\frac{v_{n}}{mu_{n}+v_{n}}\right)dx = 0 $ holds for all $ n $. If $ 1-ku^{\ast}-\frac{v^{\ast}}{mu^{\ast}+v^{\ast}} > 0 $, then $ 1-ku_{n}-\frac{v_{n}}{mu_{n}+v_{n}} > 0 $ as $ n $ is getting large. However, $ u_{n} $ is positive, so this is impossible. Similarly, $ 1-ku^{\ast}-\frac{v^{\ast}}{mu^{\ast}+v^{\ast}} < 0 $ is impossible either. Hence, $ 1-ku^{\ast}-\frac{v^{\ast}}{mu^{\ast}+v^{\ast}} = 0 $. Using the same argument leads to $ -a-bv^{\ast}+\frac{u^{\ast}}{mu^{\ast}+v^{\ast}} = 0 $. Consequently, $ (u^{\ast}, v^{\ast}) = (\tilde{u}, \tilde{v}) $.

Theorem 2.2. (Lower Bounds). Assume that $ d $ and $ D $ are fixed positive constants. Then there exist positive constants $ c_{i} = c_{i}(d, D, \Lambda) $, $ i = 1, 2 $, such that when $ d_{1}, d_{2}\geq d $ and $ \frac{d_{12}}{d_{1}} $, $ \frac{d_{21}}{d_{2}}\leq D $, the positive solution $ (u, v) $ of system (1.4) satisfies

Proof. By a straightforward calculation, we have

and

Then, Lemma 2.2 indicates that there exist positive constants $ C_{1}^{\ast} = C_{1}^{\ast}(d, \Lambda) $ and $ C_{2}^{\ast} = C_{2}^{\ast}(d, \Lambda) $ such that $ \max \limits_{\overline{\Omega}} \phi \leq C_{1}^{\ast}\min \limits_{\overline{\Omega}} \phi $ and $ \max \limits_{\overline{\Omega}} \psi \leq C_{2}^{\ast}\min \limits_{\overline{\Omega}} \psi $. Thus we obtain

and

Now, we estimate the positive lower bounds of $ u $ and $ v $. Suppose that (2.5) is not true. Then there exists a sequence $ \{d_{1, n}, d_{2, n}, d_{12, n}, d_{21, n}\}_{n = 1}^\infty $ with $ (d_{1, n}, d_{2, n}, d_{12, n}, d_{21, n})\in [d, \infty)\times [d, \infty)\times (0, \infty)\times (0, \infty) $ such that the positive solution $ (u_{n}, v_{n}) $ of system (1.5) satisfies

and

For (2.8), it follows from the standard regularity theorem of elliptic equations ^[29] that there exists a subsequence of $ \{(u_{n}, v_{n})\}_{n = 1}^\infty $, still denoted by $ \{(u_{n}, v_{n})\}_{n = 1}^\infty $, and two nonnegative functions $ u, v\in C^2(\overline{\Omega}) $ satisfying $ (u_{n}, v_{n})\rightarrow (u, v) $ as $ n\rightarrow\infty $. Assume that $ (d_{1, n}, d_{2, n}, d_{12, n}, d_{21, n})\rightarrow (d_{1}, d_{2}, d_{12}, d_{21})\in [d, \infty)\times [d, \infty)\times (0, \infty)\times (0, \infty) $. In view of inequalities (2.6) and (2.7), it is easy to see that either $ \max \limits_{\overline{\Omega}} u_n\rightarrow0 $ or $ \max \limits_{\overline{\Omega}} v_n\rightarrow0 $, as $ n\rightarrow\infty $.

So, there are three possible cases.

If $ \max \limits_{\overline{\Omega}} u_n\rightarrow0 $ and $ \max \limits_{\overline{\Omega}} v_n\rightarrow0 $, then $ (u_{n}, v_{n})\rightarrow (0, 0) $ uniformly on $ \overline{\Omega} $, which is a contradiction to Lemma 2.3.

If $ \max \limits_{\overline{\Omega}} u_n\rightarrow0 $ and $ \max \limits_{\overline{\Omega}} v_n\rightarrow \overline{v} $, where $ \overline{v} $ is a positive constant. By integrating the second equation of system (2.8) in $ \Omega $, it gives

Then we get $ v_n\rightarrow-\frac{a}{b} $, which yields a contradiction to $ \overline{v} > 0 $. Hence, $ \min \limits_{\overline{\Omega}} u > 0 $.

Similarly, if $ \max \limits_{\overline{\Omega}} u_n\rightarrow \overline{u} $ and $ \max \limits_{\overline{\Omega}} v_n\rightarrow 0 $, where $ \overline{u} $ is a positive constant. By integrating the first equation of system (2.8) in $ \Omega $, it gives

Then $ \overline{u} = \frac 1k $. It implies that $ (u_{n}, v_{n})\rightarrow \left(\frac 1 k, 0 \right) $ uniformly on $ \overline{\Omega} $. Apparently, this leads to a contradiction to Lemma 2.3. Consequently, $ \min \limits_{\overline{\Omega}} v > 0 $.

3.   Non-constant positive steady states

In this section, we study the non-existence and existence of non-constant positive steady states of system (1.5).

3.1.   Non-existence of non-constant positive steady states

To consider the non-existence of non-constant solutions of system (1.5) in this subsection, for convenience, we denote

Theorem 3.1. Let $ d_{2}^* $ be a fixed positive constant and satisfy $ \mu_{1}d_{2}^* > \frac{1}{m} $, where $ \mu_1 $ is the least positive eigenvalue of $ -\Delta $ on $ \Omega $ under the Neumann boundary condition. Then there exists a positive constant $ D_{1} = D_{1}(\Lambda, d_{2}^*) $ such that when $ d_{1}\geq D_{1} $ and $ d_2\geq d_2^* $, system (1.5) with $ d_{12} = d_{21} = 0 $ has no non-constant positive solution.

Proof. Suppose that $ \textbf{w} = (u, v)^\mathit{T} $ is a positive solution of system (1.5). Let $ \tilde{\varphi} = \frac{1}{|\Omega|}\int_{\Omega}\varphi dx $ for any $ \varphi\in L^1(\Omega) $. Multiplying the first two equations of (1.5) by $ u-\tilde{u} $ and $ v-\tilde{v} $, respectively, and then integrating on $ \Omega $, by integration by parts we obtain

In view of Theorems 2.1 and 2.2, using Young's inequality to (3.1) we find

for some positive constant $ L $, where $ \varepsilon $ is the arbitrary small positive constant arising from Young's inequality.

Using Poincaré's inequality, we see that $ \mu_1\int_{\Omega}(u-\tilde{u})^2dx\leq \int_{\Omega}|\nabla u|^2dx $ and $ \mu_1\int_{\Omega}(v-\tilde{v})^2dx\leq \int_{\Omega}|\nabla v|^2dx $, where $ \mu_1 $ is the least positive eigenvalue of $ -\Delta $ on $ \Omega $ under the Neumann boundary condition. It follows from inequality (3.2) that

Choosing a sufficiently small $ \varepsilon_0 > 0 $ such that $ d_{2}^*\mu_{1}\geq \frac 1m+\varepsilon_0L $, and taking $ D_{1}\triangleq \frac 1{\mu_1}(1+\frac L{\varepsilon_0}) $, we arrive at the desired result $ (u, v) = (\tilde{u}, \tilde{v}) $.

3.2.   Existence of non-constant positive solutions

From the discussion in the preceding subsection, we know that when the cross-diffusion terms are absent, there might be no non-constant positive solutions for system (1.5). In this subsection, we shall discuss the existence of non-constant positive solutions of system (1.5) with respect to cross-diffusion coefficients $ d_{21} $ and $ d_{12} $ as the other parameters $ d_1 $ and $ d_2 $ are fixed by means of the Leray-Schauder degree theory.

To facilitate the discussion, we rewrite system (1.5) as

where $ \textbf{w} = (u, v)^\mathit{T} $, $ \mathit{\boldsymbol{\Phi}}(\textbf{w}) = (\phi, \psi)^\mathit{T} $, and $ \textbf{F}(\textbf{w}) = (f(u, v), \, g(u, v))^\mathit{T} $.

Let $ \textbf{X} = \left\{\textbf{w}\in \left[C^1(\overline{\Omega})\right]^2 \Big|\frac{\partial\textbf{w}}{\partial\nu} = \textbf{0} \ \text{on}\ \partial\Omega \right\} $, and define

where $ c $ is a positive constant that is guaranteed to exist by Theorems 2.1 and 2.2.

Assume that

Since $ \mathit{\boldsymbol{\Phi}}_{\textbf{w}}(\textbf{w}) = \left( $$\begin{matrix} d_{1} & d_{12}\\ d_{21} & d_{2} \end{matrix}$$ \right) $, the determinant $ \det \mathit{\boldsymbol{\Phi}}_{\textbf{w}}(\textbf{w}) $ is nonzero for all non-negative $ \textbf{w} $, $ \mathit{\boldsymbol{\Phi}}_{\textbf{w}}^{-1}(\textbf{w}) $ exists and $ \det\mathit{\boldsymbol{\Phi}}_{\textbf{w}}^{-1}(\textbf{w}) $ is of the same sign as $ \det\mathit{\boldsymbol{\Phi}}_{\textbf{w}}(\textbf{w}) $. Thus, $ \textbf{w} $ is a positive solution of system (3.3) if and only if

where $ (\textbf{I}-\Delta)^{-1} $ is the inverse of $ \textbf{I}-\Delta $ in $ \textbf{X} $ under the homogeneous Neumann boundary condition. Since $ \textbf{G}(\cdot) $ is a compact perturbation of the identity operator, for any $ \mathcal{B} = \mathcal{B}(c) $, the Leray-Schauder degree of $ \deg(\textbf{G}(\cdot), \textbf{0}, \mathcal{B}) $ is well-defined if $ \textbf{G}(\textbf{w})\neq 0 $ on $ \partial\mathcal{B} $.

Note that

where

We recall that if $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $ is invertible, the index of $ \textbf{G} $ at $ \widetilde{\textbf{w}} $ is defined by

where $ \gamma $ is the total number of eigenvalues of $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $ with negative real parts (counting multiplicities), then the degree $ \deg(\textbf{G}(\cdot), \textbf{0}, \mathcal{B}) $ is equal to the sum of the indices over all isolated solutions when $ \textbf{G} = \textbf{0} $ in $ \mathcal{B}(c) $, provided that $ \textbf{G}\neq \textbf{0} $ on $ \partial\mathcal{B} $.

Let $ 0 = \mu_{0} < \mu_{1} < \mu_{2} < \cdots $ be the eigenvalues of the operator $ -\Delta $ on $ \Omega $ under the homogeneous Neumann boundary condition and $ E(\mu_{i}) $ be the eigenspaces with respect to $ \mu_{i} $. Let $ \{\phi_{ij}; j = 1, 2, \cdots, \dim E(\mu_{i})\} $ be a set of orthonormal basis of $ E(\mu_{i}) $ and $ \textbf{X}_{ij} = \{\textbf{c}\phi_{ij}|\textbf{c}\in \mathbb{R}^2\} $.

Denote

Then

We refer to the decomposition above in the following discussions of the eigenvalues of $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $. We know that $ \textbf{X}_{ij} $ is invariant under $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $ for each $ i\in \mathbb{N} $ and each $ j\in [1, \dim E(\mu_{i})]\cap\mathbb{N} $, i.e., $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}})\textbf{w}\in \textbf{X}_{ij} $ for any $ \textbf{w}\in \textbf{X}_{ij} $. Thus, $ \lambda $ is an eigenvalue of $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $ on $ \textbf{X}_{ij} $ if and only if it is an eigenvalue of the matrix

Hence, $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $ is invertible if and only if the matrix

is non-singular for any $ i\geq 0 $.

Denote

We observe that if $ H(\mu_{i})\neq 0 $, then for each $ 1\leq j\leq \dim E(\mu_{i}) $, the number of negative eigenvalues of $ D_{\textbf{w}}\textbf{G}(\widetilde{\textbf{w}}) $ on $ \textbf{X}_{ij} $ is odd if and only if $ H(\mu_{i}) < 0 $.

We summarize our result as follows.

Theorem 3.2. Assume that the matrix $ \mu_{i}\bf{I}-\mathit{\boldsymbol{\Phi}}_{\bf{w}}^{-1}(\widetilde{\bf{w}}) \bf{F}_{\bf{w}}(\widetilde{\bf{w}}) $ is non-singular for an arbitrary $ i\geq 0 $. Then there holds

where $ \sigma = \sum \limits_{i\geq 0, \, H(\mu_{i}) < 0}\dim E(\mu_{i}) $.

According to the above Theorem, we need to consider the sign of $ H(\mu_{i}) $ in order to calculate the index of $ (\textbf{G}(\cdot), \widetilde{\textbf{w}}) $. In addition, by (3.6) we have

Hence, we need to consider the signs of $ \det\big\{\mathit{\boldsymbol{\Phi}}_{\textbf{w}}^{-1}(\widetilde{\textbf{w}})\big\} $ and $ \det \big\{\mu\mathit{\boldsymbol{\Phi}}_{\textbf{w}}(\widetilde{\textbf{w}})-\textbf{F}_{\textbf{w}}(\widetilde{\textbf{w}})\big\}, $ respectively.

By a direct calculation we get

where

Let $ \tilde{\mu}_{1} $ and $ \tilde{\mu}_{2} $ be the two roots of $ \mathcal{A}(\mu) = 0 $ with $ Re\{\tilde{\mu}_{1}\}\leq Re\{\tilde{\mu}_{2}\} $. Then $ \tilde{\mu}_{1}\tilde{\mu}_{2} = \frac C A $, which is of the same sign as $ A $.

Next, we discuss the dependence of $ \mathcal{A}(\mu) $ on $ d_{12} $ and $ d_{21} $, respectively. Due to the following limits:

it follows from (3.7) that

Note that the above two limits hold only when $ d_{12} $ (or $ d_{21} $) is chosen to be large enough. This is certainly possible if $ A = d_1d_2-d_{12}d_{21} < 0 $ for the fixed $ d_1 $ and $ d_2 $. In this case, we have

Based on the above analyses, in summary we obtain the following results.

Theorem 3.3. Assume $ A < 0 $. Then there exists a positive constant $ d_{12}^* $ such that when $ d_{12}\geq d_{12}^* $, both of the two roots $ \tilde{\mu}_{1}(d_{12}) $ and $ \tilde{\mu}_{2}(d_{12}) $ of $ \mathcal{A}(\mu) = 0 $ are real and satisfy

where

Theorem 3.4. Assume $ A < 0 $. Then there exists a positive constant $ d_{21}^* $ such that when $ d_{21}\geq d_{21}^* $, both of the two roots $ \tilde{\mu}_{1}(d_{21}) $ and $ \tilde{\mu}_{2}(d_{21}) $ of $ \mathcal{A}(\mu) = 0 $ are real and satisfy

where

The following theorem is regarding the existence of non-constant positive solutions to system (3.3) with respect to the cross-diffusion coefficient $ d_{12} $, while all of other parameters are fixed.

Theorem 3.5. Suppose that $ A < 0 $, and the parameters $ \Lambda $, $ d_{1} $, $ d_{2} $ and $ d_{21} $ are fixed. Let $ \bar{\mu} $ be given by (3.9). If $ \bar{\mu}\in (\mu_{n}, \mu_{n+1}) $ for some $ n\geq 1 $, and the sum $ \sigma_{n} = \sum\limits_{i = 1}^{n}\dim E(\mu_{i}) $ is odd, then there exists a positive constant $ d_{12}^* $ such that when $ d_{12}\geq d_{12}^* $, system (3.3) has at least one non-constant positive solution.

Proof. According to Theorem 3.3, there exists a positive constant $ d_{12}^* $ such that, if $ d_{12}\geq d_{12}^* $, then (3.10) holds and

It suffices to prove that for all $ d_{12}\geq d_{12}^* $, system (3.3) has at least one non-constant positive solution. By the way of contradiction, we assume that this is not true for some $ d_{12}\ (\geq d_{12}^*) $. By applying the homotopy invariance of the topological degree, we can see a contradiction explicitly.

For any fixed $ d_{12} $ that satisfies $ d_{12}\geq d_{12}^* $, we take $ \hat{d}_2\geq d_{2}^* $ and $ \hat{d}_1\geq D_1 $, where $ \mu_{1}d_{2}^* > \frac{1}{m} $ and $ D_{1} = D_{1}(\Lambda, d_{2}^*) $ are given by Theorem 3.1. For $ t\in [0, 1] $, we define

Consider the system

Then $ \textbf{w} $ is a non-constant positive solution of system (3.3) if and only if it is a positive solution of system (3.14) when $ t = 1 $. It is obvious that $ \widetilde{\textbf{w}} $ is the unique positive constant solution of system (3.14) for any $ t\in[0, 1] $. From (3.5), we know that for any $ t\in[0, 1] $, $ \textbf{w} $ is a positive solution of system (3.3) if and only if

Analogous to (3.6), we set

It is easy to see that $ \textbf{G}(1; \textbf{w}) = \textbf{G}(\textbf{w}) $ and

In particular, we obtain

where

More specifically, when $ t = 1 $, from (3.6) and (3.7) we have

where

and $ \mathcal{A}(\mu) $ is defined by (3.7).

According to (3.10), (3.13) and (3.15), we deduce that

Therefore, zero is not an eigenvalue of the matrix $ \mu_{i}\textbf{I}-\mathit{\boldsymbol{\Phi}}_{\textbf{w}}^{-1}(\widetilde{\textbf{w}}) \textbf{F}_{\textbf{w}}(\widetilde{\textbf{w}}) $ for any $ i\geq 0 $, and

is odd. It follows from Theorem 3.2 that

When $ t = 0 $, we have

where

and we use $ \mathcal{\hat{A}}(\mu) $ to represent $ \mathcal{A}(\mu) $ given in (3.7) under the restriction of $ d_{12} = d_{21} = 0 $. In this case, by Theorem 3.1 it implies that $ \textbf{G}(0; \textbf{w}) $ = 0 only has the positive constant solution $ \widetilde{\textbf{w}} $ in $ \textbf{X}^+ $. By a direct calculation we have

and so $ H(0, \mu_{i}) > 0 $ for all $ i\geq 0 $.

Discussing in the same manner, we can prove that

According to Theorems 2.1 and 2.2, there exists a positive constant $ c $ such that the positive solution of system (3.14) satisfies $ c^{-1} < u $ and $ v < c $ for any $ t\in[0, 1] $. Thus for any $ t\in [0, 1] $, there holds $ \mathit{\boldsymbol{\Phi}}(t; \textbf{w})\neq 0 $ on $ \partial\mathcal{B}(M) $. By the homotopy invariance of the topological degree, we have

Note that both $ \mathit{\boldsymbol{\Phi}}(1; \textbf{w}) = 0 $ and $ \mathit{\boldsymbol{\Phi}}(0; \textbf{w}) = 0 $ have the unique positive solution $ \widetilde{\textbf{w}} $ in $ \mathcal{B}(M) $. From (3.16) and (3.18) we get

which yields a contradiction with (3.19).

Processing in an analogous way as we just did in the proof of Theorem 3.5, we can obtain the following result regarding the existence of non-constant positive steady states for system (3.3) with respect to the cross-diffusion coefficient $ d_{21} $. So, we omit the proof.

Theorem 3.6. Suppose that $ A < 0 $, and the parameters $ \Lambda $, $ d_{1} $, $ d_{2} $ and $ d_{12} $ are fixed. Let $ \bar{\bar{\mu}} $ be given by (3.11). If $ \bar{\bar{\mu}}\in (\mu_{n}, \mu_{n+1}) $ for some $ n\geq 1 $, and the sum $ \sigma_{n} = \sum\limits_{i = 1}^{n}\dim E(\mu_{i}) $ is odd, then there exists a positive constant $ d_{21}^* $ such that when $ d_{21}\geq d_{21}^* $, system (3.3) has at least one non-constant positive solution.

Acknowledgments

This work is supported by NSF of China (No. 41575004) and UTRGV Faculty Research Council Award 1100127.

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.