Towards a robust algorithm to determine topological domains from colocalization data

1.   Introduction

The numerical experiment of Fermi, Pasta, Ulam and Tsingou (FPUT) in 1955 ^[18] has been of great influence to physics in many respects. The idea of the experiment was related to the role of chaos on the foundations of statistical mechanics. As chaotic systems are highly irregular, like stochastic ones, they lose memory of initial conditions rapidly, in agreement with ergodic hypothesis. In this perspective, the result of Poincaré about the non existence in Hamiltonian systems of first integrals of motion, other than the energy or those due to a particular symmetry, seems positive. In his early theoretical activity, Fermi generalised the result of Poincaré showing that in Hamiltonian systems with $ N > 2 $ degrees of freedom no smooth surface can divide the phase space into two regions containing invariant sets. From this correct result, Fermi deduced that non-integrable Hamiltonian systems are generically ergodic and, even in absence of a rigorous proof, the ergodic problem was considered basically solved. However, Fermi came back to the problem after the war with this numerical experiment, probably too much absorbed by the development of the just born quantum mechanics in the meanwhile.

With one of the first available computers, they investigated the dynamics of a simple system of springs and masses, where the force is only between nearest neighbours. The novelty consisted in the methodology (it was one of the first numerical studies), but also in the fact that the force was not linear. In the case of linear forces, it is known that the Hamiltonian of the system can be diagonalized, the eigenstates are linear waves, and there is no interaction between them, namely the initial energy distribution among the modes does not change over time. Fermi and collaborators wanted to test whether introducing a small nonlinear term in the equations of motion (they used quadratic, cubic and split-linear terms) would allow energy to spread among the linear modes, and attain equipartition, confirming the earlier idea of Fermi that ergodic hypothesis can be considered true, giving a dynamical justification to statistical mechanics. However, this was not the case and instead quasi-periodic motion was observed or, at most, just a few modes close to the ones initially excited were active for the whole simulation time.

The surprising results of FPUT generated a lot of interest, and sparked research that resulted in a large body of work, as witnessed by an excellent review ^[23]. In particular, even though ergodicity and chaos have been clarified to be largely irrelevant for statistical mechanics of macroscopic systems, that is when $ N\gg1 $ ^[30,33,35], the existence of solitons arise from a possible explanation of the FPUT phenomenology ^[46]. Moreover, the FPUT experiment was the first to show that numerical simulations are a powerful instrument to get physical insights of complex phenomena, and therefore an indispensable tool for theoretical progress. In parallel, at the same time, it was shown by mathematicians via the KAM theorem ^[25,28,31] that generic non-integrable Hamiltonian systems are not ergodic for small perturbations. This fundamental result showed that the first guess by Fermi was incorrect, even though in high dimensional systems ($ N > $ 2) the presence of KAM tori does not preclude chaotic orbits because of the Arnold diffusion mechanism.

Despite these outstanding developments and considerable efforts, a clear and exhaustive explanation of the FPUT problem is still lacking. In particular, while there is some consensus concerning the metastability picture ^[3,22], the precise mechanisms driving to equipartition on very long time-scales is still elusive. One crucial point is that studies have focused on peculiar initial conditions and the specific phenomena that emerge from them in the short or medium timescales. For example, in the original experiments and in most of the successive studies the initial conditions consisted in exciting the low-frequency modes ^[2], which leads to the formation of coherent nonlinear structures, that is solitons, at least in the short-time. Some attention has been focused also on high-frequency initial conditions and this led to the study of breathers. However, it is difficult to understand all these peculiar directions in one larger vision of the FPUT problem. The problem with generic initial conditions seems to be yet more relevant from a general perspective, as recognised in an important recent contribution ^[8].

In the present work, we propose a more unifying picture; therefore, we seek universality traits that can explain the dynamics in a way that is only weakly dependent on the particular microscopic processes of the nonlinear chain in consideration. For this reason, we will consider generic initial conditions that are randomly out of equilibrium, involving low and high modes. Moreover, we will use tools and methods of the so-called Wave Turbulence (WT) theory. Originally introduced in fluid dynamics, WT is a statistical mechanics theory of weakly interacting waves, and it has been recently applied in relation to one dimensional anharmonic chains. In some sense, our approach is in line with the recent results that have clearly showed that the $ \alpha $-FPUT chain is a perturbation of Toda lattice, which is an integrable system ^[1]. Our main claim is that the irreversible transfer of energy in the spectrum in a weakly nonlinear system is achieved by exact resonant wave-wave interactions. In the context of the FPUT system, this idea was around already in the sixties, see ^[19]. Such resonances are the base for the WT theory and are responsible for the phenomenon of thermalization.

In this paper we give an overview on resonances and WT in a comprehensive manner as well as present new results regarding the limit of a large number of modes, providing some insight in the fundamental mechanics of anharmonic chains. Our main result is the establishment of the power-law scaling of the equipartition time $ T_\text{eq} $ as a function of the nonlinearity strength (to be defined precisely later). In varying the number of elements in the chain, we show the crossover between two different scaling laws (lower exponent for large systems, that is the thermodynamic limit, steeper for smaller ones).

We remark that some of the ideas presented here have partially appeared in a series of papers by the same group of authors ^[5,36,41,42]. All the simulations presented on the $ \alpha $ and $ \beta $ FPUT problem are performed with a different class of initial conditions with respect to our previous work. Moreover, the $ \alpha $ and $ \beta $ FPUT simulations for large values of the number of particles are completely new.

2.   The models

We consider Hamiltonian systems of the form

where $ H_{\text{lin}} $ is the integrable Hamiltonian, corresponding to a linear dispersive dynamics, and $ H_{\text{nonlin}} $ that contains the anharmonicity of the potential. More in particular we will deal with the $ \alpha $, $ \beta $-FPUT and the discrete nonlinear Klein-Gordon (DNKG) (also called the $ \phi^4 $) systems, all characterized by the quadratic Hamiltonian

where $ N $ is the number of elements in the chain, $ q_j $ is the $ j $-th coordinate and $ p_j $ its conjugate momentum and $ m $ models the linear part of the site-potential. For the $ \alpha $ and $ \beta $-FPUT systems $ m = 0 $. The nonlinear part of the Hamiltonian for the three models is given by:

Without loss of generality, we use the same parameter $ \beta $ in front for nonlinearity in the DNKG and the $ \beta $-FPUT. We will use periodic boundary conditions. It should be noted, given an initial energy, that there is a finite probability that the $ \alpha $-FPUT chain breaks up, especially for large $ N $, since the nonlinear part of the Hamiltonian is not bounded from below. While being an inherently ill-posed problem, it has been shown that for low enough energies the $ \alpha $-FPUT chain can be stable for long times ^[7]. For the other models, we restrict ourselves to the case where the quartic terms are positive, that is $ \beta > 0 $, so that no blow-ups can occur. The parameter $ m $ is constrained to be greater than zero in the DNKG model, and we can anticipate that it will play a secondary role since we are interested in the effects of the nonlinear interactions. The presence of the quadratic finite difference terms in the linear Hamiltonian is important, because without that the eigenstates of the linear system would not be waves.

Our approach is of perturbative nature, hence we need a way to quantify the nonlinearity strength. In general, the linear and nonlinear parts of the Hamiltionan are not conserved separately, but only the total Hamiltonian is. However, in typical situations where the nonlinear interactions are not too strong, operatively, we define the following nondimensional parameter for the $ \alpha $-FPUT

and for the $ \beta $-FPUT and DNKG

$ h_\text{nlin}^{(\alpha)}(j) $ is the nonlinear part of the Hamiltonian density of the $ j $-th particle in the for $ \alpha $-FPUT. The absolute value in Eq (2.4) is necessary because $ h_\text{nlin}(j) $ can be negative and cancellations in the sum would cause an incorrect accounting of the nonlinearity strength. The different scalings in Eqs (2.4) and (2.5) are due to the different degrees of nonlinearity between the $ \alpha $-FPUT and the other two models. Definitions (2.4) and (2.5) allows us to refine our statement that the nonlinearity must be small, that is, we require that the parameters are much less than one. In general, they fluctuate over time, so an appropriate averaging is needed to have a meaningful estimate of the nonlinearity strength. The parameters are further discussed when presenting the numerical results.

2.1.   Fourier space

The eigenstates of the quadratic Hamiltonian are waves, hence it is useful to work in Fourier space. We define the direct and inverse discrete Fourier transform of the $ q_j $ variables,

and similar definitions for $ \hat p_k $. We will use the convention that $ 0\leq k < N $, and we note $ \hat q^*_k = \hat q_{N-k} $ and $ \hat p^*_k = \hat p_{N-k} $. After this change of variables, and using $ \sum_{j = 0}^{N-1} e^{i2\pi (k_1-k_2)j/N} = N\delta_{k_1-k_2} $ with $ \delta^{(N)}_{k_1+k_2+...} = \delta(k_1+k_2+... \mod N) $ that is the Kronecker's delta modulo $ N $, the linear part of the Hamiltonians can be written as

where we have defined the linear dispersion relation

(we recall that $ m = 0 $ for the FPUT models). The nonlinear part of the Hamiltonians couple the modes and can be interpreted as n-wave collision terms. For the sake of brevity, we denote $ \hat q_{j} = \hat q_{k_j} $ and $ \delta^{(N)}_{1+2+...} = \delta(k_1+k_2+... \mod N) $. For the FPUT models we obtain

where the collision matrices $ \widetilde{A}_{1, 2, 3} $ and $ \widetilde{B}_{1, 2, 3} $ are (after symmetrization)

The complex exponential is relevant only when crossing Brillouin zones in the sum of wave numbers. For the DNKG model, it turns out that the interaction matrix is equal to unity, hence the nonlinear part of the Hamiltonian is simply

From Eq (2.7), we can further simplify the problem using the normal modes representation,

as the linear part of the Hamiltonians becomes simply

whereas the nonlinear terms in the FPUT models and in the DNKG become (after renaming $ N-k_i = k'_i $ where needed and dropping the prime)

with the interaction matrices given by

The nonlinear terms show that a nonlinearity in physical space turns into n-mode collision terms such as $ a_1a_2a_3\delta^{(N)}_{1+2-3} $. From the Hamilton equations, we can obtain the dynamical equations $ \dot{a}_k = -i(1/N)\delta H/\delta a_k^* $, which read for the $ \alpha $-FPUT

and for the $ \beta $-FPUT and DNKG

These types of Hamiltonians are the canonical form of Hamiltonians for system composed of interacting particles or waves. If nonlinearity is small in the above mentioned sense, then there is a well developed theory called Wave Turbulence theory, which is described in detail in ^[17,38] and briefly in the subsequent section.

The number of modes in the nonlinear terms defines the collision order, that is the $ \alpha $-FPUT contains 3-wave collisions, while $ \beta $-FPUT DNKG 4-wave collisions (we will see that the effective collision order in the $ \alpha $-FPUT is also of the 4-wave type). The number of non-conjugate and conjugate variables (which matches the number of positive vs. negative terms in the Kronecker's deltas) defines different collision processes, e.g., $ a_1a_2a_3\delta^{(N)}_{1+2+3} $ is a $ 3\rightarrow 0 $ collision process (annihilation), while $ a_1a_2a^*_3a^*_4\delta^{(N)}_{1+2-3-4} $ is a $ 2\rightarrow 2 $ collision process (scattering).

The WT approach starts from the equations of motion in the canonical variables $ a_k $. Note that so far we have not taken any approximation; we only made the choice of using periodic boundary conditions.

3.   Wave-Turbulence theory in a nutshell

When the number of modes is large, the microscopic dynamics given by Eqs (2.18) and (2.19) do not provide much analytical insight and a statistical approach is needed. WT is the general statistical theory valid in the weak-nonlinear regime. While the theory has been recently developed for higher-order statistical observables ^[10,16,38], the core of the WT is the kinetic equation developed for the prediction of the energy spectrum. The basic statistical observable is the two point correlator $ \langle a_1a_2^*\rangle $ which, under the hypothesis of homogeneity, it is given by

with $ n_k = n(k, t) $ the wave actions spectral density, i.e., the Fourier transform of the autocorrelation function of $ a(x, t) $. The average is over an ensemble of realizations of the system with the same initial linear energy $ H_\text{lin} $. Then, the energy spectrum that gives the mean energy per mode is

The evolution equation for the wave action spectral density can be obtained by various techniques ^{[10,16,17,38,39,40]}. The main issue is due to the fact that calculating the evolution of $ n_k $ from the equation of motion (2.18) or (2.19), one encounters the well know problem of the BBGKY hierarchy ^[14], that is, the evolution of lower order correlators depends on higher order correlators and a closure problem arises. Different approaches have been used in the past, see for example ^[40] for a recent discussion. Accordingly to ^[39], a natural asymptotic closure arises because of the smallness of higher order cummulants. A closure was also obtained with a quasi-gaussian approximation which allowed to express higher cumulants in terms of lower ones ^[17]. It is sufficient to make a random-phase approximation and to consider initial conditions which have also random amplitudes ^{[10,12,13,16,38]}. The random phase assumption is generally deemed to be solid because the linear waves decorrelate quickly even in the linear regime, hence it is expected that such property still holds true in the weakly nonlinear regime, as corroborated by numerical experiments ^[9]. The resulting kinetic equation can be obtained in the thermodynamic limit $ N\rightarrow \infty $. Generally also the continuum limit is taken at the same time, and both physical $ {\bf x} $ and momentum space $ {\bf k} $ are continuous.

The main concept underneath the kinetic equation is the existence of conservation laws associated to the wave scattering processes. Indeed, each nonlinear term in the Eqs (2.18) and (2.19) contains an appropriate Kroneker $ \delta $ function over wave numbers. Depending on the shape of the dispersion relation, it may be possible to associate also a related conservation of energy. To be more specific, let us consider for example the scattering processes,

contained in Eq (2.18), then the main question is to verify if a similar relation holds for frequencies, i.e.,

Eqs (3.3) and (3.4) define a resonant manifold in wave number space, whose existence, as anticipated, depends only the analytical form of the dispersion curve $ \omega_k $. If Eqs (3.3) and (3.4) are satisfied for the same wave numbers, then we are dealing with a resonant process which, according to the kinetic equation, will lead to an irreversible transfer of energy.

There are two main types of wave systems that are typically considered in the framework of WT: The one dominated by three wave resonances and by four wave resonances (higher order are also possible). Examples of the systems dominated by three wave resonances include capillary waves on a surface of fluid and internal waves in the ocean. Examples of four wave resonant systems include gravity waves on deep water, as well as the celebrated 2D-Nonlinear Schrödinger equation.

For capillary waves on a surface three wave resonant interactions are possible and a kinetic equation can be derived ^[17]:

where $ {\bf k} $ is a two dimensional wave vector, $ {\mathrm{d}}{\bf k}_{23} = {\mathrm{d}}{\bf k}_{2} {\mathrm{d}}{\bf k}_{3} $ and $ \left \{({\bf k}_1 \leftrightarrow {\bf k}_2)\right \} $ implies the same integral with $ {\bf k}_1 $ and $ {\bf k}_2 $ exchanged. $ A_{123} $ is a matrix that can be derived directly from the dynamical equations for capillary waves.

For surface gravity waves in deep water, it can be show that the leading order resonant process is the four-wave one, characterized by the following resonant process:

The appropriate kinetic equation describing such process is

Note that in both kinetic equation the interaction matrix is squared. The latter equation, with a transport term, a forcing term due to the wind and term mimicking the dissipation, is integrated daily for operationally ocean wave forecasting pourposes, see ^[27].

The kinetic Eqs (3.5) and (3.7) have a number of important properties. First of all, it can be shown that both equations conserves the total energy and momentum:

The kinetic equation for four-wave interactions preserves also the number of waves (particles) in the scattering:

The kinetic Eq (3.7) is reminiscent of the Boltzmann equation for hard spheres ^[44] and there exists an entropy function

such that $ \mathrm{d}S/\mathrm{d}t\geq0 $ (the same entropy can be defined for the three wave kinetic equation). The equilibrium is reached when $ \mathrm{d}S/\mathrm{d}t = 0 $, i.e., at the Rayleigh-Jeans distribution:

where $ T $ is some normalization constant linked to the total energy and $ \mu $ is a chemical potential linked to the conservation of the total number of particles (3.1) and it is zero in the case of a three wave process; $ {\bf u} $ is a constant vector associated to momentum conservation. We observe that in isotropic conditions $ {\bf u} $ = 0, and when $ \mu = 0 $ then WT predicts a relaxation towards equipartition of energy. In this framework, exact resonances bring the system to thermalization with a time-scale which is proportional to the coupling coefficient in front of the collision integral.

Some remarks are in order.

● Given a physical dispersive waves system, it has to be checked if exact resonances are allowed. In some cases, only trivial collisions or processes which are not able to transfer energy are found. In those cases, it is necessary to pursue the perturbative procedure and derive a kinetic equation with higher-order processes to check if at some point resonances are found. This issue is related to the dispersion relation, and in physical phenomena 3-, 4-, 5- and 6-wave processes have been recognised ^[38]. In other cases, it can be shown that no exact resonances exist and therefore no exchange of energy is possible, as rigorously shown to be the case for integrable systems ^[47]. Other systems may show some resonances which are not yet able to transfer energy among modes because resonating waves belong to isolated clusters ^[6].

● The WT framework is an asymptotic theory valid in the weakly nonlinear regime. If the nonlinearity is not small, different effects can play a role. In particular, the broadening of the frequencies due to the finite value of the nonlinear coupling, may trigger some resonances which were not present in the weak asymptotic limit, therefore allowing a more efficient transfer of energy.

In the present paper, we estimate the time scale of equipartition; therefore, it is of major importance to be able to derive a kinetic equation for our chain models. One should note that chains are intrinsically discrete in physical space and, for a finite number of masses, also the Fourier space is discrete. This issue makes the derivation of the kinetic equation not straightforward and, only in the thermodynamic limit, a formal derivation of the kinetic equation is possible. We shall deal with these points in the following section in some detail.

4.   Resonance and effective Hamiltonians in the thermodynamic limit

We consider the thermodynamic limit which consists in taking the number of particles going to infinity, $ N\rightarrow \infty, $ keeping constant the mass linear density. The general linear dispersion relation becomes

with $ k $ real in the interval $ 0\le k < 2\pi $. We consider interaction processes from $ X $ to $ Y $ waves for which the following equations are satisfied:

Our goal is to find resonances. Once the leading order resonance (lowest value of $ X $ and $ Y $) has been found, using tools from Hamiltonian mechanics, an effective Hamiltonian can be established and a kinetic equation can be built.

The first trivial observation is that resonances of the type $ X $ to 0 are excluded for all three models; this is because $ \omega_k\geq0 $, and it is equal to zero only for $ m = 0 $ for mode $ k = 0 $ which does not play any role in the dynamics (for $ m = 0 $).

4.1.   Three-wave resonant interactions in the $ \alpha $-FPUT

The leading order nonlinearity in the evolution equation for the $ \alpha $-FPUT is cubic; this implies three-wave interactions of the form 2 $ \rightarrow $ 1, 1 $ \rightarrow $ 2 or 3 $ \rightarrow $ 0 (the latter have been already excluded). It is known, see for example ^[5,37], that the function $ f_k = 2|\sin(k/2)| $ is a subadditive function, i.e.,

The equality holds only for $ k_1 $ or $ k_2 = l 2\pi $, with $ l \in \mathbb{Z} $; those wave numbers do not enter into the dynamics. The subadditivity implies the non existence of three-wave resonant interactions for $ m = 0 $.

4.2.   Four-wave resonant interactions in the $ \alpha $, $ \beta $-FPUT and DNKG models

The $ \beta $-FPUT and DNKG models include processes involving four waves, while, at first sight, the $ \alpha $-FPUT model does not include them; however, as it will be shown in the following, the absence of three-wave resonances allows for a perturbative approach on the $ \alpha $-FPUT model that leads to four and higher order wave-wave interaction processes. In ^[5] it has been shown that resonant processes 3 $ \rightarrow $ 1 or 1 $ \rightarrow $ 3 are excluded for the FPUT models, i.e., in the case $ m $ = 0. In the Appendix we show that this implies that also for the case of $ m\ne0 $ there are no such processes. It turns out that in the thermodynamic limit there exist, apart from trivial resonances $ k_1 = k_2 = k_3 = k_4 $ or $ k_1 = k_3 $, $ k_2 = k_4 $, a nontirvial resonant manifold for interactions of the type $ 2\rightarrow 2 $ (see Figure 1 for a visualization of the case $ m = 0 $, similar result apply for $ m > 0 $). The result has been obtained using the software Mathematica Wolfram.

4.3.   The effective Hamiltonian and the kinetic equation for $ \alpha $, $ \beta $-FPUT and DNKG models

The effective Hamiltonian is obtained by removing all non resonant interactions from the original one. As standard in Hamiltonian systems, this can be carried out through a canonical change of variables (quasi-identity transformation), from the normal modes $ a_k $ to some other variables $ b_k $, such that in the new variables the nonresonant terms are removed from the Hamiltonian, generating higher order nonlinearities. It is worth stressing that one has to ensure the canonicity of the transformation, at least up to the order of the new interaction terms that appear in the new variables. For example, to remove all the three-wave terms in the $ \alpha $-FPUT model one uses

where the integral corresponds to three integrals from 0 to $ {2\pi} $ and not from $ -\infty $ to $ +\infty $ and $ \delta_{2\pi} $ account for periodicity of the Fourier space; this is because of the discreteness of our system in physical space. In Eq (4.4) we recognize terms equivalent to the nonlinear interactions in Eq (2.18). The matrices $ X^{(i)}_{1, 2, 3} $ are determined by inserting Eq (4.4) into the $ \alpha $-FPUT Hamiltonian and by grouping the terms corresponding to different wave processes. The transformation generates four-wave interactions (and higher) and again one has to look for resonances and remove the non resonant ones. The calculation leads to the following effective Hamiltonian for the $ \alpha $-FPUT

For the $ \beta $-FPUT and for the DNKG a transformation is used to remove the 3 $ \rightarrow $ 1, 1 $ \rightarrow $ 3 and 4 $ \rightarrow $ 0 terms, so that the effective Hamiltonian takes the form:

For an interested reader, a comprehensive procedure for removing three and four-wave interactions, is presented in ^[15,32,34]. All three models are dynamically described by the Zakharov equation:

where the coefficient $ W_{1, 2, 3, 4} $ takes different form, depending on the particular system under consideration. Its actual analytical form is irrelevant in our discussion (except in those cases for which the coefficient is zero on the resonant manifold ^[48,49]); it is just sufficient to mention that it is proportional to $ \alpha^2 (A_{1, 2, 3})^2 $ for the $ \alpha $-FPUT model and to $ \beta B_{1, 2, 3, 4}^{(\beta, KG)} $ for the $ \beta $-FPUT and DNKG models.

The Zakharov equation is the starting point for developing the statistical theory, i.e., the wave kinetic equation, which takes the following form (see for details ^[10,17,38]):

Note that, because of the $ \delta^{(2\pi)} $, instead of $ \delta $, the momentum is not conserved. The time scales, $ T_\text{eq} $, of four wave resonant interaction, which lead to a thermalized state, are:

for the $ \alpha $-FPUT model and

for the DNKG and $ \beta $-FPUT models.

We stress that the theory developed in this section is asymptotic and valid when the thermodynamic limit and the weak non-linear limit are taken, in the given order. It is important to wonder if the scaling laws obtained can be observed in actual finite-size systems and in particular in numerical experiments. We expect a positive answer, at least for sufficient large $ N $ and small nonlinearity. Indeed, it is well known that a small nonlinearity cause a frequency shift of the linear modes, and also a stocasticization of the frequencies, or in other words, a broadening ^[11,26]. It is reasonable to assume that resonances do not need to be satisfied exactly in practical applications ^[29]. It is sufficient that broadening of frequencies becomes comparable with the spacing of the frequencies, which decreases with the number of modes, so that $ \omega_k $ becomes continuous in the thermodynamic limit. In this sense, the discrete representation should converge to the continuous theory, and the higher the number of modes the smaller the nonlinearity required to be in agreement with the theory. We shall check this argument with extensive numerical simulations in the following.

5.   Discrete exact resonances

In many interesting cases, the number of modes $ N $ is not too large, like for instance in the original FPU numerical experiments. In this case, it is not possible to consider the system a good approximation of the continuous one, and it has to be studied in its discrete form. As mentioned, one should recall that in discrete systems the condition in the Kroneker $ \delta $ over wave numbers should be intended mod $ N $.

5.1.   Four-wave resonant interactions, effective Hamiltonian and itegrability

The first problem is to find out if discrete exact resonances exist and at which order. The previous discussion on three-wave resonance still applies here, hence three-wave resonances are always excluded from the $ \alpha $-FPUT model. Concerning 4-wave resonances, the only process that is potentially active for the dispersion relation (2.8) is the scattering process $ 2\rightarrow 2 $. These resonances have been considered extensively in ^[5,41,42], and we will recap here the results. Obviously, even discrete processes of the type $ X\rightarrow X $ admit trivial resonances of the type

or $ k_1 = k_2 = k_3 = k_4 $. These processes, however, do not result into an exchange of energy, but rather cause a frequency shift of the linear modes ^[38]. Because the system is periodic and the dispersion relation is symmetric,

it turns out that nontrivial resonances of the type $ 2\rightarrow 2 $ are possible with the crossing of Brillouin zones (Umklapp scatterings). For $ N $ even, these resonances take the form

and are known as pairing-off resonances ^[5]. However, one can easily check that these resonances are all disconnected, and they actually give rise to integrable dynamics ^[24,43]. In ^[42] other special resonances have been considered for some very specific values of $ m\ne 0 $, but they are limited in number and they do not appear in general to be able to cover the whole Fourier space (a detailed study should be performed for such specific cases).

The effective integrable Hamiltonian, up to four-wave interactions for the $ \alpha $, $ \beta $ and DNKG equations (with $ m $ different for those special values for which other resonant quartets exists), can be recast as follows:

where $ c.c. $ denotes complex conjugate. The first three terms depend on the moduli of the amplitudes only and underline an integrable dynamics (Birkhoff normal form); interestingly, the last term does not break integrability (resonant Birkhoff normal form) ^[24,43], due to the relations (5.2) and the following symmetries:

valid for all admissible values of $ k_1, k_2 $. It can be proven that $ N-1 $ functionally independent invariants exist and are in involution (for $ \alpha $ and $ \beta $-FPUT see the proof of integrability in ^[24,43]). We present these invariants in a way that highlights the fact that the resonant quartets are disconnected:

For each $ k = 1, \ldots, \lfloor N/4\rfloor $, define an irreducible quartet as the set $ Q_k = \left\{b_k, b_{-k}, b_{\frac{N}{2}-k}, b_{-\frac{N}{2}+k}\right\} $. There are four different modes in $ Q_k $, except for the degenerate case $ k = N/4 $, valid when $ N/4 $ is integer, where $ Q_{N/4} $ has two different modes. In the non-degenerate case, the following four invariants depend on the four modes in $ Q_k $:

● 3 quadratic invariants:

● 1 quartic invariant:

In the degenerate case, valid when $ N/4 $ is integer, we have $ Q_{N/4} = \left\{b_{\frac{N}{4}}, b_{-\frac{N}{4}}\right\} $ and the following two invariants depend on the two modes in $ Q_{N/4} $:

● 1 quadratic invariant:

● 1 quartic invariant:

Thus, in terms of counting, any irreducible quartet (degenerate or not) contributes with a number of invariants that is equal to the number of modes in the quartet. Finally, notice that the mode $ b_{\frac{N}{2}} $ is not in any irreducible quartet. In fact, the following is an invariant: $ |b_{\frac{N}{2}}|^2 $.

It is thus easy to show by simple counting of the modes in the irreducible quartets that the system has a total of $ N-1 $ functionally independent invariants:

1. When $ N/4 $ is not integer, the irreducible quartets give a total of $ 4 \times \lfloor N/4 \rfloor = N - 2 $ invariants. The missing invariant is $ |b_{\frac{N}{2}}|^2 $.

2. When $ N/4 $ is integer, we get a total of $ 4 \times (N/4 -1) = N -4 $ invariants from the non-degenerate quartets, plus $ 2 $ invariants from the degenerate quartet $ Q_{N/4} $, totalling again $ N - 2 $ invariants. The missing invariant is $ |b_{\frac{N}{2}}|^2 $.

The result shows the asymptotic integrability of the DNKG model up to four wave interactions and justifies the metastable states observed in numerical simulations previously performed ^[22].

5.2.   Higher order resonances and break-down of integrability

For the discussion above, we see that the 3- and 4-wave collision terms cannot be effective in bringing the system to equipartition. The isolated resonant quartets of the 4-wave integrable Hamiltonian do not bring the system to a thermalized state and resonances at higher order are to be investigated. For all discrete models considered here we have to perform an extra canonical change of variables, from the normal modes $ b_k $ to some other variables $ c_k $, such that in the new variables the nonresonant terms are removed from the Hamiltonian. The question is now what is the leading order resonant wave interaction. In ^[41], only power-of-two values of $ N $ were investigated (akin to the original paper on the $ \alpha $-FPUT problem) and five-wave interactions were excluded on numerical grounds. From a more recent investigation ^[5], it turned out that five-wave resonant interactions exist only if $ N $ is divisible by 3 when $ m = 0 $. When $ N = 2^a 3^b $ with $ a, b > 1 $, the resulting five-wave clusters are connected and, in principle, a thermalized state might be reached, but this requires further study, to be discussed in a subsequent paper.

Excluding such specific values of $ N $, six-wave resonant interactions are the leading order processes: It is always possible to find resonant six-wave tuples that are all interconnected and cover the whole Fourier space. These resonances are due to the same symmetries of $ \omega_k $ and are of the form:

Such resonances are valid for even and odd values of $ N $. Additional resonances can be found both in pairing-off form for even $ N $, and recently also other resonances not in pairing-off form have been found ^[5], but they are not necessarily to cover the whole Fourier space and we will not discuss them. Another six-wave processes is theoretically possible, that is $ 4\rightarrow 2 $. Explicit formulas for $ 4\rightarrow 2 $ resonances have been found recently in^[5], at least for $ N $ divisible by 3.

Excluding those specific values of $ N $ for which five wave interactions and $ 4\rightarrow 2 $ (or $ 4\rightarrow 2 $) exist, the six wave interaction Hamiltonian for the $ \alpha $, $ \beta $-FPUT and DNKG equation can be written as

where $ \delta_N $ is the Kronecker modulo $ N $. The new matrix interaction can be calculated ^[34], but its precise form is not relevant to our scope.

5.3.   The time scale of thermalization

The next step to be taken in order to evaluate the thermalisation time-scale should be the derivation of the corresponding kinetic equation, as done in the continuous case. Unfortunately, the kinetic equation can be rigorously derived only in the thermodynamic limit, that is $ N\rightarrow\infty $. Deriving a discrete version ($ N $ finite) of the kinetic equation poses significant mathematical problems ^[16].

Here, we make the conjecture that the time scale for thermalization in the discrete dynamics corresponding to the 6-wave interaction given by Eq (5.7) is at the leading order equivalent to the corresponding continuous 6-wave process. We also assume that the integrable part of the dynamics does not lead to any irreversible transfer of energy and the irreversible dynamics is fully contained in the six-wave interaction term. Our conjecture is therefore tantamount to saying that the thermalisation time-scale in the discrete case will be always inversely proportional to the square of the coupling coefficient $ Z_{1, 2, 3, 4, 5, 6} $ in the six by Eq (5.7), the latter coefficient being proportional to $ \alpha^{4} $ in the $ \alpha $-FPUT model and $ \beta^{2} $ in the $ \beta $-FPUT and DNKG system. We get the following estimates for the thermalisation time-scale for the $ \alpha $-FPUT model

and

for the $ \beta $-FPUT, DNKG models. The argument used in the discrete case is always made for the limit of vanishing nonlinearity, where only exact resonances are important. However, the presence of a small but finite nonlinearity is expected to broaden the frequencies. In the case of a small number of modes $ N $, that is in the present discrete case, an important difference with respect to the continuous case is expected. Since the wave-space is discrete, a large enough nonlinearity may cause a sufficient broadening to trigger resonances which are not in the exact-resonance manifolds and are found at a lower-order than the exact ones. Therefore, we can expect that at small $ N $ and sufficient nonlinearity the transfer of energy can be made through lower-order processes on smaller time-scales. A definite answer on the role of quasi-resonance is beyond the scope of the present manuscript.

5.4.   Final remarks on the Wave Turbulent approach

Concluding the theoretical analysis, the WT formalism applied to the different anharmonic chains leads to consider the problem of transfer of energy as related to the collisions between waves in the system. In this framework, the energy is redistributed among modes if resonances exist which connect the whole wave-space. In the thermodynamic limit, the theory predicts that 4-wave processes are the leading order process in all chains and this fact allows a transparent estimate of the equipartition time-scale. In the case of a finite small $ N $, we have considered the system intrinsically discrete and we have searched for the exact discrete resonances. We have seen that in this case, 4-waves processes are not able to transfer energy among modes, nor 5-wave collisions. The leading order is found to be 6-waves. Although we are not able to write the corresponding discrete kinetic equation, we have made the hypothesis that the same reasoning as in the continuous case can be followed, at least when looking at statistical observables like equipartion time-scale. In this way, an estimate of this time-scale is obtained always proportional to the square of the nonlinear coupling coefficient. Moreover, also when $ N $ is small, nonlinear effects can be important. We expect that the broadening of the frequencies due to nonlinearity can trigger lower-order process to transfer energy among modes when it becomes of the same order of the spacing in the frequency space, which is inversely proportional to $ N $. The discrete case stands therefore on a less rigorous ground and the conjectures proposed can be only verified numerically a posteriori.

6.   Numerical simulations

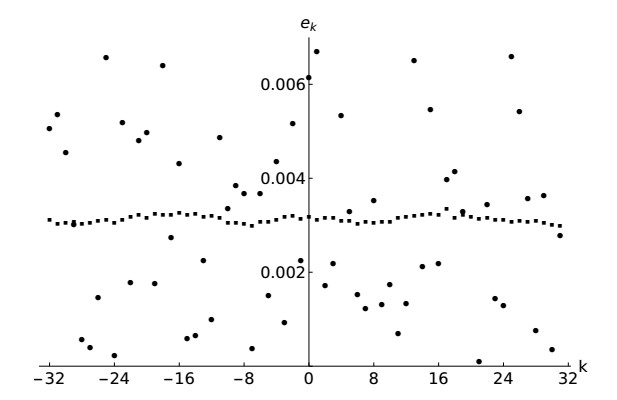
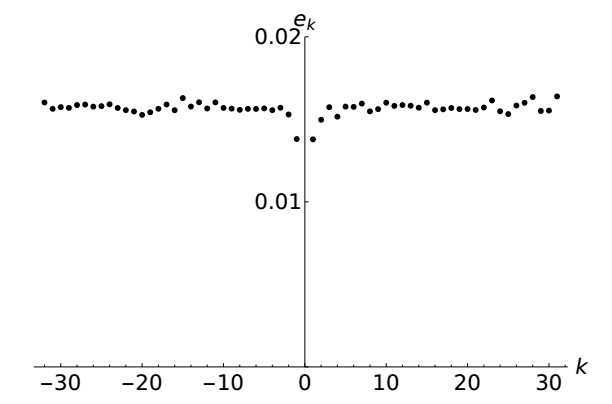
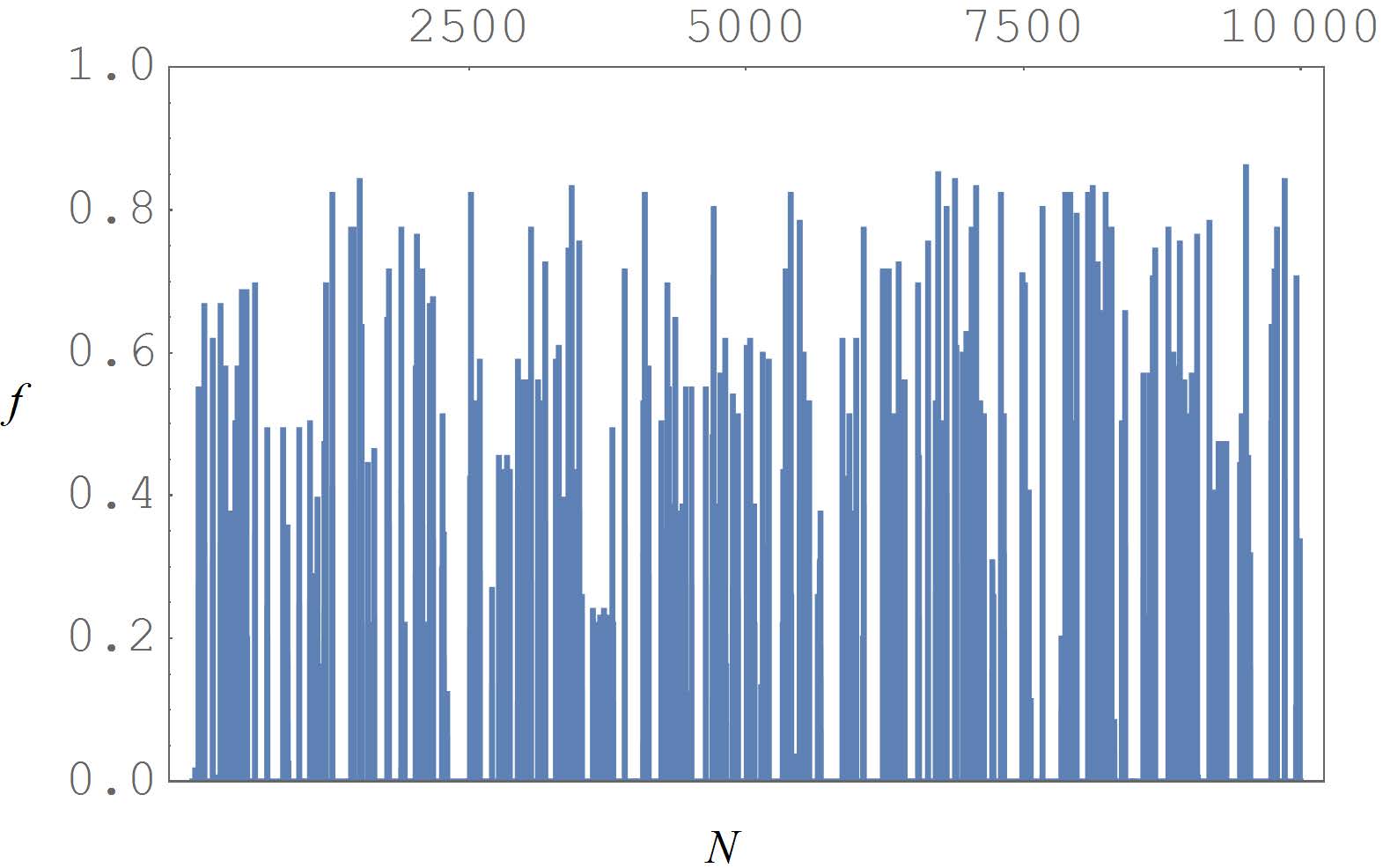
We now present the result of numerical simulations in support of the previous discussion. The Eqs (2.18) and (2.19) have been implemented in physical space, with a symplectic algorithm of the sixth order ^[45]. It is important to use a high-order integration scheme that preserves accurately the energy of the system, because simulation times are very long compared to the typical wave periods. The initial random energy per mode, $ e_k $, was drawn from an uniform distribution, and then scaled in order to obtain the desired total linear energy $ E $ and an initial number of particles $ \mathcal{N} $ compatible with a final relaxation distribution with $ \mu = 0 $ in Eq (3.11), in order to better observe equipartition. Each wave number has the same energy per mode $ e_k $ for different members of the ensemble. The initial condition is out of equilibrium. As an example, we show the initial distribution of $ e_k $ for the simulations of the DNKG system with $ N = 64 $ in Figure 2, together with its final thermalized state. The linear energy $ E $ and the wave action $ \mathcal{N} $ change only for one part in $ 10^4 $ across the whole simulation time, being quasi-conserved quantities.

Each realization in the ensemble shares the same initial energy per mode, but phases are randomized. This scheme of initialization ensures that all the realization share the same initial linear energy. The time step was set to $ 0.1 $ in all simulations, and it was checked that from beginning to the end of the simulation the total energy is conserved up to one part in $ 10^7 $. The computation is very easy to parallelize, since ensemble averages need to be computed. For this reason we implemented the code on GPU hardware, which is powerful when the code can be parallelized.

The parameter $ \alpha $ and $ \beta $ are chosen in such a way that the nonlinear energy is small compared to the linear one and the parameters $ \epsilon_{\alpha} $ and $ \epsilon_{\beta, KG} $ are small. We will present the results of $ T_\text{eq} $ as a function of $ \epsilon_{\alpha} $ and $ \epsilon_{\beta, KG} $.

In our numerical simulations we monitor the approach to equipartition using the entropy

where

Such entropy is a discretized version of Eq (3.10) and has the useful property that at equipartition then $ S'_\text{WT} = 0 $ and it is greater than zero in any other state. This expression preserves the monotonicity of the WT entropy with an inverted sign ($ \mathrm{d}S'_\text{WT}/\mathrm{d}t\leq0 $, $ S'_\text{WT} = 0 $ at equipartition).

In numerical simulations, the entropy shows some fluctuations and never reaches exactly zero, because the simulation time is finite, but most importantly because the ensemble size is finite. In the following, we will determine $ T_\text{eq} $ looking at the time when the entropy crosses a threshold value from above. The selection of the threshold depends on the ensemble size and the number of particles, but it does not depend on the degree of nonlinearity. Generally we chose a value of $ S'_\text{WT} $ two orders of magnitude smaller than that of the initial conditions.

6.1.   Small number of particles, discrete resonances

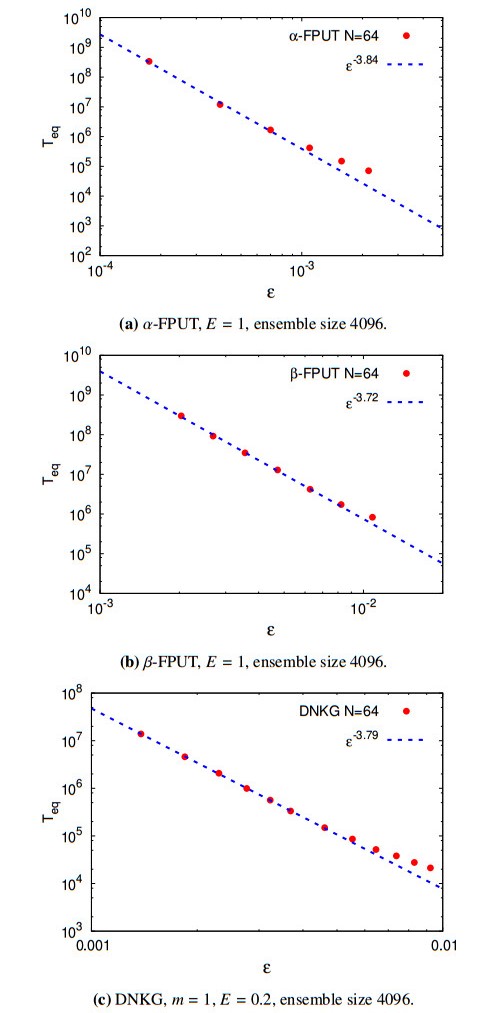
We first present the results on the case of a limited number of particles, $ N = 64 $, so that discrete resonances need to be considered. To recap, we expect for the $ \alpha $-FPUT system the scaling

and for $ \beta $-FPUT and DNKG systems the scaling

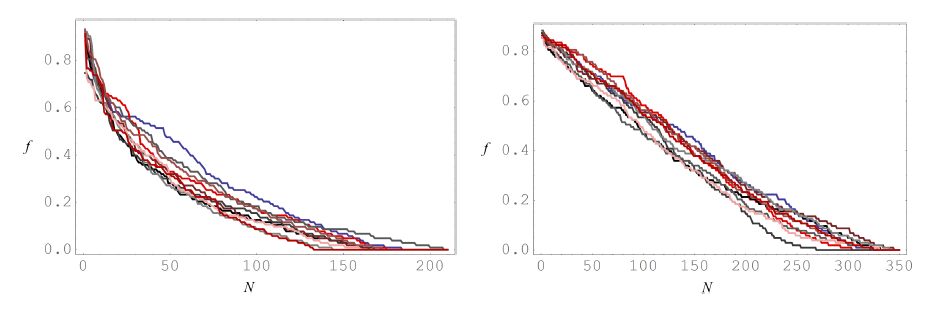
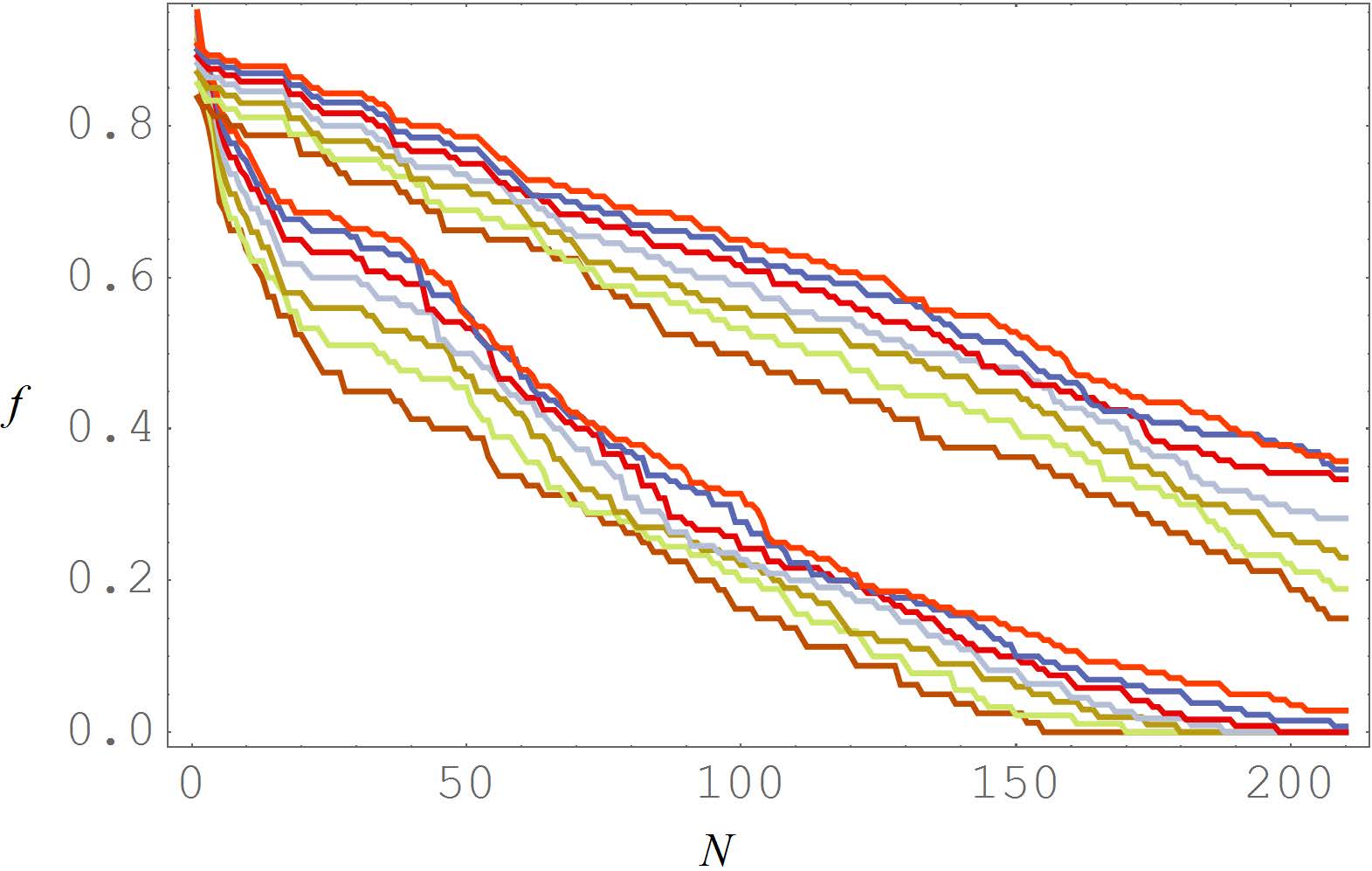
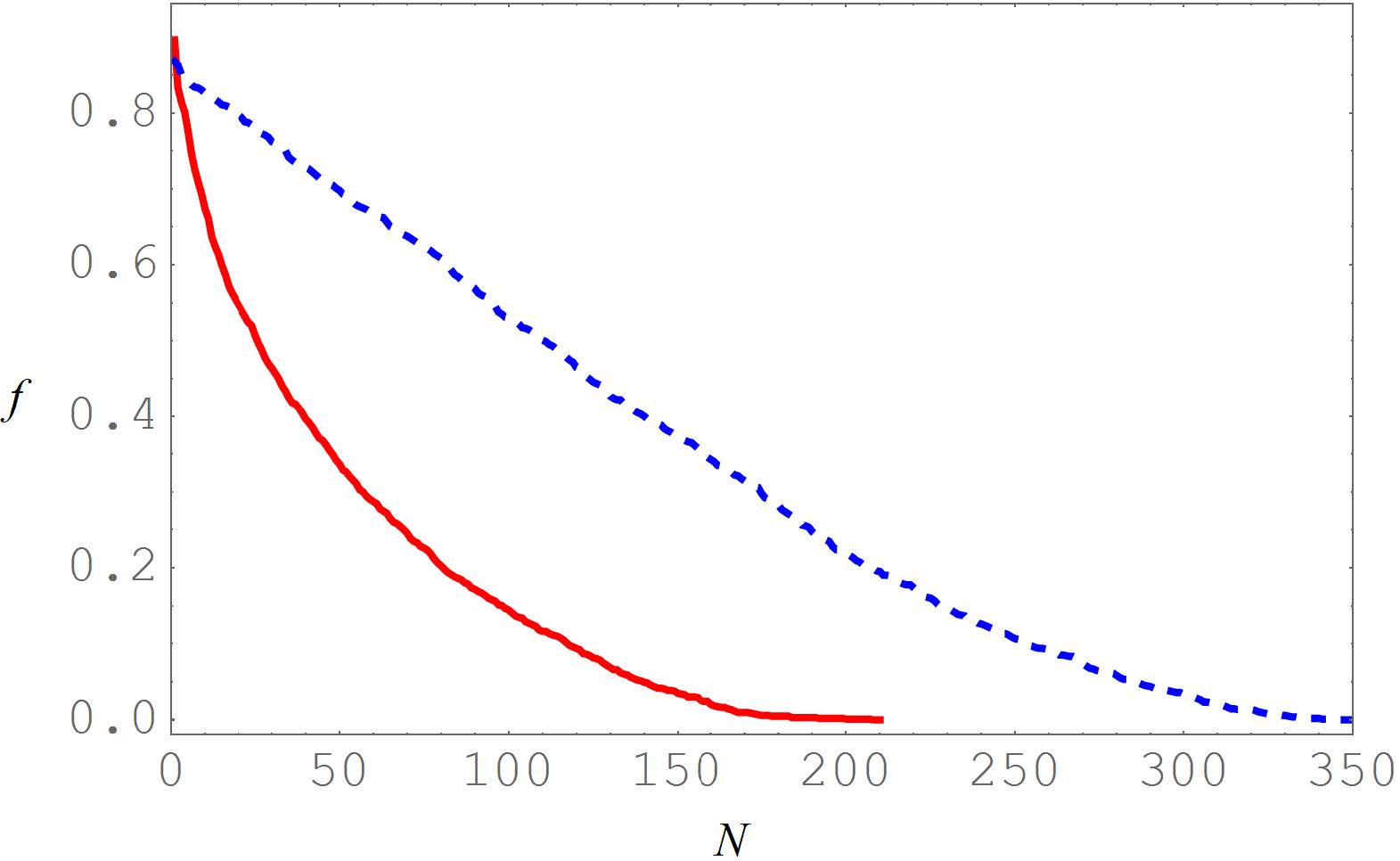
We show the results of the simulations for $ N = 64 $ in Figure 3. A line obtained from a fitting procedure has also been included. We see a good alignment with the expected power-laws for all the three models. We chose $ m = 1 $ in the DNKG model arbitrarily: In ^[42] it is argued that since the resonances in the discrete case do not depend on $ m $, then in the scope of the thermalization dynamics the value of $ m $ is not relevant. However, we should add here a comment for the limit of $ m $ very small. In such cases, the contribute to $ H_\text{nlin} $ increases for the low frequency modes. On the other hand, for the FPUT systems the nonlinearity depends on a power of the finite differences, which are approximately proportional to $ k $, hence the contribute to the nonlinear part of the Hamiltonians for modes with small $ k $ does not grow. As a consequence, in the case of the DNKG system with $ m = 0 $, a complete thermalization of the lower modes would invalid the weak-nonlinear assumption, because the nonlinearity would be too high. What is observed actually (see Figure 4) is a partial thermalization of the system, with the lower modes stationary at a lower energy than equipartition.

6.2.   Large number of particles, continuous resonances

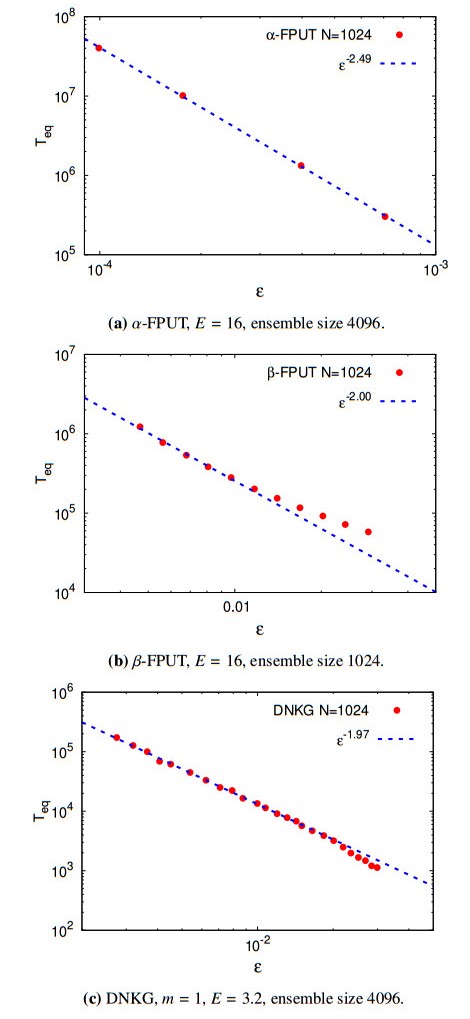
We now present the results of numerical simulations for the continuous resonance manifold. The expected results are

for the $ \alpha $-FPUT system, and

for $ \beta $-FPUT and DNKG systems. The number of particles and the strength of the nonlinearity necessary to observe the continuous resonances are not something predicted by our treatment. However, estimates of the frequency broadening are available in ^[36,38], and they can be compared to the typical frequency spacing for a fixed number of particles. We point out that in general a higher value for $ m $ in Eq (2.8) makes the frequency gaps smaller among modes, hence the DNKG model in general requires a small number of particles to observe the continuous resonances.

In Figure 5 we show the results for simulations with $ N = 1024 $, again with $ m = 1 $ for the DNKG system. The figure highlight a reasonable agreement between numerics and the theoretical predictions. A discussion of the numerical results is reported hereafter.

7.   Discussion and relation to other results in the literature

Before entering in the discussion, we summarise our numerical results here below:

7.1.   Discussion on the Thermodynamic limit

We mention that the formal derivation of the Wave Kinetic equation is made by taking the large box limit ($ N \rightarrow \infty $) and then the small nonlinearity assumption is made. By looking at the above fitting numbers, for the DNKG and $ \beta $-FPUT systems the agreement with the prediction from WT theory is remarkable, despite the fact that the simulations are done for large but finite $ N $. Any numerical simulation, by definition, is performed with finite $ N $. In this respect we recall that, besides transferring energy, two are the main effects of nonlinearity: (i) nonlinear shift of the frequencies and (ii) broadening of the frequencies ^[36]. If the broadening is large enough, then two adjacent frequencies can be connected and the system can be considered as continuous (even if the simulation is performed with a finite number of masses). The continuous limit assumed in the Wave Kinetic equation is therefore achieved numerically, with finite $ N $, with a subtle balance between the Fourier spacing (which is proportional to $ 1/N $) and the broadening.

The correct recipe to be used in numerical simulations is still not fully understood theoretically; however, results show clearly that, for a given (large) $ N $, if the nonlinearity is too small, then the discrete effects (lack of four-wave resonant interactions) may start taking place and consequently slopes steeper than predicted are observed. In our DNKG and $ \beta $-FPUT simulations discussed in the manuscript, a proper balance between Fourier spacing and broadening is achieved. For the $ \alpha $-FPUT system, unfortunately the thermodynamic limit was never reached in our simulations. The reason is that the range in which simulations can be performed in the $ \alpha $-FPUT system corresponds to very weak nonlinearity, for which discrete effects start dominating. For larger nonlinearity (and large $ N $), the probability of a blowup becomes very large ^[7], making it impossible to run simulations. In practice, the $ \alpha $-FPUT system would need a higher level of nonlinearity in order to show the expected scaling due to the continuous resonant manifold. More specifically, for $ N = 1024 $, the $ \alpha $-FPUT system starts showing very often blowups beyond $ \epsilon\simeq 0.03 $, making it difficult to obtain the ensemble averages that we use in our treatment. The thermodynamic limit is very difficult to reach in the $ \alpha $-FPUT and this is why a steeper slope is observed. One more thing should be considered: in order to derive the Wave Kinetic Equation, a canonical transformation that removes the three wave nonresonant interaction is performed. The convergence of such transformation is unknown in the thermodynamic limit. Note that for fixed $ N $, if a simulation of the DNKG or $ \beta $-FPUT would have been carried out for weaker nonlinearity, a steeper power law would have been observed because of discreteness and possible higher order effects.

In ^[3] the authors perform a large number of simulations mainly with the $ \alpha+\beta $ model. For this model, our WT prediction for the equipartition time is $ 1/\epsilon^2 $ when $ \beta\ne \beta_{T} $; note that our $ \epsilon $ is proportional to $ \beta $. The result obtained in their simulation is $ 1/\epsilon^{2.25} $, which is definitely not far from the WT prediction. We may attribute this behaviour to an effect of discreteness in their simulations at low energies. As mentioned before, for a given value of $ N $, as the nonlinearity becomes small, the effect of discreteness starts emerging and this leads to a deviation form the WT prediction. Interestingly, the WT theory is able to predict the slopes shown in Figure 5 of ^[3]: For $ \beta = \beta_T $, $ \gamma = \gamma_T $ and $ \delta \ne \delta_T $ ($ \gamma $ and $ \delta $ are the coefficients of higher order interactions in the one dimensional chains and the subscript $ T $ corresponds to the Toda lattice coefficients) of the the prediction in the thermodynamic limit from WT theory would be $ 1/\epsilon^4 $ (it is a simple and straightforward calculation to show this). The physical reason is that for those parameters the first nontrivial resonant interaction is the six-wave one (the coefficient in the collision integral calculated on the resonant manifold would be zero for lower-order resonances, namely five-wave and four-wave resonances). Numerical simulations in ^[3] show a slope of -3.95 and -3.97, which are very close to -4, the prediction from WT theory. For $ \beta = \beta_T $ and $ \gamma\ne\gamma_T $ then it is easy to show that the first nontrivial interactions are the five-wave interactions which, according to our theory, give a slope of -3. Numerical simulations show -2.98 and -3.05. We think that the agreement of our WT theory prediction with the numerical results provided in ^[3] is not a coincidence.

We also remark that in WT theory the time of thermalization is estimated from the kinetic equation using a dimensional argument; this implies that the collision integral should be of order one and the predicted time scale would then given by the power of the small parameter $ \epsilon $ in front of the integral. When $ \beta\simeq\beta_T $, the four-wave collision integral is not of order one (for $ \beta = \beta_T $ it is actually zero). Interestingly, for $ \beta \gg \beta_T $ the prediction of our theory is $ 1/\beta^2 $, exactly what is observed in the simulations ^[3] (note that our small parameter $ \epsilon $ is proportional to $ \beta $).

At about the same time of the submission of the present manuscript, two paper have been submitted in the ArXiv, see ^[20,21]. Those authors perform similar simulations to ours but including other models. Their results are consistent with ours. As in our case, some deviations from WT are observed for $ \alpha $-FPUT and for very low nonlinearity in the $ \beta $-FPUT.

Concluding this part on the thermodynamic limit, we wish to stress that, despite not being fully rigorous, the Wave Turbulence theory offers a very good tool to predict the thermalization time scale in the broad regime consisting of the combination of weak nonlinearity and large-box limit, and its predictions apply to several results obtained from numerical simulations from different independent groups; the region of applicability of the theory (for example in terms of parameter space, discreteness, etc.) is still unclear and should be further investigated, both phenomenologically and rigorously. Further work should be performed for the $ \alpha $-FPUT which, apart from blowups, requires a canonical transformation before applying the WT theory. This could be problematic in the limit of small wave numbers.

7.2.   Discussion on the discrete limit with finite $ N $

While in the thermodynamic limit the boundary conditions should not matter, when $ N $ is not so large, boundary conditions may play a role. We must make clear from the beginning that in ^[3] and ^[4] the authors studied the FPUT system with fixed ends, i.e., in the case where all resonances are trivial, see ^[43]. In contrast, the FPUT system we study has nontrivial 4-wave resonances and 6-wave resonances: although in our case the resulting 4-wave resonant clusters of interacting modes are isolated and consequently lead to integrable systems, the resulting 6-wave resonant clusters are not isolated. They are typically connected via 4 common modes in the case of $ N $ even. This connectivity generically produces non-integrable systems. Therefore, from the point of view of energy transfers across Fourier modes in normal-form coordinates, the system we consider is much more active and thus one expects to see differences with respect to the system studied in ^[3,4]. At the same time, it is difficult to assess quantitatively these differences, because of a lack of a rigorous theoretical framework. Our scaling prediction for the time to equipartition relies on dimensional analysis of the kinetic equation, whose hypotheses do not necessarily hold in the discrete case.

Having made that clarification we now proceed to discuss our rationale. First, as mentioned previously, in the discrete case the hypotheses leading to the kinetic equation do not hold and therefore any prediction based on the kinetic equation is a conjecture. Second (not a conjecture), as mentioned above, in the discrete case $ 4 $-wave resonant interactions exist and are of umklapped type; they form isolated groups so these interactions are not efficient for thermalization. Therefore, for any specific value of $ N $ one applies formally a transformation of variables to normal-form coordinates, where the nonresonant terms are removed to obtain a discrete system containing $ 6 $-wave interactions (note that at this level, a thermodynamic limit would not make sense, because in such a limit, $ 4 $-wave interactions would dominate).

The normal-form coordinates satisfy a system of evolution equations where the only energy-transfer terms arise from $ 4 $-wave resonant interactions (forming isolated groups of $ 4 $ modes each) and $ 6 $-wave resonant interactions (which connect those isolated groups). With such a discrete system we may only conjecture that the time scale of interactions would be given by the square of the coefficient in front of the highest-order nonlinearity in the system (the prediction is made on spectrum and not amplitudes) This brings a scaling of $ -4 $. Now, numerical simulations show less steep values than predicted. In ^[3,4] for the discrete case a stretched exponential is considered. Based on this, we tried to fit our data with a stretched exponential and the fitting parameter is somehow consistent with the one obtained in ^[4]. More specifically, we can fit a stretched exponential if we include in the fit large values of nonlinearity. In contrast, when we restricted the fit to small values of nonlinearity, a power law seemed to be more appropriate. We do not exclude that for lower nonlinearity, other effects, such as for example higher order resonances ^[20], may take place, changing the behaviour of the curve. Despite the fact that our predictions seem plausible and not far from numerics, at the moment it is very difficult to make a final statement on the scaling of these discrete weakly nonlinear systems and further work is definitely needed.

8.   Conclusions

In this work, we have presented recent results on the dynamics of nonlinear chains, focusing on the thermalisation time. We have proposed to encompass the behaviour of all systems of this kind within the Wave Turbulence framework. In this context, the universal mechanism invoked to lead the systems to equipartition is the resonance among different modes, at least when generic initial conditions are considered. The scaling of the thermalization time $ T_\text{eq} $ as a function of the nonlinearity level of the system is obtained from the theory. The results show curves that can be fitted by power-laws for all the cases considered, with an exponent dependent on the order of the active resonances in the system. Although the point of view is rather different, present results are not in contradiction with the most recent and accurate estimates obtained also for particular low-wavenumber initial conditions ^[3]. Since the resonant manifold is significantly different in the discrete and thermodynamic $ N\rightarrow\infty $ limit, we have considered the two cases separately, and they lead to two different scalings. Notably, large-size chains reach equipartition faster.

Our aim in this paper has been to present the results anticipated in works ^[36,41,42] in an unified manner to underline how our approach can be systematic, rather than dependent on the particular features of the systems. In the thermodynamic limit, we have shown that there exists a resonant manifold of $ 2\rightarrow 2 $ waves. We have analysed numerically the thermodynamic limit $ N\rightarrow\infty $ for the $ \alpha $ and $ \beta $-FPUT systems, as done previously for the DNKG chain. In the discrete case, for $ N $ a power of two (which excludes the existence of five-wave resonant interactions ^[5]), we have extensively verified that, for all the considered systems, the leading order interaction consists of six wave interactions. All the results seem to indicate a universal route to thermalization predicted. We have also shown that, besides the $ \alpha $ and $ \beta $-FPUT systems, also the DNKG equation is asymptotically integrable, if the expansion is truncated at four wave interactions.

Acknowledgments

M. O. has been funded by Progetto di Ricerca d'Ateneo CSTO160004. M.O. was supported by the ``Departments of Excellence 2018-2022'' Grant awarded by the Italian Ministry of Education, University and Research (MIUR) (L.232/2016). Simulations were run on GPU hardware provided at the OCCAM facility, University of Turin.

Conflict of interest

The authors declare no conflict of interest.

Appendix

Let's define the function $ f_k = 2 |\sin(k/2)| $ as the linear dispersion relation for the $ \alpha $ and $ \beta $- FPUT models which corresponds to the general dispersion relation, $ \omega_k $, when $ m = 0 $. In ^[5] it has been shown that all processes $ X \rightarrow 1$ are forbidden for the dispersion relation $ f_k $.

where the equality holds only for wave numbers equal to 2$ l\pi $, with $ l\in{\mathbb{Z}} $. Here we show that

for any value of $ m > 0$. In order to show it, we square (8.2) and, after re-arranging, we get:

The function $ f_k $ is $ m $-independent, while $ \omega_k $ with $ m\ne0 $ is proportional to $ m $. The terms of the type $ -\omega_{k_i}^2 $ all cancel out. It is easy to observe that $ F(k_1, k_2, .., k_X; m) $ is an increasing monotonic function of $ m $. For $ m = 0 $, because of the inequality in (8.1), the $ F(k_1, k_2, .., k_X; 0)\ge 0 $; then, for its monotonicity, for any $ m > 0 $, $ F(k_1, k_2, .., k_X; 0) > 0 $. This proves that there are no resonances in the DNKG model of the type $ X\rightarrow $ 1.