This review describes the physiology of normal bone tissue as an introduction to the subsequent discussion on bone remodeling and biomechanical stimulus. As a complex architecture with heterogeneous and anisotropic hierarchy, the skeletal bone has been anatomically analysed with different levelling principles, extending from nano- to the whole bone scale. With the interpretation of basic bone histomorphology, the main compositions in bone are summarized, including various organic proteins in the bone matrix and inorganic minerals as the reinforcement. The cell populations that actively participate in the bone remodeling—osteoclasts, osteoblasts and osteocytes—have also been discussed since they are the main operators in bone resorption and formation. A variety of factors affect the bone remodeling, such as hormones, cytokines, mechanical stimulus and electromagnetic stimulus. As a particularly potent stimulus for bone cells, mechanical forces play a crucial role in enhancing bone strength and preventing bone loss with aging. By combing all these aspects together, the information lays the groundwork for systematically understanding the link between bone physiology and orchestrated process of mechanically mediated bone homoestasis.
1.
Introduction
Bone is a natural composite composed of a mineral phase and an organic matrix. It has remarkable mechanical strength and fracture toughness, and plays a significant role as an endocrinal organ in regulating the global mineral and nutrient homeostasis (e.g. FGF23 made by osteocytes for phosphate disposal, and osteocalcin produced by osteoblasts and osteocytes for efficient glucose utilization) [1]–[3]. With respect to most other organs and tissues in the human body, bone repair and regeneration contribute to perfect healing without the production of any fibrotic scars, representing the structural and mechanical commensuration with surrounding undamaged counterparts [4],[5]. Except the sesamoid bones, the adult human bone skeleton has a total of 213 bones, in which the appendicular skeleton, axial skeleton and auditory ossicles have 126, 74 and 6 bones, respectively [6]. During life, each bone continuously undergoes modelling and remodeling to alter shape, preserve strength and maintain mineral homeostasis. The predominant bone growth in childhood relies on bone modelling while in adulthood bone remodeling take its place for bone metabolism [7]. Bone remodeling is a process that old bone is removed and new bone is formed with the mineralization of newly synthesized bone matrix. The primary cells involved in bone remodeling are osteoblasts and osteoclasts [8]. By tightly coupling their functions, the resorption of old damaged bone and formation of new bone can be implemented sequentially. Acting as the mechanosensor and endocrine cells, osteocytes and lining cells are also indispensable in bone remodeling [9]. Terminally differentiated from osteoblasts, these cells construct a functional syncytium with osteoblasts within the bone tissue to promote the bone formation. Like muscles, the natural bone can increase its mass under high loadings and atrophy without external force applied. The adaptation of bone architecture to biomechanical stimulus has attracted a great attention during these decades with the most well-known theory proposed by Julius Wolff in 1892 [10]. His idea can be simply concluded into a rule that the bone structure can be autonomously adjusted by adapting to the applied mechanical load. In adult skeleton, exercise with frequent mechanical stimulus can not only reduce the bone resorption during bone turnover, but provide a better mechanical performance and a more youthful skeleton.
2.
The physiology of bone tissue
2.1. The hierarchical structure of bone
Due to its hierarchical architecture with heterogeneous arrangement, the complex organization of natural bone has been defined into varying distinct levels, spanning from nano- to whole-bone scales [11]. To better investigate this biologically-derived material with high irregularity, it's extremely important to figure out how many levels and which level is employed for a specific type of the bone. For instance, Weiner and Wagner proposed that lamellar bone can be classified into 7 levels relied on the hierarchical structure while Reznikov et al. adapted this scheme with 9 levels considering the presence of ordered and disordered materials in this bone type [12],[13]. All these user-oriented leveling methodologies aim at providing optimal strategies to depict natural bone tissues under specific conditions. Based on different research projects, molecular biologists and quantum chemists may use the nano- or sub-nanoscale leveling approaches for the mechanism study while morphological biologist may shift to macro- or mesoscale standards to characterize the bone skeleton.
With respect to the macro- or mesoscopic level, the skeletal system is composed of 20% inner trabecular bone surrounded by 80% outer cortical bone [14]. However, different bones or different sites within a bone have varying ratios of trabecular to cortical bones. In vertebra, the ratio reaches at 1:3 while the femoral head has a ratio of 1:1 [15]. As a dense and solid tissue, the high modulus (i.e. 16–23 GPa) of cortical bone provides a structural support to stabilize the inner porous structure [16]. In contrast, the honeycomb-like network of trabecular bone with soft textures and low modulus (i.e. 1–2 GPa) endows the tissue metabolism and bone marrow hematopoiesis with a favorable environment [17],[18]. On the microscopic scale, both trabecular and cortical bones are composed of repeating osteons. Trabecular osteons with semilunar shape has various plates and rods with the average thickness of 50∼400 mm to form an interconnecting framework with high porosities (40–90%) [18]. Also known as Haversian systems, cortical osteons in cylindrical shape has a branching network with a 200∼400 mm width at their base. Compared to trabecular bones, the porosity of cortical bones is normally lower than 5% but affected by bone modelling at different stages of human life [19]. Although structural discrepancies exist in the whole skeletal system, the basic components constructing the bone tissue are always the same, contributing to the structural consistence at the nanoscale level [20].
2.2. The molecular components of bone
As a mineralized composite, the main composition involved in the bone architecture can be categorized as an organic phase and an inorganic phase. Accounting for around 85% organic bone proteins, type I collagen (300 nm long, 1.1–1.5 nm wide) plays a vital role in the formation of bone matrix [21]. It is a triple helical biomolecule composed of highly repeated amino acid residues (glycine-X-Y), in which X and Y are normally proline and hydroxyproline [22]. With the incorporation for trace amounts of other type collagens, these molecules are self-assembled together into microfibrils with varying diameters via hydrophobic and electrostatic forces [23]. The collagenous microfibrils are then directed and agammaegated into fibrils with the aid of another minor bone matrix protein called fibronectin. Genetic studies have demonstrated that the source of this key protein mainly comes from the liver circulation although human bone can also synthesize fibronectin [24]. Another liver secretory glycoprotein named Fetuin (or α2-HS glycoprotein) has also found at high levels in bone tissues and regulate the bone mineralization via binding to transforming growth factor-β (TGF-β) or bone morphogenetic protein (BMP) [25]. In addition, the bone produces nearly 10% non-collagenous proteins (NCPs) with a great significance in matrix mineralization, cell signaling and tissue metabolism [26]. Thousands of NCPs in the extracellular matrix (ECM) have been found up to now and can be broadly divided into several categories based on their internal featured groups, such as small leucine-rich group, small cysteine-rich group, small integrin-binding N-glycosylated group and γ-carboxyglutamic acid group [27],[28]. Recent research showed that some NCPs (e.g. osteocalcin, osteopontin and osteonectin) have the “glue” effect to enhance the bonding between collagenous fibrils and apatites [29]. However, the roles of each NCP are still not well defined at present since many of them seem to have multiple functions, including the regulation of bone mineral tunerover, modelling, remodeling and cell activity.
The inorganic content of natural bone is mostly hydroxyapatite (HA), a thermodynamically stable biomineral [Ca10(PO4)6(OH)2] with the Ca/P ratio keeping at less than 1.67 [30]. Compared to geological HA crystals, the biosynthesized counterparts are very small, measuring the largest dimension of only around 200 Å. The small and poorly crystalized HA normally has higher solubility, thereby facilitating the mineral metabolism during the bone growth [31]. Since the bone HA is a flexible material, the phosphate and hydroxyl sites can be replaced with carbonate, magnesium, sodium and acid phosphate ions. Nevertheless, the improper incorporation of some other ions may result in low mineralization, impaired mechanical performance and increased fracture risk [32]. As the chief reinforcer of collagenous matrix, the HA content has a vital impact on the strength and stiffness of bone. By using full-atomistic calculations to assess the mechanical properties of collagen matrix with altering HA concentrations, it was proposed that the stress-bearing capacity of this three-dimensional collagen-fiber network can be raised up to four times [33]. Bone minerals are initially deposited at the space between the ends of collagen fibrils [34]. In vitro studies testified that some acidic NCPs promote the ordered deposition of HA by regulating the content, shape and size of apatites formed while the detailed in vivo HA mineralization process remains obscure [35]. Besides, Vitamin D also plays an indirect role in stimulating the HA crystallization through maintain serum calcium and phosphorus at ample concentrations for passive deposition [36].
3.
Cells in bone remodeling
3.1. Osteoclasts
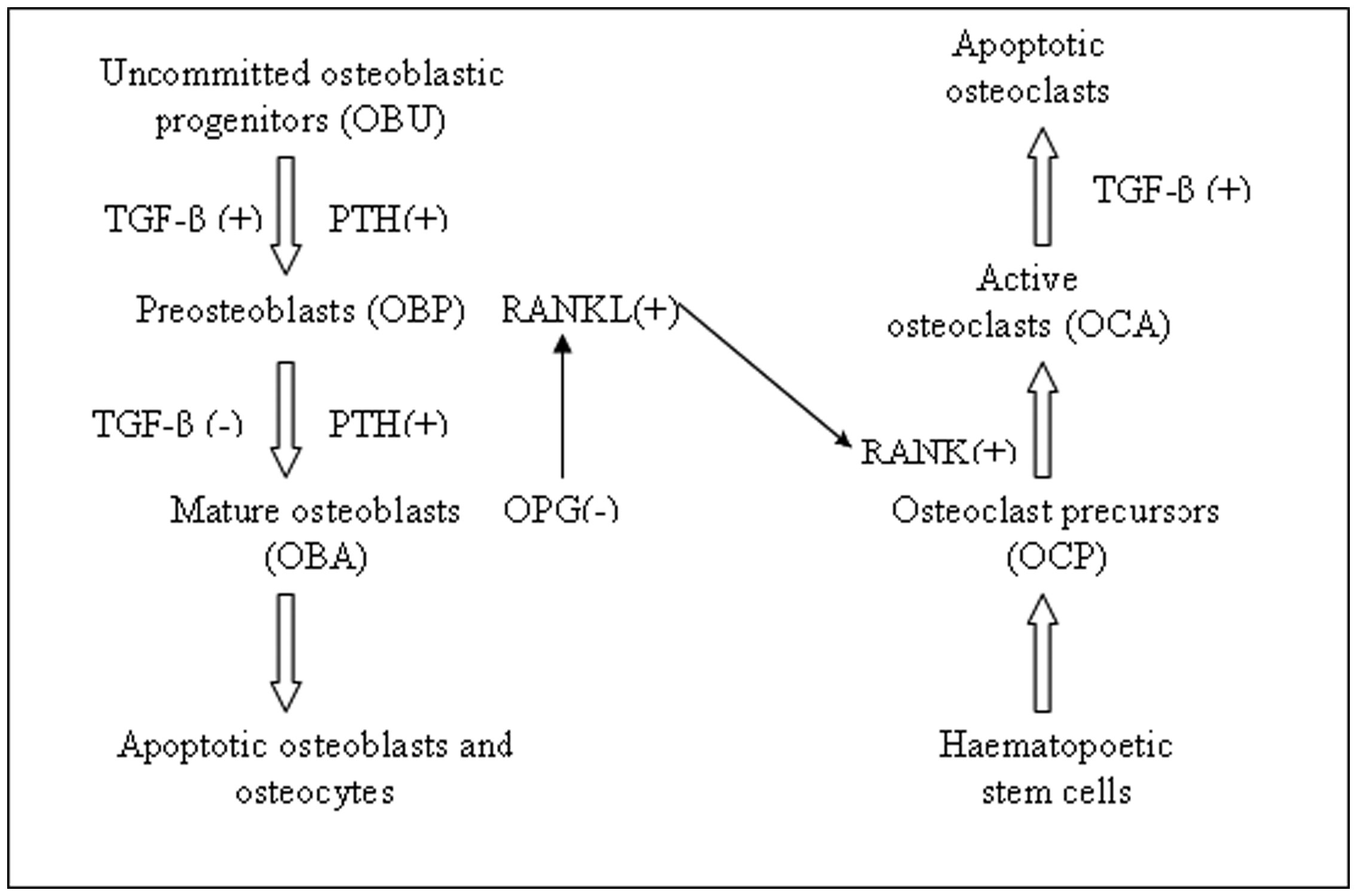
Derived from the hematopoietic monocyte macrophage lineage, osteoclasts are large multi-nucleated cells capable of bone resorption [37]. It has been demonstrated both in vivo and in vitro that the differentiation, proliferation and activity of osteoclasts are closely related to two key cytokines: macrophage colony-stimulating factor 1 (M-CSF) and receptor activator of NF-κB ligand (RANKL) [38],[39]. Through binding directly to the receptor (i.e. c-fms) on the membrane of osteoclast progenitors, M-CSF can not only facilitate their proliferation but up-regulate the cell activity, preventing the occurrence of apoptosis [40]. Yoshida et al. found that the rodents suffered from severe osteoporosis after mutating the coding gene of M-CSF owing to the generation of functionally inactivated M-CSF [39]. Belonging to the Tumor Necrosis Factor (TNF) gene family, RANKL is mainly expressed on the surface of immature osteoblasts or marrow stromal cells with the positive expression being achieved by systemic and local factors such as parathyroid hormone (PTH), interferon-1 (IL-1) or prostaglandins [41]–[43]. Basically, the binding between RANKL on osteoblast surface and RANK on osteoclast surface is realized via the cell-cell interaction so as to induce the osteoclast formation [44]. However, osteoblasts can also synthesize osteoprotegerin (OPG), a soluble decoy receptor that can firmly attach onto the ligand RANKL and limit the osteoclast activity. Therefore, the relative contents of RANKL and OPG expressed by osteoblasts have a crucial influence on the differentiation, proliferation and function of osteoclasts [45],[46]. A bone cell model with RANK/RANKL/OPG signaling pathway between osteoblasts and osteoclasts, PTH and the dual action of TGF-β is illustrated in Figure 1 [47]. In case of inflammatory dysfunction like rheumatoid arthritis, the ratio of RANKL to OPG to a certain extent will be increased, resulting in the enhanced osteoclastogenesis [48].
The bone resorption is commenced by migrating non-polarized, mature osteoclasts onto the bone matrix. The attachment of these osteoclasts leads to the formation of podosomes that employ various integrins and cytoskeletal proteins to construct an actin core and ring complex [49]. By interplaying with bone matrix proteins (e.g. osteopontin and vitronectin), osteoblasts are polarized with the cell membrane transforming into three different domains, including the basolateral membrane (BM) unattached to the bone, the sealing zone (SZ) closely contacted with bone matrix and the ring-shaped ruffled border (RB) encompassed by the sealing zone [50],[51]. Since the SZ has a diffusion barrier around the RB to sustain a stable proton and protease concentration in this resorption compartment, a disruption on the formation of SZ or RB may largely hamper the bone resorption [52],[53]. In order to dissolve the mineral HA in bone, an acid environment (pH∼4.5) is created with the pumping and translocation of protons via the action of carbonic anhydrase and V-type ATPase, respectively. The hydrochloric acid secreted by osteoclasts initiates the decomposition of bone minerals into calcium and phosphate ions [54]. With the demineralization of the bone material, two major proteases are engaged into the degradation of the bone organic phase: lyosomal cathepsin K and matrix metalloprotein-9 (MM9). The former is mainly responsible for degrading type-1 collagen under the acidic milieu while the latter plays a crucial role in removing the collagenous layer on bone surface to initiate the bone resorption and digesting the remaining collagen pits after cathepsin K degradation [55],[56]. The decomposed calcium and phosphate ions after bone resorption are endocytosed, transported and then released by osteoclasts into the blood stream, in which the high concentration of these ions may cause the podosomal disassembly and osteoclast apoptosis [57],[58]. Up to now, numerous substances have been demonstrated to restrict the bone resorption by facilitating their apoptosis, including TGB-β, estrogen, calcium, tamoxifen, bisphosphonates, denosumab (a monoclonal antibody against RANKL), etc [59]–[61]. However, bisphosphonates are the only drugs approved by FDA to treat diseases with high bone turnover (e.g. osteoporosis and Paget's disease of bone) [62].
3.2. Osteoblasts
As the primary cells for bone formation, osteoblasts are originated from pluripotent mesenchymal stem cells. These cells have a great potential to differentiate into a variety of musculoskeletal tissues (e.g. cartilage, muscle, ligament, tendon and bone) based on various regulatory transcription factors and biochemical factors that act on them [63]. The osteoblast precursor cells proliferate once the osteoblast lineage is transformed from skeletal stem cells. Several protein and signaling pathways are involved into the regulation of osteoblast differentiation and proliferation, such as BMPs from the large super family of TGF-β and wnt signaling pathways. It has been shown that BMPs can not only induce osteoblast differentiation via Smad dependent signaling pathway, but initiate the expression of osteoblast-derived proteins like osteocalcin and alkaline phosphatase [64],[65]. By activating a series of intracellular signaling cascade, wnt proteins play a crucial role in bone formation as facilitators for the expression of osteoblastogenic transcription factors (e.g. Osterix and Runx2) [66]. Moreover, the canonical wnt signaling is closely related to the anabolic effects of PTH on bone growth, which can regulate calcium homeostasis and prevent the apoptosis of osteoblasts and osteocytes [67]. Results showed that the sympathetic nervous system can also affect the osteoblast function by stimulating β adrenergic receptors on its cell membrane so as to increase bone resorption and reduce bone formation, finally leading to the occurrence of osteoporosis [68].
With the further maturation into cuboidal osteoblasts, these cells function as clusters along the bone surface, engaging in the production of bone matrix by synthesizing and depositing type I collagen [69]. The osteoblast is also responsible for the mineralization of this newly formed bone osteoid by locally secreting the phosphate from with the aid of osteocalcin and alkaline phosphatase. The HA crystal is formed by coordinating these phosphates with calcium from the extracellular fluid [70]. The proper ratio of organic matrix to mineral is vital to strike an optimal balance between stiffness and flexibility of the bone structure. Normally, the human bone contains approximately 60% inorganic HA, 10% water and 30% polymer matrix collagen fibers and other organics [71],[72]. Apart from their role in bone growth, osteoblasts are also involved in the modulation of osteoclast activity by expressing M-CSF, RANKL or OPG [73]. Mature osteoblasts after bone formation may lead to apoptosis or coalescence into inhomogeneous population with bone-lining cells. Some of them may even convert into osteocytes, being encased and trapped into the matrix. This phenomenon is greatly affected by the age of mammals and bone types [74].
3.3. Osteocytes
Accounting for more than 90% of all cells in bone, the abundance of osteocytes highlights the significance in shaping and maintaining bone mass in the skeletal structure [75]. The terminal differentiation of osteoblast lineage after bone formation contributes to the birth of pre-osteocytes residing in the unmineralized osteoid with various matrix proteins, in which most of them are type I collagen [76]. Along with the osteoid mineralization via a precisely controlled process, these encased cells mature further, digest off over 70% organelles and cytoplasm, and finally become dentritic-like osteocytes with a star-shape appearance [77],[78]. By virtue of these long, slender dentrites on cell surface, osteocytes are highly linked with other cells (e.g. osteoblasts and osteocytes) through the lacunar-canalicular network both in the bone matrix and on the bone surface. Nutrients, oxygen and other metabolites from blood vessels thus can be transported to bone cells, as well as the delivery of signaling molecules between each other. This largely facilitates the communication in whether neighboring cells or far-apart cells without direct contact [79].
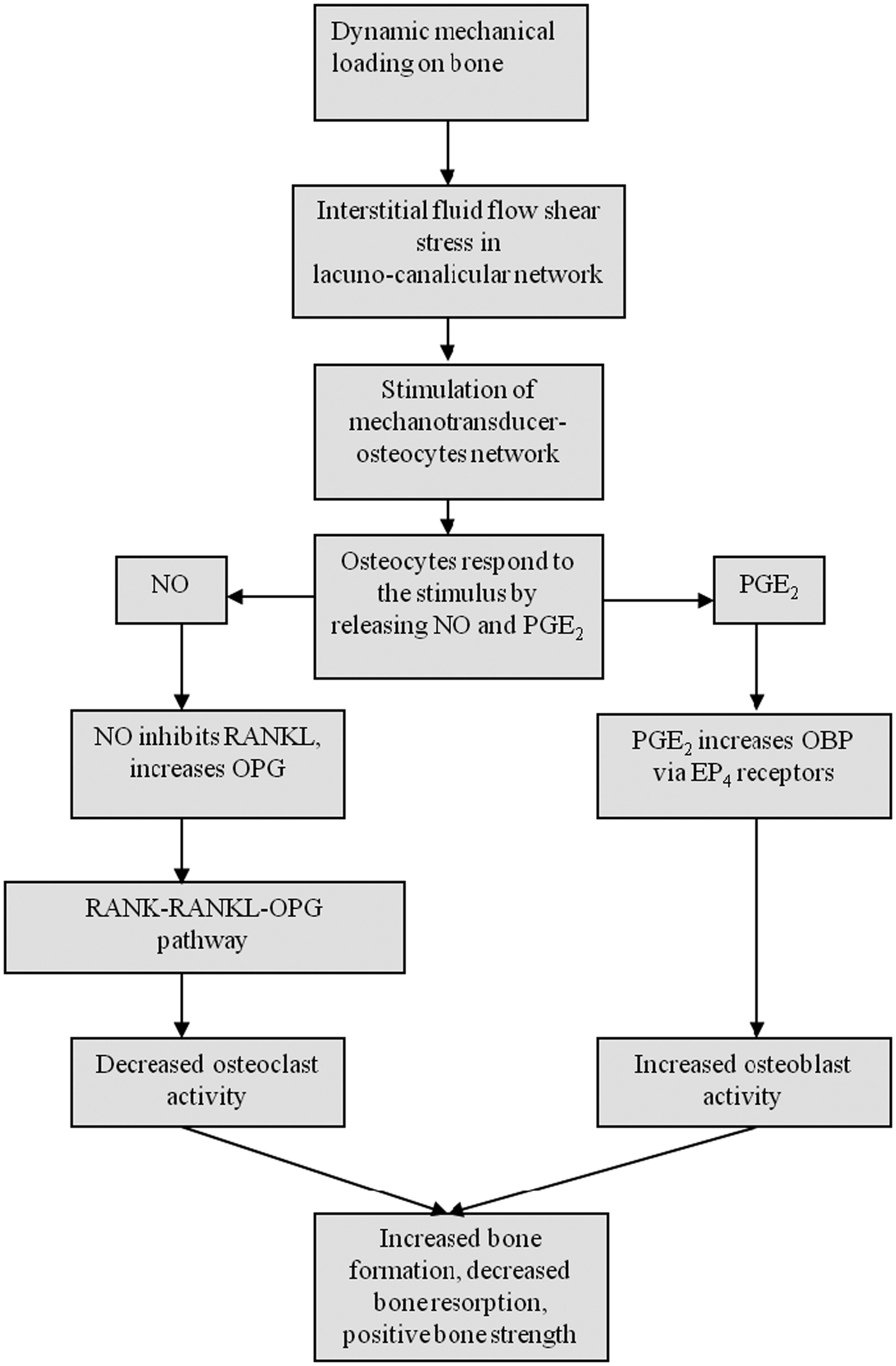
Osteocytes located in the osteoid have the capacity to sense the applied stress on bone and give a proper response. This action has been widely accepted as “mechanostat” for the bone growth and bone loss [80]. The microdamage within the bone structure caused by mechanical forces (e.g. walking, jumping and resistance training) is detected by these monitoring cells with a fine modulation of bone remodeling by sending corresponding signals to regulate the activity of osteoblasts and osteoclasts [81]. Numerous messengers have been identified in recent years, such as nitric oxide, sclerostin, prostaglandin E2, RANKL and insulin-like growth factor-1 (IGF-1). Further research may therapeutically provide useful strategies for the treatment of some bone diseases like osteoporosis, osteopetrosis and osteopenia [82]. In addition to mechanical signaling, osteocytes can also sense signals from various metabolites. For instance, with aging, the drop of estrogen level in human body leads to the death of these cells and associated bone mass decrease [83].
4.
The bone remodeling process
Bone remodeling is a process that the existing bone is replaced and renewed to sustain the mechanical properties of bone and mineral homeostasis [84]. The discrete packets of old bone are continuously removed and refilled with newly synthesized organic matrix, in which the mineralization with HA deposition follows to form new bone so as to reduce the accumulation of bone microdamages. It occurs before birth and continues throughout the whole lifetime [31]. Five stages are involved into the bone remodeling cycle: activation, resorption, reversal, formation and termination. A coupled mechanism that regulates the bone resorption and formation via osteoclasts and osteoblasts is established during the remodeling via the temporary anatomical structures called “Basic Multicellular Units (BMUs)” [85]. The sequential arrangement of bone cells within the active BMUs is critical to ensure each phase of bone remodeling is orderly proceeded. Although remodeling sites are thought to begin in a random fashion, specific damaged areas that need to be repaired could be targeted for the bone health [86].
As the first stage of bone remodeling to turn the quiescent state, activation involves the recruitment of monocyte-macrophage osteoclast precursor from the circulation after detecting the initiating signals. These related signals can be either hormone (e.g. PTH and estrogen) from the alteration of systemic homeostasis or from external mechanical stimuli [87]. Details on the correlation of physical forces and biological signal generation for remodeling will be discussed in the next section. With the detection of these signals, the endosteum is lifted from the bone surface by lining cells and the endosteal membrane is degraded by the introduction of collagenase and osteoclast precursors [88]. The osteoclasts then differentiate and bind to the bone surface by the interaction between integrin receptors of their cytoplasmic membranes and RGD (arginine, glycine and asparagine)-containing peptides in matrix proteins, to form SZ domain in the bone resorption compartment [89].
It takes approximately 2–4 weeks to complete the bone resorption during each remodeling cycle. As the main player for this stage, osteoclasts secrete hydrogen ions through proton pumps on their membranes so as to decrease the bone-resorbing compartment pH to around 4.5. The acidic microenvironment created by resorbing osteoclasts facilitates the mobility of bone minerals [90]. These cells also secrete other enzymes from their lysosomes to digest the organic matrix of bone, such as tartrate-resistant acid phosphatase, matrix metalloproteinase, cathepsin K, etc [91]. This contributes to the formation of various cavities where saucer-shaped Howship's lacunae and Haversian canals are generated in trabecular and cortical bone, respectively. The apoptosis of multinucleated osteoclasts symbolizes the end of bone resorption phase.
The transition from bone resorption to bone formation is regarded as reversal stage, during which a bunch of mononuclear cells (i.e. monocytes, preosteoblasts and osteocytes) are recruited in those cavities to start the new bone formation [92]. Although coupling signals employed in this phase to shift from the end of bone resorption to the beginning of bone formation are still unclear, various bone matrix-derived factors have been put forward to be the reversal signal candidates, including TGF-β, BMP, platelet derived growth factor, fibroblast growth factor, etc [93],[94]. For instance, TGF-β content in bone matrix has a close association with bone turnover indices like serum osteocalcin and alkaline phosphatase that are osteoblast-yielded proteins to facilitate collagen matrix and minerals synthesis. By hindering RANKL production from osteoblasts, TGF-β negatively affects the amount and activity of osteoclasts to decrease the bone resorption [95],[96]. Osteoblast-linage cells gradually replace osteoclast to be the main protagonist in the next phase.
Normally, the bone formation process needs 4–6 months to complete. The new collagenous matrix with HA mineralized and deposited inside is achieved by the regulation from osteoblasts. These cells secretes small, membrane-bound matrix vesicles that incorporates a large amount of calcium, phosphate and enzymes to digest mineralization inhibitors (e.g. pyrophosphate and proteoglycans) [97]. The new bone is synthesized with osteoblasts surrounded and entombed within this new bone matrix, giving rise to the transformation to osteocytes and bone-lining cells. Via the gap junctions built from the cytoplasmic processes of osteocytes, a functional syncytium is created from the wide canalicular network with the connection among osteoblasts, bone-lining cells and other osteocytes [98]. In the end, 50% to 70% of osteoblasts undergo apoptosis with the balance converting to osteoblasts and bone-lining cells [99]. Moveover, acting as a blood-bone barrier, lining cells inhabited on the bone surface can not only regulate the flow of mineral ions into and out of bone extracellular fluid, but possess the capacity to redifferentiate into osteoblasts under the stimuli of related hormone (e.g. PTH) and mechanical forces [100].
After around 30 days of the osteoid formation, the mineral deposition is initiated and lasts for 90 days in trabecular bone and 130 days in cortical bone. After that, a quiescent phase comes with the final termination of bone remodeling [101]. The adult cortical bone turnover is at the rate of 2–3% per year, which is adequate to preserve the bone mechanical strength. The rate of trabecular bone turnover is found to be higher due to the requirement of maintaining the mineral metabolism [31]. The newly formed bone with a relatively low mineral content facilitates the ion exchange with the extracellular fluid. Usually, the endosteal bone has more old bone resorption than new bone formation, opposite to the situation occurred in periosteal bone. Since the net change in endosteal resorption becomes larger than that in perosteal formation with aging, human bone contents decrease with higher risk of stress fracture [102].
5.
Biological effects of mechanical stimulus
Mechanical stimulus produces a profound influence on bone remodeling. Under no or low loading situations, the bone turnover leans to a rapid loss of bone mass due to the bone resorption surpassing the bone formation. Conditions like long-term bed rest, cast immobilization and microgravity (e.g. astronauts in weightless environment of a space station or shuttle) may result in this type of bone loss and mineral reduction which might be ascribed to the lack of convective fluid flow within the canalicular network [103]. In contrast, overuse or increased loadings such as resistance training and long-distance running can stimulate the bone remodeling with more bone gain by first eliciting microcracks and focal damage in the bone tissue. As is well known, the main purpose of bone remodeling is to continuously replace and renew the old bone tissue. If the damage with microcracks accumulates faster than the “repairing” process via the combination between compromised bone resorption of osteoclasts and new bone formation of osteoblasts, larger cracks develop and eventually propagate to an unrepaired stress fracture [104].
The increased number of bone remodeling sites with mechanical stimulus is realized by programmed cell death in osteocytes [105]. The mechanism underlying osteocyte apoptosis is still not well explain but may be generated from the direct cell damage via microcracks in bone tissue or the above-mentioned reduced convective fluid flow. The impacts of mechanical loadings on bone remodeling adhere to a U-shaped curve, where the remodeling level is raised up under disuse or overload conditions [106]. A range of loading called physiological range also can be observed in which the bone turnover level drops to be minimum. Compared to the bone remodeling, periosteal bone formation shows a steady upward trend with the increased loading, implying that the mechanism regulating bone growth and modelling is different with that regulating bone remodeling.
The adaptive response of bone remodeling under mechanical stimulus is highly site oriented. Well-established mathematical and numerical methods were employed for analyzing the complex remodeling process [107]–[115]. Further, researchers have conspicuously seen that at the entire skeletal system, only the bone with certain loadings may undergo adaptation [116],[117]. This phenomenon is well supported from human research regarding the skeleton health indices in athletes. For instance, racquet sports (e.g. tennis) players have higher bone mineral density and cortical bone content for their racquet arm than those in the unloaded arm [118]. The site-oriented deposition of new bone plays a significant role in bone functional progress. It aims at the specific bone with frequent high loadings to increase the burn formation and enhance its strength, while not unnecessarily increases the whole bone mass or density [119].
Differentiated from osteoblasts, Osteocytes within the bone matrix and lining cells on the bone surface are thought to be the chief mechanosensors in skeletal system [120]. Their abundance and high connectivity contributes to the precise detection of mechanical strains like an antenna. The targeted ablation of osteocytes via the injection of diphtheria toxin in mice results in fragile bone with intracortical porosity, trabecular bone loss and adipose tissue proliferation in marrow space while the unloading-induced bone loss is restricted, which demonstrates the role of osteocytes in mechanotransduction [121]. As the most and second most cells in bone tissue, the total number of these two types of cells is 20 folds relative to that of osteoblasts and osteoclasts [122]. When osteocytes are subjected to the bone deformation, they detect this mechanical force and secrete several messengers, such as prostaglandins and nitric oxide [123]. During this process, the external force pushes extracellular fluid with certain viscosity back and forth through the extracellular space, yielding the corresponding shear stress on osteocyte membrane and drag force on ECM proteins. The magnitude of the fluid force depends on the loading rate, verifying that bone tissue is more sensitive to dynamic forces [124]. On the other hand, the average strain exerted on bone matrix should be lower than 0.7% (7000 µε) since too large strain will permanently damage the bone. Strains in the normal locomotor range between 500 µε and 2500 µε while this strain will be amplified at the cellular level [125]. The theoretical model depicts that cells can has 3–7 fold deformation compared to the average strain in bone tissue. Recently, another mechanotransducer (i.e. Piezo1) for various biological processes has been found to be crucial in bone formation via the disruption of osteogenesis from osteoblasts [126]. In addition, the latest models have been published for the bone remodeling mechanism under the corresponding mechanical stimulations [127]–[130]. We also developed a bone cell population dynamics model that not only has a great consistence with experiment results on bone mineral content and bone fracture energy under different loading schemes, but predict the real-time development pattern of these values for each loading scheme, which is hard to be monitored via experiments (Figure 2) [131].
6.
Conclusion
As the main mechanical support in the skeletal system, natural bones are a complex, hierarchical composite with a reinforcing phase and a matrix phase. The reinforcing phase is mainly composed of HA mineral to provide high rigidity and stiffness, while the matrix phase is mostly consisted of collagen fibrils to give flexibility and resilience to the bone. At certain time intervals or in response to damages with microcracks, the complex bone remodeling will be initiated with the engagement of primary bone cells (e.g. osteoclasts, osteoblasts and osteocytes) and a variety of factors that regulate the differentiation, proliferation and activity of these cells. Mechanical stimulus is a simple and effective scheme to modulate the bone gain and loss, thereby indirectly affecting the bone stiffness and strength. With the more discovered knowledge on the cellular and molecular mechanisms involved in bone cell mechano-transduction, new schemes for therapeutic intervention can be created via triggering proper mechano-signaling cascades without applying any force onto the bone.









 DownLoad:
DownLoad: