1. Introduction
G protein-coupled receptors (GPCRs) mediate cellular communication by regulating signal transduction through heterotrimeric G proteins and β-arrestins. This family of receptors represent one of the most important therapeutic targets for the pharmaceutical industry [1], and, as such, its members are key targets for structure determination. Crystallisation of GPCRs has proved to be one of the biggest challenges in structural biology in recent years, but one that has ultimately been overcome by technical innovation. The development and application of novel methodologies, including T4 lysozyme fusion proteins [2], conformational thermostabilisation [3] and lipidic cubic phase crystallisation [4,5], has resulted in 277 structures of 54 different receptors being determined to date [6]. These have provided unparalleled insight into the mechanism of ligand binding and receptor activation, and are currently being used by the pharmaceutical industry to facilitate the development of novel therapeutic compounds [7]. However, it has become evident that to understand the activation mechanism of individual receptors, and to fully exploit the potential of structure-based drug design, each receptor should ideally be characterised in a minimum of four distinct conformational states, bound to either: an inverse agonist; an agonist; an agonist and G protein; or an agonist and arrestin [8].
Structural and functional characterisation of GPCRs in their active conformation [8], i.e. bound to a heterotrimeric G protein [9] or β-arrestin [10], has proved to be particularly challenging, due to the large size, instability and conformational dynamics of these complexes [11,12]. Whilst it is true that structure determination of receptors bound to native signalling proteins is most desirable, the success rate of crystallising these complexes has been particularly low. Therefore, driven by the need to expedite the structure determination of receptors in their active conformation, a number of G protein mimetics have been developed, including G protein-derived peptides [13,14], nanobodies [15] and mini G proteins [16]. The aim of these surrogates is to bind the receptor and stabilise its active conformation, whilst eliminating the problems inherent to native signalling proteins. However, these mimetics have both advantages and disadvantages compared to heterotrimeric G proteins. The C-terminal peptide (GαCT) from the G protein α-subunit (Gα) is the smallest and simplest of the G protein mimetics, and it has facilitated the determination of numerous active-state rhodopsin structures [13,17,18,19,20,21,22]. However, such peptides do not appear to efficiently stabilise the active conformation of other receptors, and are therefore of limited use for studying the wider GPCR family. Nanobodies have proved to be effective G protein surrogates that are able to induce comparable pharmacological and structural changes in the receptor to those elicited by heterotrimeric G proteins [23,24,25,26,27]. Their small size and rigid structure makes them particularly well suited to X-ray crystallography applications [28], but their inability to recapitulate the native GPCR-G protein interface means that these structures do not provide insight in to the molecular determinants of G protein coupling specificity. They also require laborious immunisation and selection procedures that must be performed for each receptor being studied. Mini G proteins (see Section 2) induce comparable pharmacological and structural changes in the receptor to those elicited by heterotrimeric G proteins, retain their natural coupling specificity [16,29] and recapitulate the native GPCR-G protein interface [30]. Mini G protein versions of at least one member of the four G protein families have been developed, they can therefore be used off-the-shelf to study a wide variety of receptors. However, the Gq class proved difficult to develop, and required the construction of chimeric proteins that are less biologically relevant [29].
Clearly, none of these surrogates represent a silver bullet for characterising GPCRs in their active conformation, and the stability of individual receptors remains a key factor in the success of structural studies. Nonetheless, together they comprise a toolkit of binding proteins that have greatly simplified the characterisation of active-state GPCRs, and have provided valuable insight into the mechanism of receptor activation. Mini G proteins are the latest addition to this toolkit, and, in this review, I present an overview of their current applications to study the structure and function of GPCRs.
2. Development of mini G proteins
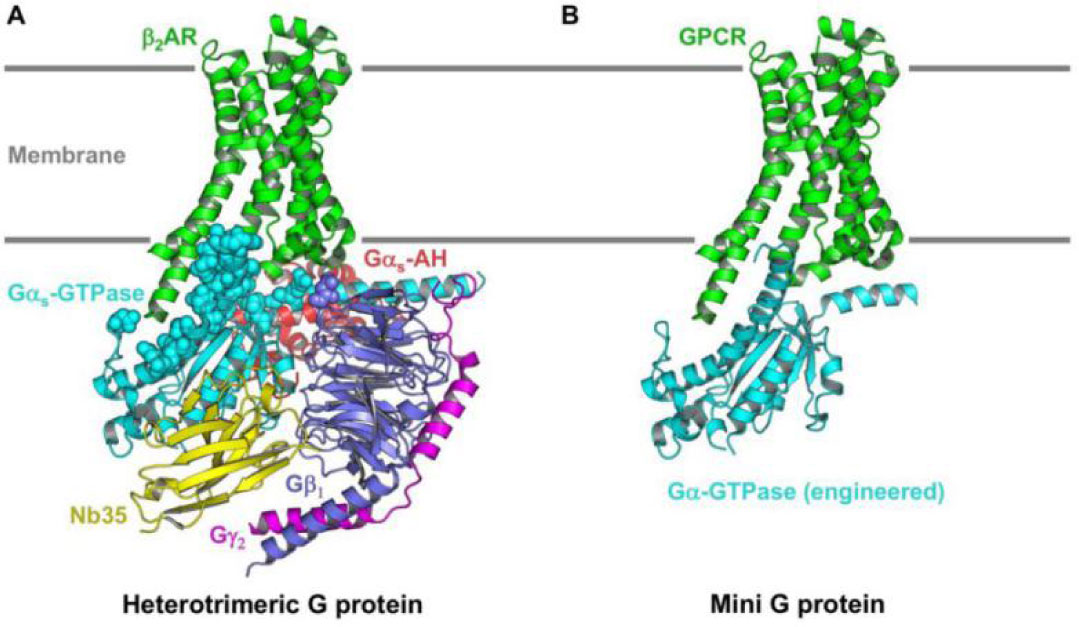
The observation that led to the development of mini G proteins came from structure of the β2-adrenergic receptor (β2AR) in complex with heterotrimeric Gs [9]. Despite the G protein having a molecular weight of over 90 kDa, the structure revealed that virtually all of the molecular contacts that it formed with the receptor were mediated by the ∼30 kDa GTPase domain from Gαs (Gαs-GTPase). The original mini G protein (mini-Gs) was constructed by isolating the Gαs-GTPase domain (Figure 1), and engineering it to increase its thermostability and reduce conformational dynamics. This was achieved using rational design mutagenesis, based primarily on the structure of Arl2 [31], the small G protein that is most structural similarity to Gαs [32]. The optimal construct contained deletions in three key regions, namely the α-helical domain (Gα-AH), switch III and the N-terminus. The Gα-AH domain was the most conformationally dynamic region in the β2AR-Gs complex [9,11]; its deletion not only reduced conformational dynamics, but also enabled the Gα-GTPase domain to couple receptors in the absence of the G protein βγ subunits (Gβγ) [16]. Switch III was disordered in the receptor-bound conformation [9], and is completely absent from small G proteins. Its deletion was designed to replace this flexible region with the defined secondary structure elements found in Arl2 [16,30,31]; this resulted in an increase in both the thermostability and expression level of the mini G protein [16]. The N-terminal helix normally interacts with Gβγ, and is therefore not explicitly required in the mini G protein. Deletion of the complete N-terminus had a detrimental effect on both the thermostability and expression level of the mini G protein, consequently, only residues 1-25 were deleted. Nevertheless, this removed a substantial region of conformationally dynamic protein, and also eliminated the lipidation sites that tether Gα to the cell membrane [33]. The optimal construct also contained seven point mutations [16], none of which were located within the receptor-binding site. The G49D, E50N, A249D and S252D mutations were designed to stabilise the nucleotide-binding pocket and phosphate-binding loop; they resulted in increased thermostability of the mini G protein, as well as increased expression levels. The L272D mutation was incorporated to conformationally constrain the flexible switch II region. The I372A and V375I mutations, which are located within the α5 helix, were designed to stabilise the receptor-bound conformation of the mini G protein, particularly in the presence of detergent, by improving packing of the α5 helix against the core of the protein. The I372A mutation was also shown to render the complex largely resistant to dissociation by cellular concentrations of guanine nucleotides [16]. Residue I372 appears to act as a relay, transmitting the conformational rearrangements induced by receptor binding from the α5 helix to the nucleotide-binding pocket; the I372A mutation appears to prevent the propagation of these conformational changes, and thus uncouples receptor binding from nucleotide exchange [16]. The final mini-Gs construct was shown to induce a shift in the agonist-binding affinity of both the β1-adrenergic receptor (β1AR) and the adenosine A2A receptor (A2AR) comparable to that elicited by Gs, demonstrating that it functioned as an effective mimetic of the heterotrimeric G protein [16,30]. To prove that mini-Gs could facilitate the structure determination of a receptor in its active state, it was crystallised in complex with A2AR, and the structure solved at 3.4 Å resolution [30,34] (see Section 3.2). Comparison of this structure with that of β2AR-Gs revealed striking similarities in the organisation of the complex. Critically, the α5 helix and C-terminus of the mini G protein undergo comparable conformational changes to those observed in the heterotrimeric G protein, demonstrating that the mini G protein does indeed recapitulate the native GPCR-G protein interface [30].
Following the successful development of mini-Gs, the concept was transferred to the other classes of heterotrimeric G proteins; the goal being to convert at least one member of each family into a mini G protein [29]. To date, this has been directly achieved for members of the Gs, Gi and G12 families (see Table 1 for details), but only indirectly for Gq family members (discussed below). Mini-Gq could not be expressed in a functional form, so instead a chimera was constructed, in which residues from mini-Gs that interact with either A2AR or β2AR in the respective crystal structures [9,30] were mutated to match those found in Gq. This approach is not ideal since it cannot account for structural differences between Gs and Gq, or variations in the molecular contacts that they form with Gs- or Gq-coupled receptors, respectively. Nonetheless, the mini-Gs/q chimera did interact with Gq-coupled receptors such as the neurotensin receptor (NTSR1) and the angiotensin II receptor (AT1R), and did not bind Gs-coupled receptors such as A2AR [29]. Therefore, it is a useful tool for the functional characterisation of Gq-coupled receptors, but, since it is unlikely to fully stabilise the receptor in its active state or perfectly recapitulate the native GPCR-G protein interface, it may not be the best option for structural studies. Development of mini-Gi also proved difficult, and so a chimera with mini-Gs (mini-Gs/i) was constructed. This has been used successfully in cell-based assays (see Section 4.2), although mini-Go remains the best Gi family member for structural studies (see Table 1).
Table 1. Mini G proteins.
| Family |
Mini G proteins |
GPCRs shown to bind in vitroa |
GPCRs shown to bind in vivob |
Structures determined |
| Gs |
mini-Gs |
A2AR |
A2AR |
A2AR-mini-Gs |
|
|
|
|
A2AR-mini-Gs-β1γ2c |
|
|
β1AR |
|
|
|
|
|
β2AR |
|
|
|
|
D1R |
|
|
|
|
D5R |
|
|
|
|
V2R |
|
|
mini-Golf |
A2AR |
|
|
| Gi |
mini-Gi1 |
5-HT1BR |
|
|
|
mini-Gs/i1d |
5-HT1BR |
|
|
|
|
|
α2A-AR |
|
|
|
|
A1R |
|
|
|
|
CB1R |
|
|
|
|
D2R |
|
|
|
|
M4R |
|
|
mini-Go1 |
5-HT1BR |
|
5-HT1BR-mini-Go1-β1γ2c |
|
|
Rhodopsin |
|
Rhodopsin-mini-Go1 |
| Gq |
mini-Gs/qd |
NTSR1 |
|
|
|
|
AT1R |
AT1R |
|
|
|
|
ETAR |
|
|
|
|
M3R |
|
|
|
|
5-HT2AR |
|
| G12 |
mini-G12 |
None |
Nonee |
|
a Detergent-solubilised or membrane embedded GPCRs.
b Primary coupling interactions.
c Heterotrimeric versions of the mini G proteins.
d Chimeric mini G proteins.
e Only secondary coupling interactions have been observed for mini-G12 in vivo [35]. |
Mini G proteins have a number of advantages in structural biology applications, compared to the heterotrimeric G proteins from which they were derived, including their smaller size (∼27 kDa), reduced conformational dynamics, increased solubility and improved thermostability, particularly in short-chain detergents. They also exhibit additional characteristics that have broadened their range of applications, including: (i) their high-level expression (up to 100 mg/l) in E. coli [36], which makes them both simple and inexpensive to produce in large quantities, and thus ideal for high-throughput screening applications (see Section 3.1); (ii) their potential modification to restore binding to Gβγ, which is particularly useful in cryo-electron microscopy (cryo-EM) applications (see Section 3.2); and (iii) their resistance to dissociation from the receptor by physiological concentrations of GTP [16], which allows them to be used in cell-based assays (see Section 4.2).
3. Structural biology applications of mini G proteins
Mini G proteins have been used to both improve the properties of receptors for structural studies (see Section 3.1), and to facilitate structure determination of GPCRs in their active state (see Section 3.2). To date, structures of three different receptors have been solved in complex with mini G proteins, using either X-ray crystallography or cryo-EM, namely A2AR [30,37], the serotonin 5-HT1B receptor (5-HT1BR) [38] and rhodopsin [39]. Interestingly, structures of the A2AR complex have been solved using both approaches, which has enabled direct comparison of these techniques [37].
3.1. Thermostabilisation of GPCRs for structural studies
GPCRs are extremely labile when extracted from the membrane by detergent solubilisation, and the relative stability of individual receptors is a key factor in whether or not their structure can be determined. At present, structures have been reported for only ∼15% of non-olfactory GPCRs encoded in the human genome. Considering that these receptors have often been selected for characterisation based on their above-average stability, it is telling that the vast majority have only had their structures determined bound to an antagonist, which is typically the most stable conformation. One solution to this problem has been the development of conformational thermostabilisation, which uses systematic mutagenesis coupled with a radioligand binding assay to stabilise detergent-solubilised receptors in a defined conformational state [3]. This approach has previously been used to increase the thermostability of either antagonist- or agonist-bound receptors sufficiently to facilitate their crystallisation [3,40,41,42]. Notably, conformational thermostabilisation of A2AR in the presence of an agonist alone did not result in stabilisation of the fully active state, but rather a biologically relevant intermediate-active conformation [40,41,43,44,45,46]. This suggests that in order to stabilise the fully active state of the receptor, both the agonist and G protein must be present during the selection process.
Using heterotrimeric G proteins in this type of conformational thermostabilisation procedure poses several problems. First, G proteins are composed of multiple subunits, which may be susceptible to dissociation when heated in the presence of detergent. Second, to ensure saturation of the receptor, the G protein must be added at a relatively high concentration (ideally in the micromolar range), which would potentially require hundreds of milligrams of G protein to conduct a full screen. Third, the heterotrimer must be expressed in insect cells using the baculovirus expression system, which means that producing large quantities of pure protein is both time consuming and expensive. In contrast, mini G protein are small, single domain proteins that are highly expressed in E. coli, and stable even in harsh detergent [16]. The advent of mini G proteins has therefore enabled conformational thermostabilisation to be applied to an agonist-GPCR-G protein complex, namely the corticotrophin-releasing factor receptor 1 (CRF1R) in complex with the peptide agonist sauvagine and mini-Gs [47]. The initial screen identified 17 individual point mutations that increased the apparent melting temperature (Tm) of the sauvagine-CRF1R-mini-Gs complex by up to 5.1 °C. These results are comparable to those obtained during the initial thermostability screen of agonist-bound A2AR [40], which ultimately resulted in its successful crystallisation [41], suggesting that conformational thermostabilisation is indeed a viable approach for stabilising agonist-GPCR-G protein complexes.
3.2. Structure determination of GPCRs in their active conformation
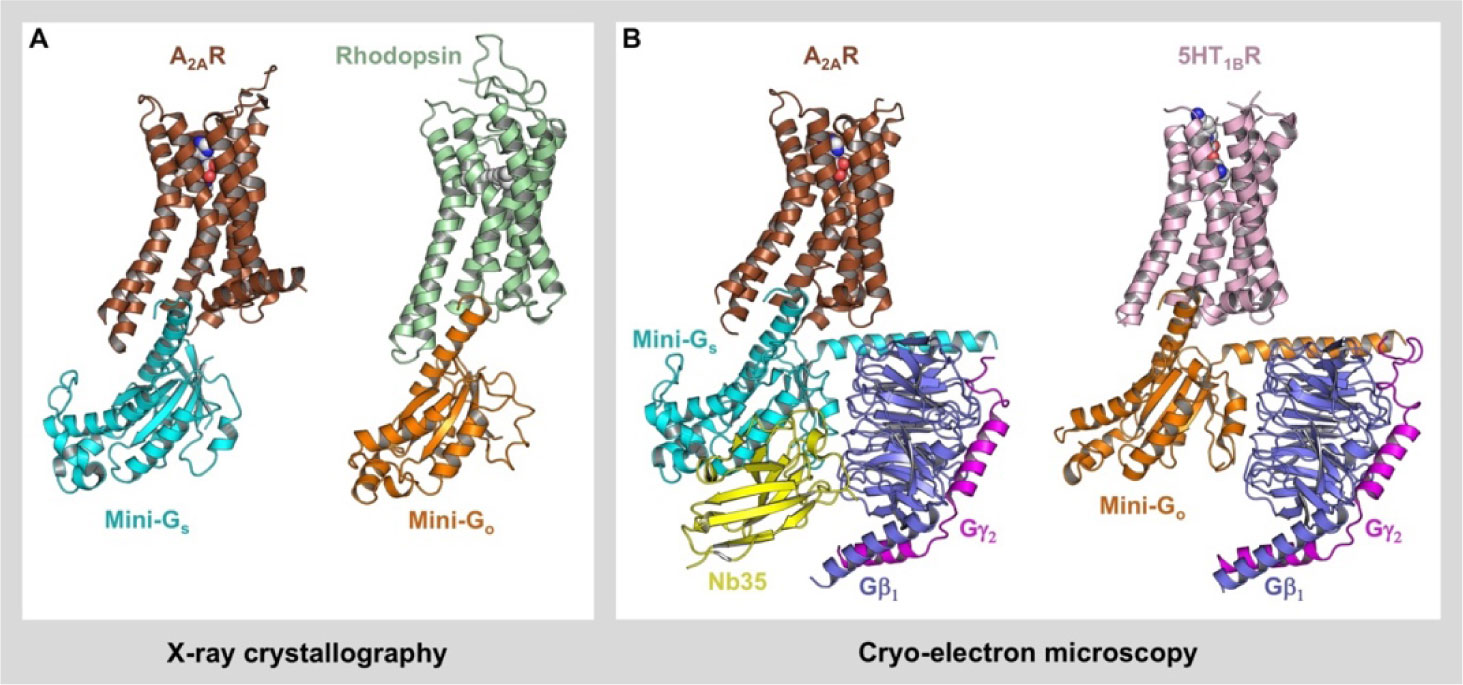
Mini G proteins were originally developed to facilitate structure determination of receptors in their active conformation using X-ray crystallography. Only one structure of a GPCR bound to a heterotrimeric G protein has been solved using this approach, namely the β2AR-Gs complex, and even this required a nanobody (Nb35) to stabilise the complex sufficiently to enable its crystallisation [9] (Figure 1A). Mini G proteins have facilitated the determination of two additional structures by X-ray crystallography. The structure of A2AR bound to mini-Gs and the agonist NECA was solved at 3.4 Å resolution by vapour diffusion crystallisation in the detergent octylthioglucoside (OTG) [30] (Figure 2A). This was the first structure of A2AR to be solved in its active conformation, and it completed a series of structures comprising the inactive, intermediate-active and active states that provided unparalleled insight in the activation mechanism of this receptor [48]. The structure of rhodopsin bound to mini-Go and all-trans retinal was solved at 3.1 Å resolution by vapour diffusion crystallisation in the detergent octyl glucose neopentyl glycol (OGNG) [39] (Figure 2A). In the visual system, rhodopsin naturally couples to transducin (Gt), which is a member of the Gi family; attempts to construct a mini G protein version of Gt were unsuccessful, so crystallisation was performed using another Gi family member, mini-Go (see Table 1). This structure revealed that a common active conformation of rhodopsin is responsible for coupling both the G protein and arrestin [10,39]. It is noteworthy that both of these mini G protein complexes were crystallised by vapour diffusion, since high-quality crystals could not be obtained using LCP. The β2AR-Gs complex however was crystallised using LCP [9], so this method should also be compatible with mini G proteins. It is likely that further screening will be required to identify the optimal combination of detergent, lipids and additives to successfully crystallise mini G protein complexes using this approach.
Recent advances in cryo-EM have brought this technique to the forefront of efforts to determine structures of GPCR-G protein complexes. During the past two years it has accounted for structures of three receptors in complex with Gs, namely the calcitonin receptor (CTR) [49], the calcitonin gene-related peptide (CGRP) receptor [50] and the glucagon-like peptide 1 receptor (GLP-1R) [51], as well as three receptors in complex with Gi, namely the μ-opioid receptor (μOR) [52], the adenosine A1 receptor (A1R) [53] and rhodopsin [54]. Despite the fact that cryo-EM is currently limited to proteins larger than ∼65 kDa [55], which is similar to that of a receptor in complex with a mini G protein, it has not yet proved possible to resolve such complexes using this approach. However, mini G proteins can easily be modified to restore binding to Gβγ [16], and these heterotrimeric versions have facilitated the determination of two structures using cryo-EM. The structure of A2AR bound to mini-Gs-β1γ2 and the agonist NECA was solved at 4.1 Å resolution in the detergent lauryl maltose neopentyl glycol (LMNG) [37] (Figure 2B). The organisation of the interface in this structure was virtually identical to that in the A2AR-mini-Gs complex solved using X-ray crystallography, which further validates the use of mini G proteins as surrogates for heterotrimeric G proteins. The structure of 5-HT1BR bound to mini-Go-β1γ2 and the agonist donitriptan was solved at 3.8 Å resolution in the detergent decylmaltoside (DM) [38] (Figure 2B). This was the first structure of a receptor to be solved in complex with Go, and it provided unique insight into the molecular determinants of G protein coupling specificity.
At present, it is unclear whether the heterotrimeric versions of mini G proteins have a significant advantage over native heterotrimeric G proteins in cryo-EM applications. While mini G proteins do lack the conformationally dynamic Gα-AH domain [16], this is not necessarily an advantage in cryo-EM, since flexible regions can easily be masked and omitted from data processing. Furthermore, cryo-EM is compatible with milder long-chain detergents, in which the stability of complexes composed of either a mini G protein or heterotrimeric G protein appear to be similar [16], although this has not been extensively tested. The use of mini G protein heterotrimers does enable shorter chain detergents such as DM to be screened during sample preparation for cryo-EM; an approach that significantly improved the homogeneity of the 5-HT1BR complex (R. Nehmé, personal communication). Furthermore, if technical developments continue to reduce the protein size limit for cryo-EM [56], then, in the future, it may be possible to determine structures of GPCRs in complex with the mini G protein alone. This would significantly increase the throughput of complex preparation and screening, which should translate into an increased rate of successful structure determination.
4. Applications of mini G proteins for the functional characterisation of GPCRs
Mini G proteins have been used in a number of applications to functionally characterise GPCRs. In vitro, they have been used to develop a suite of easy-to-use assays that are capable of reporting mini G protein binding to either membrane-embedded or detergent-solubilised receptors. They have also been used in a cutting-edge native mass spectrometry study to identify endogenous lipids that modulate GPCR-G protein interactions. In vivo, they have been used to develop a sensitive assay that is capable of accurately quantifying mini G protein coupling to variety of receptors.
4.1. Characterising G protein coupling to GPCRs in vitro
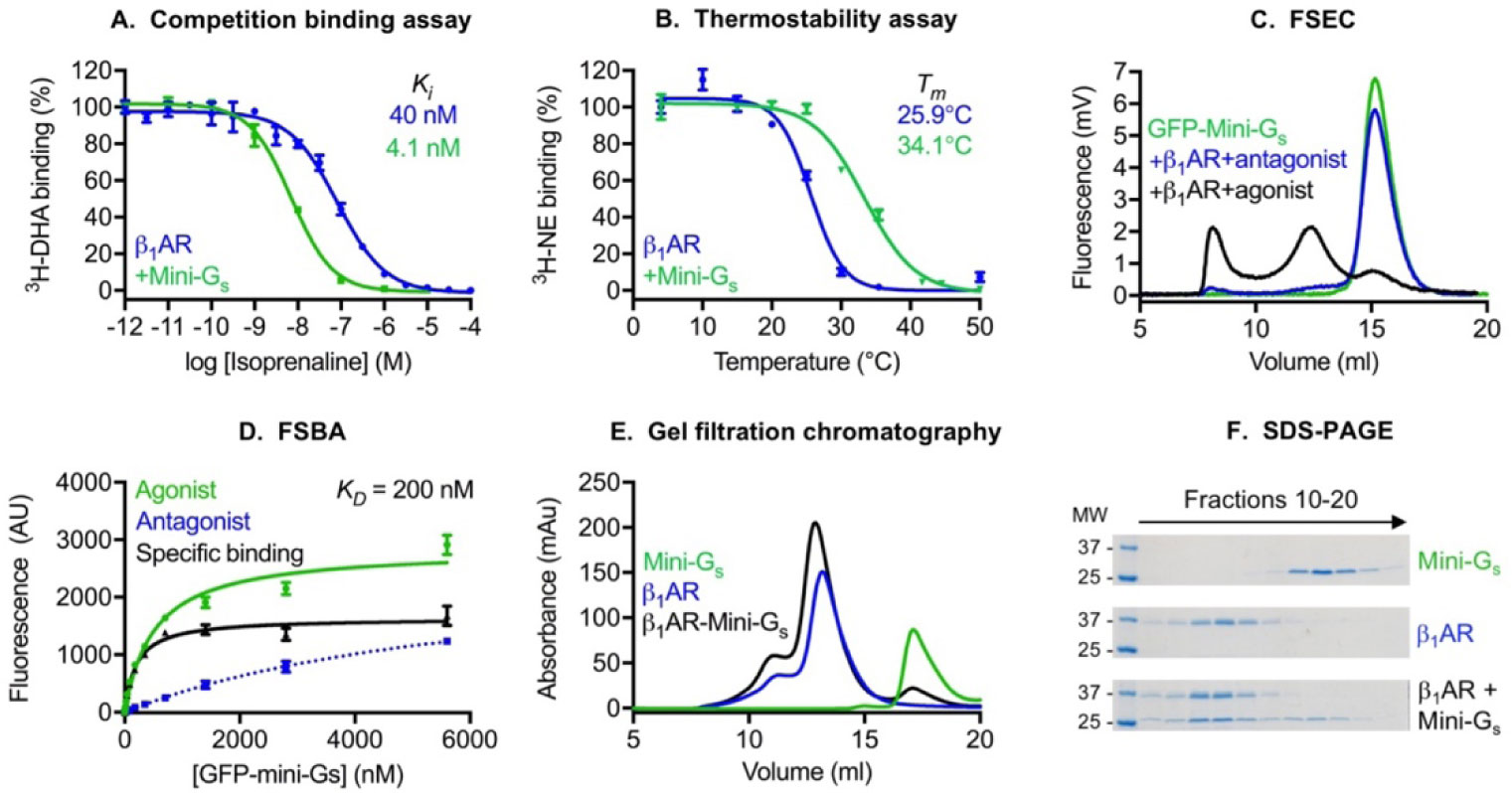
In many cases, simply detecting G protein binding to a receptor in vitro is extremely challenging, particularly when working with detergent-solubilised samples. This means that there is no single assay that is suitable for characterising G protein coupling to the entire GPCR family. Therefore, five different assays have been developed to monitor mini G protein coupling to a range of different GPCRs. First, a competition binding assay was used to demonstrate mini G protein coupling to membrane-embedded A2AR [30,37], β1AR [16] and 5-HT1BR [29]. This assay measures the inhibitory constant (Ki) of an agonist binding to a receptor in either the presence or absence of a mini G protein (Figure 3A). For many receptors, G protein binding elicits a significant increase (10 to 100-fold) in their agonist-binding affinity [57], and, in these cases, the competition binding assay can be used to reliably measure mini G protein coupling. The advantages of this assay are that it is very sensitive and can be performed in high-throughput format. The disadvantages are that a radiolabelled antagonist is required for each receptor being investigated and some receptors exhibit only a small shift in agonist-binding affinity upon G protein coupling, in which case this assay is not suitable. Second, a thermostability assay [3] was used to report binding of mini G proteins to detergent-solubilised A2AR [29,30], AT1R [29], β1AR [16], CRF1R [47], NTSR1 [29] and 5-HT1BR [29]. This assay measures the apparent Tm of a non-purified detergent-solubilised receptor in the presence of either an agonist, or both an agonist and a mini G protein (Figure 3B). All receptors that have been tested in this assay display higher thermostability when bound to both the agonist and mini G protein, compared to the agonist alone; this response can therefore be used as a reliable indicator of mini G protein coupling. The advantages of this assay are that it can be used to evaluate the stability of the complex in different detergents and can be performed in high-throughput. The main disadvantage is that, in this format, a radiolabelled agonist is required for each receptor being investigated. However, it may be possible to use a different type of thermostability assay that does not require a radioligand, such as differential scanning fluorimetry (DSF) [58], although this has not been tested. Third, fluorescence size exclusion chromatography (FSEC) was used to evaluate mini G protein coupling to non-purified detergent-solubilised A2AR, β1AR and 5-HT1BR [29]. In this approach, samples of a GFP-tagged mini G protein, either alone or mixed with a non-purified detergent-solubilised receptor bound to either an agonist or antagonist, are loaded onto a gel filtration column and GFP signal in the eluate is monitored using a fluorescence detector. A shift in the retention volume of the GFP-tagged mini G protein peak in the presence of the agonist-bound receptor is indicative of complex formation (Figure 3C). The advantages of this assay are that it uses non-purified receptor samples and it allows rapid screening of detergent or buffer conditions for optimal complex formation. The disadvantages are that only a low concentration of GFP-tagged mini G protein can be used in the assay and high detergent concentrations are often required for efficient membrane solubilisation, which can affect the stability of the complex. Fourth, a fluorescence saturation binding assay (FSBA) was used to estimate the affinity of mini G protein binding to detergent-solubilised A2AR, β1AR and 5-HT1BR [29]. This assay measures the apparent equilibrium dissociation constant (KD) of a GFP-tagged mini G protein binding to a non-purified detergent-solubilised receptor, immobilised on a microtiter plate via its histidine tag, in the presence of either an agonist or antagonist (Figure 3D). The main advantage of this assay is that it can be used to estimate G protein binding affinity in different detergents or buffers. The main disadvantage is that the affinity of the interaction is likely to be affected by the presence of detergent, and thus is not representative of native interactions within the cell. Fifth, analytical gel filtration chromatography was used to demonstrate mini G protein binding to A2AR [29], β1AR [16] and 5-HT1BR [29]. In this approach, samples of purified receptor and mini G protein, either individually or mixed, are resolved by analytical gel filtration chromatography. A decrease in the retention volume of the mixed sample, compared to the receptor alone, indicates complex formation (Figure 3E). Also, co-elution of the receptor and mini G protein, which is assessed by SDS-PAGE analysis of the gel filtration eluate, gives a reliable indication of coupling (Figure 3F). The advantages of this method are that it can be used to screen detergents or buffer conditions for optimal complex formation and it enables the stability of a complex to be assessed over a period of days. The main disadvantage is that it requires a significant quantity of purified receptor, which can be challenging to obtain.
Mini G proteins have also been used to study the effect of endogenous lipids on the G protein coupling selectivity of A2AR, β1AR and NTSR1 using native mass spectrometry [59]. Hotspots were identified on the cytoplasmic surface of the receptors that specifically bound phosphatidylinositol-4,5-bisphosphate (PtdIns(4,5)P2). This lipid appears to function as an allosteric modulator of G protein binding, by both stabilising the active state of the receptor and mediating bridging interactions with the G protein. Mini G proteins proved ideal for this application, since they are more stable than heterotrimeric G proteins, and, whilst nanobodies could also be used, they did not bind PtdIns(4,5)P2 and thus did not recapitulate the native bridging interactions.
4.2. Characterising G protein coupling to GPCRs in vivo
Mini G proteins have been used to measure G protein coupling to GPCRs in live mammalian cells using confocal microscopy, bioluminescence resonance energy transfer (BRET) spectroscopy and luciferase complementation [35]. Initially, confocal microscopy was used to demonstrate agonist-dependent recruitment of mini-Gs (fused to the fluorescent protein venus) to membrane-localised β2AR. This confirmed that the resistance of mini G protein complexes to dissociation by cytosolic concentrations of guanine nucleotides makes them ideally suited to cell-based applications. Next, a BRET spectroscopy assay was developed using mini G proteins from each of the four families. Mini-Gs and mini-G12 were both well expressed in mammalian cells, but neither mini-Gq or mini-Gi were expressed in a soluble form, therefore the chimeric versions of these proteins, mini-Gs/i and mini-Gs/q, were used (see Table 1). BRET was measured between venus-tagged versions of these mini G proteins and a panel of GPCRs (fused to the Renilla luciferase Rluc8). The cytosolic localisation of mini G proteins means that they displayed a significantly higher BRET signal-to-noise ratio than heterotrimeric G proteins [60,61], which are tethered to the membrane through lipid anchors [33]. The assay was able to accurately profile coupling of the mini G proteins to a panel of receptors including: The α2A-adrenergic receptor (α2A-AR); A1R; A2AR; AT1R; β2AR; the cannabinoid receptor type 1 (CB1R); the D1, D2 and D5 dopamine receptors (D1R, D2R and D5R, respectively), the endothelin A receptor (ETAR); the M3 and M4 acetylcholine receptors (M3R and M4R, respectively); the serotonin 5-HT2A receptor (5-HT2AR); and the vasopressin receptor 2 (V2R; see Table 1). The mini G proteins, including the two chimeras, were shown to maintain appropriate coupling specificity in vivo (see Table 1). Furthermore, their secondary coupling interactions were also accurately reported, and in the case of D1R and D5R, previously unknown secondary interactions were also identified. The assay was also able to precisely report the efficacy of agonists, partial agonists, antagonists and inverse agonists at β2AR by measuring mini-Gs coupling [35]. Similar results were obtained when the assay was modified to use luciferase complementation [62], demonstrating the versatility of this assay format. Confocal microscopy and BRET spectroscopy were also used to measure mini G protein recruitment to receptors localised to intracellular compartments, including A1R in the Golgi apparatus and β2AR in early endosomes [35]. Thus, mini G proteins can be used as biosensors for monitoring the subcellular localisation and internalisation of receptors in a similar manner to nanobodies [63,64].
5. Conclusions and future perspectives
Mini G proteins have facilitated the structure determination of three different receptors in their active state, and have enabled the development of a novel methodology to thermostabilise agonist-GPCR-G protein complexes. These structures have provided valuable insight into the mode of agonist binding, the mechanism of receptor activation, and the molecular determinants of G protein coupling specificity. Their potential applications in structure-based drug design means there is high demand for structures of all GPCRs to be solved in their active state; both cryo-EM and X-ray crystallography will be key techniques in determining these structures, and mini G proteins have proven to be useful tools in both approaches. Beyond structural biology, mini G proteins have been used to develop a range of assays that have facilitated the characterisation of G protein coupling both in vitro and in vivo. The cell-based BERT spectroscopy assay will have immediate applications in GPCR drug discovery, enabling the efficacy and functional selectivity [65] of novel drug candidates to be measure at potentially any receptor. It will also facilitate the characterisation of allosteric modulators that can be used to enhance the receptor subtype specificity of orthosteric ligands [66]. The construction of some mini G protein subtypes has proved difficult, particularly Gq family members, thus further work is required to complete development of the full mini G protein panel. The relatively high degree of sequence homology shared by the different mini G proteins means that it should be possible to use gene shuffling approaches to pinpoint areas responsible for the poor stability of certain subtypes. This would enable the development of more biologically relevant chimeras in which only minimal regions of the mini G protein need to be substituted to achieve optimal expression and stability [67]. Although a number of different tools are available for characterising receptors in their active state, the fact that mini G proteins can be used off-the-shelf without the need for laborious receptor-specific development makes them an ideal first choice in many applications. Further development and modification of mini G proteins should result in many more novel applications being identified, particularly in relation to GPCR functional studies. Therefore, in the future, mini G proteins will continue to contribute to our understanding of these important receptors, and aid in the development of drugs to treat a wide variety of diseases.
Acknowledgements
This work was supported by funding from a BBSRC/EPSRC grant awarded to WISB (BB/M017982/1). I thank Rony Nehmé for comments on the manuscript.
Conflict of interest
The author is an inventor on a patent application covering mini G proteins, but has no other conflict of interest.









 DownLoad:
DownLoad: