Plant cell wall composition and enzymatic deconstruction

Thatiane Rodrigues Mota; Dyoni Matias de Oliveira; Rogério Marchiosi; Osvaldo Ferrarese-Filho; Wanderley Dantas dos Santos; Thatiane Rodrigues Mota; Dyoni Matias de Oliveira; Rogério Marchiosi; Osvaldo Ferrarese-Filho; Wanderley Dantas dos Santos

doi:10.3934/bioeng.2018.1.63

AIMS Bioengineering

2018, Volume 5, Issue 1: 63-77. doi: 10.3934/bioeng.2018.1.63

Previous Article Next Article

Review Topical Sections

Plant cell wall composition and enzymatic deconstruction

Laboratory of Plant Biochemistry, Department of Biochemistry, State University of Maringá, PR, Brazil

Received: 20 December 2017 Accepted: 14 March 2018 Published: 30 March 2018

Cellulosic ethanol is one the most prominent technologies capable of replacing the use of fossil fuels in an observable horizon of technological development. The complexity of plant biomass, however, continues to challenge our ability to convert it into biofuels efficiently. Highly complex and cross-linked polysaccharides, hydrophobic and protein adsorbent polymers, and crystalline supramolecular structures comprise some of the structures that shield the plant cell contents (and the shield structures themselves) against predators. In response, a sophisticated enzymatic weaponry, with its associated chemical and physical mechanisms, is necessary to overcome this recalcitrance. Here we describe basic information about chemical composition of lignocellulosic biomass and the enzymatic arsenal for lignocellulose deconstruction into fermentable sugars.

Keywords:

Citation: Thatiane Rodrigues Mota, Dyoni Matias de Oliveira, Rogério Marchiosi, Osvaldo Ferrarese-Filho, Wanderley Dantas dos Santos. Plant cell wall composition and enzymatic deconstruction[J]. AIMS Bioengineering, 2018, 5(1): 63-77. doi: 10.3934/bioeng.2018.1.63

Related Papers:

[1]	Adam Sullivan, Folashade Agusto, Sharon Bewick, Chunlei Su, Suzanne Lenhart, Xiaopeng Zhao . A mathematical model for within-host Toxoplasma gondii invasion dynamics. Mathematical Biosciences and Engineering, 2012, 9(3): 647-662. doi: 10.3934/mbe.2012.9.647
[2]	Cameron Browne . Immune response in virus model structured by cell infection-age. Mathematical Biosciences and Engineering, 2016, 13(5): 887-909. doi: 10.3934/mbe.2016022
[3]	A. D. Al Agha, A. M. Elaiw . Global dynamics of SARS-CoV-2/malaria model with antibody immune response. Mathematical Biosciences and Engineering, 2022, 19(8): 8380-8410. doi: 10.3934/mbe.2022390
[4]	Joan Ponce, Horst R. Thieme . Can infectious diseases eradicate host species? The effect of infection-age structure. Mathematical Biosciences and Engineering, 2023, 20(10): 18717-18760. doi: 10.3934/mbe.2023830
[5]	Yanxia Dang, Zhipeng Qiu, Xuezhi Li . Competitive exclusion in an infection-age structured vector-host epidemic model. Mathematical Biosciences and Engineering, 2017, 14(4): 901-931. doi: 10.3934/mbe.2017048
[6]	Yue Deng, Siming Xing, Meixia Zhu, Jinzhi Lei . Impact of insufficient detection in COVID-19 outbreaks. Mathematical Biosciences and Engineering, 2021, 18(6): 9727-9742. doi: 10.3934/mbe.2021476
[7]	Junyuan Yang, Rui Xu, Xiaofeng Luo . Dynamical analysis of an age-structured multi-group SIVS epidemic model. Mathematical Biosciences and Engineering, 2019, 16(2): 636-666. doi: 10.3934/mbe.2019031
[8]	Andrey V. Melnik, Andrei Korobeinikov . Lyapunov functions and global stability for SIR and SEIR models withage-dependent susceptibility. Mathematical Biosciences and Engineering, 2013, 10(2): 369-378. doi: 10.3934/mbe.2013.10.369
[9]	Kento Okuwa, Hisashi Inaba, Toshikazu Kuniya . An age-structured epidemic model with boosting and waning of immune status. Mathematical Biosciences and Engineering, 2021, 18(5): 5707-5736. doi: 10.3934/mbe.2021289
[10]	Yanfeng Liang, David Greenhalgh . Estimation of the expected number of cases of microcephaly in Brazil as a result of Zika. Mathematical Biosciences and Engineering, 2019, 16(6): 8217-8242. doi: 10.3934/mbe.2019416

Abstract

1. Introduction

One of interactions between three types of populations is known as non-transitive, cyclic competition or a rock-paper-scissors relationship, that is, type $ A $ is stronger than type $ B $, and type $ B $ is superior to type $ C $, which in turn is better than $ A $. We can find several examples of this kind of interaction in nature; the most well-known are bacteria (e.g., ^[1,2,3,4]) and lizards (e.g., ^[5,6,7]).

Barreto et al. ^[8] proposed phenotypic and genotypic cyclic competition models to clarify the fact that three throat morphs in male lizards, known as orange, blue, and yellow, are maintained with a rock-paper-scissors relationship. Both models have the same equilibrium, but the latter gives a wider stability region than the former. Barreto et al. ^[8] analyzed their model by fixing all payoffs except two elements, which are given by variable parameters. However, such a case is difficult to manage because an internal equilibrium depends on these parameters. Then we consider an alternative setting as an internal equilibrium with equal frequencies for all phenotypes independent of parameters, namely, we use symmetric conditions of parameters to obtain global insights into the dynamics in this simplified system for the convenience of analysis.

In this paper, we re-examine stability conditions under the following situations: symmetric parameters for the phenotypic model, cyclic allele dominance rule, and spatial structure. We obtain the following results: (ⅰ) Cyclic allele dominance rule in a genotypic model gives a wider stable region of internal equilibrium than the allele dominance rule observed in lizards. (ⅱ) Spatial structure drastically changes the dynamical behavior, especially when all three phenotypes coexist in almost all the parameter spaces when both competition and dispersal occur locally.

In the next section, we review the phenotypic model and its corresponding genotypic model proposed by ^[8] and then restrict these models with two parameters to generate an internal equilibrium independent of the parameters. In section 3, we derive local stability conditions for each model. We consider cyclic allele dominance rule in section 4. In section 5, we investigate the effects of spatial structure on the stability of the internal equilibrium.

2. The phenotypic model and its corresponding genotypic model

First, we consider a phenotypic model of cyclic competition, or a rock-paper-scissors game, following ^[8]. There are three phenotypes $ O, B, $ and $ Y $. $ O $ has a better strategy than $ B $, and $ B $ is superior to $ Y $, which is, in turn, surpasses $ O $. When we use a payoff matrix in Table 1, this relation can be expressed by $ M_{OY} < M_{OO} < M_{OB}, M_{BO} < M_{BB} < M_{BY}, $ and $ M_{YB} < M_{YY} < M_{YO} $, where $ M_{IJ} $ is a payoff of focal individual $ I \in \{O, B, Y\} $ against an opponent $ J \in \{O, B, Y\} $.

Table 1. Payoff matrix of rock-paper-scissors game. $ M_{IJ} $ is a payoff of focal individual $ I \in \{O, B, Y\} $ against an opponent $ J \in \{O, B, Y\} $. The following magnitude relations hold: $ M_{OY} < M_{OO} < M_{OB}, M_{BO} < M_{BB} < M_{BY}, M_{YB} < M_{YY} < M_{YO} $.

	Individual $ J $
Individual $ I $	$ O $	$ B $	$ Y $
$ O $	$ M_{OO} $	$ M_{OB} $	$ M_{OY} $
$ B $	$ M_{BO} $	$ M_{BB} $	$ M_{BY} $
$ Y $	$ M_{YO} $	$ M_{YB} $	$ M_{YY} $

| Show Table

DownLoad: CSV

Using these payoffs obtained by the competition between two phenotypes, the dynamics of phenotypic model are defined as

$\begin{eqnarray} p_{O, n+1} & = & \frac{W_O}{W} p_{O, n}, \end{eqnarray}$ $

(2.1)

$\begin{eqnarray} p_{B, n+1} & = & \frac{W_B}{W} p_{B, n}, \end{eqnarray}$ $

(2.2)

$\begin{eqnarray} p_{Y, n+1} & = & \frac{W_Y}{W} p_{Y, n}, \end{eqnarray}$ $

(2.3)

with $ p_{O, n}, p_{B, n}, $ and $ p_{Y, n} $ as the fractions of phenotypes $ O, B, $ and $ Y $, respectively, at generation $ n $. Here $ W_O, W_B, $ and $ W_Y $ are the fitnesses of phenotypes $ O, B, $ and $ Y $, respectively, and $ W $ is the average fitness of the population:

$\begin{eqnarray} W_O & = & M_{OO} p_{O, n}+M_{OB} p_{B, n}+M_{OY} p_{Y, n}, \end{eqnarray}$ $

(2.4)

$\begin{eqnarray} W_B & = & M_{BO} p_{O, n}+M_{BB} p_{B, n}+M_{BY} p_{Y, n}, \end{eqnarray}$ $

(2.5)

$\begin{eqnarray} W_Y & = & M_{YO} p_{O, n}+M_{YB} p_{B, n}+M_{YY} p_{Y, n}, \end{eqnarray}$ $

(2.6)

$\begin{eqnarray} W & = & W_O p_{O, n} + W_B p_{B, n} + W_B p_{Y, n}. \end{eqnarray}$ $

(2.7)

This is a standard model of the rock-paper-scissors game (e.g., ^[9,10]).

At equilibrium we have

$\begin{equation} W = W_O = W_B = W_Y \end{equation}$ $

(2.8)

by eqs.(2.1)–(2.3). A unique internal equilibrium solution for the above simultaneous equations (2.8) with $ p_O + p_B + p_Y = 1 $ is

$\begin{eqnarray} p_O & = & \frac{M_1}{M_1 + M_2 + M_3}, \end{eqnarray}$ $

(2.9)

$\begin{eqnarray} p_B & = & \frac{M_2}{M_1 + M_2 + M_3}, \end{eqnarray}$ $

(2.10)

$\begin{eqnarray} p_Y & = & \frac{M_3}{M_1 + M_2 + M_3}, \end{eqnarray}$ $

(2.11)

where

$\begin{eqnarray} M_1 & = & M_{OB}(M_{BY}-M_{YY}) + M_{BB}(M_{YY}-M_{OY}) + M_{YB}(M_{OY}-M_{BY}), \end{eqnarray}$ $

(2.12)

$\begin{eqnarray} M_2 & = & M_{OY}(M_{BO}-M_{YO}) + M_{BY}(M_{YO}-M_{OO}) + M_{YY}(M_{OO}-M_{BO}), \end{eqnarray}$ $

(2.13)

$\begin{eqnarray} M_3 & = & M_{OO}(M_{BB}-M_{YB}) + M_{BO}(M_{YB}-M_{OB}) + M_{YO}(M_{OB}-M_{BB}). \end{eqnarray}$ $

(2.14)

We have another three equilibria $ (1, 0, 0), (0, 1, 0), $ and $ (0, 0, 1) $ as the boundary equilibria $ (\hat{p}_O, \hat{p}_B, \hat{p}_Y) $.

Next we move to a genotypic model corresponding to the above phenotypic model by the genotypic allele dominance rule in which an allele $ o $ dominates over two others, $ y $ and $ b $, and an allele $ y $ dominates $ b $. In other words, genotypes $ oo, oy, $ and $ ob $ are phenotype $ O $, genotypes $ yy $ and $ yb $ are phenotype $ Y $, and genotype $ bb $ is phenotype $ B $ (Table 2).

Table 2. Allele dominance rule (Ⅰ). An allele $ o $ is dominant to other alleles $ y $ and $ b $, then three genotypes $ oo $, $ oy $, and $ ob $ correspond to a phenotype $ O $. An allele $ y $ is dominant to an allele $ b $, then two genotypes $ yy $ and $ yb $ correspond to a phenotype $ Y $. An allele $ b $ is recessive to other alleles, then only one genotype $ bb $ corresponds to a phenotype $ B $.

Genotype		Phenotype
$ oo, oy, ob $	$ \to $	$ O $
$ yy, yb $	$ \to $	$ Y $
$ bb $	$ \to $	$ B $

| Show Table

DownLoad: CSV

Then phenotypic frequencies can be expressed by the genotypic frequencies $ g_{ij, n} \ (i, j \in \{o, y, b\}) $ at generation $ n $ as follows:

$\begin{eqnarray} p_{O, n} & = & g_{oo, n} + g_{oy, n} + g_{ob, n}, \end{eqnarray}$ $

(2.15)

$\begin{eqnarray} p_{Y, n} & = & g_{yy, n} + g_{yb, n}, \end{eqnarray}$ $

(2.16)

$\begin{eqnarray} p_{B, n} & = & g_{bb, n}. \end{eqnarray}$ $

(2.17)

Therefore the fitness of each genotype becomes

$\begin{eqnarray} W_O & = & W_{oo} = W_{oy} = W_{ob}, \end{eqnarray}$ $

(2.18)

$\begin{eqnarray} W_Y & = & W_{yy} = W_{yb}, \end{eqnarray}$ $

(2.19)

$\begin{eqnarray} W_B & = & W_{bb}. \end{eqnarray}$ $

(2.20)

Considering the above relationships of fitnesses and frequencies, first, the genotypic frequencies at generation $ n $ change:

$\begin{equation} \tilde{g}_{ij, n} = \frac{W_{ij}}{W} g_{ij, n} \qquad (i, j \in \{o, y, b\}). \end{equation}$ $

(2.21)

Second, the allele frequencies $ \tilde{f}_i \ (i \in \{o, y, b\}) $ at generation $ n $ are

$\begin{eqnarray} \tilde{f}_{o, n} & = & \tilde{g}_{oo, n} + \frac{1}{2} \tilde{g}_{oy, n} + \frac{1}{2} \tilde{g}_{ob, n}, \end{eqnarray}$ $

(2.22)

$\begin{eqnarray} \tilde{f}_{y, n} & = & \tilde{g}_{yy, n} + \frac{1}{2} \tilde{g}_{yb, n} + \frac{1}{2} \tilde{g}_{oy, n}, \end{eqnarray}$ $

(2.23)

$\begin{eqnarray} \tilde{f}_{b, n} & = & \tilde{g}_{bb, n} + \frac{1}{2} \tilde{g}_{yb, n} + \frac{1}{2} \tilde{g}_{ob, n}. \end{eqnarray}$ $

(2.24)

Third, assuming random mating gives the genotypic frequencies at generation $ n+1 $, $ g_{ij, n+1} \ (i, j \in \{o, y, b\}) $ as

$\begin{eqnarray} g_{ij, n+1} & = & 2\tilde{f}_{i, n} \tilde{f}_{j, n} \quad \mbox{if $i \ne j$}, \end{eqnarray}$ $

(2.25)

$\begin{eqnarray} g_{ii, n+1} & = & \tilde{f}_{i, n}^2, \end{eqnarray}$ $

(2.26)

then we can describe the above relations and dynamics (2.15)–(2.26) with only variables representing the genotypic frequencies $ g_{ij, n} (i, j \in \{0, y, b\}) $ as

$\begin{eqnarray} g_{oo, n+1} & = & \left(\frac{W_O}{W}\right)^2\left(g_{oo, n} + \frac{1}{2} g_{oy, n} + \frac{1}{2} g_{ob, n}\right)^2, \end{eqnarray}$ $

(2.27)

$\begin{eqnarray} g_{oy, n+1} & = & 2\frac{W_O}{W}\left(g_{oo, n} + \frac{1}{2} g_{oy, n} + \frac{1}{2} g_{ob, n}\right) \\ && \times \left\{\frac{W_Y}{W}\left(g_{yy, n} + \frac{1}{2} g_{yb, n}\right) + \frac{1}{2} \frac{W_{O}g_{oy, n}}{W}\right\}, \end{eqnarray}$ $

(2.28)

$\begin{eqnarray} g_{ob, n+1} & = & 2\frac{W_O}{W}\left(g_{oo, n} + \frac{1}{2} g_{oy, n} + \frac{1}{2} g_{ob, n}\right) \\ && \times \left(\frac{W_{B}g_{bb, n}}{W} + \frac{1}{2} \frac{W_{Y}g_{yb, n}}{W} + \frac{1}{2} \frac{W_{O}g_{ob, n}}{W}\right), \end{eqnarray}$ $

(2.29)

$\begin{eqnarray} g_{yy, n+1} & = & \left\{\frac{W_Y}{W}\left(g_{yy, n} + \frac{1}{2} g_{yb, n}\right) + \frac{1}{2} \frac{W_{O}g_{oy, n}}{W}\right\}^2, \end{eqnarray}$ $

(2.30)

$\begin{eqnarray} g_{yb, n+1} & = & 2\left\{\frac{W_Y}{W}\left(g_{yy, n} + \frac{1}{2} g_{yb, n}\right) + \frac{1}{2} \frac{W_{O}g_{oy, n}}{W}\right\} \\ && \times \left(\frac{W_{B}g_{bb, n}}{W} + \frac{1}{2} \frac{W_{Y}g_{yb, n}}{W} + \frac{1}{2} \frac{W_{O}g_{ob, n}}{W}\right), \end{eqnarray}$ $

(2.31)

$\begin{eqnarray} g_{bb, n+1} & = & \left(\frac{W_{B}g_{bb, n}}{W} + \frac{1}{2} \frac{W_{Y}g_{yb, n}}{W} + \frac{1}{2} \frac{W_{O}g_{ob, n}}{W}\right)^2, \end{eqnarray}$ $

(2.32)

where

$\begin{eqnarray} W_O & = & M_{OO} (g_{oo, n} + g_{oy, n} + g_{ob, n})+M_{OB} g_{bb, n}+M_{OY} (g_{yy, n} + g_{yb, n}), \end{eqnarray}$ $

(2.33)

$\begin{eqnarray} W_B & = & M_{BO} (g_{oo, n} + g_{oy, n} + g_{ob, n})+M_{BB} g_{bb, n}+M_{BY} (g_{yy, n} + g_{yb, n}), \end{eqnarray}$ $

(2.34)

$\begin{eqnarray} W_Y & = & M_{YO} (g_{oo, n} + g_{oy, n} + g_{ob, n})+M_{YB} g_{bb, n}+M_{YY} (g_{yy, n} + g_{yb, n}), \end{eqnarray}$ $

(2.35)

$\begin{eqnarray} W & = & W_O(g_{oo, n} + g_{oy, n} + g_{ob, n}) + W_B g_{bb, n} + W_Y(g_{yy, n} + g_{yb, n}). \end{eqnarray}$ $

(2.36)

Using the above equations, we can obtain the following relations:

$\begin{eqnarray} g_{oo, n+1}+\frac{1}{2}g_{oy, n+1}+\frac{1}{2}g_{ob, n+1} & = & \frac{W_O}{W} \left(g_{oo, n}+\frac{1}{2}g_{oy, n}+\frac{1}{2}g_{ob, n}\right), \end{eqnarray}$ $

(2.37)

$\begin{eqnarray} g_{yy, n+1}+\frac{1}{2}g_{yb, n+1}+\frac{1}{2}g_{oy, n+1} & = & \frac{W_Y}{W} \left(g_{yy, n}+\frac{1}{2}g_{yb, n}\right)+ \frac{1}{2}\frac{W_O}{W}g_{oy, n}, \end{eqnarray}$ $

(2.38)

$\begin{eqnarray} g_{bb, n+1}+\frac{1}{2}g_{yb, n+1}+\frac{1}{2}g_{ob, n+1} & = & \frac{W_B}{W} g_{bb, n}+\frac{1}{2}\frac{W_Y}{W} g_{yb, n}+ \frac{1}{2}\frac{W_O}{W} g_{ob, n}. \end{eqnarray}$ $

(2.39)

At equilibrium, by eq.(2.37), we have

$\begin{equation} W = W_O. \end{equation}$ $

(2.40)

By eq.(2.38) and eq.(2.40), we have

$\begin{equation} W = W_Y. \end{equation}$ $

(2.41)

By eqs.(2.39)–(2.41), we have

$\begin{equation*} W = W_B. \end{equation*}$ $

Therefore, because we also have the same relationships (2.8) for genetypic model, we have the same phenotypic equilibrium (2.9)–(2.11) with eqs.(2.12)–(2.14) as the corresponding phenotypic model.

3. Stability condition for equilibrium $ (1/3, 1/3, 1/3) $

The payoff matrix includes nine payoffs and is a little complicated. Following ^[8], we reduce it to two values. We fix the values of the payoffs at 1 for the competitions between the same phenotypes, but we also adopt the symmetric cases --- namely, we give a larger payoff $ \alpha > 1 $ to a stronger competitor and a smaller one $ \beta < 1 $ to a weaker competitor (Table 3), which results in the same equilibrium fractions of $ 1/3 $ for all three phenotypes ^[9].

Table 3. Payoff matrix with only two parameters. We obtain the same equilibrium fractions of $ 1/3 $ for all three phenotypes. Parameter ranges are given by $ 0 < \beta < 1 < \alpha $.

	Opponent Individual
Focal Individual	$ O $	$ B $	$ Y $
$ O $	$ 1 $	$ \alpha $	$ \beta $
$ B $	$ \beta $	$ 1 $	$ \alpha $
$ Y $	$ \alpha $	$ \beta $	$ 1 $

| Show Table

DownLoad: CSV

By using this reduced payoff matrix, eqs.(2.1)–(2.7) become

$\begin{eqnarray} p_{O, n+1} & = & \frac{(p_{O, n}+\alpha p_{B, n}+\beta p_{Y, n})p_{O, n}}{(p_{O, n}+\alpha p_{B, n}+\beta p_{Y, n})p_{O, n} + (\beta p_{O, n}+ p_{B, n}+\alpha p_{Y, n})p_{B, n} +(\alpha p_{O, n}+\beta p_{B, n}+ p_{Y, n})p_{Y, n}}, \end{eqnarray}$ $

(3.1)

$\begin{eqnarray} p_{B, n+1} & = & \frac{(\beta p_{O, n}+ p_{B, n}+\alpha p_{Y, n})p_{B, n}}{(p_{O, n}+\alpha p_{B, n}+\beta p_{Y, n})p_{O, n} + (\beta p_{O, n}+ p_{B, n}+\alpha p_{Y, n})p_{B, n} +(\alpha p_{O, n}+\beta p_{B, n}+ p_{Y, n})p_{Y, n}}, \end{eqnarray}$ $

(3.2)

$\begin{eqnarray} p_{Y, n+1} & = & \frac{(\alpha p_{O, n}+\beta p_{B, n}+ p_{Y, n})p_{Y, n}}{(p_{O, n}+\alpha p_{B, n}+\beta p_{Y, n})p_{O, n} + (\beta p_{O, n}+ p_{B, n}+\alpha p_{Y, n})p_{B, n} +(\alpha p_{O, n}+\beta p_{B, n}+ p_{Y, n})p_{Y, n}}. \end{eqnarray}$ $

(3.3)

By eqs.(2.12)–(2.14),

$\begin{equation*} M_1 = M_2 = M_3 = \alpha^2+\beta^2 -(\alpha+\beta+\alpha\beta) + 1, \end{equation*}$ $

so that an internal equilibrium (2.9)–(2.11) becomes

$\begin{equation} p_O = p_Y = p_B = \frac{1}{3}. \end{equation}$ $

(3.4)

The linearized system of eqs.(3.1)–(3.3) about an internal equilibrium (3.4) gives the following Jacobian matrix:

$\begin{equation*} \frac{1}{3(1+\alpha+\beta)} \begin{pmatrix} 4+\alpha+\beta & -2+\alpha-2\beta & -2-2\alpha+\beta \\ -2-2\alpha+\beta & 4+\alpha+\beta & -2+\alpha-2\beta \\ -2+\alpha-2\beta & -2-2\alpha+\beta & 4+\alpha+\beta \end{pmatrix}. \end{equation*}$ $

Then the characteristic equation of the linearized system becomes

$\begin{equation*} \lambda(\lambda^2 + a_1 \lambda + a_2) = 0, \end{equation*}$ $

where

$\begin{eqnarray} a_1 & = & -\frac{4+\alpha+\beta}{1+\alpha+\beta}, \end{eqnarray}$ $

(3.5)

$\begin{eqnarray} a_2 & = & \frac{4+2(\alpha+\beta)+\alpha^2+\beta^2}{(1+\alpha+\beta)^2}. \end{eqnarray}$ $

(3.6)

Jury conditions or Schur-Cohn criteria (e.g., ^[11]) for second-degree characteristic equations $ \lambda^2 + a_1 \lambda + a_2 = 0 $ are known as

$\begin{equation} |a_1| \lt 1 + a_2 \lt 2. \end{equation}$ $

(3.7)

Because $ a_1 < 0 $ from eq.(3.5), the left inequality of eq.(3.7) becomes $ -a_1 < 1 + a_2 $, that is, $ a_1 + a_2 + 1 > 0 $, which holds by the calculation using eqs.(3.5)–(3.6):

$\begin{equation*} a_1 + a_2 + 1 = \frac{(1-\alpha)^2+(1-\beta)^2+(\alpha-\beta)^2}{2(1+\alpha+\beta)^2} \gt 0. \end{equation*}$ $

The right inequality of eq.(3.7) $ 1 + a_2 < 2 $, that is, $ a_2 -1 < 0, $ gives

$\begin{equation} \alpha\beta \gt 1. \end{equation}$ $

(3.8)

Notice that it is symmetric with respect to $ \alpha $ and $ \beta $; namely, eq.(3.8) does not change when $ \alpha $ and $ \beta $ are exchanged.

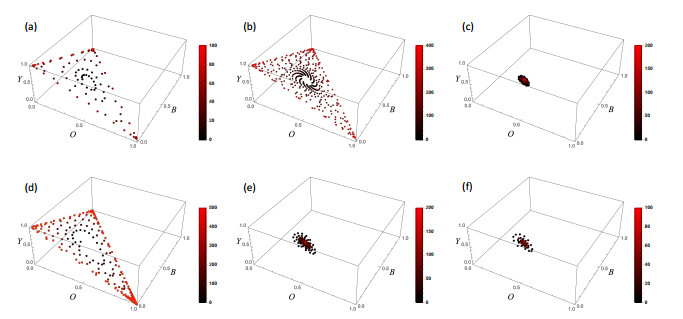
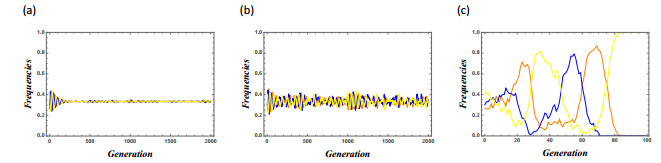
Indeed, it is known that eq.(3.8) becomes a globally asymptotic stable condition, which can be checked using the Lyapunov function ^[9]. If eq.(3.8) does not hold, then we can observe the trajectory of the heteroclinic cycle between three vertices in the triangular space for three phenotypic frequencies ^[9] similar to the three-species Lotka-Volterra cyclic competition model ^[12] (See Figure 1(a) and (b)).

Figure 1. Trajectories of phenotypic frequencies. (a)-(c) for eqs.(3.1)-(3.3), (d)-(f) for eqs.(2.27)-(2.36) with Table 3. $ \beta $ is fixed to $ 0.3 $. $ \alpha = 2 $ for (a) and (d), $ \alpha = 3 $ for (b) and (e), $ \alpha = 4 $ for (c) and (f). Figure 2(a) tells us that internal equilibrium is unstable for (a), (b) and (d), but stable for (c), (e) and (f). Colorbars indicate the time steps of the dynamics.

DownLoad: Full-Size Img PowerPoint

Figure 2. Stable and unstable region on parameter spaces of the equilibrium point (3.4) for (a) allele dominance rule (Ⅰ) and (b) allele dominance rule (Ⅱ). $ \alpha $ and $ \beta $ indicate payoffs for strong and weak competitors, respectively. Green, red and yellow regions indicate stable for both phenotypic and genotypic models, stable for genotypic model but unstable for phenotypic one and unstable for both phenotypic and genotypic models, respectively. Allele dominance rule (Ⅱ) has larger stability region than (Ⅰ).

DownLoad: Full-Size Img PowerPoint

On the other hand, for a genotypic model, we get the following unique internal equilibrium by eqs.(2.27)–(2.36):

$\begin{eqnarray} g_{oo} & = & \frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{2}, \end{eqnarray}$ $

(3.9)

$\begin{eqnarray} g_{oy} & = & \left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{2}-1\right), \end{eqnarray}$ $

(3.10)

$\begin{eqnarray} g_{ob} & = & \frac{2}{3}\left(\sqrt{3}-\sqrt{2}\right), \end{eqnarray}$ $

(3.11)

$\begin{eqnarray} g_{yy} & = & \frac{1}{3}\left(\sqrt{2}-1\right)^2, \end{eqnarray}$ $

(3.12)

$\begin{eqnarray} g_{yb} & = & \frac{2}{3}\left(\sqrt{2}-1\right), \end{eqnarray}$ $

(3.13)

$\begin{eqnarray} g_{bb} & = & \frac{1}{3}. \end{eqnarray}$ $

(3.14)

Of course,

$\begin{eqnarray*} p_O & = & g_{oo} + g_{oy} + g_{ob} = \frac{1}{3}, \\ p_Y & = & g_{yy} + g_{yb} = \frac{1}{3}, \\ P_B & = & g_{bb} = \frac{1}{3}. \end{eqnarray*}$ $

We can say that an internal equilibrium does not depend on the parameters $ \alpha $ nor $ \beta $ on either the phenotyic or genotypic models.

The characteristic equation of the linearized system of eqs.(2.27)–(2.32) with eqs.(2.33)–(2.36) about an internal equilibrium (3.9)–(3.14) becomes

$\begin{equation*} \lambda^4(\lambda^2 + a_1 \lambda + a_2) = 0, \end{equation*}$ $

where

$\begin{eqnarray} a_1 & = & -\frac{2\sqrt{3}}{3(1+\alpha+\beta)} \left\{\left(2\sqrt{2}+2-\sqrt{3}\right)+\left(2\sqrt{3}-\sqrt{2}-1\right)(\alpha+\beta)\right\}, \end{eqnarray}$ $

(3.15)

$\begin{eqnarray} a_2 & = & \frac{1}{(1+\alpha+\beta)^2} \left[8\sqrt{2}-11+4\sqrt{3}\left(\sqrt{2}-2\right) \right. \\ &+& \left\{2\sqrt{2}\left(4+\sqrt{3}\right)-\left(6\sqrt{3}+5\right)\right\}(\alpha^2+\beta^2) \\ &+& 2\left\{4+3\sqrt{3}-\sqrt{2}\left(4+\sqrt{3}\right)\right\}(\alpha+\beta) \\ &-& \left. 2\left\{2\sqrt{2}\left(2+\sqrt{3}\right)-\left(7+2\sqrt{3}\right)\right\}\alpha\beta \right]. \end{eqnarray}$ $

(3.16)

Noticing that $ a_1 < 0 $ from eq.(3.15), the left inequality of eq.(3.7) holds because, using eqs.(3.15)–(3.16),

$\begin{eqnarray*} && a_1 + a_2 + 1 \\ & = & \frac{4\sqrt{3}\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{2}-1\right)}{3(1+\alpha+\beta)^2} \left\{(1-\alpha)^2+(1-\beta)^2+(\alpha-\beta)^2\right\} \gt 0. \end{eqnarray*}$ $

The right inequality of eq.(3.7) $ a_2 -1 < 0 $ becomes

$\begin{equation} \sqrt{2}\left(\sqrt{3}+1\right)\left(\sqrt{3}+\sqrt{2}\right)(\alpha\beta-1) + \alpha(\alpha-1)+\beta(\beta-1) \gt 0, \end{equation}$ $

(3.17)

which is a quadratic inequation on $ \alpha $ or $ \beta $ and is also symmetric with respect to $ \alpha $ and $ \beta $.

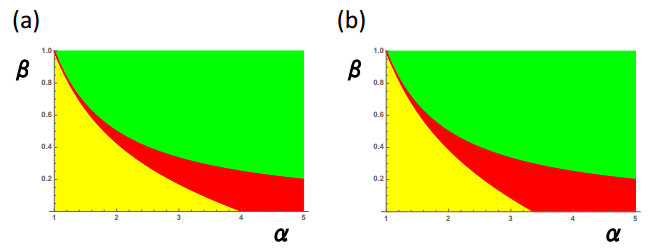
Figure 2(a) shows the local stability region obtained by eq.(3.8) and eq.(3.17). We can observe their dynamics by numerical simulations (Figure 1).

4. Cyclic allele dominance rule expands the stability region of the internal equilibrium

Common side-blotched lizards have an allele dominance rule (Ⅰ), that is, an allele $ o $ for an orange throat is the most dominant over others, an allele $ y $ for a yellow one is intermediate, and an allele $ b $ for a blue one is the most recessive (Table 2). In other words, this allele dominance rule has three kinds of alleles: most dominant, intermediate, and most recessive. We refer to these as $ o $, $ y $, and $ b $, respectively.

Although perhaps we have not yet discovered it in realistic genetic systems, we can theoretically consider another allele dominance rule (Ⅱ), that is, all alleles having intermediate dominance: $ o $ dominant over $ y $, $ y $ over $ b $, and $ b $ over $ o $ (Table 4). This rule could be called as a "cyclic allele dominance rule." Similarly, in this rule, we name these alleles $ o $, $ y $, and $ b $, and any allele can be replaced by another one.

Table 4. Allele dominance rule (Ⅱ). An allele $ o $ is dominant to an allele $ y $, then two genotypes $ oo $ and $ oy $ correspond to a phenotype $ O $. An allele $ y $ is dominant to an allele $ b $, then two genotypes $ yy $ and $ yb $ correspond to a phenotype $ Y $. An allele $ b $ is dominant to an allele $ o $, then two genotypes $ bb $ and $ ob $ correspond to a phenotype $ B $.

Genotype		Phenotype
$ oo, oy $	$ \to $	$ O $
$ yy, yb $	$ \to $	$ Y $
$ bb, ob $	$ \to $	$ B $

| Show Table

DownLoad: CSV

A calculation for allele dominance rule (Ⅱ) similar to that for allele dominance rule (Ⅰ) reveals that the boundary of local stability obtained from the Jury condition (3.7) is determined by

$\begin{equation} 8(\alpha\beta-1)+\alpha(\alpha-1)+\beta(\beta-1) = 0, \end{equation}$ $

(4.1)

which only differs from the first calculation in the smaller coefficient of $ \alpha\beta-1 $ compared to eq.(3.17). Figure 2(b) shows the local stability region by allele dominance rule (Ⅱ) using eq.(4.1), which clearly has a larger stability region than rule (Ⅰ).

From a theoretical point of view, we should also consider the cases with the same allele dominance rules but with different cyclic competitive strengths. Then another possible combination exists, that is, Table 2 with $ \alpha < 1 $ and $ \beta > 1 $. However, this combination gives the same stability regions as Figure 2(a) by the symmetry of the boundary equation (3.17) on the parameters $ \alpha $ and $ \beta $; eq.(3.17) does not change when $ \alpha $ and $ \beta $ are exchanged. On the other hand, it is trivial that no qualitative difference exists between the two cases: Table 4 with $ \alpha > 1 $ and $ \beta < 1 $ and Table 4 with $ \alpha < 1 $ and $ \beta > 1 $.

5. Spatial simulation

Barreto et al. ^[8] showed the same stabilizing effect in a genetic system of lizards as the previous section of this paper. Here we introduce a spatial structure into a phenotypic model and consider its effects on population dynamics.

The phenotypic model includes two processes: competition and reproduction. When we add a spatial structure into this model, we restrict the spatial range, both for the opponents against a focal individual and for the dispersion of offspring by reproduction. When we set such a spatial restriction as a whole or as a neighborhood, we consider four distinct cases: (a) global competition and global dispersion, (b) global competition and local dispersion, (c) local competition and global dispersion, and (d) local competition and local dispersion.

The Monte Carlo simulation procedures for the above four cases use the following algorithm (See the C program code in the Electronic Supplementary Materials):

(ⅰ) We prepare a two-dimensional square lattice space, each-side with a size of 100, so that the total number of sites on a whole lattice becomes $ N = 100\times 100 = 10000 $. We use a periodic boundary condition. The states $ O $, $ Y $, and $ B $ are randomly distributed according to the initial fractions: $ (p_O, p_Y, p_B) = (0.3, 0.3, 0.4) $, respectively.

(ⅱ) The first process is competition, which determines the payoffs after games against randomly chosen opponents. All individuals experience this process. The payoffs for all the sites $ i \ ( = 1, \ldots, N) $ in a whole population with size $ N $ are determined in order; the site $ (\ell, m) $ with $ x $-coordinate $ \ell \ (\ell = 1, \ldots, 100) $ and $ y $-coordinate $ m \ (m = 1, \ldots, 100) $ on the two-dimensional square lattice is numbered $ (\ell-1)\times 100 + m $. An individual $ I \in\{O, B, Y\} $ is included on the site $ i $. Another site $ j $ is randomly chosen in a whole population in the cases of (a) and (b) or, in the cases of (c) and (d), in the nearest neighboring four individuals. An individual $ J \in\{O, B, Y\} $ is included on the site $ j $. Two individuals $ I $ and $ J $ compete and an individual $ I $ gets a payoff by a payoff matrix (Table 3). All the payoffs are transferred to their offspring, and they are gathered in one offspring pool in the cases of (a) and (c) or, in the cases of (b) and (d), in local offspring pools. Here, we use lower cases for the sites and corresponding upper cases for the states of the individuals on those sites.

(ⅲ) The second process is dispersion, which gives positions of offspring selected from the offspring pool. The model is discrete-generation: all individuals die, and the states at the next time steps for all the sites $ i \ ( = 1, \ldots, N) $ in a whole population with size $ N $ are replaced in order. For each site, an individual is randomly chosen from a whole pool for (a) and (c) or from each local pool for (b) and (d); this choice is made in proportion to the relative payoff against total payoffs in a whole population in the cases of (a) and (c) or in the nearest neighboring four individuals in the cases of (b) and (d). In other words, this random selection depends on $ \frac{W_O}{W}, \frac{W_Y}{W} $, and $ \frac{W_B}{W} $. After the previous process (ⅱ), all the individuals have their own payoffs. In the cases of (a) and (c), we can then calculate $ W, W_O, W_Y $, and $ W_B $ as the total payoffs for, respectively, a whole population, phenotype $ O $, phenotype $ Y $, and phenotype $ B $. In the cases of (b) and (d), we can obtain $ W, W_O, W_Y $, and $ W_B $ as the total payoffs for, respectively, a local population, phenotype $ O $ in the local population, phenotype $ Y $ in the local population, and phenotype $ B $ in the local population. Here a local population is restricted to individuals on five sites: the focal site and its nearest neighboring four sites.

(ⅳ) The above procedures (ⅱ) and (ⅲ) are repeated for $ 10000 \ ( = 100 \times 100) $ time steps for each parameter combination of $ \alpha = 1, 1.05, 1.10, \ldots, 5 $ and $ \beta = 0, 0.05, 0.10, \ldots, 1 $. The repetition of the simulations is 100 for each parameter combination, and we record the fraction of the coexistence of the three phenotypes.

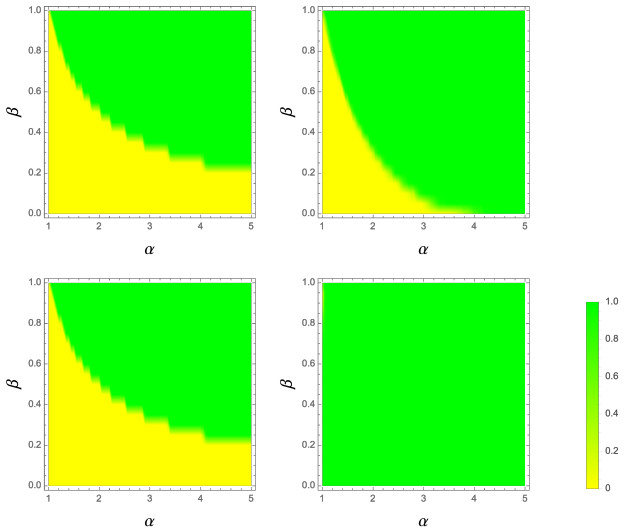
We show the results of the Monte Carlo simulation by the above algorithm in Figure 3. Case (a) completely coincides with Figure 2(a). Case (b) gives a wider coexistence region due to local dispersion. Case (c) has the same result as case (a) because the global dispersal produces the same effect with random choices of opponents from the population. Case (d) shows coexistence in almost all the simulations for the entire parameter space. Therefore, we can conclude that locally limited interactions between individuals strongly promote the coexistence of all phenotypes.

Figure 3. Phase diagram for coexistence and non-coexistence. Each parameter $ \alpha $ or $ \beta $ is set for every 0.05 increment. Initial values are given as $ (p_O, p_B, p_Y) = (0.3, 0.3, 0.4) $. Simulation runs are repeated for 100 times for each parameter set and their fractions are shown by continuous gradation between green and yellow. Green indicates coexistence until the end of simulations. Yellow corresponds to non-coexistence in which one phenotype goes extinct, and then an inferior phenotype disappears and ultimately only one phenotype survives, due to finite size of the system. (Upper left panel) global competition and global dispersion; (Upper right panel) global competition and local dispersion; (Lower left panel) local competition and global dispersion; (Lower right panel) local competition and local dispersion.

DownLoad: Full-Size Img PowerPoint

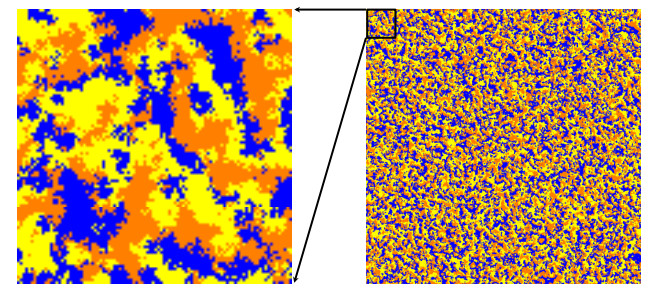
In case (d), individuals with the same phenotypes tend to cluster and adopt collective behavior, so changes of state occur only on the boundaries between these clusters, causing a slower change of total population and stabilization (See Figure 4). Indeed ^[13] already reached such a conclusion from a continuous-time cyclic competition model that also calculated the average domain size or boundary length at a steady state. This spatial structure in the population is gradually produced by both local competition and local dispersion, and, in turn, also gives different results in competition and dispersion, either globally or locally.

Figure 4. Snapshot of spatial pattern by Monte Carlo simulation of phenotypic model on two-dimensional square lattice space after some time. Both competition and dispersion occur locally. We can observe that several dozens of same phenotypic individuals are clustering. (Right panel) The whole spatial pattern with $ 1000 \times 1000 $ lattice sites. (Left panel) The upper left part of spatial pattern with $ 100 \times 100 $ lattice sites. Colors indicate $ O, B, Y $ as orange, blue, yellow, respectively. $ \alpha = 2.0 $ and $ \beta = 0.3 $.

DownLoad: Full-Size Img PowerPoint

6. Discussion

Similar to ^[8], we show the difference between the phenotypic model and its corresponding genotypic model, but we can also give an explicit condition using a simplified system. In addition, we investigate other allele dominance rules to clarify their effects on the stability of internal equilibrium compared to the allele dominance rule observed in lizards. Unfortunately, however, we cannot specify the mechanism by which the genotypic model stabilizes the system more than the phenotypic model. To discover it, we need to find models other than cyclic competition in which the genotypic models give different dynamic behaviors than the corresponding phenotypic models.

A recent proposal by ^[14] may have important implications for future work in this area. As they point out, the present three-strategy payoff matrix can be built up as the sum of nine independent Fourier components, $ \mathbf{g}(1), \ldots, \mathbf{g}(9) $, with orthogonality and normalization:

$\begin{eqnarray*} \begin{pmatrix} 1 & \alpha & \beta \\ \beta & 1 & \alpha \\ \alpha & \beta & 1 \end{pmatrix} & = & (1+\alpha+\beta) \cdot \frac{1}{3} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix} \\ &+& \frac{\sqrt{2}}{2}(2-\alpha-\beta) \cdot \frac{1}{\sqrt{18}} \begin{pmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{pmatrix} \\ &+& \frac{\sqrt{6}}{2}(\beta-\alpha) \cdot \frac{1}{\sqrt{6}} \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & -1 \\ -1 & 1 & 0 \end{pmatrix} \\ & = & (1+\alpha+\beta) \mathbf{g}(1) + \frac{\sqrt{2}}{2}(2-\alpha-\beta) \mathbf{g}(8) + \frac{\sqrt{6}}{2}(\beta-\alpha) \mathbf{g}(9), \end{eqnarray*}$ $

where we have $ \mathbf{g}(1), \mathbf{g}(8) $, and $ \mathbf{g}(9) $ as irrelevant constant terms, a coordination (Potts) component that equally favors the formation of one of the homogeneous states, and a cyclic (rock-paper-scissors) component, respectively. This formulation may offer more detailed insights into dynamical behaviors if we examine cases with various combinations of coefficients corresponding to the strengths of these components.

The intuitive reason local competition and local dispersion both stabilize an internal equilibrium is that several dozens of identical phenotypic individuals gather and adopt collective behavior, restricting phenotypic changes on the boundary. To investigate their stabilization mechanisms in detail, we should further rely on other kinds of analysis, especially spatial pattern formation, which may play an important role in stabilizing the dynamics. So far, the concept of "vortex" has been proposed to characterize the spatial pattern ^[15,16,17], and it has also been shown that clockwise or anti-clockwise rotating spiral patterns with characteristic sizes emerge that yield finite size effects by cyclic competition models or rock-paper-scissors games in physics ^{[18,19,20,21]} and evolutionary games ^[22,23]. More precisely, the coexistence of three strategies transforms into one of the homogeneous states after a suitable relaxation time if the characteristic length of patterns exceeds a threshold value comparable to the system size. Here we use a small lattice space size $ (100 \times 100) $ for Figure 3, but we should further investigate these finite size effects using a larger lattice space, such as $ 1000 \times 1000 $, as in Figure 4.

In this paper, we only show whether three phenotypes can coexist or not in the long run using a Monte Carlo simulation. However, we can expect an internal equilibrium to be asymptotically stable for the case of coexistence in larger Monte Carlo systems than in smaller ones (Figure 5).

Figure 5. Time series of frequencies by Monte Carlo simulation of phenotypic model on two-dimensional square lattice space. Both competition and dispersion occur locally. We can confirm that fluctuations are due to the effect of finite size of lattice sites. The numbers of lattice sites are (a) $ 1000 \times 1000 $, (b) $ 100 \times 100 $, (c) $ 10 \times 10 $. All phenotypes survived after 2000 Monte Carlo steps in (a) and (b), but in (c) $ B $ went extinct around 70 generations by chance, and then $ O $ died out almost inevitably (but not definitely because of finite system size) because $ Y $ is stronger than $ O $. Colors indicate $ O, B, Y $ as orange, blue, yellow, respectively. Initial frequencies are $ (p_O, p_B, p_Y) = (0.3, 0.3, 0.4) $. $ \alpha = 2.0 $ and $ \beta = 0.3 $.

DownLoad: Full-Size Img PowerPoint

Here we can only show the condition of the locally asymptotic stability of a genotypic model. We expect that condition to be replaced by global stability, but we leave it as a future problem.

In addition, we would like to examine a genotypic model in a lattice space and clarify whether it becomes more stable than a phenotypic model and to what degree its stability can be evaluated by, for example, the return time of perturbation to an internal equilibrium.

Throughout this paper, we use only symmetric conditions of parameters to obtain global insights into the dynamics, then we should study more complicated models with symmetry-breaking interactions, including the parameter setting of ^[8], in future research.

Acknowledgements

I sincerely appreciate Prof. Akira Sasaki for giving me useful comments and encouraging me. I would also like to thank three anonymous reviewers whose comments were helpful in revising the manuscript.

Conflict of interest

The author declares no conflict of interest.

References

[1]	Santos WDD, Gómez ED, Buckeridge MS, (2011) Bioenergy and the Sustainable Revolution, In: Buckeridge MS, Goldman GH. Routes to Cellulosic Ethanol. Springer Science and Business Media, LCC, 1 Ed., New York, 15–26.
[2]	Jaiswal D, Souza APD, Larsen S, et al. (2017) Brazilian sugarcane ethanol as an expandable green alternative to crude oil use. Nat Clim Change 7: 788–792. doi: 10.1038/nclimate3410
[3]	Saini JK, Saini R, Tewari L (2015) Lignocellulosic agriculture wastes as biomass feedstocks for second-generation bioethanol production: Concepts and recent developments. Biotech 5: 337–353.
[4]	Buckeridge MS, Dos Santos WD, Mas T, et al. (2016) The cell wall architecture of sugarcane and its implications to cell wall recalcitrance, In: Lam E, Carrer H, Da Silva JA, et al. Compendium of Bioenergy Plants: Compendium of Bioenergy Plants, Boca Raton, FL: CRC Press, 31–50.
[5]	Poovaiah CR, Nageswara-Rao M, Soneji JR, et al. (2014) Altered lignin biosynthesis using biotechnology to improve lignocellulosic biofuel feedstocks. Plant Biotechnol J 12: 1163–1173. doi: 10.1111/pbi.12225
[6]	Torres AF, Visser RGF, Trindade LM (2015) Bioethanol from maize cell walls: Genes, molecular tools, and breeding prospects. GCB Bioenergy 7: 591–607. doi: 10.1111/gcbb.12164
[7]	Balat M (2011) Production of bioethanol from lignocellulosic materials via the biochemical pathway: A review. Energ Convers Manage 52: 858–875. doi: 10.1016/j.enconman.2010.08.013
[8]	Souza APD, Leite DCC, Pattathil S, et al. (2013) Composition and structure of sugarcane cell wall polysaccharides: Implications for second-generation bioethanol production. BioEnergy Res 6: 564–579. doi: 10.1007/s12155-012-9268-1
[9]	Gupta A, Verma JP (2015) Sustainable bio-ethanol production from agro-residues. Renew Sust Energ Rev 41: 550–567. doi: 10.1016/j.rser.2014.08.032
[10]	Sims REH, Mabee W, Saddler JN, et al. (2010) An overview of second generation biofuel technologies. Bioresource Technol 101: 1570–1580. doi: 10.1016/j.biortech.2009.11.046
[11]	Amorim HV, Lopes ML, Oliveira JVC, et al. (2011) Scientific challenges of bioethanol production in Brazil. Appl Microbiol Biotechnol 91: 1267–1275. doi: 10.1007/s00253-011-3437-6
[12]	Verardi A, Blasi A, Molino A, et al. (2016) Improving the enzymatic hydrolysis of Saccharum officinarum L. bagasse by optimizing mixing in a stirred tank reactor: Quantitative analysis of biomass conversion. Fuel Process Technol 149: 15–22.
[13]	Limayem A, Ricke SC (2012) Lignocellulosic biomass for bioethanol production: Current perspectives, potential issues and future prospects. Prog Energy Combust Sci 38: 449–467. doi: 10.1016/j.pecs.2012.03.002
[14]	Goldemberg J, Coelho ST, Guardabassi P (2008) The sustainability of ethanol production from sugarcane. Energ Policy 36: 2086–2097. doi: 10.1016/j.enpol.2008.02.028
[15]	Rocha GJM, Gonçalves AR, Oliveira BR, et al. (2013) Steam explosion pretreatment reproduction and alkaline deligniﬁcation reactions performed on a pilot scale with sugarcane bagasse for bioethanol production. Ind Crop Prod 35: 274–279.
[16]	Buckeridge MS, Santos WDD, Souza AP, (2010) Routes for cellulosic ethanol in Brazil, In: Cortez LAB. Sugarcane Bioethanol, R&D for productivity and sustainability, Blucher, 992.
[17]	Kou L, Song Y, Zhang X, et al. (2017) Comparison of four types of energy grasses as lignocellulosic feedstock for the production of bio-ethanol. Bioresource Technol 241:434–429.
[18]	Álvarez C, Manuel RF, Bruno D (2016) Enzymatic hydrolysis of biomass from wood. Microb Biotechnol 9: 149–156. doi: 10.1111/1751-7915.12346
[19]	Malinovsky FG, Fangel JU, Willats WGT (2014) The role of the cell wall in plant immunity. Front Plant Sci 5: 178.
[20]	Payne CM, Knott BC, Mayes HB, et al. (2015) Fungal cellulases. Chem Rev 115: 1308–1448. doi: 10.1021/cr500351c
[21]	Khare SK, Pandey A, Larroche C (2015) Current perspectives in enzymatic saccharification of lignocellulosic biomass. Biochem Eng J 102: 38–44. doi: 10.1016/j.bej.2015.02.033
[22]	Jørgensen H, Kristensen JB, Felby C (2007) Enzymatic conversion of lignocellulose into fermentable sugars: Challenges and opportunities. Biofuels Bioprod Biorefin 1: 119–134.
[23]	Le GH, Florian F, Jean-Marc D, et al. (2015) Cell wall metabolism in response to abiotic stress. Plants 4: 112–166. doi: 10.3390/plants4010112
[24]	Pauly M, Keegstra K (2008) Cell-wall carbohydrates and their modiﬁcation as are source for biofuels. Plant J 54: 559–568. doi: 10.1111/j.1365-313X.2008.03463.x
[25]	Höfte H, Voxeur A (2017) Plant cell walls. Curr Biol 27: R865–R870. doi: 10.1016/j.cub.2017.05.025
[26]	Carpita NC, Gibeaut DM (1993) Structural models of primary cell walls in flowering plants: Consistency of molecular structure with the physical properties of the walls during growth. Plant J 3: 1–30. doi: 10.1111/j.1365-313X.1993.tb00007.x
[27]	Chundawat SPS, Beckham GT, Himmel ME, et al. (2011) Deconstruction of lignocellulosic biomass to fuels and chemicals. Annu Rev Chem Biomol Eng 2: 121–145. doi: 10.1146/annurev-chembioeng-061010-114205
[28]	Meents MJ, Watanabe Y, Samuels AL (2018) The cell biology of secondary cell wall biosynthesis. Ann Bot.
[29]	Turner S, Kumar M (2018) Cellulose synthase complex organization and cellulose microfibril structure. Philos Trans 376: 20170048.
[30]	Himmel ME, Ding SY, Johnson DK, et al. (2007) Biomass recalcitrance: Engineering plants and enzymes for biofuels production. Science 315: 804–807. doi: 10.1126/science.1137016
[31]	Carpita NC, Mccann MC, (2000) The cell wall, In: Buchanan BB, Gruissem W, Jones RL, Biochemistry and molecular biology of plants. Rockville: IL: American Society of Plant Physiologists, 1367.
[32]	Abramson M, Shoseyov O, Shani Z (2010) Plant cell wall reconstruction toward improved lignocellulosic production and processability. Plant Sci 178: 61–72. doi: 10.1016/j.plantsci.2009.11.003
[33]	Van dWT, Dolstra O, Visser RG, et al. (2017) Stability of cell wall composition and saccharification efficiency in miscanthus across diverse environments. Front Plant Sci 7: 2004.
[34]	Pauly M, Keegstra K (2016) Biosynthesis of the plant cell wall matrix polysaccharide xyloglucan. Annu Rev Plant Biol 67: 235–259. doi: 10.1146/annurev-arplant-043015-112222
[35]	Oliveira DM, Finger-Teixeira A, Mota TR, et al. (2016). Ferulic acid: A key component in grass lignocellulose recalcitrance to hydrolysis. Plant Biotechnol J 13: 1224–1232.
[36]	Kozlova LV, Ageeva MV, Ibragimova NN, et al. (2014) Arrangement of mixed-linkage glucan and glucuronoarabinoxylan in the cell walls of growing maize roots. Ann Bot 114: 1135–1145. doi: 10.1093/aob/mcu125
[37]	Srivastava PK, Kapoor M (2017) Production, properties, and applications of endo-β-mannanases. Biotechnol Adv 35: 1–19. doi: 10.1016/j.biotechadv.2016.11.001
[38]	Biswal AK, Atmodjo MA, Li M, et al. (2018) Sugar release and growth of biofuel crops are improved by downregulation of pectin biosynthesis. Nat Biotechnol.
[39]	Voragen AGJ, Coenen GJ, Verhoef RP, et al. (2009) Pectin, a versatile polysaccharide present in plant cell walls. Struct Chem 20: 263–275. doi: 10.1007/s11224-009-9442-z
[40]	Mohnen D (2008) Pectin structure and biosynthesis. Curr Opin Plant Biol 11: 266–277. doi: 10.1016/j.pbi.2008.03.006
[41]	Nguyen TN, Son S, Jordan MC, et al. (2016) Lignin biosynthesis in wheat (Triticum aestivum L.): Its response to waterlogging and association with hormonal levels. BMC Plant Biol 16: 1–16.
[42]	Ragauskas AJ, Beckham GT, Biddy MJ, et al. (2014) Lignin valorization: Improving lignin processing in the biorefinery. Science 344: 1246843. doi: 10.1126/science.1246843
[43]	Santos WDD, Ferrarese MDLL (2008) Ferulic acid: An allelochemical troublemaker. Funct Plant Sci Biotechnol 2: 47–55.
[44]	dos Santos WD, Ferrarese ML, Nakamura CV, et al. (2008) Soybean (Glycine max) root lignification induced by ferulic acid the possible mode of action. J Chem Ecol 34: 1230–1241. doi: 10.1007/s10886-008-9522-3
[45]	Liu Q, Luo L, Zheng L (2018) Lignins: Biosynthesis and Biological Functions in Plants. Int J Mol Sci 19: 335.
[46]	Salvador VH, Lima RB, dos Santos WD, et al. (2013) Cinnamic acid increases lignin production and inhibits soybean root growth. PLoS One 8: e69105. doi: 10.1371/journal.pone.0069105
[47]	Oliveira DMD, Finger-Teixeira A, Freitas DLD, et al. (2017) Phenolic Compounds in Plants: Implications for Bioenergy, In: Buckeridge MS, de Souza AP, Advances of Basic Science for Second Generation Bioethanol from Sugarcane, Springer Int Publishing, 39–52.
[48]	Boerjan W, Ralph J, Baucher M (2003) Lignin biosynthesis. Annu Rev Plant Biol 166: 63–71.
[49]	Moreira-Vilar FC, Siqueira-Soares RC, Finger-Teixeira A, et al. (2014) The acetyl bromide method is faster, simpler and presents best recovery of lignin in different herbaceous tissues than klason and thioglycolic acid methods. PLoS One 9: e110000. doi: 10.1371/journal.pone.0110000
[50]	Santos WDD, Marchiosi R, Vilar FCW, et al. (2014) Polyvalent Lignin: Recent Approaches in Determination and Applications, In: Lu F, Lignin: Structural analysis, applications in biomaterials and ecological significance, New York: Nova Publishers, 1–26.
[51]	Fornalé S, Rencoret J, Garcíacalvo L, et al. (2017) Changes in cell wall polymers and degradability in maize mutants lacking 3′- and 5′-O-methyltransferases involved in lignin biosynthesis. Plant Cell Physiol 58: 240–255.
[52]	Lima RB, Salvador VH, dos Santos WD, et al. (2013) Enhanced lignin monomer production caused by cinnamic acid and its hydroxylated derivatives inhibits soybean root growth. PLoS One 8: e80542. doi: 10.1371/journal.pone.0080542
[53]	Saritha M, Arora A, Lata (2012) Biological Pretreatment of Lignocellulosic Substrates for Enhanced Delignification and Enzymatic Digestibility. Indian J Microbiol 52: 122–130. doi: 10.1007/s12088-011-0199-x
[54]	Henrissat B, Bairoch A (1993) New families in the classification of glycosyl hydrolases based on amino acid sequence similarities. Biochem J 293: 781–788. doi: 10.1042/bj2930781
[55]	Lombard V, Ramulu HG, Drula E, et al. (2014) The carbohydrate-active enzymes database (CAZy). Nucleic Acids Res 42: D490–D495. doi: 10.1093/nar/gkt1178
[56]	Bourne Y, Henrissat B (2001) Glycoside hydrolases and glycosyltransferases families and functional modules. Curr Opin Struc Biol 11: 593–600. doi: 10.1016/S0959-440X(00)00253-0
[57]	Hashimoto H (2006) Recent structural studies of carbohydrate-binding modules. Cell Mol Life Sci 63: 2954–2967. doi: 10.1007/s00018-006-6195-3
[58]	Boraston AB, Bolam DN, Gilbert HJ, et al. (2004) Carbohydrate-binding modules: Fine-tuning polysaccharide recognition. Biochem J 382: 769–781. doi: 10.1042/BJ20040892
[59]	Davies G, Henrissat B (1995) Structures and mechanisms of glycosyl hydrolases. Structure 3: 853–859. doi: 10.1016/S0969-2126(01)00220-9
[60]	Terrapon N, Lombard V, Drula E, et al. (2017) The CAZy Database/the Carbohydrate-Active Enzyme (CAZy) Database: Principles and Usage Guidelines, In: Aoki-Kinoshita K (eds), A Practical Guide to Using Glycomics Databases. Springer, Tokyo, 117–131.
[61]	Segato F, Dias B, Berto GL, et al. (2017) Cloning, heterologous expression and biochemical characterization of a non-specific endoglucanase family 12 from Aspergillus terreus NIH2624. BBA 1865: 395–403.
[62]	Segato F, Damásio AR, de Lucas RC, et al. (2014) Genomics review of holocellulose deconstruction by aspergilli. Microbiol Mol Biol Rev 78: 588–613. doi: 10.1128/MMBR.00019-14
[63]	Olsen JP, Alasepp K, Kari J, et al. (2016) Mechanism of product inhibition for cellobiohydrolase Cel7A during hydrolysis of insoluble cellulose. Biotechnol Bioeng 113: 1178–1186.
[64]	Grange DC, Haan R, Zyl WH (2010) Engineering cellulolytic ability into bioprocessing organisms. Appl Microbiol Biotechnol 87: 1195–1208. doi: 10.1007/s00253-010-2660-x
[65]	Damásio ARL, Rubio MV, Gonçalves TA, et al. (2017) Xyloglucan breakdown by endo-xyloglucanase family 74 from Aspergillus fumigatus. Appl Microbiol Biotechnol 101: 2893–2903. doi: 10.1007/s00253-016-8014-6
[66]	Dodd D, Cann IKO (2009) Enzymatic deconstruction of xylan for biofuel production. GCB Bioenergy 1: 2–17. doi: 10.1111/j.1757-1707.2009.01004.x
[67]	Damásio ARDL, Pessedela BC, Segato F, et al. (2012) Improvement of fungal arabinofuranosidase thermal stability by reversible immobilization. Process Biochem 47: 2411–2417. doi: 10.1016/j.procbio.2012.09.024
[68]	Wilkens C, Andersen S, Dumon C, et al. (2017) GH62 arabinofuranosidases: Structure, function and applications. Biotechnol Adv 35: 792–804. doi: 10.1016/j.biotechadv.2017.06.005
[69]	Wu L, Jiang J, Kallemeijn W, et al. (2017) Activity-based probes for functional interrogation of retaining β-glucuronidases. Nat Chem Biol 13: 867–873 doi: 10.1038/nchembio.2395
[70]	Bornscheuer UT (2002) Microbial carboxyl esterases: Classification, properties and application in biocatalysis. FEMS Microbiol Rev 26: 73–81. doi: 10.1111/j.1574-6976.2002.tb00599.x
[71]	Krastanova I, Guarnaccia C, Zahariev S, et al. (2005) Heterologous expression, purification, crystallization, X-ray analysis and phasing of the acetyl xylan esterase from Bacillus pumilus. BBA 1748: 222–230.
[72]	Wong DWS (2006) Feruloyl esterase, a key enzyme in biomass degradation. Appl Biochem Biotechnol 133: 87–111. doi: 10.1385/ABAB:133:2:87
[73]	Dilokpimol A, Mäkelä MR, Aguilarpontes MV, et al. (2016) Diversity of fungal feruloyl esterases: Updated phylogenetic classification, properties, and industrial applications. Biotechnol Biofuels 9: 231. doi: 10.1186/s13068-016-0651-6
[74]	Faulds CB, Mandalari G, Curto RBL, et al. (2006) Synergy between xylanases from glycoside hydrolase family 10 and 11 and a feruloyl esterase in the release of phenolic acids from cereal arabinoxylan. Appl Microbiol Biotechnol 71: 622–629. doi: 10.1007/s00253-005-0184-6
[75]	Wong DWS, Chan VJ, Liao H, et al. (2013) Cloning of a novel feruloyl esterase gene from rumen microbial metagenome and enzyme characterization in synergism with endoxylanases. J Ind Microbiol Biotechnol 40: 287–295.
[76]	Pérezrodríguez N, Moreira CD, Torrado AA, et al. (2016) Feruloyl esterase production by Aspergillus terreus CECT 2808 and subsequent application to enzymatic hydrolysis. Enzyme Microb Tech 91: 52–58. doi: 10.1016/j.enzmictec.2016.05.011
[77]	Oliveira DM, Salvador VH, Mota TR, et al. (2016) Feruloyl esterase from Aspergillus clavatus improves xylan hydrolysis of sugarcane bagasse. AIMS Bioeng 4: 1–11. doi: 10.3934/bioeng.2017.1.1
[78]	Garg G, Singh A, Kaur A, et al. (2016) Microbial pectinases: An ecofriendly tool of nature for industries. Biotech 6: 47.
[79]	Kant S, Vohra A, Gupta R (2013) Purification and physicochemical properties of polygalacturonase from Aspergillus niger MTCC 3323. Protein Expres Purif 87: 11–16.
[80]	Chen Q, Jin Y, Zhang G, et al. (2012) Improving production of bioethanol from duckweed (Landoltia punctata) by pectinase pretreatment. Energies 5: 3019–3032. doi: 10.3390/en5083019
[81]	Kataria R, Ghosh S (2011) Saccharification of Kans grass using enzyme mixture from Trichoderma reesei for bioethanol production. Bioresource Technol 102: 9970–9975. doi: 10.1016/j.biortech.2011.08.023
[82]	Oberoi HS, Vadlani PV, Nanjundaswamy A, et al. (2011) Enhanced ethanol production from Kinnow mandarin (Citrus reticulata) waste via a statistically optimized simultaneous saccharification and fermentation process. Bioresource Technol 102: 1593–1601.
[83]	Shanmugam VK, Gopalakrishnan D (2016) Screening and partial purification for the production of ligninase enzyme from the fungal isolate Trichosporon asahii. Braz Arch Biol Technol 59: e160220.
[84]	Vrsanska M, Voberkova S, Langer V, et al. (2016) Induction of laccase, lignin peroxidase and manganese peroxidase activities in white-rot fungi using copper complexes. Molecules 21: E1553. doi: 10.3390/molecules21111553
[85]	Pan L, Zhao H, Yu Q (2017) miR397/Laccase gene mediated network improves tolerance to fenoxaprop-P-ethyl in Beckmannia syzigachne and Oryza sativa. Front Plant Sci 23: 879.
[86]	Kameshwar AKS, Qin W (2016) Recent developments in using advanced sequencing technologies for the genomic studies of lignin and cellulose degrading microorganisms. Int J Biol Sci 12: 156–171. doi: 10.7150/ijbs.13537
[87]	Rastogi M, Shrivastava S (2017) Recent advances in second generation bioethanol production: An insight to pretreatment, saccharification and fermentation processes. Renew Sust Energ Rev 80: 330–340. doi: 10.1016/j.rser.2017.05.225
[88]	Huang R, Su R, Qi W, et al. (2011) Bioconversion of lignocellulose into bioethanol process intensification and mechanism research. BioEnerg Res 4: 225–245. doi: 10.1007/s12155-011-9125-7
[89]	Lygin AV, Upton J, Dohleman FG, et al. (2011) Composition of cell wall phenolics and polysaccharides of the potential bioenergy crop-Miscanthus. Global Change Biol Bioenergy 3: 333–345. doi: 10.1111/j.1757-1707.2011.01091.x
[90]	Wei Y, Li X, Yu L, et al. (2015) Mesophilic anaerobic co-digestion of cattle manure and corn stover with biological and chemical pretreatment. Bioresource Technol 198: 431–436. doi: 10.1016/j.biortech.2015.09.035
[91]	Balat M, Balat H (2009) Recent trends in global production and utilization of bio-ethanol fuel. Appl Energ 86: 2273–2282. doi: 10.1016/j.apenergy.2009.03.015
[92]	Cianchetta S, Maggio BD, Burzi PL, et al. (2014) Evaluation of selected white-rot fungal isolates for improving the sugar yield from wheat straw. Appl Biochem Biotechnol 173: 609–623.
[93]	Behera S, Arora R, Nandhagopal N, et al. (2014) Importance of chemical pretreatment for bioconversion of lignocellulosic biomass. Renew Sust Energ Rev 36: 91–106. doi: 10.1016/j.rser.2014.04.047
[94]	Safari A, Karimi K, Shafiei M (2017) Dilute alkali pretreatment of softwood pine: A biorefinery approach. Bioresource Technol 234: 67–76. doi: 10.1016/j.biortech.2017.03.030
[95]	Rabemanolontsoa H, Saka S (2016) Various pretreatments of lignocellulosics. Bioresource Technol 199: 83–91. doi: 10.1016/j.biortech.2015.08.029
[96]	Zhu Z, Simister R, Bird S, et al. (2015) Microwave assisted acid and alkali pretreatment of Miscanthus biomass for biorefineries. AIMS Bioeng 2: 446–468.
[97]	Tang C, Shan J, Chen Y, et al. (2017) Organic amine catalytic organosolv pretreatment of corn stover for enzymatic saccharification and high-quality lignin. Bioresource Technol 232: 222–228. doi: 10.1016/j.biortech.2017.02.041
[98]	Silva ASD, Inoue H, Endo T, et al. (2010) Milling pretreatment of sugarcane bagasse and straw for enzymatic hydrolysis and ethanol fermentation. Bioresource Technol 101: 7402–7409. doi: 10.1016/j.biortech.2010.05.008
[99]	Chemat S, Lagha A, AitAmar H, et al. (2004) Comparison of conventional and ultrasound-assisted extraction of carvone and limonene from caraway seeds. Flavour Frag J 19: 188–195. doi: 10.1002/ffj.1339
[100]	Sipponen MH, Rahikainen J, Leskinen T, et al. (2017) Structural changes of lignin in biorefinery pretreatments. Nord Pulp Pap Res J 32: 547–568.
[101]	Fang H, Zhao C, Song XY, et al. (2013) Enhanced cellulolytic enzyme production by the synergism between Trichoderma reesei RUT-30 and Aspergillus niger NL02 and by the addition of surfactants. Biotechnol Bioprocess Eng 18: 390–398. doi: 10.1007/s12257-012-0562-8

This article has been cited by:

1.	Kwassi H. Degue, Denis Efimov, Abderrahman Iggidr, 2016, Interval estimation of sequestered infected erythrocytes in malaria patients, 978-1-5090-2591-6, 1141, 10.1109/ECC.2016.7810443
2.	Kwassi H. Degue, Jerome Le Ny, Estimation and outbreak detection with interval observers for uncertain discrete-time SEIR epidemic models, 2020, 93, 0020-7179, 2707, 10.1080/00207179.2019.1643492
3.	Pierre-Alexandre Bliman, Bettina D’Avila Barros, 2017, Chapter 3, 978-3-319-54210-2, 31, 10.1007/978-3-319-54211-9_3
4.	A. Iggidr, M. O. Souza, State estimators for some epidemiological systems, 2019, 78, 0303-6812, 225, 10.1007/s00285-018-1273-3
5.	Kwassi H. Degue, Jerome Le Ny, 2018, An Interval Observer for Discrete-Time SEIR Epidemic Models, 978-1-5386-5428-6, 5934, 10.23919/ACC.2018.8431758
6.	Derdei M. Bichara, Aboudramane Guiro, Abderrahman Iggidr, Diene Ngom, State and parameter estimation for a class of schistosomiasis models, 2019, 315, 00255564, 108226, 10.1016/j.mbs.2019.108226
7.	David Jaurès Fotsa-Mbogne, Improvement of disease dynamics monitoring through systematic screening and patchy structure: application to Neissera Meningitidis, 2021, 40, 2238-3603, 10.1007/s40314-021-01417-6
8.	M. S. Vinogradova, S. B. Tkachev, O. S. Tkacheva, Using an Observer in a Sliding Mode for Modeling Antiangiogenic Therapy, 2019, 2412-5911, 52, 10.24108/mathm.0618.0000165
9.	Kwassi H. Degue, Denis Efimov, Abderrahman Iggidr, Interval observer design for sequestered erythrocytes concentration estimation in severe malaria patients, 2021, 58, 09473580, 399, 10.1016/j.ejcon.2020.08.012
10.	S. Bowong, L. Mountaga, A. Bah, J. J. Tewa, J. Kurths, Parameter and state estimation in aNeisseria meningitidismodel: A study case of Niger, 2016, 26, 1054-1500, 123115, 10.1063/1.4971783
11.	Awais Khan, Xiaoshan Bai, Muhammad Ilyas, Arshad Rauf, Wei Xie, Peiguang Yan, Bo Zhang, Design and Application of an Interval Estimator for Nonlinear Discrete-Time SEIR Epidemic Models, 2022, 6, 2504-3110, 213, 10.3390/fractalfract6040213
12.	D. Bouhadjra, A. Alessandri, P. Bagnerini, A. Zemouche, 2022, A High-Gain Observer for Stage-Structured Susceptible-Infectious Epidemic Model with Linear Incidence Rate, 978-1-6654-5196-3, 1336, 10.23919/ACC53348.2022.9867230
13.	D. Bichara, A. Iggidr, M. Oumoun, A. Rapaport, G. Sallet, Identifiability and Observability via decoupled variables: Application to a malaria intra-host model, 2023, 56, 24058963, 576, 10.1016/j.ifacol.2023.10.1629
14.	F. Hamelin, A. Iggidr, A. Rapaport, G. Sallet, M. Souza, About the identifiability and observability of the SIR epidemic model with quarantine, 2023, 56, 24058963, 4025, 10.1016/j.ifacol.2023.10.1384
15.	Nik Cunniffe, Frédéric Hamelin, Abderrahman Iggidr, Alain Rapaport, Gauthier Sallet, 2024, Chapter 2, 978-981-97-2538-0, 9, 10.1007/978-981-97-2539-7_2

Reader Comments

Your name:*

Email:*
© 2018 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Bioengineering

1.2

Metrics

Article views(11002) PDF downloads(1730) Cited by(63)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(2) / Tables(1)

AIMS Bioengineering

Plant cell wall composition and enzymatic deconstruction

Related Papers:

Abstract

1. Introduction

2. The phenotypic model and its corresponding genotypic model

3. Stability condition for equilibrium $ (1/3, 1/3, 1/3) $

4. Cyclic allele dominance rule expands the stability region of the internal equilibrium

5. Spatial simulation

6. Discussion

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Bioengineering

Plant cell wall composition and enzymatic deconstruction

Related Papers:

Abstract

1. Introduction

2. The phenotypic model and its corresponding genotypic model

3. Stability condition for equilibrium $ (1/3, 1/3, 1/3) $

4. Cyclic allele dominance rule expands the stability region of the internal equilibrium

5. Spatial simulation

6. Discussion

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog