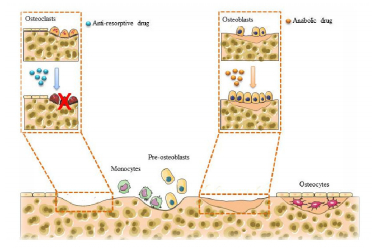
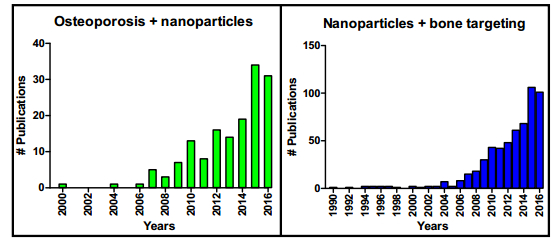
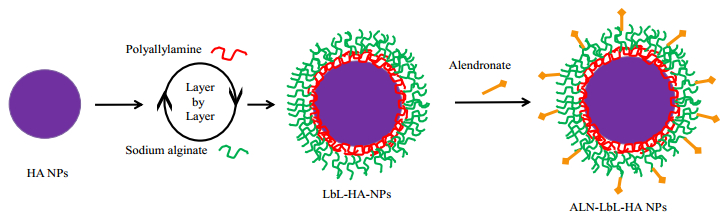
Osteoporosis is by far the most frequent metabolic disease affecting bone. Current clinical therapeutic treatments are not able to offer long-term solutions. Most of the clinically used anti-osteoporotic drugs are administered systemically, which might lead to side effects in non-skeletal tissues. Therefore, to solve these disadvantages, researchers have turned to nanotechnologies and nanomaterials to create innovative and alternative treatments. One of the innovative approaches to enhance osteoporosis therapy and prevent potential adverse effects is the development of bone-targeting drug delivery technologies. It minimizes the systemic toxicity and also improves the pharmacokinetic profile and therapeutic efficacy of chemical drugs. This paper reviews the current available bone targeting drug delivery systems, focusing on nanoparticles, proposed for osteoporosis treatment. Bone targeting delivery systems is still in its infancy, thus, challenges are ahead of us, including the stability and the toxicity issues. Newly developed biomaterials and technologies with potential for safer and more effective drug delivery, require multidisciplinary collaboration between scientists from many different areas, such as chemistry, biology, engineering, medicine, etc, in order to facilitate their clinical applications.
1.
Introduction
Fractional calculus is a field of applied mathematics that deals with derivatives and integrals of arbitrary orders [6,9,11,17]. Recently, fractional partial differential equations play an important role in interpretation and modeling of many of realism matters appear in applied mathematics and physics including fluid mechanics, electrical circuits, diffusion, damping laws, relaxation processes, optimal control theory, chemistry, biology, and so on [7,13,14,15,16]. Therefore, the search of the solutions for fractional partial differential equations is an important aspect of scientific research.
Many powerful and efficient methods have been proposed to obtain numerical solutions and analytical solutions of fractional partial differential equations. The most commonly used ones are: Adomian decomposition method (ADM) [5], variational iteration method (VIM) [18], new iterative method (NIM) [8], fractional difference method (FDM) [11], reduced differential transform method (RDTM) [1], homotopy analysis method (HAM) [3], homotopy perturbation method (HPM) [4].
The main objective of this paper is to present a new numerical technique called modified generalized Taylor fractional series method (MGTFSM) to obtain the approximate and exact solutions of Caputo time-fractional biological population equation. The proposed algorithm provides the solution in a rapid convergent series which may lead to the solution in a closed form. The main advantage of the proposed method compare with the existing methods is, that method solves the nonlinear problems without using linearization and any other restriction.
Consider the following Caputo time-fractional biological population equation
with the initial condition
where Dαt=∂α∂tα is the Caputo fractional derivative operator of order α, 0<α≤1,u=u(x,y,t),(x,y)∈R2,t>0 denotes the population density and F represents the population supply due to birth and death, α is a parameter describing the order of the fractional derivative.
The plan of our paper is as follows: In Section 2, we present some necessary definitions and properties of the fractional calculus theory. In Section 3, we will propose an analysis of the modified generalized Taylor fractional series method (MGTFSM) for solving the Caputo time-fractional biological population equation (1.1) subject to the initial condition (1.2). In Section 4, we present three numerical examples to show the efficiency and effectiveness of this method. In Section 5, we discuss our obtained results represented by figures and tables. These results were verified with Matlab (version R2016a). Section 6, is devoted to the conclusions on the work.
2.
Basic definitions
In this section, we present some basic definitions and properties of the fractional calculus theory which are used further in this paper. For more details see, [9,11].
Definition 2.1. A real function u(X,t), X=(x1,x2,...,xn)∈RN,N∈N∗,t∈R+, is considered to be in the space Cμ(RN×R+), μ∈ R, if there exists a real number p>μ, so that u(X,t)=tpv(X,t), where v ∈C(RN×R+), and it is said to be in the space Cnμ if u(n)∈Cμ(RN×R+),n∈N.
Definition 2.2. The Riemann-Liouville fractional integral operator of order α≥0 of u∈Cμ(RN×R+),μ≥−1, is defined as follows
where Γ(.) is the well-known Gamma function.
Definition 2.3. The Caputo time-fractional derivative operator of order α>0 of u∈Cn−1(RN×R+),n∈N, is defined as follows
For this definition we have the following properties
(1)
(2)
Definition 2.3. The Mittag-Leffler function is defined as follows
For α=1, Eα(z) reduces to ez.
3.
Analysis of modified generalized Taylor fractional series method (MGTFSM)
Theorem 3.1. Consider the Caputo time-fractional biological population equation of the form (1.1) with the initial condition (1.2).
Then, by MGTFSM the solution of equations (1.1)-(1.2) is given in the form of infinite series which converges rapidly to the exact solution as follows
where ui(x,y) the coefficients of the series and R is the radius of convergence.
Proof. In order to achieve our goal, we consider the following Caputo time-fractional biological population equation of the form (1.1) with the initial condition (1.2).
Assume that the solution takes the following infinite series form
Consequently, the approximate solution of equations (1.1)-(1.2), can be written in the form of
By applying the operator Dαt on equation (3.2), and using the properties (1) and (2), we obtain the formula
Next, we substitute both (3.2) and (3.3) in (1.1). Therefore, we have the following recurrence relations
We follow the same analogue used in obtaining the Taylor series coefficients. In particular, to calculate the function un(x,y),n=1,2,3,.., we have to solve the following
where
Now, we calculate the first terms of the sequence {un(x,y)}N1.
For n=1 we have
Solving G(x,y,0,α,1)=0, yields
For n=2 we have
Applying Dαt on both sides of equation (3.4) gives
Solving Dαt{G(x,y,t,α,2)}↓t=0=0, yields
To calculate u3(x,y), we consider G(x,y,t,α,3) and we solve
we have
and so on.
In general, to obtain the coefficient function uk(x,y) we solve
Finally, the solution of equations (1.1)-(1.2), can be expressed by
The proof is complete.
4.
Test examples
In this section, we test the validity and efficiency of the proposed method to solve three numerical examples of Caputo time-fractional biological population equation.
We define En to be the absolute error between the exact solution u and the approximate solution un, as follows
Example 4.1. Consider the Caputo time-fractional biological population equation in the form
with the initial condition
By applying the steps involved in the MGTFSM as presented in Section 3, we have the solution of equations (4.1)-(4.2) in the form
and
So, the solution of equations (4.1)-(4.2), can be expressed by
where Eα(htα) is the Mittag-Leffler function, defined by (2.3).
Taking α=1 in (4.3), we have
which is an exact solution to the standard form biological population equation [10].
Example 4.2. Consider the Caputo time-fractional biological population equation in the form
with the initial condition
By applying the steps involved in the MGTFSM as presented in Section 3, we have the solution of equations (4.4)-(4.5) in the form
and
So, the solution of equations (4.4)-(4.5), can be expressed by
where Eα(tα) is the Mittag-Leffler function, defined by (2.3).
Taking α=1 in (4.6), we have
which is an exact solution to the standard form biological population equation [12].
Example 4.3 Consider the Caputo time-fractional biological population equation in the form
with the initial condition
By applying the steps involved in the MGTFSM as presented in Section 3, we have the solution of equations (4.7)-(4.8) in the form
and
So, the solution of equations (4.7)-(4.8), can be expressed by
where Eα(htα) is the Mittag-Leffler function, defined by (2.3).
Taking α=1 in (4.9), we have
which is an exact solution to the standard form biological population equation [2].
5.
Numerical results and discussion
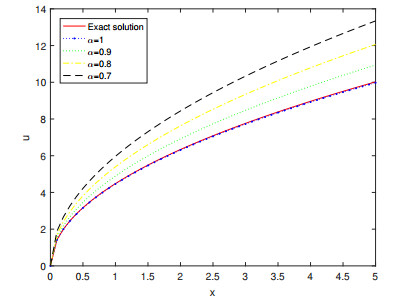
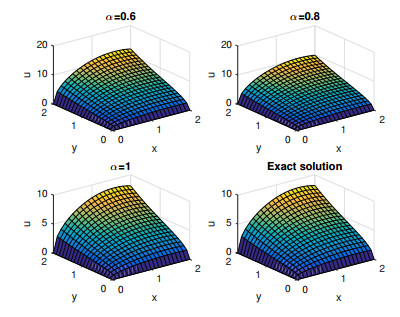
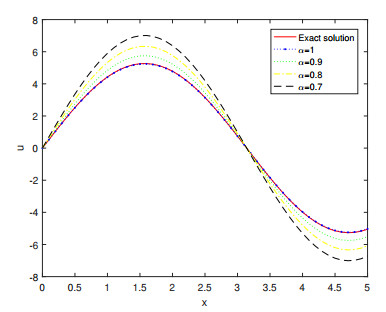
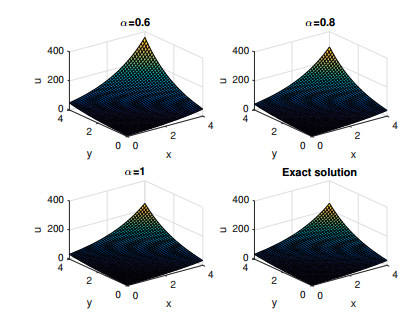
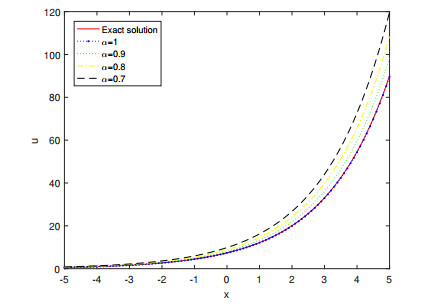
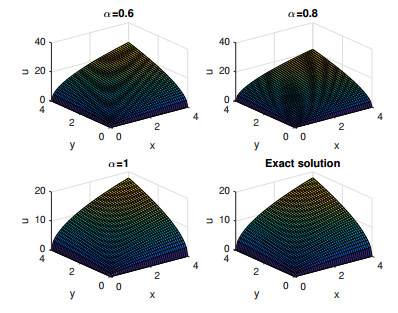
In this section the numerical results for Examples 4.1, 4.2 and 4.3 are presented. Figures 1, 3 and 5 represents the surface graph of the exact solution and the approximate solution u6(x,y,t) at α=0.6,0.8,1. Figures 2, 4 and 6 represents the behavior of the exact solution and the approximate solution u6(x,y,t) at α=0.7,0.8,0.9,1. These figures affirm that when the order of the fractional derivative α tends to 1, the approximate solutions obtained by MGTFSM tends continuously to the exact solutions. Tables 1–3 show the absolute errors between the exact solution and the approximate solution u6(x,y,t) at α=1 for different values of x,y and t. These tables clarifies the convergence of the approximate solutions to the exact solutions.
In addition, numerical results have confirmed the theoretical results and high accuracy of the proposed scheme.
Remark 5.1. In this paper, we only apply Six terms to approximate the solutions, if we apply more terms of the approximate solutions, the accuracy of the approximate solutions will be greatly improved.
6.
Conclusion
In this paper, a new numerical technique called modified generalized Taylor fractional series method (MGTFSM) has been successfully applied for solving the Caputo time-fractional biological population equation. The method was applied to three numerical examples. The results show that the MGTFSM is an efficient and easy to use technique for finding approximate and exact solutions for these problems. The obtained approximate solutions using the suggested method is in excellent agreement with the exact solutions. This confirms our belief that the effciency of our technique gives it much wider applicability for general classes of fractional problems.
Acknowledgments
The authors are very grateful to the guest editors of this special issue and would like to express their sincere thanks to the referees for the careful and noteworthy reading of the paper and for their constructive comments and suggestions which are improved the paper substantially.
Conflict of interest
The authors declare that there is no conflict of interest in this paper.









 DownLoad:
DownLoad: