1. Introduction
Molecular techniques developed in last few years, can be successfully used for qualitative and quantitative analyses. The increased knowledge in computer science in bioinformatic and computational biology make DNA/RNA probes design easier and faster then in the past. Specific computer programs allow the utilization of database as EMBL site (http://www.ebi.ac.uk/embl/), NCBI (http://www.ncbi.nlm.nih.gov/) and DDBJ (http://www.ddbj.nig.ac.jp/) that give the availability of many sequence genomes. The knowledge of the target sequence is an important starting point for the design of the probe (stretch of the nucleic acid single strand sequence) to make it specific. The length of the probes can varies from 15 to 60 bp depending on their utilization. Shorter probes (primers) can be used in couples to produce millions-fold PCR products, while longer can be used alone or in couple to functionalize various kinds of surfaces, from Au, glass, silicon nitride, plastic, carbondiimide and graphene surfaces [1,2,3,4,5,6] and build a biosensor. DNA/RNA probes have been used in various research fields such as food [7,8,9], environment [10,11,12], medical [13,14,15] and veterinary [16,17,18] applications to improve the specificity of the analyses, as they recognize their complementary sequence, and the sensitivity of the analyses. These probes can be used to detect various microorganisms present in samples down to strain level [19,20,21] without the requirement of a classical microbiological culture step in specific media and subsequent plate count, isolation, and identification by biochemical methods. This advantage reduce the time required for the identification of pathogens that can be responsible for food poising and subsequently affect human health. Moreover, DNA stretches, labelled or labelled free, are cheap then antibodies making interesting their application in new technologies, such as diagnostics.
2. Probe Design and Production
The first step requires the comparison of the target sequences among various microorganisms that show similarities. This is obtained by the alignment of DNA sequences downloaded by data bank from the web and using several kind of software such as ClustalW2 (http://www.clustal.org/), MAFFT (http://mafft.cbrc.jp/alignment/software/), MUSCLE (http://www.drive5.com/muscle/downloads.htm) or T-Coffee (http://tcoffee.org/Projects/tcoffee/).
Once selected the sequence that will represent the target, the designed probe is subjected to: i) evaluation about the potential mismatching location caused by the chosen sequence probe, and the possibility of secondary structure formations, such as hairpins, selfdimer and cross-dimer, before the synthesizing of the probe by using automated DNA synthesizers, ii) an in “silico” evaluation using specific software that test the probe against a whole genome list of selected microorganisms which are possible competitors of the target organism in the sample, iii) an evaluation of the specificity of the sequence of the probe, testing against DNAs from various non-target microorganisms, iv) optimization of the hybridization conditions [22]. Primers are used for the Polymerase Chain Reaction that has become a standard method in various research fields, and makes possible the detection and analysis of limited amounts of DNA molecules. PCR can be used for the identification of unknown DNA, for cloning DNA, and it can be used both on DNA and complementary DNA (cDNA). The critical parameter is the correct design of PCR primers, that often dictates the success or failure of the PCR technique [23]. A couple of specific primers (forward and reverse) are used to amplify the target region, which will be defined at both ends by the primer sequences; this PCR is often used to detect pathogens as the presence or absence of the expected product corresponds to the presence or absence of the pathogen. The unique annealing of the two primers to the template with high efficiency and high specificity to obtain unique, specific products is fundamental for a successful reaction.
3. PCR Methods
Foodborne pathogens responsible for the vast majority of illnesses are Listeria monocytogenes, Salmonella, Campylobacter, Escherichia coli O157:H7, Staphylococcus aureus, Clostridium perfringens, Toxoplasma gondii and Norovirus [24].
As reported by Manzano et al. [25] PCR was simple and fast when detecting L. monocytogenes in food matrices. A detection limit of 30 CFU/ml or g of L. monocytogenes was obtained without enrichment in milk using Mar1 and Mar2 primers located in the iap gene.
Another example of application in food is the study conducted by Aznar and Alarcon [26] that studied factors affecting PCR for the detection of L. monocytogenes in food matrices. PCR is compared with traditional culture methods on artificially and naturally contaminated foods such as meat, milk, fish, diary and ready to eat products. Among the six pair of primers tested, and designed on hlyA, iap, and 16S rRNA gene, the higher sensitivity was obtained for the primers designed in the hlyA gene, with a detection limit of 10-1 CFU/mL. Malorny et al. [27] conducted a study to evaluate specific PCR-based methods for Salmonella detection. The detection limit estimated for artificially contaminated minced beef (25 g) and broiler carcass-rinse (100 mL) was about 5 cells.
Yamamoto [28] reported data about the utilization of PCR for the specific detection of pathogens in clinical samples. In this case PCR was able to detect successfully the presence of Chlamydia pneumoniae in most of the samples tested demonstrating the importance of primer design for specificity and sensitivity. Al-Dragy and Baqer [29] used a multiplex PCR to detect Escherichia coli O157:H7 in human patient stools using a multiplex PCR.
The introduction of novel reagents, robust detection chemistries and instrumentation platforms allowed to upgrade the PCR to Quantitative PCR (qPCR) method, sometimes also called Real-Time PCR, which allows precise quantification of specific nucleic acids in a complex mixture even if the starting amount of material is at a very low concentration. qPCR increased the rapidity of the detection in comparison to the agarose gel electrophoresis by the inclusion of fluorescent reporter molecules that enable the quantification of PCR products in real time by monitoring the amplification of a target sequence using fluorescent technology. Mainly two different methods of detection of the amplicons are used, the non specific DNA-binding, which uses a dye (sybrgreen) to give the information about the presence or absence of the amplicon and the labelled probes. This last has three kinds of probes that can be used, the method based on cleavage, the molecular beacons and FRET probes. TaqMan® probes, based on 5' to 3' cleavage by Taq DNA polymerase exonuclease activity, can be used for both quantification and mutation detection. Molecular Beacons are probes that contain a stem-loop structure, with a fluorophore and a quencher at their 5' and 3' ends, respectively [30]. Scorpions® primers are suitable for both quantitative Real-Time PCR and genotyping/end-point analysis of specific DNA targets. de Boer et al. [31] developed a qPCR method to analyse 926 poultry sample for the presence of Campylobacter using three couple of primers designed on glyA gene [labeling with FAM (6-carboxyfluorescein) and MGB (minor grove binding)], hipO gene (labeling with VIC and TAMRA at 5' and 3' end respectively), and 16S rDNA [labeling with FAM (6-carboxyfluorescein) and MGB (minor grove binding)] respectively for C. jejuni, C. coli and Campylobacter spp. Gianfranceschi et al. [32] in 2013 published a study on the validation of an alternative detection strategy based on an ISO enrichment coupled to a consolidated real-time PCR assay for the detection of L. monocytogenes in artificially contaminated soft cheese. The lower detection obtained with qPCR is down to 1 CFU in 25 g of sample. qPCR to detect L. monocytogenes in pork meat artificially contaminated was also used by Gattuso et al. [33] in 2014. The detection limit obtained was 8 CFU/sample (25 g) using an incubation period of about 27 h in an enrichment broth, according to ISO method for Listeria. These two last studies [32,33] were based on the research of Lazzaro et al. [34] which used a co-amplification of the gene hly and the internal amplification control (IAP), using two labelled probes with FAM and the second with HEX (Hexachloro-fluorescein) respectively. This method was used to confirm that a negative result was not due to the presence of inhibitors in food.
Brooks et al. [35] used qPCR based on the utilization of the non specific DNA-binding to study possible sources of pathogens like Salmonella and Campylobacter and the possible presence of antibiotic resistance genes analysing litter and soil samples. Vendrame et al. [36] also developed a qPCR method to enumerate cells of Oenococcus oeni, directly, in must and wine using the non specific DNA-binding method (sybrgreen was used as a dye). The utilization of propidium monoazide to treat samples allowed the enumeration of Oenococcus oeni viable cells down to a detection limit of 0.33 log CFU/mL (2.14 CFU/mL) in must, and 0.69 log CFU/mL (4.90 CFU/mL) in wine, lower than previously developed qPCR protocols (Figure 1).
Minguzzi et al. [37] applied the qPCR for uncultured bacteria and virus and optimized for a simultaneous detection of Candidatus Phytoplasma prunorum and Plum pox virus in prunus. The fluorogenic label probe had a TAMRA (dye 6-carboxytetramethylrhodamin) quencher as reporter.
In the last years, the use of qPCR, was widely utilized for the detection of viruses in several water sources like sewage, irrigation and processing, river, drinking water to check the capability of the different concentration methods. The aim is the monitoring of the environmental contamination, the pathway transmission and the possible source of the outbreak. Calgua at al. [38] made a study on the concentration and quantification of human adenoviruses (HAdV), JC polyomaviruses (JCPyV) and noroviruses genogroup II (NoV) from urban sewage using JJV2F and COG2R primers and the RING2-TP probe, fluorogenic probe for NLV GII, while Gimenez, et al. [39] evaluated the presence of HAdV, JCPyV, and NoV on human faecal contamination of water with label probe with FAM and TAMRA. De Keuckelaere et al. [40] tried to detect murine norovirus-1 (MNV-1) and MS2 bacteriophages in processing water and several source water, but only MNV-1 was detected by qPCR. The probe had FAM (6-carboxyfluorescein) like reporter and for MGBNFQ minor groove binder with a 3' nonfluorescent like quencher.
Faye and co-workers [41] developed a qPCR method to detect a genetic diversity of Zika Virus. The NS5 gene was chosen to design the primers that were tested also on mosquitoes. The probe used contained the fluorescent quencher and reporter TAMRA and FAM respectively. The RNA quantification was performed with the dye RiboGreen, specific for ssRNA. The result showed that the detection limit of the established qPCR assay was 0.5 PFU/mL more sensitive then RT-PCR.
4. Hybridization Based Methods
The possible inhibition of the amplification step due to the presence of contaminants in the samples affecting the activity of DNA polymerase has encouraged the evaluation of different techniques able to overcome this step. Direct hybridization seems a good solution as probes, from 25 to 60 bp, can be used in hybridization methods. The presence of the probe can be detected using specific labelling molecules that are bond to one end (5' or 3') of the DNA probe or at both ends. The labels are often incorporated into the molecule probe, like isotopes as 32P, 35S, 125I and 3H that were the first type of labelling, or attached by covalent cross linkage bound to the probe like the enzymes. These last ones require the presence of a compound/spencer to avoid steric hindrance and allow the functionality.
Today the non-radioactive labelling is preferred for safety reasons and also for the cost including the radioactive waste disposal. Although the advantage of the radioactive labelling, the higher sensitivity reached, down to 0.1 pg (32P has the highest sensitivity to detect a single copy of gene in 0.5 μg DNA [42]), to reduce the risks for operators the non-radioactive labelling has been used in molecular biology techniques. Biotin, fluorophores and enzymes allowed to reach a good sensitivity, simplicity and safety, thus increasing the possible applications. When using biotin it is necessary a second molecular reporter such as avidin or streptavidin (with high affinity for biotin) directly linked by alkaline phosphatase or peroxidase. The presence of the probe takes place thanks to a chemical reaction that needs an antibody and specific enzymes. A blue colour can be obtained that is proportional to the concentration of the target molecule that allow the binding of the labelled probe in a ratio 1:1 using a chromogenic substrate. Photon are produced using luminol as a substrate, generating light that is then detected.
When using digoxigenin, an antibody (Anti-DIG) with alkaline phosphatase is coupled to obtain the detection of the labelled probe to develop a blue colour in the presence of a chromogen substrate BCIP/NBT (5-bromo-4-chloro-3-indolyl phosphate and nitro-blue tetrazolium chloride) [43]. DIG labeling is also used in PCR-ELISA to detect and quantify the PCR product directly after immobilization on a microplate [44,45]. The principle is the utilization of a PCR step followed by biotinylated DNA immobilization on a microplate and detection. Specific DNA oligonucleotides (probes) are labelled with biotin and used to detect DIG-labelled PCR amplicons. PCR-ELISA can be applied for various purposes such as the detection of viral genomes like papillomavirus in clinical samples, the detection of malaria in an in field test [46], and also for quantitative monitoring like for Leishmania parasite quantitation in livestock and cytomegalovirus infection in bone marrow transplant recipients [47,48].
4.1. Blotting techniques
To overcome amplification steps in pathogen detection using molecular biology techniques, hybridization techniques offered a feasible solution. The development of nitrocellulose and nylon membranes made it possible to bind DNA molecules to the surfaces allowing the possibility to hybridize a short specific stretch of labelled DNA (probe). Some tests were developed to optimize the concentration of the probes used to highlight the presence of the target. Length, concentration and modification of the probes influence the hybridization step. Long probes, can be highly specific for the target sequence, and at the same time allow hairpin formations that can reduce efficiency in hybridization to the target. Molecules such as radioactive phosphates, biotin, fluorophores and enzymes are mostly used to label DNA probes. Companies are available to add tags to nucleic acids during synthesis and to purify the labelled probes before their utilization at laboratory level. Tags can be added at both 5' or 3' end or can be incorporated throughout the sequence, depending on the sensitivity to be reachedand on the sample that has to be analyzed.
Specific hybridization depends strictly from the temperature and the ionic strength (salt concentration), usually according to the following:
for DNA probe more length than 100 pb:
Tm = 81.5 °C + 16.6 log M + 0.41 (% C +G)
for oligonucleotides probe ≈ 20 base:
Tm = 4 °C (G +C number) + 2 °C (A + T number)
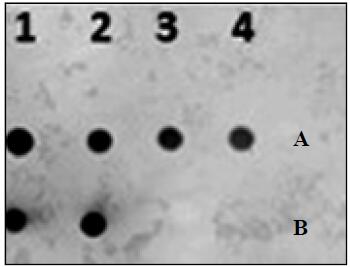
Mostly, the detection happens thanks to a colorimetric reaction due to labelled Ab Anti-Digoxigenin. The presence of blue spots indicate the presence of the target in the spotted DNA sample (positivity) (Figure 2). Lower salt and higher temperature close to the Tm, reduce the background and the non-specific binding. Comparing TE buffer and KH2PO4 buffer, both at 1 M, Peterson et al. [49] didn't obtain substantial difference on the final densities of probes and on kinetics of hybridization.
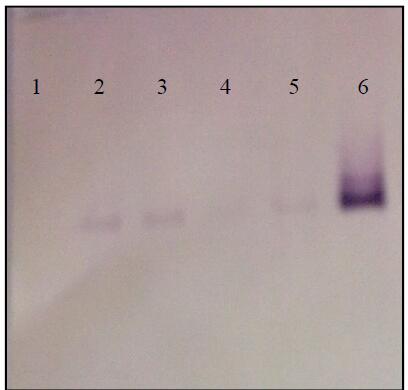
Twelve intestinal pathogens (Salmonella spp., Brucella spp., Escherichia coli O157:H7, Clostridium botulinum, Bacillus cereus, Clostridium perfringens, Vibrio parahaemolyticus, Shigella spp., Yersinia enterocolitica, Vibrio cholerae, Listeria monocytogenes and Staphylococcus aureus) were detected using a reverse dot blot method by Xing et al. [50]using DNA probes from 30 to 48 bp. According to Cecchini et al. [51] it is possible to use dot blot and Southern blot techniques for the detection of an unculturable bacterium, in Figure 3 is reported the Southern blot of the detection of the unculturable Candidatus Arthromitus in the intestinal content of trout. Chen et al. [52] used the reverse dot blot for the environmental monitoring, they simultaneously detected five type of harmful algae of the Chinese cost. Each probe was created by PCR and spotted onto a nitrocellulose sheet. The detection limit was 10 cells.
5. Probe Utilization in DNA Based Biosensors
Last decade new technologies faced the molecular techniques field and made it possible to couple the nucleic acids probes to a new field of interest, the construction of biosensors, devices employing biological recognition properties for a selective, specific, sensitive, rapid and cheap bioanalysis. Figure 4 shows a scheme of a biosensor based on DNA.
Probe density, influenced by immobilization conditions, such as ionic strength, interfacial electrostatic potential, affects the hybridization. A low probe density allows 100% of the probe to hybridize following the Langmuir-like kinetic, while a high probe density can drop to 10% the probe hybridization [49]. High density can suffer from problems due to steric interactions and repulsive electrostatic charge.
Probes can be used in couples (capture and detection) or singularly, based on the detection system used in the biosensor which are divided in various types on the detection mode: Optical, Electrochemical, Magnetic, etc.
Some kinds of biosensors need the use of tagged probes, others can use not labelled probes. Specificity is an important goal to pinpoint in biosensor construction, especially when the target molecule is at low concentration in respect to non-target molecules. To avoid a false positive result or an overestimation of the target due to non-correct hybridization between the DNA probe and the DNA target sequence, strategies can be used. To avoid a non specific biding in general a blocking solution like bovine serum albumin (BSA) or salmon sperm DNA or polyethylene glycol is used to cover the biosensor active surface after the biofunctionalization. It serves to occupy each free binding not specific site before the addition of the sample. The concentration of the probe on the surface (glass, metal, etc.) depends also on the strategy used to bind the probe.
Nestorova et al. [53] described the utilization of biotinylated probes for the construction of a thermophile biosensor. The hybridization between the DNA target and the probe is detected by the release of heat. This thermoelectric method avoided the utilization of enzyme based reactions or fluorescent labeling of the probes.
5.1. Fiber optic biosensors
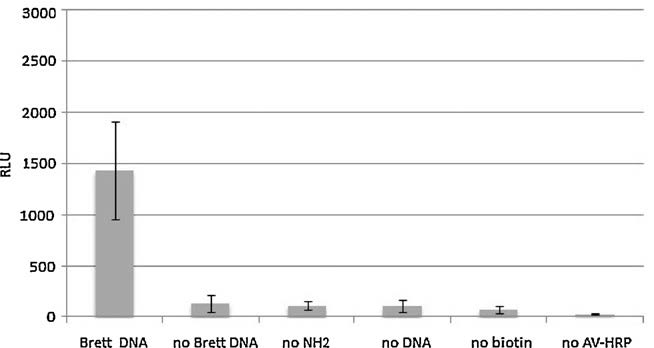
A fiber optic biosensor is a device that uses a biological compound (DNA molecule/probe, antibody, etc.) as a bioreceptor and a fiber optic as transducer. At first the development of an optical signal was obtained using antibodies attached to the glass fiber to detect toxic molecules and/or pathogens bacteria and viruses. The immobilisation technique is responsible for the stability of the bound between the sensing surface and the bioreceptor, avoiding any interference with the system activity. The sensitivity is an essential requisite for a biosensor that has to be used for diagnostic purposes. Wijesuriya et al. [54] evaluatedregeneration and reuse of antibody-coated fibre optic biosensors as a means of reducing routine laboratory analysis costs and time, now the possibility to reuse DNA based biosensors is also investigated. The advantages of fiber-optic biosensors are inertness, the compatibility to surface modifications and the low cost. In fact, Ferguson et al. [55] used a fiber-optic DNA microarray sensor to monitor multiple DNA sequences in parallel. They obtained a LOD of 10 fM by labelling DNA targets with fluorescent labels. Almadidy et al. [56]used a SYBR 101 succidimidyl ester (reactive dye) to label the amine-modified oligonucleotide, 25 mer length, that was shown to be sufficiently selective to hybridize genomic target from E. coli bacteria in water samples using an optical fiber biosensor. The detection of the target was obtained by coupling two DNA probes, the capture, which shows a modification at one end to allow attachment to the surfaces as function of the modification obtained on the glass, and the detection probe, usually labelled to produce a detectable luminous signal. Cecchini et al. [57] optimized a fibre glass biosensor based on the binding of DNA oligos targeting the ITS1-ITS2 sequences, for the detection of a spoiler yeast, Brettanomyces bruxellensis, that causes unpleasant aromas in wines. The method resulted sensitive (200 RLU were the LOD) for the direct detection of the yeast avoiding a PCR step. In Figure 5 are reported the results from the optimization step. Yin et al. [58] developed a DNA based biosensor to detect ssDNA. The system, based on a thin-core fiber modal interferometer (TCFMI), used a layer-by-layer (LbL) self-assembly technology and reached the sensitivity of 0.27 nm/matched-base.
5.2. Optic biosensor based on localized surface plasmon resonance (LSPR)
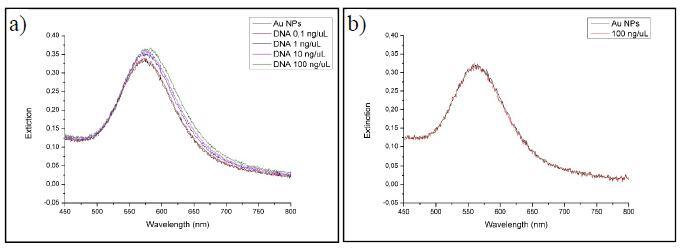
DNA free probes can be also applied to optic biosensor based on localized surface plasmon resonance (LSPR). The phenomenon of the LSPR is created when an electromagnetic field, such as light, hit gold nanoparticles (AuNPs) producing absorption and scattering caused by electron collective oscillation on the Au surface. Changes in the reflection index of biofunctionalized AuNPs using DNA probes can be monitored by the LSPR peak wavelength shift and used for the construction of a biosensor. Last years there was an increased interest in modifying surfaces of AuNPs by the addition of DNA probes to apply for the detection of microorganisms, especially pathogens in food, medical and environmental samples.
A preliminary test to detect Listeria monocytogenes was performed by optimizing the experimental conditions. DNAs from L. monocytogenes and Salmonella enteritidis has been used for the purpose. A specific DNA probe designed in the iap gene sequence of L. monocytogenes has beenbound to the surface of AuNPs by the addition of a thiol group at 5' end and used to capture DNA from the target organism L. monocytogenes and S. enteritidis, used as a negative control. The shift obtained for the two pathogens is reported in Figure 6. The minimum concentration tested and able to produce a positive shift for L. monocytogenes was 1 ng/µL. This method allows the direct detection of the pathogen avoiding an enrichment method of 24-48 h as reported in ISO methods for Listeria. LSPR can also be used for the detection of gene mutation, in fact it was used by Yoo and co-workers [59] that tested the possibility to detect the point mutation of the gene BGH3 associated with corneal dystrophies by using a multispot gold-capped nanoparticle array (MG-NPA) chip. The detection limit was of 1 pM target DNA. Also other authors used LSPR for applications in medical field, Endo at al. [60] developed a LSPR label-free biosensor. A gold-capped nanoparticle layer substrate was immobilized with peptide nucleic acids (PNAs) to detect a point mutation of the necrosis factor (TNF-α) that is involved in inflammation and edema in many acute and chronic disease state, such as ischemia and reperfusion injury. The detection limit obtained was of 0.677 pM target DNA. Cheng et al. [61] studied the point mutation of apolipoprotein E gene (ApoE) which is linked with theAlzheimer's disease, by using LSPR on Au nanoparticle (AuNP)-modified indium tin oxide (ITO).
5.3. Electrochemical biosensors
Free DNA probes can be used also in electrochemical biosensors. An electrode is used as a transducer to encode target-receptor binding in an electrochemical signal that can be voltametric, potenziometric, amperometric and impedimetric/conduttometric.
Using a DNA probe as a bio-receptor the target is DNA, but Qu et al. [62] used DNA as bio-receptor to detect cadmium, a metal used in agriculture and industry that can be accumulated in the environment and in animal organs. The biosenor was built using ssDNA, with a thiol group at one end, that showed high sensitivity for cadmium salts when tested on sodium salts, copper salts, magnesium salts, plumbum salts and zinc salts. The current signal increased from 1 to 20 ng/L, and a detection limit for the target (cadmium) was obtained at 0.3 ng/L. A thiolated DNA probe was also used by Patel et al. [63] to detect the bacterium Neisseria gonorrhoeae. The detection limit for this bacterium that causes meningitis was of 70 ng/L by immobilizing the probe onto an Au surface deposited on glass slide.
The results obtained by biosensors which use DNA probes are affected also by the method used to immobilize the probe. Li et al. [64] tested a new method, based on a covalent immobilization of target ssDNA (modified at the 5'with an amino group) on Au electrode. A mixture of MPTMS/GPTMS was used for a certain time to produce a self-assembled sol-gel film (MPTMS-GPTMSA) on an Au electrode. The detection limit of the biosensor was 8.57 × 10-10 M for ssDNA [65].
An emergent electrochemical biosensor bases on Field effect transistor (FET) for DNA detection analysis. This biosensor is composed by a source, drain and gate electrodes, and the sensing mechanism is based on the changing of the density charge [66]. Nanomaterials such as silicon nanowires (SiNW-FET) and carbon nanotubes (CNT-FET), configured with FETs, have attracted great attention because they are an ideal biosensor for the high sensitivity, for the small size, and large surface in respect to the volume. Indeed, silicon nanowires (SiNWs) have recently been developed to function as a transducer for ultrasensitive biosensors because the analyte affects the current flow through the whole area of the diameter of the NW rather than just at the surface. Lin and co-worker [67] detected the virus of avian influenza (AI) using poly-crystalline silicon nanowire-FET. They have tested a range of detection of the DNA target between fM to pM. Rahman et al. [68] propose a new approch to detect dengue virus, a combination of SiNW-FET and plasma oxygen for to detect and improve the signal. In both cases the probes used for the functionalization of the surface were modified with a -NH2 group at one end, requiring for this reason a chemical modification of the biosensor using aminopropyltriethoxysilane (APTES) and Gluteraldehyde. Gao et al. [69] used the biosensor for the simultaneous detection of the viruses of Avian InfluenceH1N1 and H5N1 Their test shown the possibility to develop e multiplex detection biosensor immobilizing the H5N1 probe on the surface and using H1N1 like negative control and H5N1 like positive control, both of them at the concentration of 10 mM. A decrease of the current was registered only with the H5N1. The capture probe used was modified with a carboxyl group to bind the ammine group of the modified SINW surface.
Instead Zhang and Ning [70] conducted a study to detect the Dengue serotype 2 virus using a PNA (Peptide Nucleic Acid ) probe with a length of 16 nt used at several concentration from 1 fM to 100 fM obtained after RT-PCR. They shown that the lower limit detection was 10 fM and that was not necessary the purification of the sample.
5.4. Mechanical biosensors based on quartz crystal microbalance (QCM)
The QCM is a mass sensitive detector that relies on a bulk acoustic wave frequency shift due to the mass changes from the capture of the analyte by the DNA probes bound on the surface of the crystal.
This technique can be associated with PCR as reported by Dell'Atti et al. [71] in a study on the detection of Human Papilloma Virus (HPV) strains in scraping cervical samples, used degenerate probes and amplification products as targets for measurements. They demonstrated the possibility to regenerate the DNA probes attached to the surface by chemical and fast reaction. QCM eliminates the need for labels and offers the potential advantage of rapidity and real-time monitoring of DNA hybridisation, and specificity.
Hao et al. [72] developed a QCM biosensor for the detection of Bacillus anthracis, a spore forming bacterium used in 2001 for terroristic attacks in the USA. The targets were two specific sequences, the Ba813 chromosomal, and the pag gene in plasmid pXO1. Based on the Hz values obtained the LOD was 3.5 × 102 CFU/mL for both the Ba813 chromosom and the pag gene.
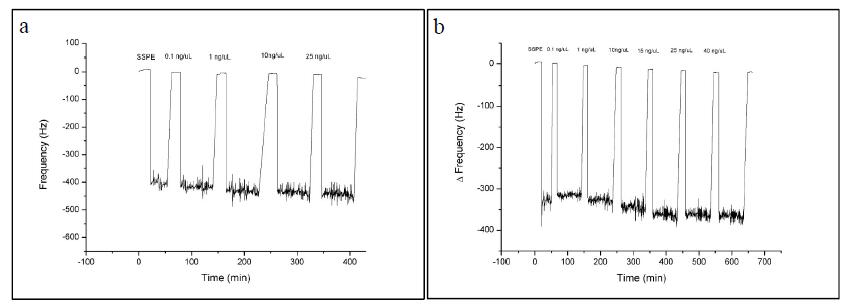
Microbalance-DNA probe method was used also by Moa et al. [73] to detect bacteria in water samples. Skladal et al. [74] reported the use of a biotinylated probe for the detection of HCV virus on a QCM biosensor. Avidin (streptavidin)-modified piezoelectric crystals were used as the probes were biotinylated at the 5' end. In this study the real samples were subjected to reverse transcriptase reaction to obtain cDNA which was then amplified and used for testing four different probes using the piezoelectric sensor. A work with QCM was conducted on Brettanomyces bruxellensis by Vizzini [75] to optimize working conditions and probe concentration. The experiment was performed in 15 µL SSPE (20 ×: NaCl 3 M, NaH2PO4, anhydrous 230 mM, EDTA 2 ×, H2O 25 mM) buffer, first the hybridization condition were evaluated using the sequence complementary to the probe as a target at 0.1,1,10,25 ng/μL, then the thiolated DNA probe specific for B. bruxellensis was used at 100 ng/µL after 75 min immobilization on the gold surface of the crystal. The specific hybridization was obtained by incubation at 53 °C. The results reported in Figure 7 show that there is proportional increase in the Hz values both using the complementary and the thiolated probes inducing to suppose that a quantitative evaluation of the target can be done with this system.
6. Alternative Probe
6.1. LNA (locked nucleic acid)
LNA are DNA or RNA sequences with one or more nucleotides modified, named locked nucleic acid. The methylene binding allows the locking on the DNA target. The melting temperature of this probe is higher than normal probes, and for this reason they can be shorter and can identify short DNA and RNA sequences. Due to the high resistance to degradative nucleases activity these LNA probes have been increasingly used in the last years. Their thermal stability and increased sensitivity and specificity allow for discrimination of single point mutations [76,77] and various applications. Yoon et al. [78] used the LNA probe in qPCR to detect the mutation of embB gene in codon 306, in Micobacterium tubercolosis, responsible for the Ethambutol (drug) resistance. The probe, labelled at 5' and at 3' ends with a FAM and Iowa Black FQ™ (IABkFQ) respectively, and located between the primers, can have two/three LNA (A, T) can be introduced to obtain a modified probe that can reach higher binding efficiency. This due to the additional methylene bridge between the 2'oxygen and the 4'carbon of the ribose ring in comparison with unmodified probe [79].
Wang et al. [80] had used the LNA probe with three nucleotide substitution to detect HBV in plasma a serum human sample and compared it with the TaqMan. The LNA probe has shown a better sensitivity (40 IU/mL against 80 IU/mL) and stability of the fluorescent signal. In fact the LNA showed a 1% decrease against 36% of TaqMan.
Nitecki et al. [81] applied the qPCR to detect L. monocytogenes and E. coli in raw salmon like an alternative method based on plate count. The LNA probes were designed on hly and stx genes respectively. The probes were labelled in different ways at 5' Rox and BHQ2 for the Listeria probe and 5' Hex and 3' BHQ1 for Escherichia probe. Both probes detected a range from 106 to 103 CFU/mL with a percentage of success of 100%, whereas when the target was at 102 CFU/mL the successful percentage was lower, about 80% for E. coli and 60% for L. monocytogenes. Instead with a lower concentration the probability of detection decrease from 0 to 20% for E. coli and close to 0% for L. monocytogenes.
The application of this kind of probe was largely studied with FISH technique by several researchers.
Priya et al. [82] studied the detection of bacterial endosymbionts, for example Arsenophonus and Portiera in the bacteriocites of Bemisia tabaci insect.
Rohdea et al. [83] detected Yersinia pestis by LNA probe design on 23S RNA with only one nucleotide modified. An other application by Rohdea et al. [84] was for Campylobacter, in this study the application of LNA confirmed the strong binding with the DNA target in comparison with utilization of DNA probes. A higher signal was obtained with LNA probe with the modification of three nucleotides.
Fontenete et al. [85] tried to develop three probes modified and labelled with Fluorescein phosphoramiditeusing the technique fluorescent in vivo hybridization (FIVH) to detect Helicobacter pylori in humans.
6.2. PNA probe
PNA probe is an artificial DNA sequence with the same properties to hybridize a complementary DNA or RNA strand. The backbone is composed by N-(2-aminoethyl) glycine units which are linked by peptide bound, it has the advantage that it is not charged, which gives a better stability and resistance to enzyme degradation. The artificial backbone is not recognized by polymerase, thus it can not be used in techniques based on PCR, but it can be used in FISH and in the biosensor field.
Santos and co-workers [86] optimized the standard condition of the FISH to detect bacteria using PNA probeEUB338. The sequence of the probe, that was labelled at the N terminus with AlexaFluor488, was universal, thus able to recognize the 16S RNA sequence in bacteria. The PNA FISH was used to identify several Candida species directly from blood cultures [87]. An interesting application was conducted by Ahn and coworkers [88]. They detected Mycoplasma fermentans and Mycoplasma hyorhinis using Fluorescence Melting Curve Analysis (FMCA). The PNA probe was labelled with two fluorescent molecules, dyes (HEX) and quencher (Dabcyl). Moreover recent studies have shown a trend, the modification of the PNA probe to increase the bound with DNA or RNA. Vilaivan [89] developed a PNA modified: Pyrrolidinyl PNA with α/β-Dipeptide Backbone (acpc PNA), its structure and stereochemistry take several advantages: a major affinity and stability to bound DNA or RNA, the inability to form self hybrids and a selectivity for antiparallel/parallel strand.
Teengam et al [90] used a acpc PNA probe to detect papillomavirus (HPV) using a paper based electrochemical biosensor and measuring the impedance by spectroscopy. The probe was modified at N-terminal with the addition of three glutamic acids that were negatively charged, and was labelled by anthroquinone to allow the immobilization and the exchange of electron with the G-PANI respectively. When DNA was hybridized on the probe there was a decrease of the current signal for the rigidity of the structure that limits the electrons transfer.
7. Conclusions
The utilization of primers for PCR based methods, and probes for hybridization based methods, is now a widely known technique used in various fields of application. These methods based on the utilization of stretches of DNA demonstrated their flexibility in classical biology and nanotechnology. The usefulness of DNA probes in the construction of biosensors helped diagnostics in many fields making them very interesting for rapidity, specificity and sensitivity. Design and labelling of probes became more interesting for scientists that spent time to improve both aspects. Researches on new molecules able to label probes avoiding risks for operators, simplicity of labelling techniques, and the high sensitivity obtained by new dyes, allowed the utilization of DNA probes, both single strand or double strand, in nanotechnology applications. Biosensors could benefit from these last discoveries, in fact, different transducers were and still are under evaluation to optimize the sensitivity of the devices and reusability, aspect that could open new frontiers for the application of DNA based biosensors in an in-line application. Portability is still an objective for biosensors to obtain a point of care (POC) requested in all kinds of diagnostics.
Aknowledgment
Authors thank Prof. Elena Rodica Ionescu and Prof. Pierre-Michel Adams at the Universite' de Technologie de Troyes, for the scientific support in LSPR and QCM experiments.
Conflict of Interest
All authors declare no conflicts of interest in this review.









 DownLoad:
DownLoad: