1. Introduction
Soil microorganisms are one of the most important indicators of soil fertility. Microorganisms play important roles in the decomposition of organic materials and the cycling of carbon, nitrogen, phosphorus, sulfur and several other nutrients in soil [1,2,3]. Microorganisms can also degrade xenobiotic compounds such as petroleum hydrocarbons and pesticides [4,5,6,7,8].
In the last century, agrochemicals such as chemical fertilizers and pesticides have been developed to enhance agricultural productivity [8]. Food and vegetable yields have been significantly enhanced but at the cost of risks to human health and the environment. Chemical fertilizers and pesticides have the potential to cause significant environmental hazards, including reductions in the number and activities of soil microorganisms [9,10].
To protect soil microorganisms from the harmful effects of agrochemicals, it is necessary to either minimize the use of agrochemicals or increase the abundance and activities of soil microorganisms to accelerate the biodegradation process. In our previous study, we developed a method to stimulate soil microorganisms and microbial nutrient cycling activities through the control of total carbon (TC), total nitrogen (TN), and the C/N ratio in petroleum hydrocarbon-polluted soils [11]. Microbial stimulation also led to improvements in the bioremediation of polluted soils.
In this study, the relationship between bacterial biomass and organic materials in agricultural soils was investigated. The aim of the study was to stimulate soil microorganisms in pesticide-contaminated soil by manipulating soil organic materials.
2. Materials and Methods
2.1. Analysis of agricultural soil samples for chemical properties
Soils were collected from various agricultural fields from Hokkaido to Okinawa in Japan. A composite sample from about five randomly selected points in a field was taken from the top 10-cm soil layer after removing a few centimeters of the surface crust. The TC in the soil samples was determined using the total organic carbon analyzer (TOC-VCPH; Shimadzu, Kyoto, Japan) and the solid sample combustion unit (SSM-5000A; Shimadzu, Kyoto, Japan). To analyze TN, total phosphorus (TP), and total potassium (TK), soil was digested in a Kjeldahl digestion unit (Gerhardt, Königswinter, Germany) and filtered (ADVANTEC No. 6; Toyo Roshi Co. Ltd., Tokyo, Japan). TN, TP, and TK in the filtrate were determined by the indophenol blue method [13], the molybdenum blue method [14], and atomic absorption spectrophotometry (Hitachi, Tokyo, Japan), respectively. Soil pH (1:2.5 soil-to-water suspension, w/v) was analyzed using a pH meter (LAQUA F-72, Horiba, Kyoto, Japan).
2.2. Estimation of bacterial biomass in agricultural soils
Bacterial biomass in the soils was measured by quantification of the environmental DNA (eDNA) using the slow-stirring method [15]. To extract the eDNA from the soils, a 1.0-g soil sample was mixed with 8.0 mL of DNA extraction buffer (100 mM tris(hydroxymethyl)aminomethane, 100 mM sodium EDTA, 100 mM sodium dihydrogen orthophosphate, 1.5 M sodium chloride, and 1% (w/v) hexadecyltrimethylammonium bromide) and 1.0 mL of 20% (w/v) sodium dodecyl sulfate solution; the suspension was agitated with a propeller for 20 min. The suspension was centrifuged at 5,000 × g for 10 min, then about 700 µL of supernatant was transferred into a 1.5 mL micro tube and 700 µL of chloroform-isoamyl alcohol was slowly added. The mixture was centrifuged at 18,000 × g for 10 min followed by a further addition of 300 µL of isopropanol and precipitation by centrifugation at 18,000 × g for 20 min. The pellet of crude nucleic acid was dissolved in TE buffer (10 mM Tris-HCl and 1 mM EDTA, pH 8.0) after drying. The extracted eDNA was quantified based on the intensity of the eDNA bands after electrophoresis on an agarose gel using Kodak 1D 3.6 Image Analysis Software (Kodak, CT, USA). The bacterial biomass in the soil was estimated by using the equation Y = 1.70 × 108X (r2 = 0.96), where Y and X are the bacterial biomass g−1 soil and the amount of eDNA, respectively [15].
2.3. Agricultural practices in the fields rich in TC and TN but low in bacterial biomass
Two representative fields rich in TC and TN but low in bacterial biomass (field A and B) were investigated for agricultural practices (Table 1). In field A, watermelon-tomato cropping system was practiced for more than 30 years, while only solanaceous crops were planted for more than 40 years in field B. Both of the fields were treated with chemical fertilizers and pesticides. Pesticides were used in both fields almost every year since they were first cultivated. In field A, dichloropropane-dichloropropene (D-D) (250 kg/ha) and fosthiazate (200 kg/ha) were used for controlling root-knot nematodes in watermelon and tomato. Field B was fumigated with chloropicrin (220 L/ha) to protect solanaceous crops from bacterial wilt.
Table 1.Agricultural practices in fields A and B.
| Field | Cropping system | Cropping history | Target pest | Pesticide(s) |
| Name | Rate |
| A | Watermelon-tomato | >30 years | Root-knot nematode | 1. DD* | 250 kg/ha |
| 2. Fosthiazate | 200 L/ha |
| B | Solanaceous crops | >40 years | Broad spectrum | 1. Chloropicrin | 220 L/ha |
| * Dichloropropane-dichloropropene |
Properties of the pesticides used in field A and B are shown in Table 2. Among the three pesticides, fosthiazate seems most toxic followed by dichloropropane-dichloropropene and chloropicrin.
Table 2.Properties of the pesticides used in fields A and B.
| Pesticide | Log Pow* | Toxicity in rat | Reference |
| Oral, LD50 (mg/kg) | Dermal, LD50 (mg/kg) |
| Dichloropropane-dichloropropene | 1.4-2.28 | 140 | 2,100 | [16] |
| Fosthiazate | 1.752 | 51-73 | 861-2,396 | [17] |
| Chloropicrin | 2.09 | 250 | - | [16] |
| * n-octanol/water partition coefficient |
2.4. Effect of organic materials on bacterial biomass in pesticide-contaminated soil
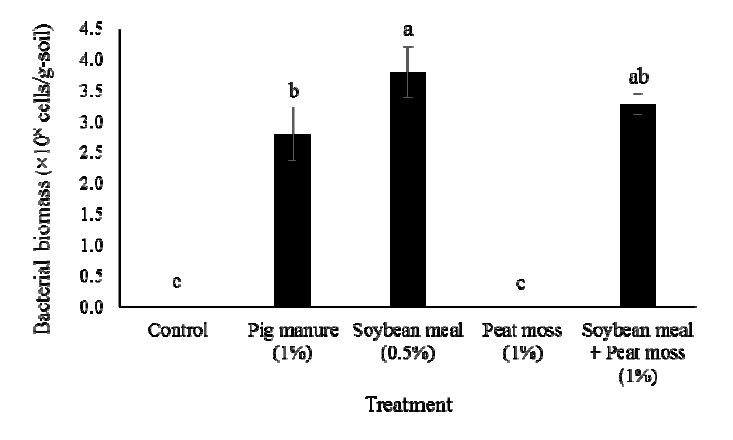
To investigate the effect of treatment with organic materials on bacterial biomass in pesticide-contaminated soil, soil from field A was sampled, filled into sterile pots (200 g/pot, 25% moisture content) and incubated with the following five treatments: 1) untreated control; 2) pig manure (1% w/w); 3) soybean meal (0.5%); 4) peat moss (1% w/w); and 5) soybean meal (0.5%) + peat moss (1%). Soybean meal and peat moss were autoclaved and dried at 60 °C for 3 days before treatment, while non-autoclaved pig manure was used for the treatment. The TC, TN, C/N ratio and bacterial biomass in each organic material are shown in Table 3. Sterile distilled water was added frequently to maintain the moisture content throughout the incubation period. After 1 month of incubation of the treated soils at 22 °C (12 h) / 18 °C (12 h), soil bacterial biomass was analyzed by the slow-stirring method [15].
Table 3.Total carbon (TC), total nitrogen (TN) and carbon/nitrogen (C/N) ratio of the organic materials used in this study.
| Organic material(s) | TC (mg/kg) | TN (mg/kg) | C/N ratio | Bacterial biomass (× 108 cells/g) |
| Pig manure | 287,000 | 24,100 | 11.9 | 11.9 |
| Soybean meal | 446,800 | 77,000 | 5.8 | ND |
| Peat moss | 504,200 | 5,020 | 100.4 | ND |
| Soybean meal + peat moss (0.27:0.73, w/w) | 488,700 | 24,400 | 20.0 | ND |
3. Results
3.1. Analysis of bacterial biomass, TC, and TN in agricultural soils
Bacterial biomass, TC and TN in 427 agricultural soil samples were analyzed for the construction of an agricultural soil database (Table 4). Levels of bacterial biomass were categorized into the following six groups: 1) extremely low (<1.0 × 108 cells/g); 2) very low (1.0 × 108 to 2.9 × 108 cells/g); 3) low (3.0 × 108 to 4.4 × 108 cells/g); 4) medium (4.5 × 108 to 5.9 × 108 cells/g); 5) high (6.0 × 108 to 9.9 × 108 cells/g); and 6) very high (≥10.0 × 108 cells/g). Bacterial biomass varied in accordance to TC and TN contents in the soil. In the soils with very high bacterial biomass, average TC and TN were 35,200 mg/kg and 1,550 mg/kg, respectively, while average TC and TN in the soils with low bacterial biomass were 17,470 mg/kg and 890 mg/kg, respectively. These results suggest that TC and TN are closely related to bacterial biomass in the soil.
Table 4.Relationship between bacterial biomass and soil organic matter level in agricultural soils.
| Bacterial level | Organic matter | Number of sample |
| Category | Bacterial biomass (× 108 cells/g) | TC (mg/kg) | TN (mg/kg) |
| Extremely low | < 1.0 | 23,540 | 880 | 35 |
| Very low | 1.0–2.9 | 17,470 | 890 | 30 |
| Low | 3.0–4.4 | 23,110 | 1,040 | 41 |
| Medium | 4.5–5.9 | 23,450 | 1,170 | 38 |
| High | 6.0–9.9 | 27,480 | 1,160 | 91 |
| Very high | >10.0 | 35,200 | 1,550 | 192 |
3.2. Investigation of soils with low bacterial biomass in soils
Thirty-five soil samples with extremely low bacterial biomass (< 1.0 × 108 cells/g) were analyzed for TC, TN, TP, TK, and pH (Table 5). Seven samples (samples 1 to 7) contained TC less than 10,000 mg/kg, and 15 samples (samples 21 to 35) contained TC above 20,000 mg/kg. Average values of TC, TN, TP, and TK in 35 samples were 23,540, 880, 1,971, and 6,375 mg/kg, respectively. Similarly, average soil pH was 6.34. Although TC, TN, C/N ratio, TP, TK, and pH in most of the samples seem at suitable levels, an extremely low bacterial biomass indicate the possibility of pollution in the soil.
Table 5.Chemical properties of the soils with extremely low level of bacterial biomass (< 1.0 × 108 cells/g).
| Sample number | TC (mg/kg) | TN (mg/kg) | C/N ratio | TP (mg/kg) | TK (mg/kg) | pH | Bacterial biomass (× 108 cells/g) |
| 1 | 1,230 | 270 | 4.6 | 370 | 3,680 | 6.65 | ND |
| 2 | 1,580 | 200 | 7.9 | 220 | 3,980 | 7.60 | ND |
| 3 | 1,802 | 350 | 5.1 | 1,040 | 1,560 | 6.69 | ND |
| 4 | 3,584 | 240 | 14.9 | 290 | 4,300 | 7.35 | 0.8 |
| 5 | 3,992 | 290 | 13.8 | 2,330 | 16,220 | 6.86 | ND |
| 6 | 7,673 | 530 | 14.5 | 370 | 5,670 | 6.50 | ND |
| 7 | 8,462 | 410 | 20.6 | 610 | 860 | 6.51 | 0.9 |
| 8 | 13,640 | 810 | 16.8 | 870 | 10,940 | 6.42 | ND |
| 9 | 15,010 | 840 | 17.9 | 2,380 | 5,760 | 7.77 | 0.5 |
| 10 | 15,720 | 630 | 25.0 | 600 | 11,560 | 6.71 | 0.8 |
| 11 | 17,110 | 600 | 28.5 | 1,070 | 4,060 | 5.95 | 0.1 |
| 12 | 17,410 | 640 | 27.2 | 2,460 | 6,990 | 5.72 | 0.9 |
| 13 | 17,560 | 500 | 35.1 | 6,940 | 4,790 | 5.67 | ND |
| 14 | 18,280 | 850 | 21.5 | 2,220 | 3,530 | 6.10 | 0.1 |
| 15 | 18,480 | 580 | 31.9 | 980 | 3,430 | 5.50 | 0.1 |
| 16 | 18,530 | 1,560 | 11.9 | 3,120 | 6,560 | 5.44 | ND |
| 17 | 19,000 | 990 | 19.2 | 880 | 4,820 | 5.50 | 0.9 |
| 18 | 19,490 | 960 | 20.3 | 3,310 | 5,540 | 6.67 | ND |
| 19 | 19,570 | 960 | 20.4 | 2,250 | 10,200 | 5.82 | ND |
| 20 | 19,620 | 380 | 51.6 | 1,940 | 4,830 | 6.22 | ND |
| 21 | 20,230 | 670 | 30.2 | 1,100 | 4,010 | 6.12 | 0.1 |
| 22 | 20,980 | 1,180 | 17.8 | 3,900 | 6,890 | 6.62 | 0.4 |
| 23 | 21,590 | 930 | 23.2 | 1,690 | 4,880 | 5.93 | 0.7 |
| 24 | 22,740 | 1,120 | 20.3 | 2,740 | 6,480 | 5.53 | ND |
| 25 | 23,680 | 840 | 28.2 | 1,990 | 10,230 | 6.27 | 0.8 |
| 26 | 23,710 | 880 | 26.9 | 1,980 | 7,720 | 5.56 | 0.3 |
| 27 | 26,520 | 960 | 27.6 | 2,200 | 6,300 | 7.28 | ND |
| 28 | 32,400 | 930 | 34.8 | 3,140 | 3,610 | 6.25 | ND |
| 29 | 35,000 | 890 | 39.3 | 1,870 | 10,540 | 7.10 | ND |
| 30 | 35,460 | 950 | 37.3 | 1,740 | 17,370 | 6.90 | ND |
| 31 | 41,650 | 1,420 | 29.3 | 4,890 | 3,190 | 6.77 | ND |
| 32 | 42,000 | 1,270 | 33.1 | 3,040 | 2,600 | 6.80 | ND |
| 33 | 46,860 | 2,880 | 16.3 | 2,520 | 1,750 | 6.30 | ND |
| 34 | 72,750 | 2,180 | 33.4 | 460 | 14,110 | 5.49 | 0.7 |
| 35 | 99,710 | 1,020 | 97.8 | 1,520 | 4,180 | 5.46 | ND |
| Average | 23,540 | 880 | 25.8 | 1,970 | 6,375 | 6.34 | - |
| * ND=not detected (< 6.6 × 106 cells/g) |
3.3. Investigation of soils with extremely low levels of bacterial biomass but high TC and TN
Average values of TC, TN, C/N ratio, and bacterial biomass in two representative fields (fields A and B) with extremely low bacterial biomass (< 6.6 × 106 cells/g-soil) but high TC (≥22,500 mg/kg) and TN (≥990 mg/kg) are shown in Table 6. In both fields TC was ≥22,500 mg/kg and TN was ≥990 mg/kg. C/N ratio in field A and B was 15 and 21, respectively.
Table 6.Soil properties in two agricultural fields used in this study (n = 2).
| Field | Value | TC (mg/kg) | TN (mg/kg) | C/N ratio | Bacterial biomass* |
| A | Average | 22,500 | 1,500 | 15 | ND |
| SD | 3,535 | 141 | 1.4 | - |
| B | Average | 23,000 | 990 | 21 | ND |
| SD | 2,828 | 127 | 0 | - |
| * ND=not detected (< 6.6 × 106 cells/g) |
Data suggest that long-term use of nematicidal and bactericidal pesticides significantly reduced bacterial biomass in soils, even with high levels of TC and TN and optimum C/N ratio.
3.4. Stimulation of bacterial biomass in pesticide contaminated soils through the control of TC and TN
To increase the bacterial biomass and improve bioremediation processes in pesticide-polluted soils, soil sampled from field A was treated with different organic materials. After 1 month of incubation under laboratory conditions, bacterial biomass in soil treated with pig manure, soybean meal, and a mixture of soybean meal and peat moss increased from below the detection limit to 2.8 × 108, 3.8 × 108 and 3.3 × 108 cells/g, respectively (Figure 1). Bacterial biomass did not increase in the soil treated with peat moss only and in the untreated soil (control). The results suggested that microorganisms in pesticide-polluted soils were stimulated by the application of nitrogen-rich organic materials.
4. Discussion and Conclusion
Microorganisms are in intimate contact with the soil environment and as such are considered ideal monitors of pollution [18,19]. The results reported here indicate that long-term use of a broad spectrum fumigant (chloropicrin) and nematicidal pesticides (DD and fosthiazate) reduced the abundance of soil bacteria. Detrimental effects of chloropicrin on bacteria have been reported previously, such as mutagenesis [20] and reduction in biomass and activity [21]. Similarly, nematicides can cause suppression and alteration of the soil microflora [22]. Usually, the harmful effects of pesticides on soil microorganisms are manifested only at high concentrations [23,24]. However, a significant reduction in microbial dehydrogenase activity by DD was observed even when applied at the usual field rate [25]. Therefore, the use of these pesticides over long time periods appears detrimental for both the abundance and activities of soil microorganisms.
TC, TN, and C/N ratio are closely related to the number and activities of microorganisms in soil [12]. In this study, bacterial biomass were positively related to TC and TN, but some soil samples with relatively lower TC also contained high amount of bacterial biomass (data not shown). Higher bacterial biomass even in low TC might be due to a suitable C/N ratio in those soils.
In this study, bacterial biomass below the detection level (< 6.6 × 106 cells/g) was observed in two pesticide-polluted soils, which was substantially lower than the average bacterial biomass in agricultural soils (~ 6.0 × 108 cells/g) [11]. High bacterial biomass (< 1.0 × 109 cells/g) has been reported in petroleum hydrocarbon-polluted agricultural soils [4,5,15]. Therefore, the environmental impact of pesticide pollution is more severe than that of petroleum hydrocarbon pollution.
In this study, bacterial biomass was enhanced by applying some organic materials. Although, the bacterial biomass of 2.8 × 108 cells/g in the pig manure treated soil may include both introduced and stimulated microorganisms, a significant enhancement of the bacterial biomass in the soils applied with autoclaved organic materials (soybean meal and the mixture of soybean meal and peat moss) clearly indicated that indigenous microorganisms in pesticide polluted soils can be stimulated by using nitrogen-rich organic materials.
Stimulation of soil microorganisms through the control of soil organic matter (TC, TN, and C/N ratio) has been demonstrated as an efficient method to enhance bioremediation of agricultural soils polluted by petroleum hydrocarbons [4]. In this study, treatment of a pesticide-polluted soil with nitrogen-rich organic materials led to an increase in the soil bacterial biomass by up to 3.8 × 108 cells/g. The efficiency of organic material treatment in increasing abundance of microorganisms was lower when compared with that in petroleum hydrocarbon-polluted soils. Manipulation of soil properties (TC, TN, and C/N ratio) using organic materials has the potential to accelerate bioremediation processes in pesticide-polluted agricultural soils.
Acknowledgements
The authors acknowledge the support of CCP program.
Conflict of Interest
The authors have no conflict of interest to disclose.









 DownLoad:
DownLoad: