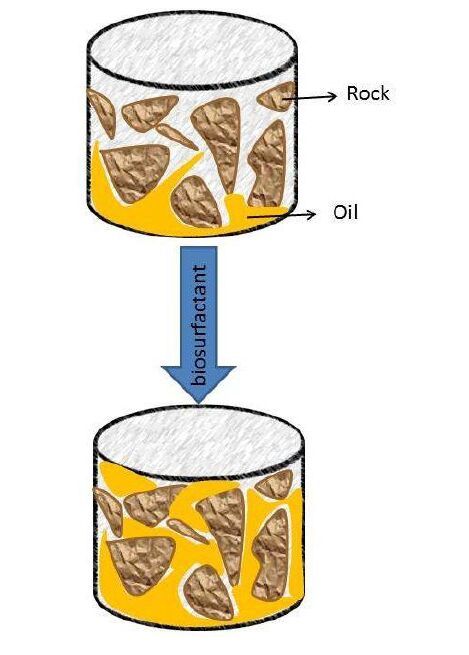
Many toxic substances have been introduced into environment through human activities. These compounds are danger to human health when they are ultimately or immediately in contact with soil particles. A conventional method to reduce, degrade and remove these substances is associated with some risk. In recent years, microorganisms have proved a unique role in the degradation and detoxification of polluted soil and water environments and, this process has been termed bio reclamation. The diversity of bioemulsifiers/biosurfactants makes them an attractive group and important key roles in various fields of industrial as well as biotechnological applications such as enhanced oil recovery, biodegradation of pollutants, and pharmaceutics. Environmental application of microbial surfactant has been shown as a promising due to solubilization of low solubility compounds, low toxicity observed and efficacy in improving biodegradation. However, it is important to note that full scale tests and more information is require to predict the behavior and model of surfactant function on the remediation process with biosurfactants. The purpose of this review is to describe the state of art in the potential applications of biosurfactants in remediation of environmental pollution caused by oil and heavy metal.
1.
Introduction
Let R,Z, and N be the sets of all real numbers, integers, and natural numbers, respectively. Here and below, for a,b∈N with a<b, we use the notation Z(a,b):={a,a+1,⋯,b}.
In recent years, difference equations as mathematical models to describe a variety of practical problems in the fields of economy, biology, disease prevention and control, environmental protection, etc., have attracted great attention and there have been a lot of outstanding works in theory and actual application; see, for example, [1,2].
In the paper, we consider the following discrete Dirichlet boundary value problem involving the mean curvature operator
where ϕ(s)=s√1+κs2,κ>0 is a constant [3], T is a given positive integer, △ is the forward difference operator defined by △u(k)=u(k+1)−u(k),△2u(k)=△(△u(k)),q(k)≥0 for all k∈Z(1,T),λ is a real positive parameter, and f(k,⋅)∈C(R,R) for each k∈Z(1,T).
When q(k)=0 for all k∈Z(1,T), the problem (1.1) is the discrete analogy of one-dimensional prescribed mean curvature equations with Dirichlet boundary conditions
The existence of (positive) solutions of the above problem has been studied by using the variational method, the standard techniques from bifurcation theory, fixed point index, and Kresnoselskii's fixed point theorem (see [4,5,6] and the references therein).
Note that when κ=0, the problem (1.1) degenerates into the classical second-order difference equation boundary value problem
The existence of (positive) solutions to the problem (1.2) has been well known with various qualitative assumptions of nonlinearity f ([7,8,9]).
When κ=1, the problem (1.1) is the ordinary discrete mean curvature problem
which has aroused the interest of many scholars recently [10,11,12]. Their approaches are variational. The existence of (positive) solutions to the problem (1.3) depends on the behavior at zero or infinity of the potential F(k,u)=∫u0f(k,s)ds. In [10,11], the oscillating behavior of F at +∞ played an important role in obtaining an infinite number of positive solutions to the problem (1.3). Chen and Zhou [12] obtained at least three positive solutions of the problem (1.3) with q(k)=0 for all k∈Z(1,T), where the primitive F on the nonlinear datum satisfies that lim sups→+∞F(k,s)|s|<α (α is a positive constant). Meanwhile, the case that the potential F satisfies lim infs→∞F(k,s)|s|>β (β is a positive constant) has been also discussed. They obtained at least two nontrivial solutions based on a two-critical-point theorem (Theorem 2.1) established in [13]. It is an important tool in obtaining at least two positive solutions of the Laplacian or the algebraic boundary value problems (see, for instance, [15,16]). However, it is relatively less used to look for positive solutions to the mean curvature boundary value problems.
Inspired by this, we will apply the two-critical-point theorem to establish the existence of at least two positive solutions for the problem (1.1) in this paper. As a special case of our main theorem, the existence of two positive solutions for the problem (1.1) with κ=1 and all q(k)=0 is obtained in Remark 4. The result improves Theorem 2 [12], where the author establishes the existence of only two nontrivial solutions without providing sign information for them under stronger hypotheses on the potential F. In Theorem 2 [12], the bilateral limit assumption on F(k,s)|s| at ∞ ensures that the energy functional of that problem is anticoercive, which consequently guarantees the establishment of the Palais-Smale condition—a pivotal requirement for applying critical point theorems. In our paper, the bilateral limit on the potential F is weakened to a unilateral limit at +∞, and then the energy functional of the problem (1.1) loses its anticoercivity. However, with the help of some inequality techniques, it is proven that the energy functional still satisfies the Palais-Smale condition. Moreover, in our main result (Theorem 3.1), the existence of at least two positive solutions is established without any asymptotic condition of the potential F at 0 and with no requiring that f(k,0)>0 for any k∈Z(1,T). In fact, the algebraic conditions in Theorem 3.1 are more general than the conditions that the potential F is subquadratic at 0 and superlinear at +∞ (see Corollary 3.1).
In 2003, Guo and Yu [17] first used the variational method to study the periodic solutions of second-order difference equations. Since then, for nonlinear difference systems, many scholars have used the variational method to study the existence of various solutions, such as periodic solutions, subharmonic solutions, and homoclinic solutions [18,19,20]. For general references on difference equations and their applications, we refer the reader to monographs [21,22] and the references therein.
This paper is organized as follows: In section 2, some definitions and results are collected. Some estimations of equivalence of the norm are provided. Moreover, Lemma 2.1 is presented to guarantee us to obtain positive solutions rather than nontrivial solutions to the problem (1.1). Section 3 is devoted to our main result. Lemma 3.1 is given to ensure the Palais-Smale condition of the functional on this basis. Some consequences of our main result are presented together with three examples.
2.
Preliminaries
2.1. Relevant notations and inequalities
Consider the T dimensional Banach space
endowed with the norm ‖⋅‖ as
Moreover, the space S can also be equipped with the following equivalent norms:
respectively. It is easy to know that for all u∈S,
By Theorem 12.6.1 in [21], we have for all u∈S,
where λj=4sin2jπ/2(T+1) for all j∈Z(1,T). By virtue of Lemma 2.2 in [23], we get for all u∈S,
Note that v(0)=v(T+1)=0 for all v∈S, we have
for all u,v∈S.
2.2. Variational framework
Let
for all s∈R.
Remark 2.1. In fact, the nonnegative solution of the following problem
is the nonnegative solution of the problem (1.1). To obtain positive solutions to the problem (1.1), we only need to search for positive solutions to the problem (2.5) now.
Consider two functionals Φ and Ψ defined respectively on S by
and
F+(k,s)=∫s0f(k,t+)dt for all (k,s)∈Z(1,T)×R. Obviously,
for all k∈Z(1,T), and Φ,Ψ∈C1(S,R), which means that Φ and Ψ are two continuously Gâteaux-differentiable functionals defined on S. By (2.4), we have that for any u,v∈S,
and
We define Iλ:S→R by
Clearly, Iλ∈C1(S,R) and for any u,v∈S,
Remark 2.2. For any u,v∈S, I′λ(u)(v)=0 if and only if
for all u∈S and k∈Z(1,T). In other words, a critical point of Iλ on S corresponds to a solution to the problem (2.5).
For the problem (1.1), we are interested in the existence of positive solutions rather than nontrivial ones. To the end, we present an assumption on f(k,0) as follows.
(H1) f(k,0)≥0,∀k∈Z(1,T).
Lemma 2.1. If (H1) holds, then any nonzero critical point of the functional Iλ on S is a positive solution to the problem (1.1).
Proof. In fact, taking Remarks 2.1 and 2.2 into account, it is sufficient to verify that any nontrivial solution u of the problem (2.5) is positive, that is, u(k)>0 for all k∈Z(1,T).
Notice that ϕ is a strictly monotonically increasing and odd function on R. By standard computation, we can conclude that
for all k∈Z(1,T+1). By a direct computation, we get
for all k∈Z(1,T). For any nontrivial solution u of the problem (2.5), combining Eqs (2.4), (2.8) and (2.9) with assumption (H1), we obtain that
Hence △u−(0)=△u−(1)=⋯=△u−(T)=0. Recalling that u(0)=u(T+1)=0 for any u∈S, we have u−(k)=0 for all k∈Z(1,T). Thus u is nonnegative.
Next, we further prove that u is positive. Otherwise, there exists some k0∈Z(1,T) such that u(k0)=0, then
Clearly, ϕ(△u(k0))≤ϕ(△u(k0−1)). Because ϕ is a strictly monotonically increasing homomorphism, we get △u(k0)≤△u(k0−1). Hence, u(k0+1)+u(k0−1)≤0. As a result, u(k0±1)=0. Then iterating the process, we have that u(k)=0 for all k∈Z(1,T). In short, u is zero somewhere in Z(1,T). Then it is zero identically. This contradicts the nontriviality of u. The proof is ended. □
Let (X,‖⋅‖) be a real Banach space and φ∈C1(X,R). φ is said to satisfy the Palais-Smale condition ((PS) condition), if any sequence {un}⊂X for which {φ(un)} is bounded and φ′(un)→0 as n→∞ possesses a convergent subsequence in X.
The following two-critical-point theorem is given by Bonanno and D'Aguì in 2016 [13].
Theorem 2.1. [13] Let X be a real Banach space, and let Φ,Ψ:X→R be two functionals of class C1 such that infXΦ=Φ(0)=Ψ(0)=0. Assume that there are r∈R and ˜u∈X, with 0<Φ(˜u)<r, such that
for each
the functional Iλ=Φ−λΨ satisfies the (PS) condition, and it is unbounded from below. Then for each λ∈Λ, the functional Iλ admits at least two nonzero critical points uλ,1,uλ,2 such that Iλ(uλ,1)<0<Iλ(uλ,2).
3.
Result and discussion
3.1. The Palais-Smale condition
Let
where F(k,s)=∫s0f(k,t)dt for all (k,s)∈Z(1,T)×R. Here and below, when L∞=0, we think 1L∞=∞. Before we come to a conclusion, let's give a lemma on the (PS) condition.
Lemma 3.1. If L∞>0 and (H1) hold, then Iλ satisfies the (PS) condition, and it is unbounded from below for all λ∈(√(T+1)λT+Q√κL∞,+∞), where Q:=(∑Tk=1|q(k)|2)12.
Proof. Because S is finite dimensional, it is sufficient to show that any (PS) sequence of Iλ is bounded on S. Let {un}⊂S be a sequence such that {Iλ(un)} is bounded and I′λ(un)→0 as n→∞.
First, we claim that {u−n} is bounded. According to (2.8) and (2.9), we have for all n∈N and k∈Z(1,T+1),
and
By (3.1) and (3.2), we can estimate the derivative of Φ at un in the direction of −u−n that
To put it simply,
And, from the condition (H1), it follows that
Combining (3.3) and (3.4), we have
for all λ>0 and n∈N. Moreover, by the definition of the functional Φ, we obtain, for all u∈S,
which implies that
for all u∈S. Thus, it is clear that for all u∈S,
So combining (3.5) and the above inequality, we have
Also, from limn→∞I′λ(un)=0, it follows that
As a result, we obtain
By standard computation, the above equation is transformed into
which means that limn→∞‖u−n‖=0. Hence our claim is proved. So there is M>0 such that 0≤u−n(k)≤M for all k∈Z(1,T) and n∈N.
Next, we prove that {un} is bounded. If {un} is not bounded, we may assume, going if necessary to a subsequence, that ‖un‖→∞(n→∞). Taking L∞>0 into account, we fix λ>√(T+1)λT+Q√κL∞ and fix l=l(λ) such that for all k∈Z(1,T),
then for all k∈Z(1,T), there is a δk>0 such that
Meanwhile, for all k∈Z(1,T) and s∈[−M,δk],
Hence, for all k∈Z(1,T),
On account of (2.1), we obtain that for all n∈N,
where η=∑Tk=1η(k). Using the Cauchy-Schwarz inequality, we get that for all n∈N,
Therefore, from the previous two inequalities and (2.2), it follows that for all n∈N,
When ‖un‖→+∞(n→∞), by √(T+1)λT+Q√κ−λl<0, we have limn→∞Iλ(un)=−∞. This leads to a contradiction. Hence {un} is bound and Iλ satisfies the (PS) condition.
Finally, we prove that Iλ is unbounded from below. Let {un} be such that un=u+n for any n∈N and ‖u+n‖→∞(n→∞). Arguing as before, we obtain that
So limn→∞Iλ(un)=−∞. Our conclusion follows. □
3.2. Main result
Below, our main result is presented.
Theorem 3.1. Suppose that (H1) holds and there exist two positive constants c and d with d<c such that
and
Then for each
the problem (1.1) possesses at least two positive solutions, where q:=∑Tk=1q(k).
Proof. By Lemma 2.1, it is enough to prove that Iλ has at least two nonzero critical points. We apply Theorem 2.1 by putting X=S,Iλ=Φ−λΨ where Φ,Ψ are the functions introduced in (2.6) and (2.7).
Clearly, infSΦ=Φ(0)=Ψ(0)=0. Also notice that F+(k,s)=F(k,s) for all (k,s)∈Z(1,T)×[0,+∞). From the conditions (H1),(H2) and (H3), it follows that L∞>0 and Λ+ is non-degenerate. Then Lemma 3.1 ensures that the function Iλ satisfies the (PS) condition and it is unbounded from below for λ∈Λ+.
For fixed λ∈Λ+, there exists c>0 such that λ≤−1κ+√4c2κ(T+1)+1κ2∑Tk=1maxs∈[0,c]F(k,s). Put r:=−1κ+√4c2κ(T+1)+1κ2. We claim that
If Φ(u)≤r, by (3.6), we get that ‖u‖2≤κΦ2(u)+2Φ(u)≤κr2+2r=4c2T+1. Thus, from the inequality (2.3), it is clear that
The assertion is verified. Therefore, we obtain
Now, we look for ˜u∈S in Theorem 2.1. Define ˜u∈RT+2 as ˜u(k)=d(0<d<c) for all k∈Z(1,T) and ˜u(0)=˜u(T+1)=0. Clearly, ˜u∈S. It is easy to see that
and hence we get
Therefore, from (3.7), (3.9), and (H3), it follows that
and Λ+⊂Λ. Moreover, since 0<d<c, and again by virtue of the condition (H3), we obtain that
On account of (3.8) and (3.10), we get that 0<Φ(˜u)<r. Thus, (2.10) holds. Hence Theorem 2.1 ensures that Iλ admits two nonzero critical points. This completes the proof. □
Remark 3.1. Indeed, condition (H1) implicitly covers both f(k,0)>0 and f(k,0)=0 cases. Theorem 3.1 holds true under either sub-case of condition (H1).
Remark 3.2. If all f(k,⋅) are nonnegative on [0,c](c>0), then maxs∈[0,c]F(k,s)=F(k,c) for all k∈Z(1,T). According to Theorem 3.1, it is enough to assume that there is a positive constant d with d<c such that
Remark 3.3. When κ=1 and q(k)=0 for all k∈Z(1,T) (Q=0 and q=0), the conditions in Remark 3.2 are more general than those of Theorem 2 in [12], where f(k,s) is required to be positive for all (k,s)∈Z(1,T)×[−c,c] rather than nonnegative, and the potential F is assumed to possess asymptotic behavior not only at +∞ but also at −∞. Here, the two solutions we obtain are positive, while the solutions in Theorem 2 of [12] are only nontrivial. Obviously, our main result improves Theorem 2 in [12].
Now, we present two particular cases of Theorem 3.1.
Corollary 3.1. Assume that (H1) holds,
and
for all k∈Z(1,T). Then for each λ∈(0,λ∗), where
the problem (1.1) admits at least two positive solutions.
Proof. Let λ∈(0,λ∗) and c>0 such that
Taking (3.11) into account, we get that lim sups→0+F(k,s)√1+κs2−1=+∞. As a result, there is d>0 with d<c such that κ2+q∑Tk=1F(k,d)√1+κd2−1>1λ. Note that L∞=+∞, so Theorem 3.1 ensures the conclusion. □
Corollary 3.2. Assume that f(k,⋅)=f for all k∈Z(1,T) and f is a continuous function such that
and
Then, for each
the problem (1.1) admits at least two positive solutions.
Proof. In fact, Corollary 3.2 is a consequence of Corollary 3.1. It is easy to see that (3.13) implies f(0)≥0, and (3.11) and (3.12) can be derived from (3.13) and (3.14), respectively. □
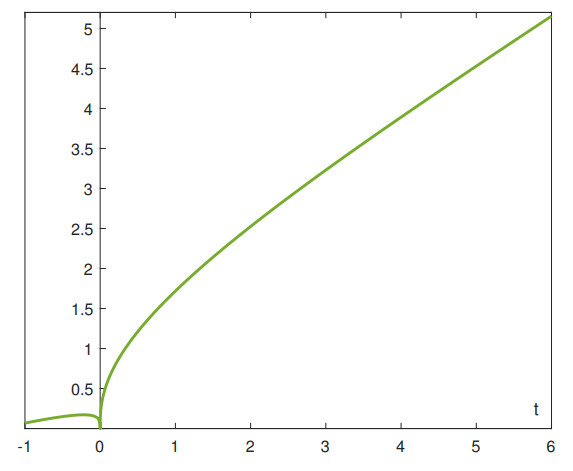
Example 3.1. For each λ∈(0,−1κ+√4κ(T+1)+1κ2(3e−1)T), the problem
admits at least two positive solutions. Here, the nonlinearity f(t)=e3√t−1 satisfies the conditions of Corollary 3.2 and
The image of f(t) is shown in Figure 1.
Example 3.2. For each λ∈(0,−1κ+√4κ(T+1)+1κ2T(T+1)), the problem
admits at least two positive solutions. It is easy to see that f(k,t)=k√t(cost+2) satisfies the assumptions of Corollary 3.1 and
Figure 2 displays the functional plot of f(k,t) for k∈(0,100).
Remark 3.4. We observe that Theorem 2 in [12] cannot be applied in the previous two examples with κ=1 and q(k)=0 for all k∈Z(1,T), since f(k,0)>0 is assumed there.
Example 3.3. Consider the boundary value problem (1.1) with κ=1,q(k)=0 and
for all k∈Z(1,T). Clearly, if t∈(0,43), then f(t)>0; and if t∈(43,2π), then f(t)<0. Such a relationship is visually apparent in Figure 3. A straightforward calculation yields
for all k∈Z(1,T).
Obviously, L∞(k)=lim infs→+∞F(k,s)s=2π−1 for all k∈Z(1,T), then
Letting T=3,c=5, and d=1, we obtain
and
It follows that
and
From f(k,0)=f(0)=2>0 and the preceding relations, all conditions of Theorem 3.1 hold. Thus for each λ∈(√(T+1)λTL∞,−1+√4c2T+1+1∑Tk=1maxs∈[0,c]F(k,s))≈(0.687,1.034), the boundary value problem (1.1) has at least two positive solutions.
Remark 3.5. The potential function F in the above example lacks superlinearity at +∞, failing to satisfy the conditions of Corollaries 3.1 and 3.2. Nevertheless, Theorem 3.1 still guarantees the existence of two positive solutions for the problem (1.1) in Example 3.3.
4.
Conclusions
In this paper, we consider a generalized difference mean curvature problem, which includes the conventional one and the classical second-order difference equation boundary value problem. The main novelties of this research are as follows:
(1) The existence of two positive solutions rather than nontrivial solutions for our problem is established based on a two-zero critical points theorem and some inequality techniques.
(2) Under the assumption of the unilateral limit of F(k,s)|s| at +∞ on the potential F(k,s)=∫s0f(k,t)dt instead of the bilateral limit at ∞, it is proved that without anticoercivity the energy functional associated with our problem still satisfies the Palais-Smale condition that plays a key role in the critical point theorem.
(3) Our principal result can be applied to cases with nonlinear terms where f(k,0)>0 but also to cases where the nonlinear terms satisfy f(k,0)=0.
(4) It is also worth mentioning that the algebraic conditions in our main result are more general than the subquadraticity at 0 and the superlinearity at +∞ for the potential F.
In fact, due to the previous (1)–(3), our main result extends Theorem 2 in [12].
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is supported by the National Nature Science Foundation of China (No.10901071, No.11501054, and No.12301186).
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad: