Systemic centrality and systemic communities in financial networks

1.   Introduction

Systemic risk could be defined as the risk that problems affecting one institution could spill over and threaten other firms. Systemic risk, hence, could be mapped into different dimensions. One is too-connected-to-fail risk, where the failure of a highly interconnected firm could pose risks to its counterparties. A second one is too-important-to-fail, where the failure of a firm have a large impact within a group of firms even if the system-wide impact is not large. Finally, another dimension of systemic risk is too-big-to-fail, where the firm may account for a large share of the system or financial activities.^*

^*See Chan-Lau (2013) for a textbook treatment.

In systemic risk assessment, financial networks have rapidly become important visualization and analytical tools in the policy making community. They are useful for examining interconnectedness and systemic risk in the financial system. When extended to include important non-financial firms, networks also serve for assessing linkages between firms in the financial sector and the real economy. Network analysis is far from a theoretical exercise. It guides macroprudential surveillance by evaluating how shocks could propagate across the financial system and by identifying what firms contribute the most to financial contagion.

To cite some examples, the Financial Stability Board (FSB) has recommended policy measures to address the risks posed by systemically important financial institutions (FSB, 2011). The systemic importance of a financial firm depends partly on the level of connectedness of the institution to the financial system (BCBS, 2013). Some of the measures the FSB recommended aim to reduce the risk spillovers arising from connectedness. The Office of Financial Research of the U.S. Treasury, when monitoring financial system vulnerabilities, assesses cross-institution contagion risk and cross-border contagion risk (McLaughlin et al., 2018). Finally, the International Monetary Fund determines what jurisdictions are covered by its mandatory financial sector assessment applying a community detection method to a hybrid financial network (see next section).

To place the methodological contribution presented here in context, this article briefly reviews the main types of networks policy makers typically use when examining financial stability. Then it argues that systemic risk assessment requires the evaluation of node centrality and the identification of communities within networks. The article also explains how to modify community detection methods to accommodate the too-big-to-fail dimension of systemic risk.

1.1.   Counterparty exposure vs. market-based networks

In policy applications, networks typically fall into one of two categories depending on how connections between firms are modeled. In balance-sheet or direct exposure networks, counterparty exposures connect different firms. Simulation techniques, first advanced by Eisenberg and Noe (2001), help to quantify the impact the failure of a single firm or set of firms has on the network.^† Examples of these networks, calibrated using interbank market data for individual firms, include Upper and Worms (2002), Battiston et al. (2012), Ho (2012), Chan-Lau (2010), Cont et al. (2013), and Sun and Chan-Lau (2017). Central banks, such as Banco de Mexico (2016), routinely monitor these networks to assess the stability of their countries' financial systems.

^†See Upper (2011) for more details on simulation methods and related work.

For analysts sitting outside major government and supervisory agencies it is difficult to gather counterparty exposure data on a timely basis. Besides, counterparty exposure may not explain spillovers across firms arising from exposures to similar asset classes, market sentiment, and similarity in business models. Market-based networks address some of these shortcomings. In these networks, the connections between firms correspond to some dependence measure constructed using the market prices of securities or financial contracts. Arguably, prices capture all information relevant to the risk of a firm, and the risk it poses to other firms.

Examples of market-based networks include the equity return correlation network of Mantegna (1999); the Granger causality network of Billio et al. (2012), which Chen et al. (2015) extended to incorporate tail risk; the variance decomposition network of Diebold and Yilmaz (2014), based on generalized impulse response functions, or that of Chan-Lau (2016), based on generalized forecast errors; and the forward-looking partial default correlation network, as in Chan-Lau et al. (2016), periodically updated and maintained by the Credit Research Initiative of the Risk Management Institute, National University of Singapore.^‡

^‡Monthly updates of global, regional, and country-specific systemic risk rankings of financial institutions are available at http://rmicri.org

Networks could combine information from both counterparty exposure and market-based data. For example, the analysis of a hybrid network helped the International Monetary Fund to determine what financial jurisdictions should undertake a periodical mandatory assessment of their financial sector. The strength of the connections between the jurisdictions depended on their bilateral banking exposures, country allocations in equity and fixed income portfolios, and the pairwise return correlation of national stock indices. The application of the clique-percolation detection method then served to identify the community of systemically important jurisdictions, which were then placed under a more strict surveillance regime (Demekas et al., 2013).

1.2.   Centrality and communities: two complementary views on systemic risk

Policy applications, especially of market-based financial networks, typically associate the systemic importance of a firm or node with its centrality.^§ Centrality measures look at the number of connections the firm has, whether the connections link it to other systemic firms, and whether the firm serves as a connecting bridge between any two other firms. As explained in detail below, centrality-based measures capture closely the too-connected-to-fail dimension of systemic risk and serve to construct connectedness-based risk rankings.

^§See, among others, Martinez-Jaramillo et al. (2014), who analyzed the Mexican banking system; Leon and Perez (2014) who examined the financial market infrastructure in Colombia; and Kuzubas, Omercikoglu, and Saltoglu (2013), who assessed systemic risk in the Turkish interbank market during a financial crisis period.

By switching the focus from centrality to the concept of community, it becomes possible to bring on board the too-important-to-fail dimension of systemic risk in the analysis of financial networks. A community is a subset of firms in the network sharing common connections among themselves. The community does not need to be fully connected, i.e. all firms within it do not need to be connected to each other. Regardless of whether the community and its firms are central nodes in the network, intuition suggest that some or several of them could be systemic within the community. These firms, hence, are too-important-to-fail within the local context of the community and belong in the systemically important set.

In the remainder of the paper, section 2 examines the economic intuition underlying the notions of systemic centrality and systemic communities. Section 3 provides a non-technical overview of different centrality and community detection methods that are applicable to directed, weighted financial networks. Section 4 illustrates the use of these algorithms in a global variance decomposition equity return network, based on earlier analysis in Chan-Lau (2016). Section 5 examines the core-periphery structure that characterize the largest community in the network, and section 6 presents the conclusions of the study. During the discussion, the terms firm and node are used interchangeably, as well as the terms connections, edges, links, and ties.

2.   Systemic importance in financial networks

In any network, there are nodes linked to a large number of nodes, i.e. central nodes; and sets of neighboring nodes with strong links among themselves, i.e. community nodes. A systemic node can belong in either of these two categories, or belong simultaneously in both. The existence of power laws governing the distribution of the number of edges connected to a node, i.e. its degree, suggests that only a few nodes are both central nodes and community nodes. A comprehensive assessment of systemic risk, hence, needs to look at central nodes and communities separately since there may not be substantial overlaps among both sets of nodes.

2.1.   Centrality

Borrowing from standard practice in the analysis of social networks, the systemic importance of a firm in a financial network is generally associated with its centrality. The centrality of a node is a function of the number and weight of the edges connecting it to other nodes. Several measures are available, among which the most used is the degree, or number of edges, of the node. In directed networks, where the direction of the edge matters, the degree can be further refined to in-degree, the number of edges going into the node, and out-degree, the number of edges coming out of the node. Degree matters because real world financial networks tend to be scale-free, a property first identified by Barabasi and Albert (1999) in random networks.^¶ That is, only few nodes in the network have a large number of connections.

^¶Boss et al. (2004), Cont, Santos, and Moussa (2013), and Sun and Chan-Lau (2017) find evidence supportive of the scale-free property in the Austrian interbank market, the Brazilian banking system, and the Chilean banking system respectively.

Degree, however, is only a local measure: it captures a node's links with its neighbors but fails to provide a global view of the node's connections in relation to the rest of the network. From the vantage point of financial systems, the degree of a node tells us little about whether shocks originating elsewhere in the network can reach it.

A number of other centrality measures can fill this gap, including closeness, betweenness, and eigenvector centrality. Closeness measures how far away a node is from the other nodes based on the average length of the shortest paths connecting it to them. Betweenness captures the number of instances in which a node lies in the shortest path connecting a pair of nodes. Eigenvector centrality measures the importance of a node based on how important the nodes it connects to are.

Social network analysis relies heavily on these centrality measures. In many instances, the connections between nodes, i.e. people, do not require the edges to be weighted or directed. In contrast, financial networks could exhibit directed or undirected weighted edges. The direction of the edge indicates whether one node influences another, and the weight of the edge measures how important this influence is. If the weighted edge is undirected, the economic assumption is that the connected nodes influence each other at the same time. By construction, counterparty exposure networks are directed weighted networks since the ties between nodes correspond to their bilateral obligations.

Among market-based networks, some examples of networks with undirected weighted edges include the equity correlation network of Mantegna (1999), the partial equity return correlation network of Kennett et al. (2010), and the partial default correlation network of Chan-Lau et al. (2016). Examples of market-based directed weighted networks include the Granger correlation network of Billio et al. (2012), and the variance decomposition networks of Diebold and Yilmaz (2014), and Chan-Lau (2016). More generally, directed weighted networks are the natural outcome of contagion and spillover analyses based on directional dependence measures.

Extending the centrality measures above to weighted undirected and directed networks is possible. Barrat et al. (2004) generalized the concept of degree to weighted networks, and Newman (2001) did the same for shortest paths. Opsahl, Agneessens, and Skvoretz (2010) discussed how to factor in both the weight of the edges and their number in the calculation of centrality. Eigenvector calculations in weighted directed networks may yield complex solutions if some edges have negative weights due to the asymmetry of the adjacency matrices. Adding a free parameter, typically associated with the status of a node, allows extending eigenvector-like centrality measures to directed networks. Commonly used measures include Katz centrality (Katz, 1953), alpha centrality (Bonacich, 1987; Bonacich and Lloyd, 2001), and PageRank (Page et al, 1999).^||

^||Battiston et al. (2012) proposed using a modified version of PageRank, DebtRank, to measure systemic risk in financial systems when bilateral exposure data are available.

Another possibility is to transform weighted directed financial networks, to unweighted undirected network, as in Demekas et al. (2013). If two nodes are connected by two reciprocal directed edges, both edges can be replaced by a simple average measure, i.e. arithmetic mean, geometric mean, or the harmonic mean. In some cases, node characteristics could also serve as weights. When the analysis focuses on the size of the nodes, their sizes could serve as weights in the calculation of the average measure. The undirected network could also be de-weighted, by setting the value of all the edges to the same weight, typically one. This simplification may fail to capture the direction and magnitude of the effects of one node on another. Furthermore, if the distribution of the edges' weights follow a power law, it could underweight the impact of heavy edges on the network.

2.2.   Communities

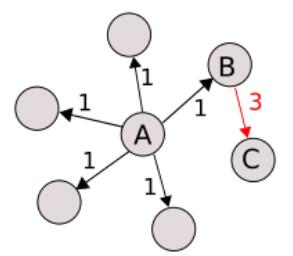
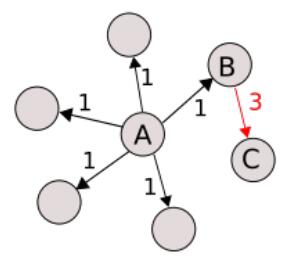
Centrality measures help to single out systemic firms in financial networks. But they may overlook features typically associated with systemic risk. Figure 1, which depicts a very simplified network, illustrates this.

Based on centrality, node A, the one with the highest degree in the network, is the systemic node. The network has weighted edges and node A, again, is the most systemic from an out-strength perspective, i.e. the sum of its weighted out-edges, or the weighted equivalent of out-degrees, is the highest in the network.

Restricting the analysis to centrality measures would overlook node B. While its external strength is about half of that of node A, the impact of node B on its only neighbor, node C, is three times as large as the impact of node A on each of its neighbors. If the directed edges represent repayment obligations from the node where the edge originates to the node where the edge ends, node B is more important for node C than node A. Arguably, node B is systemically important in the two-node community of B and C.

This simple example highlights two dimensions of systemic risk. Centrality measures captures well characteristics we associate with too-connected-to-fail (TCTF) risk. But they may fail to capture concentration risks from counterparty exposures which we associate with too-important-to-fail (TITF) risk. In the latter, the systemically importance of a node does not depend on its number of connections but rather on the node's ability to have a substantial impact on its neighbors, even if the impact is largely contained within a local neighborhood, i.e. a subetaaph of the larger graph characterizing the network. The two risk categories are not mutually exclusive: a node that belongs to the TCTF category could also be TITF and viceversa.

^**The Financial Stability Board, in its 2013 assessment methodology of global systemically important banks explicitly incorporates size and interconnectedness (BCBS, 2013). A simple way to include the size or too big to fail dimension is to weigh the ties between nodes by the size of the nodes. The community detection analysis performs this weighting in section 4.3.

TITF is consistent with the empirical distribution of edge weights in financial networks. As it is the case with centrality measures such as degree or strength, the distribution of the edges' weights also appear to follow a power law distribution. That is, most edges have relatively small weights, with only large weights associated only to a few edges. Hence, only a few firms may have a substantial impact on their neighbors owing to some few large exposures. For community detection purposes, it is possible to exploit the power law feature characterizing most financial networks as explained next.

3.   Methods

This section describes the methods the numerical example uses to calculate centrality measures and to identify systemic communities. The description emphasizes concepts and avoids to, the extent which is possible, the discussion of the underlying mathematics and solution algorithms. Interested readers can explore them in the references cited in the text.

3.1.   Centrality measures^††

^††Among several useful references on centrality measures, Newman (2001) offers an accessible introduction to non-specialists.

This section discusses four centrality measures: strength, closeness, eigenvector centrality, and the PageRank measure.

3.1.1.   Strength

The most used centrality measure of a network node is the degree, or number of ties or edges, in the case of unweighted network, or the strength, which is the degree weighted by the strength (or weight) of the ties. For a directed network, it is possible to further differentiate the degree by counting only the edges coming into a node to obtain the in-degree or in-strength, and counting only the edges originating from a node to obtain the out-degree or out-strength.^‡‡

^‡‡See Barrat et al. (2004) and Opsahl, Agneessens, and Skvoretz (2010).

The in-strength and out-strength measures are economically meaningful. In the case of variance decomposition networks, for instance, Diebold and Yilmaz (2014) propose measuring systemic risk as the total contribution of the node (or firm) to the variance of other nodes (or firms). This contribution is equivalent to the out-strength of the node. Similarly, the systemic vulnerability of a node is proportional to the contribution of other firms to its variance, or in other words, to its in-strength.

To put it precisely, let A be the network's adjacency matrix, where the i-th row and the j-th column entry, A_ij, measures the effect of node i on node j. The in-strength and out-strength of node i are, respectively, equal to the sum of the entries in column i and the sum of the entries in row i:

3.1.2.   Closeness

The closeness measure is equivalent to the mean distance from a node to the other nodes in the network. The distance between nodes is the geodesic path, or shortest path joining them. In weighted directed networks, where the edge weight corresponds to the strength of the interaction between the nodes, it is necessary to use a modified adjacency matrix, B. In this matrix, the i-th, j-th entry B_ij should be inversely proportional to the original weight of the edge, A_ij since nodes joined by edges with higher weights are closer together.

For calculation purposes, we set B_ij = 1/(1 + A_ij), for all $i \neq j$ and zero otherwise. The mean in- and out-distance of node i, $\ell_{i, in}$ and $\ell_{i, out}$ respectively, are equal to:

where n is the number of nodes in the network. The centrality of a node is inversely related to its mean distance, i.e. lower distances imply higher centrality.

3.1.3.   Eigenvector centrality

The eigenvector centrality measure, introduced by Bonacich (1987), defines the centrality of a node as the weighted sum of the centrality of its neighbors with edges pointing towards the node. For node i, its centrality $x_i$, is equal to:

In the analysis of financial networks eigenvector centrality corresponds to the importance of nodes as recipients (or sinks) of spillovers, i.e. the systemic vulnerability ranking of the node in the network. There are several reasons why a node becomes eigenvector-central. It may have incoming links from very central nodes, even if the in-degree is low; it may have a large number of incoming links, even if the connecting nodes are not that important, or it may be because of a combination of both cases above.

The eigenvector centrality measure, which in vector notation is x, should satisfy the equation:

where $\kappa_{1}$ is the largest eigenvalue of the adjacency matrix A. Although the adjacency matrix may be asymmetric, all eigenvalues are positive and real if all the matrix elements are positive. The centrality of a node is a weighted sum of the centrality of other nodes, where the weights are equal to the incoming edges' weights.

Using the eigenvector centrality measure to capture systemic risk rather than systemic vulnerability requires some adjustments. Rather than using the adjacency matrix A to perform the calculations, we use the transpose of the adjacency matrix, A^T. In the latter matrix, the entry ${A_{ij}^{T} = A_{ji}}$. Therefore, the edges entering into a node are actually the edges leaving the node. In this case, the centrality of the node depends on its influence on other nodes.

3.1.4.   PageRank

As with eigenvector centrality, the PageRank algorithm allows nodes receiving edges from a high centrality node to benefit from the centrality of the latter. However, the algorithm dilutes the received centrality in proportion to the strength of the out-edges from the high centrality node. In other words, the importance of a node on the receiving end may not be substantial if it is only one among many to which the highly central node points to. Letting x be the centrality vector, its value comes from solving the equation:

where 1 is the vector $(1, 1, 1, ...)$, and D is a diagonal matrix with diagonal elements equal to the out-degree of the node if the out-degree is different than zero, or equal to one otherwise. The formula includes a free parameter, $\alpha$, which is set equal to 0.85 in the Google search engine. The results reported in the numerical analysis below correspond to those obtained by setting the parameter to the default value Google specifies. As a robustness check, we verified that results are mostly unchanged when the parameter values takes values in the range $[0.5, 1)$.

As in the case of the eigenvector centrality measure, the PageRank centrality of a node captures the exposure of the node to other nodes in the network, or in other words, its vulnerability. But as in the case of eigenvector centrality, performing the calculations using the transpose of the adjacency matrix captures the systemic risk of the node.

3.2.   Community detection methods

When looking at networks, it is natural to think about communities within it. Roughly, a community is a subset of nodes (or subetaaph) such that the nodes interact more closely among themselves than with the rest of the network. This is quite a broad definition, which makes community detection an ill-defined problem, as noted, for instance, in Fortunato and Hric (2016), and Schaub et al. (2017). The identification problem is even more challenging in directed networks, as noted in Malliaros and Vazirgiannis (2013).

Notwithstanding the ill-defined nature of community detection, Schaub et al. (2017) suggested four different approaches to community detection able to encompass most existing methods. The cut-based approach aims at minimizing the number of edges between the nodes, independently of the intrinsic structure of the network by the successive removal of edges. The clustering approach attempts to produce densely connected communities such that nodes within a community are "close" together, and points in different communities are distant from each other.^* The stochastic equivalence approach assumes that nodes belong to the same community if they are equally likely to have ties to similar nodes. The fourth and final approach is to view a network as a dynamic building block, which associates the concept of community to the role its nodes play in the diffusion of processes through the network.

^*Fortunato and Hric (2016) refers to this perspective as the classic view on community identification.

The context of the problem should guide the choice of the community detection method. Focus on the role of edges as the transmission channel of shocks suggest that among the different perspectives, the relevant ones are the clustering perspective and the dynamical building block perspective. The methods used here include edge betweenness, a clustering method, and the map equation, or Infomap, a dynamic method. Both of these methods work for weighted directed networks.

3.2.1.   Edge betweeness

For weighted directed networks, Girvan and Newman (2002) generalize the node betweenness measure of Freeman (1977) to edges. Their algorithm starts by examining the complete graph and start eliminating, one by one, edges with high centrality in decreasing order. The centrality of an edge is defined as the number of times it lies in the shortest path between any two nodes in the network.

The intuition behind the method is that just a few edges connect different communities in the network, and these edges would be highly central since they are in the shortest path between pairs of nodes such that each one is located in a different community. By removing them, the network fragments and the community structure emerges. This method is consistent with the classic view that communities are dense subetaaphs separated from each other. Or in other words, the number of internal edges in the community largely exceeds the number of external edges connecting it to other communities (Fortunato and Hric, 2016).

Some applications in finance include, among others, Elouaer-Mrizak and Chastand (2013), who analyzed communities within the French inter-corporate network; and Wang et al. (2016), who apply the method to identify communities in equity return partial correlation networks.

3.2.2.   The map equation (Infomap)

The map equation, introduced by Rosvall and Bergstrom (2008), builds on the coding theory of Shannon(1948a, b), which looks at the most economical way to compress information flow in the network. Coding theory serves to examine the constraints the network topology imposes on the the dynamic behavior of processes taking place there. The dynamics, in turn, identify the network communities.^†

^†See Rosvall, Axelsson, and Bergstrom (2010) for a comprehensive discussion of the method.

While coding theory is likely not familiar to most financial market practitioners, the intuition is straightforward. Imagine a random walker, or drunk person, moving from one node to another node. The probability that the random walker would go to a neighboring node is proportional to the strength of the edge pointing to it. If the number of steps in the walk is large enough, the random walker would tend to spend more time walking within certain communities, as the internal edges would encourage moving between community nodes rather than exiting the community. When traversing the network, the random walker codifies the information implied by each community partition. There are a large number of paths with associated partitions. The map equation chooses the partition which requires the minimal information encoding.

There are a number of recent applications of the map equation to financial networks. Among them, Tumminello et al. (2012), using a database of trading activity of individual investors, identified clusters of investors characterized by the high synchronization of their trading activities.Vitali and Battiston (2012) examined the community structure of the global corporate network. Jiang et al. (2014) analyzed the interactions of different business sectors implied by the sectors' return correlation network. Bech et al. (2014) identified changes in lending patterns in the overnight money market, arguably triggered by the collapse of Lehman Brothers in September 2008; and Alzahrani (2016), using an extension of Infomap to bipartite networks first proposed by Alzahrani et al. (2014), uncovered the community structure of the payment transactions system of the Kingdom of Saudi Arabia.

3.2.3.   Practical issues when dealing with dense networks

Community detection methods work best for sparse networks, i.e. networks where the number of edges between nodes is substantially lower than the maximum possible amount of edges. This is typically the case for social networks and biological networks. In contrast, financial networks tend to be dense networks since they mirror a highly interconnected system. Translated into network analysis language, financial networks tend to comprise just one single giant component (Bollobas, 2001). This network characteristic, while intuitive, is of little help for singling out systemic communities. It also makes continuous monitoring difficult when resources are scarce and the number of nodes large.

There are several ways to reduce network density. Minimum spanning trees (MSTs), first developed by Kruskal (1956) and Prim (1957) and introduced in financial networks by Mantegna (1999), reduce the number of edges in a network drastically, yielding a network comprising a subset of edges connecting all vertices together while minimizing the total weight of the edges. In MST networks, systemic firms are those that are located more often in the set of shortest paths connecting any pair of nodes. One shortcoming of this method, however, is that it may yield the opposite problem, a network which is way too sparse. In these networks, the concept of community no longer applies.

Too sparse networks could also be a problem in partial correlation networks comprising a large number of nodes. Straight application of partial correlation analysis could render many nodes orphans, i.e. completely disconnected from other nodes. This situation, especially in financial networks, could be counter-intuitive since the common wisdom is that all nodes are connected in a financial network. An alternative is to use economic intuition to guide what would be otherwise a purely statistical method. For instance, Chan-Lau et al. (2016) constrain the partial correlation network by tuning a regularization or cost parameter such that there are no orphans in the resulting network.

Finally, a simpler way to reduce the density of a financial network is to use some criteria for identifying "weak" edges and removing them. We can justify this approach if the focus is on the extreme connections, or tail connections, between nodes, i.e. extreme spillovers. If the tail distribution of the edges and/or the edges' weights follow a power law, the approach is further justified. The easier implementation is to set a threshold value and to remove all edges with weights below it in case the weight directly proportional to the strength of the nodes' connection, or to remove all edges with values above it if higher edge values imply weaker connections. Once a sparser, transformed financial network is obtained, it is straightforward to calculate the centrality measures and to apply the community methods discussed above.

4.   Systemic centrality and systemic communities in the global financial system

This section applies centrality and community detection methods to the variance decomposition financial network in Chan-Lau (2016). By accounting for the overall impact of firms on the equity return variance of other firms, this method improves on pair-wise correlation methods such as those of Billio et al. (2012) and Chen et al. (2015). In contrast to the the Pesaran-Shin decomposition used by Diebold and Yilmaz (2014), the network analyzed here was based on the Lanne-Nyberg decomposition, which already embeds a unit normalization of the variance decomposition. This normalization facilitates the comparison of risk ratings and risk contributions at two different points in time.

4.1.   Data and network construction

The construction of the network used weekly equity returns, in U.S. dollars, for a sample of financial firms during the period January 1, 2001-July 31, 2016. The data sample, comprising 275 financial firms, included banks, insurance companies, and security brokers and dealers. Bloomberg LLP was the source of equity prices. Table 1 shows the distribution of firms per country and per type of firm. About one out of four firms is headquartered in the United States, and four out of ten firms are banks.

After fitting an unrestricted Vector Autoregressive (VAR) model to the equity returns time series, the value of the directed edge from firm i to firm j is set according to the contribution of firm i to the Lanne-Nyberg Generalized Forecast Error Variance Decomposition (GFEVD) of firm j over a horizon of h periods, $\lambda_{ij}(h)$ (Lanne and Nyberg, 2016):

where n is the number of firms in the network, Ω_t−1 is the information up to period $t-1$, and GI is the generalized impulse response function of Pesaran and Shin (1998):

In the above equation, e_j is a $n \times 1$ vector with all entries set to zero, except for the $j-$th entry, and A_j and Σ are the coefficient matrix corresponding to the h lag and the covariance matrix of the error terms in the moving average representation of the VAR system respectively. In the adjacency matrix of the global financial network, A, the i-th row, j-th column entry, A_ij, simply corresponds to $\lambda_{ij}(h)$, with h set equal to one hundred periods. The resulting network, calculated using a VAR specification with eight lags, is dense and fully connected, as the adjacency matrix does not have any entry with a zero value.^‡

^‡Due to the high dimensionality of the VAR system, it is necessary to estimate the system using regularization techniques. The structure of the financial network remains mostly unchanged regardless of the number of lags in the VAR specification. See Chan-Lau (2016) for details.

4.2.   Centrality measures

We calculated the centrality of each node using four different measures: strength, closeness, eigenvector centrality, and Pagerank. As described in the methods section, the calculations used the appropriate adjacency matrices. The centrality measures then served to construct ordinal risk and vulnerability rankings. Following Diebold and Yilmaz (2014), riskier firms contribute more to the variance decomposition of other firms. Similarly, firms to whom other firms contribute the most are the most vulnerable. Diebold and Yilmaz concepts of risk and vulnerability map directly into the strength measures.

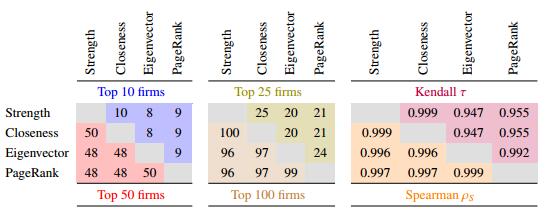
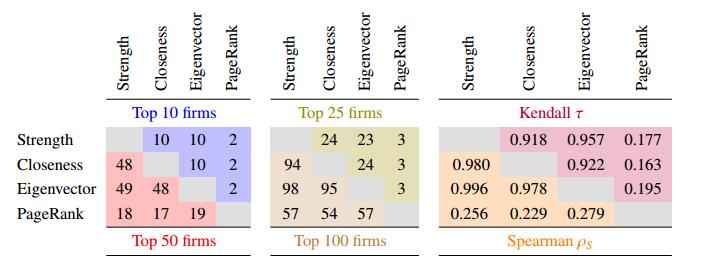
Table 2 summarize the systemic risk rankings. They are quite similar regardless of the centrality measures used. Their Kendall $\tau$ and Spearman $\rho_S$ rank correlations are well above 90 percent. Consistently, all the centrality measures yield similar risk rankings and identify the same set of firms among the top 10, 25, 50 and 100 riskiest firms in the system. It is safe to conclude that, for systemic risk identification, all four centrality measures are equally useful and that the rankings are robust to the choice of methodology.

Excluding the PageRank rankings, the results for the systemic vulnerability rankings are quite similar to those for their risk counterparts (Table 3). The rank correlations exceed 90 percent and there are substantial overlaps among the 10, 25, 50, and 100 most vulnerable firms identified by each method. The notable exception is the PageRank ranking, which differs substantially from the other rankings.

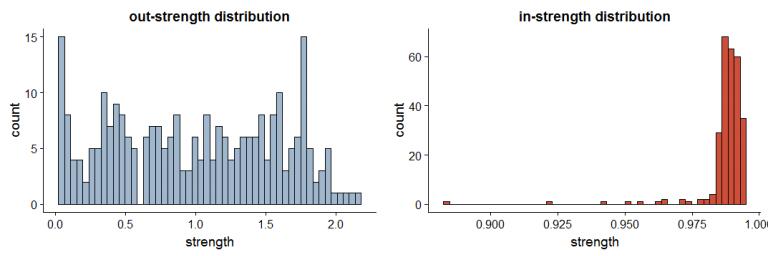
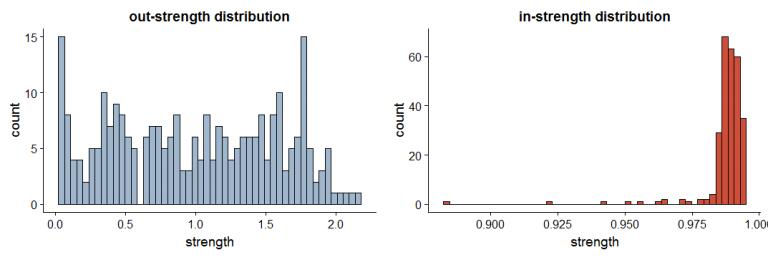
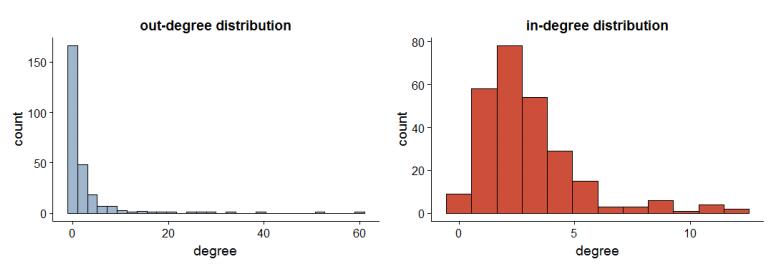
The nodes' in-strength distribution, shown in Figure 2, may explain why the PageRank rankings are so different. Compared with the out-strength distribution (left panel), which is relatively uniform, the in-strength distribution is highly skewed to the left, with the in-strength of most nodes clustered within a narrow range of values. The PageRank algorithm would tend to treat most nodes as equally important, blurring node differences.

Table 4 expands on the results in Tables 2 and 3. It shows the top ten riskiest and most vulnerable firms. Again, systemic risk rankings seem robust to the choice of centrality-based measure. This is also the case for systemic vulnerability rankings provided we exclude the PageRank centrality ranking. Note that the riskiest firms comprise a mix of large banks and insurance companies, most of them with a large international presence. The most vulnerable firms, in contrast, are relatively large players in domestic markets. These results are consistent with the in-strength and out-strength results in Chan-Lau (2016), which presents more detailed results on a regional basis.

4.3.   Community detection

The density of the network does not present problems for the calculation of the centrality measures. This is not the case for community detection. Fortunately, the distribution of the weights of the edges, or the GFEVD contributions of a firm to other firms' long term variance, follows a power law distribution. This justifies trimming the number of edges by discarding edges falling below a certain threshold.

4.3.1.   Power law distribution of edge weights

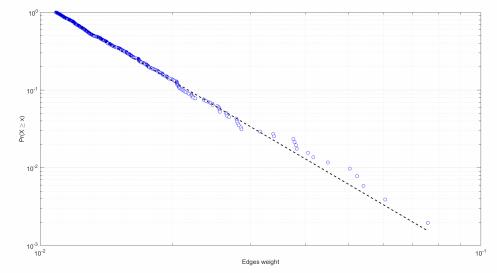
A casual examination of the histogram of the edge weights suggest that the number of edges representing a high GFEVD contribution, or return spillovers between firms, decreases rapidly. The histogram suggests that a power law distribution could capture the distribution of edge weights reliably. That is, the fraction of edges in the network, $P(k)$, with a weight exceeding the value k declines exponentially as k increases: $P(k) \sim k^{-\alpha}$, where $\alpha$ is a scaling parameter.

The estimation of the power law distribution parameters follows the methods suggested by Clauset et al. (2009). Maximum likelihood estimation allows recovering the empirical estimate of the scaling parameter, $\alpha$, given the value of a lower bound, x_min, above which the observations follow the power law:

The estimate of the lower bound, $\hat{x}_{min}$, minimizes the Kolmogorov-Smirnov statistics, or maximum distance between the cumulative distribution functions (CDFs) of the data and the fitted power law model:

where $S(x)$ is the empirical CDF for observations with values greater or equal to x_min, and $P(x)$ is the CDF for the power law model that best fits the data in the region $x \geq x_{min}$.

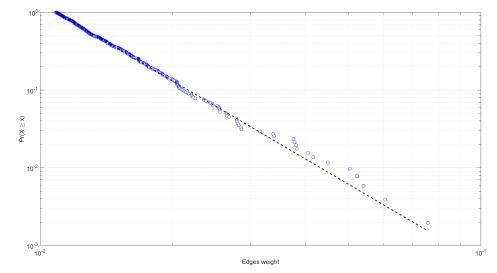
For the Lanne-Nyberg variance decomposition network, the log-log plot in Figure 3 shows that the power law fits the data well. The estimated scaling parameter of the power law distribution, $\alpha$, is 4.33, clearly indicating the presence of heavy tails in the data. The lower bound, x_min, 0.0109, corresponds to the upper 99.3 percentile of the observed edge weights, and it is about 40 times higher than the mean value of the edge weights, 0.0036.

4.3.2.   Network density reduction and the tail spillover network

Based on the evidence supporting the existence of a power law distribution, it was sensible to reduce the density of the network by removing all edges with a weight below the lower bound x_min. Compared to the original, fully connected network, which has a density of one hundred percent, the trimmed network has a density of just one percent. After removing the weak links, a number of nodes became orphan, and were removed from the network. The final number of nodes, however, is 262, just slightly below the 275 nodes in the original network. Since values above the lower bound fall in the tail of the edge weight distribution, the trimmed network is equivalent to a tail spillover network.

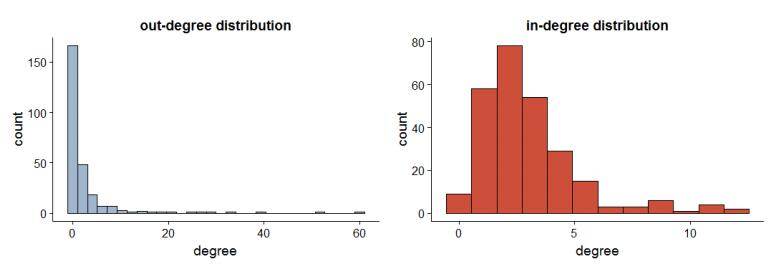
Figure 4 shows the out-degree and in-degree distributions in the trimmed network. Four out of ten nodes have an out-degree of zero, that is, they have no spillovers to other nodes in the tail spillover network. The out-degree distribution also exhibits a right fat tail, with only a few nodes with degree greater than ten, i.e. tail spillovers to ten or more firms. The in-degree distribution shows that most nodes tend to receive spillovers from five nodes or less.

4.3.3.   Edge betweenness communities

As in the case of the original network, the entries in the adjacency matrix A of the trimmed network, A_ij, correspond to the Lanne-Nyberg contribution of the node, $\lambda_{ij}(h)$, calculated according to equation (8). The adjacency matrix A characterizes an edge-weighted network, which captures the too-important-to-fail dimension of systemic risk. But the ongoing policy discussion on the designation of systemically important financial institutions also emphasizes the too-big-to-fail dimension. To explore this in detail, the analysis also looks at two additional edge weighting schemes.

The first weighting scheme associates the too-big-to-fail dimension with the asset size of the firms. To this end, it constructs an alternative adjacency matrix, B. In B, there is a link between two nodes if such a link exists in matrix A. But the weight of the link is unrelated to the Lanne-Nyberg contribution of the source node. Rather, for a source node i, the weight of the link to its outgoing nodes or children nodes, B_ij, is set equal to the share of the outgoing node on the total assets of the system:

where $a_j$ denotes the total assets of node j. In this node-weighted network, the magnitude of the spillover from node i to node j does not matter. What matters, instead, is whether j is a large node or not.

The second scheme factors in both the size of the children nodes and the magnitude of the spillovers. In the node and edge weighted-network, the adjacency matrix, C, has entries C_ij equal to:

Table 5 shows, for each of the three weighted networks, the number of communities and their sizes identified by the edge betweenness method. The calculations use networks generated by adjacency matrices with entries $Y_{ij} = 1/(1+X_{ij}), X = A, B, C \text{ for} X_{ij} > 0$ since stronger links imply a smaller distance between nodes.

Regardless of the weighting scheme, we can observe that edge-betweenness generates two large communities with about fifty and thirty communities each. Also, almost half of the nodes are orphans, i.e. isolated nodes that do not belong to any community; and about one out of four nodes belong to small communities of size ten or lower. The overlap of the two largest communities identified under the different weighting schemes is substantial (Table 6). This finding seems to imply a close association between the too-important-to-fail and too-large-to-fail dimensions of systemic risk.

Within a community subetaaph, it is feasible to identify the "riskiest" firms in the community by ranking the nodes in descending order by their out-degree or out-strength in the community subetaaph. In other words, after applying the community detection method, we can rank nodes in each community using any of the centrality measures described earlier. Similarly, the in-degree and the in-strength serve to identify the most vulnerable firms in the community. Since the trimmed networks are sparse, it is not adequate to use either the eigenvector centrality or PageRank methods. Table 7 lists the top ten riskiest and most vulnerable firms in the largest community for each of the weighted networks.

The list of the riskiest firms is similar across networks, reflecting the fact that only a few nodes have outgoing links, e.g.~they are sources of shocks. There are just eleven such nodes in the edge-weighted network, and thirteen in the other two networks. In contrast, most of the nodes in the largest community in each network are shock recipients. We could argue that the largest community resembles somewhat a core-periphery community, with a few nodes originating most of the spillovers. As in the case of the centrality-based rankings, the top riskiest firms include both large banks and insurance companies with large international operations. This class of firms is also present among the the most vulnerable firms but to a lesser extent.

The structure of the second largest community, which includes slightly more than thirty nodes, differs largely from the largest community. The number of nodes with outgoing links is similar to the number of nodes with incoming links, suggesting that nodes in the community are closely connected to each other (Table 8). Most of the firms in the second largest community are insurance companies, suggesting they naturally belong to a different segment of the global financial system. This result supports applying different regulatory and supervisory approaches to firms in each community.

4.3.4.   Infomap communities

The analysis focuses now on the communities identified using the Infomap algorithm. To detect the systemic communities, the Infomap algorithm assumes that the probability that a random walker, or shock, in economic parlance, moves from one node to another (teleportation) is proportional to the weight of the outgoing links. In an edge-weighted network, the weights correspond to the entries in the adjacency matrix A. As in the previous section, the analysis can factor in the size of the nodes of the network to incorporate the too-big-to-fail dimension of systemic risk. To accomplish this, there are two options.

The first option is to make the probability of teleportation proportional to the weights (or size) of the outgoing nodes, neglecting the weight of the links. In other words, given the weight of the node, $\omega$, the communities in the node weighted network belong to the network defined by the adjacency matrix B:

where $V_{-i}$ is the set of outgoing, or children, nodes of i. In this network, what matters is whether shocks spill over to large nodes rather than the magnitude of the impact the node has on other nodes.

The second option is to find the communities in the transformed node and edge weighted network C, where the adjacency matrix is equal to:

where A_ij are the weighted edges in the original network. In this case, the analysis takes into account both the size of the recipient nodes and the magnitude of the spillover.

Mimicking the analysis of the edge-betweenness communities, we look at the number of communities and their size generated by the Infomap algorithm (Table 9).

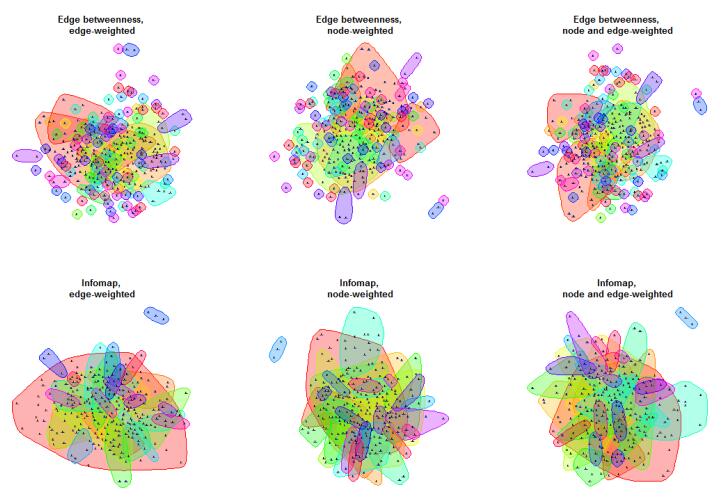
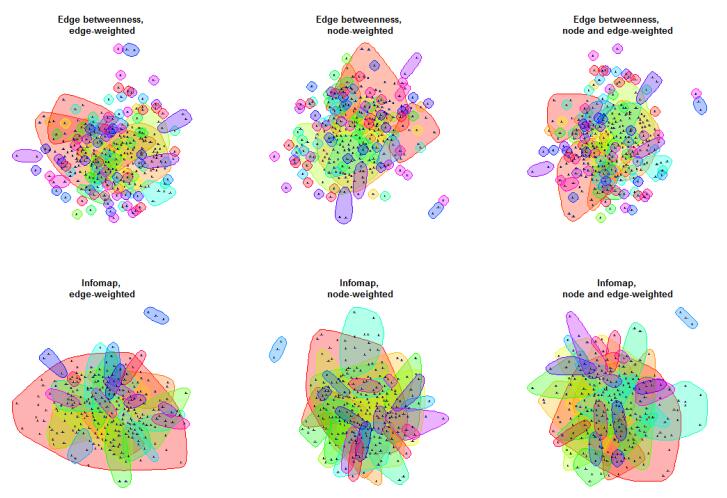
Compared with the edge-betweenness methods, the infomap algorithm seldom generates orphan nodes. It yields, however, just one big, dominant community surrounded by a large number of smaller communities. The Infomap dominant community, especially for the edge-weighted network, is larger than the ones generated using the edge-betweenness method. In the case of the edge-weighted network, the largest community encompasses almost half of the financial firms, and in the other two networks, one quarter of them. This pattern is also evident in Figure 5, which for comparison purposes shows the graphics corresponding to the edge betweenness communities.

An examination of the results show that, except for communities of two nodes or less, the Infomap algorithm generates exactly the same communities in the node-weighted and node and edge-weighted networks. This result suggests that when using the Infomap method, too-big-to-fail risk dominates too-important-to-fail risk. Further evidence of the sensitivity of the Infomap method to the weighting scheme used comes from the communities identified in the edge-weighted network. In this case, the largest systemic community comprises more than one hundred firms compared with only seventy firms in the other two networks. While the Infomap community structures are more sensitive to the weighting scheme used than the edge-betweennes communities, the former communities are better connected and there are almost no orphan nodes.

The largest systemic community comprises a large number of nodes but only a few nodes are sources of spillovers, i.e. they have outgoing edges to other nodes. The first panel in Table 10 shows that if size is not accounted for, only four out of ten nodes have outgoing links. In contrast, almost all the nodes in the community receive links from the spillover nodes. Once size is factored in, the ratio of spillover nodes falls to three out of ten. Therefore, the largest community in the networks are characterized by a core-periphery structure, a finding also supported by the edge-betweenness results.

The second panel and third panels in Table 10 list the ten riskier and most vulnerable firms respectively. Among the riskiest firms, there is almost an equal split between large banks and insurance companies, some of which with a global footprint. Among the most vulnerable firms, the majority are insurance companies. There are some notable exceptions, however, such as JPMorgan Chase, Morgan Stanley, and Nordea Bank.

In contrast to the results obtained using the edge-betweenness method, there are a number of firms that are both important spillover sources (risky firms) and the recipient of shocks (vulnerable firms). Among them we have insurance firms Alleghany, Allstate, American Financial Group, Metlife, Torchmark, and XL Group. The community detection methods do not seem to generate similar risk and vulnerability rankings, as there is little overlap between the rankings generated by the edge-betweenness and Infomap methods.

5.   The core-periphery structure in the largest community: a clique percolation verification

The edge betweenness and Infomap algorithms generate non-overlapping communities, with nodes belonging either to one community or another. Arguably, some communities may overlap and shared some nodes. One popular algorithm used to detect overlapping communities is the k-clique percolation method introduced by Palla et al. (2005). The algorithm finds k-cliques, that is, group of k nodes fully connected to each other. If two k cliques share $k-1$ adjacent nodes, they belong to the same community.

Palla et al. (2007) show we can apply the k-clique percolation method to directed graphs after specifying a hierarchical ordering of the nodes that sets the parent-child mapping of the network. Assuming such ordering is not feasible ex ante, however, the application of the method to an undirected, unweighted version of the network serves to provide an upper bound to the number of communities and their member nodes. We can exploit then this structure to verify that the largest communities have a core-periphery structure.

To see this, notice that a clique in the undirected network may not exist once we account for the edge direction, since the nodes in the clique may cease to be fully connected. The fact that the largest edge betweenness and Infomap communities have very few nodes with outgoing edges suggest that cliques, if existent, may be located in the smaller communities. The structure of the large community, therefore, would be consistent with a core-periphery model, with periphery nodes only loosely connected to each other. Clique percolation communities may also inherit this structure.

Indeed, this seems to be the case as Table 11 illustrates. The table shows the largest k-clique community for clique sizes of four, five, and six, where the latest value is the maximal clique size in the trimmed tail spillover network. The firms in the cliques overlap with those contained in the second largest community identified using the edge-betweenness method. Also, about one third to one half of the firms in the 5-clique and 6-clique communities fall within the top riskiest firms Infomap identifies, suggesting the presence of a small core in the largest Infomap community.

6.   Conclusions

Centrality measures and community identification methods are useful for assessing systemic risk in the financial system. Centrality measures are suitable to capture the too-connected-to-fail dimension of systemic risk, while community identification methods serve to single out groups of firms where some of them may play a too-important-to-fail role. Moreover, the last set of methods is also able to accommodate the too-big-to-fail characteristics of certain firms by weighting the links between firms by a measure of the firms' sizes.

To illustrate the applicability of these concepts, Ⅰ conducted a systemic risk analysis of a global financial network where firms are linked by their contribution to the variance decomposition of equity returns of other firms. This is a dense, weighted and directed financial network. Systemic risk rankings were quite similar regardless of the choice of centrality measure. For systemic vulnerability rankings, strength, closeness, and eigenvector centrality measures performed similarly. The exception was the PageRank centrality measures, which yielded rankings weakly correlated with those of other measures. This finding may be due to the existence of a power law distribution affecting the left tail of the in-strength distribution of the nodes in the network.

Community identification methods may not perform well in a fully connected network. Taking advantage of the fact that the distribution of the strength of the edges follows a power law, it was possible to reduce the density of the network by preserving only those edges with values above the power law minimum value. The trimmed network is equivalent to a tail spillover network, which focuses solely on major spillovers. Edge betweenness, a classical method, generates a consistent group of communities regardless of the edge and/or size weighting scheme used, but it leaves many nodes orphan. The map equation, or Infomap, a random walk-based method, is sensitive to the weighting scheme but generates fewer communities than edge betweenness. Under both methods, the largest community has only a few nodes with outgoing links, while most nodes have incoming links. This suggests that the largest community has a core-periphery or hub and spoke structure, which is further verified using clique percolation methods.

Arguing whether one community detection method is superior to other does not seem justified. Research in community detection methods has yet to agree on a dominant method for the simple reason that the choice of method depends on the objective of the analysts. Edge betweenness is appropriate if the analysis focuses on whether a specific node appears often in the shock transmission path. When the analysis focuses on whether shocks tend to be contained within a specific group of firms, then Infomap offers a better approach. Moreover, some of these findings may be inherent only to the variance decomposition network analyzed here. Other networks may have different characteristics, and discovering them may require using a variety of methods, as done in this article.

While the article focuses on methodology rather than policy making it is important to remark that the former could have a substantial impact on the latter, as it has been reflected in policy work at central banks and multilateral institutions. For instance, the two largest communities identified by the edge-betweenness method contain two different types of firm. This suggests that regulatory and supervisory approaches should be customized to each community. From a strictly surveillance perspective, monitoring how the communities composition evolves over time could serve to identify changes in the financial sector landscape and could point towards financial industry developments worth examining in detail.

Acknowledgments

I benefit greatly from comments by Martin Cihak and two anonymous referees. Any errors and/or omissions remain my sole responsibility.

Conflict of interest

The author declares no conflict of interest.