Cerebral vascular accidents (strokes) are a leading cause of motor deficiency in millions of people worldwide. While a complex range of biological systems is affected following a stroke, in this paper we focus primarily on impairments of the motor system and the recovery of motor skills. We briefly review research that has assessed two types of mental practice, which are currently recommended in stroke rehabilitation. Namely, action observation (AO) therapy and motor imagery (MI) training. We highlight the strengths and limitations in both techniques, before making the case for combined action observation and motor imagery (AO + MI) therapy as a potentially more effective method. This is based on a growing body of multimodal brain imaging research showing advantages for combined AO + MI instructions over the two separate methods of AO and MI. Finally, we offer a series of suggestions and considerations for how combined AO + MI therapy could be employed in neurorehabilitation.
1.
Introduction
The construction of discrete fractional sums and differences from the knowledge of samples of their corresponding continuous integrals and derivatives arises in the context of discrete fractional calculus; see [1,2,3,4,5,6] for more details. Recently, discrete fractional operators with more general forms of their kernels and properties have gathered attention in both areas of physics and mathematics; see [7,8,9,10].
In discrete fractional calculus theory, we say that $ \mathtt{F} $ is monotonically increasing at a time step $ t $ if the nabla of $ \mathtt{F} $ is non-negative, i.e., $ \bigl(\nabla \mathtt{F}\bigr)(t): = \mathtt{F}(t)-\mathtt{F}(t-1)\geq 0 $ for each $ t $ in the time scale set $ \mathbb{N}_{c_{0}+1}: = \{c_{0}+1, c_{0}+2, \ldots\} $. Moreover, the function $ \mathtt{F} $ is $ \theta- $monotonically increasing (or decreasing) on $ \mathbb{N}_{c_{0}} $ if $ \mathtt{F}(t+1) > \theta\, \mathtt{F}(t) \quad \bigl(\rm{or}\; \mathtt{F}(t+1) < \theta\, \mathtt{F}(t)\bigr) $ for each $ t\in\mathbb{N}_{a}\bigr) $. In [11,12] the authors considered $ 1- $monotonicity analysis for standard discrete Riemann-Liouville fractional differences defined on $ \mathbb{N}_{0} $ and in [13] the authors generalized the above by introducing $ \theta- $monotonicity increasing and decreasing functions and then obtained some $ \theta- $monotonicity analysis results for discrete Riemann-Liouville fractional differences defined on $ \mathbb{N}_{0} $. In [14,15,16], the authors considered monotonicity and positivity analysis for discrete Caputo, Caputo-Fabrizio and Attangana-Baleanu fractional differences and in [17,18] the authors considered monotonicity and positivity results for abstract convolution equations that could be specialized to yield new insights into qualitative properties of fractional difference operators. In [19], the authors presented positivity and monotonicity results for discrete Caputo-Fabrizo fractional operators which cover both the sequential and non-sequential cases, and showed both similarities and dissimilarities between the exponential kernel case (that is included in Caputo-Fabrizo fractional operators) and fractional differences with other types of kernels. Also in [20] the authors extended the results in [19] to discrete Attangana-Baleanu fractional differences with Mittag-Leffler kernels. The main theoretical developments of monotonicity and positivity analysis in discrete fractional calculus can be found in [21,22,23,24] for nabla differences, and in [25,26,27,28] for delta differences.
The main idea in this article is to analyse discrete Caputo-Fabrizo fractional differences with exponential kernels in the Riemann-Liouville sense. The results are based on a notable lemma combined with summation techniques. The purpose of this article is two-fold. First we show the positiveness of discrete fractional operators from a theoretical point of view. Second we shall complement the theoretical results numerically and graphically based on the standard plots and heat map plots.
The plan of the article is as follows. In Section 2 we present discrete fractional operators and the main lemma. Section 3 analyses the discrete fractional operator in a theoretical sense. In Section 4 we discuss our theoretical strategy on standard plots (Subsection 4.1) and heat map plots (Subsection 4.2). Finally, in Section 5 we summarize our findings.
2.
Basic definitions and a lemma
First we recall the definitions in discrete fractional calculus; see [2,3,5] for more information.
Definition 2.1. (see [2,Definition 2.24]). Let $ c_0\in\mathbb{R} $, $ 0 < \theta\leq 1 $, $ \mathtt{F} $ be defined on $ \mathbb{N}_{c_{0}} $ and $ \Lambda(\theta) > 0 $ be a normalization constant. Then the following operator
is called the discrete Caputo-Fabrizio fractional operator with exponential kernels in the Riemann-Liouville sense $ \mathrm{CF_{R}} $, and the following operator
is called the discrete Caputo-Fabrizo fractional operator with exponential kernels in the Caputo sense $ \mathrm{CF_{C}} $.
Definition 2.2 (see [3]). For $ \mathtt{F}:\mathbb{N}_{c_{0}-\kappa}\to\mathbb{R} $ with $ \kappa < \theta\leq \kappa+1 $ and $ \kappa\in\mathbb{N}_{0} $, the discrete nabla $ \mathrm{CF_{C}} $ and $ \mathrm{CF_{R}} $ fractional differences can be expressed as follows:
and
respectively, for each $ t\in\mathbb{N}_{c_{0}+1} $.
The following lemma is essential later.
Lemma 2.1. Assume that $ \mathtt{F} $ is defined on $ \mathbb{N}_{c_{0}} $ and $ 1 < \theta < 2 $. Then the $ \mathrm{CF_{R}} $ fractional difference is
for each $ t\in\mathbb{N}_{c_{0}+2} $.
Proof. From Definitions 2.1 and 2.2, the following can be deduced for $ 1 < \theta < 2: $
for each $ t\in\mathbb{N}_{c_{0}+2} $.
3.
Theoretical analysis results
In the following theorem, we will show that $ \mathtt{F} $ is monotonically increasing at two time steps even if $ \left({}_{{c_0}}^{C{F_R}}\nabla^{\theta}\mathtt{F}\right)(t) $ is negative at the two time steps.
Theorem 3.1. Let the function $ \mathtt{F} $ be defined on $ \mathbb{N}_{c_{0}+1} $, and let $ 1 < \theta < 2 $ and $ \epsilon > 0 $. Assume that
If $ (1-\theta)(2-\theta) < -\epsilon $, then $ \bigl(\nabla \mathtt{F}\bigr)(c_{0}+2) $ and $ \bigl(\nabla \mathtt{F}\bigr)(c_{0}+3) $ are both nonnegative.
Proof. From Lemma 2.1 and condition (3.1) we have
for each $ t\in \mathbb{N}_{c_{0}+2} $. At $ t = c_{0}+2 $, we have
where we have used $ (1-\theta) < (1-\theta)(2-\theta) < -\epsilon $ and $ \bigl(\nabla \mathtt{F}\bigr)(c_{0}+1)\geq 0 $ by assumption. At $ t = c_{0}+3 $, it follows from (3.2) that
as required. Hence the proof is completed.
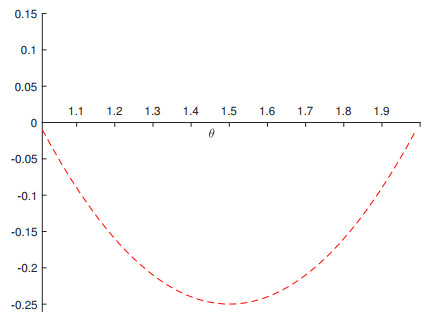
Remark 3.1. It worth mentioning that Figure 1 shows the graph of $ \theta\mapsto (1-\theta)(2-\theta) $ for $ \theta\in (1, 2) $.
In order for Theorem 3.1 to be applicable, the allowable range of $ \epsilon $ is $ \epsilon \in \bigl(0, -(2-\theta)(1-\theta) \bigr) $ for a fixed $ \theta \in (1, 2) $
Now, we can define the set $ \mathscr{H}_{\kappa, \epsilon} $ as follows
The following lemma shows that the collection $ \left\lbrace \mathscr{H}_{\kappa, \epsilon} \right\rbrace _{\kappa = c_{0}+1}^{\infty} $ forms a nested collection of decreasing sets for each $ \epsilon > 0 $.
Lemma 3.1. Let $ 1 < \theta < 2 $. Then, for each $ \epsilon > 0 $ and $ \kappa\in\mathbb{N}_{c_{0}+3} $ we have that $ \mathscr{H}_{\kappa+1, \epsilon} \subseteq \mathscr{H}_{\kappa, \epsilon} $.
Proof. Let $ \theta \in \mathscr{H}_{\kappa+1, \epsilon} $ for some fixed but arbitrary $ \kappa\in\mathbb{N}_{c_{0}+3} $ and $ \epsilon > 0 $. Then we have
Considering $ 1 < \theta < 2 $ and $ \kappa\in\mathbb{N}_{c_{0}+3} $, we have $ 0 < 2-\theta < 1 $. Consequently, we have
This implies that $ \theta \in \mathscr{H}_{\kappa, \epsilon} $, and thus $ \mathscr{H}_{\kappa+1, \epsilon} \subseteq \mathscr{H}_{\kappa, \epsilon} $.
Now, Theorem 3.1 and Lemma 3.1 lead to the following corollary.
Corollary 3.1. Let $ \mathtt{F} $ be a function defined on $ \mathbb{N}_{c_{0}+1} $, $ \theta\in(1, 2) $ and
for each $ t\in\mathbb{N}_{c_{0}+3}^{s}: = \{c_{0}+3, c_{0}+4, \ldots, s\} $ and some $ s\in\mathbb{N}_{c_{0}+3} $. If $ \theta \in \mathscr{H}_{s, \epsilon} $, then we have $ \bigl(\nabla \mathtt{F}\bigr)(t)\geq 0 $ for each $ t\in\mathbb{N}_{c_{0}+1}^{s} $.
Proof. From the assumption $ \theta \in \mathscr{H}_{s, \epsilon} $ and Lemma 3.1, we have
This leads to
for each $ t\in\mathbb{N}_{c_{0}+3}^{s} $.
Now we use the induction process. First for $ t = c_{0}+3 $ we obtain $ \left(\nabla \mathtt{F}\right)(c_{0}+3) \geq 0 $ directly as in Theorem 3.1 by considering inequalities (Eq 3.4) and (Eq 3.5) together with the given assumption $ (\nabla \mathtt{F})(c_{0}+1) \geq 0 $. As a result, we can inductively iterate inequality (Eq 3.2) to get
for each $ t\in\mathbb{N}_{c_{0}+2}^{s} $. Moreover, $ \bigl(\nabla \mathtt{F}\bigr)(c_{0}+1)\geq 0 $ by assumption. Thus, $ \left(\nabla \mathtt{F}\right)(t)\geq 0 $ for each $ t\in\mathbb{N}_{c_{0}+1}^{s} $ as desired.
4.
Numerical analysis results
In this section, we consider the methodology for the positivity of $ \nabla \mathtt{F} $ based on previous observations in Theorem 3.1 and Corollary 3.1 in such a way that the initial conditions are known. Later, we will illustrate other parts of our article via standard plots and heat maps for different values of $ \theta $ and $ \epsilon $. The computations in this section were performed with MATLAB software.
Example 4.1. Considering Lemma 1 with $ t: = c_{0}+3 $:
For $ c_{0} = 0 $, it follows that
If we take $ \theta = 1.99, \mathtt{F}(0) = 0, \mathtt{F}(1) = 1, \mathtt{F}(2) = 1.001, \mathtt{F}(3) = 1.005 $, and $ \epsilon = 0.007 $, we have
In addition, we see that $ (1-\theta)(2-\theta) = -0.0099 < -0.007 = -\epsilon $. Since the required conditions are satisfied, Theorem 3.1 ensures that $ (\nabla \mathtt{F})(3) > 0 $.
4.1. Standard plots
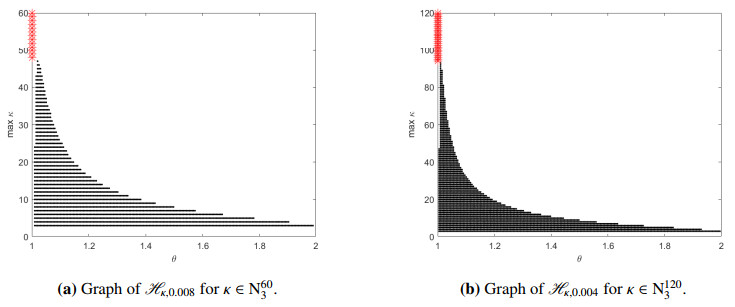
In Figure 2, the sets $ \mathscr{H}_{\kappa, 0.008} $ and $ \mathscr{H}_{\kappa, 0.004} $ are shown for different values of $ \kappa $, respectively in Figure 2a, b. It is noted that $ \mathscr{H}_{\kappa, 0.008} $ and $ \mathscr{H}_{\kappa, 0.004} $ decrease by increasing the values of $ \kappa $. Moreover, in Figure 2a, the set $ \mathscr{H}_{\kappa, 0.008} $ becomes empty for $ \kappa\geq 45 $; however, in Figure 2b, we observe the non-emptiness of the set $ \mathscr{H}_{\kappa, 0.004} $ for many larger values of $ \kappa $ up to $ 90 $. We think that the measures of $ \mathscr{H}_{\kappa, 0.008} $ and $ \mathscr{H}_{\kappa, 0.004} $ are not symmetrically distributed when $ \kappa $ increases (see Figure 2a, b). We do not have a good conceptual explanation for why this symmetric behavior is observed. In fact, it is not clear why the discrete nabla fractional difference $ {}_{{c_0}}^{C{F_R}}\nabla^{\theta} $ seems to give monotonically when $ \theta\to 1 $ rather than for $ \theta\to 2 $, specifically, it gives a maximal information when $ \theta $ is very close to $ 1 $ as $ \epsilon\to 0^+ $.
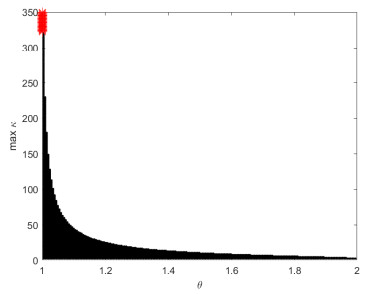
In the next figure (Figure 3), we have chosen a smaller $ \epsilon $ ($ \epsilon = 0.001 $), we see that the set $ \mathscr{H}_{\kappa, 0.001} $ is non-empty for $ \kappa > 320 $. This tells us that small choices in $ \epsilon $ give us a more widely applicable result.
4.2. Heat map plots
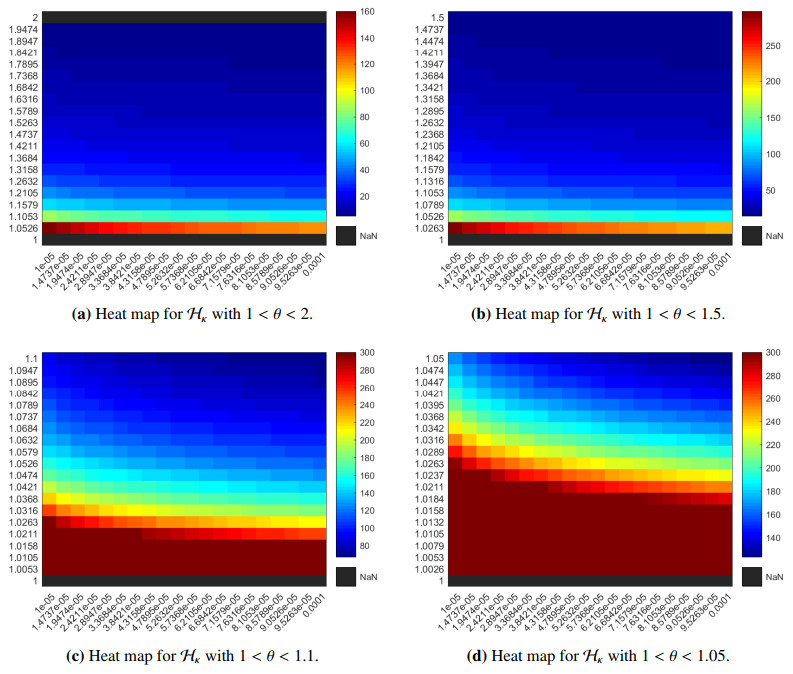
In this part, we introduce the set $ \mathcal{H}_{\kappa}: = \{\kappa:\; \theta \in \mathscr{H}_{\kappa, \epsilon}\} $ to simulate our main theoretical findings for the cardinality of the set $ \mathcal{H}_{\kappa} $ via heat maps in Figure 4a–d. In these figures: we mean the warm colors such as red ones and the cool colors such as blue ones. Moreover, the $ \theta $ values are on the $ x- $axis and $ \epsilon $ values are on the $ y- $axis. We choose $ \epsilon $ in the interval $ [0.00001 $, $ 0.0001] $. Then, the conclusion of these figures are as follows:
● In Figure 4a when $ \theta\in(1, 2) $ and Figure 4b when $ \theta\in(1, 1.5) $, we observe that the warmer colors are somewhat skewed toward $ \theta $ very close to $ 1 $, and the cooler colors cover the rest of the figures for $ \theta $ above $ 1.05 $.
● In Figure 4c, d, the warmest colors move strongly towards the lower values of $ \theta $, especially, when $ \theta\in(1, 1.05) $. Furthermore, when as $ \theta $ increases to up to $ 1.0368 $, it drops sharply from magenta to cyan, which implies a sharp decrease in the cardinality of $ \mathcal{H}_{\kappa} $ for a small values of $ \epsilon $ as in the interval $ [0.00001 $, $ 0.0001] $.
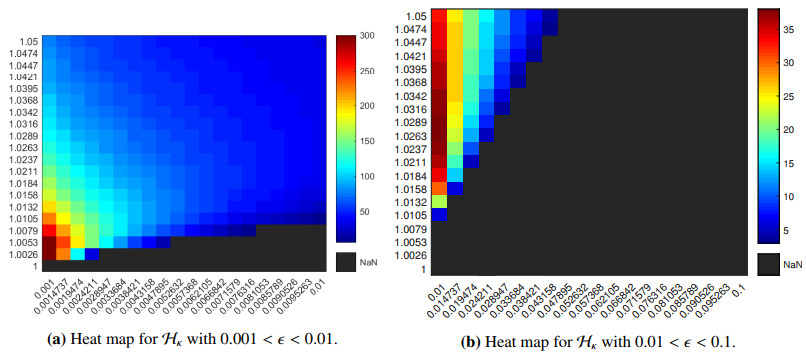
On the other hand, for larger values of $ \epsilon $, the set $ \mathcal{H}_{\kappa} $ will tend to be empty even if we select a smaller $ \theta $ in such an interval $ (1, 1.05) $. See the following Figure 5a, b for more.
In conclusion, from Figures 4 and 5, we see that: For a smaller value of $ \epsilon $, the set $ \mathscr{H}_{\kappa, \epsilon} $ tends to remain non-empty (see Figure 4), unlike for a larger value of $ \epsilon $ (see Figure 5). Furthermore, these verify that Corollary 3.1 will be more applicable for $ 1 < \theta < 1.05 $ and $ 0.01 < \epsilon < 0.1 $ as shown in Figure 4d.
Although, our numerical data strongly note the sensitivity of the set $ \mathcal{H}_{\kappa} $ when slight increasing in $ \epsilon $ is observed for $ \theta $ close to $ 2 $ compares with $ \theta $ close to $ 1 $.
5.
Concluding remarks
In this paper we developed a positivity method for analysing discrete fractional operators of Riemann-Liouville type based on exponential kernels. In our work we have found that $ (\nabla \mathtt{F})(3)\geq 0 $ when $ \left({}_{{c_0}}^{C{F_R}}\nabla^{\theta} \mathtt{F}\right)(t) > -\epsilon\, \Lambda(\theta-1)\, \bigl(\nabla \mathtt{F}\bigr)(c_{0}+1) $ such that $ \bigl(\nabla \mathtt{F}\bigr)(c_{0}+1)\geq 0 $ and $ \epsilon > 0 $. We continue to extend this result for each value of $ t $ in $ \mathbb{N}_{c_{0}+1}^{s} $ as we have done in Corollary 3.1.
In addition we presented standard plots and heat map plots for the discrete problem that is solved numerically. Two of the graphs are standard plots for $ \mathscr{H}_{\kappa, \epsilon} $ for different values of $ \kappa $ and $ \epsilon $ (see Figure 2), and the other six graphs consider the cardinality of $ \mathcal{H}_{\kappa} $ for different values of $ \epsilon $ and $ \theta $ (see Figures 4 and 5). These graphs ensure the validity of our theoretical results.
In the future we hope to apply our method to other types of discrete fractional operators which include Mittag-Leffler and their extensions in kernels; see for example [5,6].
Acknowledgements
This work was supported by the Taif University Researchers Supporting Project Number (TURSP-2020/86), Taif University, Taif, Saudi Arabia.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: